Investigation of the Application of Complex Function Theory in Underground Mine Design: A Case Study
Abstract
:1. Introduction
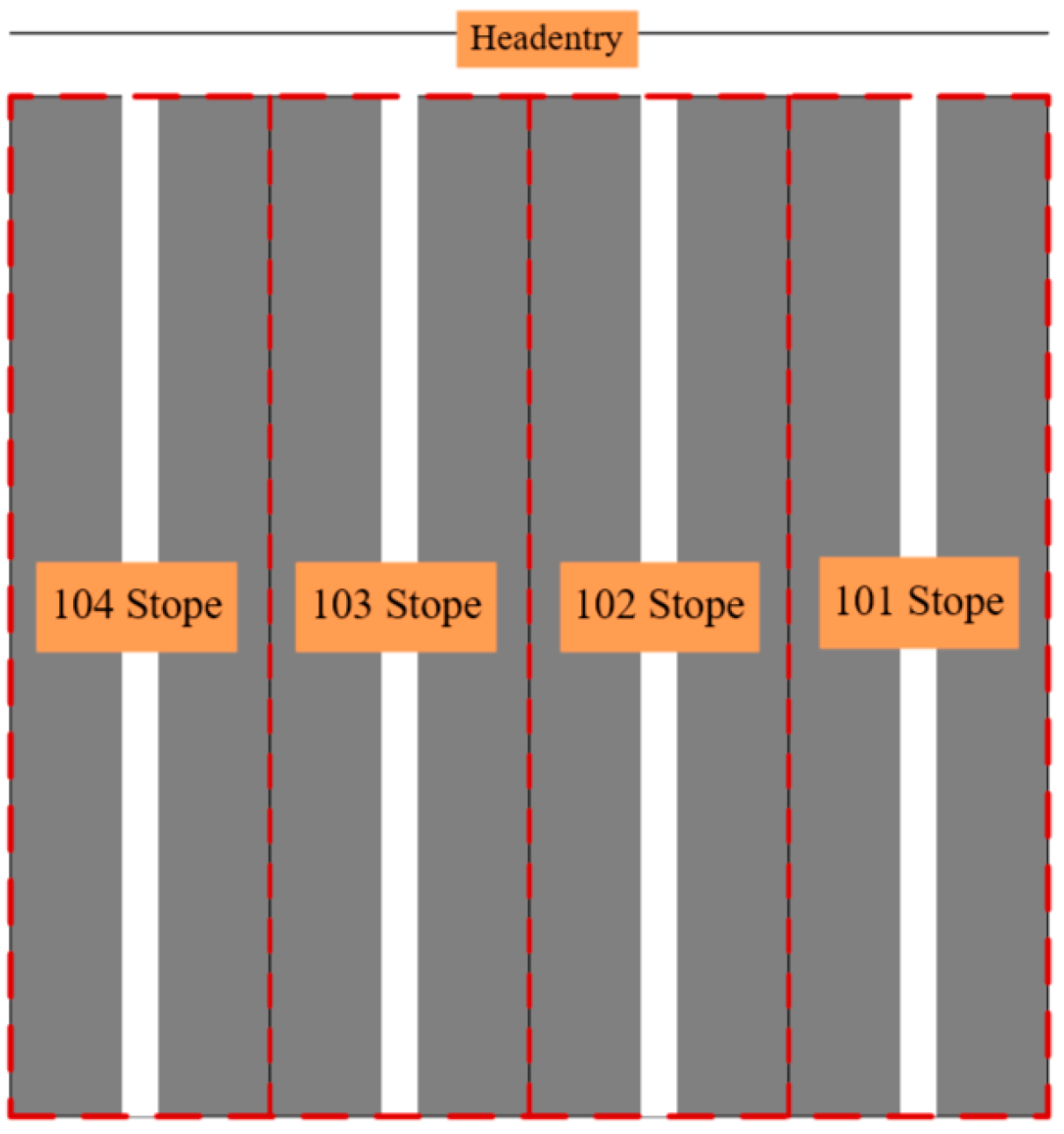
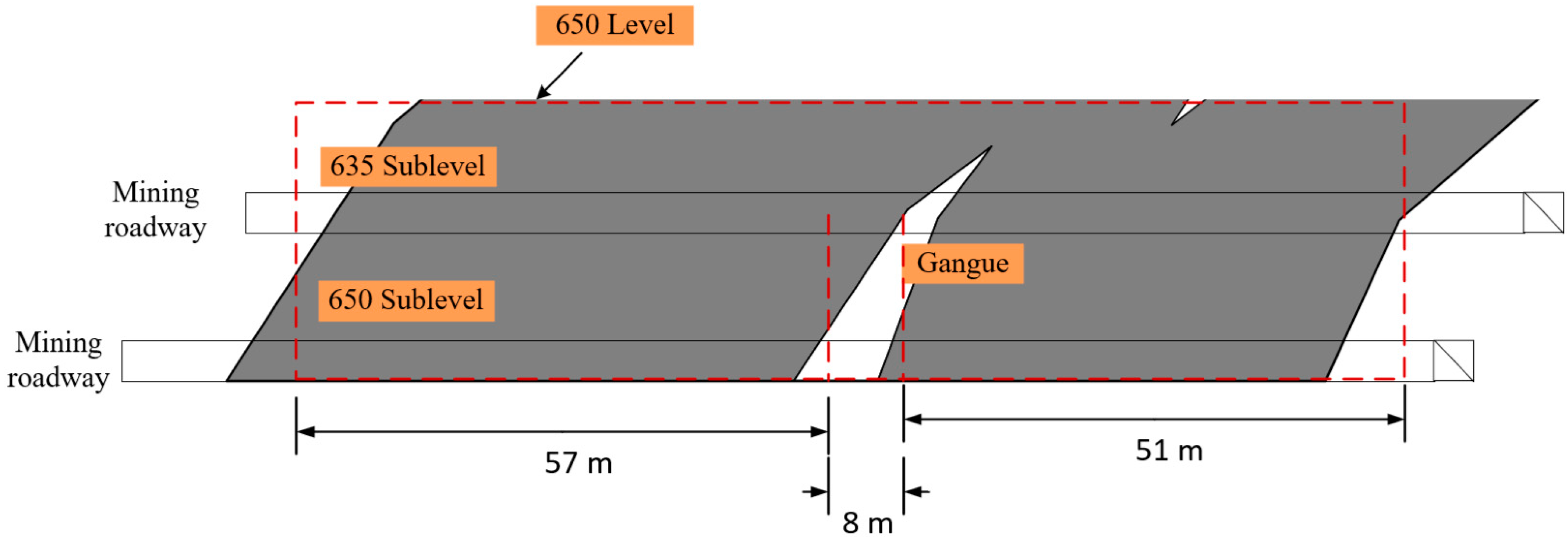
2. Engineering Background
3. Results and Analysis
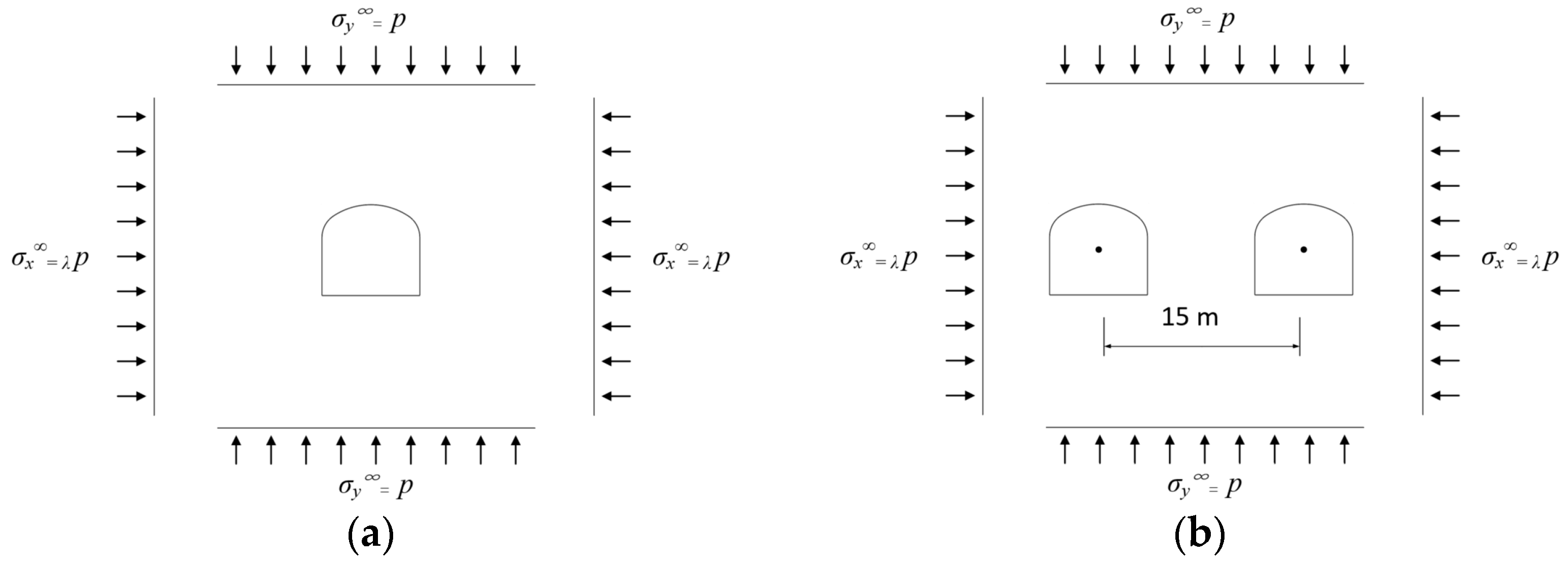
3.1. Calculation Models
3.2. Characteristics of Stress Distribution around a Single Roadway
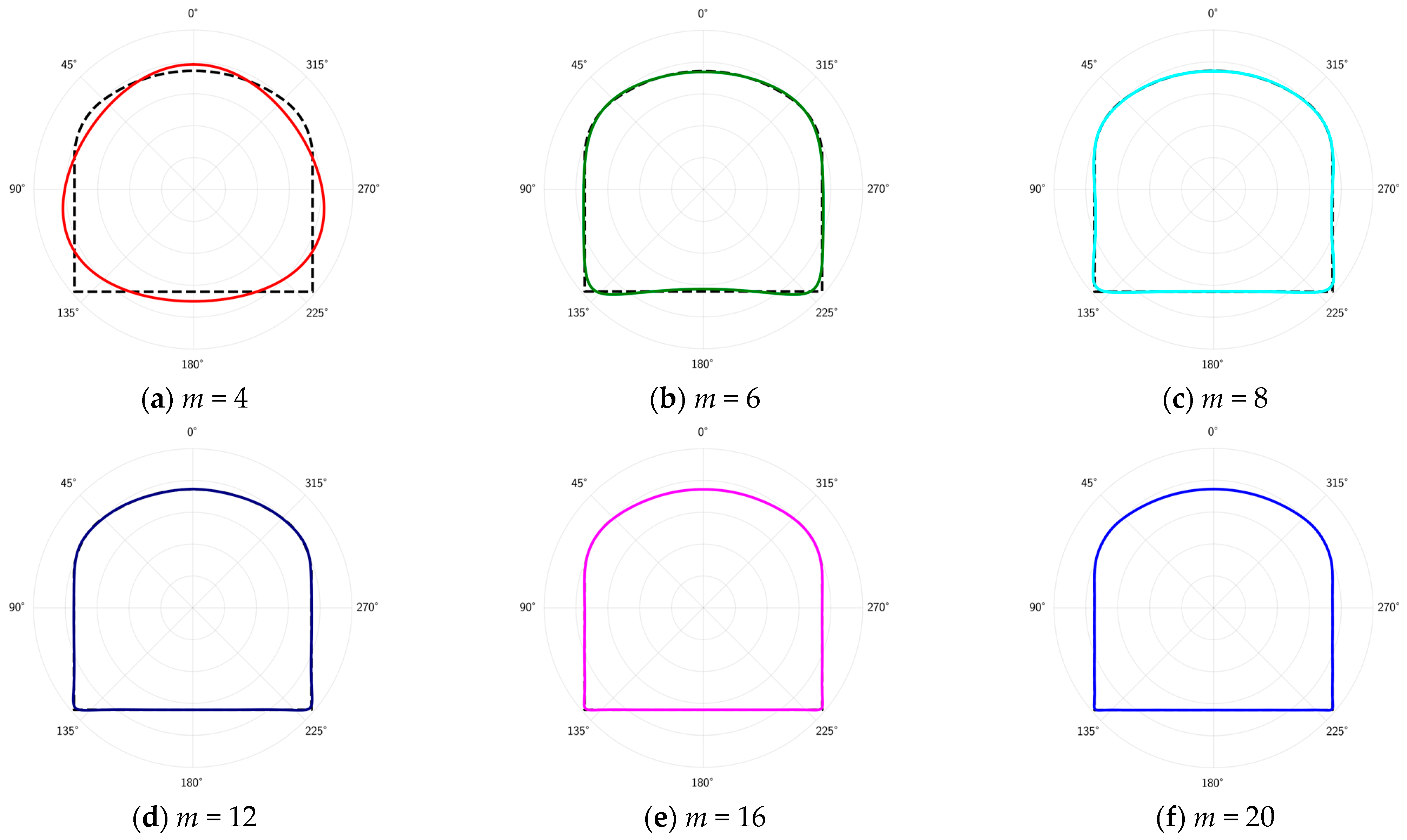
3.2.1. Solution of the Mapping Function for a Plane Containing a Single Tri-Center Arch Roadway
3.2.2. Solution of the Complex Stress Function
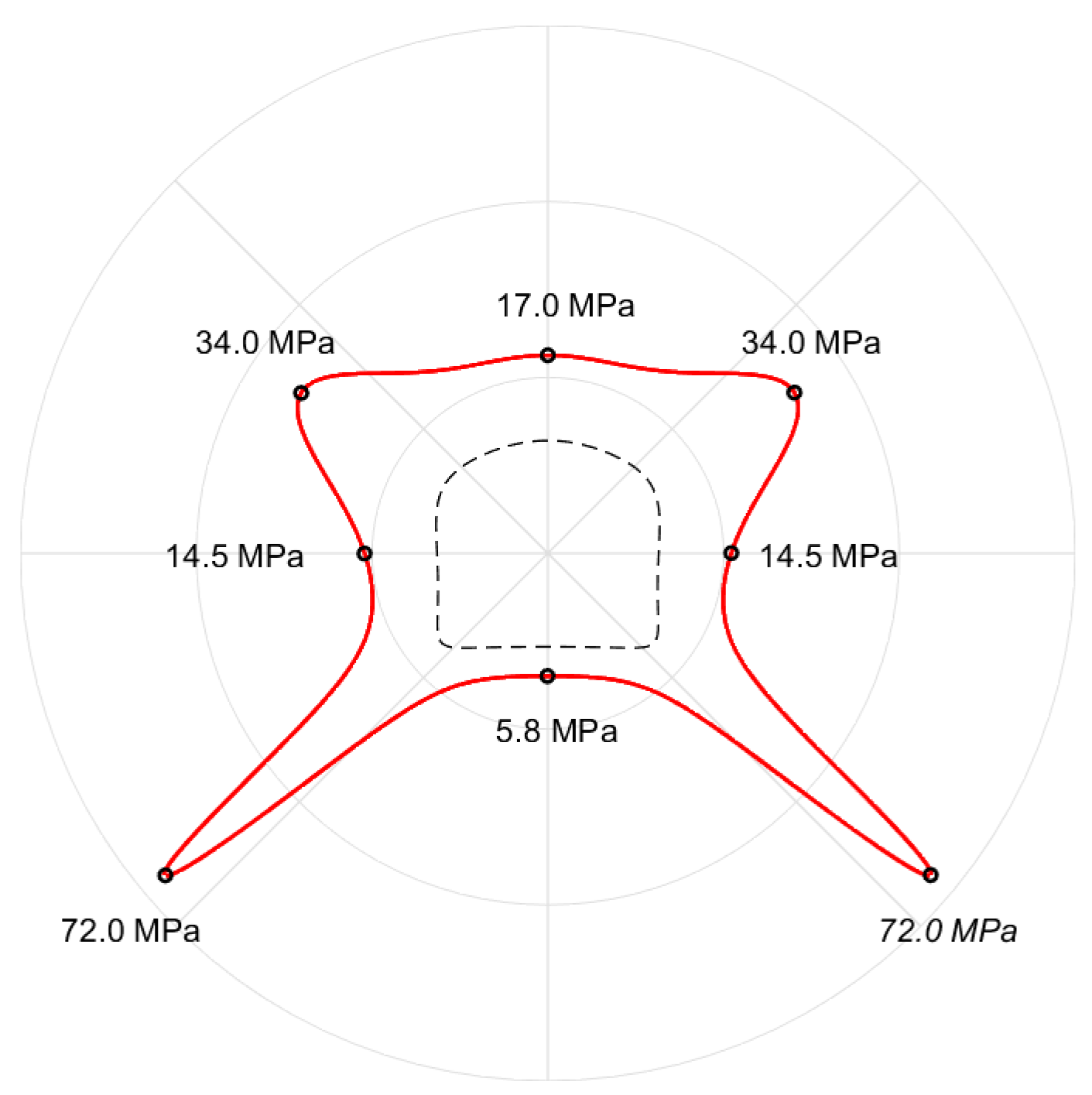
3.2.3. Characteristics of Stress Distribution around a Single Roadway
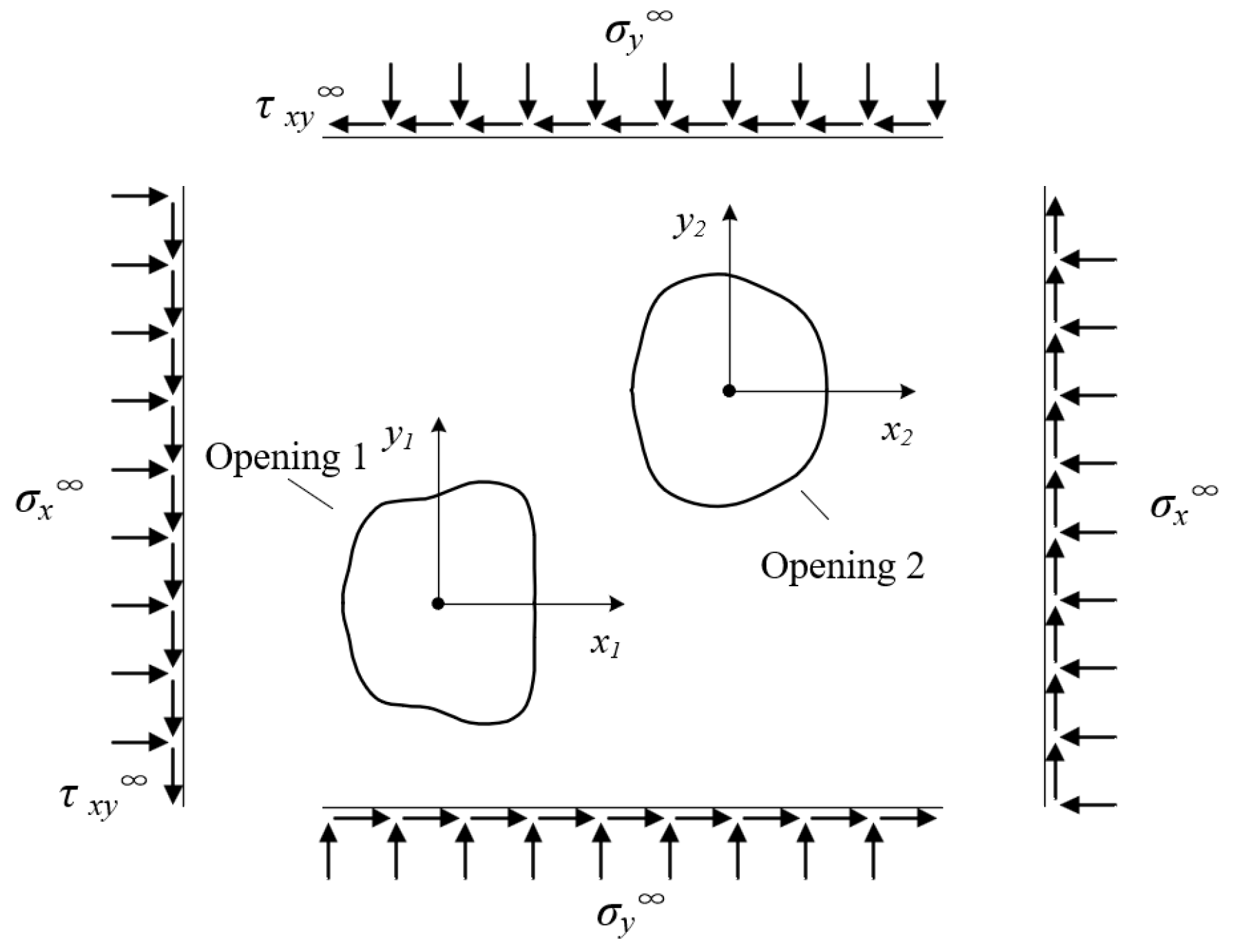
3.3. Mutual Influence between Adjacent Roadways
3.3.1. Solution of Stress Function for a Plane Containing Two Openings
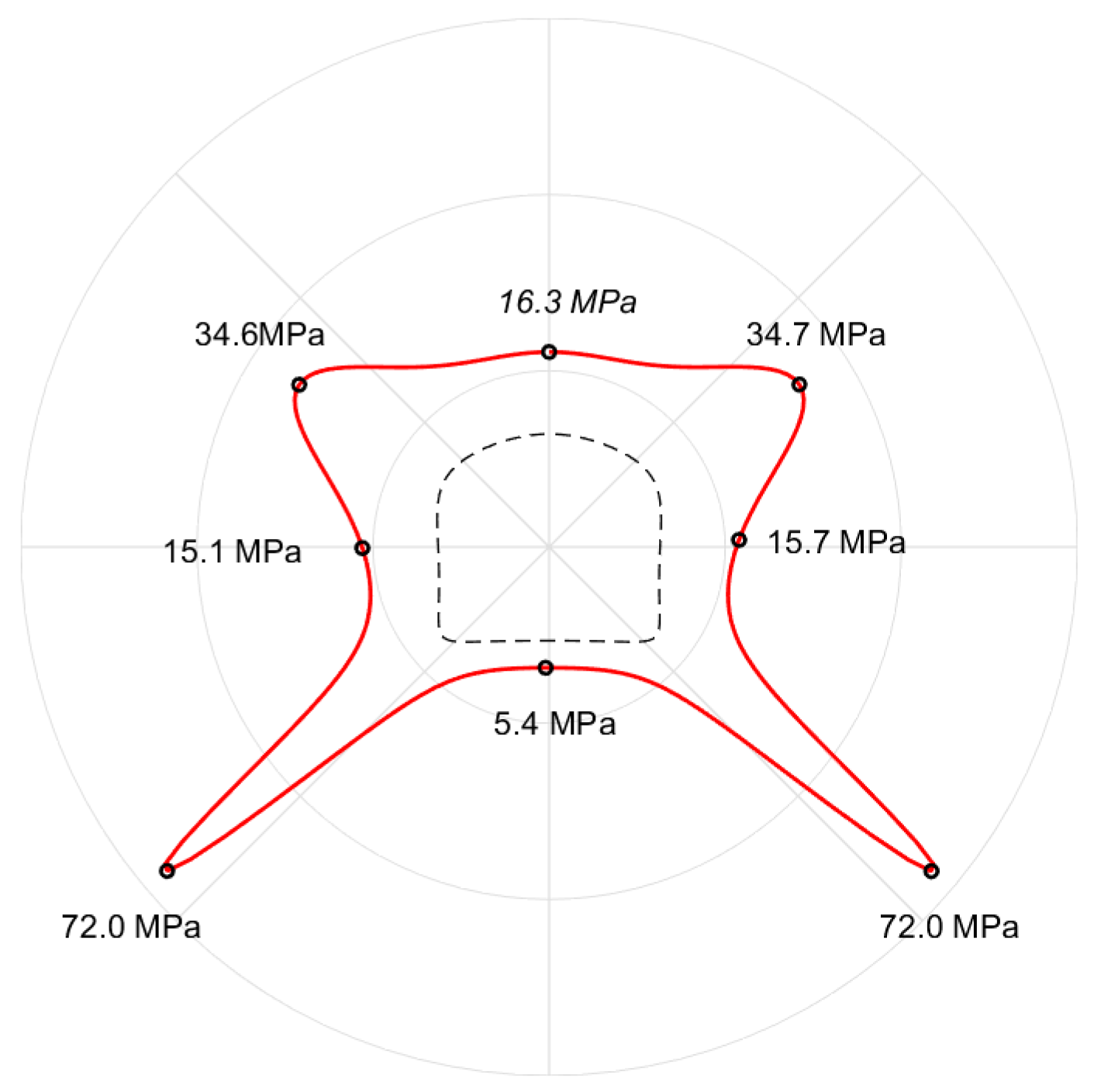
3.3.2. Impact of Adjacent Roadway on the Stress Field around the Existing Roadway
3.4. Optimization Design of Stope Pillar Parameters
4. Discussion and Conclusions
4.1. Discussion
4.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, H.; Lu, A.-Z.; Ma, Y.-C. Analytic stress solution for a circular tunnel in half plane with a concentrated force. Math. Mech. Solids 2019, 24, 3862–3879. [Google Scholar] [CrossRef]
- Cao, X.; Gong, W.; Zhou, F.; Dai, G. Stress Analytical Solution for Shallow Buried Lined Circular Tunnel Under the Deformation of Surrounding Rock Inner Edge. Geotech. Geol. Eng. 2019, 37, 3771–3780. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, L.; Alotaibi, R.; Hdeib, R. Deformation and stress theory of surrounding rock of shallow circular tunnel based on complex variable function method. Appl. Math. Nonlinear Sci. 2022, 7, 629–640. [Google Scholar] [CrossRef]
- Guo, Z.; Wu, B.; Jia, S. An analytical model for predicting the mechanical behavior of a deep lined circular pressure tunnel by using complex variable method. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 90. [Google Scholar] [CrossRef]
- Zhao, G.; Yang, S. Analytical solutions for rock stress around square tunnels using complex variable theory. Int. J. Rock Mech. Min. Sci. 2015, 80, 302–307. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, G.Y.; Liang, W.Z. Mechanical properties and fracture characteristics of pre-holed rocks subjected to uniaxial loading: A comparative analysis of five hole shapes. Theor. Appl. Fract. Mech. 2020, 105, 102433. [Google Scholar] [CrossRef]
- Tan, L.; Ren, T.; Dou, L.; Yang, X.; Qiao, M.; Peng, H. Analytical stress solution and mechanical properties for rock mass containing a hole with complex shape. Theor. Appl. Fract. Mech. 2021, 114, 103002. [Google Scholar] [CrossRef]
- Tan, L.; Ren, T.; Dou, L.; Yang, X.; Wang, G.; Peng, H. Analytical Stress Solution and Numerical Mechanical Behavior of Rock Mass Containing an Opening under Different Confining Stress Conditions. Mathematics 2021, 9, 2462. [Google Scholar] [CrossRef]
- Xiao, W.; Zhang, D.; Li, S.; Lu, J. Fracture evolution and fracture mechanism of tunnel surrounding rock: A case study based on laboratory tests and theoretical analysis. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 2617–2638. [Google Scholar] [CrossRef]
- Tu, S.; Li, Z.; Ye, Z.; Zhang, C.; Zhang, L. The Complex Function Method Roadway Section Design of the Soft Coal Seam. Math. Probl. Eng. 2016, 2016, 9291412. [Google Scholar] [CrossRef]
- Bobet, A. Deep Tunnel in Transversely Anisotropic Rock with Groundwater Flow. Rock Mech. Rock Eng. 2016, 49, 4817–4832. [Google Scholar] [CrossRef]
- Cheng, Q.-x.; Lu, A.-z.; Yin, C.-l. Analytical Stress Solutions for a Deep Buried Circular Tunnel Under an Unsteady Temperature Field. Rock Mech. Rock Eng. 2021, 54, 1355–1368. [Google Scholar] [CrossRef]
- Yu, I.W.; Sendeckyj, G.P. Multiple Circular Inclusion Problems in Plane Elastostatics. J. Appl. Mech. 1974, 41, 215–221. [Google Scholar] [CrossRef]
- Ukadgaonker, V.G. Stress analysis of a plate containing two circular holes having tangential stresses. AIAA J. 1980, 18, 125–128. [Google Scholar] [CrossRef]
- Salerno, V.L.; Mahoney, J.B. Stress Solution for an Infinite Plate Containing Two Arbitrary Circular Holes Under Equal Biaxial Stresses. J. Eng. Ind. 1968, 90, 656–665. [Google Scholar] [CrossRef]
- Kim, T.J.; Ukadgaonker, V.G. Plane stress analysis of two rigid circular inclusions. Aiaa J. 1971, 9, 2294–2296. [Google Scholar] [CrossRef]
- Ukadgaonker, V.G.; Naik, A.P. Interaction effect of two arbitrarily oriented cracks—Part I. Int. J. Fract. 1991, 51, 219–230. [Google Scholar] [CrossRef]
- Zhang, L.-Q.; Lu, A.-Z. An Analytic Algorithm of Stresses for Any Double Hole Problem in Plane Elastostatics. J. Appl. Mech. 2000, 68, 350–353. [Google Scholar] [CrossRef]
- Tan, L.; Ren, T.; Dou, L.; Yang, X.; Cai, X.; Qiao, M. Analytical stress solution for rock mass containing two holes based on an improved Schwarz alternating method. Theor. Appl. Fract. Mech. 2021, 116, 103092. [Google Scholar] [CrossRef]
- Lunder, P.J.; Pakalnis, R.C. Determination of the strength of hard-rock mine pillars. CIM Bull. 1997, 90, 51–55. [Google Scholar]



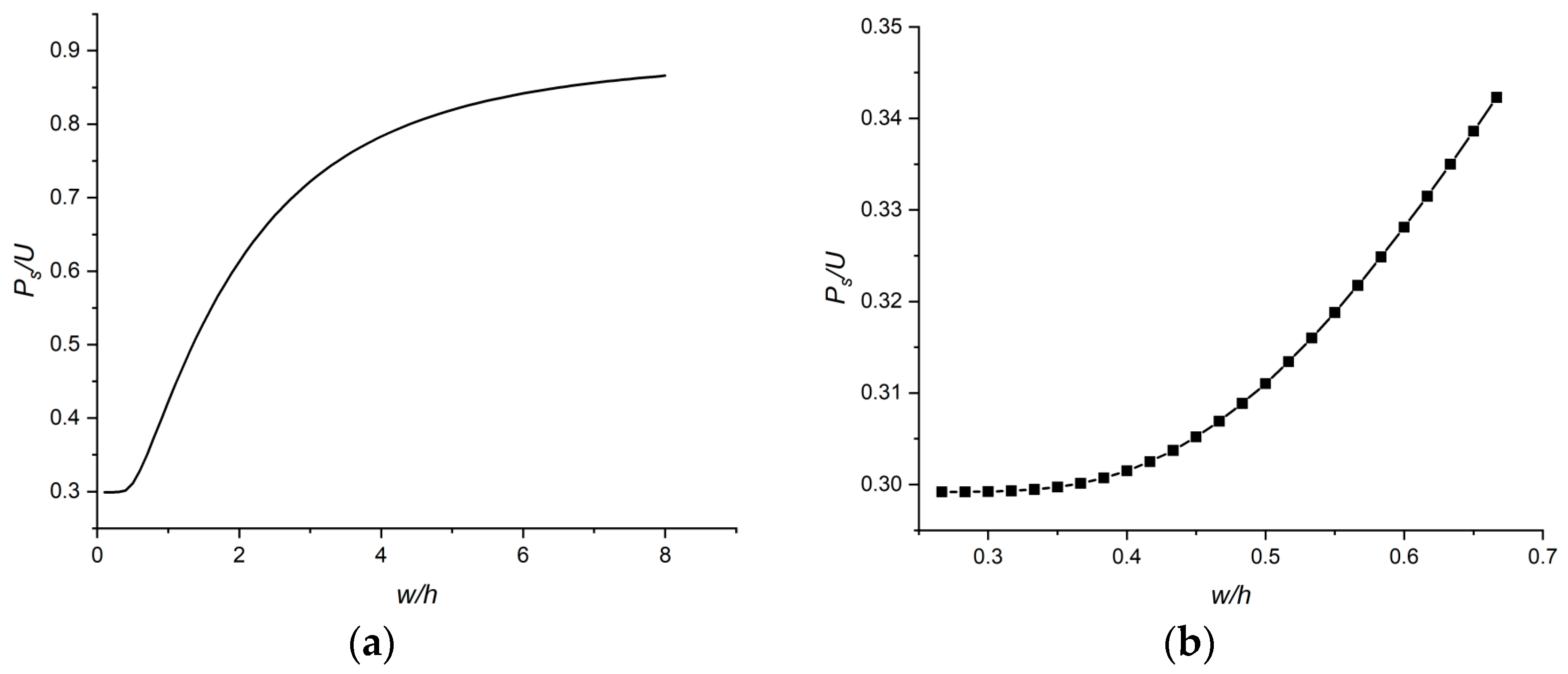

| Number | Pillar Thickness/m | Left Opening Span/m | Right Opening Span/m | w/h | Ps/U | Axial Stress in Pillar/MPa | Pillar Safety Factor |
|---|---|---|---|---|---|---|---|
| 1 | 8.00 | 57.00 | 51.00 | 0.27 | 0.299 | 45.04 | 1.04 |
| 2 | 8.50 | 56.75 | 50.75 | 0.28 | 0.299 | 43.85 | 1.07 |
| 3 | 9.00 | 56.50 | 50.50 | 0.30 | 0.299 | 42.77 | 1.10 |
| 4 | 9.50 | 56.25 | 50.25 | 0.32 | 0.299 | 41.85 | 1.12 |
| 5 | 10.00 | 56.00 | 50.00 | 0.33 | 0.299 | 40.89 | 1.15 |
| 6 | 10.50 | 55.75 | 49.75 | 0.35 | 0.300 | 39.96 | 1.18 |
| 7 | 11.00 | 55.50 | 49.50 | 0.37 | 0.300 | 39.21 | 1.20 |
| 8 | 11.50 | 55.25 | 49.25 | 0.38 | 0.301 | 38.05 | 1.24 |
| 9 | 12.00 | 55.00 | 49.00 | 0.40 | 0.302 | 37.66 | 1.26 |
| 10 | 12.50 | 54.75 | 48.75 | 0.42 | 0.303 | 36.66 | 1.30 |
| 11 | 13.00 | 54.50 | 48.50 | 0.43 | 0.304 | 36.35 | 1.31 |
| 12 | 13.50 | 54.25 | 48.25 | 0.45 | 0.305 | 35.57 | 1.35 |
| 13 | 14.00 | 54.00 | 48.00 | 0.47 | 0.307 | 34.89 | 1.38 |
| 14 | 14.50 | 53.75 | 47.75 | 0.48 | 0.309 | 34.35 | 1.41 |
| 15 | 15.00 | 53.50 | 47.50 | 0.50 | 0.311 | 33.78 | 1.45 |
| 16 | 15.50 | 53.25 | 47.25 | 0.52 | 0.313 | 33.32 | 1.48 |
| 17 | 16.00 | 53.00 | 47.00 | 0.53 | 0.316 | 32.60 | 1.52 |
| 18 | 16.50 | 52.75 | 46.75 | 0.55 | 0.319 | 32.31 | 1.55 |
| 19 | 17.00 | 52.50 | 46.50 | 0.57 | 0.322 | 31.73 | 1.59 |
| 20 | 17.50 | 52.25 | 46.25 | 0.58 | 0.325 | 31.39 | 1.62 |
| 21 | 18.00 | 52.00 | 46.00 | 0.60 | 0.328 | 30.91 | 1.67 |
| 22 | 18.50 | 51.75 | 45.75 | 0.62 | 0.332 | 30.55 | 1.70 |
| 23 | 19.00 | 51.50 | 45.50 | 0.63 | 0.335 | 30.33 | 1.73 |
| 24 | 19.50 | 51.25 | 45.25 | 0.65 | 0.339 | 29.75 | 1.79 |
| 25 | 20.00 | 51.00 | 45.00 | 0.67 | 0.342 | 29.36 | 1.83 |
| Number | Left Opening | Right Opening | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| c1 | c3 | c5 | c7 | c9 | c1 | c3 | c5 | c7 | c9 | |
| 1 | 2.538 | 0.743 | −0.387 | −0.068 | 0.024 | 2.368 | 0.579 | −0.371 | −0.054 | 0.028 |
| 2 | 2.531 | 0.736 | −0.386 | −0.067 | 0.024 | 2.361 | 0.573 | −0.370 | −0.054 | 0.028 |
| 3 | 2.524 | 0.729 | −0.386 | −0.067 | 0.024 | 2.354 | 0.566 | −0.370 | −0.053 | 0.028 |
| 4 | 2.517 | 0.723 | −0.385 | −0.066 | 0.024 | 2.347 | 0.559 | −0.369 | −0.053 | 0.028 |
| 5 | 2.510 | 0.716 | −0.384 | −0.066 | 0.024 | 2.340 | 0.552 | −0.368 | −0.052 | 0.028 |
| 6 | 2.503 | 0.709 | −0.384 | −0.065 | 0.025 | 2.333 | 0.545 | −0.368 | −0.052 | 0.029 |
| 7 | 2.496 | 0.702 | −0.383 | −0.065 | 0.025 | 2.326 | 0.538 | −0.367 | −0.051 | 0.029 |
| 8 | 2.489 | 0.695 | −0.382 | −0.064 | 0.025 | 2.318 | 0.532 | −0.366 | −0.050 | 0.029 |
| 9 | 2.482 | 0.689 | −0.382 | −0.064 | 0.025 | 2.311 | 0.525 | −0.365 | −0.050 | 0.029 |
| 10 | 2.475 | 0.682 | −0.381 | −0.063 | 0.025 | 2.304 | 0.518 | −0.365 | −0.049 | 0.029 |
| 11 | 2.467 | 0.675 | −0.380 | −0.062 | 0.026 | 2.297 | 0.511 | −0.364 | −0.049 | 0.029 |
| 12 | 2.460 | 0.668 | −0.380 | −0.062 | 0.026 | 2.290 | 0.504 | −0.363 | −0.048 | 0.029 |
| 13 | 2.453 | 0.661 | −0.379 | −0.061 | 0.026 | 2.283 | 0.497 | −0.362 | −0.047 | 0.030 |
| 14 | 2.446 | 0.655 | −0.379 | −0.061 | 0.026 | 2.276 | 0.491 | −0.362 | −0.047 | 0.030 |
| 15 | 2.439 | 0.648 | −0.378 | −0.060 | 0.026 | 2.269 | 0.484 | −0.361 | −0.046 | 0.030 |
| 16 | 2.432 | 0.641 | −0.377 | −0.060 | 0.026 | 2.261 | 0.477 | −0.360 | −0.046 | 0.030 |
| 17 | 2.425 | 0.634 | −0.377 | −0.059 | 0.027 | 2.254 | 0.470 | −0.359 | −0.045 | 0.030 |
| 18 | 2.418 | 0.627 | −0.376 | −0.059 | 0.027 | 2.247 | 0.463 | −0.359 | −0.044 | 0.030 |
| 19 | 2.411 | 0.620 | −0.375 | −0.058 | 0.027 | 2.240 | 0.456 | −0.358 | −0.044 | 0.030 |
| 20 | 2.404 | 0.614 | −0.375 | −0.057 | 0.027 | 2.233 | 0.449 | −0.357 | −0.043 | 0.031 |
| 21 | 2.397 | 0.607 | −0.374 | −0.057 | 0.027 | 2.226 | 0.443 | −0.356 | −0.043 | 0.031 |
| 22 | 2.390 | 0.600 | −0.373 | −0.056 | 0.027 | 2.218 | 0.436 | −0.355 | −0.042 | 0.031 |
| 23 | 2.382 | 0.593 | −0.372 | −0.056 | 0.028 | 2.211 | 0.429 | −0.355 | −0.041 | 0.031 |
| 24 | 2.375 | 0.586 | −0.372 | −0.055 | 0.028 | 2.204 | 0.422 | −0.354 | −0.041 | 0.031 |
| 25 | 2.368 | 0.579 | −0.371 | −0.054 | 0.028 | 2.197 | 0.415 | −0.353 | −0.040 | 0.031 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, L.; Peng, H.; Si, X.; Lin, Q. Investigation of the Application of Complex Function Theory in Underground Mine Design: A Case Study. Appl. Sci. 2023, 13, 12142. https://doi.org/10.3390/app132212142
Tan L, Peng H, Si X, Lin Q. Investigation of the Application of Complex Function Theory in Underground Mine Design: A Case Study. Applied Sciences. 2023; 13(22):12142. https://doi.org/10.3390/app132212142
Chicago/Turabian StyleTan, Lihai, Huaide Peng, Xuefeng Si, and Qibin Lin. 2023. "Investigation of the Application of Complex Function Theory in Underground Mine Design: A Case Study" Applied Sciences 13, no. 22: 12142. https://doi.org/10.3390/app132212142
APA StyleTan, L., Peng, H., Si, X., & Lin, Q. (2023). Investigation of the Application of Complex Function Theory in Underground Mine Design: A Case Study. Applied Sciences, 13(22), 12142. https://doi.org/10.3390/app132212142








