The Simulation of Dielectric Barrier Discharge for Breakdown Voltage in Starch Modification
Abstract
:1. Introduction
2. Modeling and Simulation Methods
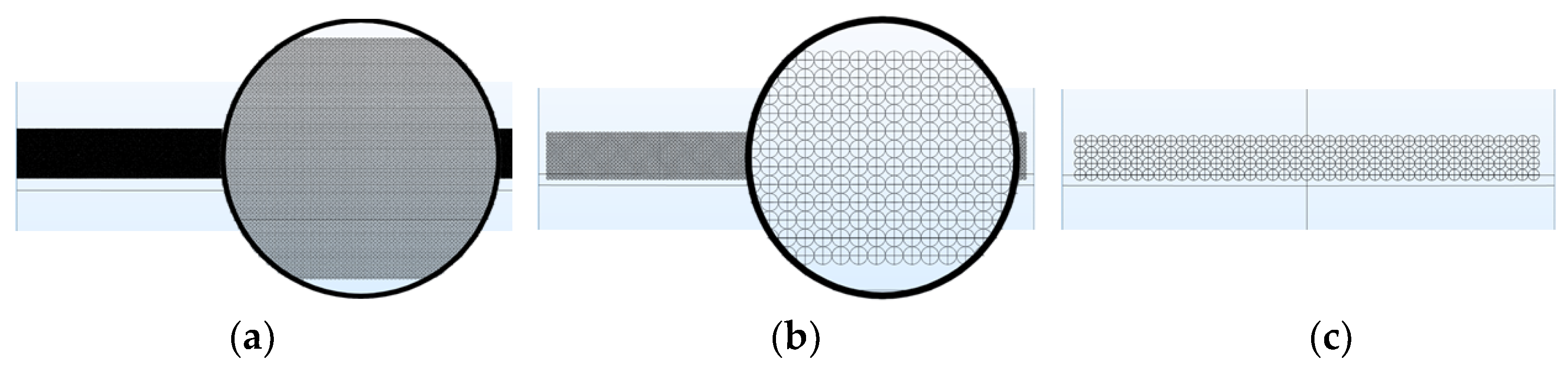
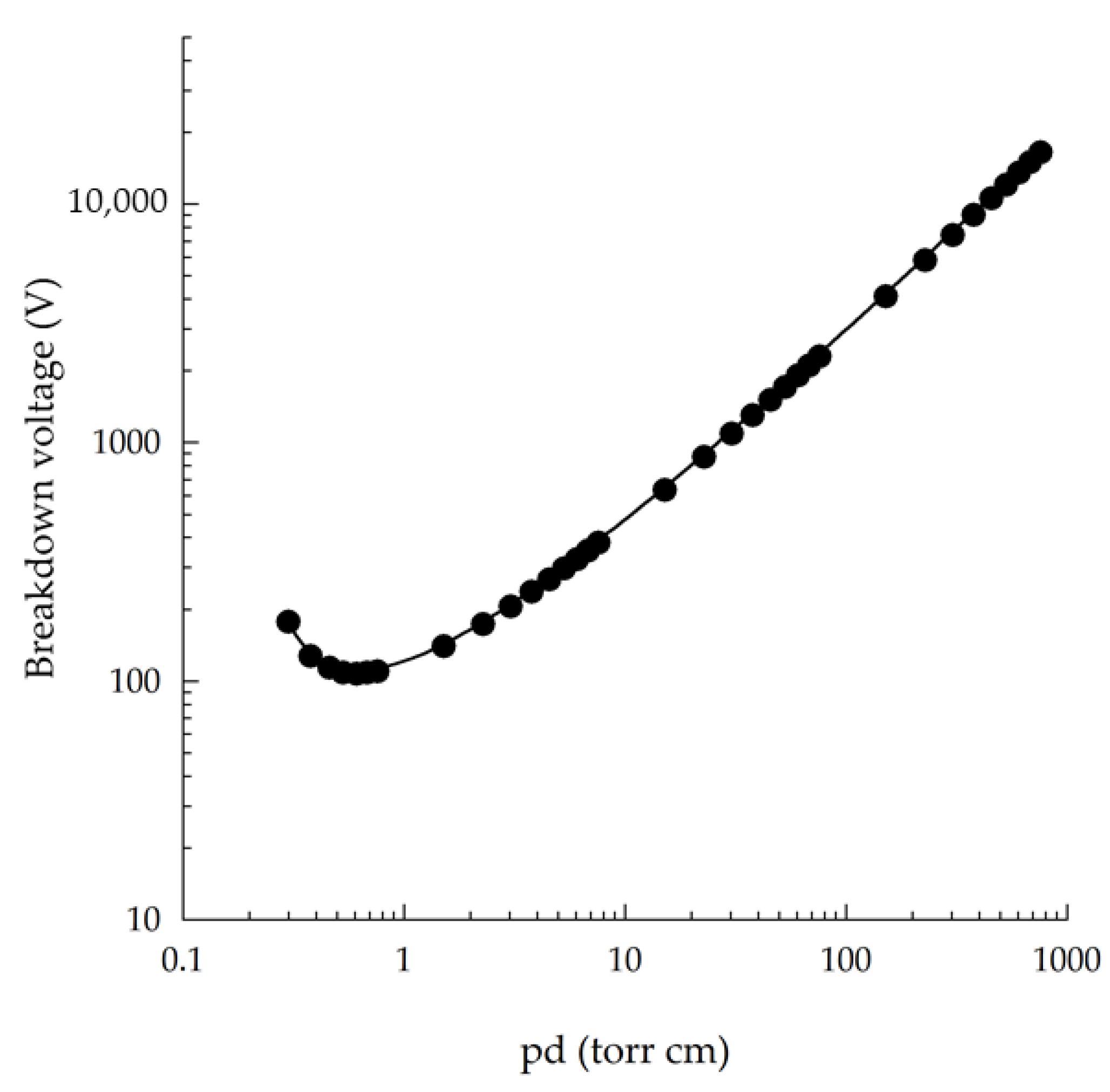
2.1. Method for Grid Independence Test
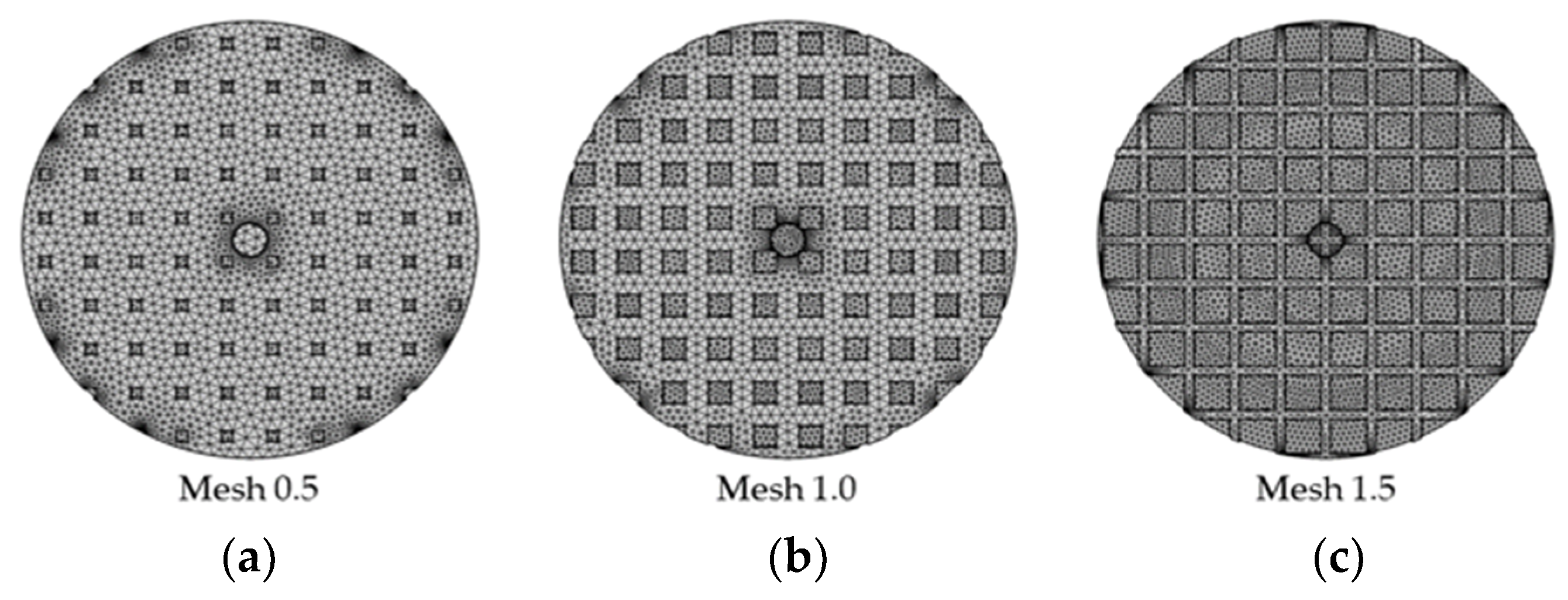
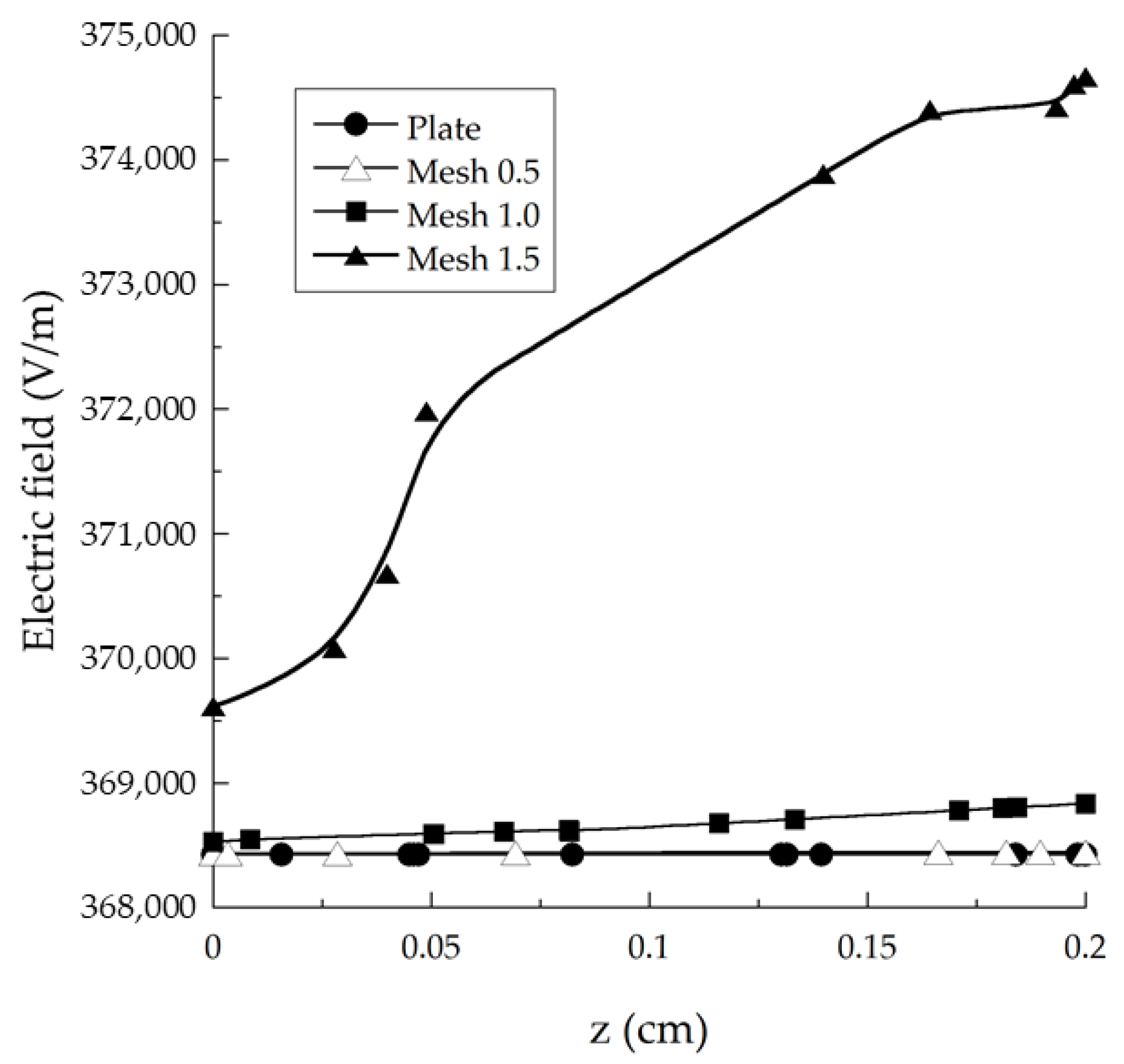
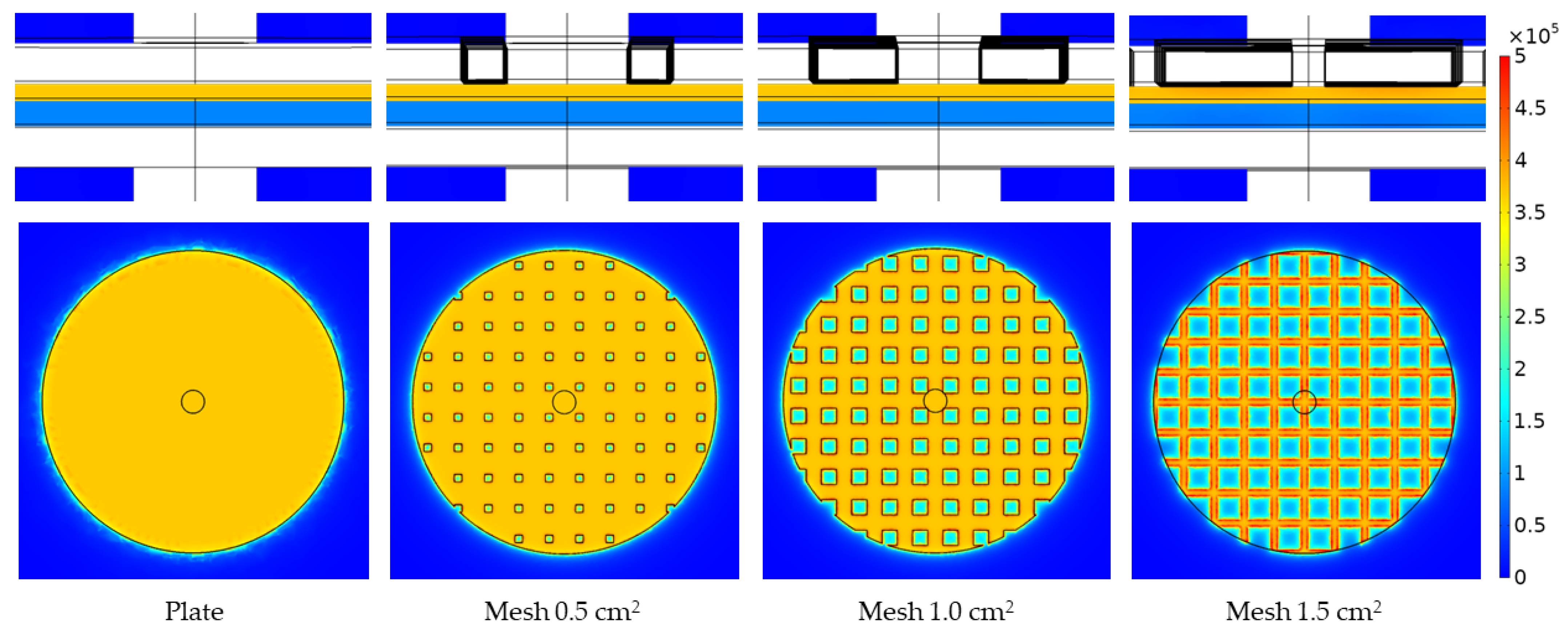
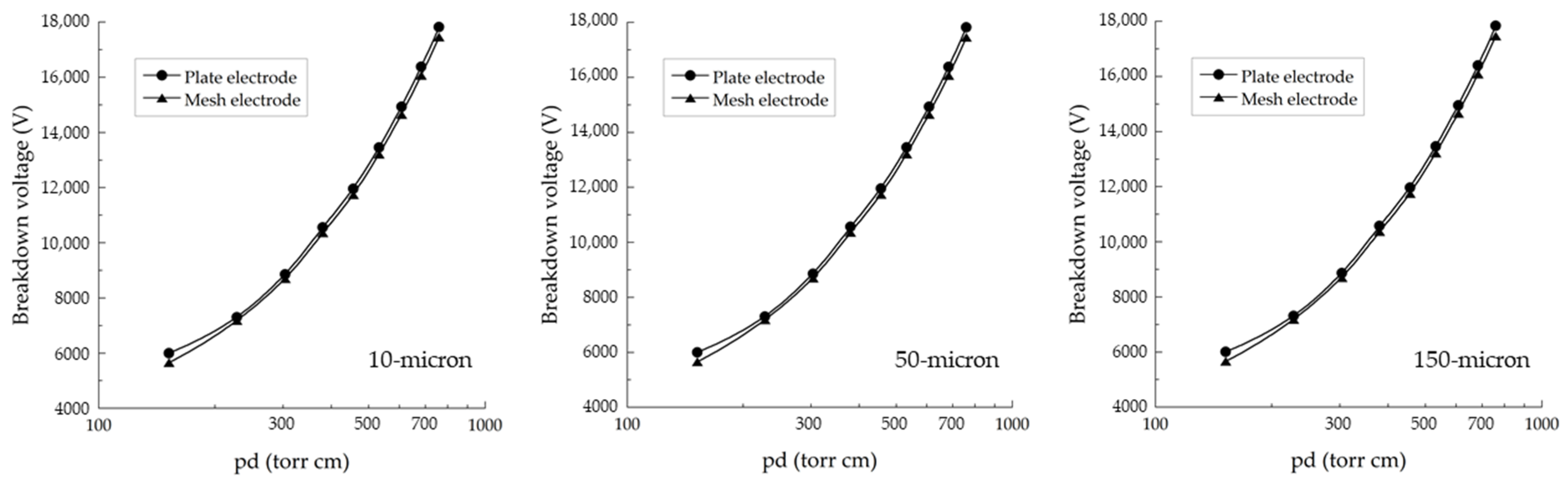
2.2. Effect of the Top Electrode’s Mesh Size
2.3. Effect of Starch Relative Permittivity
2.4. Effect of Starch Granule Shape
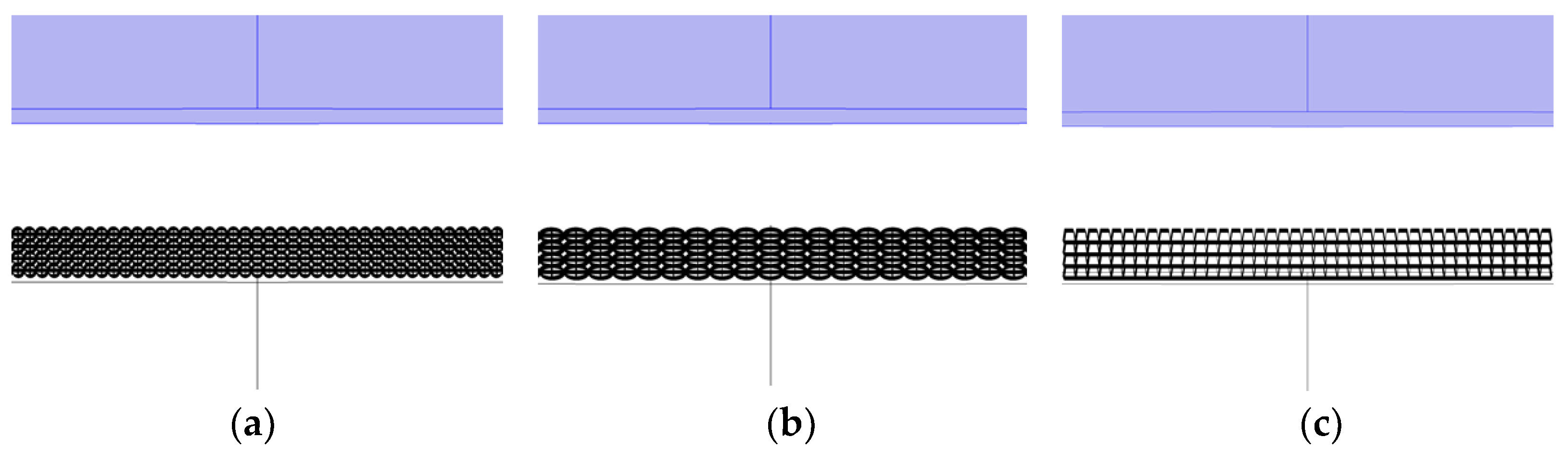
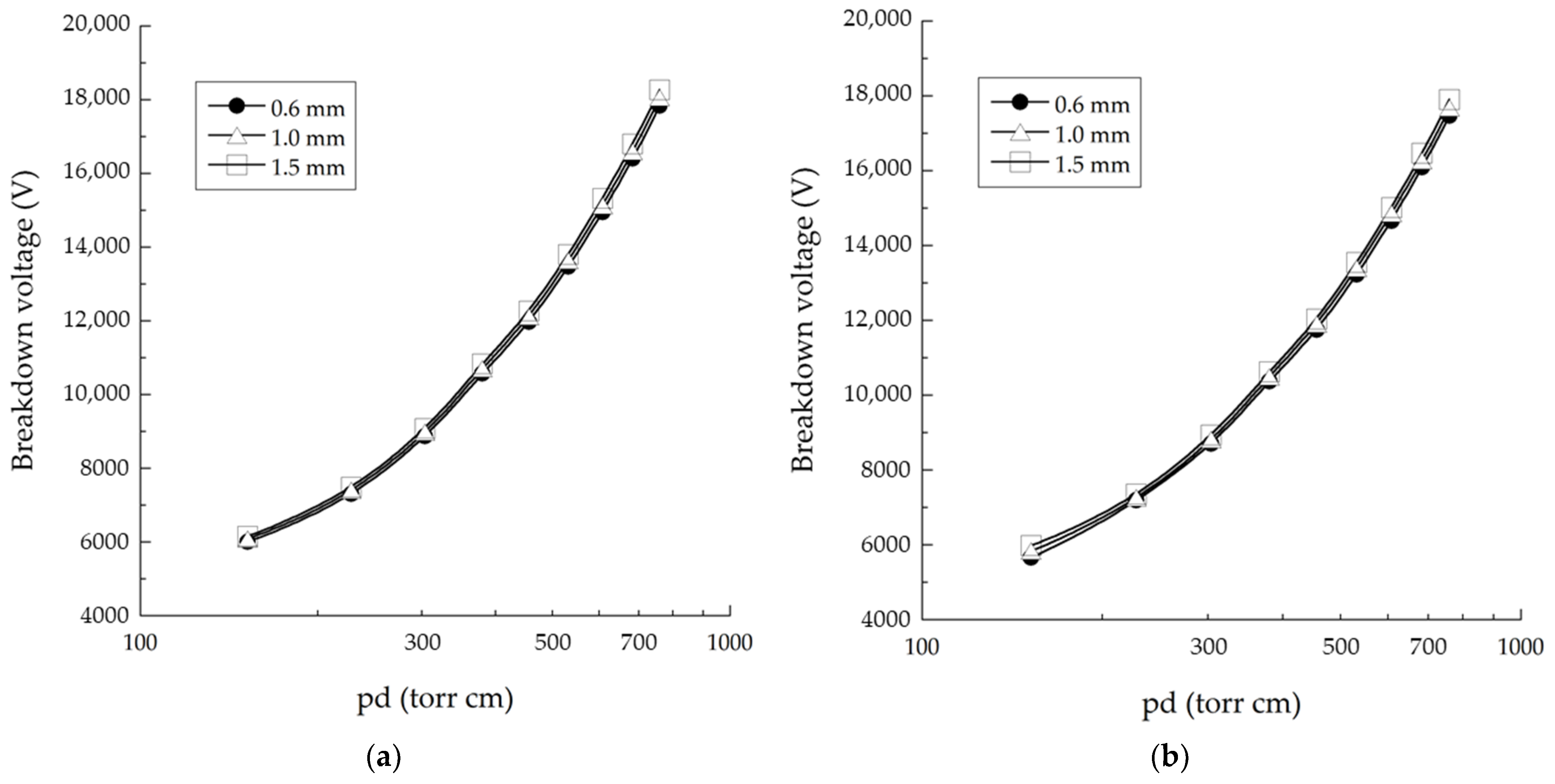
2.5. Effect of Starch Thickness Layer
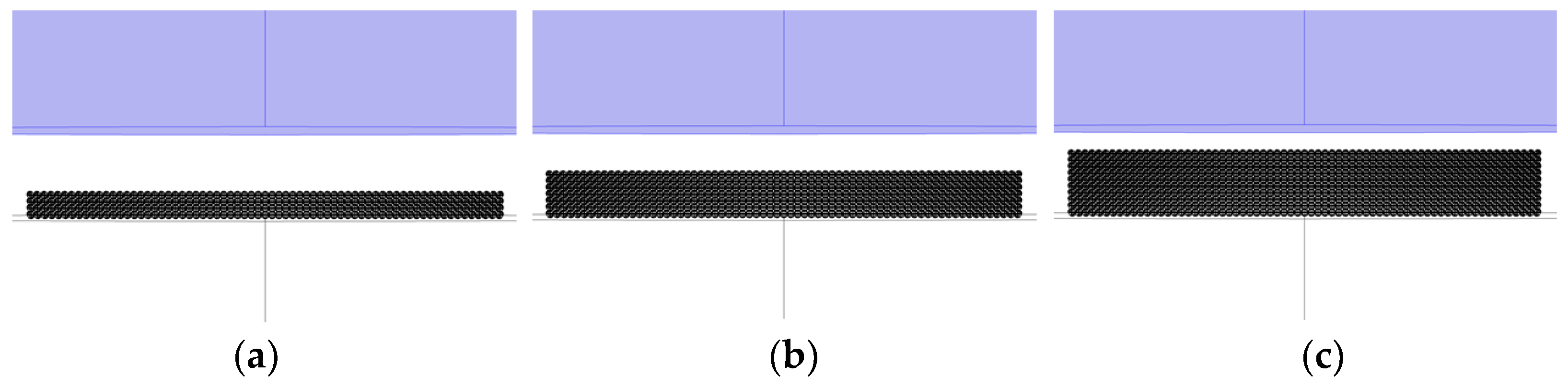
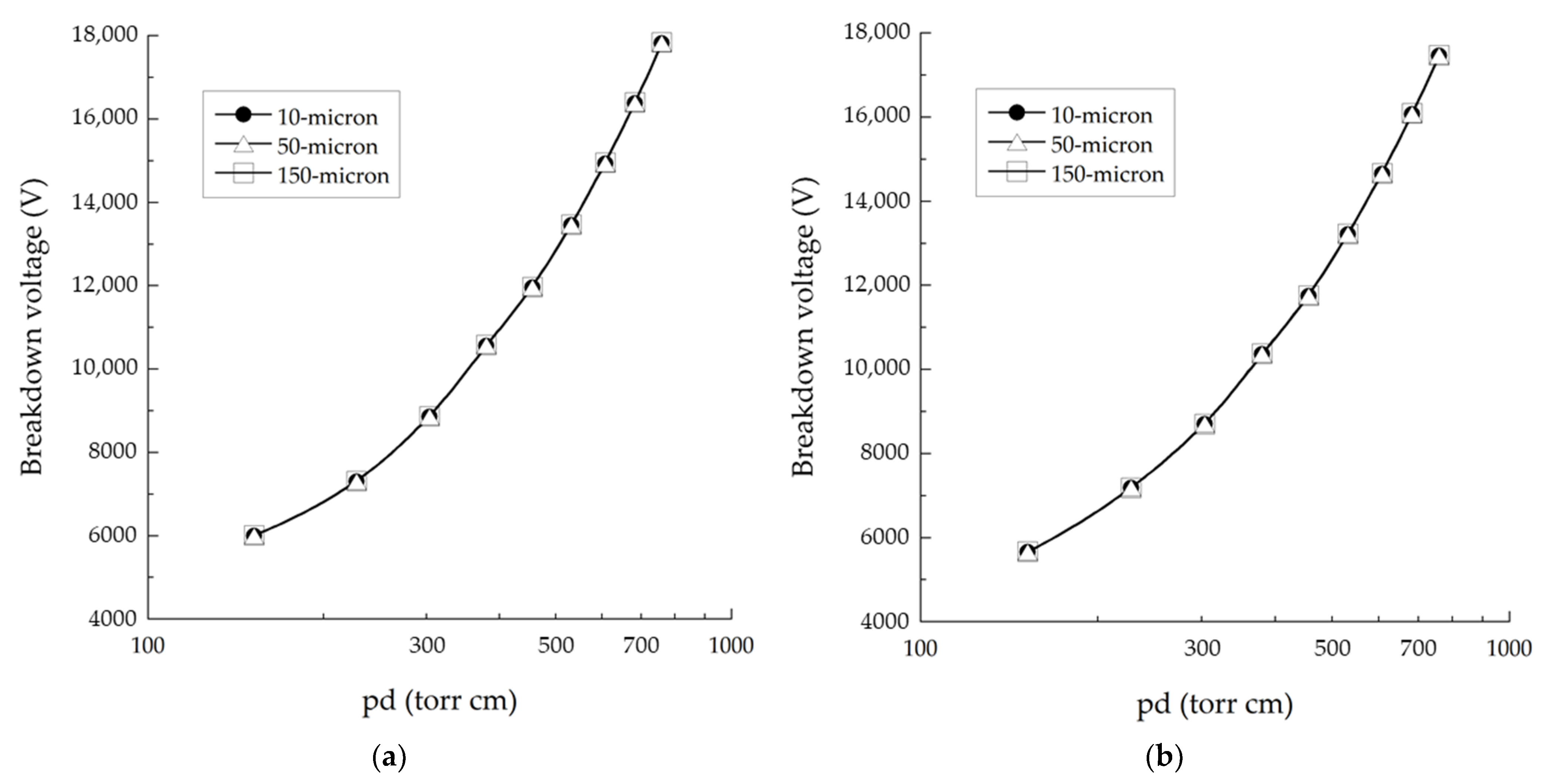
2.6. Effect of Starch Granule Diameter
3. Results and Discussion
3.1. Effect of the Model’s Mesh Type on the Electric Field
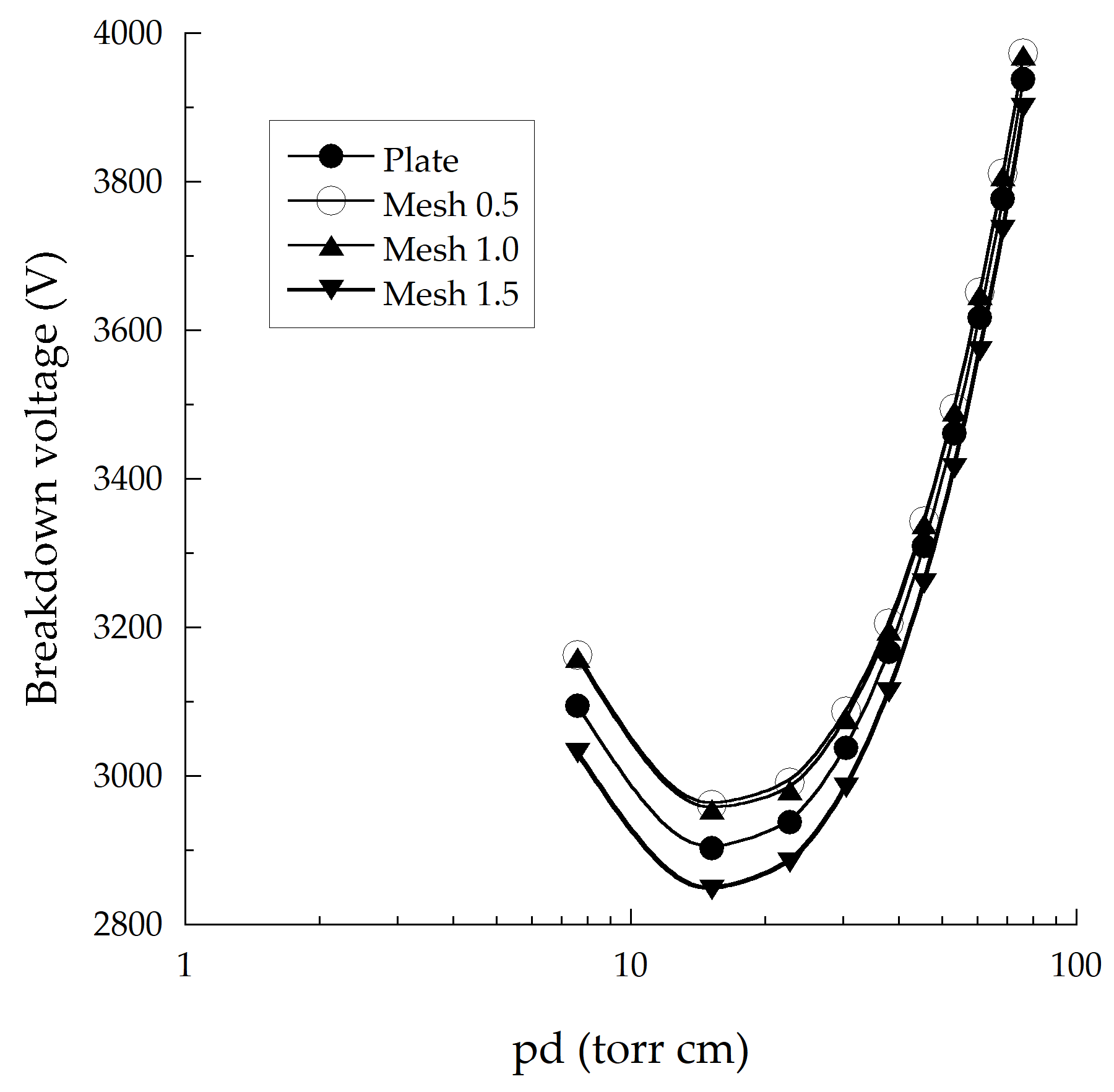
3.2. Effect of the Top Electrode’s Mesh Size
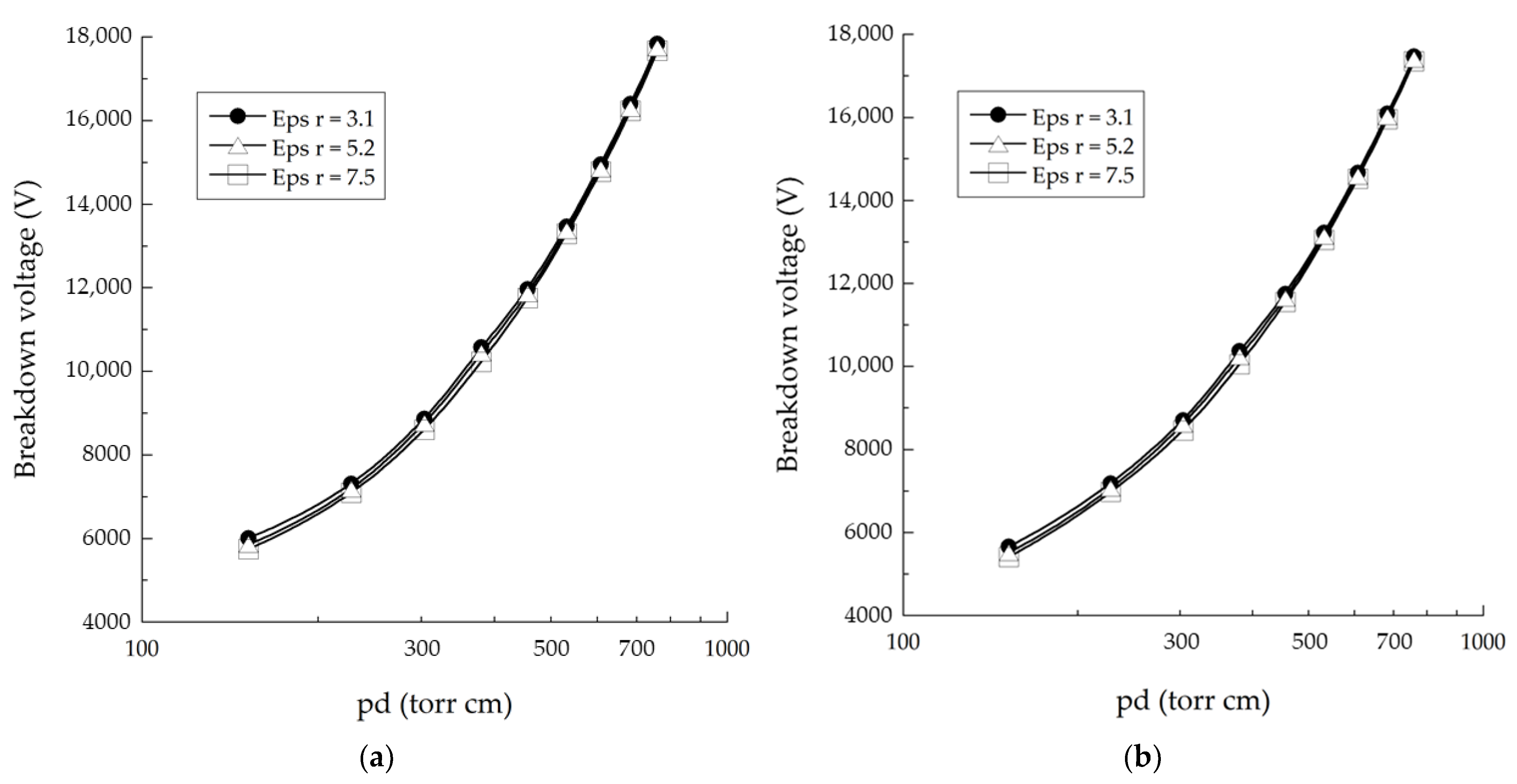
3.3. Effect of Starch Relative Permittivity
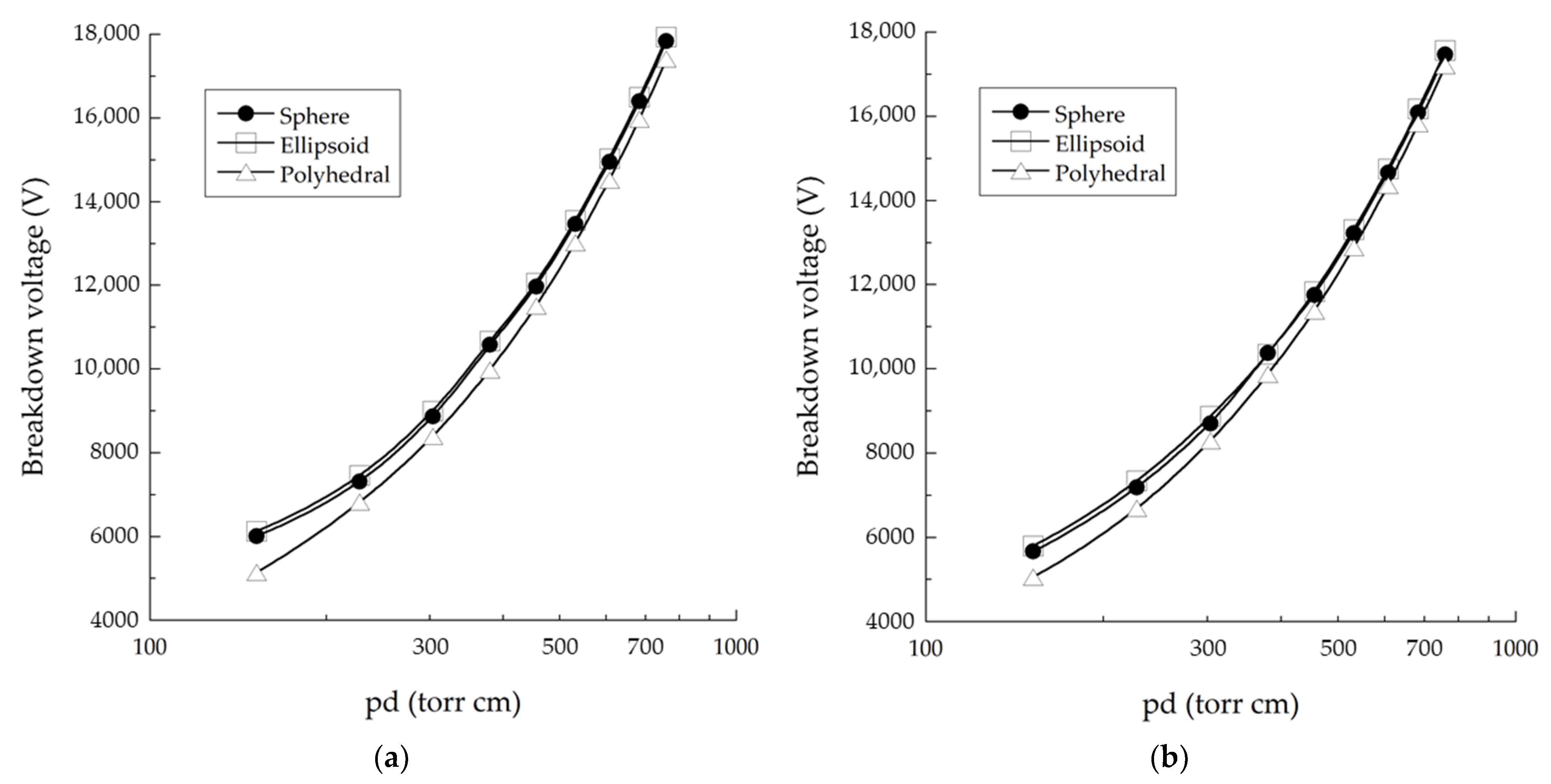
3.4. Effect of Starch Granule Shape
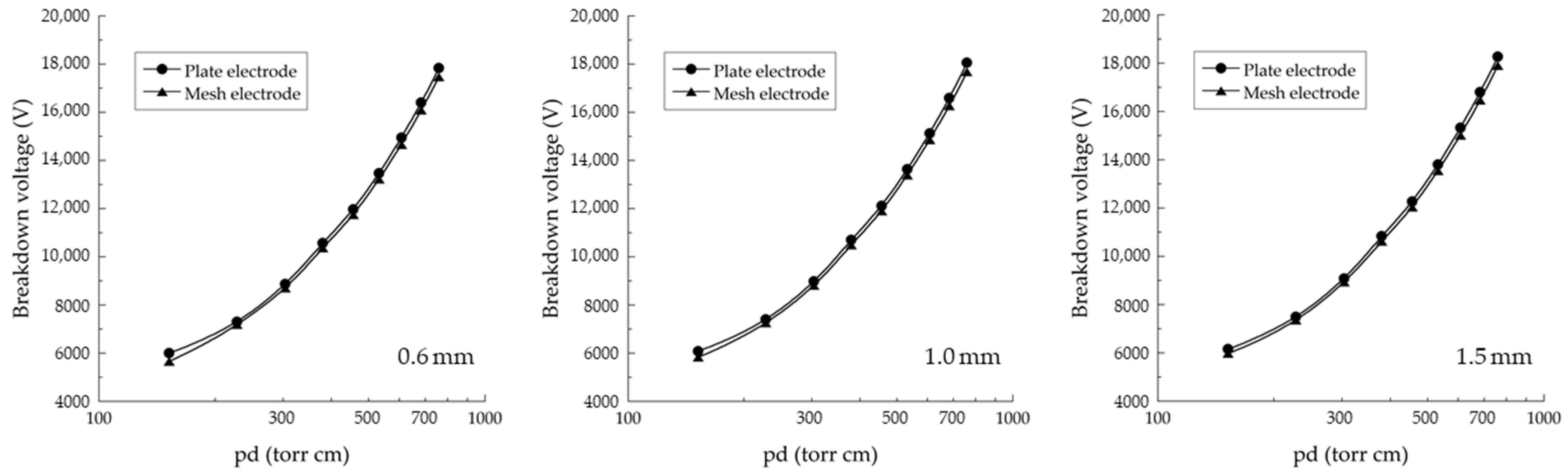
3.5. Effect of Starch Thickness Layer
3.6. Effect of Starch Granule Diameter
4. Conclusions
- The simulation results of this model were independent of the mesh when using the finer, extra fine, and extremely fine types.
- The top electrode of the plasma system can use a mesh electrode to replace the typical electrode. Based on the simulation results, this can lower the voltage required for initiating plasma production for similar conditions by approximately 2–6%.
- A higher-intensity electric field can be generated via electrodes with a larger mesh size, resulting in a lower breakdown voltage than for electrodes with a small mesh size.
- A comparison of the results for relative dielectric permittivity with different starch shows that the breakdown voltage decreases with increasing permittivity of the used starch.
- Starch with a polyhedral granule shape uses a voltage for breakdown significantly lower than that used in sphere and ellipsoid shapes.
- The thinner starch layer allows it to ionize at lower voltages while increasing the starch layer thickness requires an increase in the breakdown voltage.
- When the thickness of the starch layer is fixed, the breakdown voltage is unaffected by the starch granule diameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vamadevan, V.; Bertoft, E. Structure-function relationships of starch components. Starch-Stärke 2015, 67, 55–68. [Google Scholar] [CrossRef]
- Robyt, J. Starch: Structure, Properties, Chemistry, and Enzymology. In Glycoscience; Fraser-Reid, B.O., Tatsuta, K., Thiem, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1437–1472. [Google Scholar] [CrossRef]
- Park, S.H.; Na, Y.; Kim, J.; Kang, S.D.; Park, K.-H. Properties and applications of starch modifying enzymes for use in the baking industry. Food Sci. Biotechnol. 2018, 27, 299–312. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Gou, Q.; Yang, L.; Yu, Q.-L.; Han, L. Dielectric barrier discharge plasma: A green method to change structure of potato starch and improve physicochemical properties of potato starch films. Food Chem. 2022, 370, 130992. [Google Scholar] [CrossRef] [PubMed]
- Goiana, M.L.; de Brito, E.S.; Alves Filho, E.G.; Miguel, E.D.C.; Fernandes, F.A.N.; Azeredo, H.M.C.D.; Rosa, M.D.F. Corn starch based films treated by dielectric barrier discharge plasma. Int. J. Biol. Macromol. 2021, 183, 2009–2016. [Google Scholar] [CrossRef]
- Figueroa-Pinochet, M.F.; Castro-Alija, M.J.; Tiwari, B.K.; Jiménez, J.M.; López-Vallecillo, M.; Cao, M.J.; Albertos, I. Dielectric Barrier Discharge for Solid Food Applications. Nutrients 2022, 14, 4653. [Google Scholar] [CrossRef]
- Singh, J.; Colussi, R.; McCarthy, O.J.; Kaur, L. Chapter 8—Potato Starch and Its Modification. In Advances in Potato Chemistry and Technology, 2nd ed.; Singh, J., Kaur, L., Eds.; Academic Press: Cambridge, MA, USA, 2016; pp. 195–247. [Google Scholar] [CrossRef]
- Beh, C.Y.; Cheng, E.M.; Mohd Nasir, N.F.; Abdul Majid, M.S.; Khor, S.F.; Mohd Jamir, M.R.; Mohd Tarmizi, E.Z.; Lee, K.Y. Dielectric Properties of Hydrothermally Modified Potato, Corn, and Rice Starch. Agriculture 2022, 12, 783. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Liu, Y.; Liu, X. Starch Modification and Application. In Starch Structure, Functionality and Application in Foods; Wang, S., Ed.; Springer: Singapore, 2020; pp. 131–149. [Google Scholar] [CrossRef]
- Jayakody, L.; Hoover, R. Effect of annealing on the molecular structure and physicochemical properties of starches from different botanical origins—A review. Carbohydr. Polym. 2008, 74, 691–703. [Google Scholar] [CrossRef]
- Carvalho, A.P.M.G.; Barros, D.R.; da Silva, L.S.; Sanches, E.A.; Pinto, C.D.C.; de Souza, S.M.; Clerici, M.T.P.S.; Rodrigues, S.; Fernandes, F.A.N.; Campelo, P.H. Dielectric barrier atmospheric cold plasma applied to the modification of Ariá (Goeppertia allouia) starch: Effect of plasma generation voltage. Int. J. Biol. Macromol. 2021, 182, 1618–1627. [Google Scholar] [CrossRef]
- Compart, J.; Singh, A.; Fettke, J.; Apriyanto, A. Customizing Starch Properties: A Review of Starch Modifications and Their Applications. Polymers 2023, 15, 3491. [Google Scholar] [CrossRef]
- Pratiwi, M.; Faridah, D.N.; Lioe, H.N. Structural changes to starch after acid hydrolysis, debranching, autoclaving-cooling cycles, and heat moisture treatment (HMT): A review. Starch-Stärke 2018, 70, 1700028. [Google Scholar] [CrossRef]
- Brasoveanu, M.; Nemtanu, M.R. Behaviour of starch exposed to microwave radiation treatment. Starch-Stärke 2014, 66, 3–14. [Google Scholar] [CrossRef]
- Falsafi, S.R.; Maghsoudlou, Y.; Rostamabadi, H.; Rostamabadi, M.M.; Hamedi, H.; Hosseini, S.M.H. Preparation of physically modified oat starch with different sonication treatments. Food Hydrocoll. 2019, 89, 311–320. [Google Scholar] [CrossRef]
- Matta Junior, M.D.; Castanha, N.; dos Anjos, C.B.P.; Augusto, P.E.D.; Sarmento, S.B.S. Ozone technology as an alternative to fermentative processes to improve the oven-expansion properties of cassava starch. Food Res. Int. 2019, 123, 56–63. [Google Scholar] [CrossRef] [PubMed]
- Tian, S.; Chen, Y.; Chen, Z.; Yang, Y.; Wang, Y. Preparation and Characteristics of Starch Esters and Its Effects on Dough Physicochemical Properties. J. Food Qual. 2018, 2018, 1395978. [Google Scholar] [CrossRef]
- Shi, M.; Gu, F.; Wu, J.; Yu, S.; Gao, Q. Preparation, physicochemical properties, and in vitro digestibility of cross-linked resistant starch from pea starch. Starch-Stärke 2013, 65, 947–953. [Google Scholar] [CrossRef]
- Fonseca, L.M.; Gonçalves, J.R.; El Halal, S.L.M.; Pinto, V.Z.; Dias, A.R.G.; Jacques, A.C.; Da Zavareze, E.R. Oxidation of potato starch with different sodium hypochlorite concentrations and its effect on biodegradable films. LWT Food Sci. Technol. 2015, 60, 714–720. [Google Scholar] [CrossRef]
- Dura, A.; Blaszczak, W.; Rosell, C.M. Functionality of porous starch obtained by amylase or amyloglucosidase treatments. Carbohydr. Polym. 2014, 101, 837–845. [Google Scholar] [CrossRef]
- Thirumdas, R.; Kadam, D.; Annapure, U.S. Cold plasma: An alternative technology for the starch modification. Food Biophys. 2017, 12, 129–139. [Google Scholar] [CrossRef]
- Goiana, M.L.; Mattos, A.L.A.; de Azeredo, H.M.C.; de Freitas Rosa, M.; Fernandes, F.A.N. Influence of Dielectric Barrier Discharge Cold Plasma Treatment on Starch, Gelatin, and Bacterial Cellulose Biodegradable Polymeric Films. Polymers 2022, 14, 5215. [Google Scholar] [CrossRef]
- Sifuentes-Nieves, I.; Mendez-Montealvo, G.; Flores-Silva, P.C.; Nieto-Perez, M.; Neira-Velazquez, G.; Rodriguez-Fernandez, O.; Hernandez-Hernandez, E.; Velazquez, G. Dielectric barrier discharge and radio-frequency plasma effect on structural properties of starches with different amylose content. Innov. Food Sci. Emerg. Technol. 2021, 68, 102630. [Google Scholar] [CrossRef]
- Gupta, R.K.; Guha, P.; Srivastav, P.P. Effect of high voltage dielectric barrier discharge (DBD) atmospheric cold plasma treatment on physicochemical and functional properties of taro (Colocasia esculenta) starch. Int. J. Biol. Macromol. 2023, 253, 126772. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, M.; Kalaivendan, R.G.T.; Eazhumalai, G.; Annapure, U.S. Atmospheric pressure pin-to-plate cold plasma effect on physicochemical, functional, pasting, thermal, and structural characteristics of proso-millet starch. Food Res. Int. 2023, 173, 113444. [Google Scholar] [CrossRef] [PubMed]
- Thirumdas, R.; Trimukhe, A.; Deshmukh, R.R.; Annapure, U.S. Functional and rheological properties of cold plasma treated rice starch. Carbohydr. Polym. 2017, 157, 1723–1731. [Google Scholar] [CrossRef]
- Banura, S.; Thirumdas, R.; Kaur, A.; Deshmukh, R.R.; Annapure, U.S. Modification of starch using low pressure radio frequency air plasma. LWT 2018, 89, 719–724. [Google Scholar] [CrossRef]
- Yan, S.; Gui-Yun, C.; Ya-Jie, H.; Ye, C. Improved solubility of banana starch by dielectric barrier discharge plasma treatment. Int. J. Food Sci. Technol. 2019, 55, 641–648. [Google Scholar] [CrossRef]
- Okyere, A.Y.; Bertoft, E.; Amponsah Annor, G. Modification of cereal and tuber waxy starches with radio frequency cold plasma and its effects on waxy starch properties. Carbohydr. Polym. 2019, 223, 115075. [Google Scholar] [CrossRef]
- Zhu, Q.; Yao, S.; Wu, Z.; Li, D.; Ding, T.; Liu, D.; Xu, E. Hierarchical structural modification of starch via non-thermal plasma: A state-of-the-art review. Carbohydr. Polym. 2023, 311, 120747. [Google Scholar] [CrossRef]
- Von Engel, A. Ionized Gases; American Institute of Physics Press: New York, NY, USA, 1993; pp. 193–204. [Google Scholar]
- Chankuson, P.; Chumsri, P. The Plasma Ozonizer System for Mangosteen Storage Container to Preserve the Quality of Mangosteen. Appl. Sci. 2023, 13, 4873. [Google Scholar] [CrossRef]
- Murillo, D.; Huergo, C.; Gallego, B.; Rodríguez, R.; Tornín, J. Exploring the Use of Cold Atmospheric Plasma to Overcome Drug Resistance in Cancer. Biomedicines 2023, 11, 208. [Google Scholar] [CrossRef]
- Magureanu, M.; Bradu, C.; Parvulescu, V.I. Plasma processes for the treatment of water contaminated with harmful organic compounds. J. Phys. D Appl. Phys. 2018, 51, 313002. [Google Scholar] [CrossRef]
- Pánka, D.; Jeske, M.; Łukanowski, A.; Baturo-Ciésniewska, A.; Prus, P.; Maitah, M.; Maitah, K.; Malec, K.; Rymarz, D.; Muhire, J.d.D.; et al. Can Cold Plasma Be Used for Boosting Plant Growth and Plant Protection in Sustainable Plant Production? Agronomy 2022, 12, 841. [Google Scholar] [CrossRef]
- Xiao, D. Gas Discharge and Gas Insulation; Shanghai Jiao Tong University Press: Shanghai, China, 2015; pp. 47–122. [Google Scholar]
- Lisovskiy, V.A.; Osmayev, R.O.; Gapon, A.V.; Dudin, S.V.; Lesnik, I.S.; Yegorenkov, V.D. Electric field non-uniformity effect on dc low pressure gas breakdown between flat electrodes. Vacuum 2017, 145, 19–29. [Google Scholar] [CrossRef]
- Tschiersch, R.; Nemschokmichal, S.; Bogaczyk, M.; Meichsner, J. Self-stabilized discharge filament in plane-parallel barrier discharge configuration: Formation, breakdown mechanism, and memory effects. J. Phys. D Appl. Phys. 2017, 50, 415206. [Google Scholar] [CrossRef]
- Talaat, M.; Farahat, M.A.; Said, T. Numerical investigation of the optimal characteristics of a transverse layer of dielectric barrier in a non-uniform electric field. J. Phys. Chem. Solids 2018, 121, 27–35. [Google Scholar] [CrossRef]
- Nijdam, S.; Teunissen, J.; Ebert, U. The physics of streamer discharge phenomena. Plasma Sources Sci. Technol. 2020, 29, 103001. [Google Scholar] [CrossRef]
- Fridman, A. Plasma Chemistry; Cambridge University Press: Cambridge, UK, 2011; pp. 157–166. [Google Scholar]
- Lee, M.; Park, G.; Park, C.; Kim, C. Improvement of grid independence test for computational fluid dynamics model of building based on grid resolution. Adv. Civil Eng. 2020, 2020, 8827936. [Google Scholar] [CrossRef]
- Knotek, S.; Schmelter, S.; Olbrich, M. Assessment of different parameters used in mesh independence studies in two-phase slug flow simulations. Meas. Sens. 2021, 18, 100317. [Google Scholar] [CrossRef]
- Radmilović-Radjenović, M.; Radjenović, D.; Radjenović, B. Simulation studies of the electrode configuration effect on the breakdown phenomenon. Int. J. Adv. Res. Comput. Sci. Electron. Eng. 2019, 8, 68–72. [Google Scholar]
- Foruzan, E.; Akmal, A.A.S.; Niayesh, K.; Lin, J.; Sharma, D.D. Comparative study on various dielectric barriers and their effect on breakdown voltage. High. Volt. 2018, 3, 51–59. [Google Scholar] [CrossRef]
- Facta, M.; Umiati, N.A.K.; Warsito, A. Geometrical shape investigation for electrodes in silent discharge chamber. IOP Conf. Ser. Mater. Sci. Eng. 2017, 190, 012022. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, Z.; Zhang, B.; Chen, Y. Numerical Investigation on the Effects of Dielectric Barrier on a Nanosecond Pulsed Surface Dielectric Barrier Discharge. Molecules 2019, 24, 3933. [Google Scholar] [CrossRef] [PubMed]
- Seidela, J.V.; Castañeda-Uribeb, O.A.; Arevaloc, S.; Muñozd, F.; Proude, W.; Avila, A. Relative permittivity estimation of wheat starch: A critical property for understanding electrostatic hazards. J. Hazard. Mater. 2019, 368, 228–233. [Google Scholar] [CrossRef] [PubMed]
- Soloviev, V.R.; Selivonin, I.V.; Moralev, I.A. Breakdown voltage for surface dielectric barrier discharge ignition in atmospheric air. Phys. Plasmas 2017, 24, 103528. [Google Scholar] [CrossRef]
- Elaissi, S.; Alsaif, N.A.M. Modelling of Nonthermal Dielectric Barrier Discharge Plasma at Atmospheric Pressure and Role of Produced Reactive Species in Surface Polymer Microbial Purification. Polymers 2023, 15, 1235. [Google Scholar] [CrossRef]
- Kawagoe, Y. The Characteristic Polyhedral, Sharp-edged Shape of Compound-type Starch Granules in Rice Endosperm is Achieved via the Septum-like Structure of the Amyloplast. J. Appl. Glycosci. 2013, 60, 29–36. [Google Scholar] [CrossRef]
- Song, G.; Wang, Y.; Tan, D.Q. A review of surface roughness impact on dielectric film properties. IET Nanodielectr. 2022, 5, 1–23. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, Q.; Zhong, S.; Sun, R. Effect of surface roughness on characteristics of surface dielectric barrier discharge. High. Volt. Appar. 2016, 52, 96–100. [Google Scholar] [CrossRef]
- Hink, R.; Pipa, A.V.; Sch¨afer, J.; Caspari, R.; Weichwald, R.; Foest, R.; Brandenburg, R. Influence of dielectric thickness and electrode structure on the ion wind generation by micro fabricated plasma actuators. J. Phys. D Appl. Phys. 2020, 53, 405201. [Google Scholar] [CrossRef]
- Belinger, A.; Dap, S.; Naudé, N. Influence of the dielectric thickness on the homogeneity of a diffuse dielectric barrier discharge in air. J. Phys. D Appl. Phys. 2022, 55, 465201. [Google Scholar] [CrossRef]

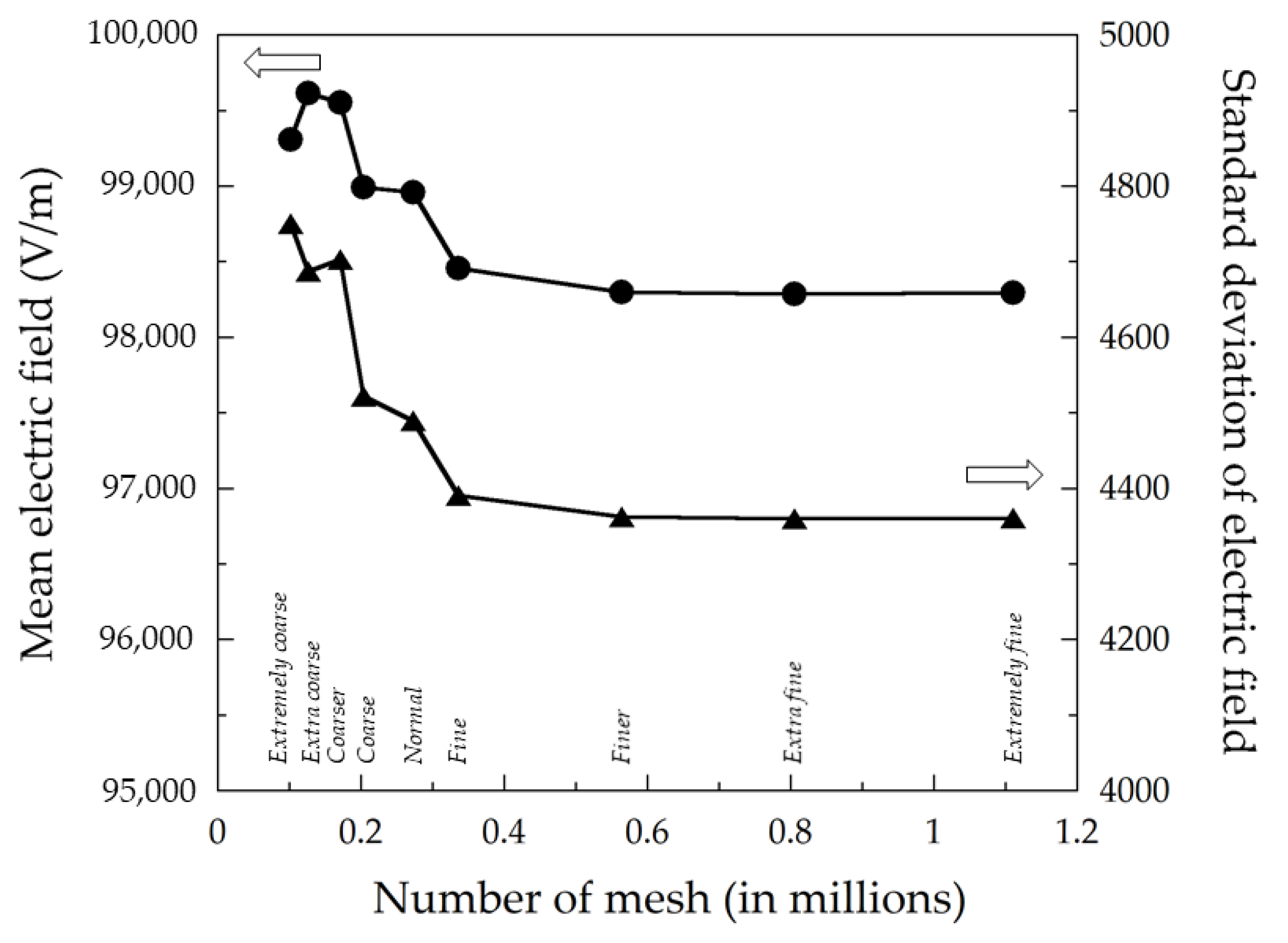


| Mesh Type | Number of Mesh (×106) |
|---|---|
| extremely coarse | 0.102 |
| extra coarse | 0.127 |
| coarser | 0.171 |
| coarse | 0.203 |
| normal | 0.273 |
| fine | 0.336 |
| finer | 0.564 |
| extra fine | 0.805 |
| extremely fine | 1.114 |
| Gap Distance (mm) | pd (torr cm) | Breakdown Voltage (V) | |||
|---|---|---|---|---|---|
| Plate | Mesh 0.5 cm2 | Mesh 1.0 cm2 | Mesh 1.5 cm2 | ||
| 0.1 | 7.6 | 3094 | 3163 | 3159 | 3031 |
| 0.2 | 15.2 | 2903 | 2961 | 2955 | 2847 |
| 0.3 | 22.8 | 2937 | 2991 | 2981 | 2900 |
| 0.4 | 30.4 | 3038 | 3087 | 3077 | 2984 |
| 0.5 | 38.0 | 3166 | 3205 | 3196 | 3113 |
| 0.6 | 45.6 | 3309 | 3343 | 3339 | 3259 |
| 0.7 | 53.2 | 3461 | 3494 | 3491 | 3414 |
| 0.8 | 60.8 | 3617 | 3651 | 3648 | 3572 |
| 0.9 | 68.4 | 3777 | 3811 | 3808 | 3735 |
| 1.0 | 76.0 | 3938 | 3973 | 3970 | 3899 |
| Gap Distance (cm) | pd (torr cm) | Breakdown Voltage (V) | |||||
|---|---|---|---|---|---|---|---|
| εr = 3.1 | εr = 5.2 | εr = 7.5 | |||||
| Plate | Mesh | Plate | Mesh | Plate | Mesh | ||
| 0.2 | 152 | 6006 | 5659 | 5854 | 5514 | 5746 | 5412 |
| 0.3 | 228 | 7307 | 7185 | 7181 | 7062 | 7091 | 6974 |
| 0.4 | 304 | 8865 | 8701 | 8758 | 8607 | 8600 | 8455 |
| 0.5 | 380 | 10,570 | 10,369 | 10,435 | 10,237 | 10,225 | 10,050 |
| 0.6 | 456 | 11,968 | 11,749 | 11,853 | 11,646 | 11,748 | 11,552 |
| 0.7 | 532 | 13,464 | 13,221 | 13,363 | 13,134 | 13,289 | 13,050 |
| 0.8 | 608 | 14,947 | 14,662 | 14,845 | 14,578 | 14,772 | 14,524 |
| 0.9 | 684 | 16,399 | 16,086 | 16,294 | 16,012 | 16,230 | 15,958 |
| 1.0 | 760.0 | 17,839 | 17,473 | 17,741 | 17,404 | 17,670 | 17,352 |
| Gap Distance (cm) | pd (torr cm) | Breakdown Voltage (V) | |||||
|---|---|---|---|---|---|---|---|
| Sphere | Ellipsoid | Polyhedral | |||||
| Plate | Mesh | Plate | Mesh | Plate | Mesh | ||
| 0.2 | 152 | 6006 | 5659 | 6123 | 5795 | 5145 | 5055 |
| 0.3 | 228 | 7307 | 7185 | 7448 | 7338 | 6818 | 6681 |
| 0.4 | 304 | 8865 | 8701 | 8994 | 8871 | 8390 | 8286 |
| 0.5 | 380 | 10,570 | 10,369 | 10,665 | 10,337 | 9969 | 9859 |
| 0.6 | 456 | 11,968 | 11,749 | 12,048 | 11,827 | 11,498 | 11,371 |
| 0.7 | 532 | 13,464 | 13,221 | 13,551 | 13,307 | 13,017 | 12,874 |
| 0.8 | 608 | 14,947 | 14,662 | 15,029 | 14,742 | 14,511 | 14,354 |
| 0.9 | 684 | 16,399 | 16,086 | 16,491 | 16,176 | 15,970 | 15,821 |
| 1.0 | 760.0 | 17,839 | 17,473 | 17,937 | 17,560 | 17,408 | 17,202 |
| Gap Distance (cm) | pd (torr cm) | Breakdown Voltage (V) | |||||
|---|---|---|---|---|---|---|---|
| 0.6 mm | 1.0 mm | 1.5 mm | |||||
| Plate | Mesh | Plate | Mesh | Plate | Mesh | ||
| 0.2 | 152 | 6006 | 5659 | 6083 | 5832 | 6158 | 5978 |
| 0.3 | 228 | 7307 | 7185 | 7400 | 7259 | 7493 | 7355 |
| 0.4 | 304 | 8865 | 8701 | 8976 | 8809 | 9086 | 8937 |
| 0.5 | 380 | 10,570 | 10,369 | 10,699 | 10,496 | 10,829 | 10,623 |
| 0.6 | 456 | 11,968 | 11,749 | 12,116 | 11,904 | 12,265 | 12,038 |
| 0.7 | 532 | 13,464 | 13,221 | 13,629 | 13,396 | 13,798 | 13,549 |
| 0.8 | 608 | 14,947 | 14,662 | 15,129 | 14,857 | 15,318 | 15,011 |
| 0.9 | 684 | 16,399 | 16,086 | 16,597 | 16,265 | 16,801 | 16,465 |
| 1.0 | 760.0 | 17,839 | 17,473 | 18,053 | 17,674 | 18,273 | 17,907 |
| Gap Distance (cm) | pd (torr cm) | Breakdown Voltage (V) | |||||
|---|---|---|---|---|---|---|---|
| 10 Micron | 50 Micron | 150 Micron | |||||
| Plate | Mesh | Plate | Mesh | Plate | Mesh | ||
| 0.2 | 152 | 5999 | 5653 | 6000 | 5655 | 6006 | 5659 |
| 0.3 | 228 | 7299 | 7178 | 7300 | 7181 | 7307 | 7185 |
| 0.4 | 304 | 8855 | 8692 | 8857 | 8694 | 8865 | 8701 |
| 0.5 | 380 | 10,558 | 10,358 | 10,560 | 10,361 | 10,570 | 10,369 |
| 0.6 | 456 | 11,955 | 11,737 | 11,957 | 11,740 | 11,968 | 11,749 |
| 0.7 | 532 | 13,449 | 13,207 | 13,451 | 13,210 | 13,464 | 13,221 |
| 0.8 | 608 | 14,930 | 14,647 | 14,933 | 14,651 | 14,947 | 14,662 |
| 0.9 | 684 | 16,381 | 16,069 | 16,383 | 16,073 | 16,399 | 16,086 |
| 1.0 | 760.0 | 17,819 | 17,454 | 17,822 | 17,458 | 17,839 | 17,473 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chankuson, P.; Chumsri, P.; Plodkaew, A. The Simulation of Dielectric Barrier Discharge for Breakdown Voltage in Starch Modification. Appl. Sci. 2023, 13, 12143. https://doi.org/10.3390/app132212143
Chankuson P, Chumsri P, Plodkaew A. The Simulation of Dielectric Barrier Discharge for Breakdown Voltage in Starch Modification. Applied Sciences. 2023; 13(22):12143. https://doi.org/10.3390/app132212143
Chicago/Turabian StyleChankuson, Pitchasak, Paramee Chumsri, and Apinun Plodkaew. 2023. "The Simulation of Dielectric Barrier Discharge for Breakdown Voltage in Starch Modification" Applied Sciences 13, no. 22: 12143. https://doi.org/10.3390/app132212143
APA StyleChankuson, P., Chumsri, P., & Plodkaew, A. (2023). The Simulation of Dielectric Barrier Discharge for Breakdown Voltage in Starch Modification. Applied Sciences, 13(22), 12143. https://doi.org/10.3390/app132212143





