Wind Load Distribution in Float Photovoltaic System
Abstract
:1. Introduction
2. PV Generation System
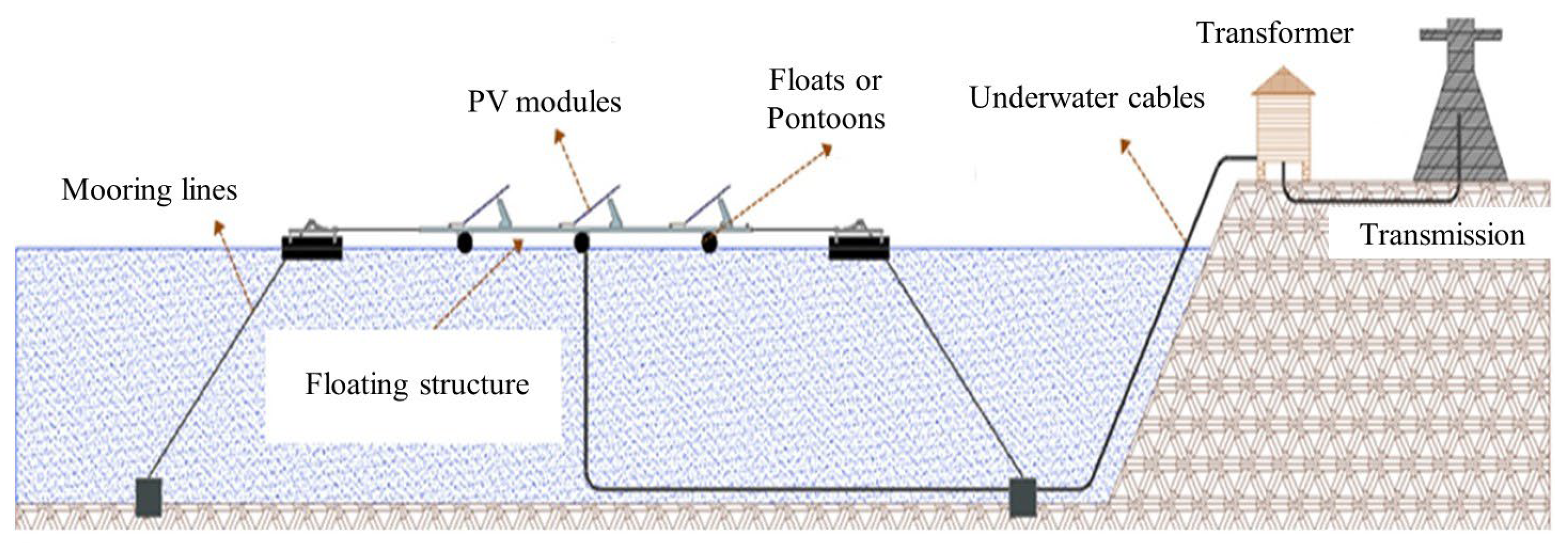
2.1. Overview
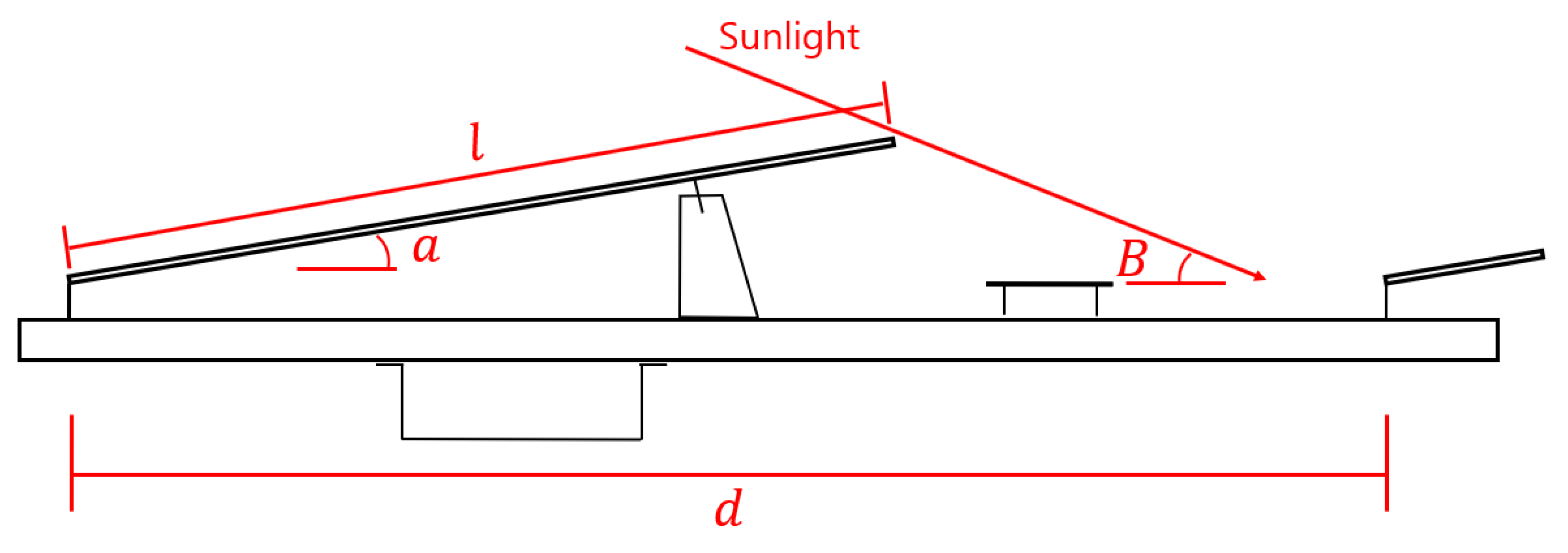
2.2. Mooring System
3. Proposed Modeling Strategy
3.1. Analysis and Design of PV Power Plants
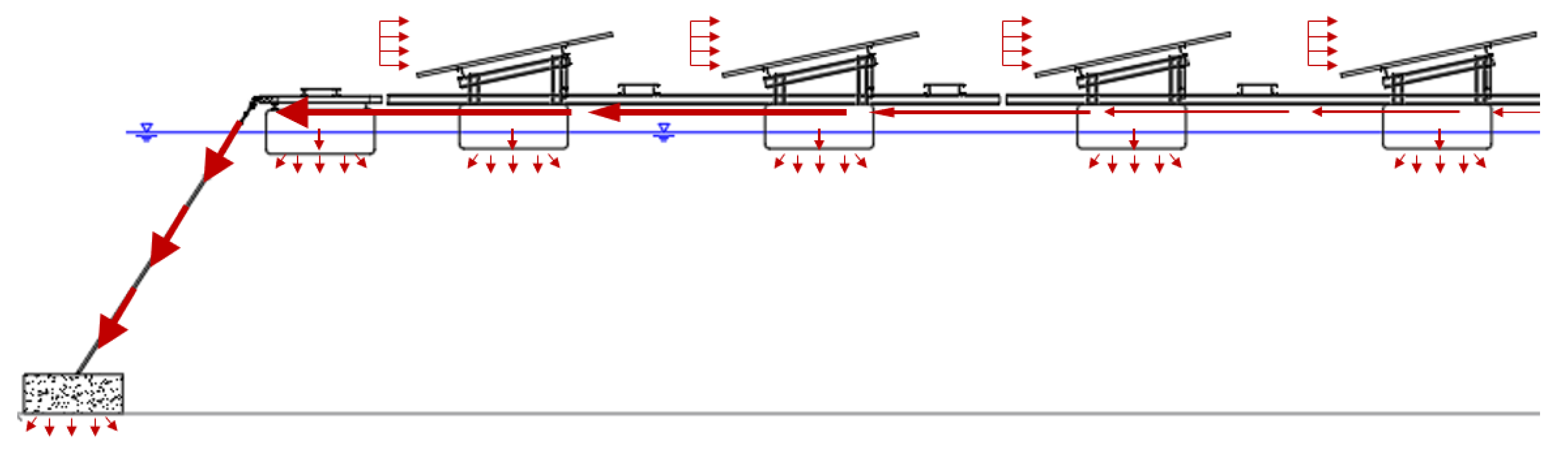
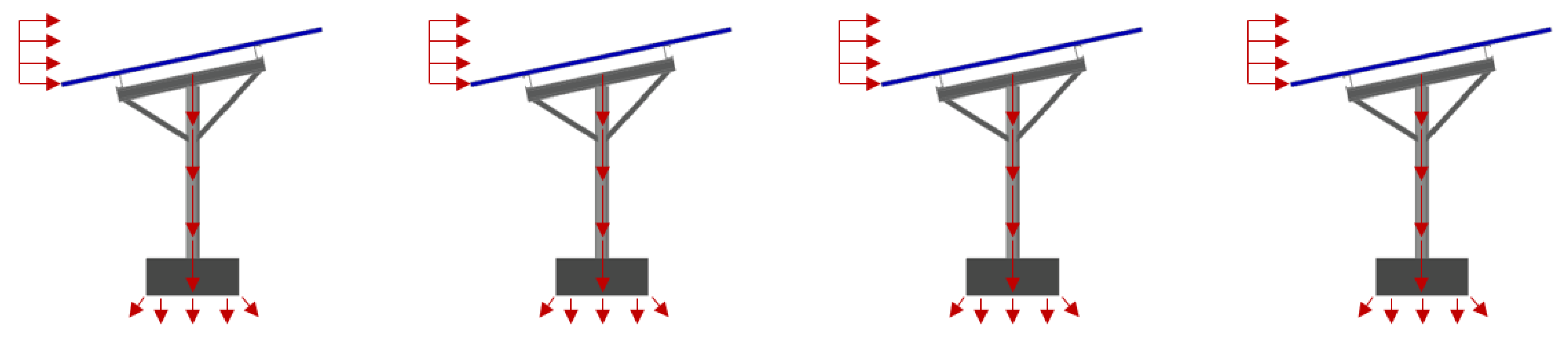
3.2. Evaluating Load Distribution
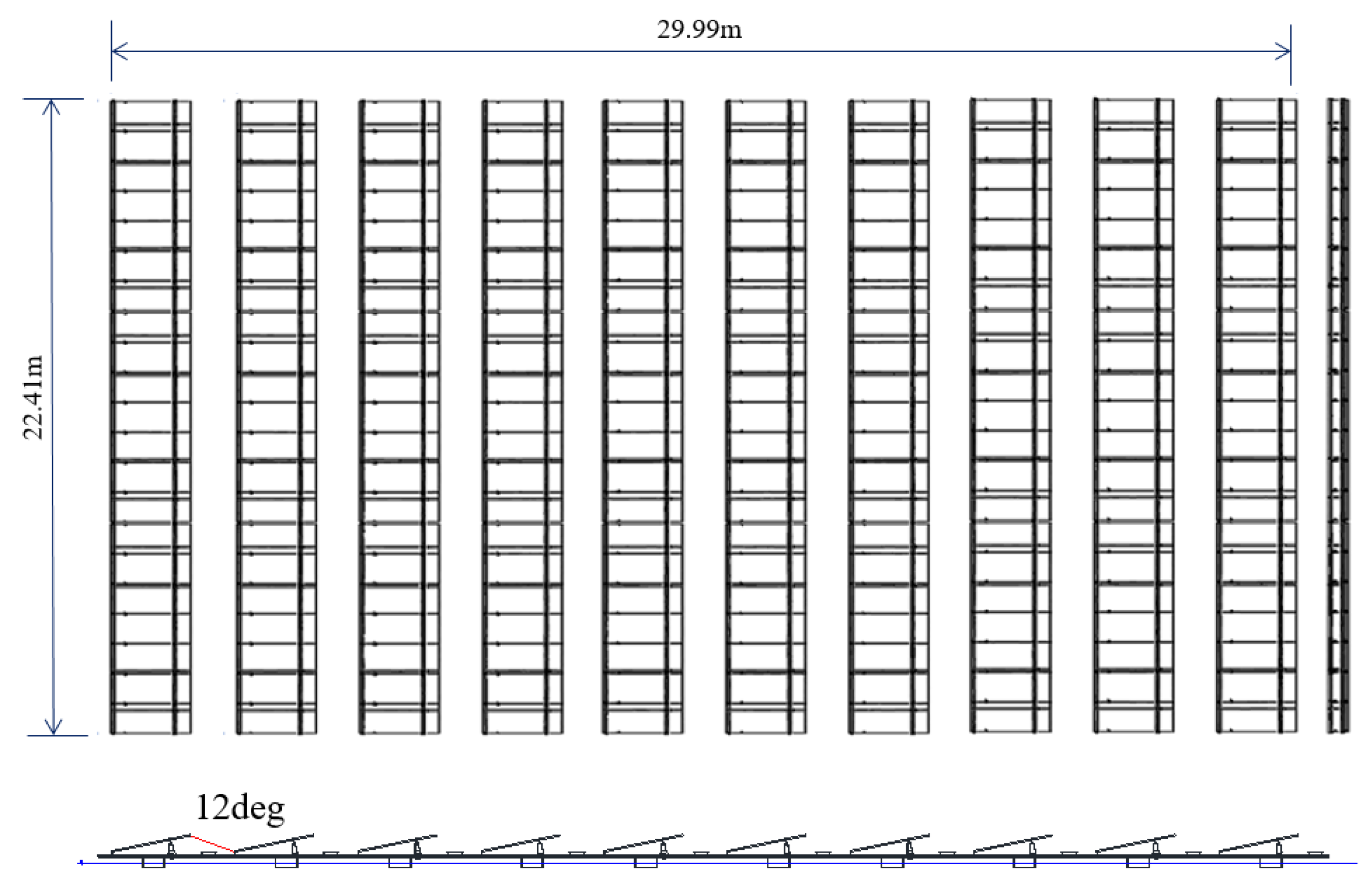
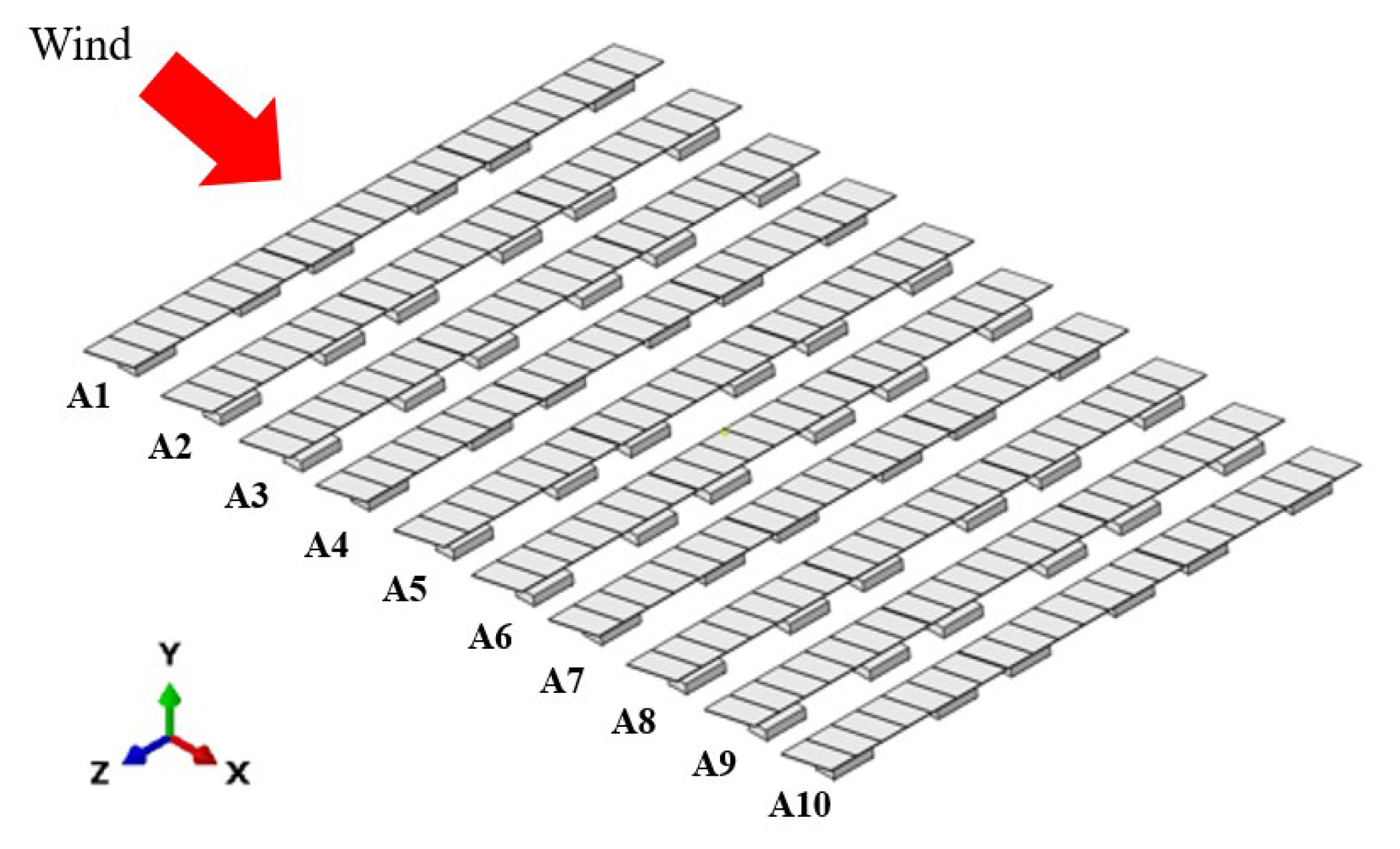
4. Modeling Description
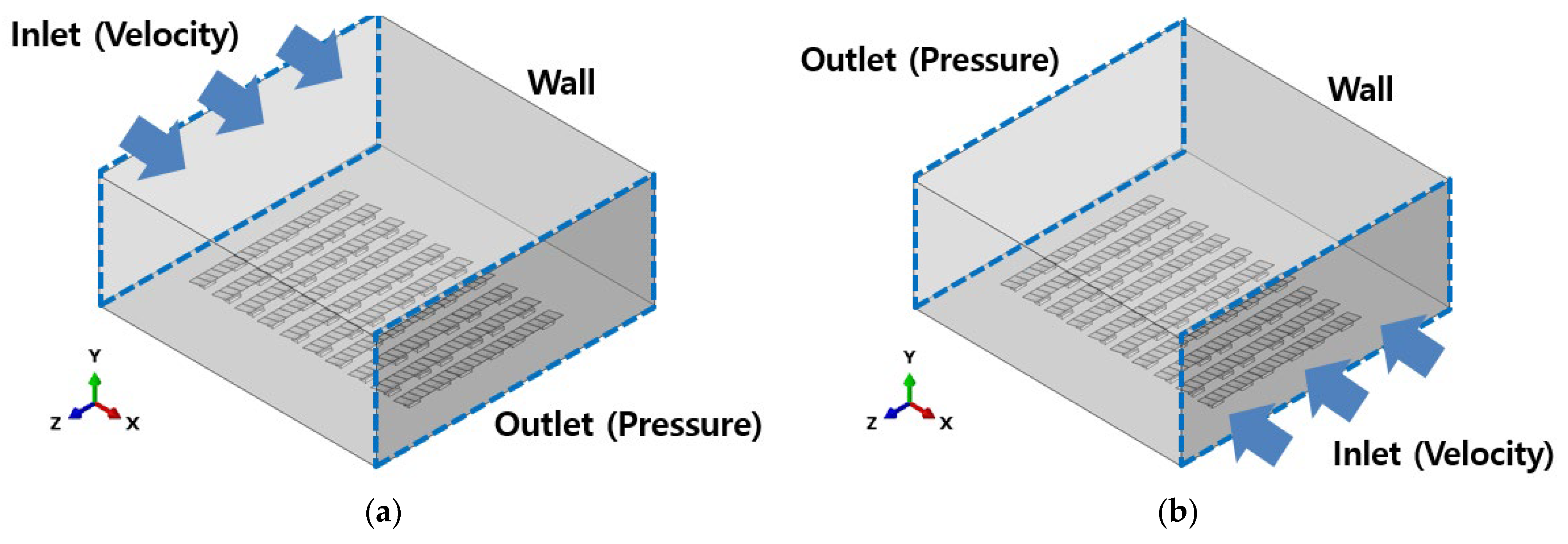
4.1. Design Variables for Wind Load Distribution for CFD Analysis
4.2. Model Evaluation Strategy
5. Results and Analysis
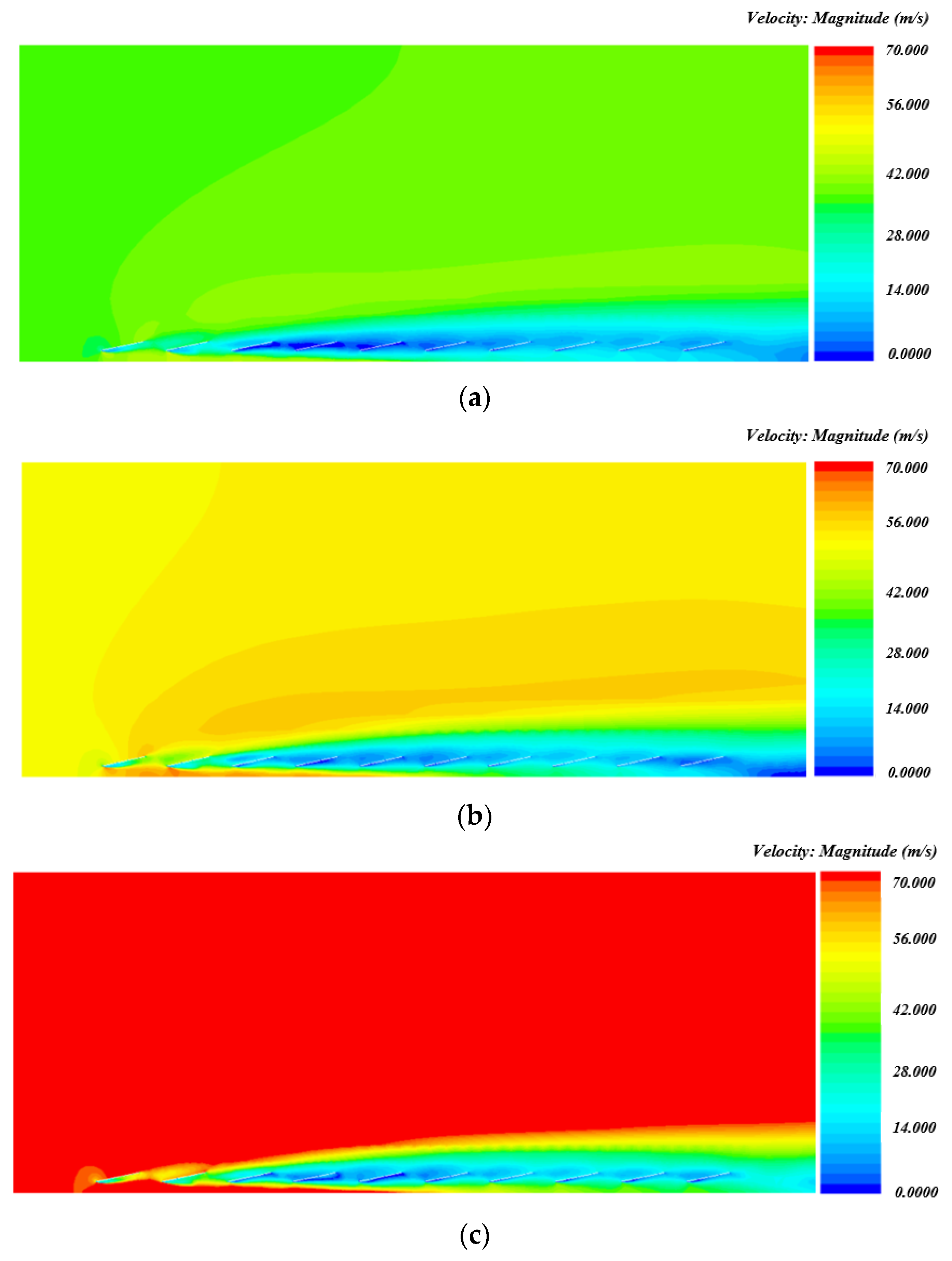
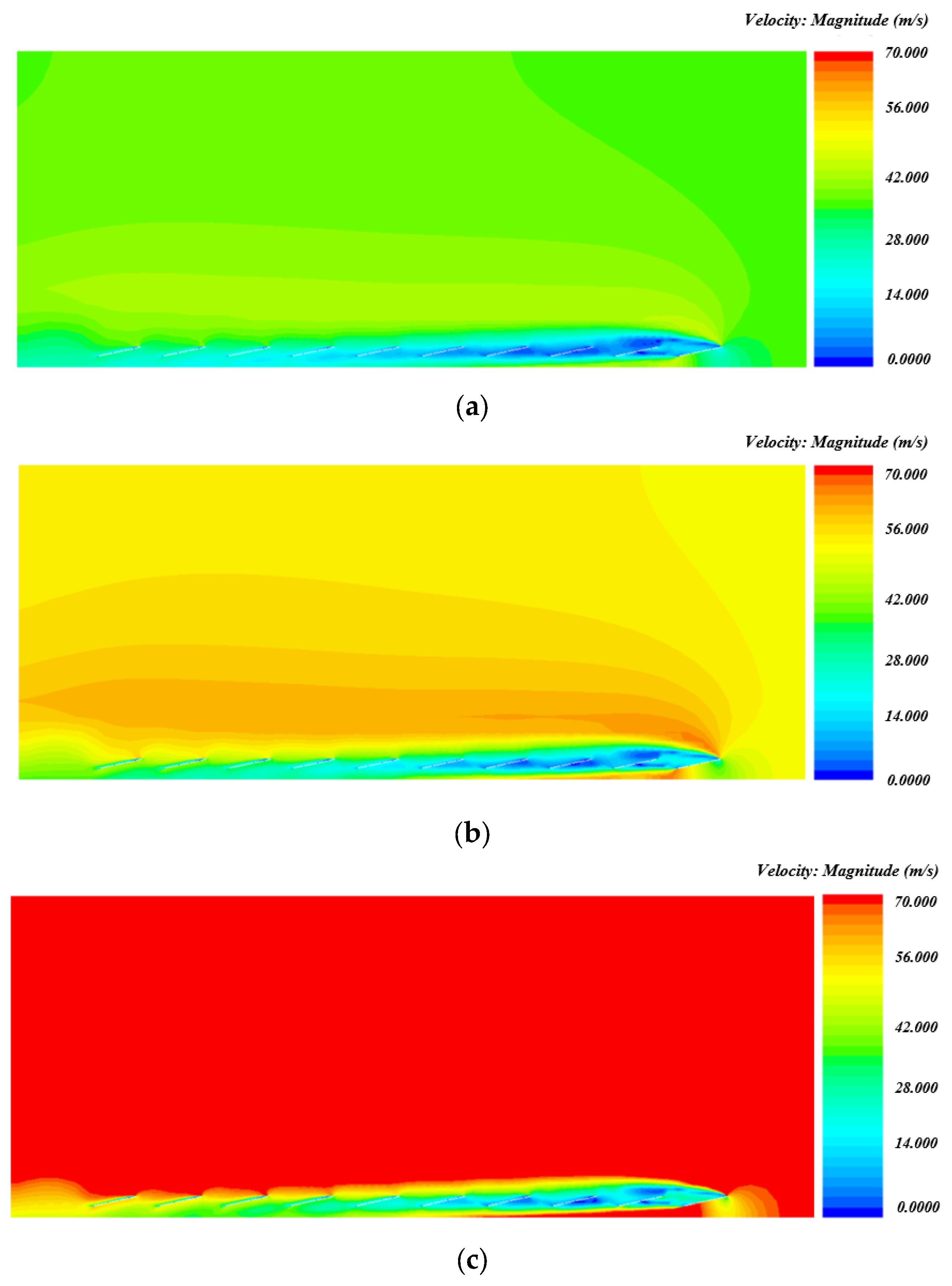
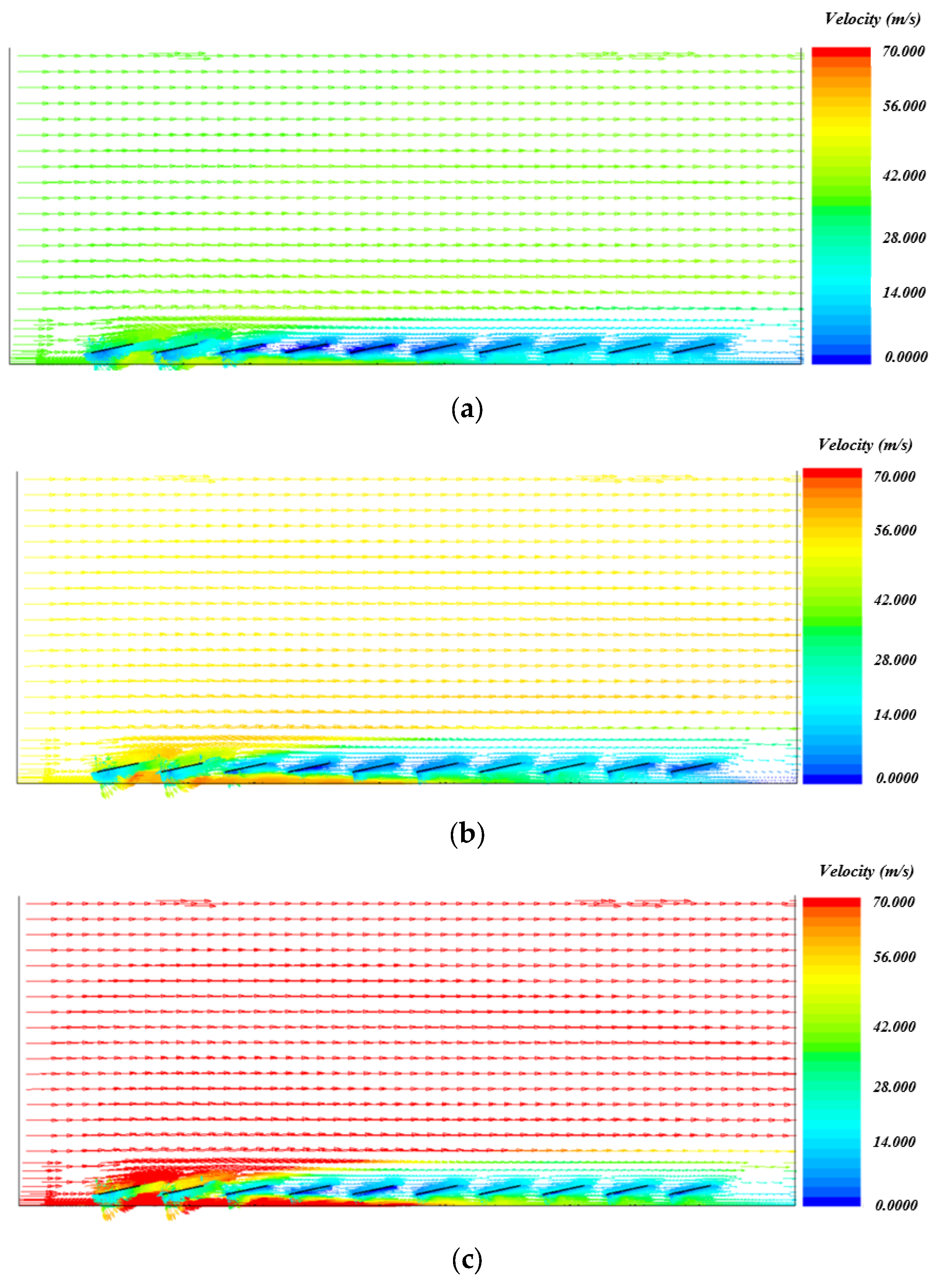
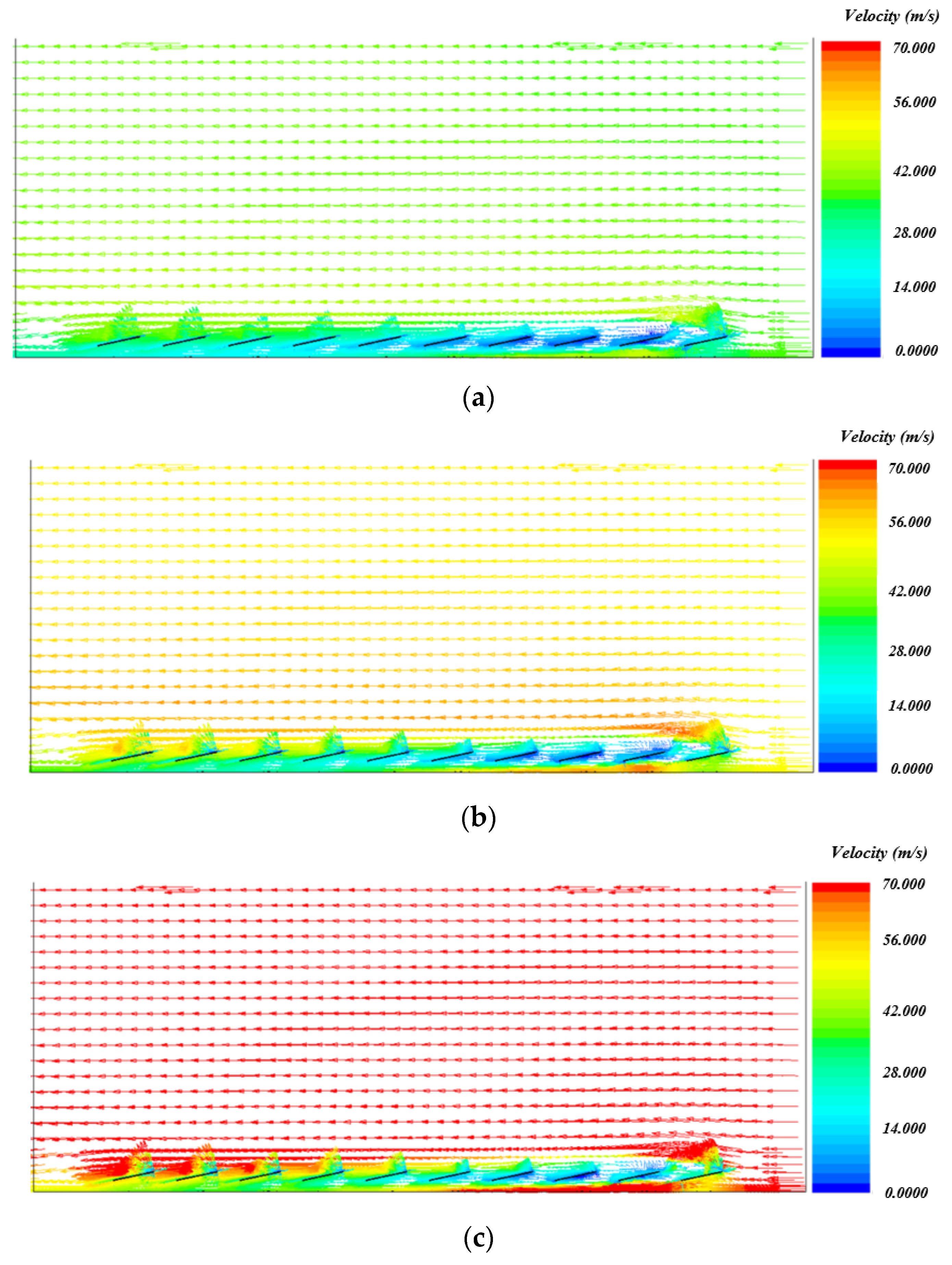
5.1. CFD Results
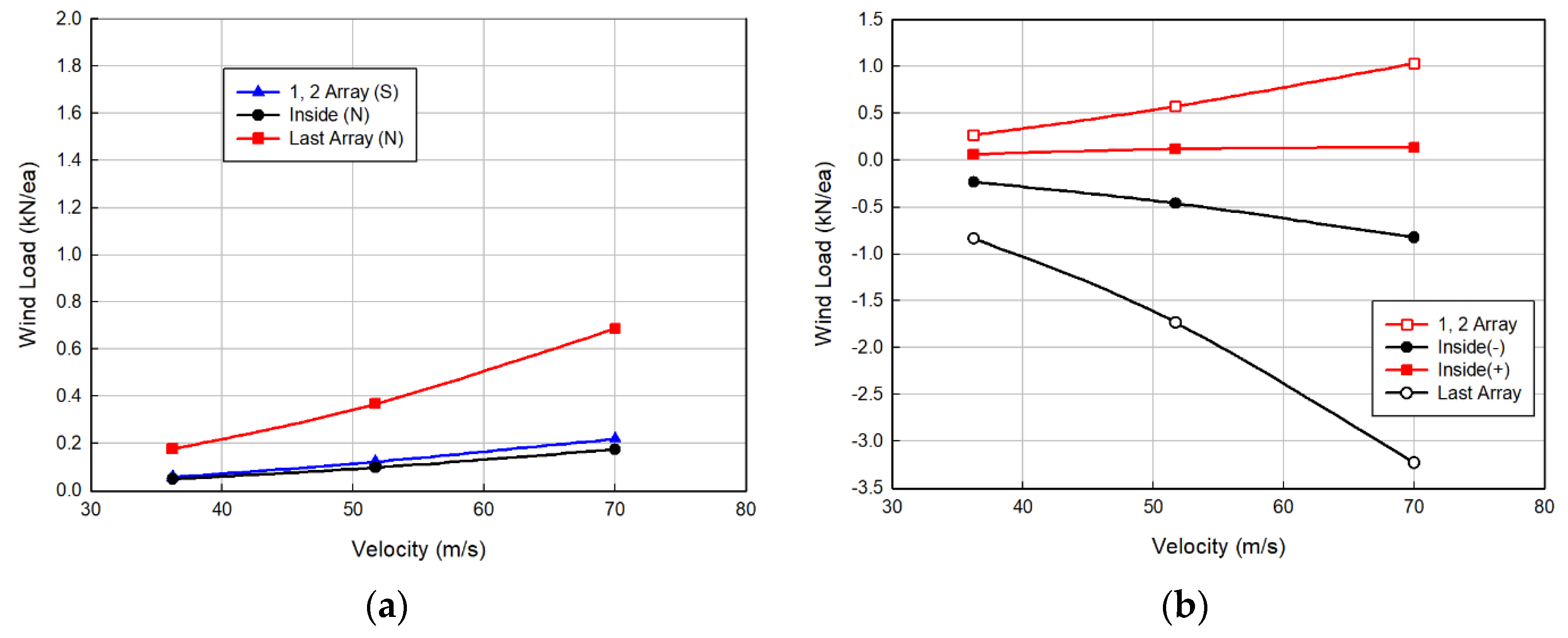
5.2. Evaluation of Wind Load Distribution
5.3. Determination of Wind Load Distribution
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yousuf, H.; Khokhar, M.Q.; Zahid, M.A.; Kim, J.; Kim, Y.; Cho, E.C.; Cho, Y.H.; Yi, J. A review on floating photovoltaic technology (FPVT). Curr. Photovolt. Res. 2020, 8, 67–78. [Google Scholar]
- Kim, S.H.; Yoon, S.J.; Choi, W.; Choi, K.B. Application of floating photovoltaic energy generation systems in South Korea. Sustainability 2016, 8, 1333. [Google Scholar] [CrossRef]
- Rosa-Clot, M.; Tina, G.M. Submerged and Floating Photovoltaic Systems: Modelling, Design and Case Studies; Academic Press: London, UK, 2017. [Google Scholar]
- Ryu, D.G.; Lee, K.B. Flow characteristics and wind loads on the solar panel and floating system of floating solar generato. J. Korea Acad.-Ind. Coop. Soc. 2019, 20, 229–235. [Google Scholar]
- Lee, C.R.; Lee, G.H.; Shim, J.Y.; Choi, D.H.; Lee, J.H. Structural safety evaluation through full modules analysis of 2 MW class floating photovoltaic power plant. J. Korean Sol. Energy Soc. 2021, 41, 109–118. [Google Scholar] [CrossRef]
- Choi, S.M.; Park, C.D.; Cho, S.H.; Lim, B.J. Effects of wind loads on the solar panel array of a floating photovoltaic system—Experimental study and economic analysis. Energy 2022, 256, 124649. [Google Scholar] [CrossRef]
- Su, K.C.; Chung, P.H.; Yang, R.Y. Numerical simulation of wind loads on an offshore PV panel: The effect of wave angle. J. Mech. 2021, 37, 53–62. [Google Scholar] [CrossRef]
- American Society of Civil Engineers. Minimum Design Loads and Associated Criteria for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2017. [Google Scholar]
- KDS 41 10 15; Load Combination. Korean Design Standard. 2019. Available online: https://www.law.go.kr/%ED%96%89%EC%A0%95%EA%B7%9C%EC%B9%99/%EA%B1%B4%EC%B6%95%EA%B5%AC%EC%A1%B0%EA%B8%B0%EC%A4%80 (accessed on 11 October 2022).
- Schellenberg, A.; Maffei, J.; Telleen, K.; Ward, R. Structural analysis and application of wind loads to solar arrays. J. Wind Eng. Ind. Aerodyn. 2013, 123, 261–272. [Google Scholar] [CrossRef]
- Kim, S.H.; Baek, S.C.; Choi, K.B.; Park, S.J. Design and installation of 500-kW floating photovoltaic structures using high-durability steel. Energies 2020, 13, 4996. [Google Scholar] [CrossRef]
- Warsido, W.P.; Bitsuamlak, G.T.; Barata, J.; Chowdhury, A.G. Influence of spacing parameters on the wind loading of solar array. J. Fluids Struct. 2014, 48, 295–315. [Google Scholar] [CrossRef]
- Wood, G.S.; Denoon, R.O.; Kwok, K.C. Wind loads on industrial solar panel arrays and supporting roof structure. Wind Struct. 2001, 4, 481–494. [Google Scholar] [CrossRef]
- Shademan, M.; Hangan, H. Wind loading on solar panels at different inclination angles. In Proceedings of the 11th Americas Conference on Wind Engineering, San Juan, PR, USA, 22–26 June 2009. [Google Scholar]
- Wu, Z.; Gong, B.; Wang, Z.; Li, Z.; Zang, C. An experimental and numerical study of the gap effect on wind load on heliostat. Renew. Energy 2010, 35, 797–806. [Google Scholar] [CrossRef]
- Choi, S.M.; Park, C.D.; Cho, S.H.; Lim, B.J. Effects of various inlet angle of wind and wave loads on floating photovoltaic system considering stress distributions. J. Clean. Prod. 2023, 387, 135876. [Google Scholar] [CrossRef]
- Kopp, G.A.; Surry, D.; Chen, K. Wind loads on a solar array. Wind Struct. 2002, 5, 393–406. [Google Scholar] [CrossRef]
- Aly, A.M. On the evaluation of wind loads on solar panels: The scale issue. Sol. Energy 2016, 135, 423–434. [Google Scholar] [CrossRef]
- Joo, H.J.; Lee, N.H.; Lee, S.W. Floating photovoltaic power generation system. Korean Soc. Adv. Compos. Struct. 2013, 4, 31–39. [Google Scholar]
- Trapani, K.; Milar, D.L. Proposing offshore photovoltaic (PV) technology to the energy mix of the Maltese islands. Energy Convers. Manag. 2013, 67, 18–26. [Google Scholar] [CrossRef]
- Dassault Systemes (DS) Sinulia Corp. ABAQUS; Dassault Systemes (DS) Sinulia Corp.: Johnston, RI, USA, 2013. [Google Scholar]



| No. | Load Combinations |
|---|---|
| 1 | 1.4 (D + F) |
| 2 | 1.2 (D + F + T) + 1.6 L + 0.5 (Lr, S, R) |
| 3 | 1.2 D + 1.6 (Lr, S, R) + (1.0 L, 0.65 W) |
| 4 | 1.2 D + 1.3 W + 1.0 L + 0.5 (Lr, S, R) |
| 5 | 0.2 D + 1.0 E + 1.0 L + 0.2 S |
| 6 | 0.9 D + 1.3 W |
| 7 | 0.9 D + 1.0 E |
| Direction | Installed Angle (Deg.) | Wind Speed (m/s) | Etc. |
|---|---|---|---|
| Forward | 12 | 36.16 | Basic wind speed 32 m/s |
| 51.74 | Basic wind speed 45 m/s | ||
| 70.00 | Recorded maximum | ||
| Backward | 36.16 | Basic wind speed 32 m/s | |
| 51.74 | Basic wind speed 45 m/s | ||
| 70.00 | Recorded maximum |
| Wind Speed (m/s) | Wind Pressure (Pa) | |
|---|---|---|
| Forward (β = 0°) | Backward (β = 180°) | |
| 36.2 | 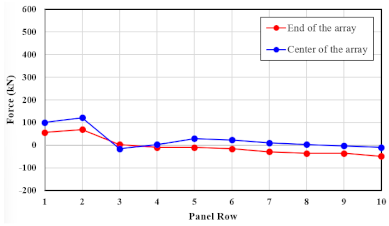 | 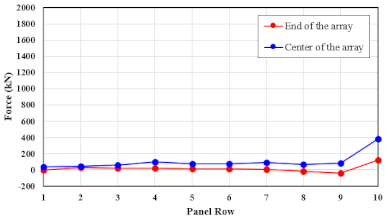 |
| 51.7 | 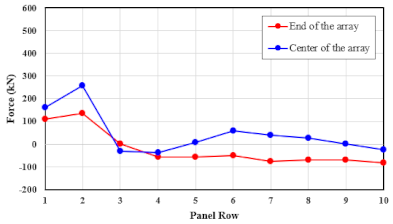 | 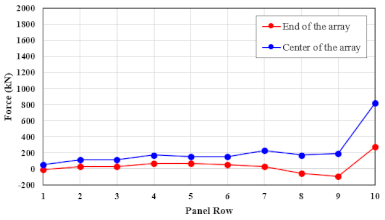 |
| 70.0 | 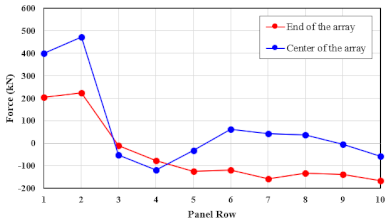 | 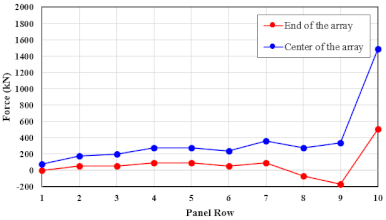 |
| Description | Wind Load (kN) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wind | Wind Speed (m/s) | Location | 1 Array | 2 Arrays | 3 Arrays | 4 Arrays | 5 Arrays | 6 Arrays | 7 Arrays | 8 Arrays | 9 Arrays | 10 Arrays |
| Forward (Horizontal) | 36.2 | Center | 0.0498 | 0.0572 | −0.0069 | 0.0009 | 0.0135 | 0.0119 | 0.0072 | 0.0038 | −0.0001 | −0.0064 |
| Edge | 0.0259 | 0.0306 | 0.0014 | −0.0031 | −0.0028 | −0.0066 | −0.0136 | −0.0151 | −0.0173 | −0.0210 | ||
| 51.7 | Center | 0.1006 | 0.1227 | −0.0125 | −0.0176 | 0.0068 | 0.0253 | 0.0178 | 0.0117 | 0.0021 | −0.0105 | |
| Edge | 0.0528 | 0.0648 | −0.0001 | −0.0241 | −0.0276 | −0.0256 | −0.0341 | −0.0314 | −0.0313 | −0.0394 | ||
| 70.0 | Center | 0.1829 | 0.2198 | −0.0229 | −0.0510 | −0.0101 | 0.0294 | 0.0230 | 0.0207 | −0.0014 | −0.0224 | |
| Edge | 0.0948 | 0.1043 | −0.0046 | −0.0343 | −0.0523 | −0.0525 | −0.0684 | −0.0612 | −0.0599 | −0.0756 | ||
| Forward (Vertical) | 36.2 | Center | 0.2345 | 0.2692 | −0.0326 | 0.0041 | 0.0634 | 0.0558 | 0.0337 | 0.0177 | −0.0003 | −0.0300 |
| Edge | 0.1218 | 0.1438 | 0.0066 | −0.0146 | −0.0134 | −0.0310 | −0.0638 | −0.0712 | −0.0815 | −0.0988 | ||
| 51.7 | Center | 0.4734 | 0.5774 | −0.0589 | −0.0830 | 0.0321 | 0.1193 | 0.0839 | 0.0551 | 0.0097 | −0.0496 | |
| Edge | 0.2485 | 0.3050 | −0.0005 | −0.1134 | −0.1300 | −0.1206 | −0.1602 | −0.1476 | −0.1473 | −0.1853 | ||
| 70.0 | Center | 0.8605 | 1.0339 | −0.1076 | −0.2398 | −0.0476 | 0.1381 | 0.1081 | 0.0973 | −0.0068 | −0.1055 | |
| Edge | 0.4461 | 0.4909 | −0.0217 | −0.1616 | −0.2459 | −0.2470 | −0.3219 | −0.2878 | −0.2820 | −0.3557 | ||
| Backward (Horizontal) | 36.2 | Center | 0.0109 | 0.0237 | 0.0274 | 0.0371 | 0.0376 | 0.0334 | 0.0492 | 0.0408 | 0.0445 | 0.1778 |
| Edge | −0.0046 | 0.0087 | 0.0107 | 0.0152 | 0.0167 | 0.0129 | 0.0137 | −0.0058 | −0.0174 | 0.0632 | ||
| 51.7 | Center | 0.0224 | 0.0472 | 0.0535 | 0.0732 | 0.0749 | 0.0660 | 0.0976 | 0.0800 | 0.0882 | 0.3680 | |
| Edge | −0.0089 | 0.0167 | 0.0198 | 0.0289 | 0.0321 | 0.0242 | 0.0276 | −0.0141 | −0.0390 | 0.1279 | ||
| 70.0 | Center | 0.0406 | 0.0851 | 0.0970 | 0.1328 | 0.1353 | 0.1179 | 0.1750 | 0.1404 | 0.1628 | 0.6864 | |
| Edge | −0.0172 | 0.0303 | 0.0356 | 0.0524 | 0.0567 | 0.0412 | 0.0458 | −0.0299 | −0.0772 | 0.2378 | ||
| Backward (Vertical) | 36.2 | Center | 0.0512 | 0.1116 | 0.1289 | 0.1745 | 0.1768 | 0.1570 | 0.2316 | 0.1918 | 0.2091 | 0.8365 |
| Edge | −0.0218 | 0.0411 | 0.0503 | 0.0715 | 0.0784 | 0.0607 | 0.0646 | −0.0274 | −0.0817 | 0.2973 | ||
| 51.7 | Center | 0.1055 | 0.2219 | 0.2517 | 0.3443 | 0.3524 | 0.3104 | 0.4594 | 0.3765 | 0.4149 | 1.7315 | |
| Edge | −0.0421 | 0.0787 | 0.0929 | 0.1358 | 0.1509 | 0.1140 | 0.1297 | −0.0664 | −0.1833 | 0.6017 | ||
| 70.0 | Center | 0.1908 | 0.4003 | 0.4567 | 0.6247 | 0.6367 | 0.5546 | 0.8235 | 0.6604 | 0.7658 | 3.2292 | |
| Edge | −0.0810 | 0.1427 | 0.1676 | 0.2463 | 0.2669 | 0.1936 | 0.2157 | −0.1409 | −0.3633 | 1.1187 | ||
| Wind Speed (m/s) | Horizontal Load (kN) | |
|---|---|---|
| Forward (β = 0°) | Backward (β = 180°) | |
| 36.2 | 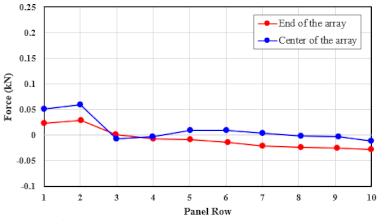 | 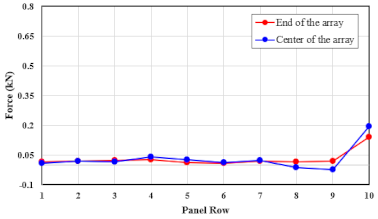 |
| 51.7 | 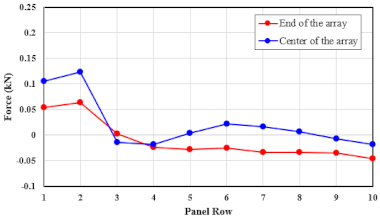 | 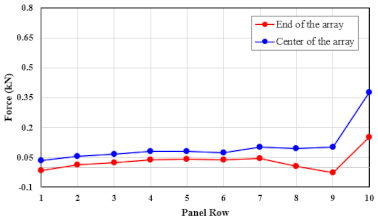 |
| 70.0 | 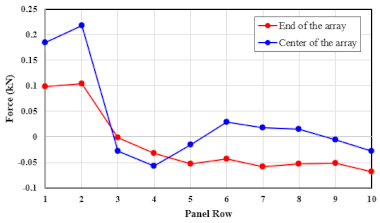 | 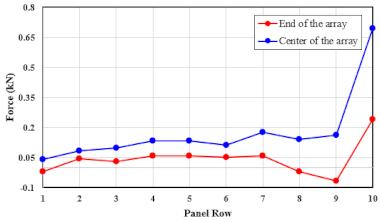 |
| Wind Speed (m/s) | Vertical Load (kN) | |
|---|---|---|
| Forward (β = 0°) | Backward (β = 180°) | |
| 36.2 |  | 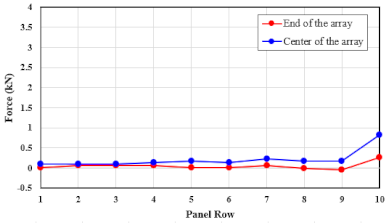 |
| 51.7 | 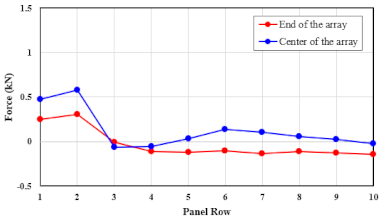 | 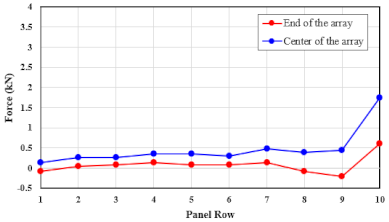 |
| 70.0 | 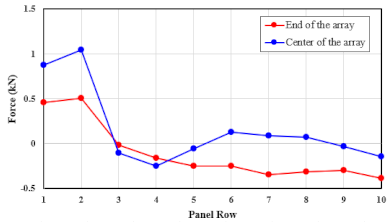 |  |
| Wind Speed (m/s) | Wind Load (kN) | ||
|---|---|---|---|
| Array 1 (A1) and Array 2 (A2) | From Array 3 (A3)~End | ||
| Horizontal direction | 36.2 | 0.0572 | 0.0135 |
| 51.7 | 0.1227 | 0.0253 | |
| 70.0 | 0.2198 | 0.0294 | |
| Vertical direction | 36.2 | 0.2692 | 0.0634 |
| 51.7 | 0.5774 | 0.119 | |
| 70.0 | 1.0339 | 0.1381 | |
| Wind Speed (m/s) | Wind Load (kN) | ||
|---|---|---|---|
| Array 1 (A1) | From Array 2 (A2)~End | ||
| Horizontal direction | 36.2 | 0.1778 | 0.0492 |
| 51.7 | 0.3680 | 0.0976 | |
| 70.0 | 0.6864 | 0.1750 | |
| Vertical direction | 36.2 | 0.8365 | 0.2316 |
| 51.7 | 1.7315 | 0.4595 | |
| 70.0 | 3.2292 | 0.8235 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joo, H.-J.; Heo, S.-J.; Kim, S.-H.; Choi, W. Wind Load Distribution in Float Photovoltaic System. Appl. Sci. 2023, 13, 12144. https://doi.org/10.3390/app132212144
Joo H-J, Heo S-J, Kim S-H, Choi W. Wind Load Distribution in Float Photovoltaic System. Applied Sciences. 2023; 13(22):12144. https://doi.org/10.3390/app132212144
Chicago/Turabian StyleJoo, Hyung-Joong, Seong-Jun Heo, Sun-Hee Kim, and Wonchang Choi. 2023. "Wind Load Distribution in Float Photovoltaic System" Applied Sciences 13, no. 22: 12144. https://doi.org/10.3390/app132212144
APA StyleJoo, H.-J., Heo, S.-J., Kim, S.-H., & Choi, W. (2023). Wind Load Distribution in Float Photovoltaic System. Applied Sciences, 13(22), 12144. https://doi.org/10.3390/app132212144






