Saturation-Based Airlight Color Restoration of Hazy Images
Abstract
:1. Introduction
2. Dehazing for Color Restoration
2.1. Atmospheric Scattering Model
2.2. Gray World Hypothesis

2.3. Gray World Hypothesis in the LAB Color Space
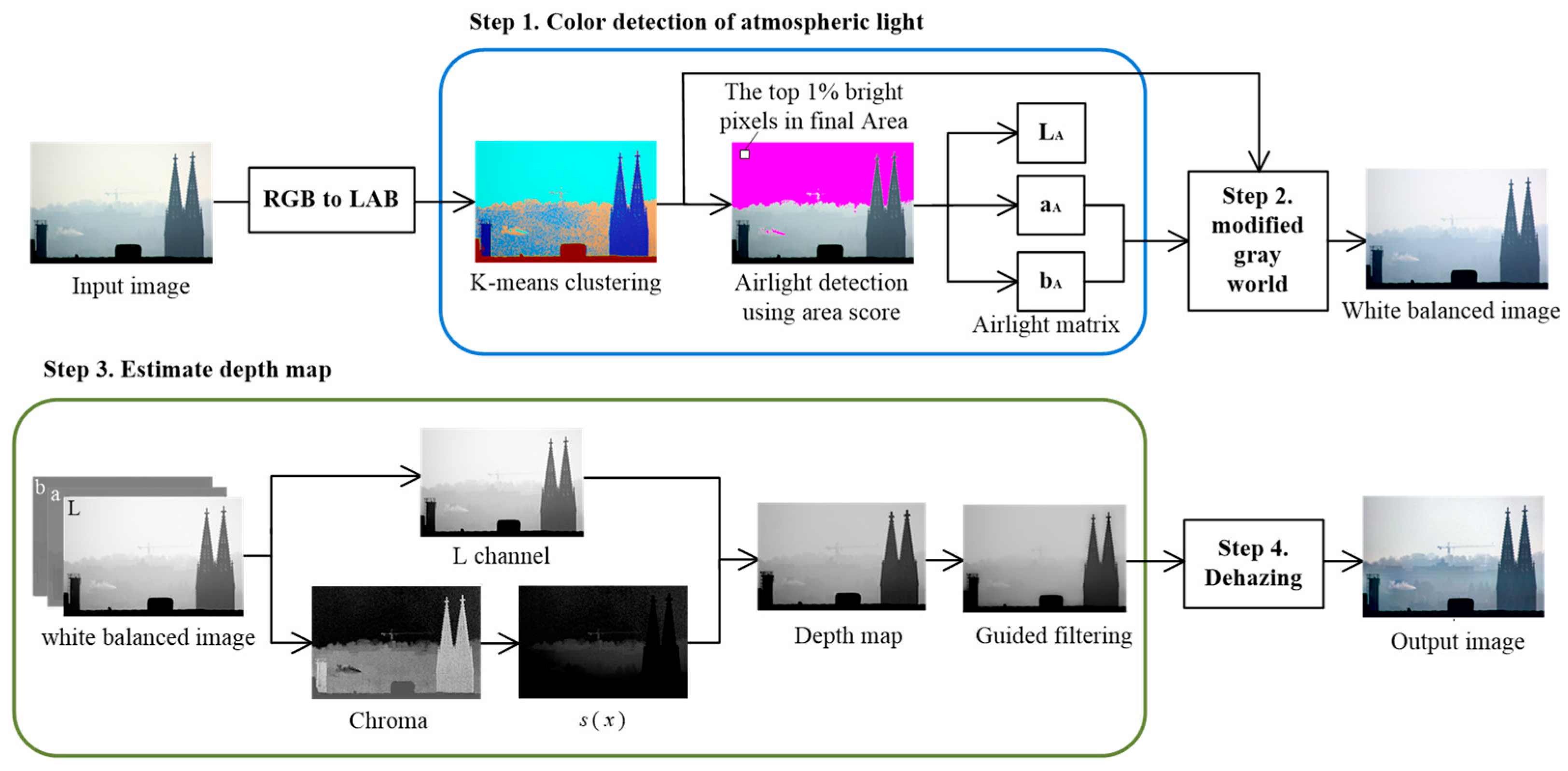
3. Proposed Dehazing Method
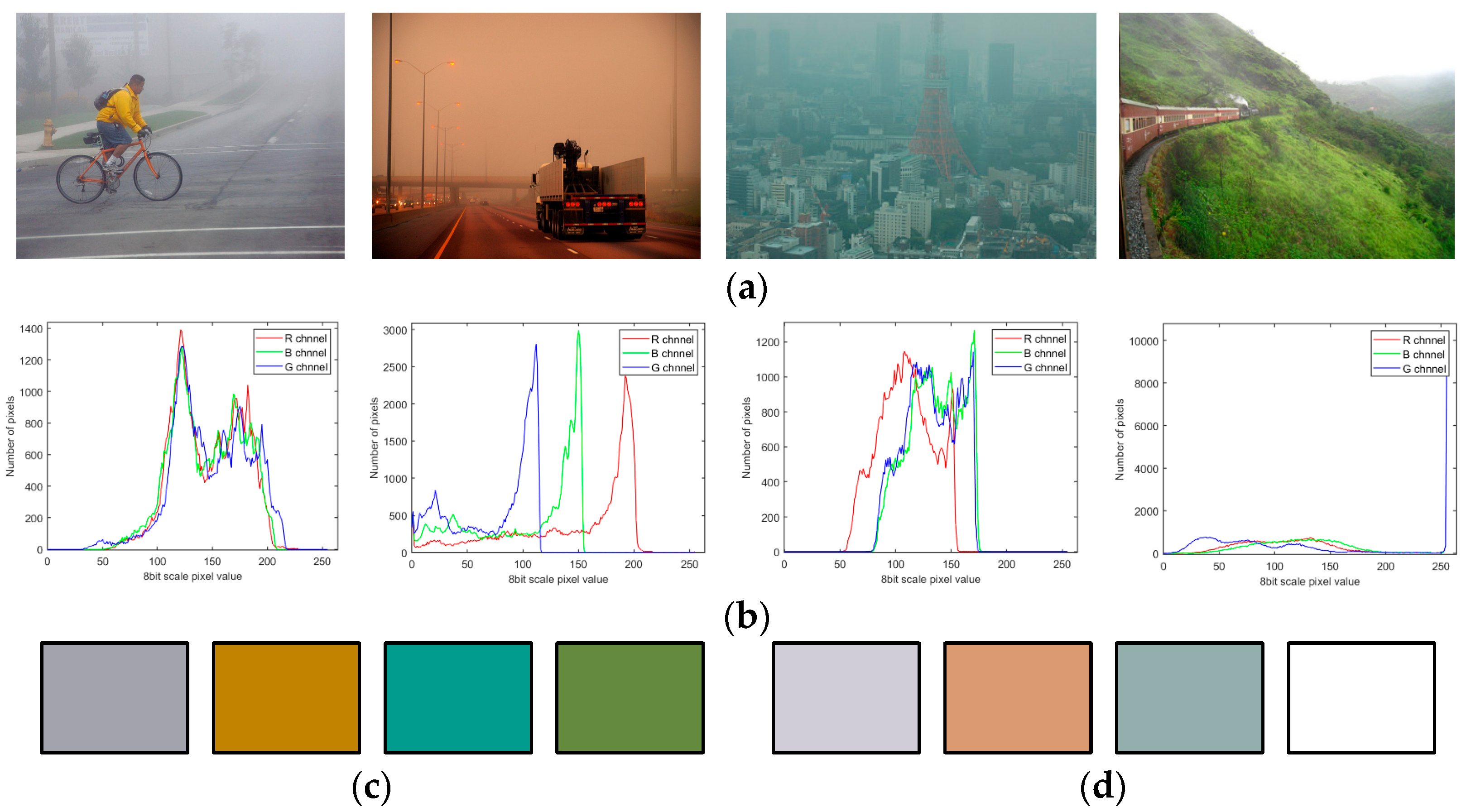
3.1. Extraction of Color Components in Airlight
- In most cases, the number of dominant colors is between 3 and 6.
- High saturation colors are often selected, with the most vivid colors almost always being chosen.
- The color that occupies the largest area is almost always chosen, regardless of its conspicuousness.
- When multiple colors are somewhat conspicuous, there is a greater likelihood that other colors will be chosen.
- Colors that differ significantly from the surrounding environment are more likely to be chosen.

3.1.1. Execution of the LAB Color Space Conversion Equation
3.1.2. Division of the Image Using K-Means Clustering
- The whole LAB color image from Equation (7) is used as the input image.
- The number of clusters “k” is set to 6 for better separation of bright objects.
- The number of repetitions is 3, which is the default value of the algorithm.
- K-means is initialized using cluster centroid initialization and the squared Euclidean distance measurement method.
3.1.3. Airlight Extraction Based on Area Scores
3.2. Improved Haze Color Correction Based on the Gray World Hypothesis
3.3. Depth Map Setting Based on Luminance and Saturation
3.3.1. Depth Map of Haze Based on Existing Studies
| Algorithm 1. Parameter estimation algorithm using multilinear regression. |
| Input dataset |
| Depth map: 450 depth map datasets on NYU ground truth images |
| L, C, a, b: 450 L, , a, b channel NYU images calculated from Section 3.1.1 |
| Output: for parameters , , , and the normal distribution of the residual zone |
| Begin |
| for index = 1:450 |
| Constant matrix with its component only at x1 = 1; x2 = L(index); x3 = C(index); |
| X = [x1 x2 x3]; Y = depth map(index); |
| Perform the multilateral regression algorithm using X as the input and Y as the output. |
| Enter the parameter and scattering of the corresponding index output to the 1, 2, 3, 4 |
| columns of the output matrix . |
| End |
| If a value with exists, the corresponding data are deleted. |
| Calculate the average of the final data on the output , and , , , . |
| End |
3.3.2. Depth Map with the Saturation Weight
- Retrieve the L, a, and b channels of the image resulting from the restoration presented in Section 3.2 and define their pixel values as , , and .
- is applied to the Gaussian distribution model of Equation (15), , to produce the random error to each location .
- Enter these into Equation (17) using , , , and to estimate , the depth map to which the weighting value of saturation is applied.
- To solve the noise of the saturation map, filtering is performed using the guide filter on .
3.4. Dehazing
4. Experimental Results and Discussions
4.1. Visual Comparison of Various Hazy Images






| Image | HRDCP | NGCCLAHE | WSDACC | Proposed | |
|---|---|---|---|---|---|
| e | Test 1 | 0.0488 | 0.0738 | 0.0669 | 0.1049 |
| Test 2 | 0.1016 | 0.1186 | −0.1143 | 0.1220 | |
| Test 3 | 0.4725 | 0.3975 | 0.0997 | 0.5101 | |
| Test 4 | 0.0583 | 0.0864 | −0.0107 | 0.0723 | |
| Test 5 | 0.4270 | 0.3816 | 0.0155 | 0.3979 | |
| Average | 0.2217 | 0.2116 | 0.0114 | 0.2415 | |
| Test 1 | 2.2533 | 1.7719 | 0.4047 | 1.3618 | |
| Test 2 | 2.9243 | 2.1153 | 1.6180 | 1.3698 | |
| Test 3 | 2.2332 | 1.7682 | 0.9952 | 1.5707 | |
| Test 4 | 2.4951 | 1.9173 | 1.0384 | 1.3632 | |
| Test 5 | 2.7109 | 1.9456 | 0.7972 | 1.6737 | |
| Average | 2.5233 | 1.9036 | 0.9707 | 1.4678 | |
| FRF | Test 1 | 0.3485 | 0.4788 | −0.0226 | 0.4585 |
| Test 2 | 0.0888 | 0.1256 | −0.2988 | 0.1285 | |
| Test 3 | 0.0783 | 0.0237 | 0.0349 | 0.1731 | |
| Test 4 | 0.3383 | 0.3456 | −0.0530 | 0.3544 | |
| Test 5 | 0.5303 | 0.4742 | −0.0401 | 0.5797 | |
| Average | 0.2768 | 0.2896 | −0.0759 | 0.3388 | |
| PIQE | Test 1 | 44.4367 | 46.4053 | 50.2147 | 40.1527 |
| Test 2 | 40.0996 | 35.7676 | 31.8466 | 29.2613 | |
| Test 3 | 43.7708 | 42.1776 | 35.8692 | 40.3450 | |
| Test 4 | 44.0385 | 42.1096 | 42.0236 | 36.5857 | |
| Test 5 | 26.1658 | 30.8974 | 38.2872 | 25.0304 | |
| Average | 39.7023 | 39.4715 | 39.6483 | 34.2750 |
4.2. Performance Evaluation Using Ground Truth Image

| Image | HRDCP | NGCCLAHE | WSDACC | Proposed | |
|---|---|---|---|---|---|
| PSNR | Column 1 | 25.6801 | 27.6232 | 12.9887 | 29.3583 |
| Column 2 | 18.3533 | 20.6083 | 13.9061 | 21.9567 | |
| Column 3 | 18.5879 | 24.1812 | 14.3154 | 25.4478 | |
| Column 4 | 30.8870 | 30.2614 | 13.8340 | 31.8312 | |
| Column 5 | 18.8900 | 19.9033 | 15.2217 | 21.8796 | |
| Column 6 | 17.9036 | 16.6909 | 13.6151 | 18.6536 | |
| Column 7 | 21.8741 | 22.5892 | 12.3425 | 23.5417 | |
| Column 8 | 23.6716 | 23.1715 | 14.6542 | 24.4558 | |
| Average | 21.9810 | 23.1286 | 13.8597 | 24.6406 | |
| CIEDE 2000 | Column 1 | 65.0429 | 58.3551 | 68.994 | 55.5198 |
| Column 2 | 80.8358 | 83.0109 | 101.178 | 70.1804 | |
| Column 3 | 71.6801 | 64.0757 | 83.9369 | 59.0298 | |
| Column 4 | 62.8703 | 60.0154 | 102.421 | 44.4957 | |
| Column 5 | 87.177 | 86.2875 | 86.9605 | 67.5862 | |
| Column 6 | 73.3669 | 74.9258 | 88.2843 | 71.7223 | |
| Column 7 | 67.9032 | 70.0154 | 97.6982 | 57.9881 | |
| Column 8 | 73.1579 | 75.1231 | 84.7146 | 62.4879 | |
| Average | 72.75426 | 71.47611 | 89.27344 | 61.12628 | |
| CIE94 | Column 1 | 40.996 | 37.9644 | 61.1512 | 35.6449 |
| Column 2 | 56.8746 | 54.1844 | 64.2783 | 51.4884 | |
| Column 3 | 55.6438 | 47.5759 | 64.1364 | 46.0510 | |
| Column 4 | 38.7339 | 39.17 | 62.4296 | 37.1594 | |
| Column 5 | 55.4124 | 53.6296 | 59.5817 | 43.9504 | |
| Column 6 | 57.1691 | 57.7260 | 64.5412 | 54.5976 | |
| Column 7 | 50.4363 | 47.0993 | 64.8543 | 45.4348 | |
| Column 8 | 46.5830 | 45.4304 | 59.5978 | 43.7097 | |
| Average | 50.2311 | 47.8475 | 62.5713 | 44.7545 |


| Image | HRDCP | NGCCLAHE | WSDACC | Proposed | |
|---|---|---|---|---|---|
| PSNR | Column 1 | 25.4914 | 34.3623 | 25.8197 | 39.6625 |
| Column 2 | 29.1756 | 35.6395 | 15.9377 | 43.3597 | |
| Column 3 | 26.6413 | 32.1664 | 26.1565 | 35.7555 | |
| Column 4 | 28.0609 | 39.7892 | 41.5410 | 55.1319 | |
| Column 5 | 24.4291 | 33.0331 | 14.5984 | 39.0183 | |
| Average | 26.7597 | 34.9981 | 24.8107 | 42.5856 | |
| CIEDE 2000 | Column 1 | 65.7187 | 57.9394 | 74.5331 | 49.2308 |
| Column 2 | 57.8792 | 53.9991 | 104.156 | 32.3133 | |
| Column 3 | 56.3077 | 56.0603 | 56.4345 | 46.6211 | |
| Column 4 | 65.2795 | 59.8458 | 50.2132 | 38.6987 | |
| Column 5 | 57.8297 | 55.5612 | 85.6416 | 47.3394 | |
| Average | 60.6029 | 56.6812 | 74.1957 | 42.8407 | |
| CIE94 | Column 1 | 45.5594 | 34.8882 | 44.2823 | 30.2724 |
| Column 2 | 45.5774 | 38.5965 | 63.0140 | 29.9591 | |
| Column 3 | 43.8257 | 36.1606 | 42.5899 | 31.0338 | |
| Column 4 | 44.7354 | 32.1035 | 32.3704 | 21.3600 | |
| Column 5 | 49.3693 | 38.4082 | 61.5174 | 31.1818 | |
| Average | 45.8134 | 36.0314 | 48.7548 | 28.7614 |
| Image | HRDCP | NGCCLAHE | WSDACC | Proposed | |
|---|---|---|---|---|---|
| Dense-HAZE | Column 1 | 0.1627 | 3.5735 | 0.3697 | |
| Column 2 | 0.2981 | 7.1377 | 0.7203 | ||
| Column 3 | 0.4315 | 10.7535 | 1.0884 | ||
| Column 4 | 0.5636 | 14.5247 | 1.4456 | ||
| Column 5 | 0.7025 | 18.1768 | 1.8046 | ||
| Average | 0.4317 | 10.8332 | 1.0857 | ||
| O-HAZE | Column 1 | 0.1963 | 4.5718 | 0.4331 | |
| Column 2 | 0.3885 | 9.0356 | 0.8792 | ||
| Column 3 | 0.6069 | 13.4543 | 1.3217 | ||
| Column 4 | 0.8094 | 17.9645 | 1.7932 | ||
| Column 5 | 1.0060 | 22.4588 | 2.2431 | ||
| Column 6 | 1.1899 | 27.0179 | 2.6768 | ||
| Column 7 | 1.3723 | 31.4922 | 3.1199 | ||
| Column 8 | 1.5712 | 36.0234 | 3.5757 | ||
| Average | 0.8926 | 20.2523 | 2.0053 |
4.3. Limitations and Discussion of the Proposed Approach
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, K.; Sun, J.; Tang, X. Single image haze removal using dark channel prior. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2341–2353. [Google Scholar]
- Tarel, J.P.; Hauti, N. Fast visibility restoration from a single color or gray level image. In Proceedings of the IEEE International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2201–2208. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, J.; Zhu, Z.; Yao, W.; Wu, S. Weighted guided image filtering. IEEE Trans. Image Process. 2015, 24, 120–129. [Google Scholar]
- Zhu, Q.; Mai, J.; Shao, L. A fast single image haze removal algorithm using color attenuation prior. IEEE Trans. Image Process. 2015, 24, 3522–3533. [Google Scholar]
- Gao, Y.; Hu, H.M.; Li, B.; Guo, Q.; Pu, S. Detail preserved single image dehazing algorithm based on airlight refinement. IEEE Trans. Multimed. 2019, 21, 351–362. [Google Scholar] [CrossRef]
- Berman, D.; Treibitz, T.; Avidan, S. Single image dehazing using haze-lines. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 720–734. [Google Scholar] [CrossRef]
- Lee, S.M.; Kang, B.S. A 4K-capable hardware accelerator of haze removal algorithm using haze-relevant features. J. Inf. Commun. Converg. Eng. 2022, 20, 212–218. [Google Scholar] [CrossRef]
- Cheon, B.W.; Kim, N.H. A modified steering kernel filter for AWGN removal based on kernel similarity. J. Inf. Commun. Converg. Eng. 2022, 20, 195–203. [Google Scholar] [CrossRef]
- Huang, S.C.; Chen, B.H.; Wang, W.J. Visibility restoration of single hazy images captured in real-world weather conditions. IEEE Trans. Circuits Syst. Video Technol. 2014, 24, 1814–1824. [Google Scholar] [CrossRef]
- Dhara, S.K.; Roy, M.; Sen, D.; Biswas, P.K. Color cast dependent image dehazing via adaptive airlight refinement and non-linear color balancing. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 2076–2081. [Google Scholar] [CrossRef]
- Peng, Y.T.; Lu, Z.; Cheng, F.C.; Zheng, Y.; Huang, S.C. Image haze removal using airlight white correction, local light filter, and aerial perspective prior. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 1385–1395. [Google Scholar] [CrossRef]
- Harald, K. Theorie der Horizontalen Sichtweite: Kontrast und Sichtweite; Keim and Nemnich: Munich, Germany, 1924; Volume 12, pp. 33–53. [Google Scholar]
- Narasimhan, S.G.; Nayar, S.K. Vision and the atmosphere. Int. J. Comput. Vis. 2002, 48, 233–254. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, D.; Ren, W.; Zhang, W. Auto color correction of underwater images utilizing depth information. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1504805. [Google Scholar] [CrossRef]
- Wang, K.; Shen, L.; Lin, Y.; Li, M.; Zhao, Q. Joint iterative color correction and dehazing for underwater image enhancement. IEEE Robot. Autom. Lett. 2021, 6, 5121–5128. [Google Scholar] [CrossRef]
- Li, H.; Zhuang, P.; Wei, W.; Li, J. Underwater image enhancement based on dehazing and color correction. In Proceedings of the IEEE International Conference on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking, Xiamen, China, 16–18 December 2019; pp. 1365–1370. [Google Scholar]
- Li, C.Y.; Guo, J.C.; Cong, R.M.; Pang, Y.W.; Wang, B. Underwater image enhancement by dehazing with minimum information loss and histogram distribution prior. IEEE Trans. Image Process. 2016, 25, 5664–5677. [Google Scholar] [CrossRef]
- Gao, G.; Lai, H.; Jia, Z.; Liu, Y.; Wang, Y. Sand-dust image restoration based on reversing the blue channel prior. IEEE Photonics J. 2020, 12, 2. [Google Scholar] [CrossRef]
- Shi, Z.; Feng, Y.; Zhao, M.; Zhang, E.; He, L. Let you see in sand dust weather: A method based on halo-reduced dark channel prior dehazing for sand-dust image enhancement. IEEE Access 2019, 7, 116722–116733. [Google Scholar] [CrossRef]
- Shi, Z.; Feng, Y.; Zhao, M.; Zhang, E.; He, L. Normalised gamma transformation-based contrast-limited adaptive histogram equalisation with colour correction for sand–dust image enhancement. IET Image Process. 2020, 14, 747–756. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Y.; Fu, X. An image dehazing approach with adaptive color constancy for poor visible conditions. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6504105. [Google Scholar] [CrossRef]
- Zuiderveld, K.J. Contrast limited adaptive histogram equalization. In Graphics Gems, 4th ed.; Academic Press Professional, Inc.: Cambridge, MA, USA, 1994; pp. 474–485. [Google Scholar]
- Gautam, S.; Gandhi, T.K.; Panigrahi, B.K. An improved air-light estimation scheme for single haze images using color constancy prior. IEEE Signal Process. Lett. 2020, 27, 1695–1699. [Google Scholar] [CrossRef]
- Lam, E.Y. Combining gray world and retinex theory for automatic white balance in digital photography. In Proceedings of the Ninth International Symposium on Consumer Electronics, Macau, China, 14–16 June 2005; pp. 134–139. [Google Scholar]
- Provenzi, E.; Gatta, C.; Fierro, M.; Rizzi, A. A spatially variant white-patch and gray-world method for color image enhancement driven by local contrast. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1757–1770. [Google Scholar] [CrossRef]
- Chang, H.; Fried, O.; Liu, Y.; DiVerdi, S.; Finkelstein, A. Palette-based photo recoloring. ACM Trans. Graph. 2015, 34, 139. [Google Scholar] [CrossRef]
- Akimoto, N.; Zhu, H.; Jin, Y.; Aoki, Y. Fast soft color segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8277–8286. [Google Scholar]
- Chang, Y.; Mukai, N. Color feature based dominant color extraction. IEEE Access 2022, 10, 93055–93061. [Google Scholar] [CrossRef]
- Kim, J.H.; Jang, W.D.; Sim, J.Y.; Kim, C.S. Optimized contrast enhancement for real-time image and video dehazing. J. Vis. Commun. Image Represent. 2013, 24, 410–425. [Google Scholar] [CrossRef]
- Liu, L.; Cheng, G.; Zhu, J. Improved single haze removal algorithm based on color attenuation prior. In Proceedings of the IEEE 2nd International Conference on Information Technology, Big Data and Artificial Intelligence, Chongqing, China, 17–19 December 2021; pp. 1166–1170. [Google Scholar]
- Wu, Q.; Ren, W.; Cao, X. Learning interleaved cascade of shrinkage fields for joint image dehazing and denoising. IEEE Trans. Image Process. 2020, 29, 1788–1801. [Google Scholar] [CrossRef]
- Ancuti, C.; Ancuti, C.O.; De Vleeschouwer, C. D-HAZY: A dataset to evaluate quantitatively dehazing algorithms. In Proceedings of the IEEE International Conference on Image Processing, Phoenix, AZ, USA, 25–28 September 2016; pp. 2226–2230. [Google Scholar]
- Choi, L.K.; You, J.; Bovik, A.C. Referenceless perceptual image defogging. In Proceedings of the Southwest Symposium on Image Analysis and Interpretation, San Diego, CA, USA, 6–8 April 2014; pp. 165–168. [Google Scholar]
- IEEE Dataport. Sand Dust Image Data. 2020. Available online: https://ieee-dataport.org/documents/sand-dust-image-data (accessed on 19 September 2023).
- Hautière, N.; Tarel, J.P.; Aubert, D.; Dumont, É. Blind contrast enhancement assessment by gradient ratioing at visible edges. Image Anal. Stereol. 2011, 27, 87–95. [Google Scholar] [CrossRef]
- Kansal, I.; Kasana, S.S. Improved color attenuation prior based image de-fogging technique. Multimed. Tools Appl. 2020, 79, 12069–12091. [Google Scholar] [CrossRef]
- Venkatanath, N.; Praneeth, D.; Bh, M.C.; Channappayya, S.S.; Medasani, S.S. Blind image quality evaluation using perception based features. In Proceedings of the 2015 Twenty First National Conference on Communications, Mumbai, India, 27 February–1 March 2015; pp. 1–6. [Google Scholar]
- Sharma, G.; Wu, W.; Dalal, E.N. The CIEDE2000 color-difference formula: Implementation notes, supplementary test data, and mathematical observations. Color Res. Appl. 2005, 30, 21–30. [Google Scholar] [CrossRef]
- McDonald, R.; Smith, K.J. CIE94-a new colour-difference formula. J. Soc. Dye Colour 2008, 111, 376–379. [Google Scholar] [CrossRef]
- Ancuti, C.O.; Ancuti, C.; Sbert, M.; Timofte, R. Dense-Haze: A Benchmark for image dehazing with Dense-Haze and haze-free images. In Proceedings of the IEEE International Conference on Image Processing, Taipei, Taiwan, 22–25 September 2019; pp. 1014–1018. [Google Scholar]
- Ancuti, C.O.; Ancuti, C.; Timofte, R.; Vleeschouwer, C.D. O-HAZE: A dehazing benchmark with real hazy and haze-free Outdoor Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 867–875. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, Y.-S.; Kim, N.-H. Saturation-Based Airlight Color Restoration of Hazy Images. Appl. Sci. 2023, 13, 12186. https://doi.org/10.3390/app132212186
Chung Y-S, Kim N-H. Saturation-Based Airlight Color Restoration of Hazy Images. Applied Sciences. 2023; 13(22):12186. https://doi.org/10.3390/app132212186
Chicago/Turabian StyleChung, Young-Su, and Nam-Ho Kim. 2023. "Saturation-Based Airlight Color Restoration of Hazy Images" Applied Sciences 13, no. 22: 12186. https://doi.org/10.3390/app132212186
APA StyleChung, Y.-S., & Kim, N.-H. (2023). Saturation-Based Airlight Color Restoration of Hazy Images. Applied Sciences, 13(22), 12186. https://doi.org/10.3390/app132212186






