Methodology for CubeSat Debris Collision Avoidance Based on Its Active ADCS System
Abstract
:1. Introduction
2. State of the Art
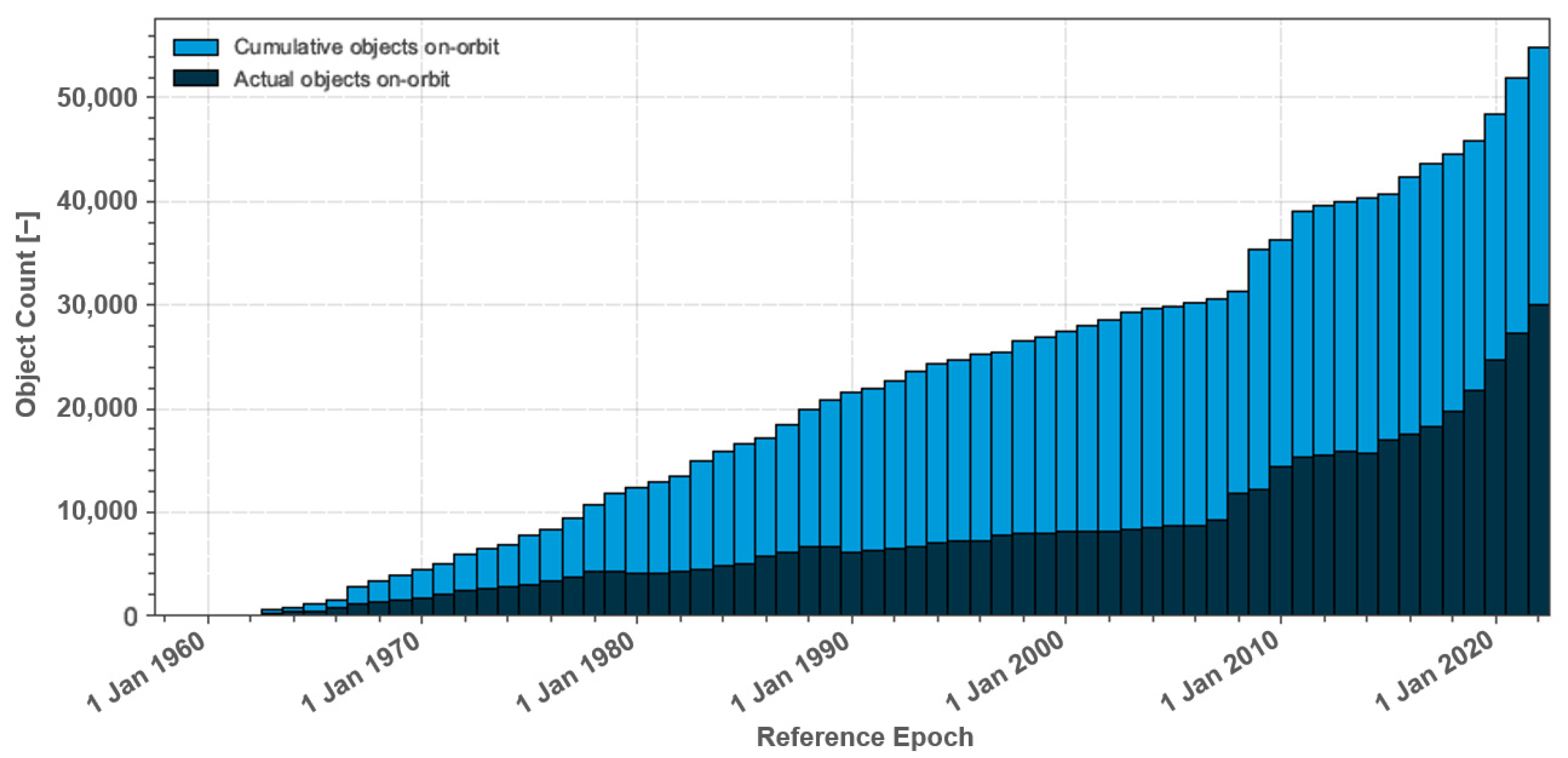
2.1. Space Debris
2.2. International Committees on Space Debris
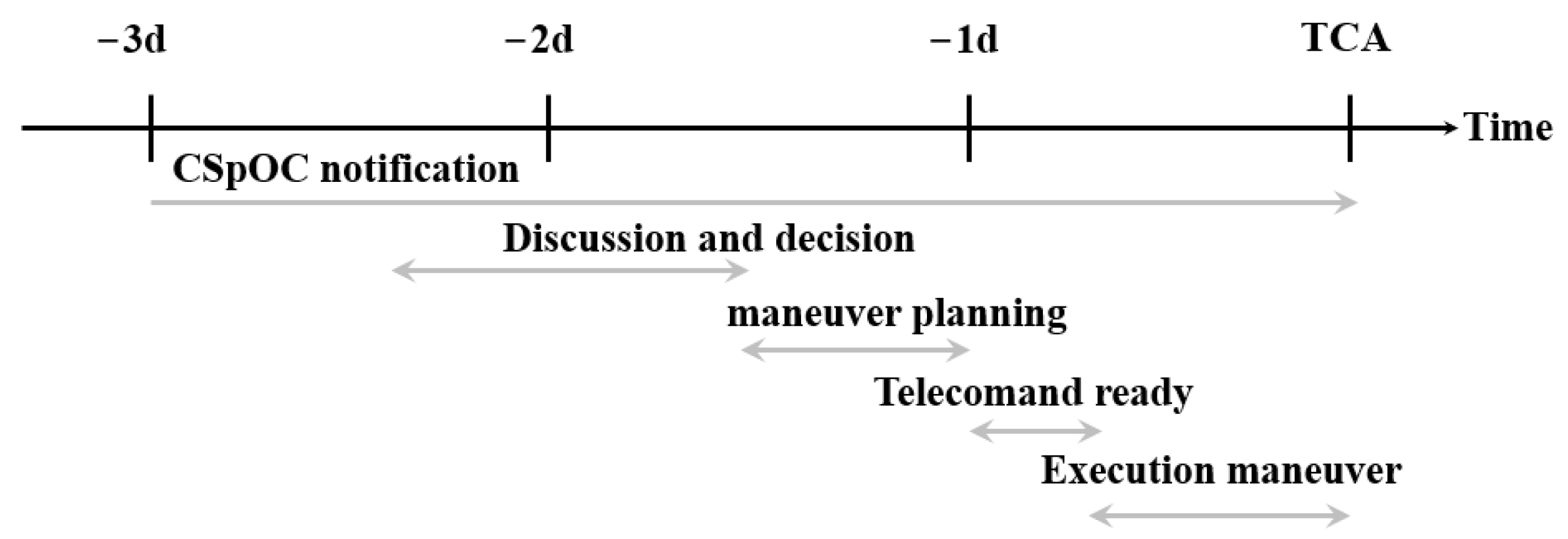
2.3. Collision Avoidance
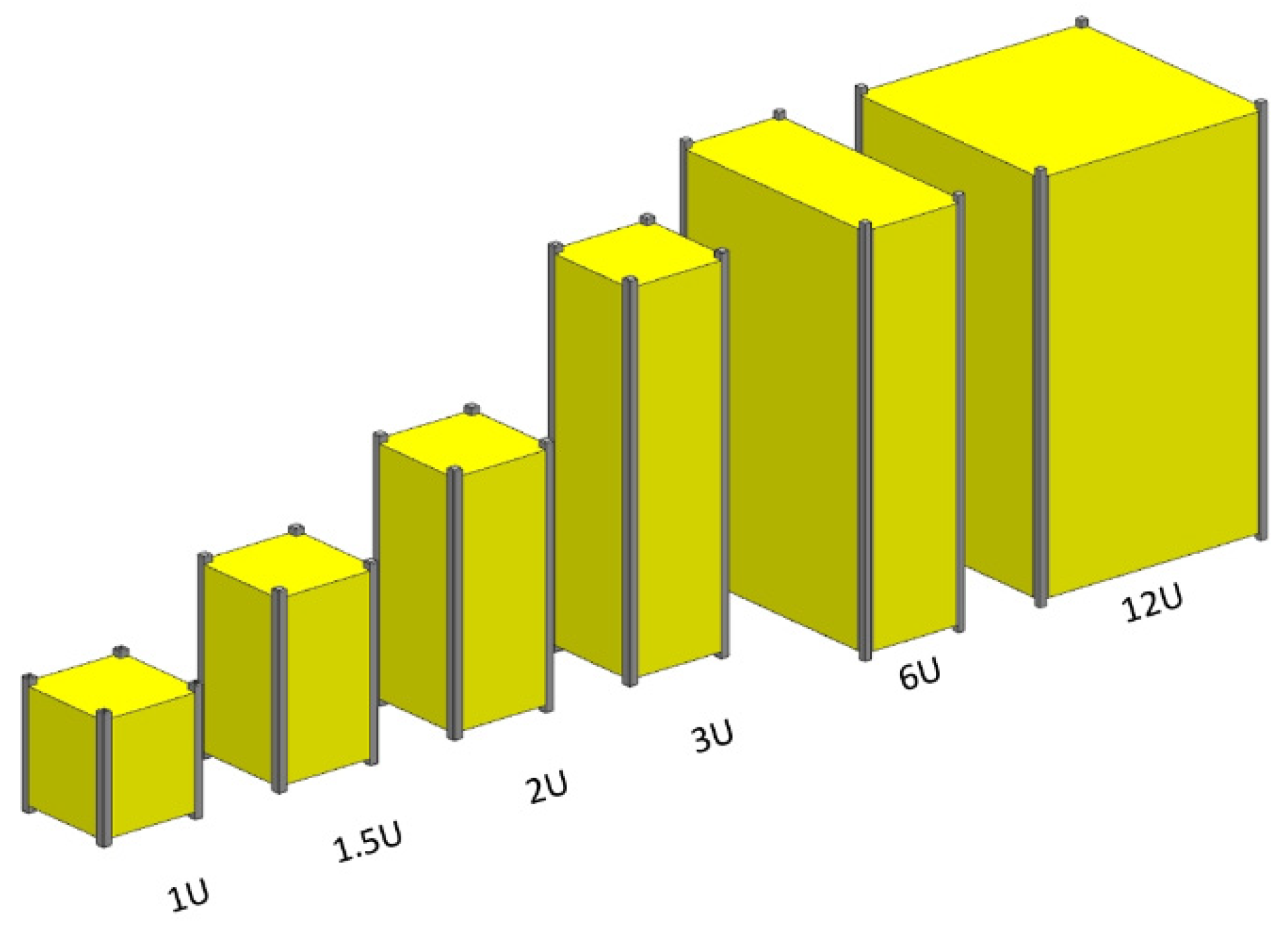
2.4. CubeSats and Space Debris
2.5. STK Software
2.6. Attitude Determination and Control Systems
3. Materials and Methods
3.1. LUME CubeSat
3.2. ADCS System
3.3. Control Algorithm
4. Results and Discussion
4.1. Distances Calculation
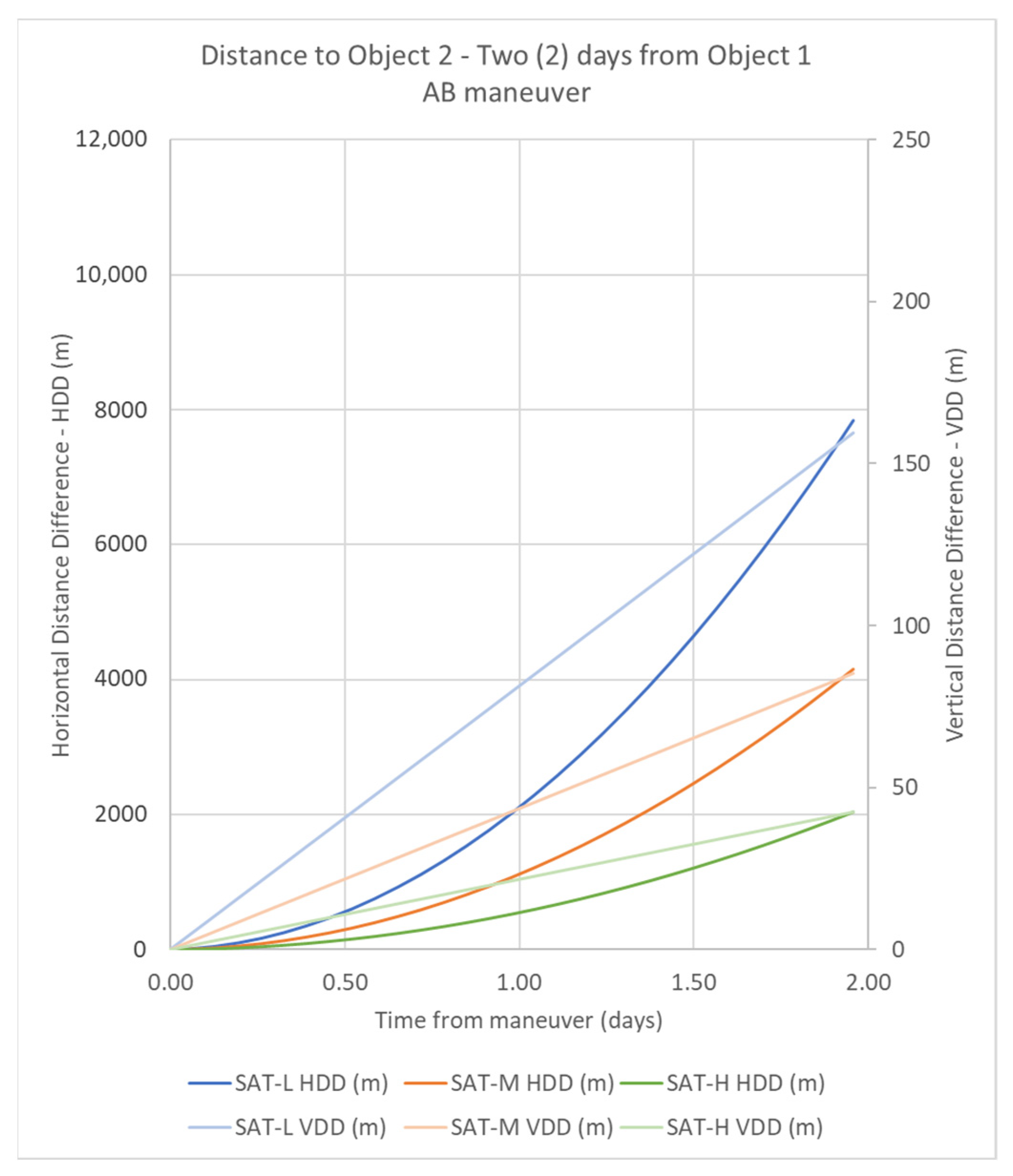
4.1.1. Maneuver AB
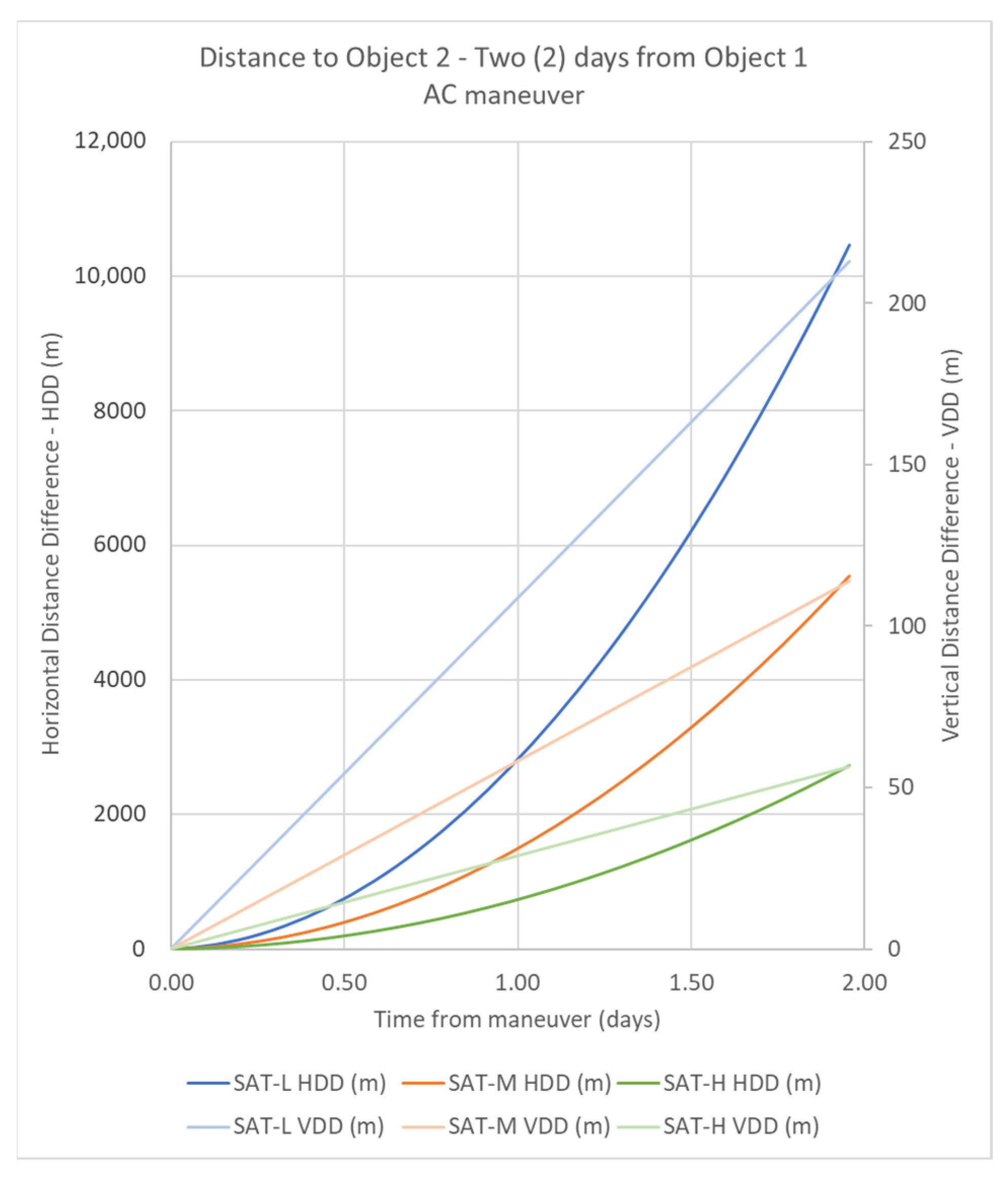
4.1.2. Maneuver AC
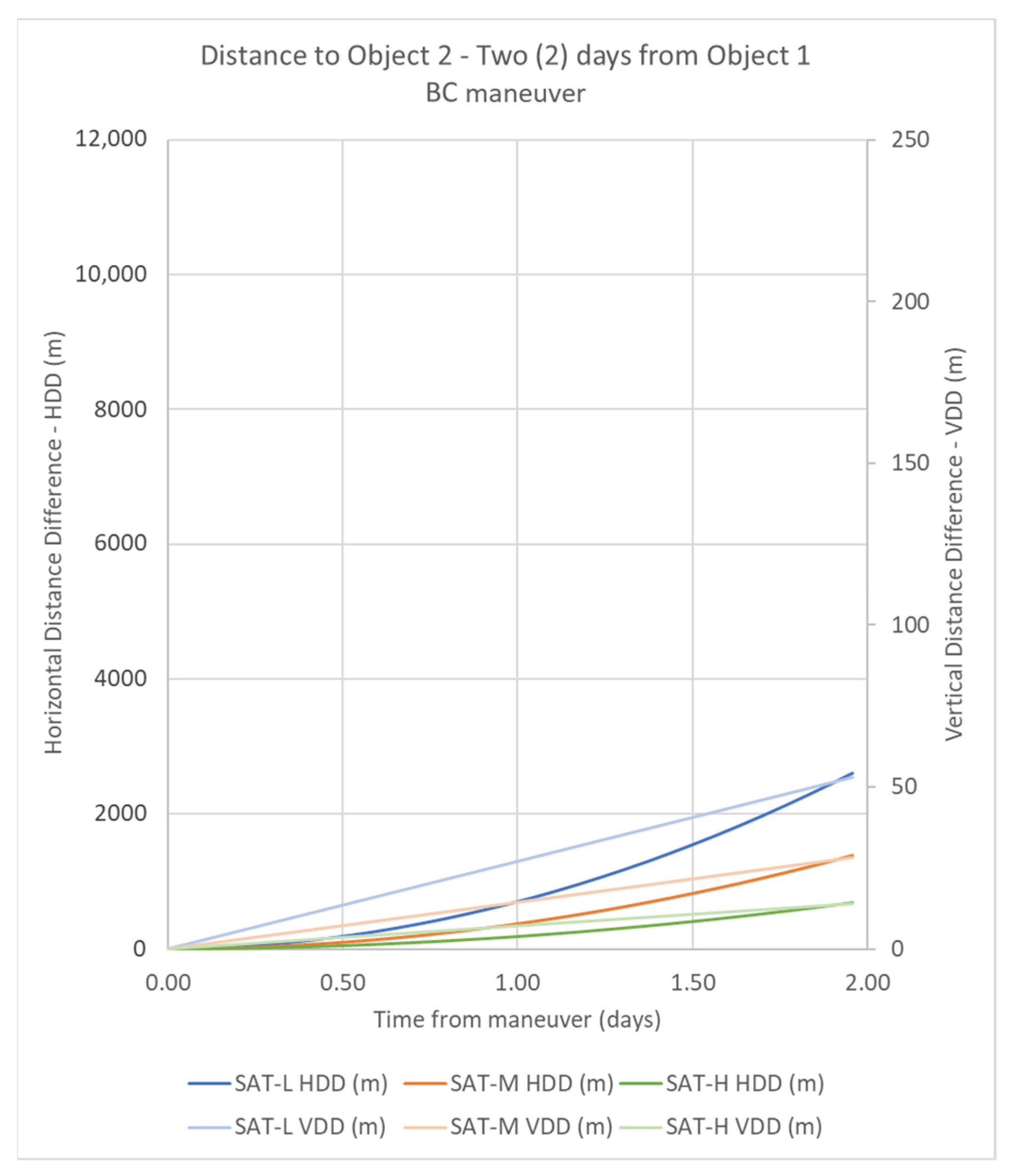
4.1.3. Maneuver BC
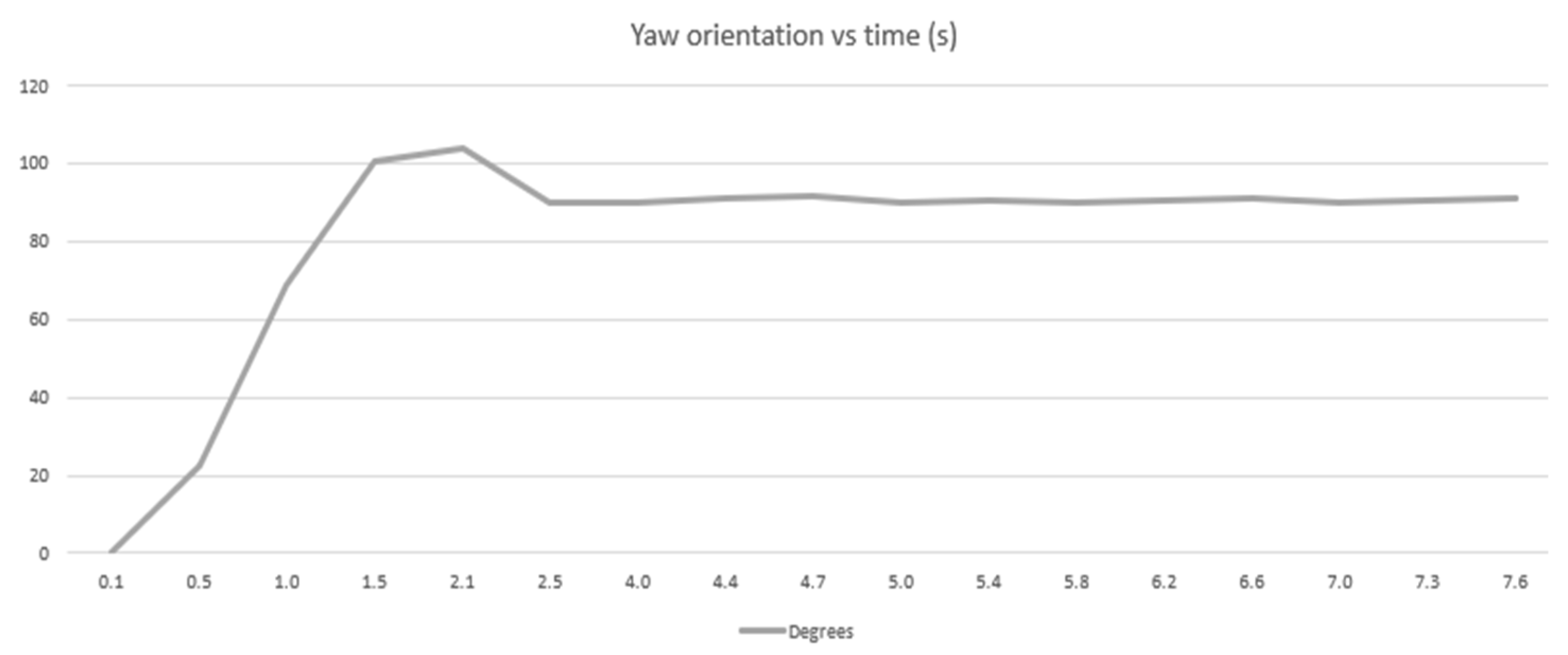
4.2. Laboratory Test
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| adrag | drag force acceleration |
| ρ | atmospheric density |
| V | satellite velocity |
| CD | drag coefficient |
| S | drag area |
| m | satellite mass |
| Yaw angle | |
| ω | Angular velocity |
| Q | Quaternioun |
| Kalman gain | |
| Acronyms/Abbreviations | |
| LEO | Low Earth Orbit |
| ADCS | Attitude Determination and Control System |
| U | Unit |
| STK | System Tool Kit |
| CDM | Conjunction Data Message |
| ESA | European Space Agency |
| ESOC | European Space Operations Centre |
| IADC | Inter-Agency Space Debris Coordination Committee |
| COPUOS | Committee on the Peaceful Uses of Outer Space |
| ISO | International Organisation for Standardisation |
| NASA | National Aeronautics and Space Administration |
| JSpOC | Joint Space Operations Center |
| SSN | Space Surveillance Network |
| ISS | International Space Station |
| SST | Space Surveillance and Tracking |
| CDS | CubeSat Design Specification |
| UAV | Unmanned Aerial Vehicle |
| SGP4 | Standard General Perturbations Satellite Orbit Model 4 |
| HPOP | High-Precision Orbit Propagator |
| CA | Conjunction Assessment |
| TCA | Time of Closest Approach |
| LVLH | Local Vertical, Local Horizontal |
| TLE | Two-Line Element |
| VDD | Vertical Distance Difference |
| HDD | Horizontal Distance Difference |
| EQM | Engineering Qualification Model |
| GISTDA | Geo-Informatics and Space Technology Development Agency |
| CDS | CubeSat Design Specification |
| UAV | Unmanned Aerial Vehicle |
| SSO | Sun Synchronous Orbit |
| KF | Kalman filter |
| EKF | extended Kalman filter |
| UKF | unscented Kalman filter |
| IMU | Inertial Measurement Unit |
| RW | Reaction wheel |
References
- NASA Website: Space Debris and Human Spacecraft. Available online: https://www.nasa.gov/mission_pages/station/news/orbital_debris.html (accessed on 25 July 2022).
- O’Reilly, D. Scopus. Available online: https://www.scopus.com/record/display.uri?eid=2-s2.0-85099955214&origin=resultslist&sort=plf-f&src=s&st1=collision+avoidance+cubesat&sid=b08453557fa8a10a6244f7da8f05a4dc&sot=b&sdt=b&sl=42&s=TITLE-ABS-KEY%28collision+avoidance+cubesat%29&relpos=5&citeCnt=3 (accessed on 11 February 2023).
- S.D. Office. ESA’s Annual Space Environment Report; The European Space Agency: Darmstadt, Germany, 2022. [Google Scholar]
- ESA’s Space Debris Office. Available online: https://www.esa.int/Safety_Security/Space_Debris/Space_debris_by_the_numbers (accessed on 9 May 2022).
- Murtaza, A.; Pirzada SJ, H.; Xu, T.; Jianwei, L. Orbital Debris Threat for Space Sustainability and Way Forward. IEEE Access 2020, 8, 61000–61019. [Google Scholar] [CrossRef]
- NASA. Top ten satellite breakups reevaluated. In Orbital Debris Quarterly News; National Aeronautics and Space Administration: Washington, DC, USA, 2016; Volume 20. [Google Scholar]
- Liou, J.C.; Johnson, N.L. Characterization of the cataloged Fengyun-1C fragments and their. Adv. Space Res. 2009, 43, 1407–1415. [Google Scholar] [CrossRef]
- The Aerospace Corporation. Understanding Space Debris Causes, Mitigations and Issues; Crosslink: Los Angeles, CA, USA, 2015; Volume 16. [Google Scholar]
- Kessler, D.J.; Cour-Palais, B.G. Collision Frequency of Satellites: The Creation of a Debris Belt. J. Geophys. Res. 1978, 83, 2637–2646. [Google Scholar] [CrossRef]
- Kessler, D.J.; Johnson, N.L.; Liou, J.C.; Matney, M. The Kessler Syndrome: Implications to Future. Am. Astronaut. Soc. 2010, 137, 2010. [Google Scholar]
- Available online: https://www.iadc-home.org/ (accessed on 15 May 2023).
- COPUOS. Available online: https://www.unoosa.org/oosa/en/ourwork/topics/space-debris/compendium.html (accessed on 5 May 2023).
- Channumsin, S. Collision avoidance strategies and conjunction risk assessment analysis tool at GISTDA. J. Space Saf. Eng. 2019, 7, 268–273. [Google Scholar] [CrossRef]
- CCSDS 508.0-B-1. Conjunction Data Message; CCSDS: Washington DC, USA, 2023. [Google Scholar]
- C.P.C. Lab. Available online: https://www.cubesat.org/s/CDS-REV14_1-2022-02-09.pdf (accessed on 5 March 2022).
- Kulu, E. Nanosats Database. 2023. Available online: https://www.nanosats.eu/ (accessed on 5 May 2023).
- Pelton, J.N. Overview of Small Satellite Technology and Systems Design. In Handbook of Small Satellites: Technology, Design, Manufacture, Applications, Economics and Regulation; Springer: Arlington, TX, USA, 2020; pp. 125–144. [Google Scholar]
- Swei, S.S.-M.; Westfall, A.J. Attitude control system design for cubesats configured with exo-brake parachute. In Proceedings of the AIAA Space and Astronautics Forum and Exposition, Long Beach, CA, USA, 13–16 September 2016; AIAA SPACE: Long Beach, CA, USA, 2016. [Google Scholar]
- NASA. TechEdSat-4 with Deployed Exobrake. 2015. Available online: https://www.nasa.gov/image-article/techedsat-4-with-deployed-exobrake/ (accessed on 15 August 2022).
- ESA. ESA—SPACE SAFETY—Deploying a Drag Sail. 2021. Available online: https://www.esa.int/ESA_Multimedia/Images/2021/04/Deploying_a_drag_sail#:~:text=ESA%E2%80%99s%20General%20Support%20Technology%20Programme%20and%20the%20space,will%20burn%20up%20after%20its%20mission%20is%20over (accessed on 15 August 2022).
- Ansys Systems Tool Kit (STK). Available online: https://www.agi.com/products/stk (accessed on 22 July 2022).
- Pelton, J.N. Stability, pointing, and orientation. In Handbook of Small Satellites: Technology, Design, Manufacture, Applications, Economics and Regulation; Springer: Arlington, TX, USA, 2020; pp. 145–188. [Google Scholar]
- Alen Space. LUME-1: Nanosatellite of the University of Vigo for Firefighting. 2018. Available online: https://alen.space/lume-1-launch/ (accessed on 15 August 2022).
- National Oceanic and Atmospheric Administration. US Standard Atmosphere; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1976.
- Lefferts, E.J.; Markley, F.L.; Shuster, M.D. Kalman filtering for spacecraft attitude estimation. J. Guid. Control. Dyn. 1982, 5, 417–429. [Google Scholar] [CrossRef]




| Rank | International Designator | Common Name | Year of Breakup | Altitude of Breakup | Cataloged Debris | Debris in Orbit | Assessed Cause of Breakup |
|---|---|---|---|---|---|---|---|
| 1 | 1999-25 | Fengyun-1C71 | 2007 | 850 | 3428 | 2880 | intentional collision |
| 2 | 1993-36 | Cosmos 2251 | 2009 | 790 | 1668 | 1141 | accidental collision |
| 3 | 1994-29 | STEP-1 Rocket Body | 1996 | 625 | 754 | 84 | accidental explosion |
| 4 | 1997-51 | Iridium 33 | 2009 | 790 | 628 | 364 | accidental explosion |
| 5 | 2006-26 | Cosmos 2421 | 2008 | 410 | 509 | 0 | unknown |
| 6 | 1986-19 | SPOT-1 Rocket Body | 1986 | 805 | 498 | 32 | accidental explosion |
| 7 | 1965-82 | OV2-1/LCS 2 Rocket Body | 1965 | 740 | 473 | 33 | accidental explosion |
| 8 | 1999-57 | CBERS 1/SACI 1 Rocket Body | 2000 | 740 | 431 | 210 | accidental explosion |
| 9 | 1970-25 | Nimbus 4 Rocket Body | 1970 | 1075 | 376 | 235 | accidental explosion |
| 10 | 2001-49 | TES Rocket Body | 2001 | 670 | 372 | 80 | accidental explosion |
| Debris Size | Mass (g) Aluminum Sphere | Kinetic Energy (J) | Equivalent TNT (Kg) | Energy Similar to |
|---|---|---|---|---|
| 1 mm | 0.0014 | 71 | 0.0003 | Baseball |
| 3 mm | 0.038 | 1910 | 0.008 | Bullets |
| 1 cm | 1.41 | 70,700 | 0.3 | Falling anvil |
| 5 cm | 176.7 | 8,840,000 | 37 | Hit by bus |
| 10 cm | 1413.7 | 70,700,000 | 300 | Large bomb |
| CubeSat Format | Drag Face | ) | Mass (kg) | Drag Area/Mass (m2/kg) | Case Study |
|---|---|---|---|---|---|
| 2U | 1U | 0.01 | 2 | 0.005 | B |
| 2U | 0.02 | 0.010 | A | ||
| 3U | 1U | 0.01 | 3 | 0.003 | C |
| 3U | 0.03 | 0.010 | A | ||
| 6U | 2U | 0.02 | 6 | 0.003 | C |
| 3U | 0.03 | 0.005 | B | ||
| 6U | 0.06 | 0.010 | A |
| Initial Position | Final Position | Maneuver | CubeSat Format |
|---|---|---|---|
| A | B | AB | 2U, 6U |
| B | A | AB | 2U, 6U |
| A | C | AC | 3U, 6U |
| C | A | AC | 3U, 6U |
| B | C | BC | 6U |
| C | B | BC | 6U |
| Orbits/Maneuvers | Semi-Major Axis (km) | VDD (m) | HDD (m) |
|---|---|---|---|
| SAT-H-AB | 6878.78 | 42.33 | 2046.32 |
| SAT-M-AB | 6838.78 | 85.36 | 4160.12 |
| SAT-L-AB | 6798.78 | 159.67 | 7845.10 |
| SAT-H_BC | 6878.78 | 14.10 | 681.72 |
| SAT-M_BC | 6838.78 | 28.42 | 1385.67 |
| SAT-L_BC | 6798.78 | 53.13 | 2611.81 |
| SAT-H_AC | 6878.78 | 56.43 | 2728.04 |
| SAT-M_AC | 6838.78 | 113.79 | 5545.80 |
| SAT-L_AC | 6798.78 | 212.80 | 10,456.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Rodríguez, D.; Orgeira-Crespo, P.; Cappelletti, C.; Aguado-Agelet, F. Methodology for CubeSat Debris Collision Avoidance Based on Its Active ADCS System. Appl. Sci. 2023, 13, 12388. https://doi.org/10.3390/app132212388
González-Rodríguez D, Orgeira-Crespo P, Cappelletti C, Aguado-Agelet F. Methodology for CubeSat Debris Collision Avoidance Based on Its Active ADCS System. Applied Sciences. 2023; 13(22):12388. https://doi.org/10.3390/app132212388
Chicago/Turabian StyleGonzález-Rodríguez, Desiree, Pedro Orgeira-Crespo, Chantal Cappelletti, and Fernando Aguado-Agelet. 2023. "Methodology for CubeSat Debris Collision Avoidance Based on Its Active ADCS System" Applied Sciences 13, no. 22: 12388. https://doi.org/10.3390/app132212388
APA StyleGonzález-Rodríguez, D., Orgeira-Crespo, P., Cappelletti, C., & Aguado-Agelet, F. (2023). Methodology for CubeSat Debris Collision Avoidance Based on Its Active ADCS System. Applied Sciences, 13(22), 12388. https://doi.org/10.3390/app132212388






