Design of a Semantic Understanding System for Optical Staff Symbols
Abstract
:1. Introduction
- The LSUS pre-trained model has the ability to recognize the pitch and duration of symbols and notes in staff images, even when they exhibit varying levels of complexity. The test results demonstrate precision and recall rates of 0.989 and 0.972, respectively, fulfilling the requirements for “intelligent score flipping” with high accuracy.
- According to the specific application of “intelligent score flipping”, a comprehensive end-to-end system model has been developed and implemented. This model converts graphical staff symbols into performance coding.
- A note-encoding reconstruction algorithm has been developed, which establishes the relationship between individual symbols based on the notation method. This algorithm outputs the pitch and duration of each note during performance.
- The SUSN dataset has been created. This dataset innovatively includes relative positional information of symbols in the staff without increasing the length of the label field. The dataset is suitable for end-to-end-type algorithm models.
2. Related Work
2.1. Optical Music Recognition
2.2. OMR Dataset
2.3. Summary
3. Materials and Methods
3.1. Dataset
- The main notes are labeled with information about the note position, pitch, and duration in the natural scale. The labeling method has two steps. Firstly, draw the bounding box: the bounding box should contain the complete note (head, stem, and tail) and the specific spatial information of the head. In other words, the bounding box is supposed to contain the 0th line to the 5th line of the staff as well as the position of the head. Then, annotate the object: the format of the label is the ’duration_pitch’ code under the natural scale (as shown in Figure 1f,g).
- Label the categories of symbols that affect the pitch and duration of the main notes as well as position information. In the score, the clef, key signature, dot, and pitch-shifting notation (sharp, flat, and natural) are the main control symbols that affect the pitch and duration of the main note, and Table 1a–c lists the control symbols identified and understood in this paper. Each of these kinds of symbols is labeled with a minimum external bounding box containing the whole symbol and category information, as shown in Figure 1a–c,e.
- Label the categories and position of the symbols of the rest. The rest is used in a score to express stopping performance for a specified duration. The symbol of the rest is labeled with a minimum external bounding box that contains the rest entirely as well as information about its category and duration. The rests identified and understood in this paper are listed in Table 1d, while the rests in the staff are labeled as shown in Figure 1d.

3.2. Low-Level Semantic Understanding Stage
3.3. High-Level Semantic Understanding Stage
- The clefs are the symbols used to determine the exact pitch position of a natural scale in the staff. It is recorded at the leftmost end of each staff, and there is also a flag that indicates the mth line in the staff. Meanwhile, it is also the first symbol considered by the NERA when encoding the pitch;
- The key signature located after the clef is the symbol used to mark the ascending or descending pitch of the corresponding notes and is expressed as a value in the NERA. The clefs and key signatures are effective within one line of staff notation;
- In accidentals, the pitch-shifting notation changes the pitch. It raises, lowers, or restores the pitch of the note on which it is applied. The dot extends the original duration of the note by half.
3.3.1. Data Preprocessing
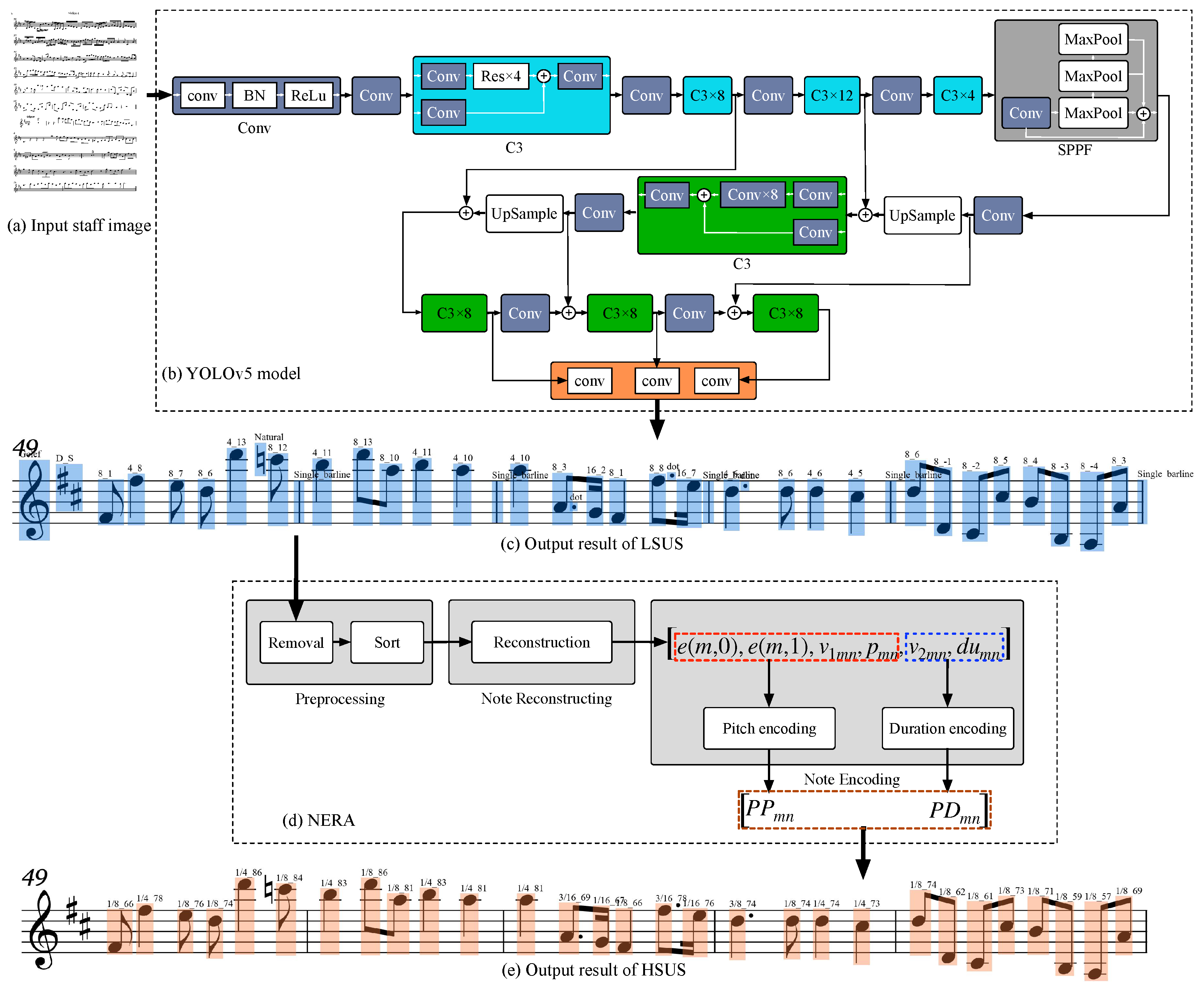
- Removal of invalid symbols. The task of this paper is to implement the encoding of the pitch and duration of staff notes during the performance. Among the numerous symbols that affect the pitch and duration of notes are the clefs, the key signatures, the accidentals, and the natural scales, while other symbols are considered invalid symbols within this article. In the preprocessing stage, invalid symbols are removed, and valid symbols are retained. We define the set of valid symbols as . The relationships among clefs, key signatures, accidentals, natural scales, the valid symbol set, and the dataset are shown in Equation (1):where clef, key signature, accidental, and natural scale are denoted by = , , , and set , respectively. Specifically, P is the space spanned by the natural scale , and is spanned by the duration . Further, the element 0 in set means there is no key signature and implies that the signature in this line is C major. Each natural scale has two pieces of information that indicate the pitch and duration, respectively. Table 2 shows the relationship between categories and sets.
- Sorting of valid symbols. The YOLOv5 algorithm in the LSUS outputs the objects, and each object is unordered with the information , where denotes the symbol’s class; denote the Cartesian coordinate values of the center point of the object bounding box; and denote the width and height. The clef is the first element of each row in the staff. Let its center point coordinate be . Denote , where D is the distance between two adjacent clefs’ center points. If the symbol is , then it goes to the same line. Next, the symbols in the same row are sorted in order by X from small to large. By this method, all valid symbols are rearranged in a new order, which is the exact order of the symbols when reading the staff.
| Algorithm 1 Algorithm for the NERA Preprocessing Part. |
| Input: The output of the LSUS. |
| Output: The staff digital information in the right order. //With M vectors and elements in each vector. |
| 1: Initialize: ;// |
| 2: while do |
| 3: |
| 4: if then |
| 5: ; //To determine whether the current symbol is a valid symbol. |
| 6: end if |
| 7: if then |
| 8: ; |
| 9: ;//If the input symbol belongs to the clefs, a new vector is created. |
| 10: else |
| 11: ; //If the valid symbols are not clefs, then continue. |
| 12: end if |
| 13: end while |
| 14: return Output |
3.3.2. Note Reconstructing
| Algorithm 2 Algorithm for the NERA Notation Reconstructing Part. |
| Input: Vector data. |
| Output: Staff notation relationship structure. |
| 1: Initialize: ;); //Maximum value of the line index according to the clef number; initializes the row index and symbolic index. |
| 2: while do |
| 3: ; //Initializes index j for symbols and index n for notes |
| 4: ; //Gets the value of the line clef and key signature. |
| 5: while do |
| 6: ; //Loop through all valid symbols in the mth line. |
| 7: if then |
| 8: ; //Assign pitch-shifting notation to the of the next note. |
| 9: else |
| 10: if then |
| 11: ;; //If it is a note, then calculate its value of pitch and duration. |
| 12: ; //Assign the note duration. |
| 13: ; //Assign the pitch of the next note. |
| 14: else |
| 15: ; //If it is a dot. |
| 16: end if |
| 17: end if |
| 18: end while |
| 19: end while |
| 20: return Output |
3.3.3. Note Encoding
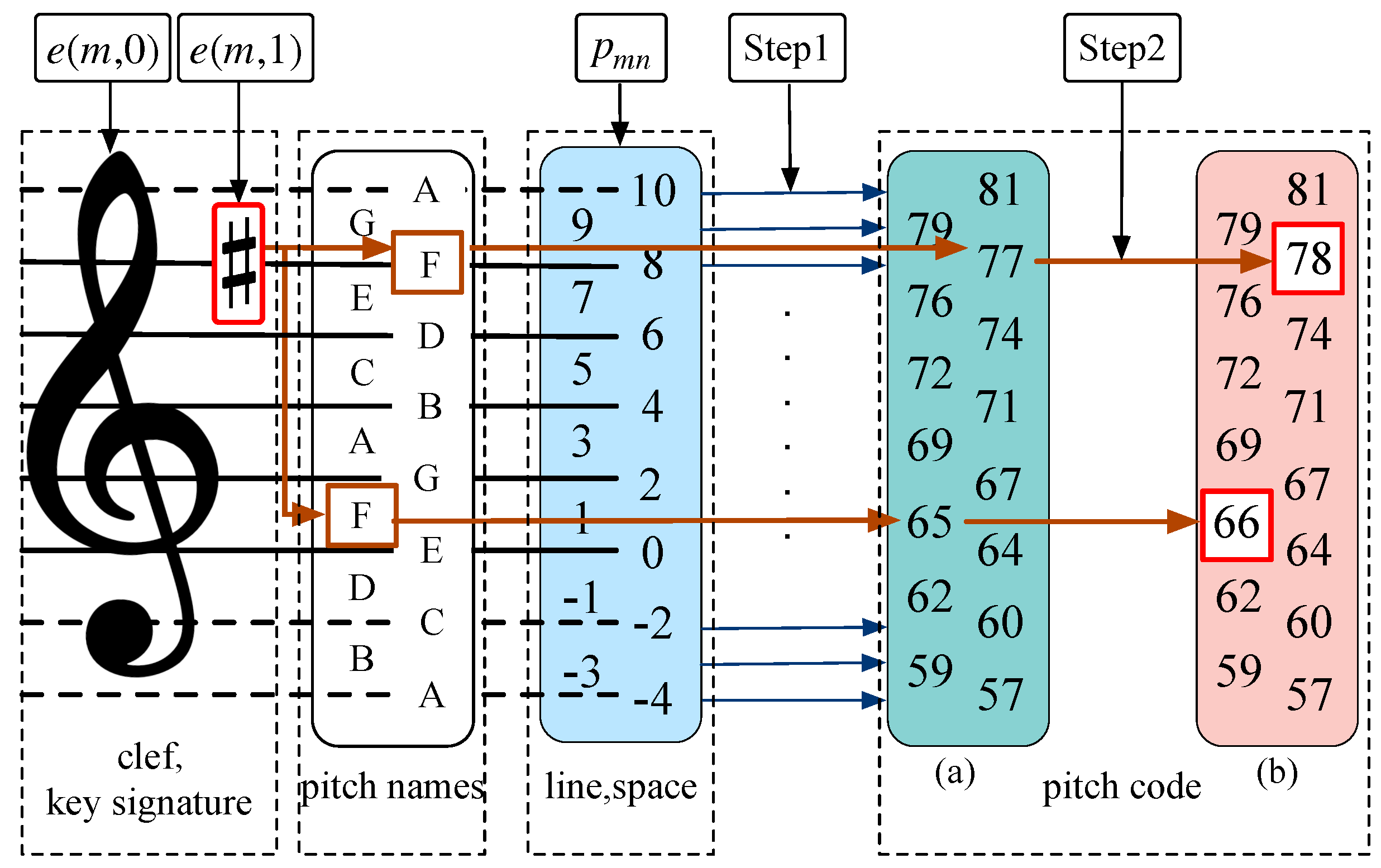
- Pitch EncodingAccording to the clef, key signature, and MIDI encoding rules, the pitch code of the natural scale is converted to a code that includes the function of clef and key signature in the mth line one by one. We define as the mapping of this strategy and obtain the converted code . The encoding process is shown in Figure 2. Then, the pitch encoding part obtains the pitch code for each note played using the MIDI encoding rules after scanning the note control vector , as shown in Equation (4):
- Duration EncodingScan each duration control vector and corresponding note duration vector , define the individual performance style coefficient as , and apply the MIDI encoding rule; then, the duration encoding strategy is shown in Equation (5):where varies according to the different performers and means that the performers’ characteristics are not considered.
3.4. System Structure
4. Results
4.1. Data
4.2. Training
4.3. Evaluation Metrics
4.4. Experiment and Analysis
4.4.1. Experiment with LSUS
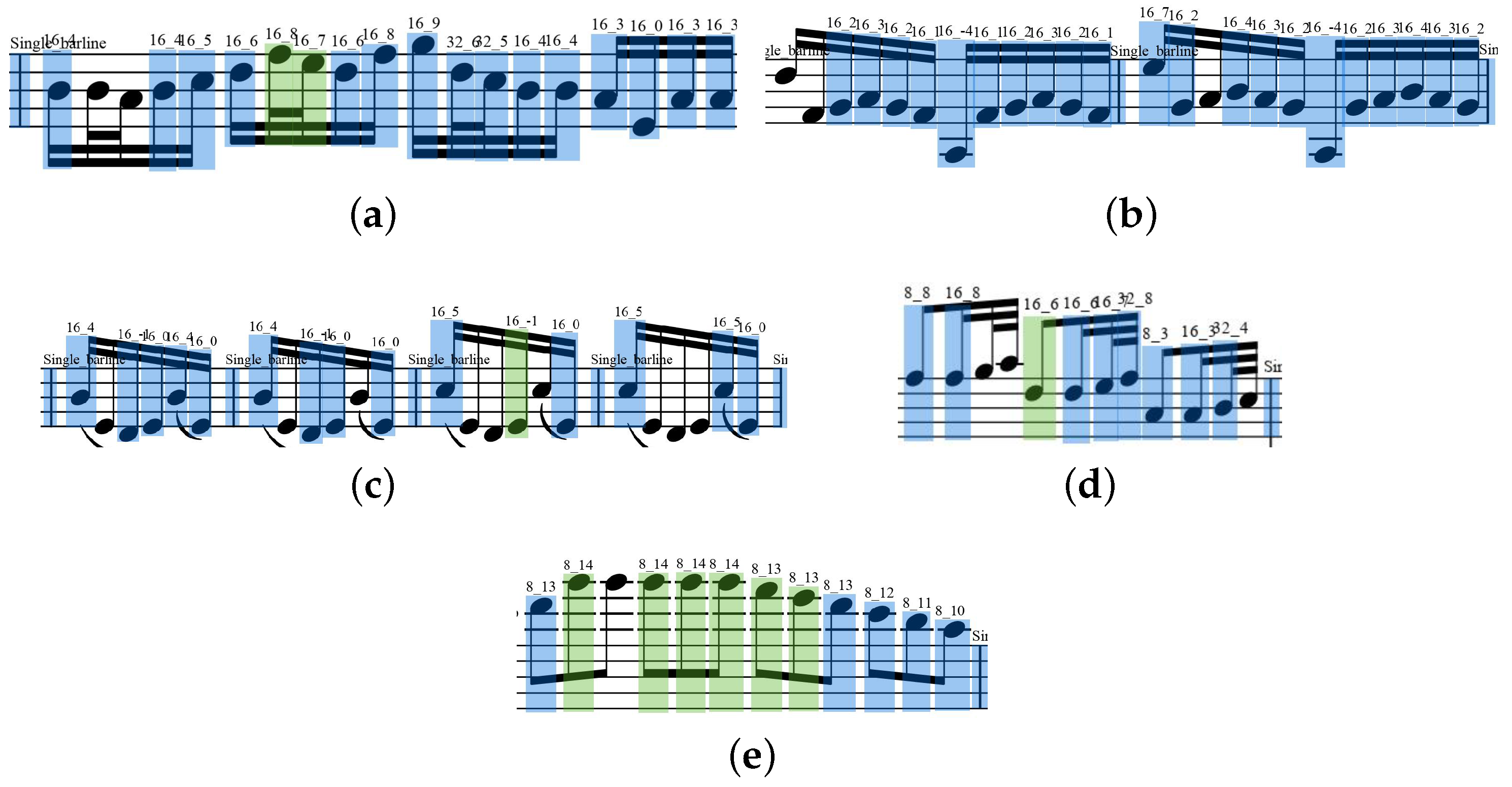
- In Staff 1, many complex note beams along with the high density of symbols result in relatively high rates of error and omission, as shown in Figure 4a;
- Staff 2 has the highest density of symbols, and its recall is relatively low, as shown in Figure 4b;
- Staff 3 has a lower complexity for each item, and its performance evaluation is better;
- The error and omission of notes in Staff 4 are mostly concentrated in the notes with longer note stems, as shown in Figure 4c;
- Staff 5 has a higher complexity for each item and very low image file size (200 kb), and its evaluation is worse than others;
- Staff 6 has a lower image file size (435 kb) and, similar to Staff 1, its notes with common note beams are tedious, as shown in Figure 4d;
- Staff 7 has a lower image file size (835 kb), but its performance evaluation is better due to the lower complexities of other attributes;
- In Staff 9, the error detection notes are those located in the higher positive line on the staff, as shown in Figure 4e.
4.4.2. Experiment with HSUS
- When the input is ideal, the error rate and the omission rate of the output result are the performance indexes of the NERA;
- The error and omission rates are the performance indexes of the whole system when the output is practical.
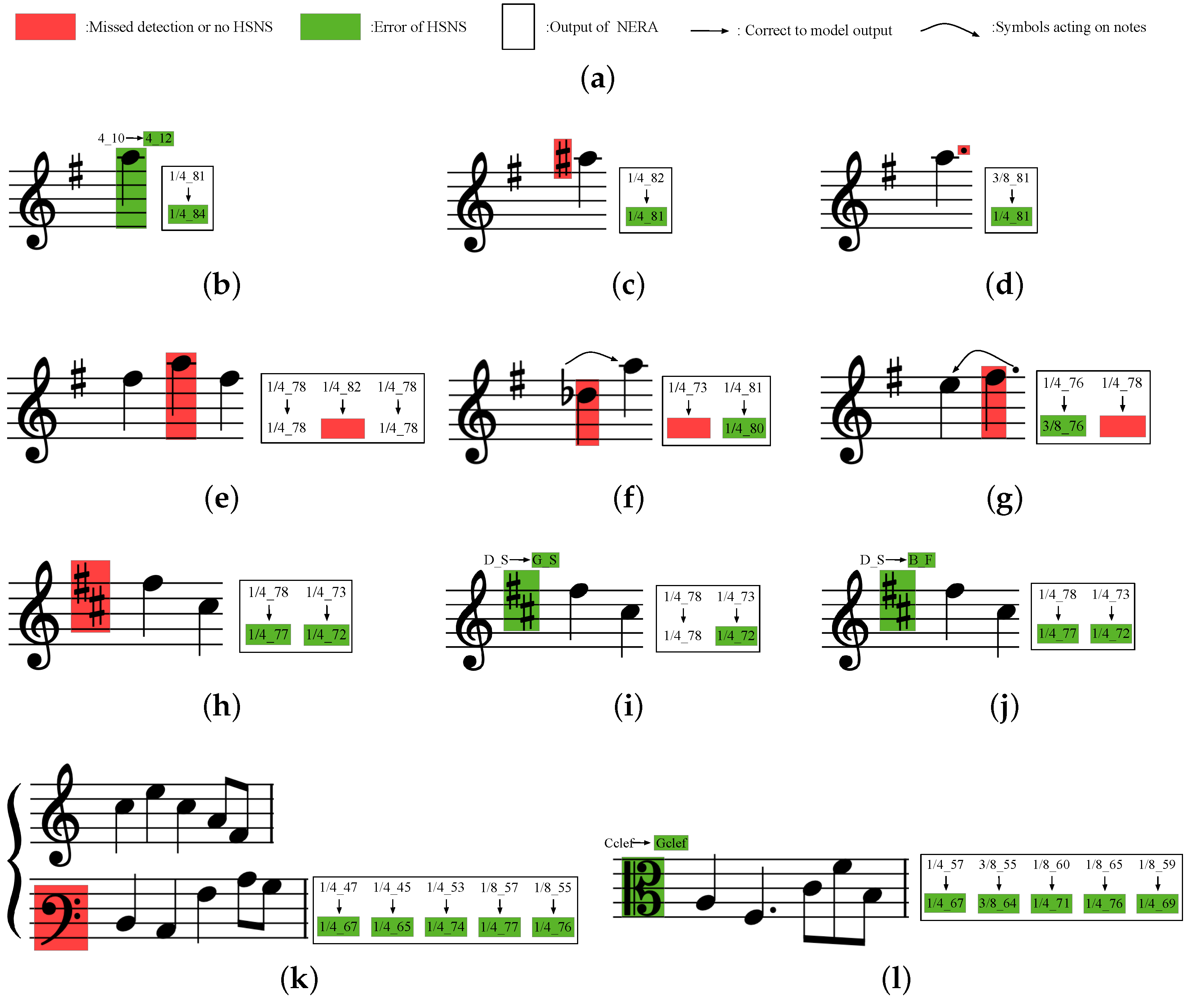
- Misidentification of the pitch and duration of natural scales can lead to errors during HSUS;
- Misidentification or omission of accidentals (sharp, flat, natural, dot) acting on natural scales can lead to errors during HSUS;
- Omission of a note affects the HSUS of the note or the preceding and following notes. There are three cases: (1) when the note is preceded and followed by separate notes, the omission of the note does not affect the semantics of the preceding and following notes; (2) when a note is preceded by a pitch-shifting notation (sharp, flat, natural) and followed by another note, the omission of the note will cause the pitch-shifting notation originally used for the note to be applied to the latter note, resulting in a pitch error at the HSUS of understanding of the latter note; (3) when the note is preceded by a note and followed by a dot, the omission of the note will cause the appendage originally used for the note to act on the preceding note, and thus the HSUS of the preceding note will be incorrectly timed;
- Misidentification or omission of the key signature will result in a pitch error in the HSUS for some notes in this line. There are three cases: (1) when the key signature is missed, the pitch of the note in the key signature range is incorrect at the HSUS; (2) when the key signature is misidentified as a key with the same mode of action, i.e., when both modes of action are the same, making the natural scale ascending (or descending) but with a different range of action, the HSUS of some of the notes will be wrong in terms of pitch; (3) when the key signature is incorrectly identified as a key with a different mode of action, the pitch will be incorrect when the note is semantically understood;
- When the clef is missed, all natural scales in this row are affected by the clef of the previous line. When the clef is incorrectly identified, an error occurs at the HSUS of all natural scales in this row.
5. Conclusions and Outlooks
5.1. Conclusions
5.2. Outlooks
- The staff notation in this paper is mainly related to the pitch and duration of musical melodies. The recognition of other symbols, such as dynamics, staccatos, trills, and characters related to the information of the staff is one of the future tasks to be solved;
- The accurate recognition of complex natural scales such as chords is a priority;
- The recognition of symbols in more complex staff images, e.g., those with larger intervals, denser symbols, and more noise in the image.
- It is important to improve the scope of accidentals, so that they can be combined with bar lines and repetition lines, etc;
- The semantic understanding of notes is based on the LSUS and, after solving the problem of the types of symbols recognized by the model, each note can be given richer expression information;
- In this paper, rests are recognized, but the information is not utilized in semantic understanding. In the future, this information and the semantic relationships of other symbols can be used to generate a complete code of the staff during performances.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LSUS | Low-Level Semantic Understanding Stage |
| HSUS | High-Level Semantic Understanding Stage |
| NERA | Note-Encoding Reconstruction Algorithm |
Appendix A
- Staff 1: Canon and Gigue in D Major (Pachelbel, Johann)
- Staff 2: Oboe String Quartet in C Minor, Violin Concerto (J.S. Bach BWV 1060)
- Staff 3: Sechs ländlerische Tänze für 2 Violinen und Bass (Woo15), Violino 1 (Beethoven, Ludwig van)
- Staff 4: Violin Concerto RV 226, Violino principale (A. Vivaldi)
- Staff 5: String Duo no. 1 in G for violin and viola KV 423 (Wolfgang Amadeus Mozart)
- Staff 6: Partia à Cembalo solo (G. Ph. Telemann)
- Staff 7: Canon in D, Piano Solo (Pachelbel, Johann)
- Staff 8: Für Elise in A Minor WoO 59 (Beethoven, Ludwig van)
- Staff 9: Passacaglia (Handel Halvorsen)
- Staff 10: Prélude n°1 Do Majeur (J.S. Bach)
References
- Moysis, L.; Iliadis, L.A.; Sotiroudis, S.P.; Boursianis, A.D.; Papadopoulou, M.S.; Kokkinidis, K.-I.D.; Volos, C.; Sarigiannidis, P.; Nikolaidis, S.; Goudos, S.K. Music Deep Learning: Deep Learning Methods for Music Signal Processing—A Review of the State-of-the-Art. IEEE Access 2023, 11, 17031–17052. [Google Scholar] [CrossRef]
- Tardon, L.J.; Barbancho, I.; Barbancho, A.M.; Peinado, A.; Serafin, S.; Avanzini, F. 16th Sound and Music Computing Conference SMC 2019 (28–31 May 2019, Malaga, Spain). Appl. Sci. 2019, 9, 2492. [Google Scholar] [CrossRef]
- Downie, J.S. Music information retrieval. Annu. Rev. Inf. Sci. Technol. 2003, 37, 295–340. [Google Scholar] [CrossRef]
- Casey, M.A.; Veltkamp, R.; Goto, M.; Leman, M.; Rhodes, C.; Slaney, M. Content-Based Music Information Retrieval: Current Directions and Future Challenges. Proc. IEEE 2008, 96, 668–696. [Google Scholar] [CrossRef]
- Calvo-Zaragoza, J.; Hajič, J., Jr.; Pacha, A. Understanding Optical Music Recognition. ACM Comput. Surv. 2020, 53, 1–35. [Google Scholar] [CrossRef]
- Rebelo, A.; Fujinaga, I.; Paszkiewicz, F.; Marcal, A.R.S.; Guedes, C.; Cardoso, J.S. Optical music recognition: State-of-the-art and open issues. Int. J. Multimed. Inf. Retr. 2012, 1, 173–190. [Google Scholar] [CrossRef]
- Calvo-Zaragoza, J.; Barbancho, I.; Tardon, L.J.; Barbancho, A.M. Avoiding staff removal stage in optical music recognition: Application to scores written in white mensural notation. Pattern Anal. Appl. 2015, 18, 933–943. [Google Scholar] [CrossRef]
- Rebelo, A.; Capela, G.; Cardoso, J.S. Optical recognition of music symbols. Int. J. Doc. Anal. Recognit. (IJDAR) 2010, 13, 19–31. [Google Scholar] [CrossRef]
- Baró, A.; Riba, P.; Fornés, A. Towards the Recognition of Compound Music Notes in Handwritten Music Scores. In Proceedings of the 2016 15th International Conference on Frontiers in Handwriting Recognition (ICFHR), Shenzhen, China, 23–26 October 2016; pp. 465–470. [Google Scholar]
- Huber, D.M. The MIDI Manual: A Practical Guide to MIDI in the Project Studio; Taylor & Francis: Abingdon, UK, 2007. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6517–6525. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. SSD: Single shot MultiBox detector. In Proceedings of the Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; pp. 21–37. [Google Scholar]
- Thuan, D. Evolution of Yolo algorithm and Yolov5: The State-of-the-Art Object Detention Algorithm. Ph.D. Thesis, Oulu University of Applied Sciences, Oulu, Finland, 2021. [Google Scholar]
- Al-Qubaydhi, N.; Alenezi, A.; Alanazi, T.; Senyor, A.; Alanezi, N.; Alotaibi, B.; Alotaibi, M.; Razaque, A.; Abdelhamid, A.A.; Alotaibi, A. Detection of Unauthorized Unmanned Aerial Vehicles Using YOLOv5 and Transfer Learning. Electronics 2022, 11, 2669. [Google Scholar] [CrossRef]
- Pacha, A.; Choi, K.Y.; Coüasnon, B.; Ricquebourg, Y.; Zanibbi, R.; Eidenberger, H. Handwritten music object detection: Open issues and baseline results. In Proceedings of the 2018 13th IAPR International Workshop on Document Analysis Systems (DAS), Vienna, Austria, 24–27 April 2018; pp. 163–168. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Hajič, J., Jr.; Dorfer, M.; Widmer, G.; Pecina, P. Towards full-pipeline handwritten OMR with musical symbol detection by U-nets. In Proceedings of the 19th International Society for Music Information Retrieval Conference, Paris, France, 23–27 September 2018; pp. 225–232. [Google Scholar]
- Tuggener, L.; Elezi, I.; Schmidhuber, J.; Stadelmann, T. Deep Watershed Detector for Music Object Recognition. arXiv 2018, arXiv:1805.10548. [Google Scholar]
- Huang, Z.; Jia, X.; Guo, Y. State-of-the-Art Model for Music Object Recognition with Deep Learning. Appl. Sci. 2019, 9, 2645. [Google Scholar] [CrossRef]
- Van der Wel, E.; Ullrich, K. Optical Music Recognition with Convolutional Sequence-to-Sequence Models. arXiv 2017, arXiv:1707.04877. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Baró, A.; Riba, P.; Calvo-Zaragoza, J.; Fornés, A. From Optical Music Recognition to Handwritten Music Recognition: A baseline. Pattern Recognit. Lett. 2019, 123, 1–8. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef]
- Tuggener, L.; Satyawan, Y.P.; Pacha, A.; Schmidhuber, J.; Stadelmann, T. The DeepScoresV2 Dataset and Benchmark for Music Object Detection. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milano, Italy, 10–15 January 2021; pp. 9188–9195. [Google Scholar]
- Hajič, J., Jr.; Pecina, P. The MUSCIMA++ Dataset for Handwritten Optical Music Recognition. In Proceedings of the 2017 14th IAPR International Conference on Document Analysis and Recognition (ICDAR), Kyoto, Japan, 9–15 November 2017; pp. 39–46. [Google Scholar]
- Calvo-Zaragoza, J.; Oncina, J. Recognition of Pen-Based Music Notation: The HOMUS Dataset. In Proceedings of the 2014 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; pp. 3038–3043. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef]
- Liu, S.; Qi, L.; Qin, H.; Shi, J.; Jia, J. Path aggregation network for instance segmentation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8759–8768. [Google Scholar]
- Lin, T.-Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 936–944. [Google Scholar]





| Classes | Images/Labels |
|---|---|
| (a) clefs |  |
| (b) key signatures |  |
| (c) accidentals | 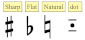 |
| (d) rests |  |
| Sets | Categories | ||
|---|---|---|---|
| Gclef, High_Gclef, DHigh_Gclef, Lower_Gclef, DLower_Gclef, Soprano_Cclef, M-soprano_Cclef, Cclef, Tenor_Cclef, Baritone_Cclef. Fclef, High_Fclef, DHigh_Fclef, Lower_Fclef, DLower_Fclef | |||
| 0, G_S, D_S, A_S, E_S, B_S, F_S, C_S, C_F, G_F, D_F, A_F, E_F, B_F, F_F | |||
| Sharp, Flat, Natural, Dot | |||
| P | |||
| Du | |||
| other | Rest1, Rest2, Rest4, Rest8, Rest16, Rest32, Rest64 | ||
| Staff | Complexity Variables | Evaluation | ||||||
|---|---|---|---|---|---|---|---|---|
| Name | Page | Type | Span | Density (Symbols) | Density (External Notes) | File Size (kb) | Precision | Recall |
| Staff 1 | 2 | 16 | 19 | 484 | 78 | 1741 | 0.968 | 0.930 |
| Staff 2 | 5 | 17 | 19 | 679 | 146 | 2232 | 0.996 | 0.988 |
| Staff 3 | 3 | 13 | 19 | 319 | 95 | 1673 | 0.997 | 0.992 |
| Staff 4 | 12 | 20 | 20 | 478 | 80 | 1741 | 0.994 | 0.981 |
| Staff 5 | 7 | 19 | 24 | 530 | 145 | 200 | 0.980 | 0.958 |
| Staff 6 | 5 | 19 | 20 | 367 | 63 | 435 | 0.992 | 0.970 |
| Staff 7 | 5 | 15 | 19 | 350 | 62 | 854 | 0.996 | 0.993 |
| Staff 8 | 3 | 13 | 20 | 441 | 40 | 1536 | 0.990 | 0.969 |
| Staff 9 | 3 | 11 | 20 | 424 | 160 | 2389 | 0.986 | 0.966 |
| Staff 10 | 2 | 17 | 18 | 315 | 86 | 1780 | 0.987 | 0.976 |
| Precision | Recall | |
|---|---|---|
| clef | 1.0 00 | 0.993 |
| key signature | 0.992 | 0.990 |
| Staff | Ideal Input | Practical Input | ||||
|---|---|---|---|---|---|---|
| Error Rate | Omission Rate | Error Rate | Omission Rate | |||
| Staff 1 | 0.006 | 0.000 | 0.052 | 0.044 | ||
| Staff 2 | 0.011 | 0.000 | 0.016 | 0.010 | ||
| Staff 3 | 0.010 | 0.000 | 0.020 | 0.006 | ||
| Staff 4 | 0.019 | 0.000 | 0.027 | 0.020 | ||
| Staff 5 | 0.013 | 0.000 | 0.044 | 0.014 | ||
| Staff 6 | 0.005 | 0.000 | 0.020 | 0.008 | ||
| Staff 7 | 0.000 | 0.000 | 0.004 | 0.010 | ||
| Staff 8 | 0.020 | 0.000 | 0.055 | 0.053 | ||
| Staff 9 | 0.022 | 0.000 | 0.037 | 0.021 | ||
| Staff 10 | 0.000 | 0.000 | 0.036 | 0.019 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, F.; Lu, Y.; Wang, G. Design of a Semantic Understanding System for Optical Staff Symbols. Appl. Sci. 2023, 13, 12627. https://doi.org/10.3390/app132312627
Lou F, Lu Y, Wang G. Design of a Semantic Understanding System for Optical Staff Symbols. Applied Sciences. 2023; 13(23):12627. https://doi.org/10.3390/app132312627
Chicago/Turabian StyleLou, Fengbin, Yaling Lu, and Guangyu Wang. 2023. "Design of a Semantic Understanding System for Optical Staff Symbols" Applied Sciences 13, no. 23: 12627. https://doi.org/10.3390/app132312627
APA StyleLou, F., Lu, Y., & Wang, G. (2023). Design of a Semantic Understanding System for Optical Staff Symbols. Applied Sciences, 13(23), 12627. https://doi.org/10.3390/app132312627








