Experimental Study on Dynamic Exhaust Law for Ventilation System of Gas Tunnel
Abstract
:1. Introduction
2. Similarity Principle
2.1. Study Object
2.2. Similarity Verification
3. Similarity Experiment
3.1. Experimental Model
3.2. Experimental Scheme
4. Results and Discussion
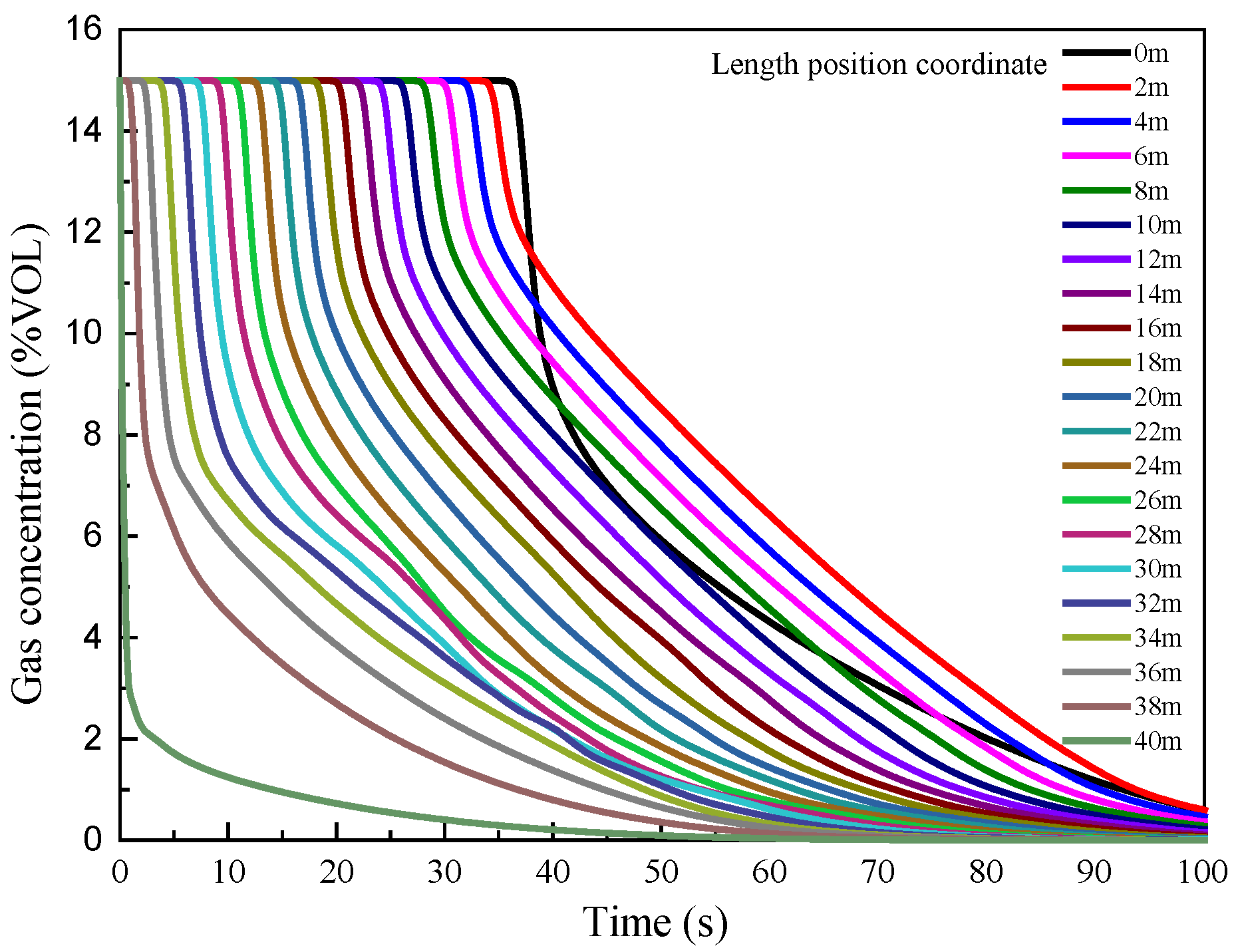
4.1. Concentration Distribution
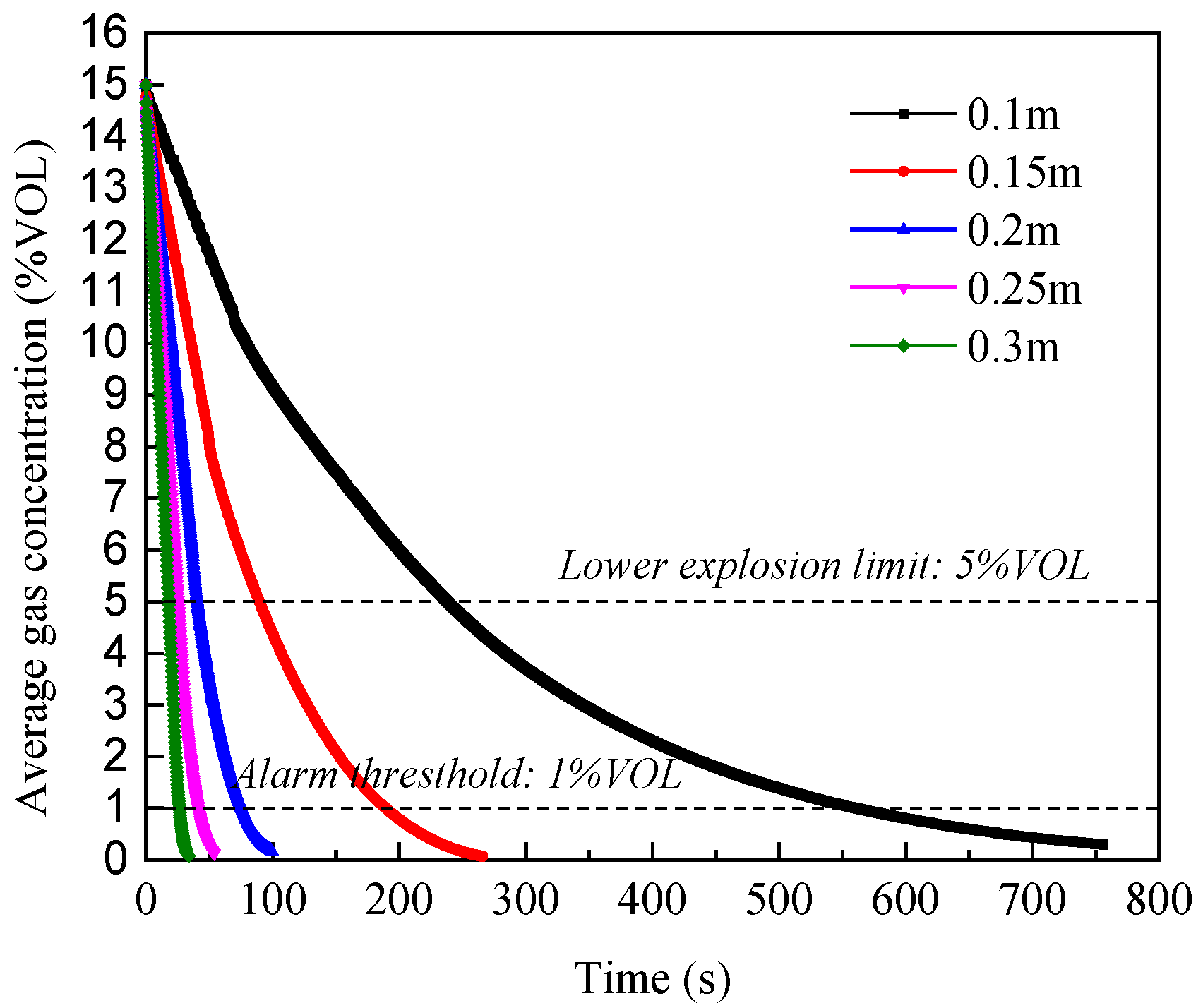
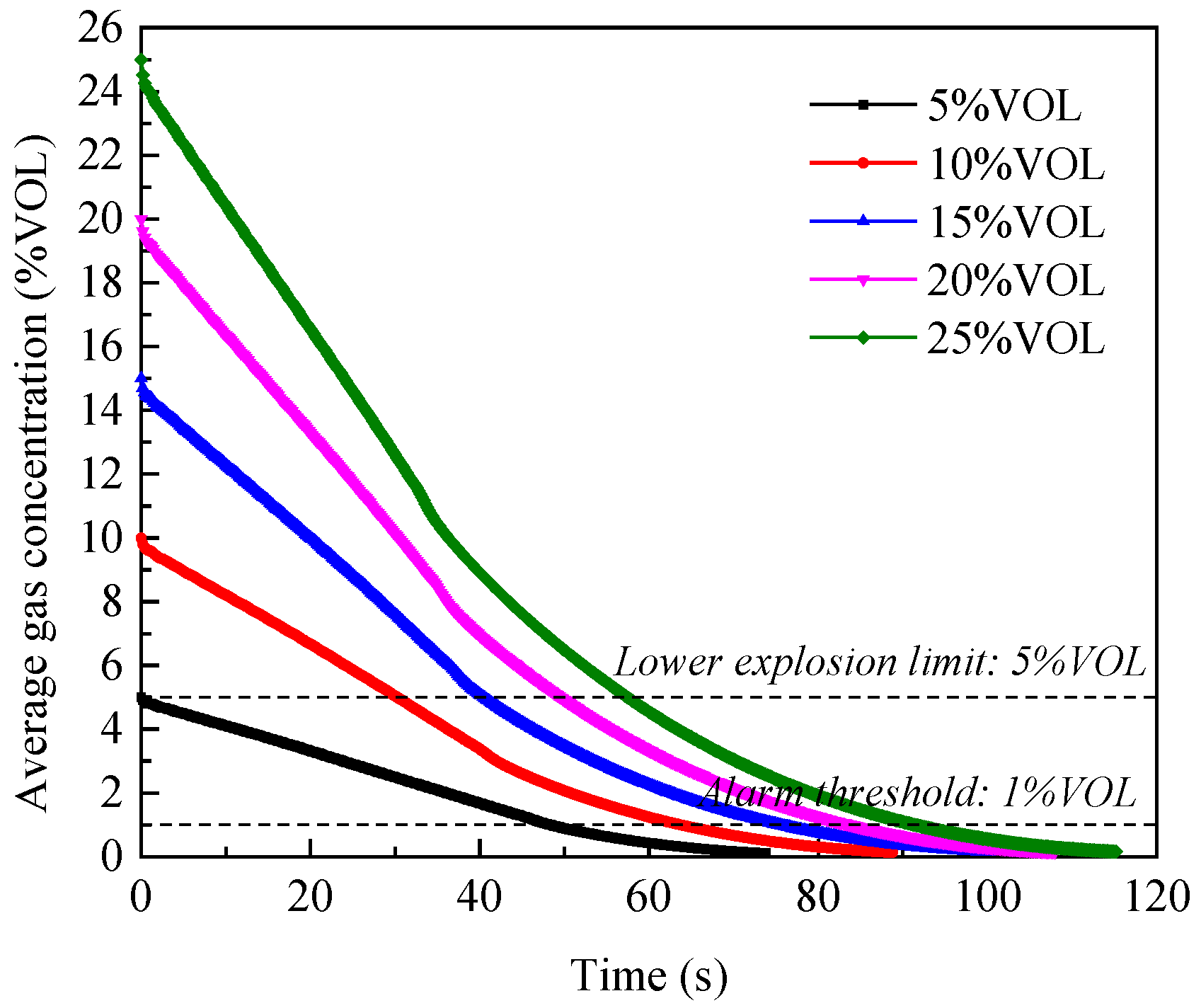
4.2. Concentration Variation
4.3. Ventilation Duration
5. Conclusions
- (1)
- In the exhaust state, the time–concentration curves of almost all positions in the gas tunnel are arranged in a regular manner and exhibit an “asymptote” distribution;
- (2)
- The variation rule of average gas concentration in the tunnel decreases linearly with time at the beginning and exponentially after a certain period of time. The segmented time point is negatively correlated with exhaust velocity, equivalent diameter of the vent and initial gas concentration;
- (3)
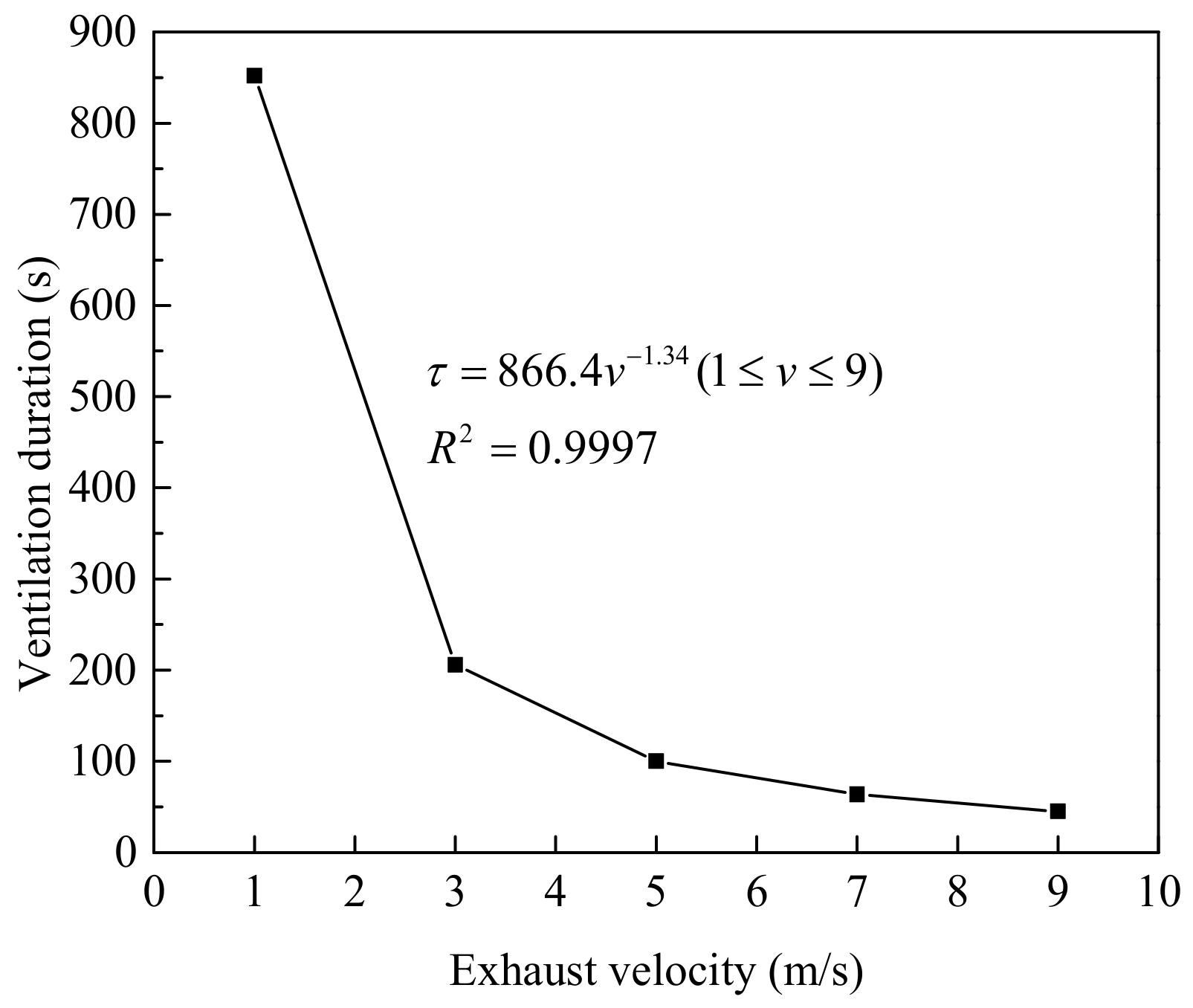
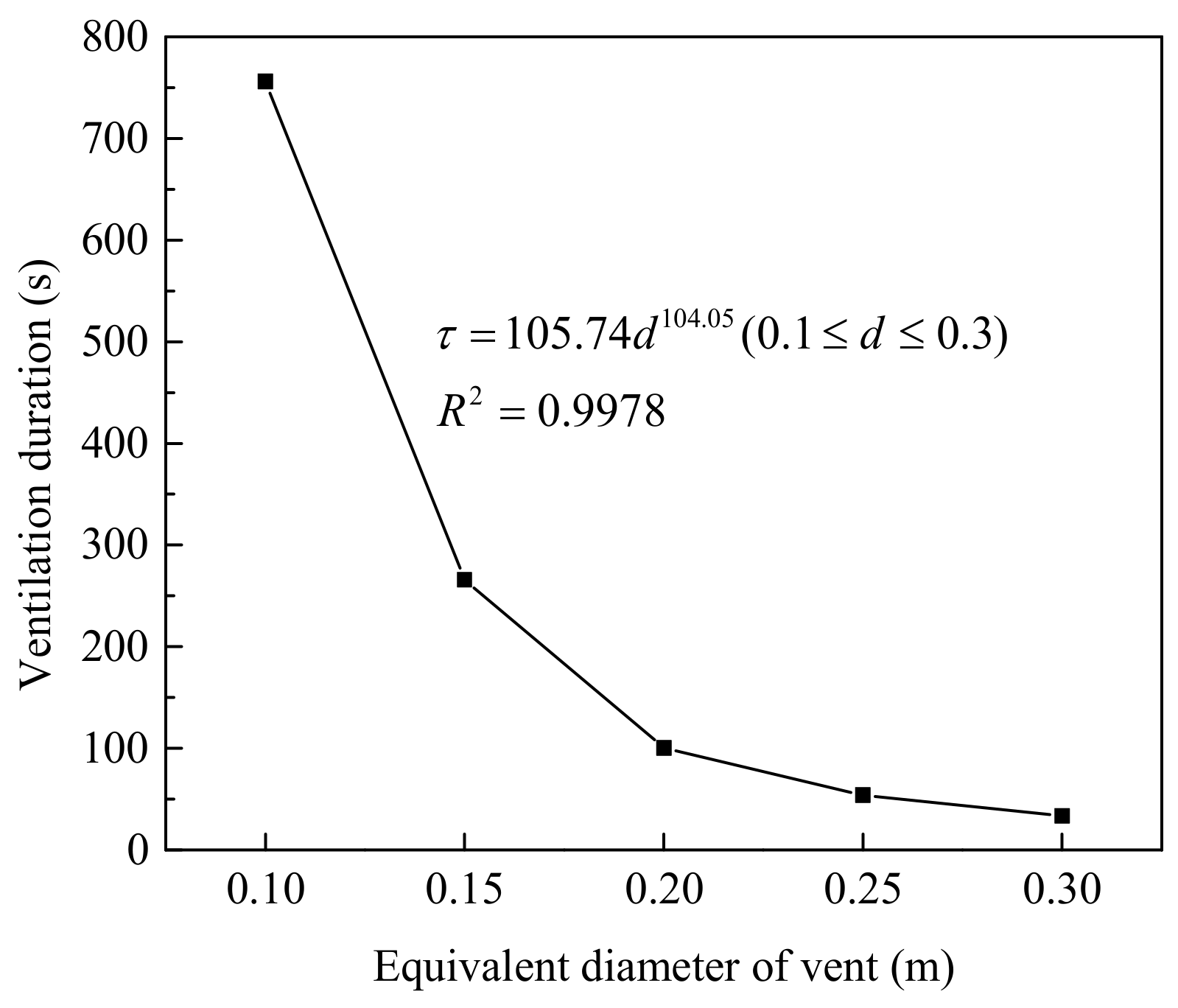
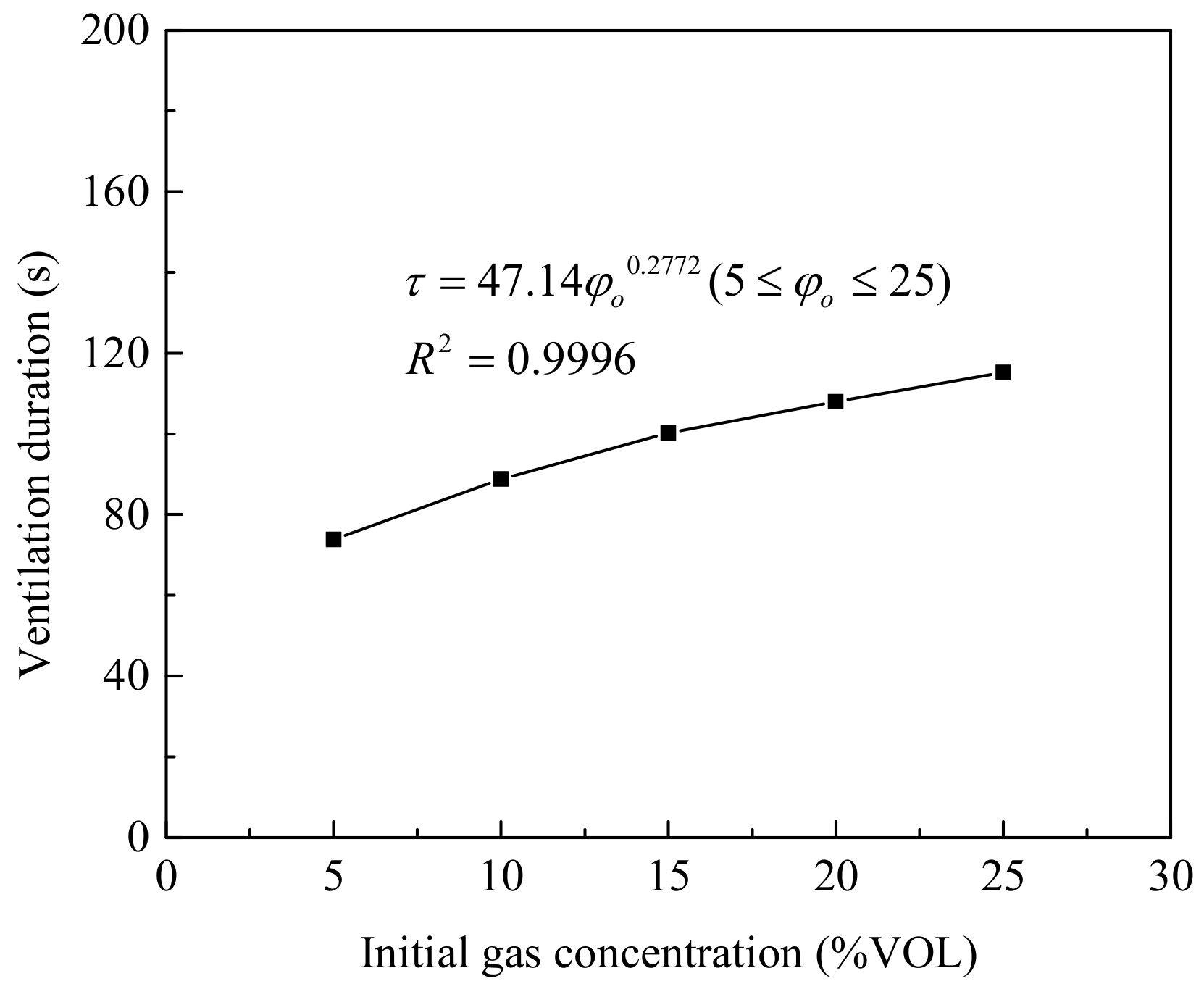
- The ventilation duration has a power function relationship with exhaust velocity, equivalent diameter of the vent and initial gas concentration. On these bases, a calculation model for the ventilation duration of actual standard gas tunnels is established, and the application scope of the model is determined;
- (4)
- The larger the exhaust speed and ventilation size, the higher the ventilation efficiency, but its increasing trend gradually slows down;
- (5)
- When the exhaust velocity exceeds 5 m/s and the equivalent diameter of the vent exceeds 0.2 m, the decreasing rate of the average gas concentration does not increase significantly, and the decreasing trend of the ventilation duration gradually slows down. Therefore, according to the similarity principle, taking efficiency, economy and other factors into account, the optimized exhaust velocity should be 5 m/s, and the equivalent diameter of the vent should be 1 m in practical engineering.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| cross-sectional area of gas tunnel (m2) | |
| area of vent (m2) | |
| a, b, c | scaling parameters |
| D | equivalent diameter of gas tunnel cross section (m) |
| d | equivalent diameter of vent (m) |
| L | length through which gas flows (m) |
| l | perimeter of vent |
| n | number of methane sensors |
| on-way resistance (Pa) | |
| Re | Reynolds number |
| T | air temperature (K) |
| t | time (s) |
| v | exhaust velocity (m/s) |
| average gas velocity in tunnel (m/s) | |
| average gas concentration (%VOL) | |
| gas concentration detected by the i-th methane sensor (%VOL) | |
| initial gas concentration (%VOL) | |
| friction factor | |
| gas viscosity (kg/ms−1) | |
| gas density (kg/m3) | |
| ventilation duration (s) | |
| ventilation duration of fire-retarding division of standard gas tunnel (s) |
References
- Liu, R.; Ren, S.; Fan, J.; Wu, F.; William, N. The air flow structure and gas dispersion behavior in gas tunnel construction through bench cut method. Therm. Sci. 2019, 23, 1417–1424. [Google Scholar] [CrossRef]
- Han, L.; Liu, H.L.; Zhang, W.G.; Ding, X.M.; Chen, Z.X.; Feng, L.; Wang, Z.Y. Seismic behaviors of utility tunnel-soil system: With and without joint connections. Undergr. Space 2022, 7, 798–811. [Google Scholar] [CrossRef]
- Canto-Perello, J.; Curiel-Esparza, J. Risks and potential hazards in utility tunnels for urban areas. Proc. Inst. Civ. Eng. Munic. 2003, 156, 51–56. [Google Scholar] [CrossRef]
- Legrand, L.; Blanpain, O.; Buyle-Bodin, F. Promoting the urban utilities tunnel technique using a decision-making approach. Tunn. Undergr. Space Technol. 2004, 19, 79–83. [Google Scholar] [CrossRef]
- Broere, W. Urban underground space: Solving the problems of today’s cities. Tunn. Undergr. Space Technol. 2016, 55, 245–248. [Google Scholar] [CrossRef]
- Yang, Y.M.; Xiong, Y.; Li, Y.Q.; Meng, X.K.; Wang, P.; Cai, T.Y. Temperature and structural responses of a single-section utility tunnel throughout fire exposure. Front. Struct. Civ. Eng. 2022, 16, 1351–1364. [Google Scholar] [CrossRef]
- Lee, J.; Lee, Y.; Park, S.; Hong, C. Implementing a Digital Twin of an Underground Utility Tunnel for Geospatial Feature Extraction Using a Multimodal Image Sensor. Appl. Sci. 2023, 13, 9137. [Google Scholar] [CrossRef]
- Liang, Y.T.; Yang, Y.L.; Guo, S.D.; Tian, F.H.; Wang, S.F. Combustion mechanism and control approaches of underground coal fires: A review. Int. J. Coal Sci. Technol. 2023, 10, 24. [Google Scholar] [CrossRef]
- Yang, W.X.; Xing, J.C.; Li, J.X.; Ling, J.H.; Hao, H.X.; Yan, Z.Q. Impacts of opening baffle of city road tunnels on natural ventilation performance. Front. Struct. Civ. Eng. 2013, 7, 55–61. [Google Scholar] [CrossRef]
- Xie, B.C.; Han, Y.X.; Huang, H.; Chen, L.N.; Zhou, Y.; Fan, C.G.; Liu, X.P. Numerical study of natural ventilation in urban shallow tunnels: Impact of shaft cross section. Sustain. Cities Soc. 2018, 42, 521–537. [Google Scholar] [CrossRef]
- Shao, Z.Z.; Tan, B.; Hu, R.L.; Song, X.Z.; Guo, Y.; Li, T.Z.; Fu, S.H.; Chen, C.H.; Wang, H.Y. Effect of periodic wide atmospheric pressure change on CO emission in closed goaf. Int. J. Coal Sci. Technol. 2023, 10, 57. [Google Scholar] [CrossRef]
- Colella, F.; Rein, G.; Borchiellini, R.; Carvel, R.; Torero, J.L.; Verda, V. Calculation and design of tunnel ventilation systems using a two-scale modelling approach. Build. Environ. 2009, 44, 2357–2367. [Google Scholar] [CrossRef]
- Liu, Q.; Nie, W.; Hua, Y.; Peng, H.T.; Liu, C.Q.; Wei, C.H. Research on tunnel ventilation systems: Dust diffusion and pollution behaviour by air curtains based on CFD technology and field measurement. Build. Environ. 2019, 147, 444–460. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, Y.; Mao, Z.L.; Bu, R.W.; Gong, J.H.; Wang, Y.X.; Yi, L.; Liang, Y. Analytical and numerical study on natural ventilation performance in single- and gable-slope city tunnels. Sustain. Cities Soc. 2019, 45, 258–270. [Google Scholar] [CrossRef]
- Hua, Y.; Nie, W.; Liu, Q.; Yin, S.; Peng, H.T. Effect of wind curtain on dust extraction in rock tunnel working face: CFD and field measurement analysis. Energy 2020, 197, 117214. [Google Scholar] [CrossRef]
- Xie, Z.W.; Xiao, Y.M.; Jiang, C.X.; Ren, Z.L.; Li, X.Q.; Yu, K.C. Numerical study on fine dust pollution characteristics under various ventilation time in metro tunnel after blasting. Build. Environ. 2021, 204, 108111. [Google Scholar] [CrossRef]
- Xue, Y.G.; Gong, H.M.; Kong, F.M.; Yang, W.M.; Qiu, D.H.; Zhou, B.H. Stability analysis and optimization of excavation method of double-arch tunnel with an extra-large span based on numerical investigation. Front. Struct. Civ. Eng. 2021, 15, 136–146. [Google Scholar] [CrossRef]
- Dastan, A.; Rahiminejad, M.; Sabz, M.; Abbasi, M.; Mokhtari, A.; Sadrizadeh, S.; Abouali, O. CFD simulations of a semi-transverse ventilation system in a long tunnel. Undergr. Space 2023, 11, 153–170. [Google Scholar] [CrossRef]
- Li, Z.; Liang, B.; Xu, M. Urban tunnel body landscape driving comprehensive evaluation study based on biomass-sensing automobile field experiment. Appl. Sci. 2023, 13, 11102. [Google Scholar] [CrossRef]
- Guo, X.S.; Fan, N.; Liu, Y.H.; Liu, X.L.; Wang, Z.K.; Xie, X.T.; Jia, Y.G. Deep seabed mining: Frontiers in engineering geology and environment. Int. J. Coal Sci. Technol. 2023, 10, 23. [Google Scholar] [CrossRef]
- Zhao, H.B.; Tu, S.H.; Liu, X.; Ma, J.Y.; Tang, L. Study of energy-efficient heat resistance and cooling technology for high temperature working face with multiple heat sources in deep mine. Int. J. Coal Sci. Technol. 2023, 10, 35. [Google Scholar] [CrossRef]
- Li, C.X.; Yang, R.S.; Wang, Y.B.; Kang, Y.Q.; Zhang, Y.T.; Xie, P. Theoretical and numerical simulation investigation of deep hole dispersed charge cut blasting. Int. J. Coal Sci. Technol. 2023, 10, 15. [Google Scholar] [CrossRef]
- Song, S.K.; Ren, T.; Dou, L.M.; Sun, J.; Yang, X.H.; Tan, L.H. Fracture features of brittle coal under uniaxial and cyclic compression loads. Int. J. Coal Sci. Technol. 2023, 10, 9. [Google Scholar] [CrossRef]
- Yoo, J.O.; Kim, J.S.; Ra, K.H. A numerical study of the effects of the ventilation velocity on the thermal characteristics in underground utility tunnel. J. Korean Tunn. Undergr. Space Assoc. 2017, 19, 29–39. [Google Scholar] [CrossRef]
- Lu, H.F.; Huang, K.; Fu, L.D.; Zhang, Z.H.; Wu, S.J.; Lyu, Y.; Zhang, X.L. Study on leakage and ventilation scheme of gas pipeline in tunnel. J. Nat. Gas Sci. Eng. 2018, 53, 347–358. [Google Scholar] [CrossRef]
- Zhang, H.T.; Zhao, Y.F. Study on underground utility tunnel fire characteristics under sealing and ventilation conditions. Adv. Civ. Eng. 2020, 2020, 9128704. [Google Scholar] [CrossRef]
- Zhang, J.H.; Dong, Y.; Chen, Y.D.; Sun, H.S.; Wu, J.K.; Liu, W.L.; Chen, J.R.; Pan, S.Q. Numerical simulation of gas ventilation mode in highway gas tunnel. Geofluids 2021, 12, 5549168. [Google Scholar] [CrossRef]
- Vauquelin, O.; Mégret, O. Smoke extraction experiments in case of fire in a tunnel. Fire Saf. J. 2002, 37, 525–533. [Google Scholar] [CrossRef]
- Ingason, H.; Li, Y.Z. Model scale tunnel fire tests with longitudinal ventilation. Fire Saf. J. 2010, 45, 371–384. [Google Scholar] [CrossRef]
- Zhao, Y.C.; Zhu, G.Q.; Gao, Y.J. Experimental study on smoke temperature distribution under different power conditions in utility tunnel. Case Stud. Therm. Eng. 2018, 12, 69–76. [Google Scholar] [CrossRef]
- Li, S.; Liu, X.F.; Wang, J.X.; Zheng, Y.L.; Deng, S.M. Experimental reduced-scale study on the resistance characteristics of the ventilation system of a utility tunnel under different pipeline layouts. Tunn. Undergr. Space Technol. 2019, 90, 131–143. [Google Scholar] [CrossRef]
- Zhang, P.; Lan, H.Q. Effects of ventilation on leakage and diffusion law of gas pipeline in utility tunnel. Tunn. Undergr. Space Technol. 2021, 105, 103557. [Google Scholar] [CrossRef]
- Qian, Q. Present state, problems and development trends of urban underground space in China. Tunn. Undergr. Space Technol. 2016, 55, 280–289. [Google Scholar]
- Zhang, P.; Lan, H.Q.; Yu, M. Reliability evaluation for ventilation system of gas tunnel based on Bayesian network. Tunn. Undergr. Space Technol. 2021, 112, 103882. [Google Scholar] [CrossRef]
- GB 50838-2015; Technical Code for Urban Utility Tunnel Engineering. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2015.
- Auvity, B.; Bellerose, M.; Tateyama, T. Experimental study of the unsteady aerodynamic field outside a tunnel during a train entry. Exp. Fluids 2001, 30, 221–228. [Google Scholar] [CrossRef]
- Zhu, P.G.; Tong, X.N.; Chen, L.; Wang, C.W.; Song, H.; Li, X.Y. Influence of opening area ratio on natural ventilation in city tunnel under block transportation. Sustain. Cities Soc. 2015, 19, 144–150. [Google Scholar] [CrossRef]
- Wang, X.; Wang, M.N.; Qin, P.C.; Yan, T.; Chen, J.; Deng, T.; Yu, L.; Yan, G.F. An experimental study on the influence of local loss on ventilation characteristic of dividing flow in urban traffic link tunnel. Build. Environ. 2020, 174, 106793. [Google Scholar] [CrossRef]
- Manzano-Miura, N.; Gloutak, D.; Bewley, G.P. Characterization of a turbulent flow with independent variation of Mach and Reynolds numbers. Exp. Fluids 2022, 63, 44. [Google Scholar] [CrossRef]
- Smith, D.R.; Gildfind, D.E.; Mee, D.J.; James, C.M.; Allsop, B.V. Magnetohydrodynamic drag force measurements in an expansion tunnel using a stress wave force balance. Exp. Fluids 2020, 61, 180. [Google Scholar] [CrossRef]
- Liu, Y.L.; Wang, Y.Z.; Li, J.H.; Tao, Y.Z.; Qiu, X. Experimental study on the large-scale turbulence structure dynamics of a counterflowing wall jet. Exp. Fluids 2022, 63, 159. [Google Scholar] [CrossRef]



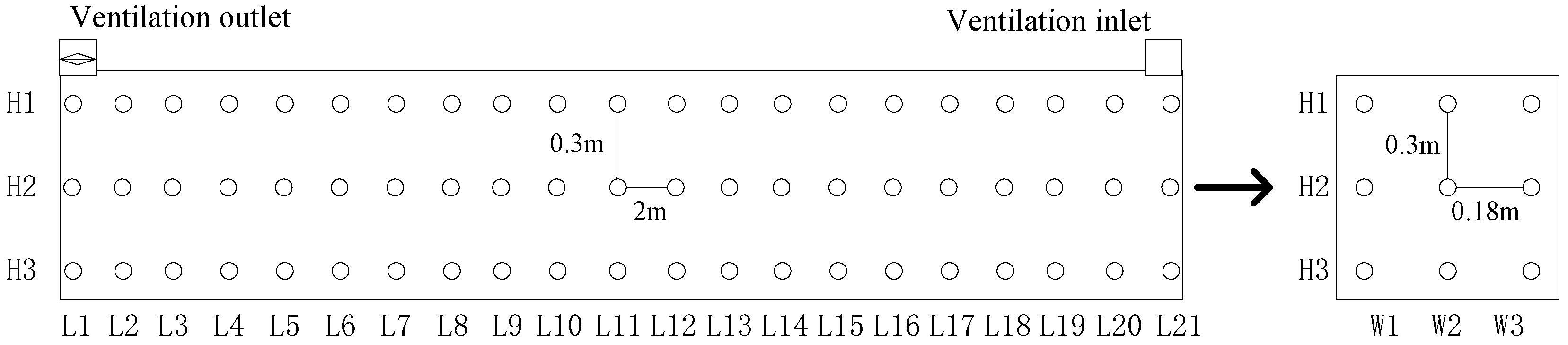

| No. | Initial Gas Concentration (%VOL) | Equivalent Diameter of the Vent (m) | Exhaust Velocity (m/s) |
|---|---|---|---|
| 1 | 15 | 0.2 | 1 |
| 2 | 15 | 0.2 | 3 |
| 3 | 15 | 0.2 | 5 |
| 4 | 15 | 0.2 | 7 |
| 5 | 15 | 0.2 | 9 |
| 6 | 15 | 0.1 | 5 |
| 7 | 15 | 0.15 | 5 |
| 8 | 15 | 0.25 | 5 |
| 9 | 15 | 0.3 | 5 |
| 10 | 5 | 0.2 | 5 |
| 11 | 10 | 0.2 | 5 |
| 12 | 20 | 0.2 | 5 |
| 13 | 25 | 0.2 | 5 |
| Exhaust Velocity (m/s) | Linear Relationship | Exponential Relationship | ||
|---|---|---|---|---|
| Linear Curve | Goodness of Fit R2 | Exponential Curve | Goodness of Fit R2 | |
| 1 | 0.999 | 0.9974 | ||
| 3 | 0.9998 | 0.9654 | ||
| 5 | 0.9995 | 0.982 | ||
| 7 | 0.9996 | 0.9875 | ||
| 9 | 0.9999 | 0.9938 | ||
| Equivalent Diameter of Vent (m) | Linear Relationship | Exponential Relationship | ||
|---|---|---|---|---|
| Linear Curve | Goodness of Fit R2 | Exponential Curve | Goodness of Fit R2 | |
| 0.1 | 0.9992 | 0.9939 | ||
| 0.15 | 0.9997 | 0.9465 | ||
| 0.2 | 0.9995 | 0.982 | ||
| 0.25 | 0.9998 | 0.9899 | ||
| 0.3 | 0.9999 | 0.9929 | ||
| Initial Gas Concentration (%VOL) | Linear Relationship | Exponential Relationship | ||
|---|---|---|---|---|
| Linear Curve | Goodness of Fit R2 | Exponential Curve | Goodness of Fit R2 | |
| 5 | 0.9998 | 0.994 | ||
| 10 | 0.9995 | 0.9857 | ||
| 15 | 0.9995 | 0.982 | ||
| 20 | 0.9996 | 0.9765 | ||
| 25 | 0.9997 | 0.972 | ||
| Exhaust Velocity (m/s) | 1 | 3 | 5 | 7 | 9 |
|---|---|---|---|---|---|
| Ventilation duration (s) | 852 | 205.8 | 100.2 | 63.6 | 45 |
| Equivalent Diameter of the Vent (m) | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 |
|---|---|---|---|---|---|
| Ventilation duration (s) | 756 | 265.8 | 100.2 | 54 | 33.6 |
| Initial Gas Concentration (%VOL) | 5 | 10 | 15 | 20 | 25 |
|---|---|---|---|---|---|
| Ventilation duration (s) | 73.8 | 88.8 | 100.2 | 108 | 115.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Lan, H.-Q. Experimental Study on Dynamic Exhaust Law for Ventilation System of Gas Tunnel. Appl. Sci. 2023, 13, 12783. https://doi.org/10.3390/app132312783
Zhang P, Lan H-Q. Experimental Study on Dynamic Exhaust Law for Ventilation System of Gas Tunnel. Applied Sciences. 2023; 13(23):12783. https://doi.org/10.3390/app132312783
Chicago/Turabian StyleZhang, Ping, and Hui-Qing Lan. 2023. "Experimental Study on Dynamic Exhaust Law for Ventilation System of Gas Tunnel" Applied Sciences 13, no. 23: 12783. https://doi.org/10.3390/app132312783
APA StyleZhang, P., & Lan, H.-Q. (2023). Experimental Study on Dynamic Exhaust Law for Ventilation System of Gas Tunnel. Applied Sciences, 13(23), 12783. https://doi.org/10.3390/app132312783






