Influence of Open Differential Design on the Mass Reduction Function
Abstract
:1. Introduction
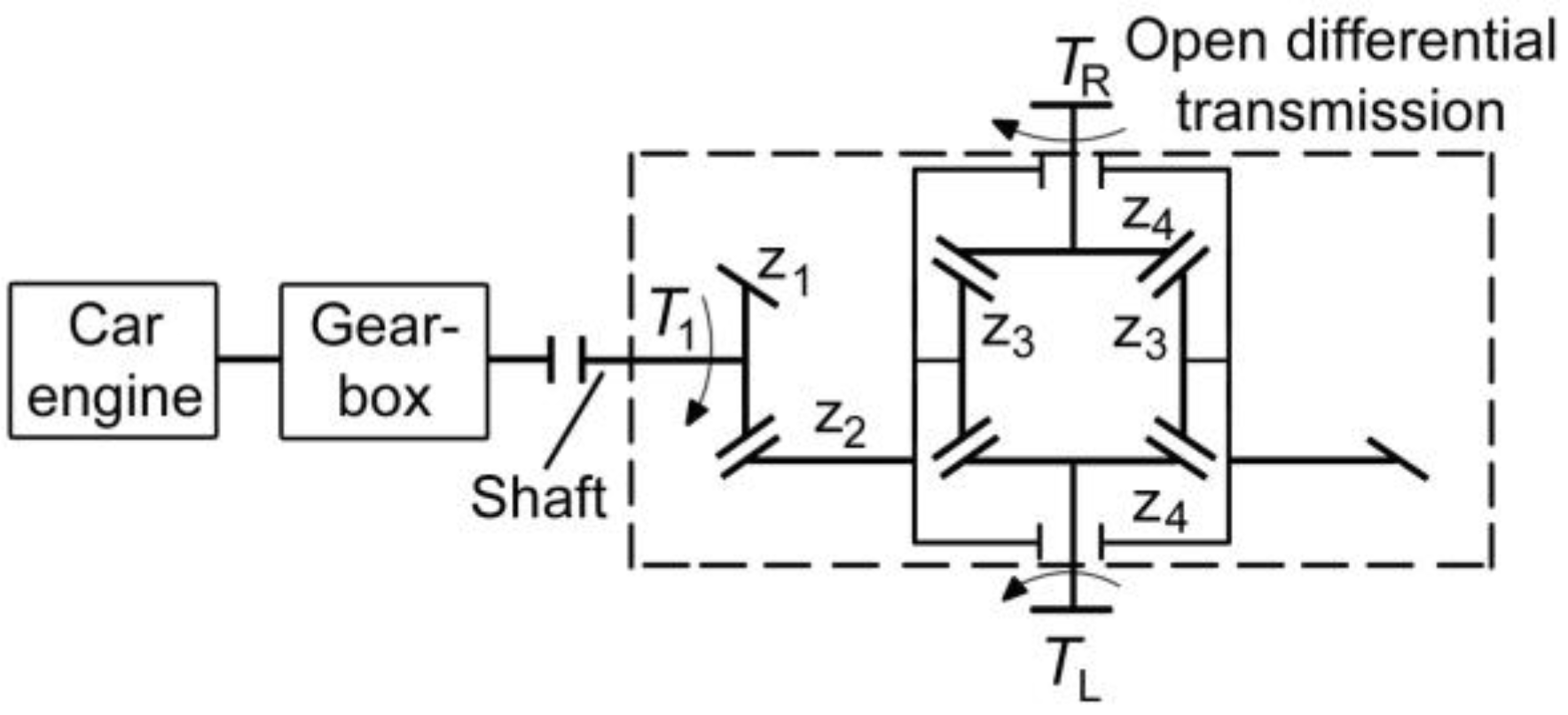
1.1. Differential Transmissions Overview
1.2. Mass Reduction Impact on Improving Energy Efficiency
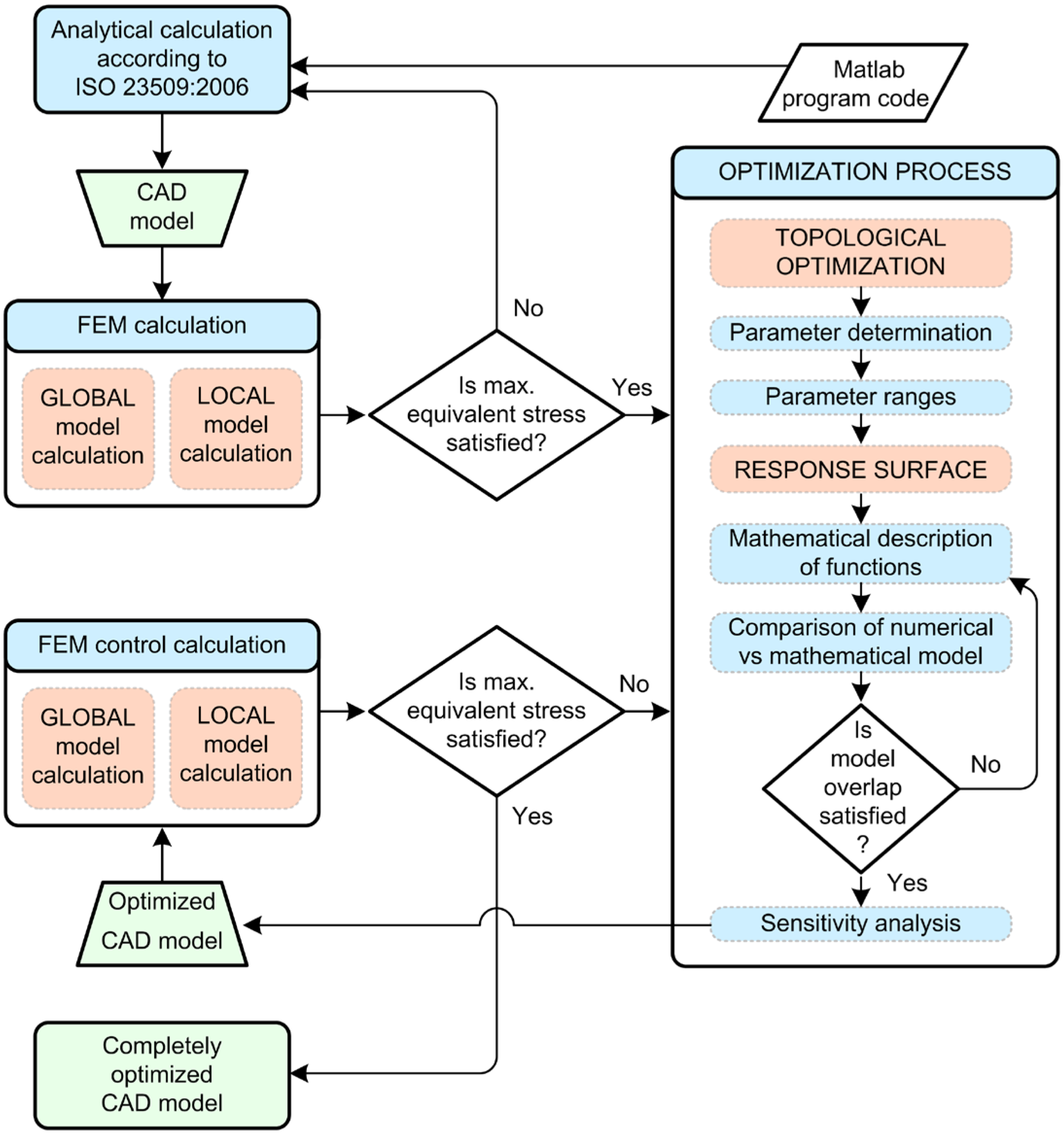
2. Proposed Methodology and Research Structure
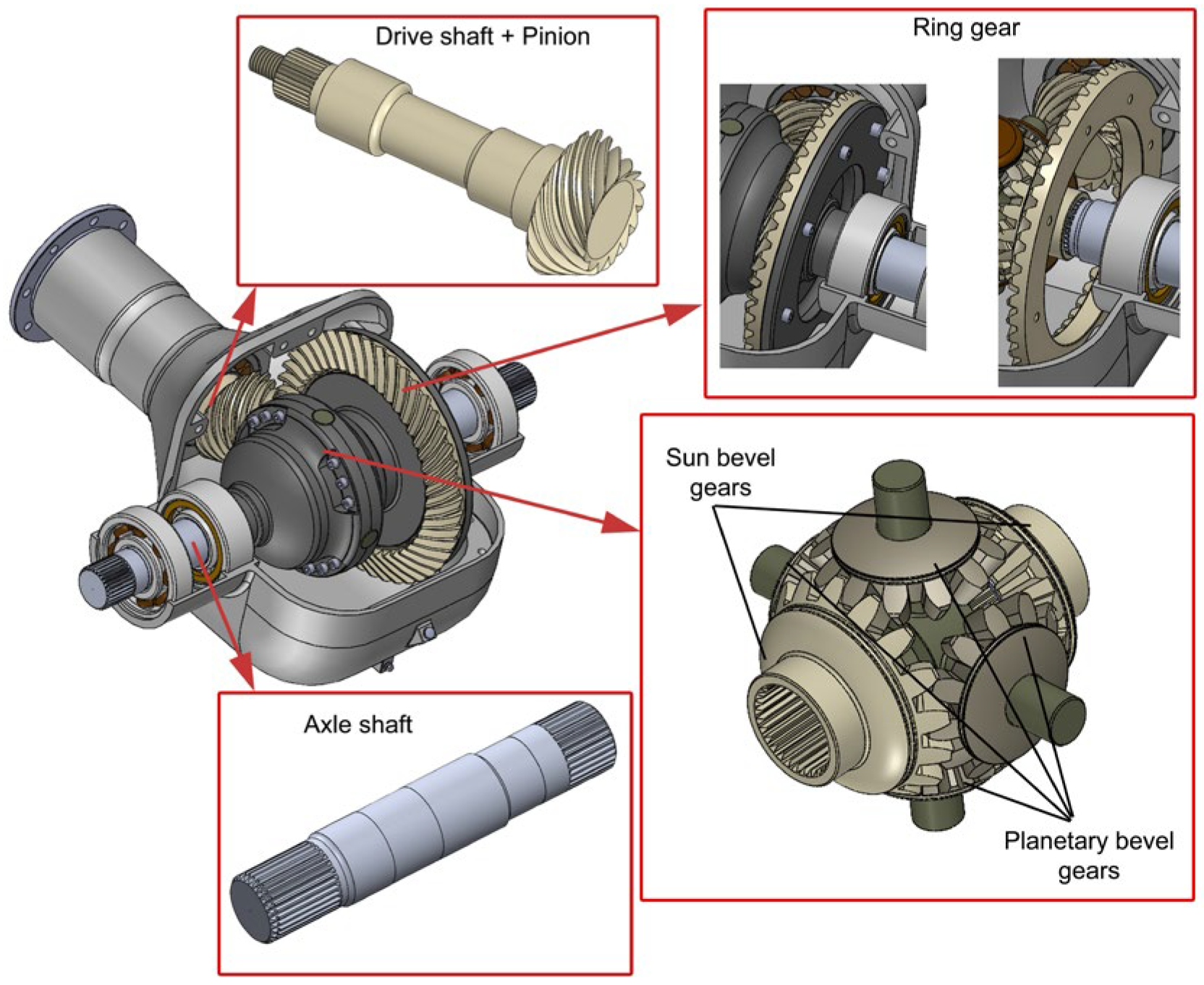
3. Design of the ODT
3.1. Design Requirements of the ODT
3.2. Loads on the Input and Output Side of the Differential Transmission
3.3. Hypoid Bevel Gears Calculation
3.3.1. Dimensioning of the Driving and Driven Hypoid Bevel Gears
3.3.2. Stress Calculation of Hypoid Bevel Gears in the Tooth Root and Tooth Face Flank
3.4. Sun and Planetary Bevel Gears Calculation
3.4.1. Dimensioning of the Planetary and Sun Bevel Gears
3.4.2. Stress Calculation of Planetary and Sun Bevel Gears in the Tooth Root and the Tooth Face Flank
4. Numerical Analysis of Differential Transmission
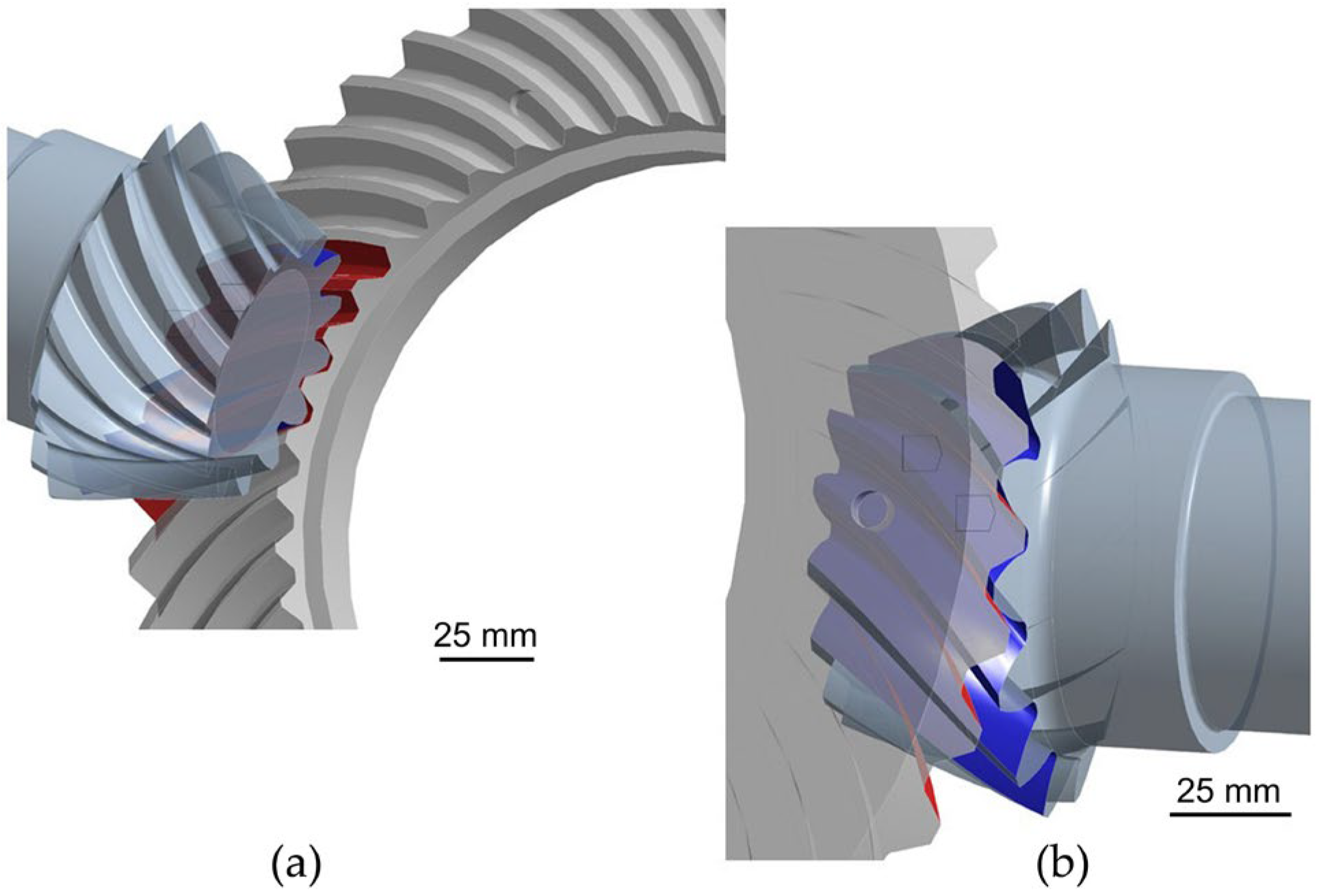
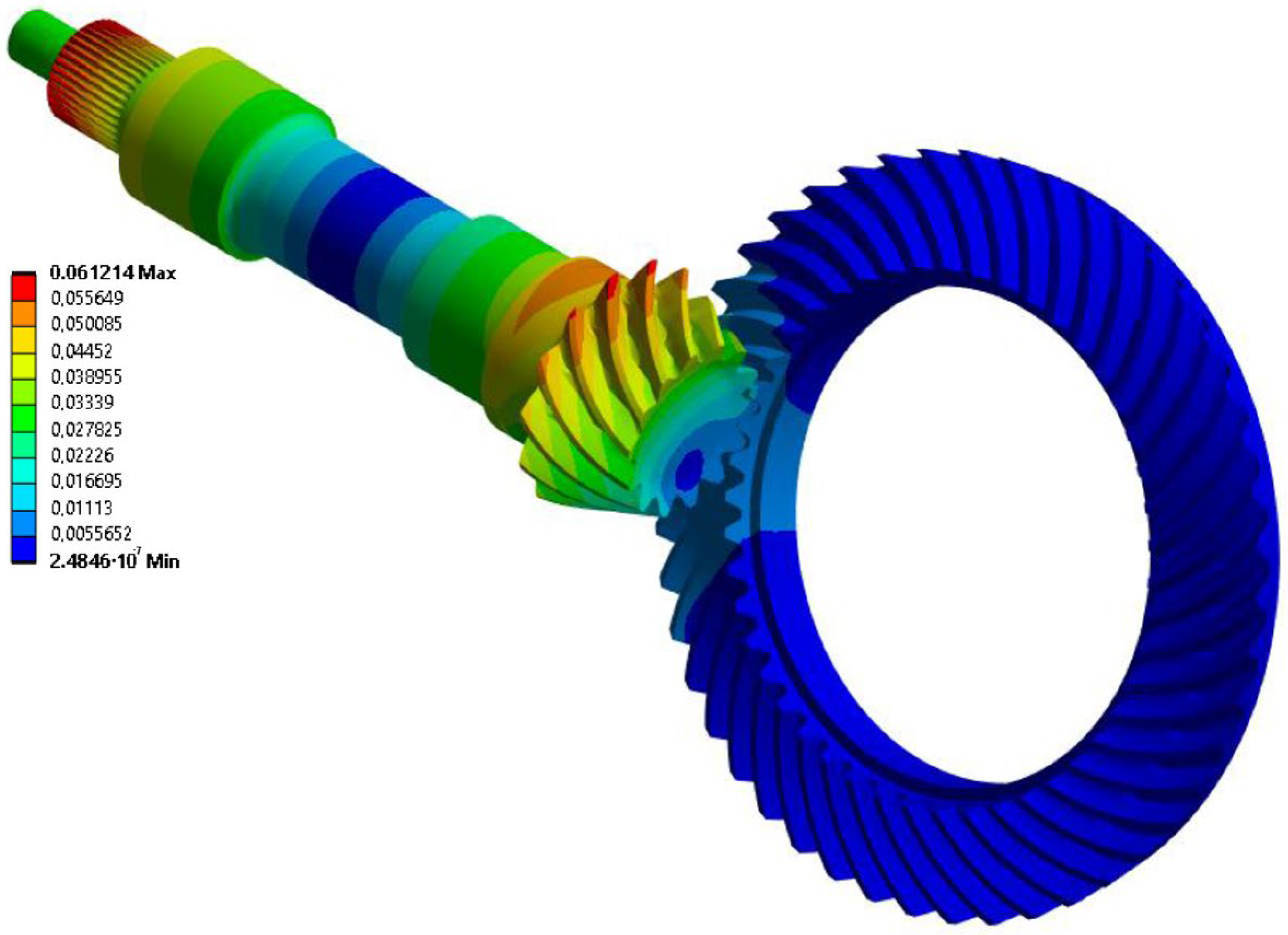
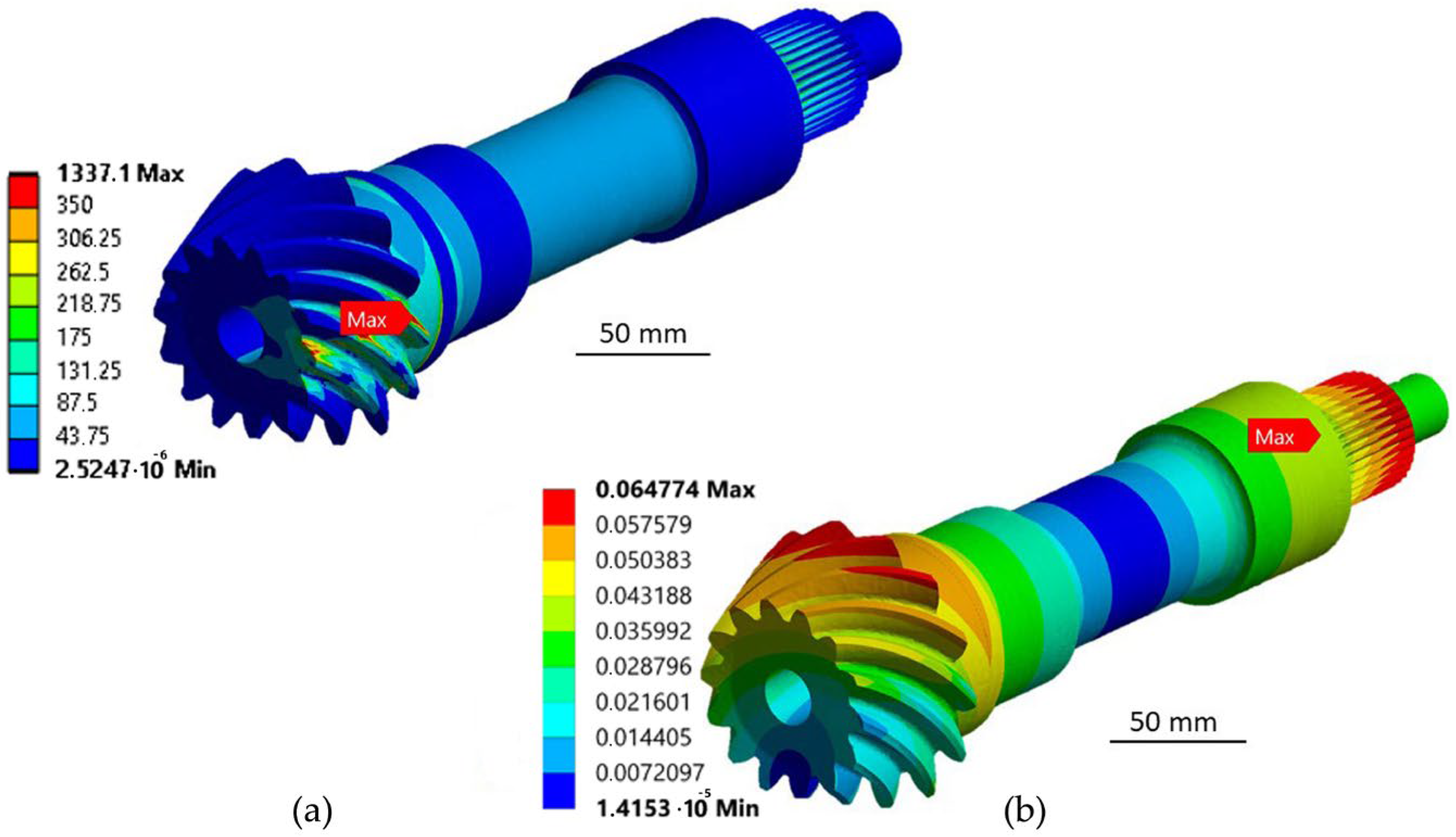
4.1. Analysis of Stress and Displacement of Bevel Gear and Pinion Gear
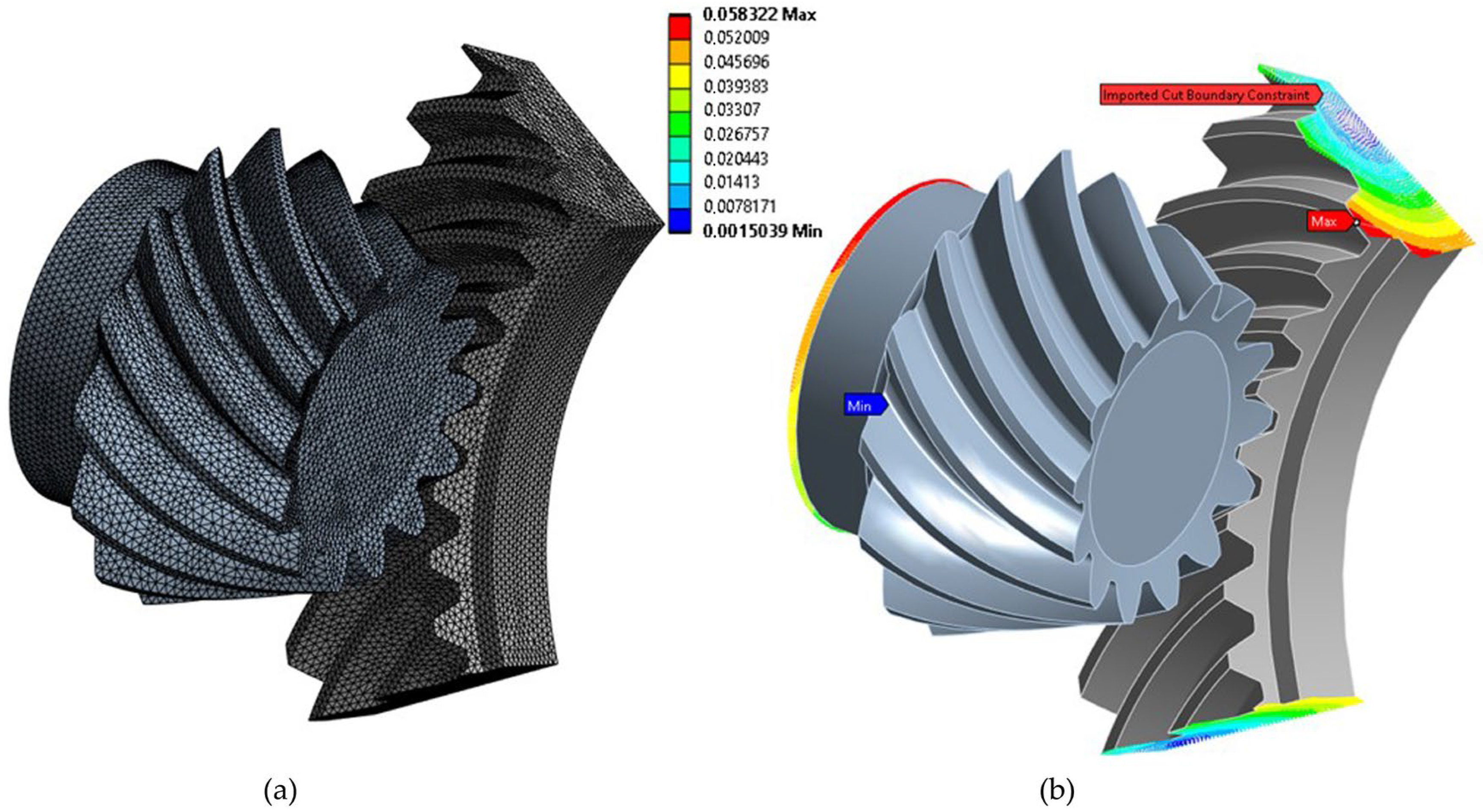
4.2. Submodeling of the Pinion and Bevel Gear
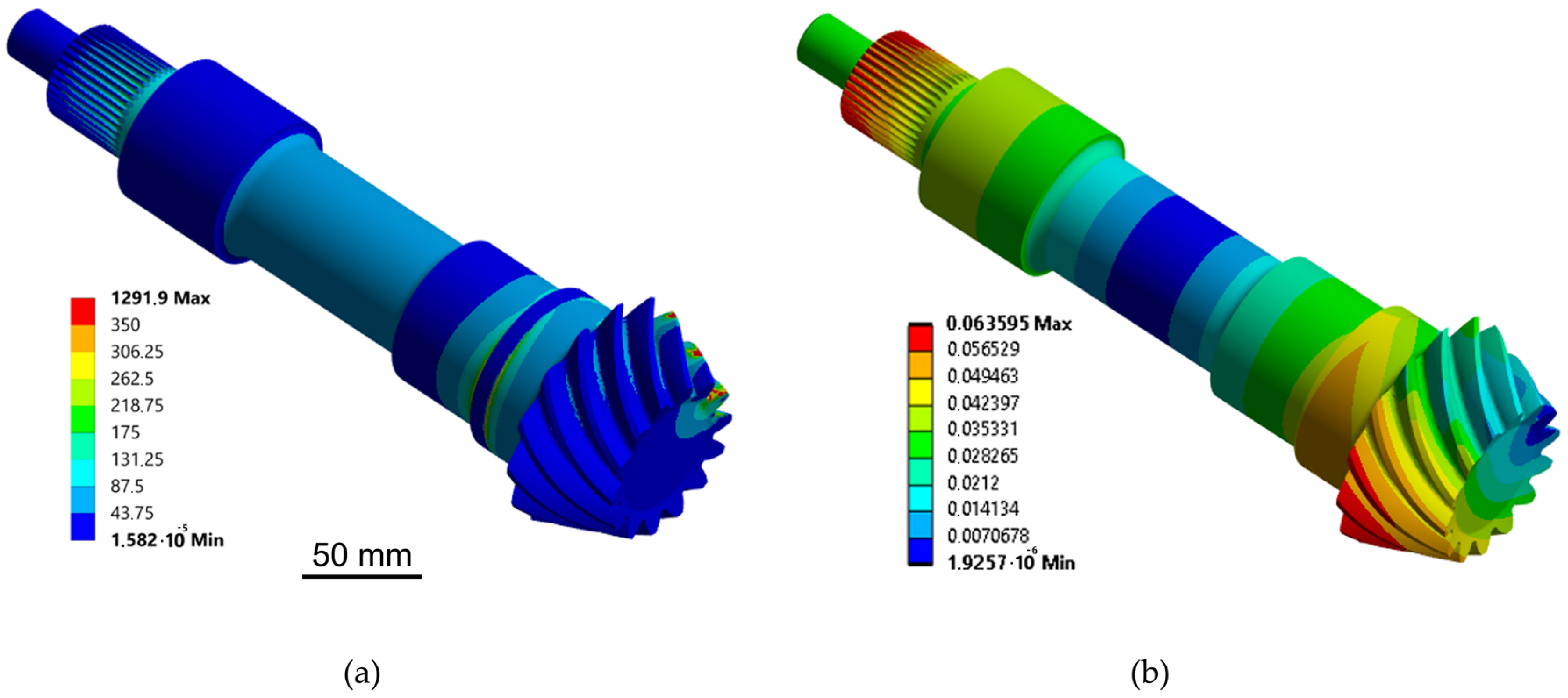
4.3. Analysis of Stress and Displacement of Drive Shaft
5. Optimization of Differential Transmission
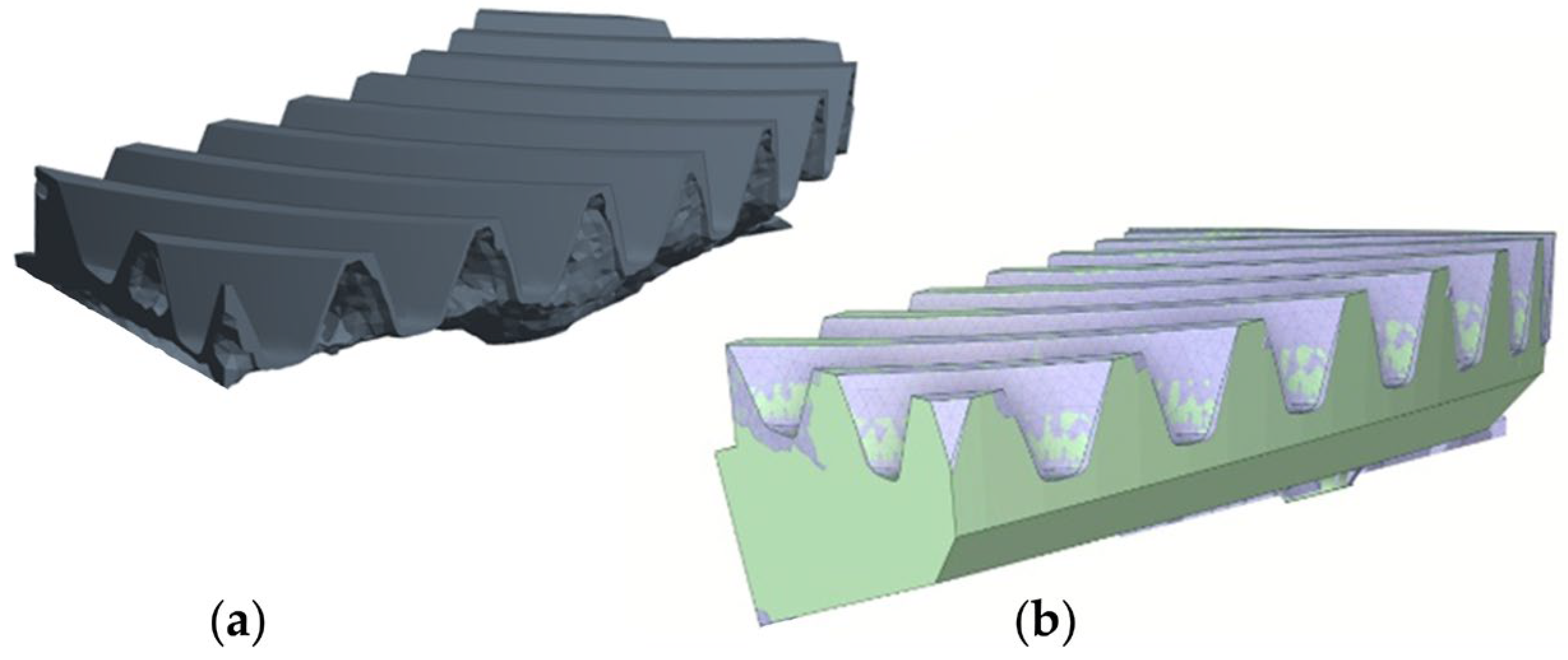
5.1. Topological Optimization and Determination of Design Parameters
5.2. RSM Model
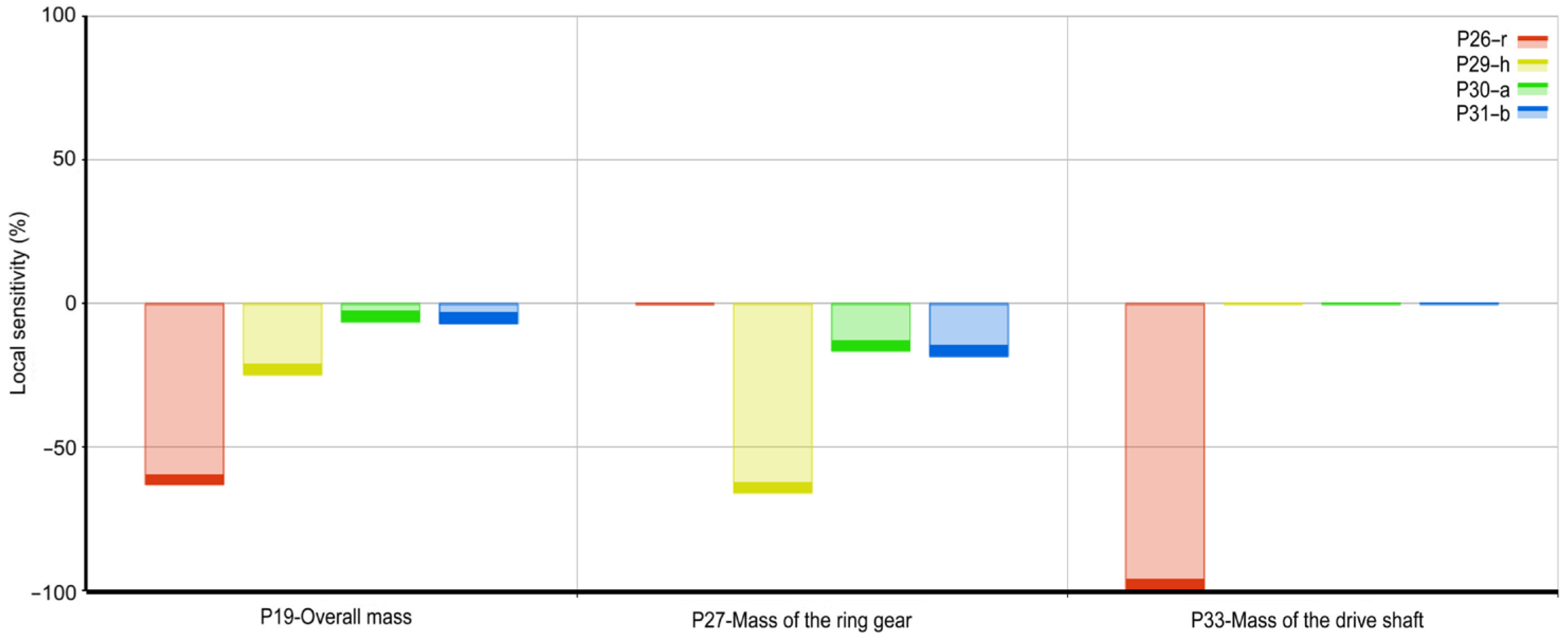
5.3. Analysis of Sensitivity of Parameter Change on Response Objective
6. Numerical Calculation of the Optimized Differential Gear
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | hypoid offset |
| av | vehicle acceleration |
| A3, A4, A5, A6, A7 | intermediate variables |
| b | tooth width |
| b1 | pinion gear face width |
| b2 | ring gear face width |
| b3 | tooth width of the planetary gear |
| b4 | tooth width of the sun gear |
| c | clearance |
| da3 | planetary gear addendum circle diameter |
| da4 | sun gear addendum circle diameter |
| dia3 | planetary gear inner addendum diameter of tooth |
| dia4 | sun gear inner addendum diameter of tooth |
| dm1 | pinion mean pitch diameter |
| dm2 | ring gear mean pitch diameter |
| dm3 | planetary gear mean pitch diameter |
| dm4 | sun gear mean pitch diameter |
| dv3 | pitch diameter of equivalent gear (planetary) |
| dv4 | pitch diameter of equivalent gear (sun) |
| dva3 | addendum diameter of equivalent gear (planetary) |
| dva4 | addendum diameter of equivalent gear (sun) |
| dvb3 | base diameter of equivalent gear (planetary) |
| dvb4 | base diameter of equivalent gear (sun) |
| dvm3 | pitch diameter of middle equivalent gear (planetary) |
| dvm4 | pitch diameter of middle equivalent gear (sun) |
| d3 | pitch circle diameter of the planetary gear |
| d4 | pitch circle diameter of the sun gear |
| F | hypoid dimensional factor |
| Ff | friction force |
| FIN | vehicle’s inertial force |
| Fmt1 | tangential force on the pinion |
| Fmt2 | tangential force on the ring gear |
| Fmt3 | tangential force on the planetary gear |
| Fmt4 | tangential force on the sun gear |
| FRI | rising resistance force |
| FRO | rolling resistance force |
| fRO | rolling resistance factor |
| FTR | traction force |
| FTRD | total resistance force of driven machine |
| Fw | reaction force in the wheel |
| g | acceleration of the earth’s gravity |
| Gv | vehicle weight force |
| h | overhang height of the ring gear |
| h3 | planetary gear whole depth |
| h4 | sun gear whole depth |
| ha3 | addendum depth for zero pair of bevel gears (planetary) |
| ha4 | addendum depth for zero pair of bevel gears (sun) |
| hf3 | dedendum depth for zero pair of bevel gears (planetary) |
| hf4 | dedendum depth for zero pair of bevel gears (sun) |
| id | transmission ratio of the differential transmission |
| i1, i2, i3, i4, i5, iR | gearbox transmission ratios |
| KFX | size influence factor |
| KFα | load distribution factor |
| KFβ | load distribution factor along the length of the tooth flank |
| KHX | factor of dimensions influence on the load capacity of the tooth flank |
| KHα | load distribution factor |
| KHβ | load distribution factor along the length of the tooth flank |
| KL | influence factor of lubricating oil |
| mall | overall mass of optimized design elements |
| mf | module considering of load of tooth face flank |
| mn | mean normal module |
| mr | module considering of load of tooth root |
| mv, max | maximum vehicle mass |
| m1 | mass of the ring gear |
| m2 | mass of the drive shaft |
| Pmax | driving machine power (engine power) |
| Po max | power on the motor output shaft |
| P1 | power delivered to the drive bevel gear (pinion gear) |
| P2 | output power of the differential transmission |
| Ra | length of the derivative of the dividing cone |
| Rmint | intermediate variable |
| Rm1 | mean cone distance of the pinion |
| Rm2 | mean cone distance of the ring gear |
| r | inner radius of the drive shaft |
| SFmin | minimum safety factor against root breakage |
| SHlim | minimum anti-pitting factor |
| SHmin | minimum safety factor against tooth flank fracture |
| TL | torques on the left drive wheel |
| torques on the left drive wheel | |
| Tmax | maximum engine torque |
| TR | torques on the right drive wheel |
| torques on the right drive wheel | |
| TW | torque on the drive wheels |
| torque on the drive wheels | |
| tzm1 | crossing point to calculation point along pinion axis |
| tzm2 | crossing point to calculation point along ring gear axis |
| T1 | input torque to the differential transmission |
| T2 | torque of the hypoid ring bevel gear (with included efficiency of the open differential) |
| torque of the hypoid ring bevel gear (without including the losses of the kinematic chain) | |
| uv | transmission ratio of supplementary bevel gears |
| YF | tooth shape factor |
| YN | is service life factor |
| YR | roughness factor |
| YS | notch action factor |
| Yβ | impact factor of tooth locking on the stress distribution in the root |
| YεV | load share factor of auxiliary gears |
| ZHV | tooth shape factor |
| ZM | material factor |
| ZN | service life factor |
| ZR | roughness influence factor |
| ZV | speed influence factor |
| ZW | influence factor of flank hardening |
| z1 | teeth number of the hypoid pinion bevel gear |
| z2 | teeth number of the hypoid ring bevel gear |
| z3 | teeth number of the planetary bevel gear |
| z4 | teeth number of the sun bevel gear |
| ZεV | coverage factor |
| αlim | limit pressure angle |
| αn | mean normal pressure angle |
| βm1 | spiral angle of hypoid pinion bevel gear |
| βm2 | spiral angle of hypoid ring bevel gear |
| γ | rising angle (slope angle) |
| δa3 | face angle of planetary gear |
| δa4 | face angle of sun gear |
| δ1 | pinion gear pitch angle |
| δ2 | ring gear pitch angle |
| δ3 | planetary gear pitch angle |
| ηc | efficiency of the cardan shaft |
| ηd | efficiency of the open differential |
| ηg | efficiency of the gearbox |
| κa3 | planetary gear teeth face angle |
| κa4 | sun gear teeth face angle |
| λ | tooth width factor |
| µ | friction factor for asphalt surface |
| ΔΣ | shaft angle departure |
| Σ | shaft angle |
| σFlim1 | amount of permanent dynamic strength for tooth root (pinion) |
| σFlim2 | amount of permanent dynamic strength for tooth root (ring gear) |
| σFlim3 | amount of permanent dynamic strength for tooth root (planetary gear) |
| σFlim4 | amount of permanent dynamic strength for tooth root (sun gear) |
| σF1 | bending stress on pinion tooth root |
| σF2 | bending stress on ring gear tooth root |
| σF3 | bending stress on planetary tooth root |
| σF4 | bending stress on sun tooth root |
| σFP1 | allowed stress on pinion tooth root |
| σFP2 | allowed stress on ring gear tooth root |
| σFP3 | allowed stress on planetary tooth root |
| σFP4 | allowed stress on sun tooth root |
| σHlim1 | permanent dynamic strength for tooth face flank (pinion) |
| σHlim2 | permanent dynamic strength for tooth face flank (ring gear) |
| σHlim3 | permanent dynamic strength for tooth face flank (planetary gear) |
| σHlim4 | permanent dynamic strength for tooth face flank (sun gear) |
| σH1 | Hertzian stress in the kinematic pole of pinion |
| σH2 | Hertzian stress in the kinematic pole of ring gear |
| σH3 | Hertzian stress in the kinematic pole of planetary gear |
| σH4 | Hertzian stress in the kinematic pole of sun gear |
| σHP1 | allowed Hertzian stress on pinion tooth face flank |
| σHP2 | allowed Hertzian stress on ring gear tooth face flank |
| σHP3 | allowed Hertzian stress on planetary tooth face flank |
| σHP4 | allowed Hertzian stress on sun tooth face flank |
| ζm | pinion offset angle in the axial plane |
| ζmp | pinion offset angle in the pitch plane |
| υm | auxiliary angle |
| ψ | contribution factor of rotating masses |
| ωmax | angular velocity at which Tmax is reached |
| ω1 | angular velocity of the hypoid pinion bevel gear |
| ω2 | angular velocity of the hypoid ring bevel gear |
References
- Veeranjaneyul, C.; Hari Babu, U. Design and structural analysis of differential gear box at different loads. Int. J. Adv. Eng. Res. Stud. 2012, 1, 65–69. [Google Scholar]
- Sivan Teja, N.; Dinesh Babu, K.; Siva Nagendra, M.; Phanideep, C.; Sai Trinadh, J. Design and analysis of differential gear box in automobiles. Int. J. Mech. Eng. Technol. 2017, 8, 175–185. [Google Scholar]
- Mohite, M.A.; Dohare, P.; Thange, R.; Dhorsinge, J.; Walunj, W. Design & Analysis of Electronically Controlled Self-locking Differential Gear Box. Int. J. Sci. Eng. Res. 2020, 11, 275–281. [Google Scholar]
- Waghmare, A.S.; Shinde, S.V.; Kavale, A.S.; Tathe, P.G. Differential Locking System. Int. J. Sci. Res. Dev. 2017, 4, 932–938. [Google Scholar]
- Huh, Y.; Kim, H.-I.; Shin, I.-H.; Koo, J.-M.; Seok, C.-S. A Study on the Differential Gearing Device with the Faculty of a Limited Slip Differential. Int. J. Precis. Eng. Manuf. 2009, 10, 91–96. [Google Scholar] [CrossRef]
- Gadola, M.; Chindamo, D. The Mechanical Limited–Slip Differential Revisited: High-Performance and Racing Car Applications. Int. J. Appl. Eng. Res. 2018, 13, 1478–1495. [Google Scholar]
- Cheli, F.; Pedrinelli, M.; Resta, F.; Travaglio, G.; Zanchetta, M.; Zorzutti, A. Development of a new control strategy for a semi-active differential for high-performance vehicle. Int. J. Veh. Mech. Mobil. 2007, 44, 202–215. [Google Scholar] [CrossRef]
- Yahiya, M.; Imaduddin, S.; Maviya, M.M.; Mujtabauddin, M.; Moulal, S. Design and Analysis of Torsen Differential. Int. J. Sci. Dev. Res. 2018, 3, 74–83. [Google Scholar]
- Directive 2012/27/EU of the European Parliament and of the Council. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2012:315:0001:0056:en:PDF (accessed on 13 December 2023).
- EN 16247-4:2022; Energy Audits—Part 4: Transport. CEN-CENELEC: Brussels, Belgium, 2022.
- Pandey, S.; Singh, N.N.; Sinha, P.K. Modeling, Design & Analysis of Differential Gear Box and its Housing through FEM, SolidWorks and Ansys Benchwork 14.0. Int. J. Eng. Sci. Res. Technol. 2017, 6, 127–139. [Google Scholar]
- Pawar, P.B.; Utpat, A.A. Analysis of Composite Material Spur Gear under Static Loading Condition. Mater. Today Proc. 2015, 2, 2968–2974. [Google Scholar] [CrossRef]
- Arul Prince, A.J.; Reddy, A.S.; Nagateja, K.; Chowdary, N.N. Design and Analysis of a Spur Gear with Composite Material. Int. J. Eng. Res. Technol. 2021, 10, 350–362. [Google Scholar]
- Demšar, I.; Černe, B.; Tavčar, J.; Vukašinović, N.; Zorko, D. Agile development of Polymer Power Transmission Systems for e-Mobility—A Novel Methodology Based on a e-Bike Drive Case Study. Polymers 2023, 15, 68. [Google Scholar] [CrossRef] [PubMed]
- Alcácer, V.; Ávila, F.; Marat-Mendes, R. Design, Manufacturing & Analysis of an ABS Differential Gear System model. In Proceedings of the 6th International Conference on Mechanics and Materials in Design, Azores, Portugal, 26–30 July 2015. [Google Scholar]
- Andersson, M. Churning Losses and Efficiency in Gearboxes. Ph.D. Thesis, Department of Machine Design, KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]
- Zou, L.; Du, M.; Jia, B.; Xu, J.; Ren, L. Numerical Simulation of the Churning Power Losses in the Automotive Hypoid Gear Reducer. J. Appl. Math. Phys. 2018, 6, 1951–1956. [Google Scholar] [CrossRef]
- Concli, F.; Gorla, C.; Della Torre, A.; Montenegro, G. Churning Power Losses of Ordinary Gears: A New Approach Based on the Internal Fluid Dynamics Simulations. Lubr. Sci. 2015, 27, 313–326. [Google Scholar] [CrossRef]
- Liu, H.; Jurkschat, T.; Lohner, T.; Stahl, K. Determination of Oil Distribution and Churning Power Loss of Gearboxes by Finite Volume CFD Method. Tribol. Int. 2017, 109, 346–354. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, L.; Gao, Y.; Kou, C.; Yang, S.; Liu, L. Research of the Optimized Management of Agricultural Machinery Allocation Path Based on Teaching and Learning Optimization Algorithm. Tech. Gaz. 2022, 29, 456–463. [Google Scholar] [CrossRef]
- Qin, Z.; Wu, Y.-T.; Lyu, S.-K. A Review of Recent Advances in Design Optimization of Gearbox. Int. J. Precis. Eng. Manuf. 2018, 19, 1753–1762. [Google Scholar] [CrossRef]
- Tharmakulasingam, R. Transmission Error in Spur Gears: Static and Dynamic Finite-Element Modeling and Design Optimization. Ph.D. Thesis, School of Engineering and Design, Brunel University, London, UK, 2009. [Google Scholar]
- Chong, T.H.; Yang, W.Y.; Lee, K.H. An Optimum Design of Planetary Gear Considering the Volume. In Proceedings of the Korean Society of Manufacturing Technology Engineering Autumn Conference, Yeosu, Republic of Korea, 17–18 October 2019. [Google Scholar]
- Noh, S.Y.; Kim, L.S.; Cho, S.H.; Lyu, S.K. Study on the Tooth Micro-geometry Optimization of Planetary Gear for Drive Reducer. J. Korean Soc. Precis. Eng. 2017, 34, 371–376. [Google Scholar] [CrossRef]
- Jeon, M.H.; Joen, N.; Kim, L.S.; Cho, S.H.; Lyu, S.K. Study on the Gear Tooth Micro-Geometry Optimization of Angle Drive Unit. J. Korean Soc. Precis. Eng. 2018, 35, 473–478. [Google Scholar] [CrossRef]
- Yaw, M.W.; Chong, K.H. Optimize Volume for Planetary Gear Train by using Algorithm Based Artificial Immune System. Int. J. Adv. Trends Comput. Sci. Eng. 2020, 9, 3757–3762. [Google Scholar] [CrossRef]
- Urbas, U.; Zorko, D.; Vukašinović, N. Machine learning based nominal root stress calculation model for gears with a progressive curved path of contact. Mech. Mach. Theory 2021, 165, 104430. [Google Scholar] [CrossRef]
- Zorko, D.; Štiglic, J.; Černe, B.; Vukašinović, N. The effect of center distance error on the service life of polymer gears. Polym. Test. 2023, 123, 108033. [Google Scholar] [CrossRef]
- Daoudi, K.; Boudi, E.M. Genetic Algorithm Approach for Spur Gears Design Optimization. In Proceedings of the International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 5–6 December 2018. [Google Scholar] [CrossRef]
- Taleb, A.A.; El Amine, M.; Sallaou, M.; Zaghar, H. Multi-level Optimization of Gear Trains with Spur Gears. In Proceedings of the 5th International Conference on Optimization and Applications (ICOA), Kenitra, Morocco, 25–26 April 2019. [Google Scholar] [CrossRef]
- Maputi, E.S.; Arora, R. Design optimization of a three-stage transmission using advanced optimization techniques. Int. J. Simul. Multidiscip. Des. Optim. 2019, 10, A8. [Google Scholar] [CrossRef]
- Gan, S.; Fang, X.; Wei, X. Parametric Analysis on Landing Gear Strut Friction of Light Aircraft for Touchdown Performance. Appl. Sci. 2021, 11, 5445. [Google Scholar] [CrossRef]
- Kalanchiam, M.; Mannai, B. Topology Optimization of Aircraft Fuselage Structure. Int. J. Aerosp. Mech. Eng. 2013, 7, 820–823. [Google Scholar] [CrossRef]
- Zhu, J.-H.; Zhang, W.-H.; Xia, L. Topology Optimization in Aircraft and Aerospace Structures Design. Arch. Comput. Methods Eng. 2016, 23, 595–622. [Google Scholar] [CrossRef]
- ISO 23509:2006; Bevel and Hypoid Gear Geometry. International Standard Organization: Geneva, Switzerland, 2006.
- Ferraiuolo, M.; Leo, M.; Citarella, R. On the Adoption of Global/Local Approaches for the Thermomechanical Analysis and Design of Liquid Rocket Engines. Appl. Sci. 2020, 10, 7664. [Google Scholar] [CrossRef]
- Guiggiani, M. The Science of Vehicle Dynamics, 1st ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 1–356. [Google Scholar]
- Salamunović, D.; Karakašić, M.; Kljajin, M.; Glavaš, H. Design of the strengthened framework for a designed concept of the sport car body. In Proceedings of the IX International Conference—Industrial Engineering and Environmental Protection (IIZS 2019), Zrenjanim, Serbia, 3–4 October 2019. [Google Scholar]
- Kljajin, M.; Ivandić, Ž.; Karakašić, M. Elementi Strojeva-Zbirka Projektno-Konstrukcijskih Zadataka, 1st ed.; Mechanical Engineering Faculty: Slavonski Brod, Croatia, 2018; pp. 1–232. [Google Scholar]
- Miltenović, Đ.; Tica, M.; Miltenović, A.; Banić, M.; Živković, S.; Mišković, Ž. Pitting of Tooth Flanks of Crossed Helical Gears made of Sintered Steel. Trans. Famena 2014, 38, 77–88. [Google Scholar]
- Decker, K.-H. Elementi Strojeva, 3rd ed.; Golden Marketing—Tehnička Knjiga: Zagreb, Croatia, 2006; pp. 1–661. [Google Scholar]
- Ansys Workbench. Available online: https://www.ansys.com/products/ansys-workbench (accessed on 10 September 2023).
- Koutromanos, I. Foundamentals of Finite Element Analysis, 1st ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2018; pp. 1–736. [Google Scholar]
- Ansys SpaceClaim. Available online: https://www.ansys.com/products/3d-design/ansys-spaceclaim (accessed on 15 September 2023).
- TuringBot. Available online: https://turingbotsoftware.com (accessed on 17 September 2023).





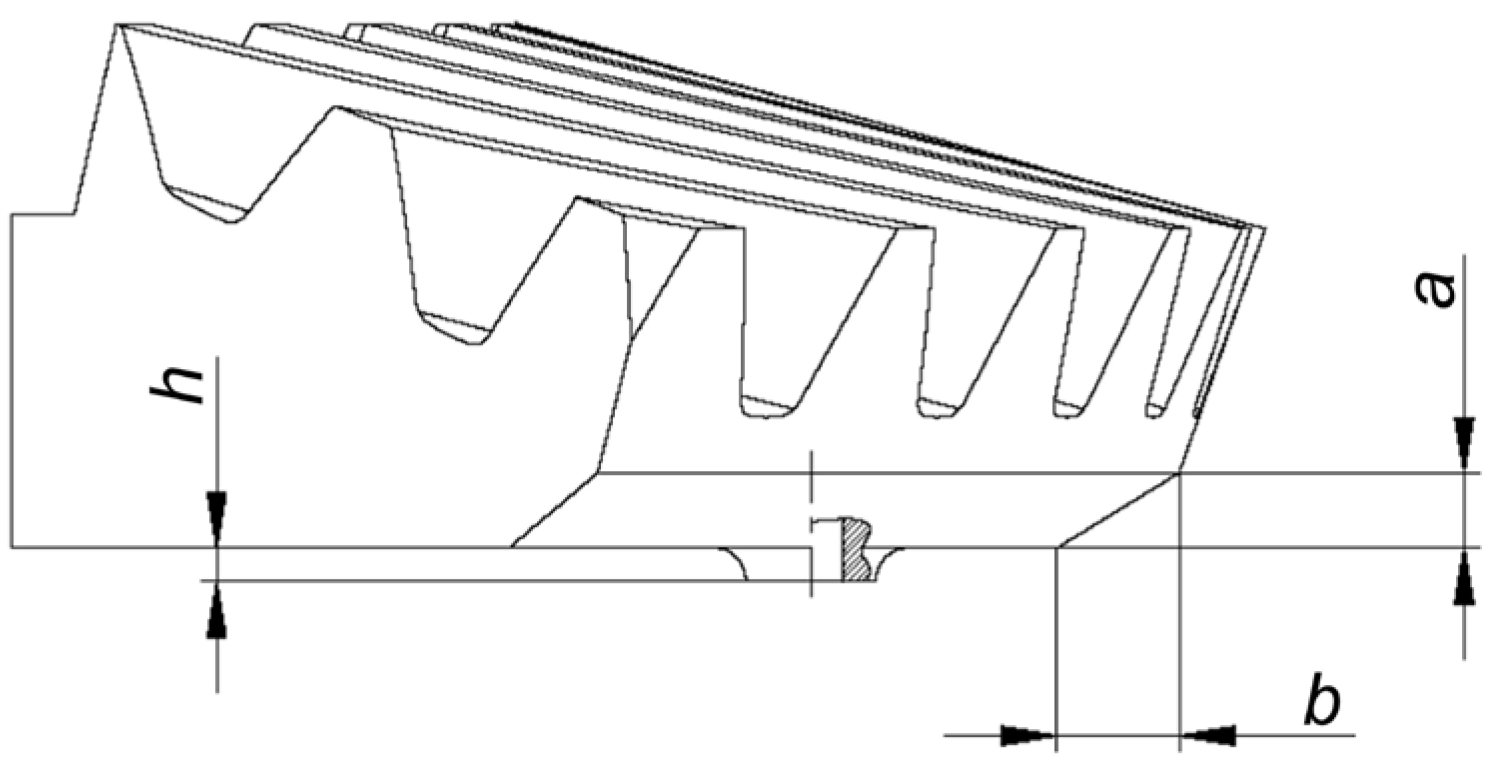
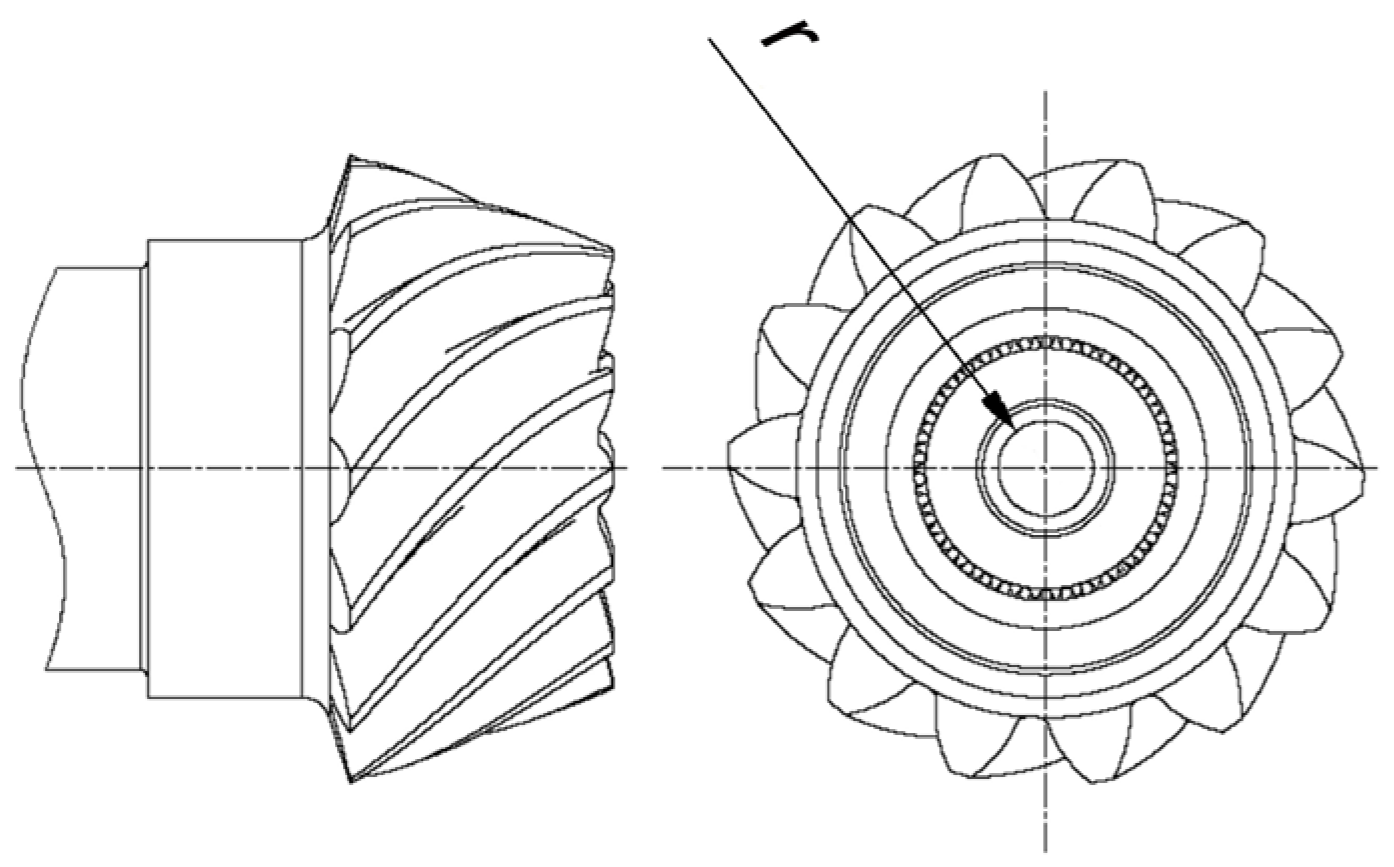



| Design Requirements | Amount |
|---|---|
| Maximum vehicle speed at the highest transmission ratio (vmax), km/h | 220 |
| Time required to reach a speed of 100 km/h (t0–100), s | 8.9 |
| Vehicle mass (mv), kg | 1550 |
| Maximum vehicle mass (mv, max), kg | 2100 |
| Vehicle acceleration (av), m/s2 | 2.5 |
| Dynamic wheel radius (rd), mm | 394.2 |
| Technical characteristics of the driving machine | |
| Max. engine torque (Tmax), Nm | 340 |
| Number of revolutions at which Tmax is reached (nTmax), min−1 | 1600 |
| Power delivered to the drive bevel gear (P1), kW | 53.05 |
| Input torque to the differential transmission (T1), Nm | 1108.14 |
| Differential Transmission Forces and Torques | Amount |
|---|---|
| Reaction force in the wheel (Fw), N | 5150.25 |
| Friction force (Ff), N | 4635.23 |
| Traction force (FTR), N | 9270.45 |
| Transmission ratio of the differential transmission (id) | 3.286 |
| Output power of the differential transmission (P2), kW | 51.457 |
| Rolling resistance force (FRO), N | 412.02 |
| Rising resistance force (FRI), N | 2153.39 |
| Vehicle’s inertial force (FIN), N | 6116.25 |
| Total resistance force of driven machine (FTRD) | 8681.66 |
| Torque of the hypoid ring bevel gear (T2), Nm | 3546.31 |
| Torque of drive wheel (TW, TR, TL), Nm | 1773.16 |
| Variables | First Iteration | Last Iteration |
|---|---|---|
| Ring gear mean pitch diameter (dm2), mm | 304.08 | 305.59 |
| Pinion offset angle in the axial plane (ζm), ° | 11.28 | 10.51 |
| Pinion offset angle in the pitch plane (ζmp), ° | 11.78 | 11.34 |
| Pinion gear pitch angle (δ1), ° | 16.59 | 22.31 |
| Ring gear pitch angle (δ2), ° | 67.57 | 67.69 |
| Mean normal module (mn), mm | 5.41 | 5.44 |
| Spiral angle of pinion (βm1), ° | 46.78 | 46.34 |
| Hypoid dimensional factor (F) | 1.196 | 1.187 |
| Pinion mean pitch diameter (dm1), mm | 110.7 | 110.36 |
| Mean cone distance of the pinion (Rm1), mm | 190.07 | 145.35 |
| Mean cone distance of the ring gear (Rm2), mm | 158.93 | 165.16 |
| Auxiliary angle (υm), ° | 10.8 | 9.74 |
| Iteration condition: () | |−47.537| < 0.019 | |−0.010| < 0.0145 |
| Geometric Quantities | Amount | |
|---|---|---|
| Pinion | Ring Gear | |
| Shaft angle departure (ΔΣ), ° | 0 | 0 |
| Pinion offset angle in the axial plane (ζm), ° | 10.68 | - |
| Pinion offset angle in the pitch plane (ζmp), ° | 11.55 | - |
| Mean normal module (mn), mm | 5.5 | 5.5 |
| Limit pressure angle (αlim), ° | −1.32 | −1.32 |
| Mean normal pressure angle (αn), ° | 20 | 20 |
| Crossing point to calculation point along ring gear axis (tzm2), mm | - | 55 |
| Crossing point to calculation point along pinion axis (tzm1), mm | 149.71 | - |
| Pinion gear | Stress on tooth root | σFP1 = 357.14 MPa | σF1 < σFP1 |
| Fmt1 = 20,082.3 N | |||
| σF1 = 226.79 MPa | |||
| Stress on tooth face flank | σHP1 = 1310.14 MPa | σH1 < σHP1 | |
| σH1 = 1286 MPa | |||
| Ring gear | Stress on tooth root | σFP2 = 357.14 MPa | σF2 < σFP2 |
| Fmt2 = 23,987 N | |||
| σF2 = 149 MPa | |||
| Stress on tooth face flank | σHP2 = 1324 MPa | σH2 < σHP2 | |
| σH2 = 852.23 MPa |
| Geometric Quantities | Mark | Amount | ||
|---|---|---|---|---|
| Planetary | Sun | Planetary | Sun | |
| Pitch circle diameter, mm | d3 | d4 | 102 | 136 |
| Length of the derivative of the dividing cone, mm | Ra | 85 | ||
| Tooth width, mm | b3 | b4 | 26 | 26 |
| Middle pitch diameter of bevel gear, mm | dm3 | dm4 | 85 | 115.2 |
| Clearance, mm | c | 2.125 | ||
| Whole depth, mm | h3 | h4 | 19.125 | 19.125 |
| Addendum depth for zero pair of bevel gears, mm | ha3 | ha4 | 8.5 | 8.5 |
| Dedendum depth for zero pair of bevel gears, mm | hf3 | hf4 | 10.625 | 10.625 |
| Addendum circle diameter, mm | da3 | da4 | 115.599 | 146.2 |
| Teeth face angle, ° | κa3 | κa4 | 5.71 | 5.71 |
| Face angle of bevel gear, ° | δa3 | δa4 | 42.58 | 58.84 |
| Inner addendum diameter of tooth, mm | dia3 | dia4 | 84.24 | 101.48 |
| Pitch diameter of middle equivalent gear, mm | dvm3 | dvm4 | 106.25 | 192 |
| Pitch diameter of equivalent gear, mm | dv3 | dv4 | 127.5 | 226.67 |
| Addendum diameter of equivalent gear, mm | dva3 | dva4 | 144.5 | 243.67 |
| Base diameter of equivalent gear, mm | dvb3 | dvb4 | 119.81 | 213 |
| Planetary gear | Stress on tooth root | σFP3 = 512.15 MPa | σF3 < σFP3 |
| Fmt3 = 15.391 N | |||
| σF3 = 274.93 MPa | |||
| Stress on tooth face flank | σHP3 = 1441.1 MPa | σH3 < σHP3 | |
| σH3 = 1400.04 MPa | |||
| Sun gear | Stress on tooth root | σFP4 = 512.5 MPa | σF4 < σFP4 |
| Fmt4 = 15.391 N | |||
| σF4 = 224.03 MPa | |||
| Stress on tooth face flank | σHP4 = 1441.1 MPa | σH4 < σHP4 | |
| σH4 = 954.44 MPa |
| Parameters | Name | Lower Value, mm | Upper Value, mm |
|---|---|---|---|
| a | Vertical chamfer of the ring gear | 1 | 7 |
| b | Horizontal chamfer of the ring gear | 1 | 13 |
| h | Overhang height of the ring gear | 1 | 3 |
| r | Inner radius of the drive shaft | 2.5 | 13.5 |
| Response | Name | Description |
|---|---|---|
| mall | Overall mass of optimized design elements | Objective function—mass reduction of the optimized design elements |
| m1 | Mass of the ring gear | Objective function—mass reduction of the ring gear |
| m2 | Mass of the drive shaft | Objective function—mass reduction of the drive shaft |
| No. | a, mm | b, mm | h, mm | r, mm | No. | a, mm | b, mm | h, mm | r, mm |
|---|---|---|---|---|---|---|---|---|---|
| 1. | 4 | 7 | 2 | 8 | 14. | 6.11 | 2.77 | 1.30 | 4.13 |
| 2. | 4 | 7 | 2 | 2.5 | 15. | 6.11 | 2.77 | 1.30 | 11.87 |
| 3. | 4 | 7 | 2 | 13.5 | 16. | 6.11 | 2.77 | 2.70 | 4.13 |
| 4. | 4 | 7 | 1 | 8 | 17. | 6.11 | 2.77 | 2.70 | 11.87 |
| 5. | 4 | 7 | 3 | 8 | 18. | 1.89 | 11.23 | 1.30 | 4.13 |
| 6. | 1 | 7 | 2 | 8 | 19. | 1.89 | 11.23 | 1.30 | 11.87 |
| 7. | 7 | 7 | 2 | 8 | 20. | 1.89 | 11.23 | 2.70 | 4.13 |
| 8. | 4 | 1 | 2 | 8 | 21. | 1.89 | 11.23 | 2.70 | 11.87 |
| 9. | 4 | 13 | 2 | 8 | 22. | 6.11 | 11.23 | 1.30 | 4.13 |
| 10. | 1.89 | 2.77 | 1.30 | 4.13 | 23. | 6.11 | 11.23 | 1.30 | 11.87 |
| 11. | 1.89 | 2.77 | 1.30 | 11.87 | 24. | 6.11 | 11.23 | 2.70 | 4.13 |
| 12. | 1.89 | 2.77 | 2.70 | 4.13 | 25. | 6.11 | 11.23 | 2.70 | 11.87 |
| 13. | 1.89 | 2.77 | 2.70 | 11.87 |
| Responses | R2 | RMSE |
|---|---|---|
| Overall mass | 0.99532 | 0.03193 |
| Mass of the ring gear | 0.99589 | 0.00149 |
| Mass of the drive shaft | 0.99988 | 0.00700 |
| Parameter | Value, mm |
|---|---|
| a | 7 |
| b | 13 |
| h | 3 |
| r | 13.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karakašić, M.; Konjatić, P.; Glavaš, H.; Grgić, I. Influence of Open Differential Design on the Mass Reduction Function. Appl. Sci. 2023, 13, 13300. https://doi.org/10.3390/app132413300
Karakašić M, Konjatić P, Glavaš H, Grgić I. Influence of Open Differential Design on the Mass Reduction Function. Applied Sciences. 2023; 13(24):13300. https://doi.org/10.3390/app132413300
Chicago/Turabian StyleKarakašić, Mirko, Pejo Konjatić, Hrvoje Glavaš, and Ivan Grgić. 2023. "Influence of Open Differential Design on the Mass Reduction Function" Applied Sciences 13, no. 24: 13300. https://doi.org/10.3390/app132413300







