Scene-Based Nonuniformity Correction Method Using Principal Component Analysis for Infrared Focal Plane Arrays
Abstract
:Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Scribner, D.A.; Sarkady, K.A.; Caulfield, J.T.; Kruer, M.R.; Katz, G.; Gridley, C.J.; Herman, C. Nonuniformity Correction for Staring IR Focal Plane Arrays Using Scene-Based Techniques. In Proceedings of the 1990 Technical Symposium on Optics, Electro-Optics, and Sensors, Orlando, FL, USA, 16–20 April 1990; Volume 1308, pp. 224–233. [Google Scholar] [CrossRef]
- Friedenberg, A.; Goldblatt, I. Nonuniformity Two-Point Linear Correction Errors in Infrared Focal Plane Arrays. Opt. Eng. 1998, 37, 1251–1253. [Google Scholar] [CrossRef]
- Harris, J.G.; Chiang, Y.-M. Nonuniformity Correction Using the Constant-Statistics Constraint: Analog and Digital Implementations. In Proceedings of the Infrared Technology and Applications XXIII, Orlando, FL, USA, 20–25 April 1997; Volume 3061, pp. 895–905. [Google Scholar] [CrossRef]
- Scribner, D.A.; Sarkady, K.A.; Kruer, M.R.; Caulfield, J.T.; Hunt, J.D.; Herman, C. Adaptive Nonuniformity Correction for IR Focal-Plane Arrays Using Neural Networks. In Proceedings of the Infrared Sensors: Detectors, Electronics, and Signal Processing, San Diego, CA, USA, 21 July 1991; Volume 1541, pp. 100–109. [Google Scholar] [CrossRef]
- Vera, E.; Torres, S. Fast Adaptive Nonuniformity Correction for Infrared Focal-Plane Array Detectors. EURASIP J. Adv. Signal Process. 2005, 2005, 560759. [Google Scholar] [CrossRef]
- Torres, S.N.; Vera, E.M.; Reeves, R.A.; Sobarzo, S.K. Adaptive Scene-Based Nonuniformity Correction Method for Infrared-Focal Plane Arrays. In Proceedings of the Infrared Imaging Systems: Design, Analysis, Modeling, and Testing XIV, Orlando, FL, USA, 21–25 April 2003; Volume 5076, pp. 130–139. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, W. Scene-Based Nonuniformity Correction Using Local Constant Statistics. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2008, 25, 1444–1453. [Google Scholar] [CrossRef] [PubMed]
- Torres, S.N.; Hayat, M.M. Kalman Filtering for Adaptive Nonuniformity Correction in Infrared Focal-Plane Arrays. J. Opt. Soc. Am. A 2003, 20, 470–480. [Google Scholar] [CrossRef] [PubMed]
- Vera, E.; Meza, P.; Torres, S. Total Variation Approach for Adaptive Nonuniformity Correction in Focal-Plane Arrays. Opt. Lett. 2011, 36, 172–174. [Google Scholar] [CrossRef] [PubMed]
- Rossi, A.; Diani, M.; Corsini, G. Bilateral Filter-Based Adaptive Nonuniformity Correction for Infrared Focal-Plane Array Systems. Opt. Eng. 2010, 49, 057003. [Google Scholar] [CrossRef]
- Hardie, R.C.; Hayat, M.M.; Armstrong, E.; Yasuda, B. Scene-Based Nonuniformity Correction with Video Sequences and Registration. Appl. Opt. 2000, 39, 1241–1250. [Google Scholar] [CrossRef] [PubMed]
- Ratliff, B.M.; Hayat, M.M.; Hardie, R.C. An Algebraic Algorithm for Nonuniformity Correction in Focal-Plane Arrays. J. Opt. Soc. Am. A 2002, 19, 1737–1747. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Chen, Q.; Gu, G.; Sui, X. Scene-Based Nonuniformity Correction Algorithm Based on Interframe Registration. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2011, 28, 1164–1176. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.-L.; Chen, Q.; Qian, W.-X.; Gu, G.; Yu, X.-L.; Liu, N. Multiframe Registration Based Adaptive Nonuniformity Correction Algorithm for Infrared Focal Plane Arrays. J. Infrared Millim. Waves 2014, 33, 122–128. [Google Scholar]
- Boutemedjet, A.; Deng, C.; Zhao, B. Edge-Aware Unidirectional Total Variation Model for Stripe Non-Uniformity Correction. Sensors 2018, 18, 1164. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Zhao, Y.; Xiang, W. Single-Frame-Based Column Fixed-Pattern Noise Correction in an Uncooled Infrared Imaging System Based on Weighted Least Squares. Appl. Opt. 2019, 58, 9141–9153. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Sui, X.; Liu, Y.; Kuang, X.; Gu, G.; Chen, Q. FPN Estimation Based Nonuniformity Correction for Infrared Imaging System. Infrared Phys. Technol. 2019, 96, 22–29. [Google Scholar] [CrossRef]
- Zhou, B.; Luo, Y.; Chen, B.; Wang, M.; Peng, L.; Liang, K. Local Spatial Correlation-Based Stripe Non-Uniformity Correction Algorithm for Single Infrared Images. Signal Process. Image Commun. 2019, 72, 47–57. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, Z.; Wang, C. An Improved Retina-like Nonuniformity Correction for Infrared Focal-Plane Array. Infrared Phys. Technol. 2015, 73, 62–72. [Google Scholar] [CrossRef]
- He, Z.; Cao, Y.; Dong, Y.; Yang, J.; Cao, Y.; Tisse, C.-L. Single-Image-Based Nonuniformity Correction of Uncooled Long-Wave Infrared Detectors: A Deep-Learning Approach. Appl. Opt. 2018, 57, D155–D164. [Google Scholar] [CrossRef] [PubMed]
- Mou, X.; Zhu, T.; Zhou, X. Visible-Image-Assisted Nonuniformity Correction of Infrared Images Using the GAN with SEBlock. Sensors 2023, 23, 3282. [Google Scholar] [CrossRef] [PubMed]
- Kuglin, C.D. The Phase Correlation Image Alignment Method. IEEE Int. Conf. Cybern. Soc. 1975, 1975, 163–165. [Google Scholar]
- Turk, M.; Pentland, A. Face Recognition Using Eigenfaces. In Proceedings of the 1991 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Maui, HI, USA, 3–6 June 1991; pp. 586–591. [Google Scholar] [CrossRef]

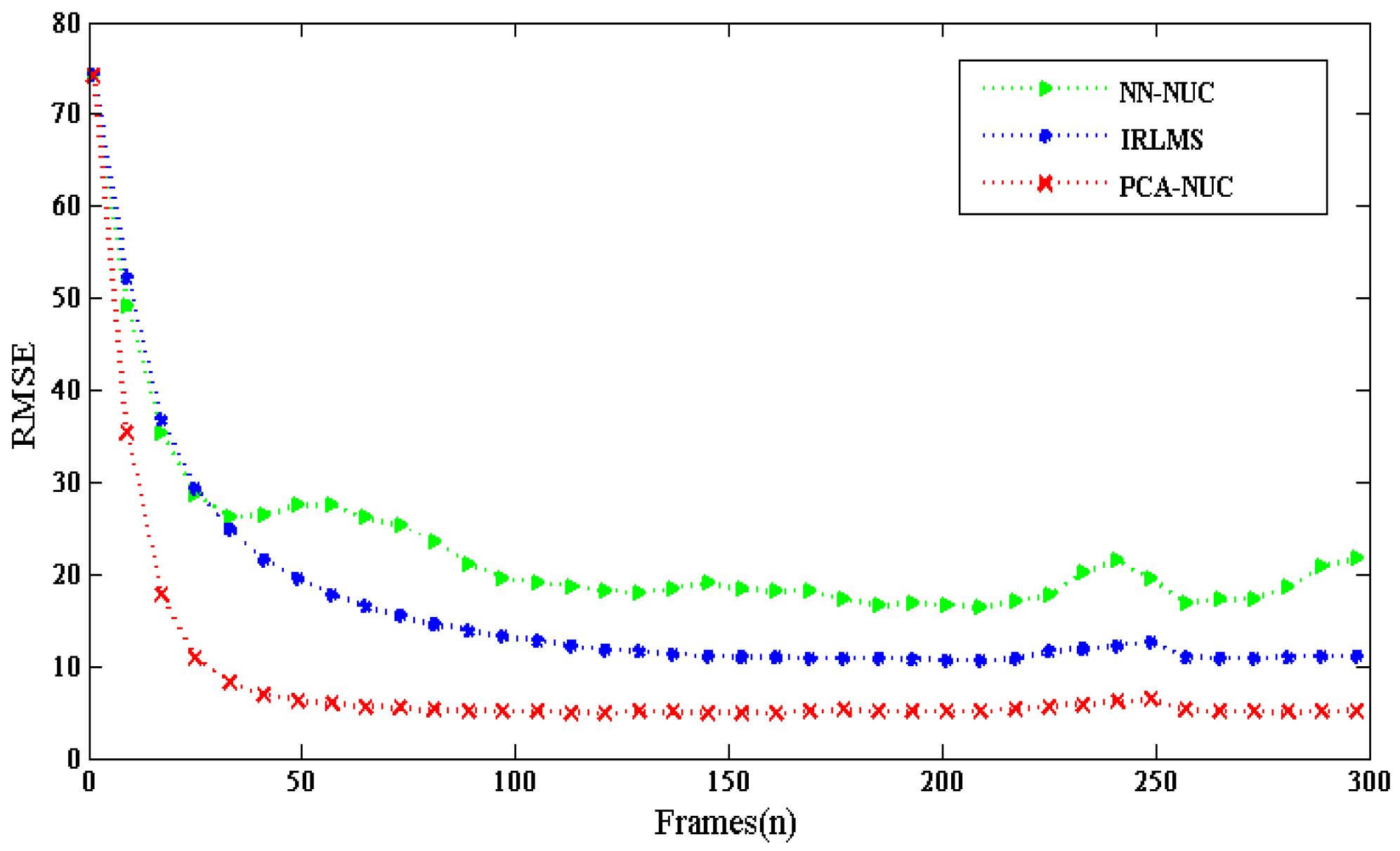
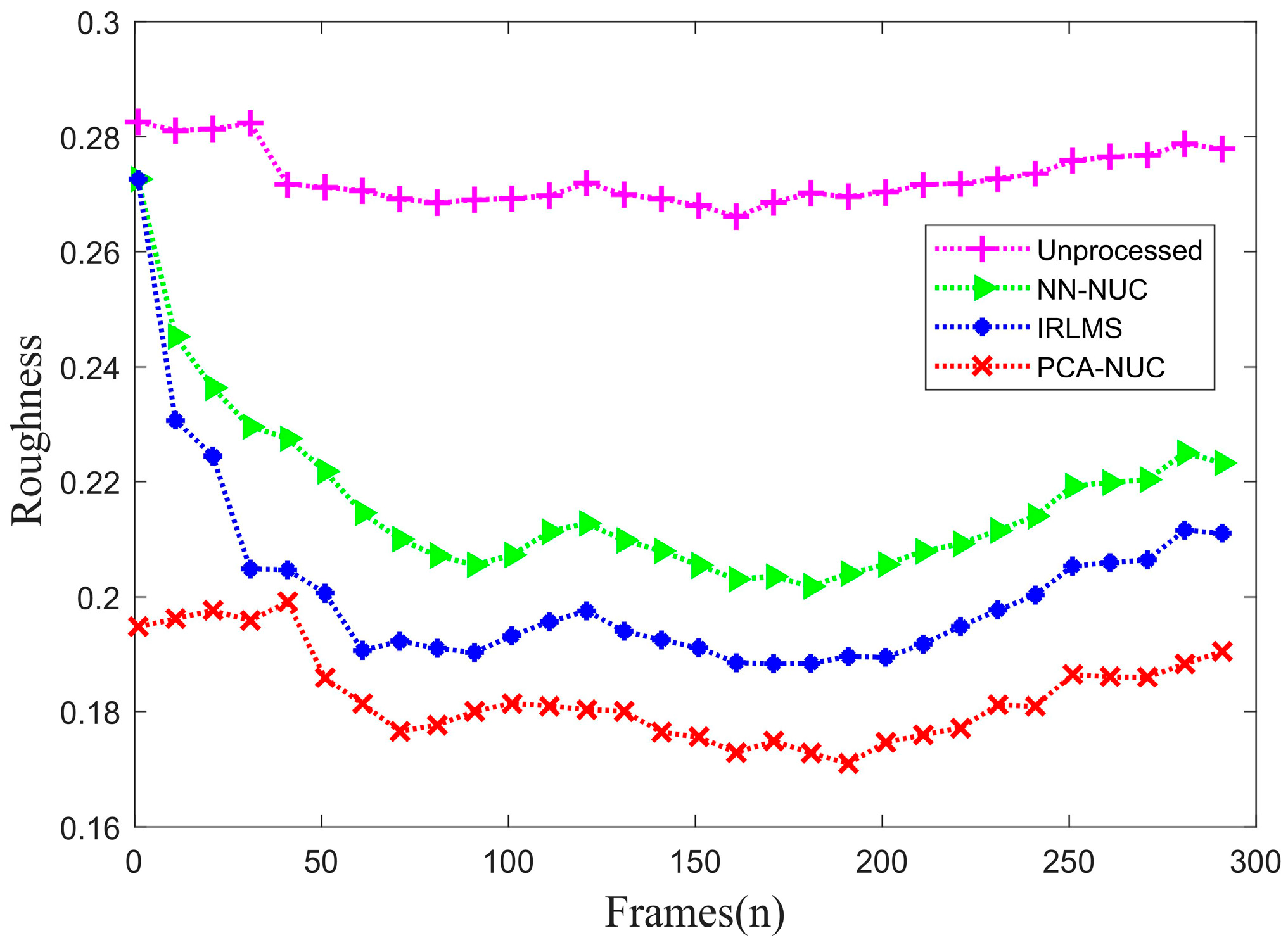


| Algorithm | Average CPU Time(s) |
|---|---|
| NN-NUC | 0.006 |
| IRLMS | 0.087 |
| PCA-NUC | 0.146 |
| Algorithm | Roughness |
|---|---|
| Unprocessed | 0.2721 |
| NN-NUC | 0.2143 |
| IRLMS | 0.1998 |
| PCA-NUC | 0.1851 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, D.; Teng, L.; Ren, J.; Tan, J.; Wang, M.; Wang, L.; Gu, G. Scene-Based Nonuniformity Correction Method Using Principal Component Analysis for Infrared Focal Plane Arrays. Appl. Sci. 2023, 13, 13331. https://doi.org/10.3390/app132413331
Lu D, Teng L, Ren J, Tan J, Wang M, Wang L, Gu G. Scene-Based Nonuniformity Correction Method Using Principal Component Analysis for Infrared Focal Plane Arrays. Applied Sciences. 2023; 13(24):13331. https://doi.org/10.3390/app132413331
Chicago/Turabian StyleLu, Dongming, Longyin Teng, Jianle Ren, Jiangyun Tan, Mengke Wang, Liping Wang, and Guohua Gu. 2023. "Scene-Based Nonuniformity Correction Method Using Principal Component Analysis for Infrared Focal Plane Arrays" Applied Sciences 13, no. 24: 13331. https://doi.org/10.3390/app132413331
APA StyleLu, D., Teng, L., Ren, J., Tan, J., Wang, M., Wang, L., & Gu, G. (2023). Scene-Based Nonuniformity Correction Method Using Principal Component Analysis for Infrared Focal Plane Arrays. Applied Sciences, 13(24), 13331. https://doi.org/10.3390/app132413331







