Animal Pose Estimation Based on 3D Priors
Abstract
:1. Introduction
- We propose a novel method for refining 2D animal pose estimation using 3D priors, which can be easily incorporated into existing 2D pose estimation methods;
- We present both conventional optimization and learning-based neural networks to implement the proposed method;
- We build a 3D animal pose dataset and manually annotate a 2D pose dataset for animal pose estimation;
- Extensive experiments are conducted to evaluate the proposed method. The experimental results show that the proposed method is effective in improving 2D animal pose estimation accuracy.
2. Related Work
2.1. The 3D Human Pose Estimation Methods
2.1.1. Deep-Learning-Based Human Pose Estimation
2.1.2. Dictionary-Based Human Pose Estimation
2.2. Animal Pose Estimation
3. Dataset Collection
3.1. Cat
3.2. Amur
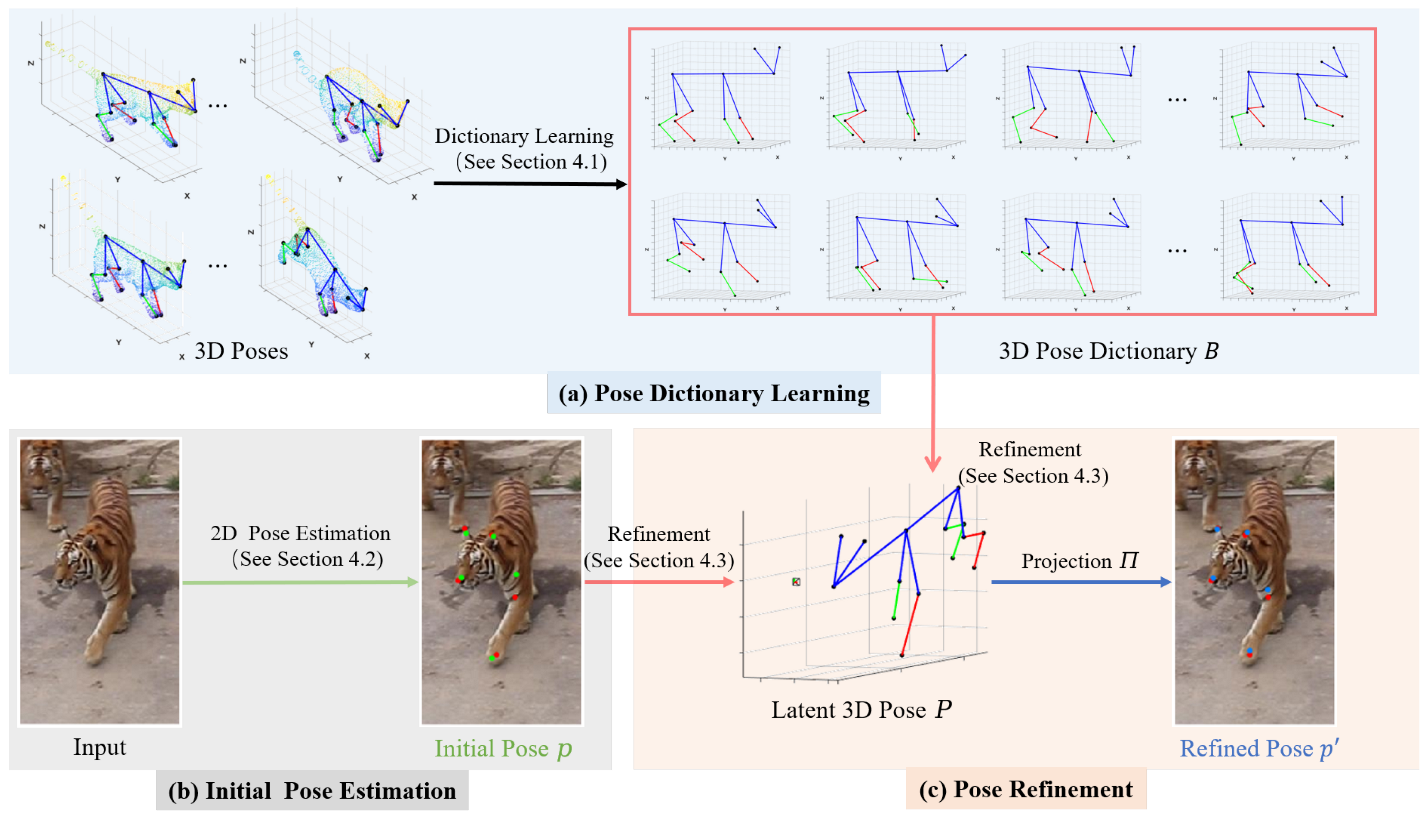
4. Proposed Method
- 1.
- Pose dictionary learning: First of all, 3D poses were generated, as described in Section 3.1. These 3D poses were then used as the training data for dictionary learning to obtain the 3D pose dictionary (see Section 4.1);
- 2.
- Initial pose estimation: The initial pose of the sample was estimated using existing pose estimation algorithms such as HRNet [25];
- 3.
- Pose refinement: The initial pose p was used together with the 3D pose dictionary B to obtain the latent 3D pose P, which was then reprojected to obtain a more accurate 2D pose (see Section 4.3).
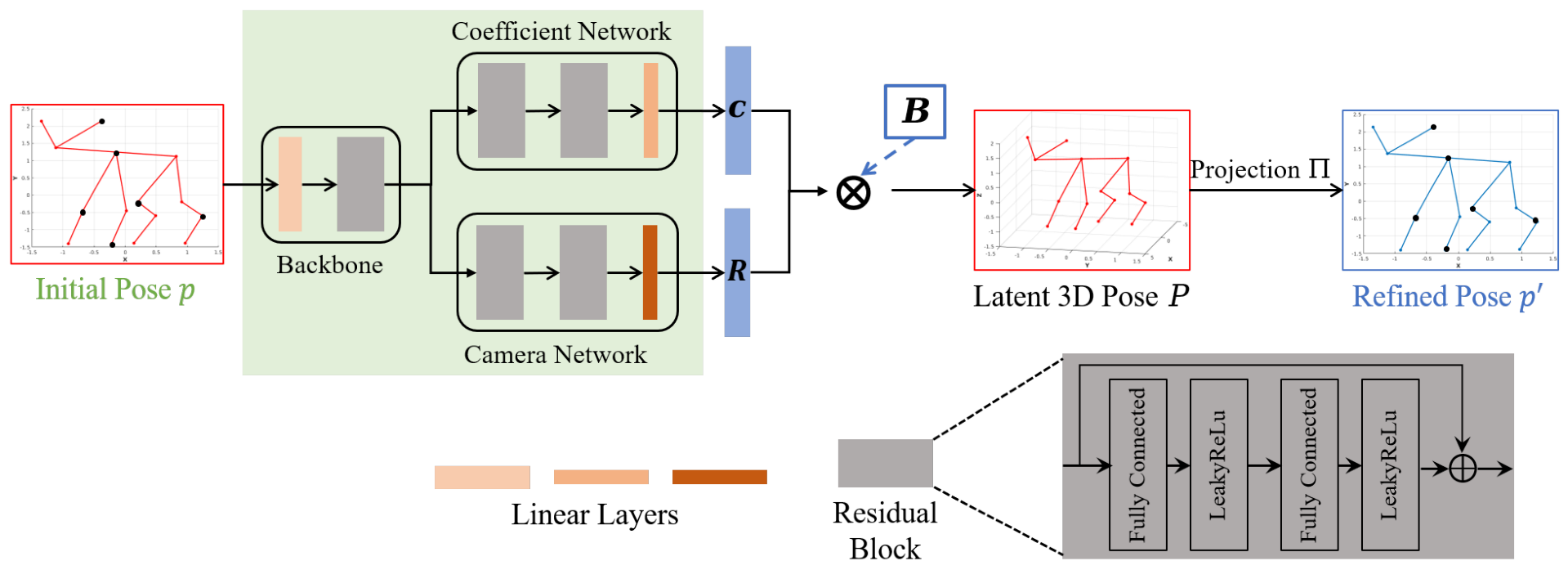
4.1. Pose Dictionary Learning
| Algorithm 1 Pose Dictionary Learning |
Input: Output:
|
4.2. Initial Pose Estimation
4.3. Pose Refinement
4.3.1. Optimization-Based Pose Refinement
| Algorithm 2 Pose Refinement |
Input: Output:
|
4.3.2. Deep-Learning-Based Pose Refinement
5. Experiments
5.1. Datasets
5.2. Experimental Setup
5.3. Results on the SA-Tiger Dataset
5.4. Results on the TD-Tiger Dataset
5.5. Results on the Amur Dataset
6. Discussions and Conclusions
6.1. Discussions
6.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mathis, A.; Mamidanna, P.; Cury, K.M.; Abe, T.; Murthy, V.N.; Mathis, M.W.; Bethge, M. DeepLabCut: Markerless Pose Estimation of User-Defined Body Parts with Deep Learning. Nat. Neurosci. 2018, 21, 1281–1289. [Google Scholar] [CrossRef] [PubMed]
- Graving, J.M.; Chae, D.; Naik, H.; Li, L.; Koger, B.; Costelloe, B.R.; Couzin, I.D. DeepPoseKit, A Software Toolkit for Fast and Robust Animal Pose Estimation Using Deep Learning. Elife 2019, 8, e47994. [Google Scholar] [CrossRef] [PubMed]
- Mathis, M.W.; Mathis, A. Deep Learning Tools for the Measurement of Animal Behavior in Neuroscience. Curr. Opin. Neurobiol. 2020, 60, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Mathis, A.; Schneider, S.; Lauer, J.; Mathis, M.W. A Primer on Motion Capture with Deep Learning: Principles, Pitfalls, and Perspectives. Neuron 2020, 108, 44–65. [Google Scholar] [CrossRef] [PubMed]
- Biggs, B.; Roddick, T.; Fitzgibbon, A.; Cipolla, R. Creatures Great and SMAL: Recovering the Shape and Motion of Animals From Video. In Proceedings of the Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; pp. 3–19. [Google Scholar]
- Zuffi, S.; Kanazawa, A.; Black, M.J. Lions and Tigers and Bears: Capturing Non-Rigid, 3D, Articulated Shape From Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3955–3963. [Google Scholar]
- Zuffi, S.; Kanazawa, A.; Berger-Wolf, T.; Black, M.J. Three-D Safari: Learning to Estimate Zebra Pose, Shape, and Texture From Images “In the Wild”. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5359–5368. [Google Scholar]
- Shih, L.Y.; Chen, B.Y.; Wu, J.L. Video-Based Motion Capturing for Skeleton-Based 3D Models. In Proceedings of the Pacific-Rim Symposium on Image and Video Technology, Tokyo, Japan, 13–16 January 2009; pp. 748–758. [Google Scholar]
- Pantuwong, N.; Sugimoto, M. A Novel Template-Based Automatic Rigging Algorithm for Articulated-Character Animation. Comput. Animat. Virtual Worlds 2012, 23, 125–141. [Google Scholar] [CrossRef]
- Pereira, T.D.; Shaevitz, J.W.; Murthy, M. Quantifying Behavior to Understand the Brain. Nat. Neurosci. 2020, 23, 1537–1549. [Google Scholar] [CrossRef] [PubMed]
- Seok, S.; Wang, A.; Chuah, M.Y.; Otten, D.; Lang, J.; Kim, S. Design Principles for Highly Efficient Quadrupeds and Implementation on the MIT Cheetah Robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3307–3312. [Google Scholar]
- Zhao, D.; Song, S.; Su, J.; Jiang, Z.; Zhang, J. Learning Bionic Motions by Imitating Animals. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Beijing, China, 13–16 October 2020; pp. 872–879. [Google Scholar]
- Ionescu, C.; Papava, D.; Olaru, V.; Sminchisescu, C. Human3. 6m: Large Scale Datasets and Predictive Methods for 3D Human Sensing in Natural Environments. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 1325–1339. [Google Scholar] [CrossRef] [PubMed]
- Zuffi, S.; Kanazawa, A.; Jacobs, D.W.; Black, M.J. 3D Menagerie: Modeling the 3D Shape and Pose of Animals. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6365–6373. [Google Scholar]
- Mu, J.; Qiu, W.; Hager, G.D.; Yuille, A.L. Learning From Synthetic Animals. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 14–19 June 2020; pp. 12386–12395. [Google Scholar]
- Li, C.; Lee, G.H. From Synthetic to Real: Unsupervised Domain Adaptation for Animal Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 1482–1491. [Google Scholar]
- Cao, J.; Tang, H.; Fang, H.S.; Shen, X.; Lu, C.; Tai, Y.W. Cross-Domain Adaptation for Animal Pose Estimation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9498–9507. [Google Scholar]
- Chen, W.; Wang, H.; Li, Y.; Su, H.; Wang, Z.; Tu, C.; Lischinski, D.; Cohen-Or, D.; Chen, B. Synthesizing Training Images for Boosting Human 3D Pose Estimation. In In Proceedings of the Fourth International Conference on 3D Vision, Stanford, CA, USA, 25–28 October 2016; pp. 479–488.
- Varol, G.; Romero, J.; Martin, X.; Mahmood, N.; Black, M.J.; Laptev, I.; Schmid, C. Learning From Synthetic Humans. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 109–117. [Google Scholar]
- Singh, P.; Bose, S.S. A Quantum-clustering Optimization Method for COVID-19 CT Scan Image Segmentation. Expert Syst. Appl. 2021, 185, 115637. [Google Scholar] [CrossRef] [PubMed]
- Mittal, H.; Pandey, A.C.; Saraswat, M.; Kumar, S.; Pal, R.; Modwel, G. A Comprehensive Survey of Image Segmentation: Clustering Methods, Performance Parameters, and Benchmark Datasets. Multimed. Tools Appl. 2022, 81, 35001–35026. [Google Scholar] [CrossRef]
- Singh, P.; Bose, S.S. Ambiguous D-means Fusion Clustering Algorithm Based on Ambiguous Set Theory: Special Application in Clustering of CT Scan Images of COVID-19. Knowl.-Based Syst. 2021, 231, 107432. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.; Li, S.; Zhao, Q.; Yang, H. Animal Pose Refinement in 2D Images with 3D Constraints. In Proceedings of the 2022-33rd British Machine Vision Conference, London, UK, 21–24 November 2022. [Google Scholar]
- Li, S.; Li, J.; Tang, H.; Qian, R.; Lin, W. ATRW: A Benchmark for Amur Tiger Re-Identification in the Wild. In Proceedings of the ACM International Conference on Multimedia, Seattle, WA USA, 12–16 October 2020; pp. 2590–2598. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep High-Resolution Representation Learning for Human Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5693–5703. [Google Scholar]
- Martinez, J.; Hossain, R.; Romero, J.; Little, J.J. A Simple Yet Effective Baseline for 3D Human Pose Estimation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2640–2649. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Zhao, W.; Wang, W.; Tian, Y. GraFormer: Graph-Oriented Transformer for 3D Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–23 June 2022; pp. 20438–20447. [Google Scholar]
- Li, W.; Liu, H.; Tang, H.; Wang, P.; Van, G.L. Mhformer: Multi-Hypothesis Transformer for 3D Human Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–23 June 2022; pp. 13147–13156. [Google Scholar]
- Wandt, B.; Rosenhahn, B. Repnet: Weakly Supervised Training of an Adversarial Reprojection Network for 3D Human Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 7782–7791. [Google Scholar]
- Li, C.; Lee, G.H. Weakly Supervised Generative Network for Multiple 3D Human Pose Hypotheses. In Proceedings of the 2020—31st British Machine Vision Conference, Virtual Event, UK, 7–10 September 2020. [Google Scholar]
- Usman, B.; Tagliasacchi, A.; Saenko, K.; Sud, A. MetaPose: Fast 3D Pose from Multiple Views without 3D Supervision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–23 June 2022; pp. 6759–6770. [Google Scholar]
- Wandt, B.; Rudolph, M.; Zell, P.; Rhodin, H.; Rosenhahn, B. Canonpose: Self-supervised Monocular 3D Human Pose Estimation in the Wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 13294–13304. [Google Scholar]
- Drover, D.; MV, R.; Chen, C.H.; Agrawal, A.; Tyagi, A.; Phuoc, H.C. Can 3D Pose be Learned from 2D Projections Alone? In Proceedings of the European Conference on Computer Vision Workshops, Munich, Germany, 8–14 September 2018.
- Chen, C.H.; Tyagi, A.; Agrawal, A.; Drover, D.; Mv, R.; Stojanov, S.; Rehg, J.M. Unsupervised 3D Pose Estimation with Geometric Self-supervision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5714–5724. [Google Scholar]
- Yu, Z.; Ni, B.; Xu, J.; Wang, J.; Zhao, C.; Zhang, W. Towards Alleviating the Modeling Ambiguity of Unsupervised Monocular 3D Human Pose Estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 8651–8660. [Google Scholar]
- Wandt, B.; Little, J.J.; Rhodin, H. ElePose: Unsupervised 3D Human Pose Estimation by Predicting Camera Elevation and Learning Normalizing Flows on 2D Poses. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–23 June 2022; pp. 6635–6645. [Google Scholar]
- Zhou, X.; Zhu, M.; Leonardos, S.; Daniilidis, K. Sparse Representation for 3D Shape Estimation: A Convex Relaxation Approach. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1648–1661. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, C.; Qiu, H.; Yuille, A.L.; Zeng, W. Learning Basis Representation to Refine 3D Human Pose Estimations. In Proceedings of the AAAI Conference on Artificial intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 8925–8932. [Google Scholar]
- Ramakrishna, V.; Kanade, T.; Sheikh, Y. Reconstructing 3D Human Pose from 2D Image Landmarks. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 573–586. [Google Scholar]
- Wang, C.; Wang, Y.; Lin, Z.; Yuille, A.L.; Gao, W. Robust Estimation of 3D Human Poses from A Single Image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2361–2368. [Google Scholar]
- Akhter, I.; Black, M.J. Pose-Conditioned Joint Angle Limits for 3D Human Pose Reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1446–1455. [Google Scholar]
- Newell, A.; Yang, K.; Deng, J. Stacked Hourglass Networks for Human Pose Estimation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 483–499. [Google Scholar]
- Wei, S.E.; Ramakrishna, V.; Kanade, T.; Sheikh, Y. Convolutional Pose Machines. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4724–4732. [Google Scholar]
- Xiao, B.; Wu, H.; Wei, Y. Simple Baselines for Human Pose Estimation and Tracking. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 466–481. [Google Scholar]
- Pereira, T.D.; Aldarondo, D.E.; Willmore, L.; Kislin, M.; Wang, S.S.-H.; Murthy, M.; Shaevitz, J.W. Fast Animal Pose Estimation Using Deep Neural Networks. Nat. Methods 2019, 16, 117–125. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Insafutdinov, E.; Pishchulin, L.; Andres, B.; Andriluka, M.; Schiele, B. DeeperCut: A Deeper, Stronger, and Faster Multi-person Pose Estimation Model. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 34–50. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Jégou, S.; Drozdzal, M.; Vazquez, D.; Romero, A.; Bengio, Y. The One Hundred Layers Tiramisu: Fully Convolutional DenseNets for Semantic Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 11–19. [Google Scholar]
- Kanazawa, A.; Kovalsky, S.; Basri, R.; Jacobs, D. Learning 3D Deformation of Animals From 2d Images. Comput. Graph. Forum 2016, 35, 365–374. [Google Scholar] [CrossRef]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A Skinned Multi-Person Linear Model. ACM Trans. Graph. 2015, 34, 1–16. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online Learning for Matrix Factorization and Sparse Coding. J. Mach. Learn. Res. 2010, 11, 19–60. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Del Pero, L.; Ricco, S.; Sukthankar, R.; Ferrari, V. Articulated Motion Discovery Using Pairs of Trajectories. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2151–2160. [Google Scholar]
- Yu, X.; Zhou, F.; Chandraker, M. Deep Deformation Network for Object Landmark Localization. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 52–70. [Google Scholar]
- Mei, J.; Chen, X.; Wang, C.; Yuille, A.; Lan, X.; Zeng, W. Learning to Refine 3D Human Pose Sequences. In Proceedings of the International Conference on 3D Vision, Québec City, QC, Canada, 16–19 September 2019; pp. 358–366. [Google Scholar]
- OpenMMLab. Available online: https://github.com/open-mmlab/mmpose (accessed on 28 July 2022).


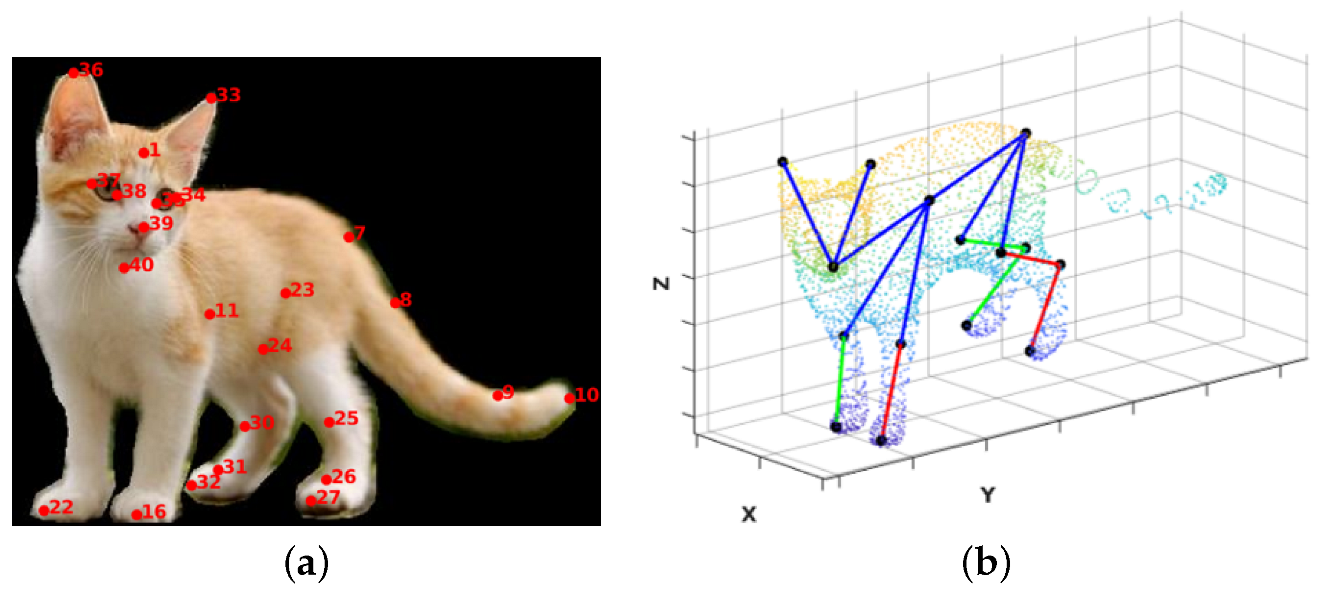



| Index | Definition | Index | Definition | Index | Definition | Index | Definition |
|---|---|---|---|---|---|---|---|
| 1 | forehead | 11 | left shoulder | 21 | right front ankle | 31 | right ankle |
| 2 | spine 0 | 12 | left front thigh | 22 | right front toe | 32 | right toe |
| 3 | spine 1 | 13 | left front shin | 23 | left thigh | 33 | left ear |
| 4 | spine 2 | 14 | left front foot | 24 | left shin | 34 | left eye outer corner |
| 5 | spine 3 | 15 | left front ankle | 25 | left foot | 35 | left eye inner corner |
| 6 | spine 4 | 16 | left front toe | 26 | left ankle | 36 | right ear |
| 7 | root of tail | 17 | right shoulder | 27 | left toe | 37 | right eye outer corner |
| 8 | tail 1 | 18 | right front thigh | 28 | right thigh | 38 | right eye inner corner |
| 9 | tail 2 | 19 | right front shin | 29 | right shin | 39 | nose |
| 10 | end of tail | 20 | right front foot | 30 | right foot | 40 | chin |
| Method | Ear | Nose | Shoulder | Front Paw | Hip | Knee | Back Paw | Tail | Center | Mean |
|---|---|---|---|---|---|---|---|---|---|---|
| GT+ | 75.9 | 75.2 | 75.5 | 75.9 | 75.0 | 74.4 | 74.1 | 75.6 | 75.8 | 75.3 |
| Ours (Optimization) | 75.6 | 77.4 | 78.3 | 76.5 | 78.3 | 76.9 | 75.1 | 80.7 | 81.1 | 77.2 |
| Ours (Fully supervised) | 85.7 | 86.2 | 89.4 | 83.5 | 86.9 | 87.9 | 87.3 | 86.2 | 95.1 | 87.3 |
| Ours (Self-supervised) | 67.2 | 65.0 | 77.7 | 69.2 | 71.9 | 76.3 | 69.4 | 71.3 | 38.7 | 67.3 |
| GT+ | 55.0 | 54.1 | 53.8 | 53.5 | 55.2 | 54.5 | 54.0 | 54.8 | 53.0 | 54.2 |
| Ours (Optimization) | 55.2 | 57.4 | 61.4 | 54.3 | 60.3 | 59.9 | 56.0 | 59.8 | 64.5 | 58.0 |
| Ours (Fully supervised) | 73.8 | 71.7 | 83.0 | 71.0 | 79.0 | 78.9 | 77.3 | 73.3 | 90.6 | 77.3 |
| Ours (Self-supervised) | 49.0 | 52.8 | 61.2 | 50.4 | 61.5 | 58.3 | 49.9 | 55.2 | 36.7 | 51.9 |
| GT+ | 40.0 | 38.5 | 38.7 | 40.6 | 39.3 | 39.3 | 39.7 | 40.3 | 39.7 | 39.7 |
| Ours (Optimization) | 41.0 | 42.8 | 46.0 | 40.6 | 48.3 | 44.8 | 41.3 | 45.5 | 54.3 | 44.2 |
| Ours (Fully supervised) | 62.0 | 60.8 | 75.1 | 59.5 | 69.7 | 69.0 | 67.4 | 63.7 | 82.8 | 67.3 |
| Ours (Self-supervised) | 37.0 | 38.9 | 48.3 | 37.4 | 49.0 | 40.9 | 36.4 | 43.0 | 34.4 | 39.7 |
| GT+ | 29.2 | 29.1 | 29.5 | 29.0 | 29.5 | 30.3 | 29.0 | 28.5 | 30.5 | 29.4 |
| Ours (Optimization) | 29.8 | 32.5 | 38.5 | 30.2 | 40.3 | 35.7 | 30.3 | 34.8 | 43.6 | 34.2 |
| Ours (Fully supervised) | 51.0 | 50.0 | 67.6 | 50.8 | 61.3 | 58.4 | 58.0 | 54.1 | 74.2 | 57.8 |
| Ours (Self-supervised) | 26.8 | 31.3 | 36.7 | 27.3 | 41.5 | 31.5 | 25.8 | 31.0 | 27.8 | 30.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, X.; Li, S.; Zhao, Q.; Yang, H. Animal Pose Estimation Based on 3D Priors. Appl. Sci. 2023, 13, 1466. https://doi.org/10.3390/app13031466
Dai X, Li S, Zhao Q, Yang H. Animal Pose Estimation Based on 3D Priors. Applied Sciences. 2023; 13(3):1466. https://doi.org/10.3390/app13031466
Chicago/Turabian StyleDai, Xiaowei, Shuiwang Li, Qijun Zhao, and Hongyu Yang. 2023. "Animal Pose Estimation Based on 3D Priors" Applied Sciences 13, no. 3: 1466. https://doi.org/10.3390/app13031466
APA StyleDai, X., Li, S., Zhao, Q., & Yang, H. (2023). Animal Pose Estimation Based on 3D Priors. Applied Sciences, 13(3), 1466. https://doi.org/10.3390/app13031466






