Earthquake Magnitude and Frequency Forecasting in Northeastern Algeria using Time Series Analysis

Abstract

This study uses two different time series forecasting approaches (parametric and non-parametric) to assess a frequency and magnitude forecasting of earthquakes above Mw 4.0 in Northeastern Algeria. The Autoregressive Integrated Moving Average (ARIMA) model encompasses the parametric approach, while the non-parametric method employs the Singular Spectrum Analysis (SSA) approach. The ARIMA and SSA models were then used to train and forecast the annual number of earthquakes and annual maximum magnitude events occurring in Northeastern Algeria between 1910 and 2019, including 287 main events larger than Mw 4.0. The SSA method is used as a forecasting algorithm in this case, and the results are compared to those obtained by the ARIMA model. Based on the root mean square error (RMSE) criterion, the SSA forecasting model appears to be more appropriate than the ARIMA model. The consistency between the observation and the forecast is analyzed using a statistical test in terms of the total number of events, denoted as N-test. As a result, the findings indicate that the annual maximum magnitude in Northeastern Algeria between 2020 and 2030 will range from Mw 4.8 to Mw 5.1, while between four and six events with a magnitude of at least Mw 4.0 will occur annually.

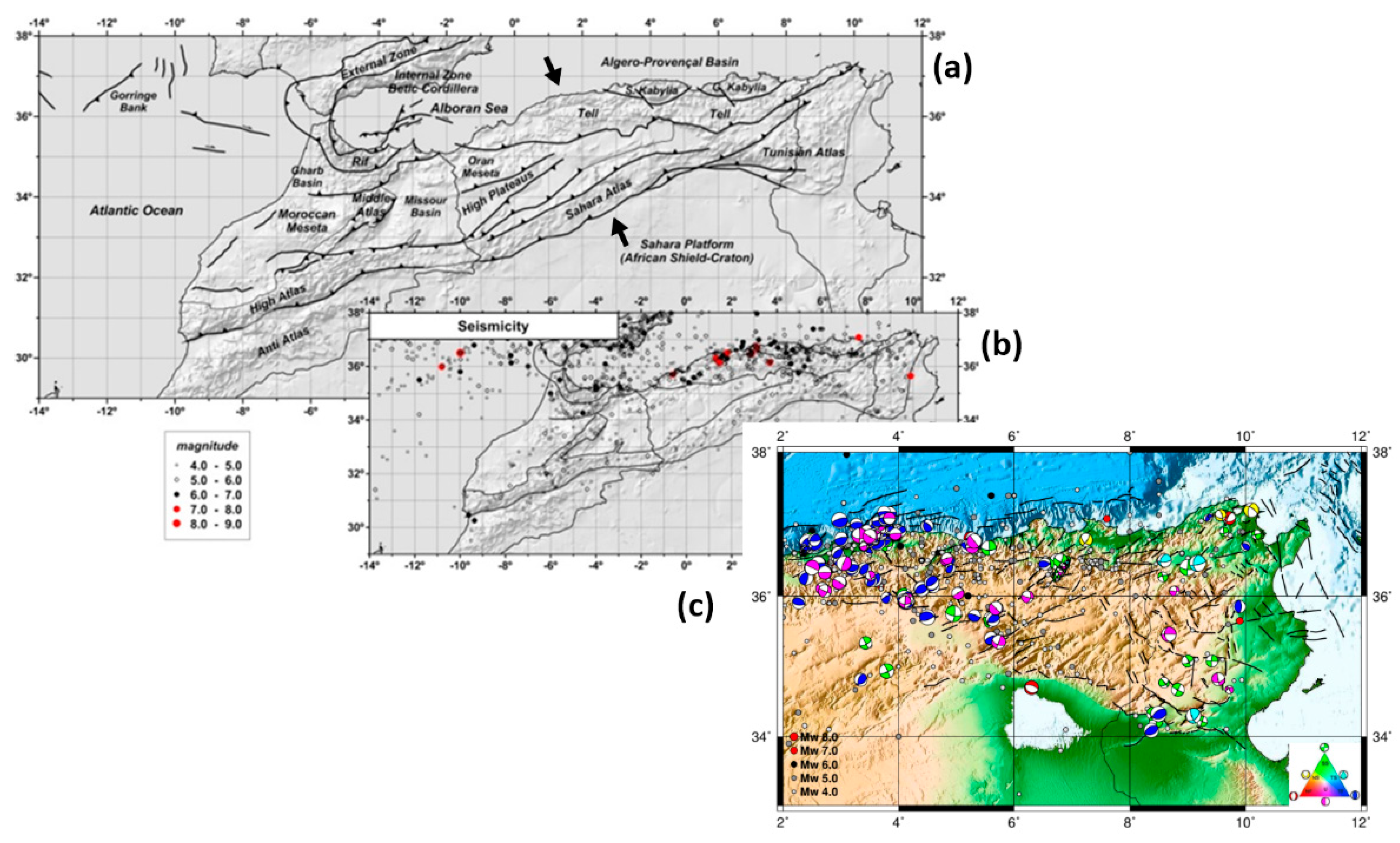
1. Introduction

Earthquakes are one of the most challenging natural disasters for populations to manage. Even though earthquakes are unpredictable and typically occur without warning, a detailed analysis of the seismic hazard and risk-reduction measures can help to reduce subsequent economic and social losses after the occurrence of an earthquake.

The north of Algeria is located on the border of the Nubian Plate, which is in a compressional movement with the Eurasian Plate [1,2,3] (Figure 1a). The origin of the seismicity in this region is the compressional movement between these two plates. Known seismic activity (Figure 1b) includes several damaging earthquakes, especially in the last 50 years, where severe earthquakes have been recorded in the El Asnam region (now Chleff), including the earthquakes of 9 September 1954 (Mw 6.8) and 10 October 1980 (Ms 7.3) (see [4]). The most recent significant event was the Zemmouri/Algiers earthquake 21 May 2003 (Mw 6.9), occurring roughly 50 km offshore from the northeast of Algiers (e.g., [5,6]). In addition, in this period, several earthquakes affected regions close to important cities and caused some damages, such as the Constantine (northeast Algeria) earthquake (Ms 5.9) of 27 October 1985.

The interest of the scientific community in approaches to reduce the risk of damaging earthquakes and related seismic risk assessments of urban areas in Northern Algeria is steadily growing in response to this seismic activity. There is always a pressing need for studies on earthquake forecasting, the implementation of building regulations, and safe constructions, especially in developing countries like Algeria, due to the severity of large earthquakes and the damage they produce. The resulting improvement in earthquake risk assessment and hazard management leads to significant savings in human life and properties.

The effects of the earthquakes previously mentioned in Northern Algeria [7] indicate the importance of improving estimates of the forecasting from different source zones. Due to its complex tectonics, the Northeastern region of Algeria was chosen as the studied area.

On both short- and long-term time periods, earthquake forecasting has significant social and economic consequences. In addition, it plays a main role in earthquake preparedness. On the basis of the quantification of patterns in seismicity data, a wide range of forecasting methods have been proposed with varied degrees of effectiveness [8,9,10,11,12,13,14,15,16,17]. For instance, Mignan [17] develops an analysis of the steady increase in seismic activity around a potential earthquake epicenter, known as the accelerating moment release (AMR) approach, while Keilis–Borok [8] presents and analyses step-by-step the topic of the earthquake prediction. A significant advance in this research field is the earthquake forecasting method based on Regional Earthquake Likelihood Models (RELM) [14,18,19,20,21]. Nowadays, a new algorithm known as pattern informatics (PI) is also emerging as an advanced method [14]. In addition, new methods based on deep learning are being developed to find a static-stress-based criterion predicting the location of aftershocks [22], as well as the interest in real-time post-seismic forecasting based on ground velocity recorded within the first hour after the mainshock by means of the perceived magnitude [23].

Several studies have been conducted from the perspective of seismic hazard assessment and forecasting. The Gutenberg Richter (GR) model [24] is widely used and states that the logarithm of the cumulative number of events is linearly proportional to the magnitude. It is worth noting that several authors [25,26,27] suggested that the extreme value distribution is a more suitable analytical model and should be employed for the distribution of the magnitude set rather than the GR model. Stochastic processes, particularly Poisson processes, are also used to forecast earthquake frequencies by taking the earthquake occurrence time into account. The Poisson model is characterized by a constant hazard function and an exponential recurrence time distribution. This assumption leads to the unsatisfying result of only time-independent seismic hazard or seismic forecasting estimates, suggesting that the probability of an earthquake at any given time is independent of its magnitude and the time since the last one, respectively. Additionally, compared to the Poisson law, the distribution of earthquakes is over-dispersed, since the events are grouped in time and location. Various other models based on stochastic processes have also been investigated to predict the number of events, such as compound Poisson [28,29], branching [15,30] and stochastic point processes [31,32]. These stochastic procedures made predicting the magnitude of the earthquake challenging. In addition, these approaches are ineffective for determining earthquake seasonality and patterns.

Recently, a few studies attempted to use forecasting models based on time series, such as the Auto-Regressive Integrated Moving Average (ARIMA) and the generalized autoregressive conditional heteroscedasticity (GARCH) models [33,34], to forecast earthquake magnitudes by considering the seasonality and trends of earthquake series. Another model, the singular spectrum analysis model, or SSA [35,36,37], is becoming more attractive in order to forecast earthquake magnitudes in a specific seismic zone. It is a reliable and advanced non-parametric time series analysis method combining dynamical systems, signal processing, multivariate statistics and traditional forecasting analysis. According to several authors [35,36,37], this approach is useful for determining the magnitude of earthquakes in a given area. The SSA model can identify significant seismic time series components exhibiting typical irregular behavior and provide accurate forecasts for them. Despite the fact that a few studies on earthquake magnitude forecasting using the SSA approach have been conducted [37], the primary goal of our study is to apply this method in Northeastern Algeria to predict earthquake magnitudes with time effects, which are frequently missed in estimates, while also capturing the dynamics of earthquake occurrences. Subsequently, the ARIMA and SSA models provided the annual maximum earthquake magnitudes for the first time in the studied area.

The root mean square error approach, usually denoted as RMSE, is a common tool for comparing different models and/or methodologies in time series [38,39]. In this study, the estimated RMSE values show that the SSA is the best model for describing the number of earthquakes and the annual maximum magnitude in this region. The seismicity in this area is continuous, and it is characterized by low-to-moderate seismic activity. Despite the interest of the scientific community in regional seismology and seismic hazards, the studied area remains of great interest due mainly to the tectonic complexity, which resulted in the identification of several active faults, the characteristics of which are still under investigation [40]. Then, this study is the first one in this region to address the issue of forecasting using time series, and it is part of the scientific community’s efforts to manage and reduce seismic risk. It is worth noting that, previously, a model has been developed for Northern Morocco and Algeria to assess the probability of exceeding magnitudes Mw 5.0 and 6.0 in 10 years [41], but assuming a Poissonian process on a spatially smoothed seismicity model. This study enabled for the spatial variation of such results.

In the current study, the consistency between the observation and the forecast is analyzed using the CSEP (Collaborative for the Study of Earthquake Predicability) test [42] in terms of the total number of events, also denoted as N-test. The results are presented as quantile scores, δ₁ and δ₂ indices. According to Nanjo et al. [43], the forecast rate is too high (an overestimation) if δ₂ is very small, and too low (an underestimation) if δ₁ is very small for the N-test. Furthermore, according to the original CSEP testing framework, a model fails the test if its score is below a significance level of 2.5%, indicating an inconsistency between the forecast and the observation.

2. Seismicity and Earthquake Database

The study area is situated in the Tell Atlas in Northeastern Algeria (Figure 1a). This important geological formation resulted from a collision caused by the Algero–Provençal Basin opening within the Nubia Plate in the Early Miocene. Furthermore, it is most likely related to the Nubian Plate subduction, which is dipping to the north [44,45].

Onshore and offshore folds and thrust faults extending from NE–SW and from E–W represent the majority of the current tectonic features (e.g., [46,47]). The compressional movement between the Nubian and Eurasian Plates causes considerable seismicity, which is mostly represented in a moderately diffused seismic area in Northern Africa in its western domain (Figure 1b). This collision zone includes Northern Algeria, where recent geodetic studies reveal an actual plate convergence rate of about 5 ± 1 mm/yr in a N60°W direction, as illustrated in Figure 1a [2,3,48,49,50]. Earthquakes with a magnitude above Mw 5.0 frequently occur in the area [7,51], sometimes causing significant damage and casualties [52,53].

Most well-studied thrusting earthquakes occur on land, including the largest-recorded Ms 7.3 10 October 1980, El Asnam earthquake [54,55,56]. Examples of destructive earthquakes in the past include the 3 January 1365, and 5 May 1716 earthquakes, both felt with intensity X (European Macroseismic Scale, EMS-98) [57]. The earthquake that struck on 2 March 1825, with a felt intensity of X–XI on the Modified Mercalli Intensity Scale (MMI), was another historical occurrence. The Mw 6.9 earthquake that struck the area under consideration on 21 May 2003 was the most recent destructive earthquake [7]. The seismicity of the studied area displayed in Figure 1b has been the subject of various studies, both on historical and instrumental seismicity. For instance, Harbi et al. [51] performed a clear and comprehensive analysis of the historical seismicity, proposing the re-appraisal of several historical events located in the region. On the other hand, recent instrumental seismicity recorded by the Algerian seismic network has also been the subject of several works [58,59,60,61,62]. Figure 1c depicts the shallow depth (h ≤ 30 km) focal mechanism data compiled in the region [44,45]; the Frohlich diagram [63] is displayed, and the Zoback classification [64] is used. In previous studies [44,45], a detailed analysis of the inversion of the focal mechanism solutions and the inferred stress pattern was performed. The tectonic framework of the Ibero–Maghrebian region is detailed from these data, and the results are found to be in agreement with more recent studies (e.g., [50]). Similar horizontal maximum principal stress directions can be seen throughout the area, and they almost exactly coincide with the previously identified horizontal P axis in the NW–SE direction, as previously established by Henares et al. [65]. Additional tectonic stress regimes have been identified, including extensional, compressional, transpressional and strike-slip schemes.

The earthquake data file considered in this analysis was obtained from a seismic catalog previously compiled [7] for Northern Algeria, which has been updated until December 2019. It is well recognized that having an up-to-date Poissonian earthquake data file is a prerequisite for any seismic hazard assessment [66,67,68,69]. A combination of available published studies, bulletins and original data was used to produce the early earthquake data file. This led to the development of a unified earthquake data file, including information on magnitude, regional extent (between 32° and 38° latitudes and between 3°W and 10°E longitude), and date range (between AD 856 and June 2008) [7].

Specifically, for the current study, this initial earthquake data file has been updated to December 2019, with data coming from the Spanish Instituto Geográfico Nacional (IGN) and the Algerian Centre de Recherche en Astronomie, Astrophysique et Geophysique (CRAAG). It is important to note that in order to maintain the magnitude homogenization, this process was performed using the same relationships between reported magnitudes and moment magnitude that were used to generate the initial catalog [7]. The initial recorded events were described using several scales (surface-wave Ms, body wave m_b, body wave from Lg phase amplitude m_bLg and local duration M_L magnitudes). The next stage was to identify and remove any dependent event or non-Poissonian earthquake (foreshocks, aftershocks and swarms). In the present study, the method of Gardner and Knopoff [70] was applied using the particular temporal and spatial window introduced in the initial catalog [7]. Figure 1b shows the spatial distribution of shallow seismicity for earthquakes with magnitudes greater than Mw 4.0 using the declustered dataset. Figure 1c, on the other hand, shows the distribution of focal mechanism solutions and seismicity with magnitudes greater than Mw 4.0.

Finally, the completeness of this catalog is performed at the base of a visual approach [71] in order to evaluate the threshold magnitude of the earthquake data file. Following previous studies [7,72], this approach is applied to our data above different magnitude values: if the cumulative annual number of earthquakes over this magnitude is approximately linear, then the seismic catalog is complete and Poissonian for a given threshold magnitude during a specific period of time. The cumulative number of events with a magnitude above Mw 4.0, 4.5, 5.0, 5.5, 6.0 and 6.5 is depicted in Figure 2. It shows that magnitudes above Mw 4.0 and 4.5 appear roughly complete and Poissonian since 1920 and 1910, with rates of 7.7 and 4.2 events/year, respectively. However, approximately since 1870 and 1885, with rates of 2.1 and 0.81 events/year, magnitudes exceeding Mw 5.5 and 5.0 can be considered complete and Poissonian, respectively. For magnitudes greater than Mw 6.0 and 6.5, they are likely complete and Poissonian since 1860 and 1700, respectively, with rates of 0.21 and 0.08 events/year.

3. Methodology Outline

The annual earthquake number series, denoted as {N_k; k ≥ 0}, and the annual maximum magnitude in Northeastern Algeria that occurred during the period from 1910 to 2019, named {m_k, k ≥ 0}, have been modelled using two different approaches. Initially, a parametric approach, abbreviated as ARIMA, was based on the Autoregressive Integrated Moving Average model, and a non-parametric approach was based on the Singular Spectrum Analysis model, abbreviated as SSA. ARIMA models [73], also known as Box–Jenkins models, are powerful tools in time series analysis aiming to describe the autocorrelations in the data and forecast values in the univariate time series that are non-stationaries, which are the time series with a trend component [74]. Usually, the notation ARIMA (p,d,q) is used, where q is the parameter of the moving average (MA) model, p is the parameter of the autoregression (AR) model, and d is the number of the differentiation procedure necessary to ensure the stationarity in the series. The extensions to ARIMA models are the Seasonal Box–Jenkins models [75], which support the direct modelling of the seasonal component of the non-stationaries time series exhibiting both the trend and seasonal fluctuations [74]. For seasonal series of a given period S, a Seasonal Autoregressive Integrated Moving Average (SARIMA, or Seasonal ARIMA) is introduced with the notation $SARIMA\left(p,d,q\right)\times {\left(P,D,Q\right)}_S$, with P and Q being the orders of the seasonal autoregressive and seasonal moving average polynomials.

Let (X_t)_t≥0 be a time series. The $ARIMA\left(p,d,q\right)$ equation model takes the form

$${\Phi }_p\left(B\right){𝛻}^d{X}_t={\mathsf{\Theta }}_p\left(B\right){\epsilon }_t$$

(1)

where ε_t is the error series representing the white noise of mean 0 and variance ${\sigma }_{\epsilon }^2$, and

$${𝛻}^d={\left(1-B\right)}^d$$

(2)

represents the difference operator of order d, being d, the order of integration required to achieve the stationarity in the data. The polynomial

$${\Phi }_p\left(B\right)=1-{\phi }_1{B}^1-{\phi }_2{B}^2-\dots -{\phi }_p{B}^p$$

(3)

corresponds to the AR term at the pth order and

$${\Phi }_p\left(B\right)=1-{\phi }_1{B}^1-{\phi }_2{B}^2-\dots -{\phi }_p{B}^p$$

(4)

is the MA polynomial at the qth order [76].

The first stage in the Box–Jenkins analysis procedure is to ensure that the analyzed series is stationary; that is, free of trend and seasonal terms. The plot of the autocorrelation (ACF) and partial autocorrelation functions (PACF) are used to determine the parameters p and q, which control substantially the model. According to Cowpertwait and Metcalfe [77], for a second-order stationary time series, the autocovariance function of the lag k is given by

$${\gamma }_k=E\left[\left(x_t-\mu \right)\left(x_{t+k}-\mu \right)\right]$$

(5)

noticing that the number of time steps between the variables is known as the lag.

The lag k autocorrelation function (ACF) ρ_k, is defined as

$${\rho }_k=\frac{{\gamma }_k}{{\sigma }^2}$$

(6)

being μ and σ² the mean and the variance of the time series, respectively, where ρ₀ = 1. In general, the partial autocorrelation function (PACF) of stationary time series at lag k is the k-th coefficient of a fitted AR(k) model; if the underlying process is AR(p), then the coefficients will be zero for all k > p. It measures the correlation between observations that are separated by k time units (e.g., x_t and x_t−k) after removing the effect of any correlation resulting by the terms at shorter lags (e.g., x_t−1,………,x_t−k−1). The Akaike information criterion [78] and the Bayesian information criterion [79], denoted as AIC and BIC, respectively, are used to select the best model, the one with minimum information criterion values and white noise error series. According to Fabozzi et al. [80], it is worth noting that the AIC criterion represents the relationship between the Kullback–Leibler measure [81] and the maximum likelihood estimation method. The Kullback–Leibler measure is developed to capture the lost information in the estimation, which means that this measure selects the good model minimizing the loss of information. Usually, the AIC criterion is given by the equation

$$AIC=-2logL\left(\tilde{\theta }\right)+ 2K$$

(7)

where θ is the set of model parameters, $L(\tilde{\theta })$ is the likelihood of the candidate model given the data when evaluated at the maximum likelihood estimate of θ, and K is the number of the estimated parameters in the candidate model.

For small samples, the corrected Akaike information criterion, denoted as AIC_c, should be used instead of the AIC criterion described previously. The relation giving the AIC_c is

$$AI{C}_c =-2 logL(\tilde{\theta })+ 2K+ \raisebox{1ex}{$\left(2K+1\right)$}\!\left/ \!\raisebox{-1ex}{$\left(N-K-1\right)$}\right.$$

(8)

where N is the number of observations. Hurvich and Tsai [82] define a small sample size as one that is less than 40. It is noteworthy that, as N increases, the third term in AIC_c approaches zero, producing the same result as the AIC criterion.

The Bayesian information criterion [79], denoted as BIC, is another model selection criterion based on the information theory but set within a Bayesian context. The difference between the BIC and the AIC criteria is that the former puts a greater penalty for the number of parameters than the latter. It is computed using the following relation

$$BIC=-2 logL(\tilde{\theta })+KlogN$$

(9)

where the terms are the same as described in the definition of the AIC criterion. As in the previous criterion, the best model is the one providing the minimum BIC value.

The Single Spectrum Analysis (SSA) model is a time series forecasting method commonly used to analyze time series with periodic oscillations. The application of the SSA method is advantageous because it encompasses decomposing a time series into simpler components, such as a gradually changing trend, oscillations and noise. Various disciplines have implemented the SSA method, including signal processing [83], nonlinear dynamics [84,85], climate data [86,87,88], medical science [89] and mathematical statistics [90]. Furthermore, when combined with neural networks or other comparable techniques, it is a powerful pre-processing tool for time series forecasting [91,92]. Decomposition and reconstruction are the two complementary processes that make up the SSA implementation algorithm.

According to Golyandina and Zhigljavsky [93], we consider a real-valued time series X = (x₁,…, x_N) with length N (N > 2), satisfying x_j ≠ 0 for at least one j. The first step in the decomposition stage, named the embedding step, consists in transforming the original time series into a sequence of L-dimensional vectors, X_i = (x_i, …, x_J)^T, where J = N − L + 1, and L is the window length. The J-formed vectors are called L-lagged vectors and present the columns of the trajectory matrix (or L-trajectory matrix) of the series X (L × J) given by

$$X=\left(\begin{array}{ccc}{x}_1& x_2& \begin{array}{cc}\cdots & x_J\end{array}\\ x_2& x_3& \begin{array}{cc}\cdots & x_{J+1}\end{array}\\ \begin{array}{c}⋮\\ x_L\end{array}& \begin{array}{c}⋮\\ x_{L+1}\end{array}& \begin{array}{cc}\begin{array}{c}\ddots \\ \cdots \end{array}& \begin{array}{c}⋮\\ x_N\end{array}\end{array}\end{array}\right)$$

(10)

The window length L is obtained through experimentation, and the appropriate L parameter is determined according to the problem being considered and some preliminary information from the time series [94]. It is worth noting that there are no general rules for the determination of this parameter. However, it is advised that for time series exhibiting seasonality, the window length can be chosen as common multiples of 12 [95].

The second step in this stage, called the singular value decomposition, consists of performing a singular value decomposition method to the trajectory matrix X. Here, we will define the matrix S = X.X^T, and denote by λ₁, λ₂, …, λ_L the eigenvalues of S that are taken in the decreasing order (λ₁ ≥ λ₂≥ … ≥ λ_L ≥ 0), and by U₁, U₂, …, U_L the orthonormal system corresponding to the eigenvalues of S. Let d = rank (X), which is equal to max{i, such that ${\lambda }_i$ > 0} and

$$V_i=X^T{U}_i/\sqrt{{\lambda }_i} \mathrm{for} i=1,\dots , d$$

(11)

Using this notation, the singular value decomposition of the trajectory matrix X can be written as

$$X=X_1+X_2+\dots +X_d$$

(12)

with

$$X_i=\sqrt{{\lambda }_i}{U}_i{V}_i^T$$

(13)

The matrices X_i, called elementary matrices, with the rank equal to one, and the set of triplets $\left(\sqrt{{\lambda }_i},U_i,V_i\right)$ are called the ith eigen-triplet of the singular values decomposition.

The second stage of the algorithm implementation corresponding to the reconstruction stage includes two other steps: the eigentriple grouping and the diagonal averaging steps. The eigentriple grouping step consists of dividing the elementary matrices $X_i$ (i = 1, …, L) into r groups, 1 ≤ r ≤ d [94]. The resulting matrices are then produced by adding the r eigen-triples in each group.

Whereas, the diagonal averaging step is based on the reconstruction of the one-dimensional series of length N, that can be considered as an approximation of the original series, by applying the diagonal averaging method on the grouped matrices that are resulted in the previous step [93,96].

In order to compare between the different approaches applied, an important convention is widely used and based on the root mean square error (RMSE) criterion [38,39], which is calculated by

$$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum }_{k=1}^N{\left(x_k-{\widehat{x}}_k\right)}^2}$$

(14)

where x_k indicates the actual value and ${\widehat{x}}_k$ represents the kth forecasted value based on the previous data. Therefore, the optimum model is the one presenting the smallest RMSE value.

4. Earthquake Magnitude Forecasting

The magnitude forecasting analysis for earthquakes with magnitudes equal to or greater than Mw 4.0 is implemented in this section using the previously described models. The data file used in this section includes the main shocks that occurred between 1910 and 2019 in Northeastern Algeria.

Figure 2 shows that the occurrence process during this time period can be approximated by a Poisson process. In this section, we will focus on two time series that represent the annual number of earthquakes and the annual maximum magnitudes in this region.

Here, we denote for j = 1, …, N by $m_j^{\left(k\right)}$ the magnitudes above Mw 4.0 of events occurred during the k-th year and define m_k as the annual maximum magnitude $\underset{0\le j\le N}{\max }{m}_j^{\left(k\right)}$ during the k-th year, whereas the number of earthquakes during the considered year, the k-th year, is denoted as N_k.

Figure 3a displays the {N_k; k ≥ 0} and {m_k, k ≥ 0} plots covering the considered time period using a threshold magnitude equal to Mw 4.0. The ARIMA and SSA time series models are then employed to forecast both the frequency and annual maximum magnitude of earthquakes using the R-packages [97] RSSA and FORECAST [98,99]. By comparing the observed and predicted values, it is critical to identify the fitting models [74]. To increase the accuracy and reduce the rate of uncertainty, we have divided the dataset into training and testing data. We have identified that between 1910 and 2000, nearly 80% of the total events in the series {N_k; k ≥ 0} and {m_k, k ≥ 0} are included, corresponding to 70 observations. As a result, we estimate that 80% of the data are composed of training data, while the remaining 20% are events that were recorded between 2001 and 2019.

Figure 3a shows two significate peaks in the {N_k; k ≥ 0} plot that refer to the high number of earthquakes that occurred between 1960 and 2003, and an important peak in the {N_k; k ≥ 0} plot corresponding to the biggest earthquakes that occurred in the studied region during this period.

The stationarity and the normality of the studied series are tested using the Augmented Dickey Fuller (ADF) [100] and the Shapiro–Wilk (SW) tests [101]. The obtained results are shown in

Table 1. Annual earthquake number and annual maximum magnitude time series stationarity (ADF) and normality (SW) tests results. ARIMA model selection using the AIC and BIC criterions are also showed.

Series	ADF Test	SW Test	Model	AIC	BIC
Eartq_Num			ARIMA (2,1,2)	4.061	4.255
	0.345	7.21 × 10−7	ARIMA (2,1,1)	3.995	4.175
			SARIMA (2,1,2) (1,0,1)(S=12)	4.068	4.294
Max_Mag			ARIMA (2,1,2)	2.169	2.364
	0.063	0.029	ARIMA (2,1,1)	2.191	2.425
			SARIMA (2,1,2) (1,0,1)(S=12)	2.198	2.425

. The ADF test indicates the non-stationarity in {N_k; k ≥ 0} and {m_k, k ≥ 0} time series with a p-value greater than 5%, and according to SW test (Table 1), the normality hypothesis is rejected for both series (p-value less than 5%). Thus, the {N_k; k ≥ 0} and {m_k, k ≥ 0} series are not normally distributed variables with non-stationary behaviour, which means that these non-parametric methods can be more appropriate for our study.

The stationarity of the data is an important hypothesis in ARIMA modelling. As a result, the first order differentiated series of {N_k; k ≥ 0} and {m_k, k ≥ 0} are computed. Figure 3b shows the differentiated resultant time series, with the two plots indicating a clear stationarity in the data. Thus, the integration parameter d is fixed in this study to 1. The p and q parameters of the ARIMA model are determined from the ACF and PACF plots of the differentiated series of {N_k; k ≥ 0} and {m_k, k ≥ 0}, respectively, which are shown in Figure 4. In the set of candidate ARIMA models, the optimum models for {N_k; k ≥ 0} and {m_k, k ≥ 0} are the ones that minimize the AIC and BIC criteria and have a normally uncorrelated residual. Hence, according to Table 1, the ARIMA (2,1,1) and ARIMA (2,1,2) models are the selected ones for {N_k; k ≥ 0} and {m_k, k ≥ 0} time series, respectively. Figure 5 illustrates the residuals analysis of the two models, where Figure 5a shows the residuals of the selected models. Figure 5b shows the ACF residual plots, indicating that the residuals of the two models are uncorrelated. Finally, Figure 5c shows that the residuals are normally distributed according to the residuals Quantile-Quantile plots (Q-Q plot) statistical test [102,103].

The second approach considered in our study is based on the SSA method. The first stage of the SSA method consists of decomposing the {N_k; k ≥ 0} and {m_k, k ≥ 0} time series into principal independent components, which are the trend, the seasonality and the noise. The second stage consists of reconstructing the original series using only the trend and the seasonality. Figure 6 indicates that the seasonality and trend components used together (blue line) describe the observed earthquake number and the annual maximum magnitude in the studied region better than the trend component alone (red line).

The parameters of the SSA model were empirically chosen based on a visual presentation and clear separability of the main independent components. According to Hassani [104], a window length less than half of the sample size is considered adequate. According to Golyandina et al. [94], for seasonal time series, this parameter must be a common multiple of the seasonality period. Several window lengths (12, 24 and 36 samples) were thus evaluated to select the best one, which has been chosen using the RMSE criterion. The reconstruction stage parameter (see Section 3), denoted r, is determined using the eigenvalues plot of the {N_k; k ≥ 0} and {m_k, k ≥ 0} series presented in Figure 7, where the slow decrease in these plots suggests the beginning of the noise component. Then, according to Figure 7, two components are used both in the reconstruction process of the {N_k; k ≥ 0} series and in the reconstruction of the {m_k, k ≥ 0} series. These results can be confirmed using the w-correlation matrices shown in Figure 8. The w-correlation matrices indicate that the first three components are uncorrelated in the {N_k; k ≥ 0} series (Figure 8a), and two components in the {m_k, k ≥ 0} series (Figure 8b). Therefore, from the w-correlation matrices, the reconstruction parameter is fixed to 3 and 2 for the {N_k; k ≥ 0} and {m_k, k ≥ 0} time series, respectively.

The first group is composed of solely the first component, which is uncorrelated to the other components. Because the second and third components are highly correlated, the pair (2,3) forms the second group. After linking the components from 4 to 8, it is shown that the fourth component has a correlation with the fifth, sixth and eighth components. In addition, the sixth component has a high correlation with the seventh component. Thus, the pairs (4,5) and (6,7), as well as the eighth component, configure the last group.

Therefore, the rest of components in {N_k; k ≥ 0} series correspond to the noise. For {m_k, k ≥ 0} series, according to the w-correlation matrix in Figure 8b, two groups can be used in the reconstruction of the original series. The first group consists of mainly the first component, whereas the second group consists of Components 2–8 and Component 12, which are all correlated with one another. As a result, all of the other components form the noise in the {m_k, k ≥ 0} series. It is worth noting that the first component in both matrices that is uncorrelated with the other component corresponds to the trend component in both series. Therefore, the reconstruction parameters in this case are fixed to 3 and 2 for the {N_k; k ≥ 0} and {m_k, k ≥ 0} time series, respectively.

Table 2. The SSA chosen model based on the RMSE of the analyzed time series.

Series	Model	RMSE
Earthq_Num	SSA (12,2)	3.847
	SSA (24,3)	3.048
	SSA (36,2)	3.426
Max_Mag	SSA (12,2)	0.314
	SSA (24,2)	0.365
	SSA (36,2)	0.395

presents the RMSE value of the candidate SSA models for the studied series. According to the results given in Table 2, the best SSA models for {N_k; k ≥ 0} and {m_k, k ≥ 0} are the SSA (24,3) and SSA (12,2) models, respectively. Figure 9 depicts the independent main component extracted from the {N_k; k ≥ 0} (a) and {m_k, k ≥ 0} (b) series, representing the trend, seasonality and noise components.

Finally, the RMSE value is used to compare the different approaches.

Table 3. Best model selected based on the RMSE value for the two considered time series.

Series	ARIMA (p,d,q) RMSE	SSA (L,r) RMSE
Earthq_Num	(2,1,1) 3.317	(24,3) 3.048
Max_Mag	(2,1,2) 0.374	(12,2) 0.314

displays the RMSE values of the ARIMA and SSA models for the {N_k; k ≥ 0} and {m_k, k ≥ 0} time series, with the smaller RMSE value indicating the better model.

As a result, the SSA (24,3) and SSA (12,2) models are the best ones for describing the number of earthquakes and the maximum magnitude series, respectively.

Table 4. Forecasted annual earthquake number and annual maximum magnitude time series from 2020 to 2030 from the selected SSA model.

Years	Series
	Earthq_Num	Max_Mag
2020	5	4.9
2021	6	5.1
2022	5	4.8
2023	5	4.9
2024	5	5.1
2025	4	5.0
2026	5	4.9
2027	6	5.0
2028	4	5.1
2029	4	5.0
2030	5	5.1

also shows the forecasted values from 2020 to 2030 using the selected SSA models. Finally, Figure 10 depicts the original (grey dashed line) and forecasted (red dashed line) series, where a stationary behavior can be observed in both time series from 2020 to 2030.

5. Validation of the Procedure

After a certain earthquake forecast method has been developed using training data and set up by best fit on real data, and before any practical implementation, it must be validated [105].

The SSA method is used to perform forecasting analysis of the earthquake data file from 1910 to 2015, with the purpose of generating forecast values and comparing them to observed values from 2016 to 2019. As previously stated, the time series are divided into two sets, the first of which includes 80% of the data used as training data [74] and encompasses the years 1910 to 1997, while the remaining 20% covers the years 1998 to 2015, considered as testing data.

The stationarity and the normality of the studied series in the considered training period are tested again using the ADF and the SW tests. The derived ADF values are 0.34 and 0.077 for the annual earthquake number and maximum magnitude, respectively, whereas the obtained SW values are 2.0 × 10⁻⁷ and 0.035 for the two investigated series, respectively. The ADF test results for the two series are higher than 5%, showing that the two series are non-stationary during the training period. Moreover, the two series are not normally distributed and exhibit a non-stationary behaviour as a result of the computed SW values. Therefore, as proceeded initially, and in order to achieve the stationarity in the data, the differentiated series of {N_k; k ≥ 0} and {m_k, k ≥ 0} are computed.

Considering the d parameter of the ARIMA model equal to 1, the ACF and PACF functions of the resultant series are used to select the p and q parameters. Thus, ARIMA (2,1,2) and ARIMA (2,1,3) are the model-candidates for the time series {N_k; k ≥ 0}, and ARIMA (2,1,2) and ARIMA (3,1,2) for the time series {m_k, k ≥ 0}, derived during the training period 1910–1997. Analyzing the annual earthquake number series, AIC values equal to 3.99 and 4.00 are obtained for the ARIMA (2,1,2) and ARIMA (2,1,3) models, respectively, whereas BIC values equal to 4.20 and 4.24 are obtained for the same model candidates, respectively. In addition, analyzing the annual maximum magnitude time series, the obtained AIC values are equal to 2.21 and 2.23 for the ARIMA (2,1,2) and ARIMA (3,1,2) models, respectively. For the same model-candidates, the BIC values are equal to 2.41 and 2.16. Thus, on the base of AIC and BIC criteria, the ARIMA (2,1,2) model is considered the best one to describe the annual earthquake number and the annual maximum magnitude during the training period.

The parameters of the SSA model are then obtained, as previously proceeded, by testing several window lengths (12, 24 and 36 samples). The best model is also derived using the RMSE criterion. Analyzing the annual earthquake number time series, the lower RMSE value equal to 3.62 is derived for the model SSA (24,2), whereas for the models SSA (12, 2) and SSA (36,2), the values are equal to 4.40 and 3.89, respectively. Concerning the annual maximum magnitude time series, the lower RMSE is derived for the model SSA (36,2), whereas for the models SSA (12,2) and SSA (36,2), the values are equal to 0.379 and 0.375, respectively. Finally, for the two considered time series, SSA (24,2) is considered the best model.

Then, using the previously described procedure, the chosen models ARIMA (2,1,2) and SSA (24,2) are used to forecast the annual number of earthquakes and the annual maximum magnitude from 2016 to 2019. Uncommonly, no events with magnitudes greater than Mw 4.0 occurred in the studied region in 2018, whereas two events with magnitudes greater than Mw 4.0 occurred in 2016, 2017 and 2019. Then, the period from 2016–2019 appears as a low seismicity epoch. That being the case, the forecasted values using the model ARIMA (2,1,2) are greater than real ones. In 2016 and 2019, about four events were predicted, and three events were predicted in 2017.

On the other hand, values found using the SSA (24,2) model are of the order of 3 for each year, and hence closer to the observed values. Regarding the annual maximum magnitude, similar values are obtained using the ARIMA (2,1,2) and SSA (24,2) models, of the order of Mw 5.0 for 2016, 2017 and 2019. These forecasted values are in agreement with the observed ones, which are equal to Mw 5.0, 4.5 and 4.7 for 2016, 2017 and 2019, respectively.

Thus, clearly the SSA (24,2) model makes it possible to find realistic results corroborating the observed data.

A statistical test is used to assess the consistency of the results obtained using the SSA algorithm in the period from 2016 to 2019. According to Schorlemmer et al. [19], to take into account the uncertainty, the likelihood test, named L-test, can be conducted by simulating the observed events. In the current study, we focus on the statistical N-test [42], which consists to test the rate forecast. The N-test is intended to measure, in a probabilistic manner, how the forecasted number of events will match the observed number of earthquakes.

Then, the N-test [19,42,106] is implemented. The N-test takes into account two linked quantile scores, δ₁ and δ₂, reflecting whether the produced sequences produced forecasted event numbers N_fore that were higher or lower than the observed values N_obs, as given in the equations

$${\delta }_1=1-P\left(\left(N_{obs}-1\right)|N_{fore}\right)$$

(15)

$${\delta }_2=P\left(N_{obs}|N_{fore}\right)$$

(16)

bearing in mind that $P\left(\omega |\lambda \right)=\frac{{\lambda }^{\omega }}{\omega !}exp\left(-\lambda \right)$.

The quantity δ₁ is the probability of observing at least N_obs, and δ₂ is the probability of observing at most N_obs. Both the overall forecast rate and observed number of events are assumed to be Poissonian and described by N_fore and N_obs, respectively. The quantity δ₂ describes the right-continuous Poisson cumulative distribution with the expectation N_fore at corresponding N_obs at the times evaluated. This score describes the fraction of forecast expectations smaller than the observed events. The probability that more than N_obs events are forecasted is given by (1 − δ₂). The problem with this approach is addressed in [42]. Instead, the δ₁ probability was added in addition to the original N-test to describe at least N_obs, in which the user only needs to be concerned about low probability values [19,42].

The quantile scores in this statistical N-test assess if the number of forecasted occurrences is inconsistent with N_obs. A small δ₁ indicates that the forecast underestimates the observed sequence, whereas a small δ₂ suggests that the forecast overestimates the number of occurrences. The forecast can thus be rejected if the probabilities of δ₁ and δ₂ are less than the effective significance level [42]. The effective significance threshold for the one-sided N-tests was set at 2.5% to coincide with a single quantile score, which corresponds to a 5% error rate for the test [42,107].

Table 5. Observed and forecasted earthquake number using the selected SSA model quantile score δ₁ and δ₂.

Year	N Observed	N Forecasted	N-Test δ1	N-Test δ2
2016	2	3.0	0.8506	0.2240
2017	2	3.2	0.8705	0.2079
2018	0	3.5	1	0.0302
2019	2	3.4	0.8865	0.1929

presents the obtained results, the observed N_obs and the forecasted number of earthquakes N_fore, and the quantile scores δ₁ and δ₂. The N-test performance can be interpreted by observing whether the quantile scores δ₁ and δ₂ fall the region between 0.025 and 1. In Figure 11, we can observe that high δ₁ scores tend to correspond to low δ₂ scores.

6. Discussion and Conclusions

The SSA technique is a well-known and effective time series analysis tool. On the studied earthquake magnitude time series, the forecasting capabilities of the SSA method were evaluated and compared with those of the standard ARIMA one, which is recognized to have a more suitable structure for forecasting.

The results of this study show that the SSA technique could be effectively applied as an algorithm for forecasting earthquake number and sizes.

According to Abacha et al. [61], the seismicity in the studied area is continuous and moderate. Several swarm sequences occurred in the recent past, showing intense activity with low magnitudes and limited time. An analysis of the series covering the years 1910 to 2015 is performed in order to validate the method employed in the current study by forecasting for the years 2016 to 2019. The forecasting values agree very well with the observed events both for the frequency and the annual maximum magnitude. Moreover, according to the recent recorded seismicity in the studied area, the forecasted magnitudes computed in the current study agree very well with the recorded seismicity during the years 2020 and 2021. The recorded magnitude events during these two years are lower than the maximum forecasted magnitudes, equal to 4.9 and 5.1, respectively. These results should to be considered as the maximum magnitude that is not exceeded.

The SSA model successfully modelled the considered data file and provided an accurate forecast of future earthquake magnitudes. Furthermore, the SSA model’s trend component is a clear deterministic component for estimating earthquake magnitude.

The N-test was employed in this study to assess the consistency between the observation and forecasting in terms of the total number of events. The results were given in terms of quantile scores δ₁ and δ₂. According to the results, the test is passed, which validates the suggested model.

The results also show that, while significant parts of the variability in those seismological time series do not appear to have an adequate time structure to be forecasted, the key components may still be identified and forecasted using the SSA model.

It is worth noting that the data file used in this study, which spans the years 1910 to the end of 2019, including events with magnitudes greater than Mw 4.0, could be modelled by an inhomogeneous Poisson process with a variable activity rate (Figure 2). A future study could forecast the number of earthquakes using such an inhomogeneous Poisson process, while the annual maximum magnitude could also be forecasted using, for instance, the extreme probability statistics [25]. An issue that appears to be a weakness of these procedures, and deserves special attention in the future, is the assessment of uncertainties of the forecasted values.