Comparison of Fatigue Performances Based on Shape Change of Rail Fastening Spring
Abstract
:1. Introduction
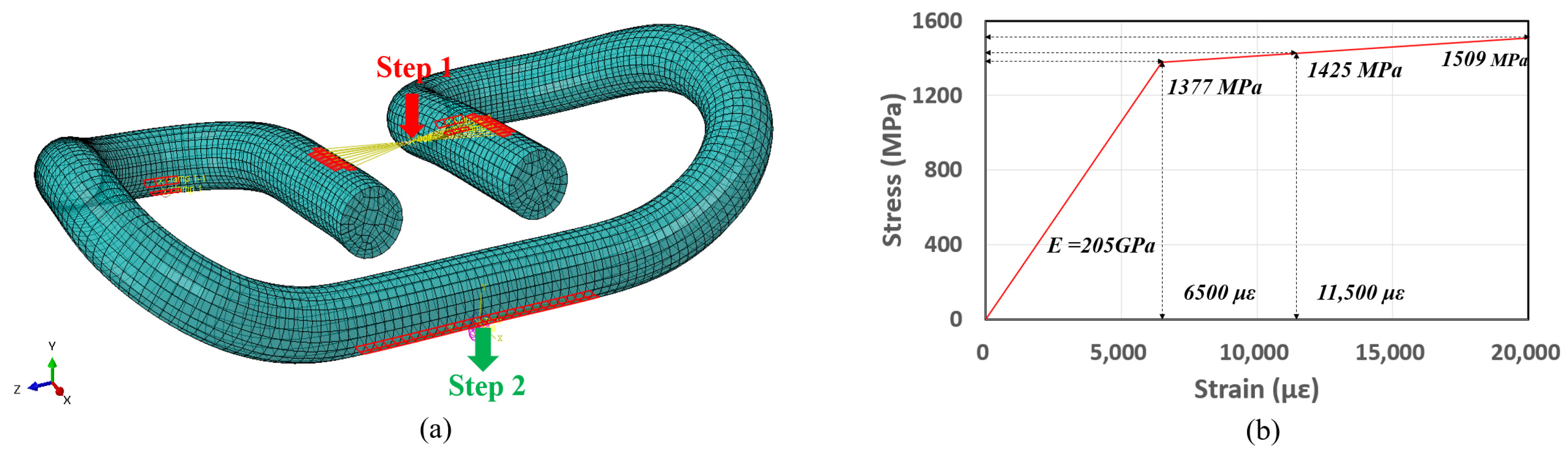
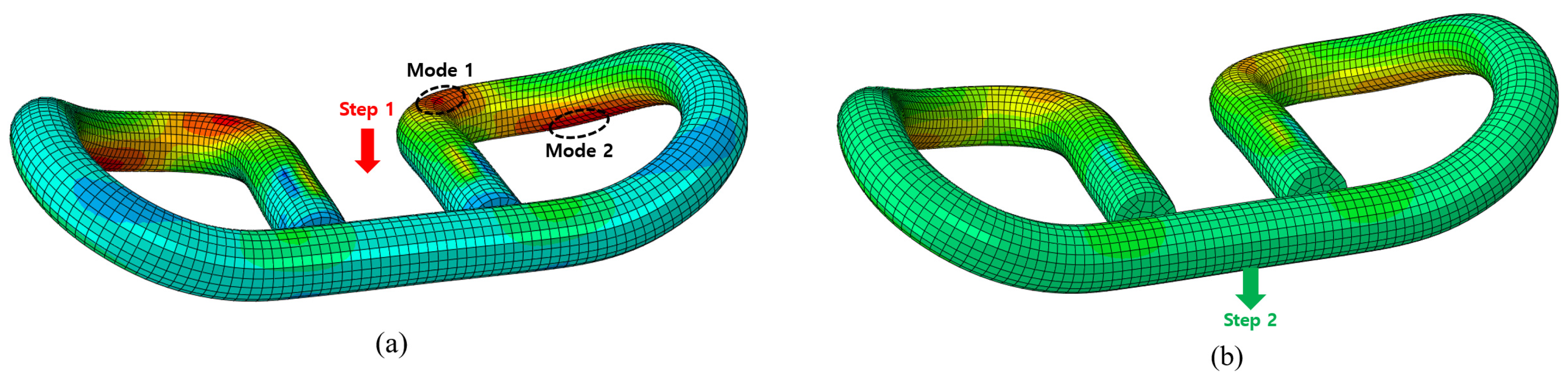
2. Finite Element Analysis
3. Comparison of Fatigue Performance Based on Fastening Spring Shapes
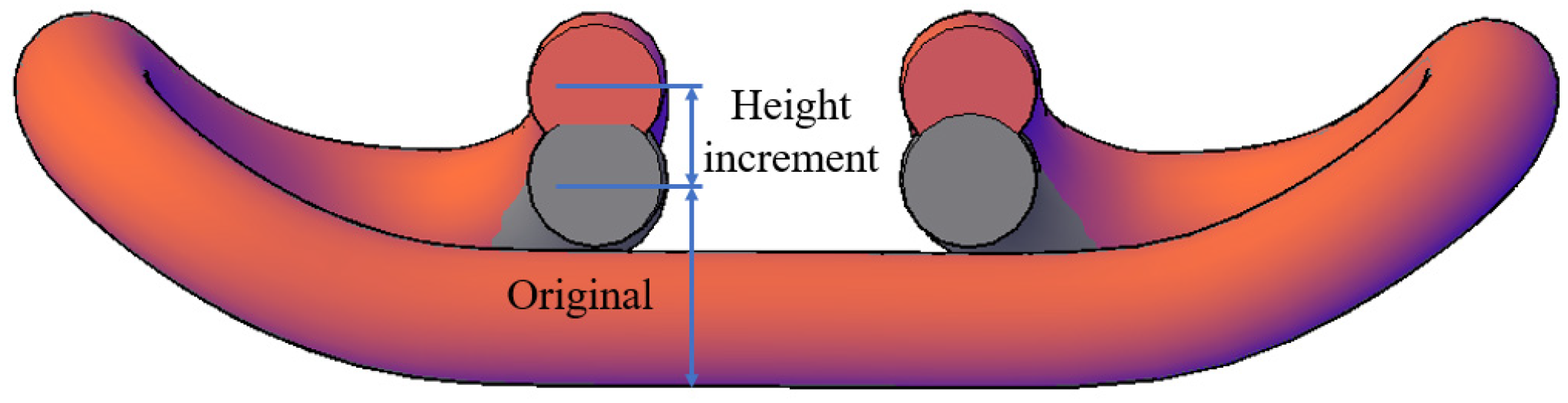
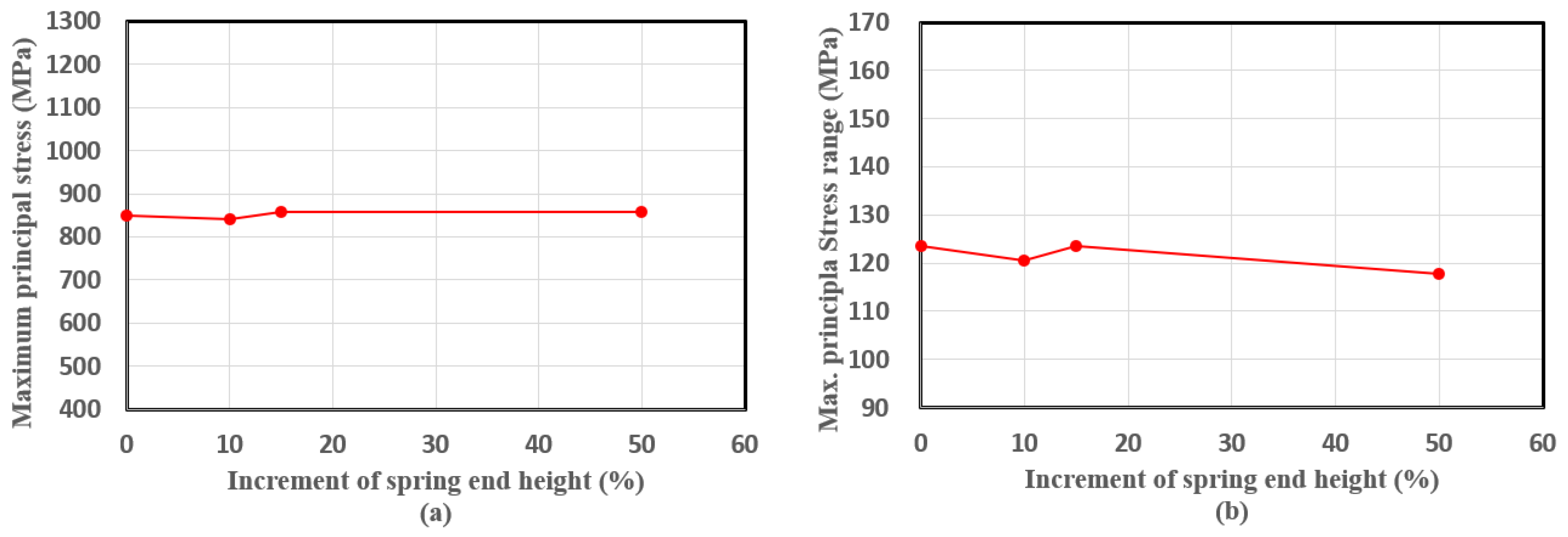
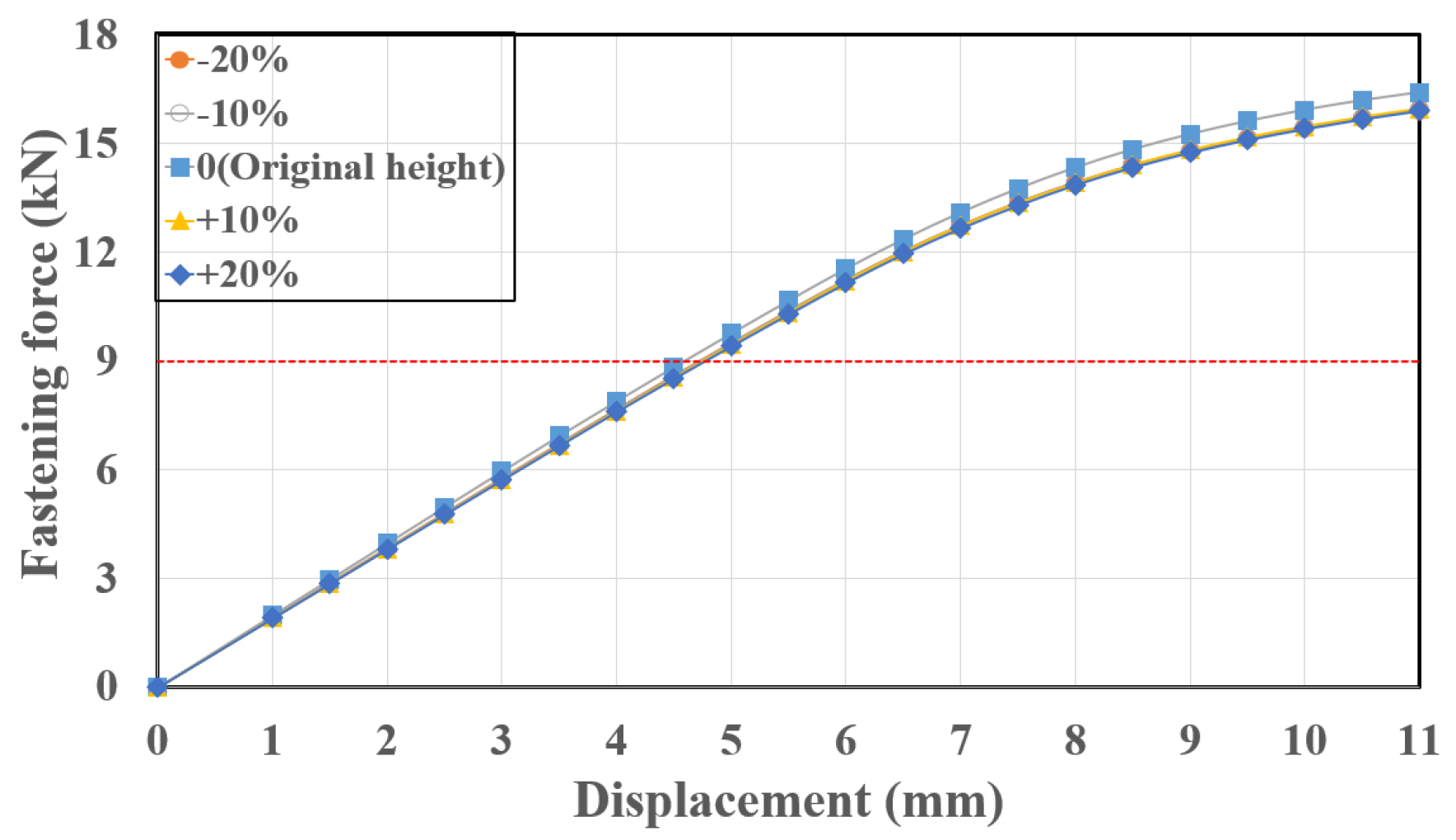
3.1. Height of the Spring End
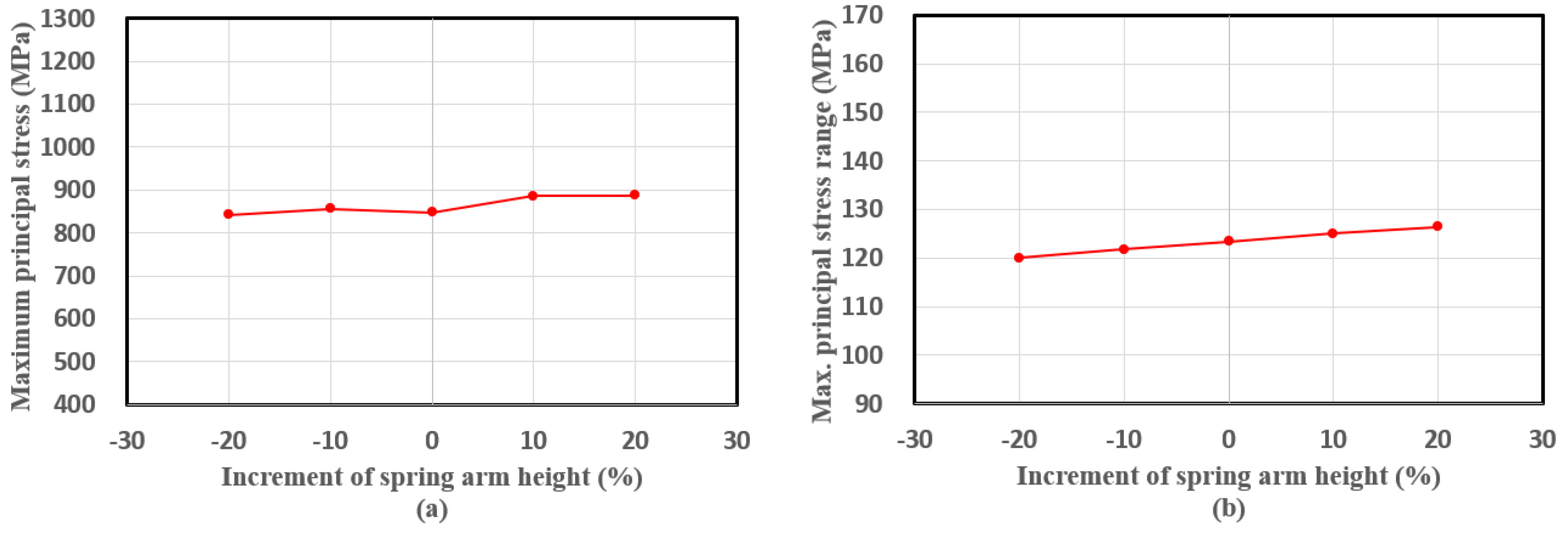
3.2. Height of the Spring Arm
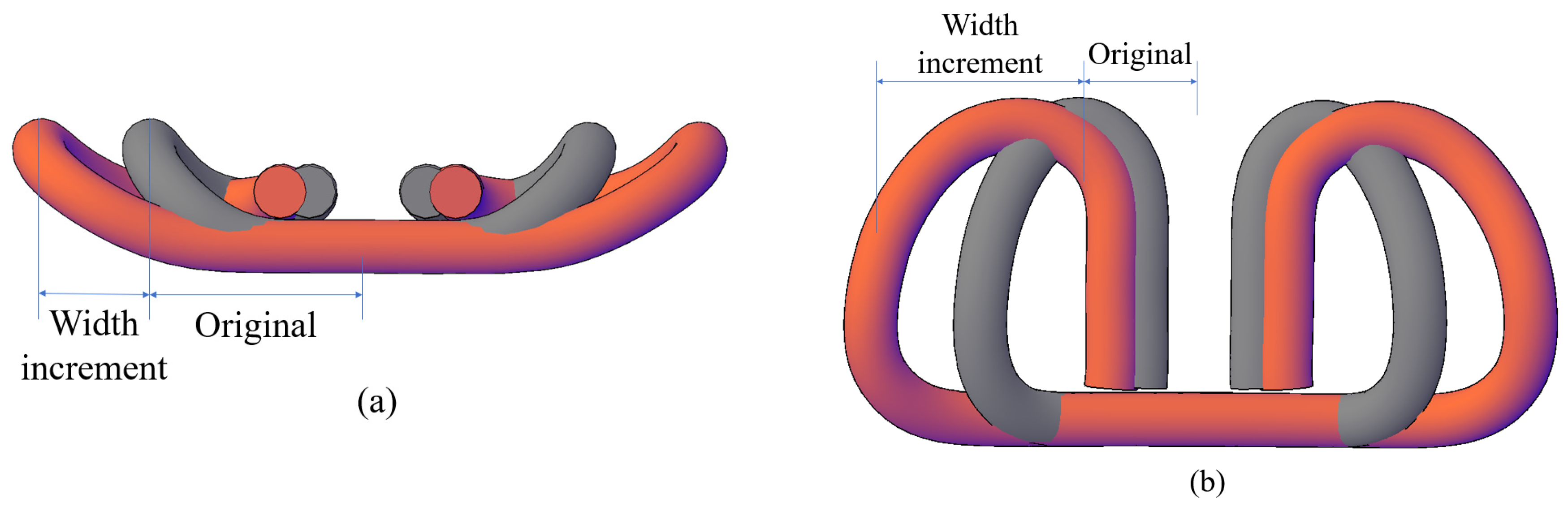
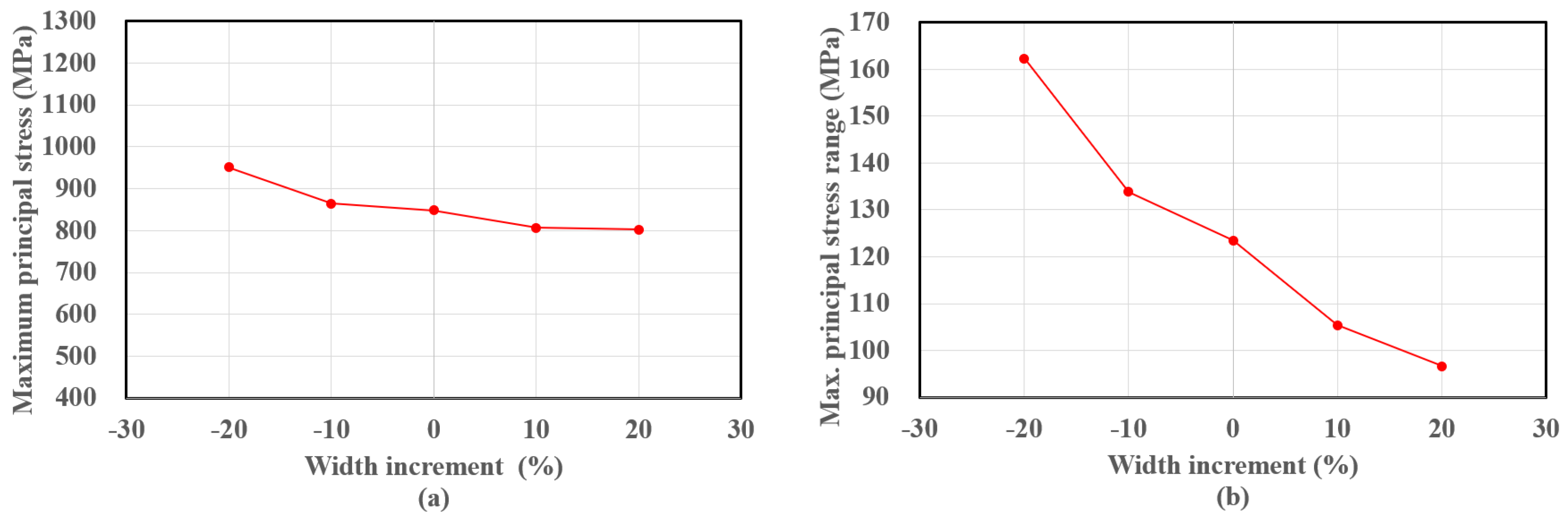
3.3. Overall Spring Width
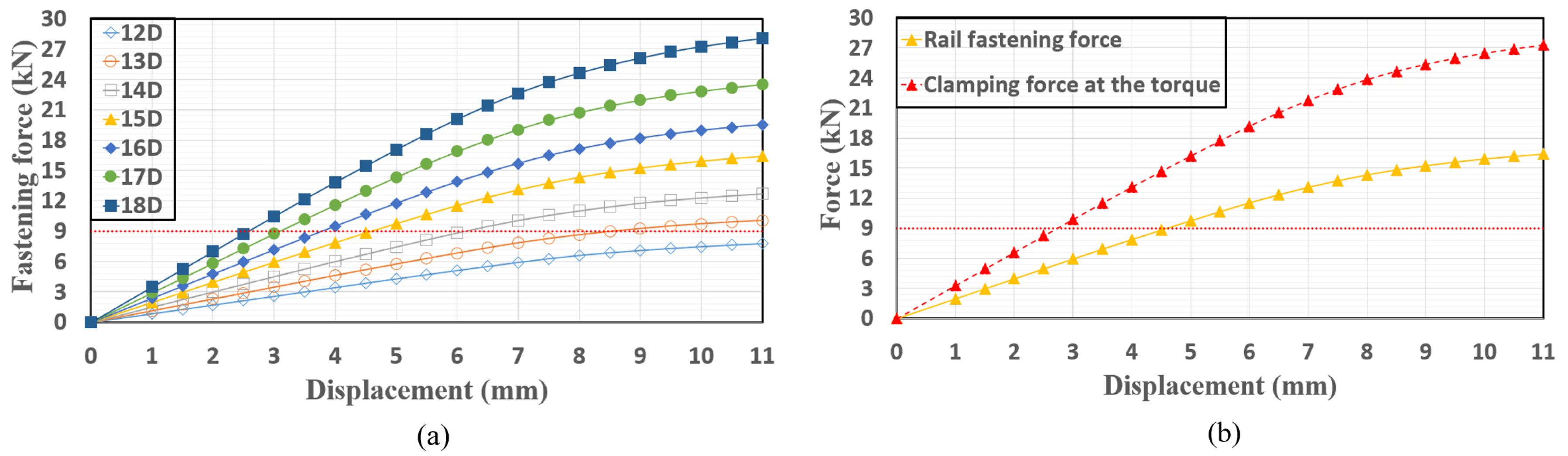
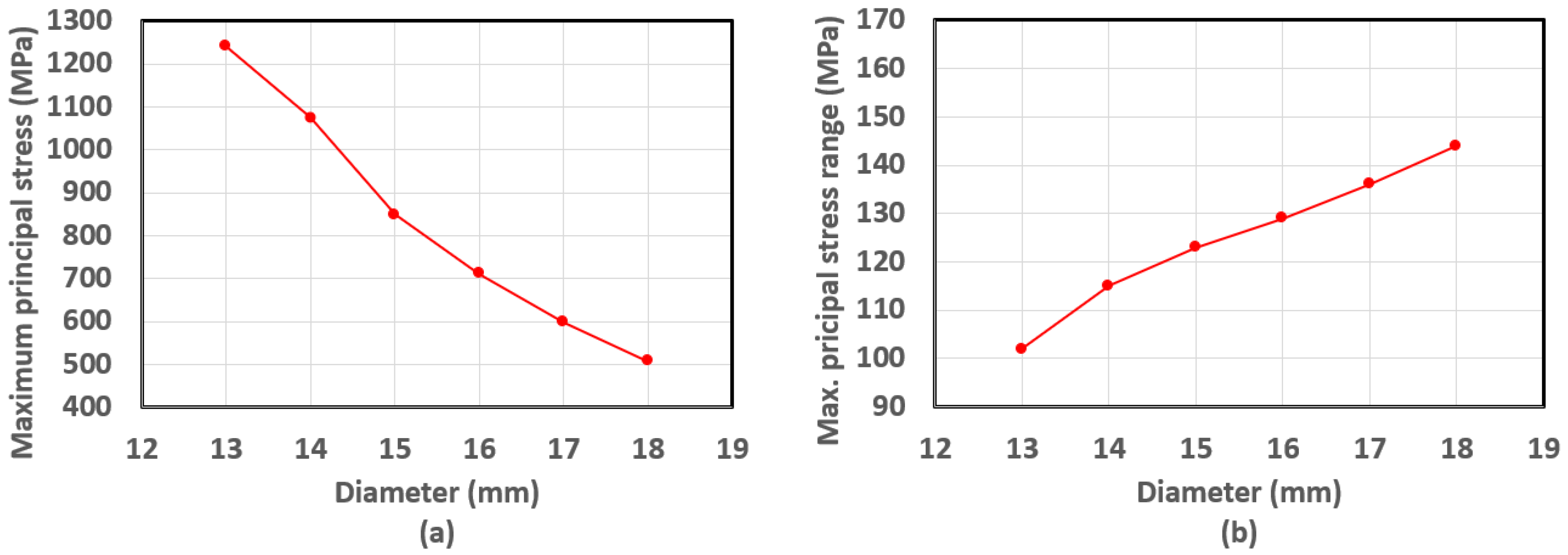
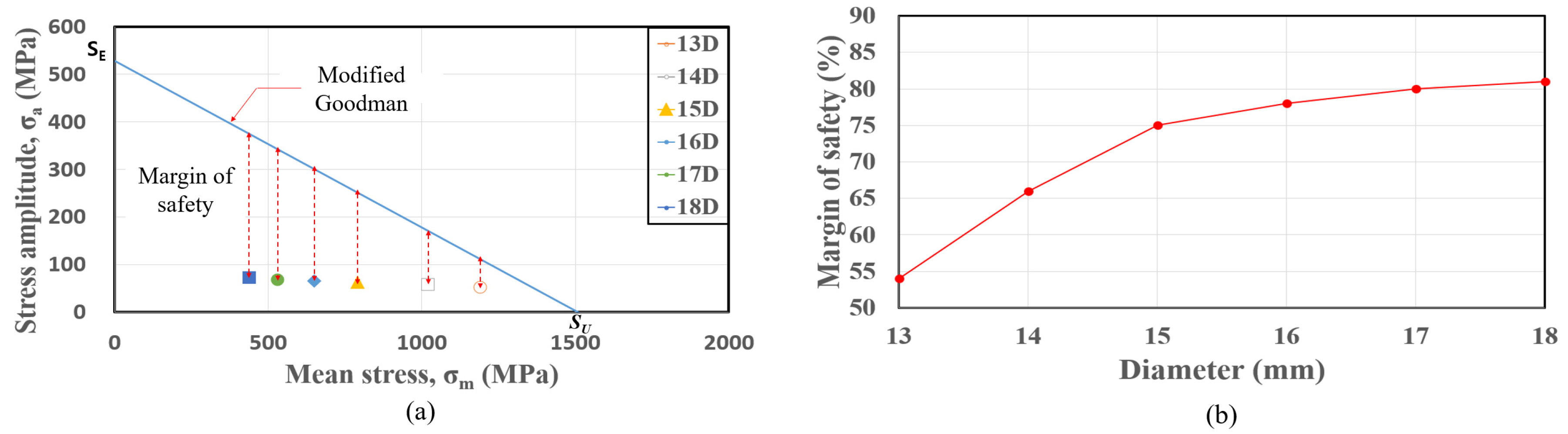
3.4. Spring Diameter
4. Conclusions
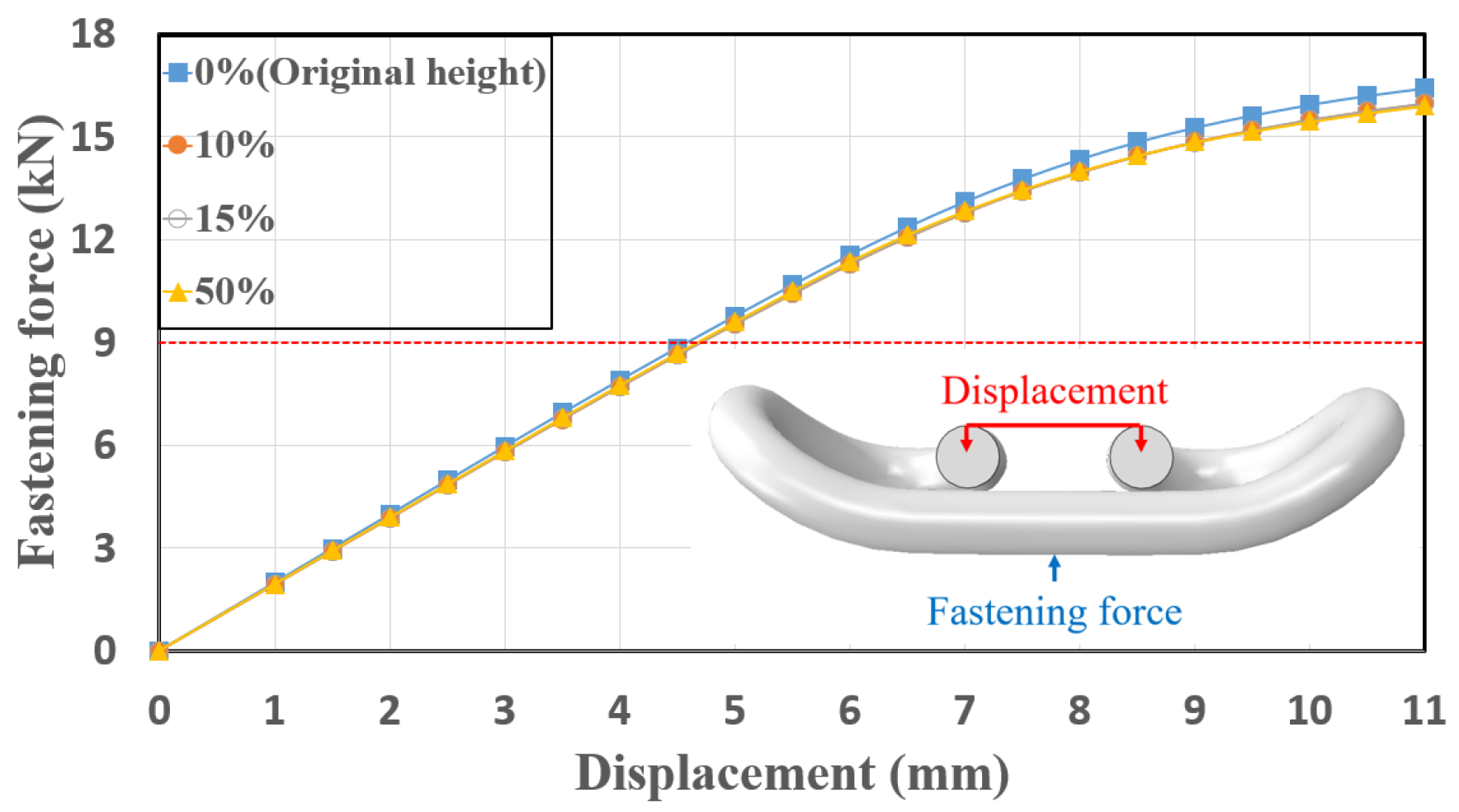
- The shape changes in the height of both the spring end and arm only slightly affected the mean stress and stress amplitude, which were the two main factors affecting the fatigue performance. This observation can be attributed to the similar internal forces (i.e., shear force and bending moment) that occurred in the critical sections with slight changes in the moment arm for each model. These two variables did not significantly change the safety margin ratio. In the case of the spring end height, the safety margin ratio was about the same (75%) when varied from 0% to 50%. In the case of the spring arm height, the safety margin ratio decreased from 75% to 73% when varied from −20% to 20%.
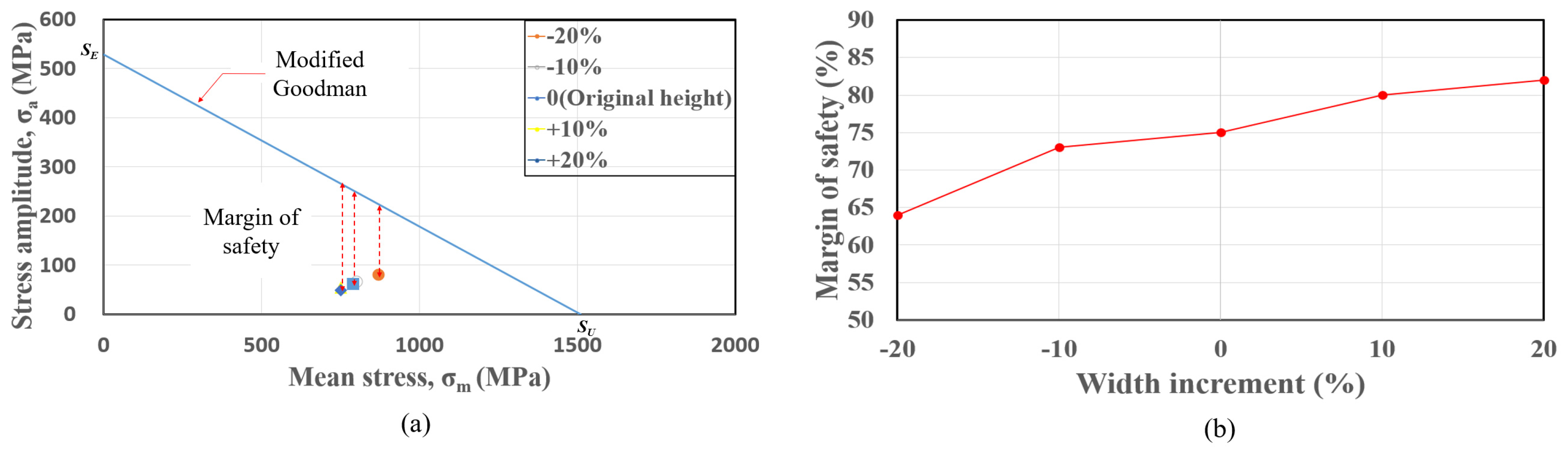
- The overall lateral width of the fastening spring significantly affected the stress condition, particularly the stress amplitude. The mean stress and stress amplitude both decreased as the width increased. With increasing width, this curvature effect on the maximum principal stress was more significant than that of the increased internal force at the critical sections. When the width increased from −20% to 20%, the safety margin ration increased from 64% to 82%.
- The variation in the maximum principal stress and the stress range according to the change in the cross-sectional diameter of the fastening spring were very remarkable. The maximum principal stress decreased as the diameter increased. In contrast, the stress range increased. The fatigue performance in the case of the modified Goodman criterion increased. For example, when the diameter was 13 mm, the safety margin was 54%, whereas in the case of the 18 mm diameter, the safety margin was 81%. It is believed that the maximum principal stress at the initial fastening has a greater dominant effect on the fatigue performance than the stress amplitude.
Author Contributions
Funding
Conflicts of Interest
References
- Oda, J.; Yamazaki, K.; Yoshida, H.; Nakada, K. An analytical and experimental investigation of rail fastening systems in travelling cranes. Int. J. Mech. Sci. 1983, 25, 935–944. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Remennikov, A. Dynamic properties of railway track and its components: A-state-of-the-art review. 2008; research online. [Google Scholar]
- Thompson, D.J.; Verheij, J.W. The dynamic behavior of rail fasteners at high frequencies. Appl. Acoust. 1997, 52, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Smutny, J. Measurement and analysis of dynamic and acoustic parameters of rail fastening. NDT Int. 2004, 37, 119–129. [Google Scholar] [CrossRef]
- Lakusic, S.; Bartos, D.; Goran, B. Experimental and numerical analysis of the rail fastening spring clips types SKL1-SKL12. In Symposium on Experimental Methods in Solid Mechanics. 22nd DANUBIA-ADRIA Symposium on Experimental Methods in Solid Mechanics; University of Parma: Parma, Italy, 2005; pp. 248–249. [Google Scholar]
- Baik, C.H.; Joo, B.G.; Choi, I.Y.; Park, Y.G. The parametric study on the performance characteristics of elastic rail fastening system on the sharp curved track. In Proceedings of the KSR Conference, Jeju, Republic of Korea, 19–21 May 2011; pp. 2163–2173. (In Korean). [Google Scholar]
- Mohammadzadeh, S.; Ahadi, S.; Nouri, M. Stress-based fatigue reliability analysis of the rail fastening spring clip under traffic loads. Lat. Am. J. Solids Struct. 2014, 11, 993–1011. [Google Scholar] [CrossRef] [Green Version]
- Tamagawa, S.; Kataoka, H.; Deshimaru, T. A fatigue limit diagram for plastic rail clips. WIT Trans. Built Environ. 2015, 39, 1–11. [Google Scholar]
- Xiao, J.H.; Yan, Z.Q.; Shi, J.; Ma, D.K. Effect of Wheel-rail impact on the fatigue performance of fastening clips in rail joint area of high-speed railway. KSCE J. Civ. Eng. 2022, 26, 120–130. [Google Scholar] [CrossRef]
- Lee, D.W.; Choi, J.Y.; Baik, C.H.; Park, Y.G. Influence of initial clamping force of tension clamp on performance of elastic rail fastening system. KSCE J. Civ. Environ. Eng. Res. 2013, 33, 1243–1251. (In Korean) [Google Scholar]
- Liu, Y.; Li, Q.T.; Jiang, X.J.; Liu, H.; Yuan, X.P.; Zhu, Z.H. The effect of material static mechanical properties on the fatigue crack initiation life of rail fastening clips. Adv. Civ. Eng. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Park, Y.C.; An, C.B.; Sim, H.B.; Kim, M.C.; Hong, J.K. Failure analysis of fatigue cracking in the tension clamp of a rail fastening system. Int. J. Steel Struct. 2019, 19, 1570–1577. [Google Scholar] [CrossRef]
- Choi, J.Y.; Kim, S.H.; Kim, S.J.; Chung, J.S. Failure analysis of tension clamps (SKL15) used in serviced urban railway tracks: Numerical analysis and experiments. Materials 2022, 15, 6354. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Park, Y.C.; Kim, M.C.; Sim, H.B. A fatigue reliability assessment for rail tension clamps based on field measurement data. Appl. Sci. 2022, 12, 624. [Google Scholar] [CrossRef]
- Han, J.G.; Park, S.S.; Kim, W.Y. A study on the design specification of KR type rail fastening spring. In Proceedings of the KSR Conference, Gangwon, Republic of Korea, 9–11 January 2017; pp. 296–298. (In Korean). [Google Scholar]
- Kim, S.H.; Fang, X.J.; Park, Y.C.; Sim, H.B. Evaluation of structural behavior and fatigue performance of a KR-type rail clip. Appl. Sci. 2021, 11, 12074. [Google Scholar] [CrossRef]
- Gao, X.G.; Wang, A.; He, Y.; Gu, X. Structural improvement of the ω-type high-speed rail clip based on a study of its failure mechanism. Shock. Vib. 2019. [CrossRef] [Green Version]
- Bannantine, J.A.; Comer, J.J.; Handrock, J.L. Fundamentals of Metal Fatigue Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Goodman, J. Mechanics Applied to Engineering; Longmans, Green and Co.: London, UK, 1899. [Google Scholar]
- UIC-774-3R; Track/Bridge Interaction: Recommendations for Calculations. International Union of Railway: Paris, France, 2001.
- KR C-08080; Railway Design Guidelines and Handbooks; Track-Bridge Longitudinal Interaction Analysis. Korea Rail Network Authority: Sejong-si, Republic of Korea, 2017. (In Korean)
- KRS TR 0014-13R; Korean Railway Standards (KRS). Rail Fastening Systems: Sejong-si, Republic of Korea, 2015. (In Korean)
- Budynas, R.G. Advanced Strength and Applied Stress Analysis, 2nd ed.; McGraw Hill: New York, NY, USA, 1999. [Google Scholar]
- Gerber, W.Z. Calculation of the allowable stresses in iron structures. Bayer Arch. Ing Ver 1874, 6, 101–110. [Google Scholar]
- Park, Y.C.; An, C.B.; Kim, M.C.; Sim, H.B. Effect of the depth of decarburized layer in SKL15 tension clamp on fatigue Strength. Appl. Sci. 2021, 11, 3841. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.-J.; Park, Y.-C.; Hu, J.-W.; Sim, H.-B. Comparison of Fatigue Performances Based on Shape Change of Rail Fastening Spring. Appl. Sci. 2023, 13, 1770. https://doi.org/10.3390/app13031770
Fang X-J, Park Y-C, Hu J-W, Sim H-B. Comparison of Fatigue Performances Based on Shape Change of Rail Fastening Spring. Applied Sciences. 2023; 13(3):1770. https://doi.org/10.3390/app13031770
Chicago/Turabian StyleFang, Xiao-Jun, Yeun-Chul Park, Jong-Wan Hu, and Hyoung-Bo Sim. 2023. "Comparison of Fatigue Performances Based on Shape Change of Rail Fastening Spring" Applied Sciences 13, no. 3: 1770. https://doi.org/10.3390/app13031770
APA StyleFang, X.-J., Park, Y.-C., Hu, J.-W., & Sim, H.-B. (2023). Comparison of Fatigue Performances Based on Shape Change of Rail Fastening Spring. Applied Sciences, 13(3), 1770. https://doi.org/10.3390/app13031770







