Evaluation and Characterization of the Influence of Solar Position Algorithm on the Performance of Parabolic Trough Solar System
Abstract
:1. Introduction
2. Calculation Methods
2.1. Optical Efficiency of Solar Trough System
2.2. Tracking Error
2.3. Solar Position Algorithms
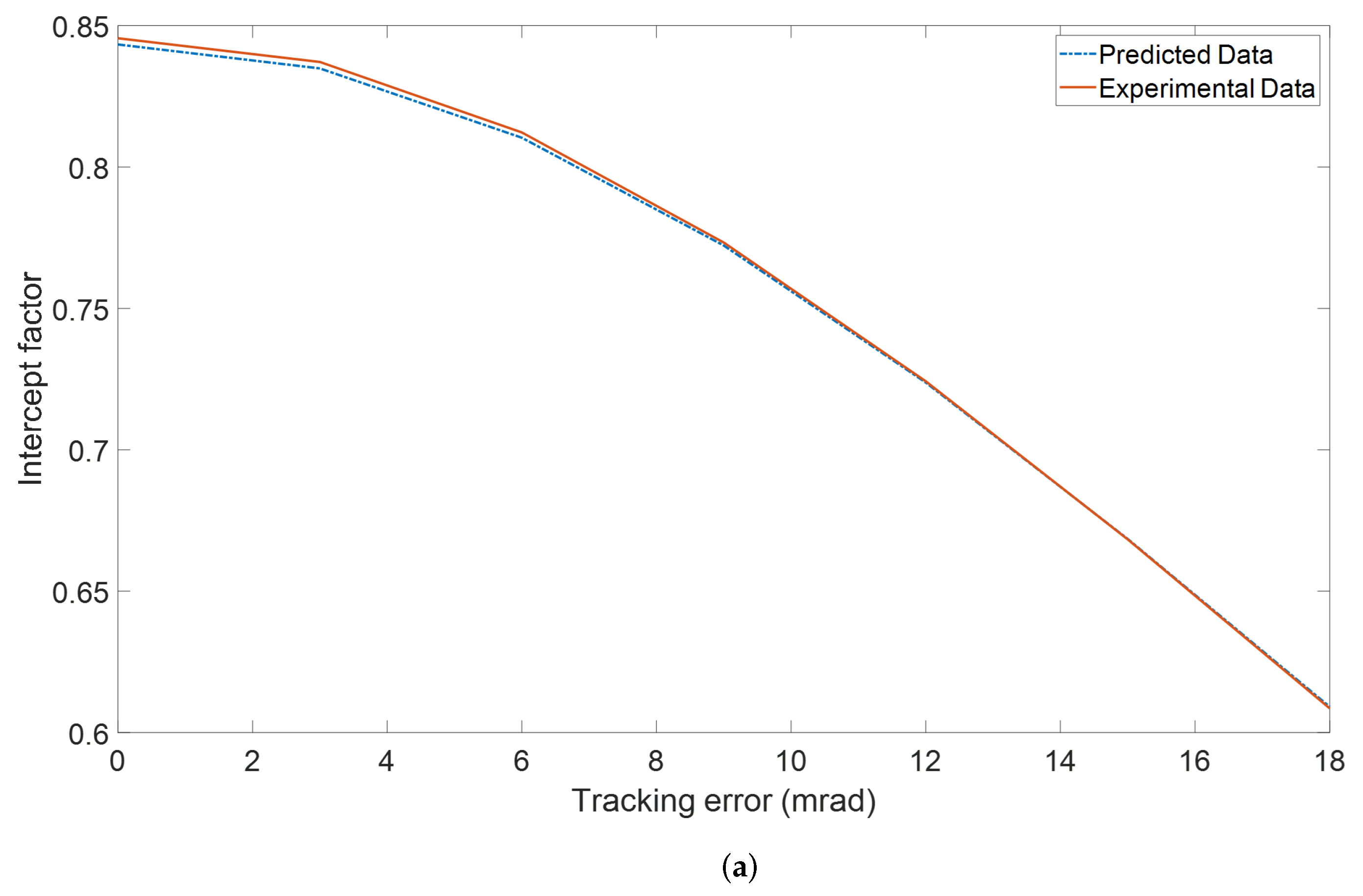
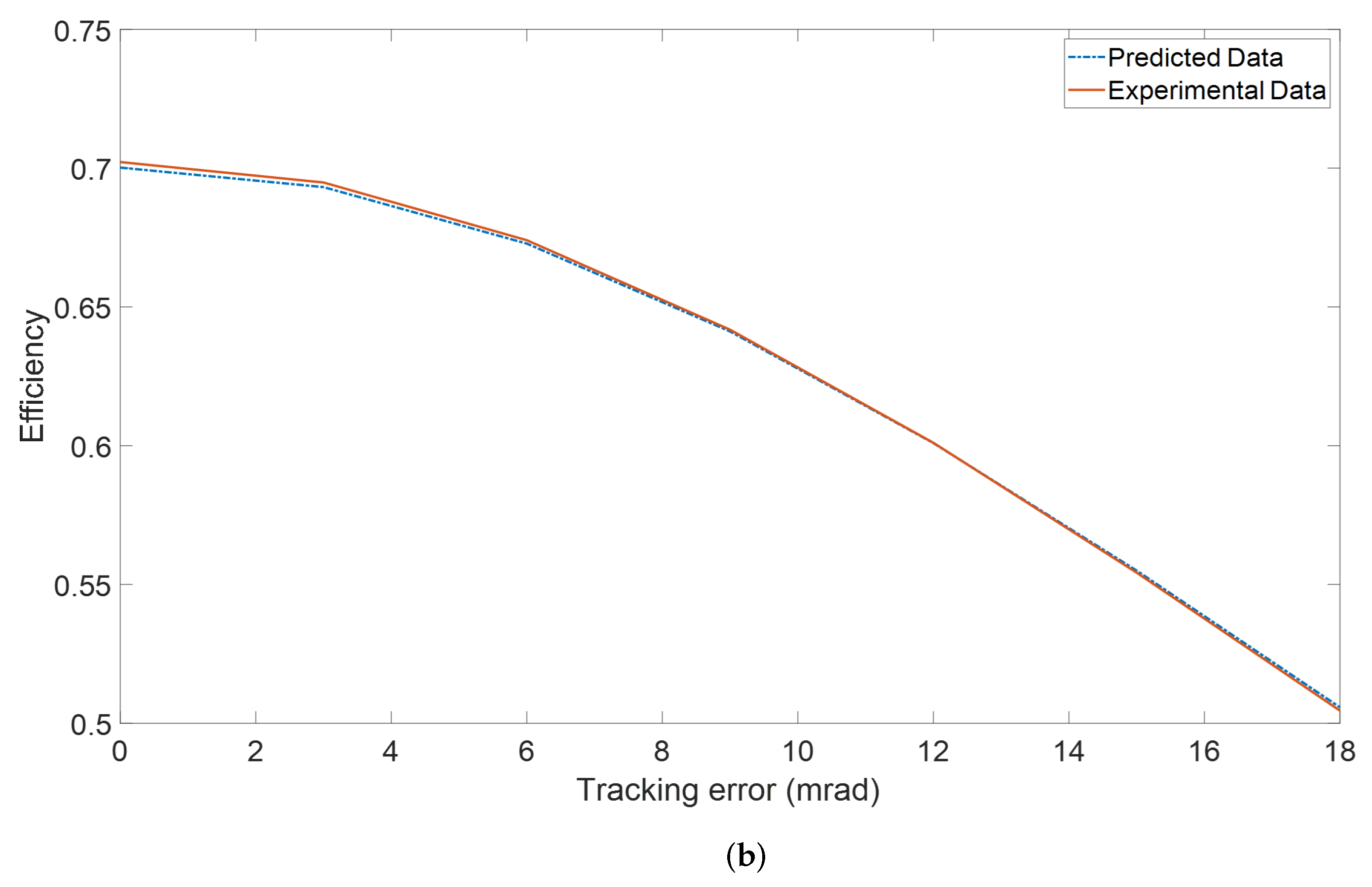
3. Model Validation
4. Results and Discussion
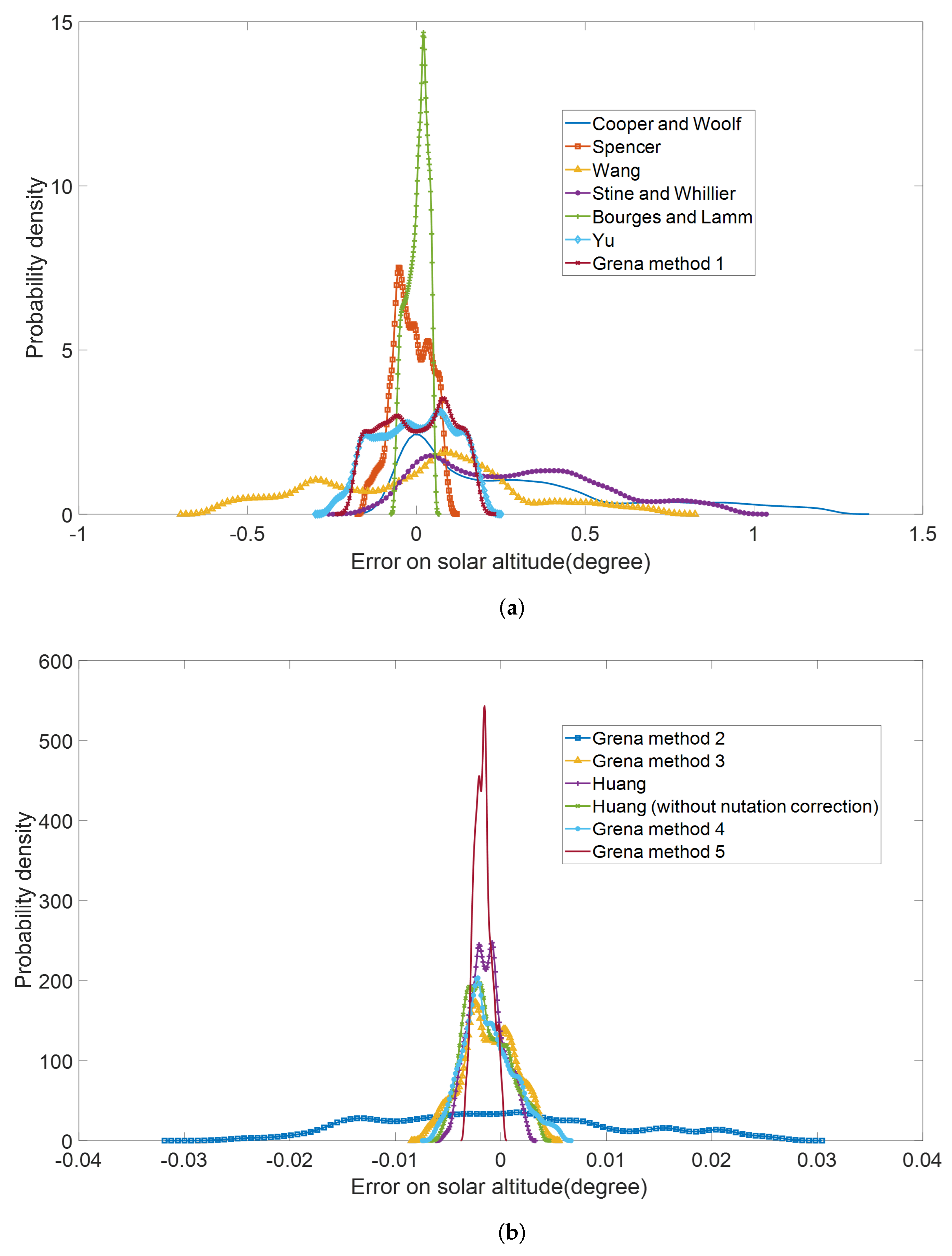
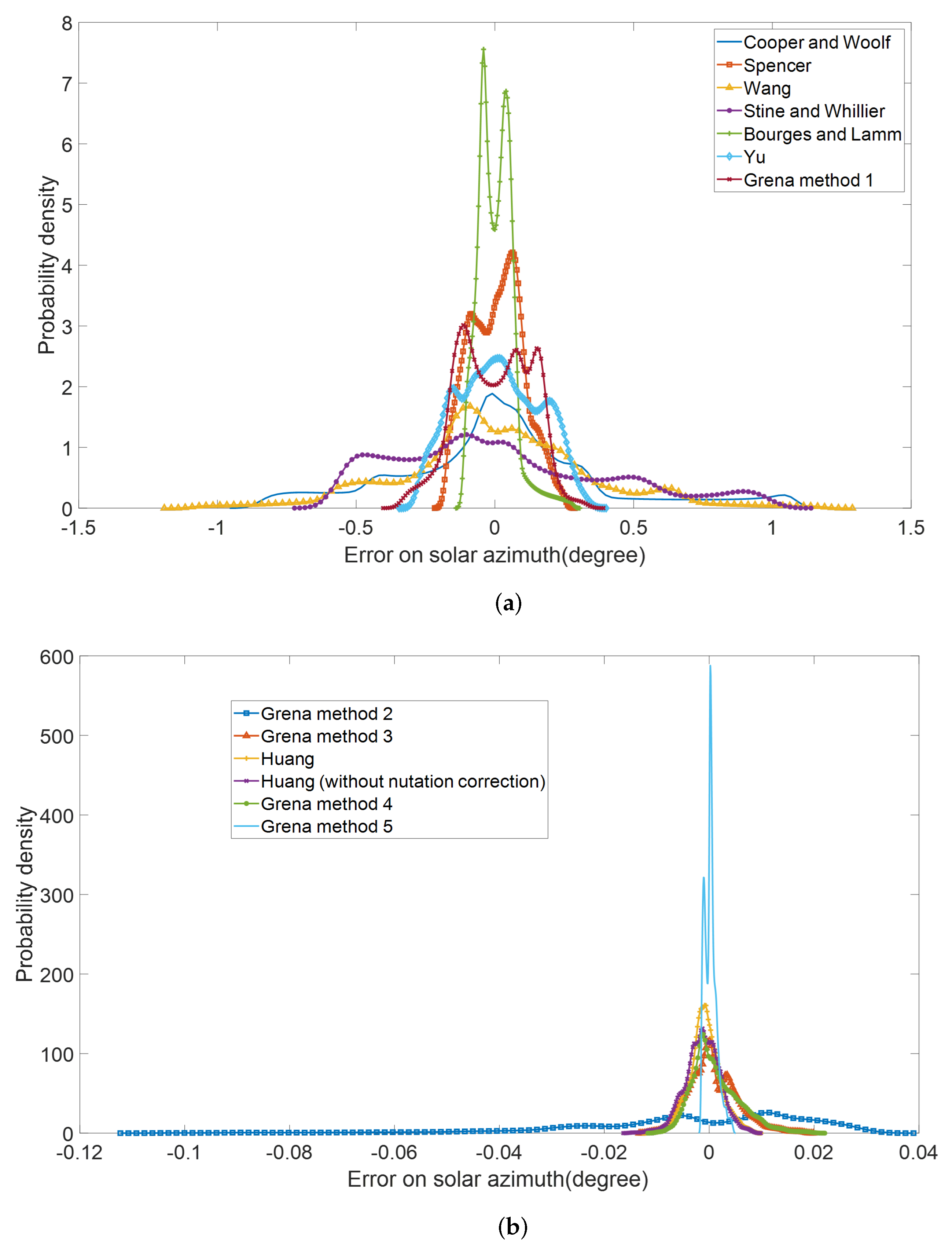
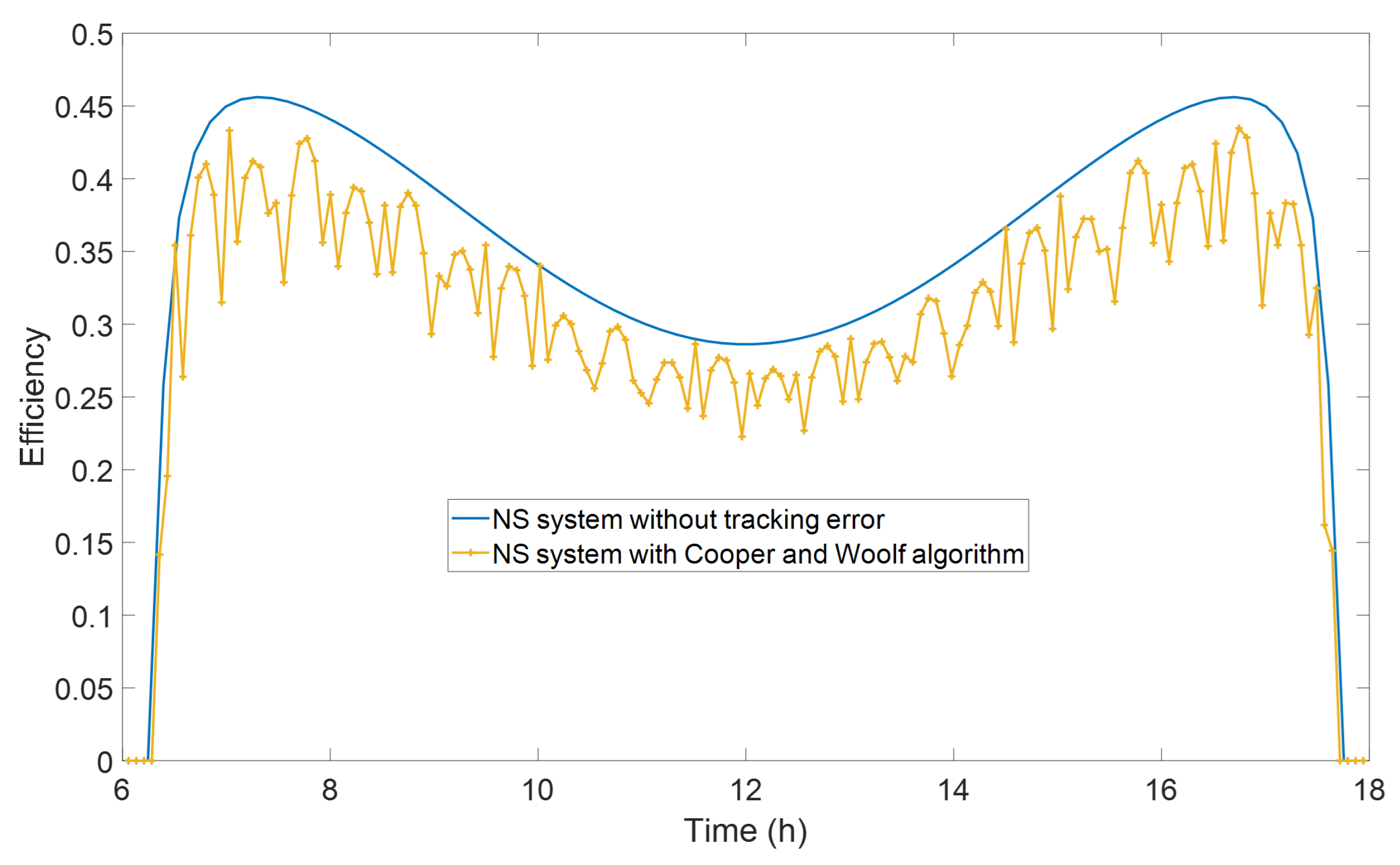
4.1. Comparison of Error Distribution of SPAs and Their Influence on Performance of System
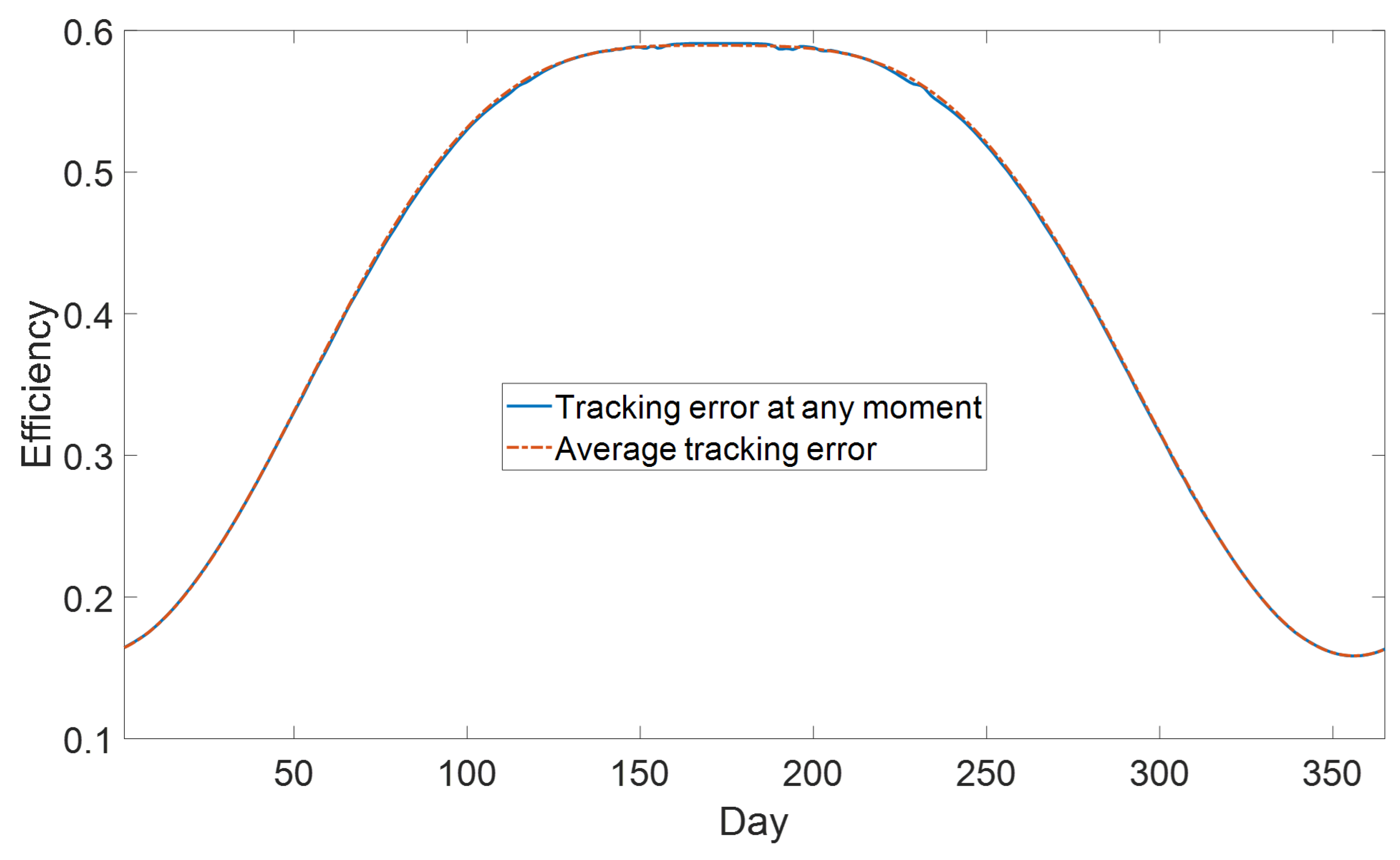
4.2. The Error Caused by Using Average Error to Evaluate the Effect of SPA’s Error on Trough Solar System
5. Conclusions
- When the average error of SPAs is used to characterize the impact of its error on system efficiency, it is a good approximation for most algorithms. Compared with the result of parabolic trough system that calculate the error of every moment, the efficiency obtained is quite similar, and most of the relative errors are of less than 0.5%;
- For the low-precision SPAs with an annual average error higher than 1.5 mrad, the relative error is within the range of 0.5% to 3% when the average error is used to evaluate its impact on the efficiency of the trough system. Most of them are less than 1%, which can represent the influence of SPA algorithm error on the performance of the system;
- The average error of SPAs is used to represent its precision characteristics. The disadvantage is that for a few algorithms with low complexity, it cannot reflect its annual periodic tracking error changes. In some moments, the error is very small, while in others, the error is large, which introduces larger error of the instantaneous efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| parameter for calculating the heat loss of receiver | |
| the energy distribution function of reflected ray in radial direction (W/m2/rad) | |
| linear brightness distribution function at transverse direction (W/m2/rad) | |
| direct normal incidence (W/m2) | |
| E | total DNI energy in a year (J/m2) |
| focus length (m) | |
| distance from the reflection point to the focus point (m) | |
| L | length of the parabolic mirror (m) |
| heat loss of receiver (W/m2) | |
| net energy power in any time (W/m2) | |
| R | radius of envelope for vacuum tube receiver (m) |
| radius of the tube receiver (m) | |
| T | temperature of receiver (K) |
| t | time (day) |
| w | half width of the trough mirror (m) |
| z | zenith |
| absorptivity of vacuum receiver | |
| azimuth | |
| reflectivity of mirror | |
| transmittance of glass envelope | |
| rim angle of the reflection point (rad) | |
| timeangle (rad) | |
| l | geographical latitude (rad) |
| solar declination (rad) | |
| angular displacement in longitudinal direction (rad) | |
| angular displacement in transverse direction (rad) | |
| maximum angle of ray to the receiver (rad) | |
| optical error (rad) | |
| tracking error (rad) | |
| the optical efficiency of parabolic trough solar collector |
References
- Thomas, A. Solar steam generating systems using parabolic trough concentrators. Energy Convers. Manag. 1996, 37, 215–245. [Google Scholar] [CrossRef]
- Fuentes-Morales, R.F.; Diaz-Ponce, A.; Peña-Cruz, M.I.; Rodrigo, P.M.; Valentín-Coronado, L.M.; Martell-Chavez, F.; Pineda-Arellano, C.A. Control algorithms applied to active solar tracking systems: A review. Sol. Energy 2020, 212, 203–219. [Google Scholar] [CrossRef]
- Blanco-Muriel, M.; Alarcón-Padilla, D.C.; López-Moratalla, T.; Lara-Coira, M. Computing the solar vector. Sol. Energy 2001, 70, 431–441. [Google Scholar] [CrossRef]
- Praveenkumar, S.; Gulakhmadov, A.; Kumar, A.; Safaraliev, M.; Chen, X. Comparative Analysis for a Solar Tracking Mechanism of Solar PV in Five Different Climatic Locations in South Indian States: A Techno-Economic Feasibility. Sustainability 2022, 14, 11880. [Google Scholar] [CrossRef]
- Hafez, A.Z.; Yousef, A.M.; Harag, N.M. Solar tracking systems: Technologies and trackers drive types—A review. Renew. Sustain. Energy Rev. 2018, 91, 754–782. [Google Scholar] [CrossRef]
- Chen, W.; Li, J. Optical performance analysis for parabolic-trough focusing collector with several tracking modes. Taiyangneng Xuebao/Acta Energiae Solaris Sin. 2003, 24, 477–482. [Google Scholar] [CrossRef]
- Spencer, J.W. Fourier series representation of the position of the Sun. Search 1971, 2, 165–172. [Google Scholar]
- Blanco, M.J.; Milidonis, K.; Bonanos, A.M. Updating the PSA sun position algorithm. Sol. Energy 2020, 212, 339–341. [Google Scholar] [CrossRef]
- Grena, R. Five new algorithms for the computation of sun position from 2010 to 2110. Sol. Energy 2012, 86, 1323–1337. [Google Scholar] [CrossRef]
- Reda, I.; Andreas, A. Solar position algorithm for solar radiation applications. Sol. Energy 2004, 76, 577–589. [Google Scholar] [CrossRef]
- Huang, W.; Hu, P.; Chen, Z. Performance simulation of a parabolic trough solar collector. Sol. Energy 2012, 86, 746–755. [Google Scholar] [CrossRef]
- Patnode, A.M. Simulation and Performance Evaluation of Parabolic Trough Solar Power Plants; University of Wisconsin Madison: Madison, WI, USA, 2006. [Google Scholar]
- Woolf, H.M. On the Computation of Solar Elevation Angles and the Determination of Sunrise and Sunset Times. 1968. Available online: https://ntrs.nasa.gov/api/citations/19680025707/downloads/19680025707.pdf (accessed on 1 June 2022).
- Cooper, P.I. The absorption of radiation in solar stills. Sol. Energy 1969, 12, 333–346. [Google Scholar] [CrossRef]
- Huang, W.; Liu, B. Solar Position Algorithm Based on the Kepler Equation. Appl. Sci. 2022, 12, 5449. [Google Scholar] [CrossRef]
- Lamm, L.O. A new analytic expression for the equation of time. Sol. Energy 1981, 26, 465. [Google Scholar] [CrossRef]
- Bourges, B. Improvement in solar declination computation. Sol. Energy 1985, 35, 367–369. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Tang, J. Comparsion of the different methods for solar position calculation. Taiyangneng Xuebao/Acta Energiae Solaris Sin. 2001, 4, 50–54. [Google Scholar] [CrossRef]
- Stine, B. Solar Energy Fundamental and Design; John, Wiley & Sons, Inc.: Hoboken, NJ, USA, 1985. [Google Scholar]
- Du, C.; Wang, P.; Ma, C.; Wu, Y. The application of day number in calculating the solar position. Taiyangneng Xuebao/Acta Energiae Solaris Sinica 2011, 32, 1640–1645. [Google Scholar]
| Parameter | Data |
|---|---|
| Focus length | 1.7 m |
| Half trough width w | 3 m |
| Length of trough L | 100 m |
| Radius of receiver tube | 0.035 m |
| Radius of envelope of receiver R | 0.055 m |
| Operation temperature of receiver T | 400 °C |
| Transverse optical error | 6 mrad |
| Longitudinal optical error | 6 mrad |
| (a) Solar Position Empirical Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|
| SPAs | Computational Cost | Tracking Method | Annual Average Tracking Error (mrad) | Annual Average Error of the Solar Azimuth (mrad) | Variance of Absolute Error of the Solar Azimuth (mrad2) | Annual Average Error of the Solar Altitude (mrad) | Variance of Absolute Error of the Solar Altitude (mrad2) | Annual Average Error of the Hour Angle (mrad) |
| Cooper and Woolf | 319 | NS | 5.75 | 6.94 | 25.618 | 5.06 | 32.08 | 2.88 |
| EW | 3.11 | |||||||
| Polar axis | 2.88 | |||||||
| Spencer | 397 | NS | 2.44 | 4.47 | 10.37 | 2.06 | 1.794 | 3.37 |
| EW | 1.47 | |||||||
| Polar axis | 3.37 | |||||||
| Stine and Whillier | 335 | NS | 6.03 | 8.48 | 25.75 | 5.19 | 17.716 | 4.93 |
| EW | 3.28 | |||||||
| Polar axis | 4.93 | |||||||
| Bourges and Lamm | 456 | NS | 1.33 | 1.68 | 1.096 | 1.16 | 0.577 | 0.89 |
| EW | 0.78 | |||||||
| Polar axis | 0.89 | |||||||
| Wang | 388 | NS | 4.22 | 5.05 | 16.015 | 3.79 | 8.833 | 1.9 |
| EW | 2.76 | |||||||
| Polar axis | 1.9 | |||||||
| Yu | 327 | NS | 2.43 | 4.16 | 6.056 | 2.08 | 1.204 | 2.84 |
| EW | 1.6 | |||||||
| Polar axis | 2.84 | |||||||
| Grena method 1 | 428 | NS | 1.82 | 3.18 | 2.922 | 1.56 | 0.787 | 2.28 |
| EW | 1.3 | |||||||
| Polar axis | 2.28 | |||||||
| (b) Solar Position Complex Algorithm | ||||||||
| SPAs | Computational Cost | Tracking Method | Annual Average Tracking Error (mrad) | Annual Average Error of the Solar Azimuth (mrad) | Variance of Absolute Error of the Solar Azimuth (mrad2) | Annual Average Error of the Solar Altitude (mrad) | Variance of Absolute Error of the Solar Altitude (mrad2) | Annual Average Error of the Hour Angle (mrad) |
| Grena method 2 | 455 | NS | 0.22 | 0.26 | 0.0725 | 0.17 | 0.0133 | 0.26 |
| EW | 0.17 | |||||||
| Polar axis | 0.26 | |||||||
| Grena method 3 | 572 | NS | 0.05 | 0.052 | 0.0030 | 0.04 | 0.0030 | 0.053 |
| EW | 0.037 | |||||||
| Polar axis | 0.053 | |||||||
| Huang (with nutation correction) | 765 | NS | 0.046 | 0.046 | 0.11 | 0.039 | 0.00047 | 0.05 |
| EW | 0.035 | |||||||
| Polar axis | 0.05 | |||||||
| Huang (without nutation correction) | 701 | NS | 0.056 | 0.054 | 0.0015 | 0.047 | 0.000615 | 0.055 |
| EW | 0.04 | |||||||
| Polar axis | 0.055 | |||||||
| Grena method 4 | 641 | NS | 0.045 | 0.049 | 0.0033 | 0.036 | 0.00066 | 0.051 |
| EW | 0.034 | |||||||
| Polar axis | 0.051 | |||||||
| Grena method 5 | 929 | NS | 0.03 | 0.012 | 0.0002 | 0.032 | 0.00019 | 0.025 |
| EW | 0.021 | |||||||
| Polar axis | 0.025 | |||||||
| Tracking Method | Time | Efficiency of System without Tracking Error | Efficiency of System with Cooper and Woolf Method | Daily Average Tracking Error (mrad) |
|---|---|---|---|---|
| north–south axis tracking system | Spring Equinox | 0.432 | 0.368 | 9.13 |
| Summer Solstice | 0.558 | 0.557 | 0.47 | |
| Autumn Equinox | 0.437 | 0.301 | 13.85 | |
| Winter Solstice | 0.142 | 0.137 | 2.05 | |
| east–west axis tracking system | Spring Equinox | 0.272 | 0.261 | 3.63 |
| Summer Solstice | 0.252 | 0.252 | 0.52 | |
| Autumn Equinox | 0.269 | 0.248 | 5.61 | |
| Winter Solstice | 0.3561 | 0.3543 | 1.3 | |
| polar axis tracking system | Spring Equinox | 0.581 | 0.579 | 1.36 |
| Summer Solstice | 0.479 | 0.478 | 0.77 | |
| Autumn Equinox | 0.58 | 0.574 | 2.38 | |
| Winter Solstice | 0.478 | 0.474 | 2.04 |
| Tracking Methods | Efficiency without Tracking Error | Efficiency with Cooper and Woolf Method | Average Annual Tracking Error (mrad) | Efficiency Calculated with Average Tracking Error | The Relative Difference |
|---|---|---|---|---|---|
| North-South axis | 0.4538 | 0.4214 | 5.5 | 0.4330 | 2.75% |
| East-West axis | 0.3447 | 0.3332 | 2.9 | 0.3403 | 2.13% |
| Polar axis | 0.5617 | 0.56 | 2.7 | 0.5552 | 0.86% |
| SPAs | Efficiency Calculated with Average Tracking Error | Efficiency Calculated with Tracking Error at Every Moment | Average Tracking Error (mrad) | The Relative Difference |
|---|---|---|---|---|
| Cooper and Woolf | 0.4330 | 0.4214 | 5.5 | 2.75% |
| Stine and Whillier | 0.4291 | 0.4140 | 6 | 3.65% |
| Wang | 0.4416 | 0.4292 | 4.2 | 2.89% |
| Spencer | 0.4494 | 0.4469 | 2.4 | 0.56% |
| Yu | 0.4498 | 0.4465 | 2.4 | 0.74% |
| Bourges and Lamm | 0.4526 | 0.4518 | 1.3 | 0.18% |
| Grena method 1 | 0.4515 | 0.4499 | 1.8 | 0.35% |
| Grena method 2 | 0.4537 | 0.4536 | 0.22 | 0.02% |
| Grena method 3 | 0.4538 | 0.4538 | 0.049 | 0% |
| Grena method 4 | 0.4538 | 0.4538 | 0.045 | 0% |
| Grena method 5 | 0.4538 | 0.4538 | 0.003 | 0% |
| Huang (without nutation correction) | 0.4538 | 0.4538 | 0.056 | 0% |
| Huang (with nutation correction) | 0.4538 | 0.4538 | 0.046 | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Zong, C.; Huang, W. Evaluation and Characterization of the Influence of Solar Position Algorithm on the Performance of Parabolic Trough Solar System. Appl. Sci. 2023, 13, 1821. https://doi.org/10.3390/app13031821
Liu B, Zong C, Huang W. Evaluation and Characterization of the Influence of Solar Position Algorithm on the Performance of Parabolic Trough Solar System. Applied Sciences. 2023; 13(3):1821. https://doi.org/10.3390/app13031821
Chicago/Turabian StyleLiu, Bowen, Chenggang Zong, and Weidong Huang. 2023. "Evaluation and Characterization of the Influence of Solar Position Algorithm on the Performance of Parabolic Trough Solar System" Applied Sciences 13, no. 3: 1821. https://doi.org/10.3390/app13031821
APA StyleLiu, B., Zong, C., & Huang, W. (2023). Evaluation and Characterization of the Influence of Solar Position Algorithm on the Performance of Parabolic Trough Solar System. Applied Sciences, 13(3), 1821. https://doi.org/10.3390/app13031821






