Cognitive Reorganization Due to Mental Workload: A Functional Connectivity Analysis Based on Working Memory Paradigms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
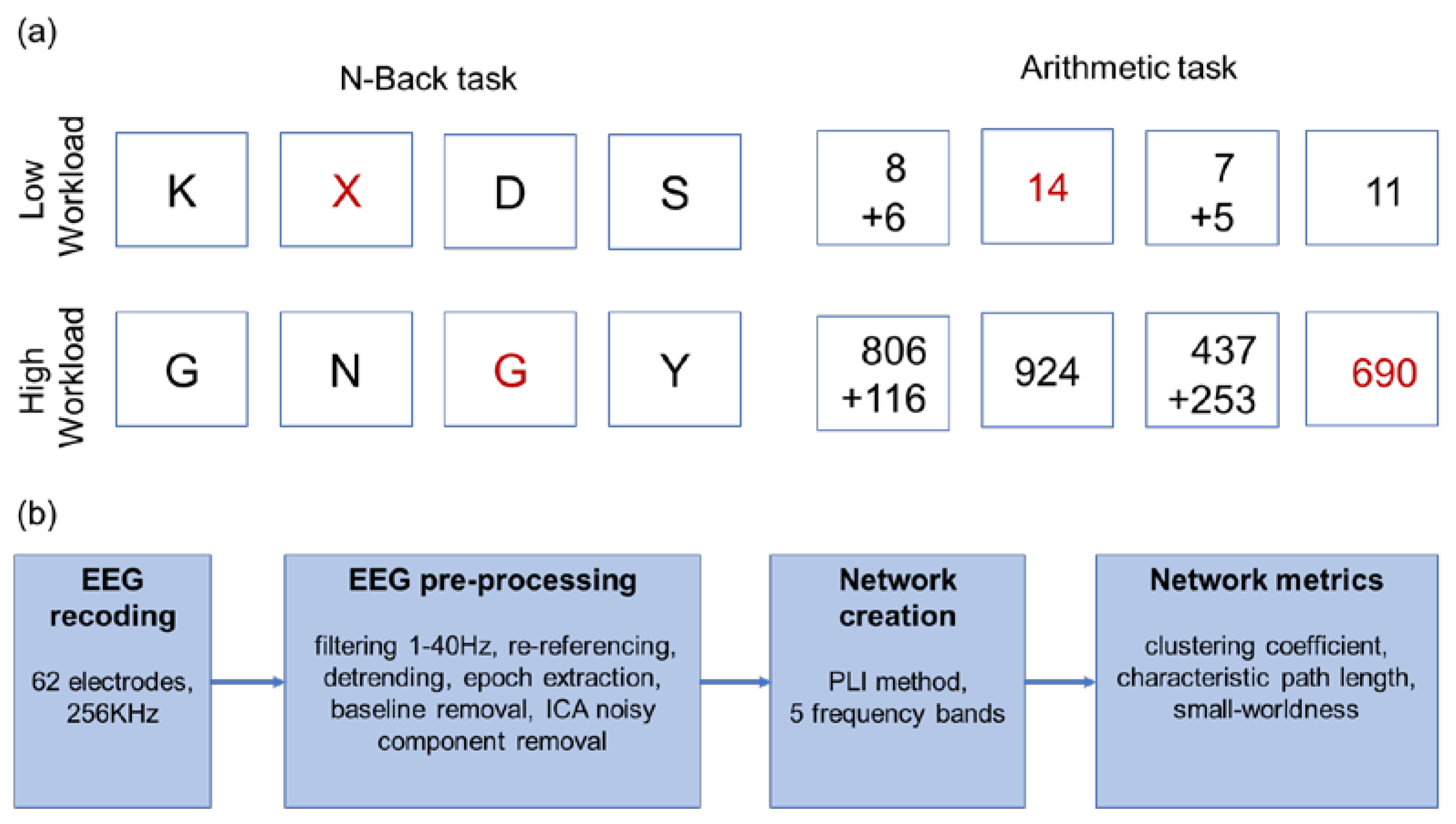
2.2. Experimental Design
2.2.1. n-Back Task
2.2.2. Mental Arithmetic Task
2.3. Data Recordings and Preprocessing
2.4. Brain Connectivity Estimation
2.5. Network Analysis
2.6. Statistical Analysis
2.7. Classification
3. Results
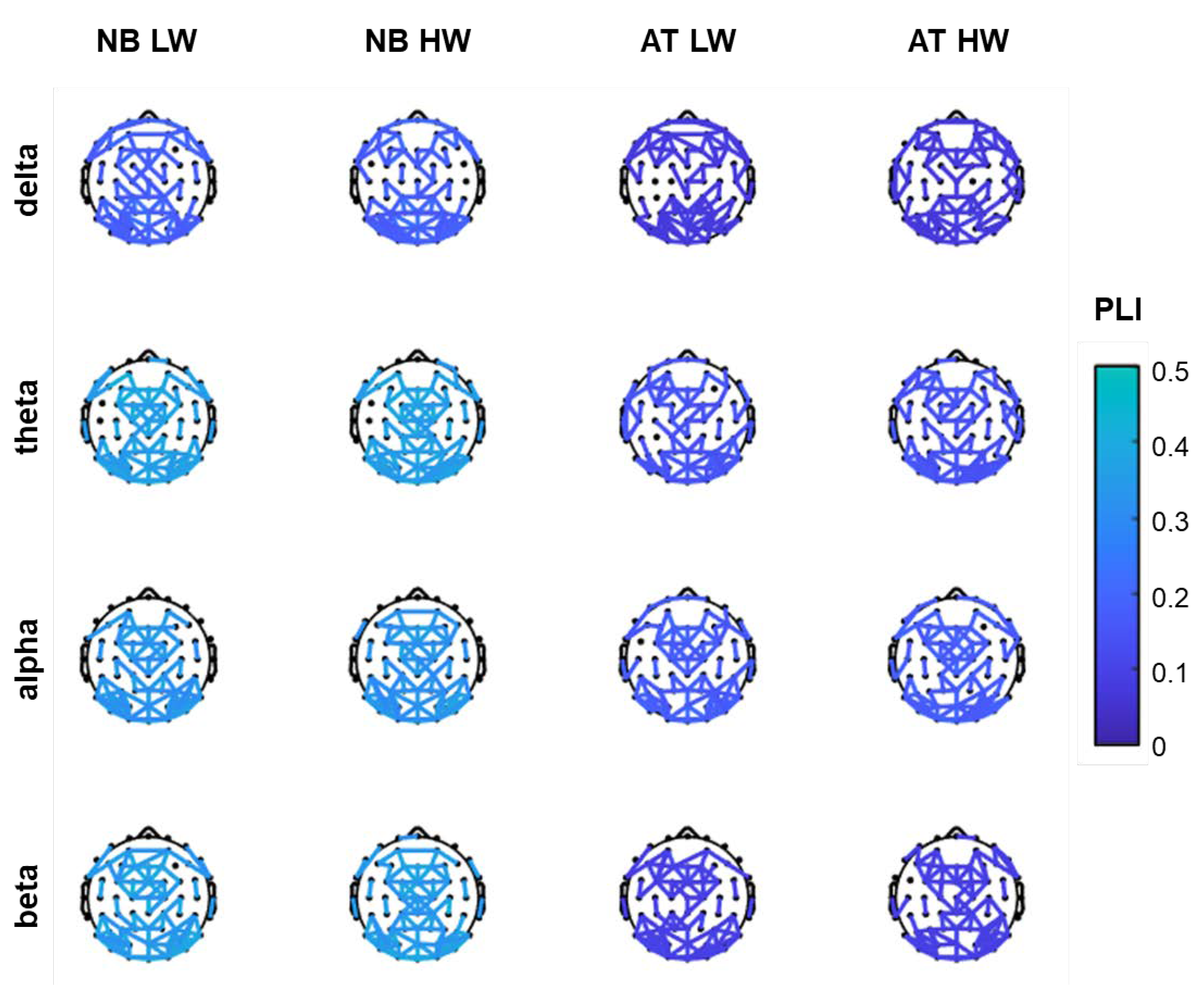
3.1. Network Topology
3.2. Network Metrics Analysis
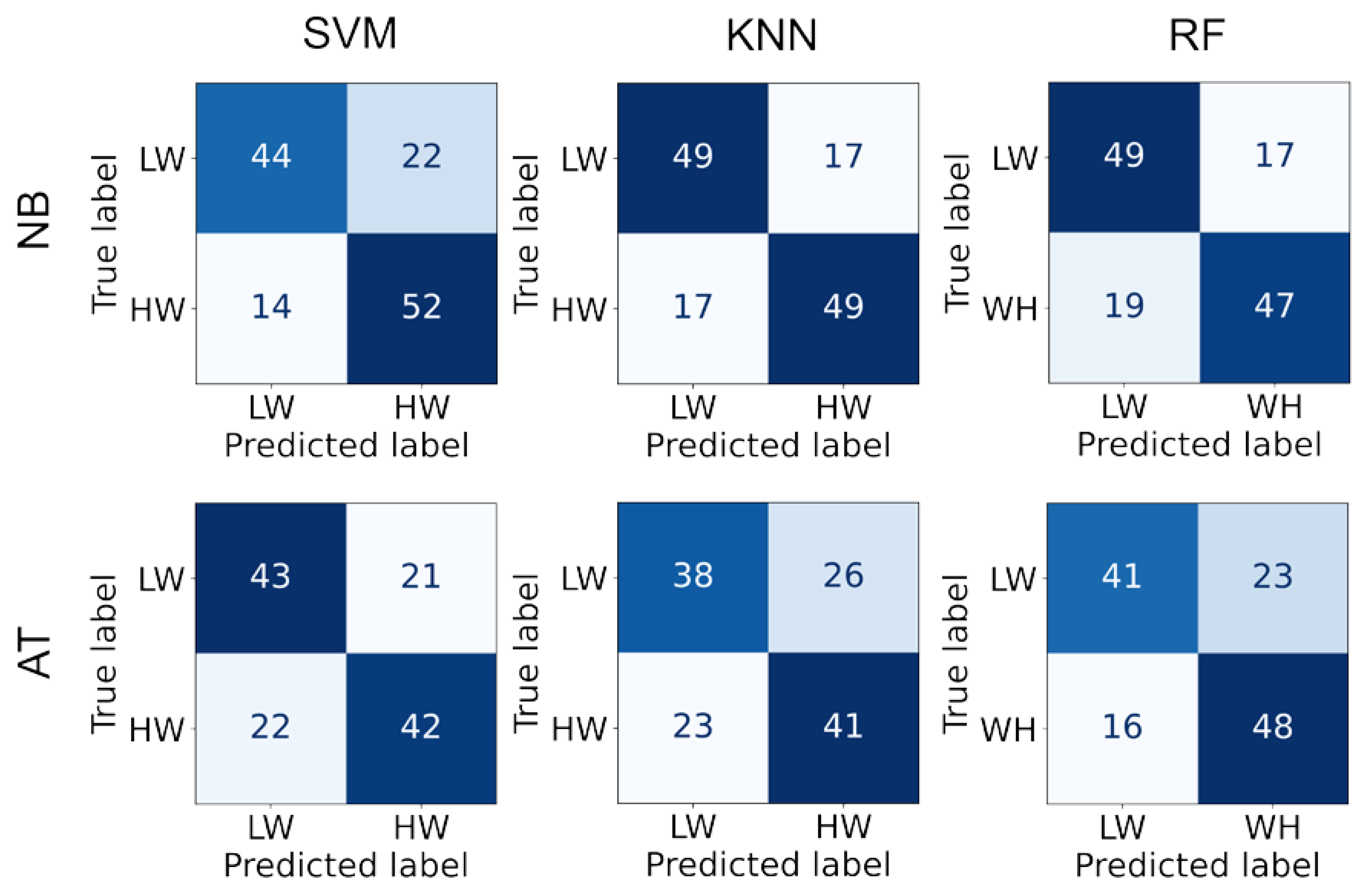
3.3. Classification
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tao, D.; Tan, H.; Wang, H.; Zhang, X.; Qu, X.; Zhang, T. A Systematic Review of Physiological Measures of Mental Workload. Int. J. Environ. Res. Public Health 2019, 16, 2716. [Google Scholar] [CrossRef] [PubMed]
- Charles, R.L.; Nixon, J. Measuring Mental Workload Using Physiological Measures: A Systematic Review. Appl. Ergon. 2019, 74, 221–232. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Huang, S.; Xu, Z.; Wang, P.; Wu, X.; Zhang, D. Cognitive Workload Recognition Using EEG Signals and Machine Learning: A Review. IEEE Trans. Cogn. Dev. Syst. 2022, 14, 799–818. [Google Scholar] [CrossRef]
- Cantin, V.; Lavallière, M.; Simoneau, M.; Teasdale, N. Mental Workload When Driving in a Simulator: Effects of Age and Driving Complexity. Accid. Anal. Prev. 2009, 41, 763–771. [Google Scholar] [CrossRef]
- Borghini, G.; Astolfi, L.; Vecchiato, G.; Mattia, D.; Babiloni, F. Measuring Neurophysiological Signals in Aircraft Pilots and Car Drivers for the Assessment of Mental Workload, Fatigue and Drowsiness. Neurosci. Biobehav. Rev. 2014, 44, 58–75. [Google Scholar] [CrossRef]
- Kakkos, I.; Dimitrakopoulos, G.N.; Gao, L.; Zhang, Y.; Qi, P.; Matsopoulos, G.K.; Thakor, N.; Bezerianos, A.; Sun, Y. Mental Workload Drives Different Reorganizations of Functional Cortical Connectivity Between 2D and 3D Simulated Flight Experiments. IEEE Trans. Neural Syst. Rehabil. Eng. A Publ. IEEE Eng. Med. Biol. Soc. 2019, 27, 1704–1713. [Google Scholar] [CrossRef]
- Aricò, P.; Borghini, G.; Di Flumeri, G.; Colosimo, A.; Pozzi, S.; Babiloni, F. A Passive Brain–Computer Interface Application for the Mental Workload Assessment on Professional Air Traffic Controllers during Realistic Air Traffic Control Tasks. Prog. Brain Res. 2016, 228, 295–328. [Google Scholar] [CrossRef]
- Roy, R.N.; Charbonnier, S.; Campagne, A.; Bonnet, S. Efficient Mental Workload Estimation Using Task-Independent EEG Features. J. Neural Eng. 2016, 13, 026019. [Google Scholar] [CrossRef]
- Di Flumeri, G.; Borghini, G.; Aricò, P.; Sciaraffa, N.; Lanzi, P.; Pozzi, S.; Vignali, V.; Lantieri, C.; Bichicchi, A.; Simone, A.; et al. EEG-Based Mental Workload Neurometric to Evaluate the Impact of Different Traffic and Road Conditions in Real Driving Settings. Front. Hum. Neurosci. 2018, 12, 509. [Google Scholar] [CrossRef]
- Lin, C.T.; Chuang, C.H.; Huang, C.S.; Tsai, S.F.; Lu, S.W.; Chen, Y.H.; Ko, L.W. Wireless and Wearable EEG System for Evaluating Driver Vigilance. IEEE Trans. Biomed. Circuits Syst. 2014, 8, 165–176. [Google Scholar] [CrossRef]
- Dehais, F.; Duprès, A.; Blum, S.; Drougard, N.; Scannella, S.; Roy, R.N.; Lotte, F. Monitoring Pilot’s Mental Workload Using ERPs and Spectral Power with a Six-Dry-Electrode EEG System in Real Flight Conditions. Sensors 2019, 19, 1324. [Google Scholar] [CrossRef] [PubMed]
- Sporns, O. The Human Connectome: A Complex Network. Ann. N. Y. Acad. Sci. 2011, 1224, 109–125. [Google Scholar] [CrossRef] [PubMed]
- Dimitrakopoulos, G.N.; Balomenos, P.; Vrahatis, A.G.; Sgarbas, K.; Bezerianos, A. Identifying Disease Network Perturbations through Regression on Gene Expression and Pathway Topology Analysis. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 5969–5972. [Google Scholar]
- Kakkos, I.; Dimitrakopoulos, G.N.; Sun, Y.; Yuan, J.; Matsopoulos, G.K.; Bezerianos, A.; Sun, Y. EEG Fingerprints of Task-Independent Mental Workload Discrimination. IEEE J. Biomed. Health Inform. 2021, 25, 3824–3833. [Google Scholar] [CrossRef]
- Dimitrakopoulos, G.N.; Kakkos, I.; Dai, Z.; Lim, J.; deSouza, J.J.; Bezerianos, A.; Sun, Y. Task-Independent Mental Workload Classification Based Upon Common Multiband EEG Cortical Connectivity. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1940–1949. [Google Scholar] [CrossRef] [PubMed]
- Shaw, E.P.; Rietschel, J.C.; Shuggi, I.M.; Xu, Y.; Chen, S.; Miller, M.W.; Hatfield, B.D.; Gentili, R.J. Cerebral Cortical Networking for Mental Workload Assessment under Various Demands during Dual-Task Walking. Exp. Brain Res. 2019, 237, 2279–2295. [Google Scholar] [CrossRef]
- Pei, Z.; Wang, H.; Bezerianos, A.; Li, J. EEG-Based Multiclass Workload Identification Using Feature Fusion and Selection. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]
- Cao, J.; Garro, E.M.; Zhao, Y. EEG/FNIRS Based Workload Classification Using Functional Brain Connectivity and Machine Learning. Sensors 2022, 22, 7623. [Google Scholar] [CrossRef]
- Gupta, A.; Siddhad, G.; Pandey, V.; Roy, P.P.; Kim, B.G. Subject-Specific Cognitive Workload Classification Using Eeg-Based Functional Connectivity and Deep Learning. Sensors 2021, 21, 6710. [Google Scholar] [CrossRef]
- Ke, Y.; Qi, H.; Zhang, L.; Chen, S.; Jiao, X.; Zhou, P.; Zhao, X.; Wan, B.; Ming, D. Towards an Effective Cross-Task Mental Workload Recognition Model Using Electroencephalography Based on Feature Selection and Support Vector Machine Regression. Int. J. Psychophysiol. 2015, 98, 157–166. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, Y.J.; Shi, Y. Real-Time Assessment of the Cross-Task Mental Workload Using Physiological Measures during Anomaly Detection. IEEE Trans. Hum.-Mach. Syst. 2018, 48, 149–160. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, X.; Zhang, W.; Chen, J. Learning Spatial-Spectral-Temporal EEG Features With Recurrent 3D Convolutional Neural Networks for Cross-Task Mental Workload Assessment. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 31–42. [Google Scholar] [CrossRef] [PubMed]
- Guan, K.; Zhang, Z.; Chai, X.; Tian, Z.; Liu, T.; Niu, H. EEG Based Dynamic Functional Connectivity Analysis in Mental Workload Tasks with Different Types of Information. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 632–642. [Google Scholar] [CrossRef] [PubMed]
- Welton, T.; Kent, D.A.; Auer, D.P.; Dineen, R.A. Reproducibility of Graph-Theoretic Brain Network Metrics: A Systematic Review. Brain Connect. 2015, 5, 193–202. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Chen, Y.; Collinson, S.L.; Bezerianos, A.; Sim, K. Reduced Hemispheric Asymmetry of Brain Anatomical Networks Is Linked to Schizophrenia: A Connectome Study. Cereb. Cortex 2017, 27, 602–615. [Google Scholar] [CrossRef]
- Xiong, X.; Yu, Z.; Ma, T.; Luo, N.; Wang, H.; Lu, X.; Fan, H. Weighted Brain Network Metrics for Decoding Action Intention Understanding Based on EEG. Front. Hum. Neurosci. 2020, 14, 232. [Google Scholar] [CrossRef]
- Guo, H.; Cao, X.; Liu, Z.; Li, H.; Chen, J.; Zhang, K. Machine Learning Classifier Using Abnormal Brain Network Topological Metrics in Major Depressive Disorder. NeuroReport 2012, 23, 1006–1011. [Google Scholar] [CrossRef]
- Li, Q.; Tao, L.; Xiao, P.; Gui, H.; Xu, B.; Zhang, X.; Zhang, X.; Chen, H.; Wang, H.; He, W.; et al. Combined Brain Network Topological Metrics with Machine Learning Algorithms to Identify Essential Tremor. Front. Neurosci. 2022, 16, 1891. [Google Scholar] [CrossRef]
- Kazeminejad, A.; Golbabaei, S.; Soltanian-Zadeh, H. Graph Theoretical Metrics and Machine Learning for Diagnosis of Parkinson’s Disease Using Rs-FMRI. In Proceedings of the 19th CSI International Symposium on Artificial Intelligence and Signal Processing, AISP 2017, Shiraz, Iran, 25–27 October 2017; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; Volume 2018, pp. 134–139. [Google Scholar]
- Jung, T.P.; Makeig, S.; Westerfield, M.; Townsend, J.; Courchesne, E.; Sejnowski, T.J. Removal of Eye Activity Artifacts from Visual Event-Related Potentials in Normal and Clinical Subjects. Clin. Neurophysiol. 2000, 111, 1745–1758. [Google Scholar] [CrossRef]
- Kakkos, I.; Ventouras, E.M.; Asvestas, P.A.; Karanasiou, I.S.; Matsopoulos, G.K. A Condition-Independent Framework for the Classification of Error-Related Brain Activity. Med. Biol. Eng. Comput. 2020, 58, 573–587. [Google Scholar] [CrossRef]
- Delorme, A.; Makeig, S. EEGLAB: An Open Source Toolbox for Analysis of Single-Trial EEG Dynamics Including Independent Component Analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef] [Green Version]
- Stam, C.J.; Nolte, G.; Daffertshofer, A. Phase Lag Index: Assessment of Functional Connectivity from Multi Channel EEG and MEG with Diminished Bias from Common Sources. Hum. Brain Mapp. 2007, 28, 1178–1193. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective Dynamics of “small-World” Networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Rubinov, M.; Sporns, O. Complex Network Measures of Brain Connectivity: Uses and Interpretations. NeuroImage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Achard, S.; Bullmore, E. Efficiency and Cost of Economical Brain Functional Networks. PLoS Comput. Biol. 2007, 3, e17. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex Networks: Structure and Dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Humphries, M.D.; Gurney, K.; Prescott, T.J. The Brainstem Reticular Formation Is a Small-World, Not Scale-Free, Network. Proc. R. Soc. B Biol. Sci. 2006, 273, 503–511. [Google Scholar] [CrossRef]
- Mencarelli, L.; Neri, F.; Momi, D.; Menardi, A.; Rossi, S.; Rossi, A.; Santarnecchi, E. Stimuli, Presentation Modality, and Load-Specific Brain Activity Patterns during n-Back Task. Hum. Brain Mapp. 2019, 40, 3810–3831. [Google Scholar] [CrossRef]
- Das Chakladar, D.; Dey, S.; Roy, P.P.; Dogra, D.P. EEG-Based Mental Workload Estimation Using Deep BLSTM-LSTM Network and Evolutionary Algorithm. Biomed. Signal Process. Control 2020, 60, 101989. [Google Scholar] [CrossRef]
- Hamann, A.; Carstengerdes, N. Investigating Mental Workload-Induced Changes in Cortical Oxygenation and Frontal Theta Activity during Simulated Flights. Sci. Rep. 2022, 12, 6449. [Google Scholar] [CrossRef]
- So, W.K.Y.; Wong, S.W.H.; Mak, J.N.; Chan, R.H.M. An Evaluation of Mental Workload with Frontal EEG. PLoS ONE 2017, 12, e0174949. [Google Scholar] [CrossRef] [Green Version]
- Dai, Z.; De Souza, J.; Lim, J.; Ho, P.M.; Chen, Y.; Li, J.; Thakor, N.; Bezerianos, A.; Sun, Y. EEG Cortical Connectivity Analysis of Working Memory Reveals Topological Reorganization in Theta and Alpha Bands. Front. Hum. Neurosci. 2017, 11, 237. [Google Scholar] [CrossRef] [PubMed]
- Sciaraffa, N.; Borghini, G.; Aricò, P.; Di Flumeri, G.; Colosimo, A.; Bezerianos, A.; Thakor, N.V.; Babiloni, F. Brain Interaction during Cooperation: Evaluating Local Properties of Multiple-Brain Network. Brain Sci. 2017, 7, 90. [Google Scholar] [CrossRef] [PubMed]
- Vecchio, F.; Miraglia, F.; Maria Rossini, P. Connectome: {Graph} Theory Application in Functional Brain Network Architecture. Clin. Neurophysiol. Pract. 2017, 2, 206–213. [Google Scholar] [CrossRef] [PubMed]
- Kitzbichler, M.G.; Henson, R.N.A.; Smith, M.L.; Nathan, P.J.; Bullmore, E.T. Cognitive Effort Drives Workspace Configuration of Human Brain Functional Networks. J. Neurosci. 2011, 31, 8259–8270. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, Y.; Li, J.; Qin, W.; Li, K.; Yu, C.; Jiang, T. Brain Anatomical Network and Intelligence. PLoS Comput. Biol. 2009, 5, e1000395. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Frequency | Workload Effect (F-Value (p-Value)) | ||
|---|---|---|---|
| Clustering Coefficient | Char. Path Length | Small-Worldness | |
| Delta | 5.91 (0.016) | 2.495 (0.115) | 2.581 (0.109) |
| Theta | 12.618 (<0.001) | 1.153 (0.284) | 8.607 (0.004) |
| Alpha | 7.785 (0.006) | 0.027 (0.869) | 7.694 (0.006) |
| Beta | 5.491 (0.02) | 4.498 (0.035) | 2.184 (0.141) |
| Algorithm | n-Back | Arithmetic Task |
|---|---|---|
| SVM | 0.733 (0.099) | 0.671 (0.088) |
| KNN | 0.731 (0.073) | 0.702 (0.091) |
| RF | 0.748 (0.124) | 0.625 (0.090) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitrakopoulos, G.N.; Kakkos, I.; Anastasiou, A.; Bezerianos, A.; Sun, Y.; Matsopoulos, G.K. Cognitive Reorganization Due to Mental Workload: A Functional Connectivity Analysis Based on Working Memory Paradigms. Appl. Sci. 2023, 13, 2129. https://doi.org/10.3390/app13042129
Dimitrakopoulos GN, Kakkos I, Anastasiou A, Bezerianos A, Sun Y, Matsopoulos GK. Cognitive Reorganization Due to Mental Workload: A Functional Connectivity Analysis Based on Working Memory Paradigms. Applied Sciences. 2023; 13(4):2129. https://doi.org/10.3390/app13042129
Chicago/Turabian StyleDimitrakopoulos, Georgios N., Ioannis Kakkos, Athanasios Anastasiou, Anastasios Bezerianos, Yu Sun, and George K. Matsopoulos. 2023. "Cognitive Reorganization Due to Mental Workload: A Functional Connectivity Analysis Based on Working Memory Paradigms" Applied Sciences 13, no. 4: 2129. https://doi.org/10.3390/app13042129






