The Influence of Interface Roughness on the Vibration Reduction Characteristics of an Under-Platform Damper
Abstract
:1. Introduction
2. Dynamic Modeling
2.1. Dynamic Modeling of a Blade with an Under-Platform Damper
2.2. Model Reduction Method
3. Characterization Method of Friction Force on Complex Dry Friction Contact Surface Based on Fractal Geometry Theory
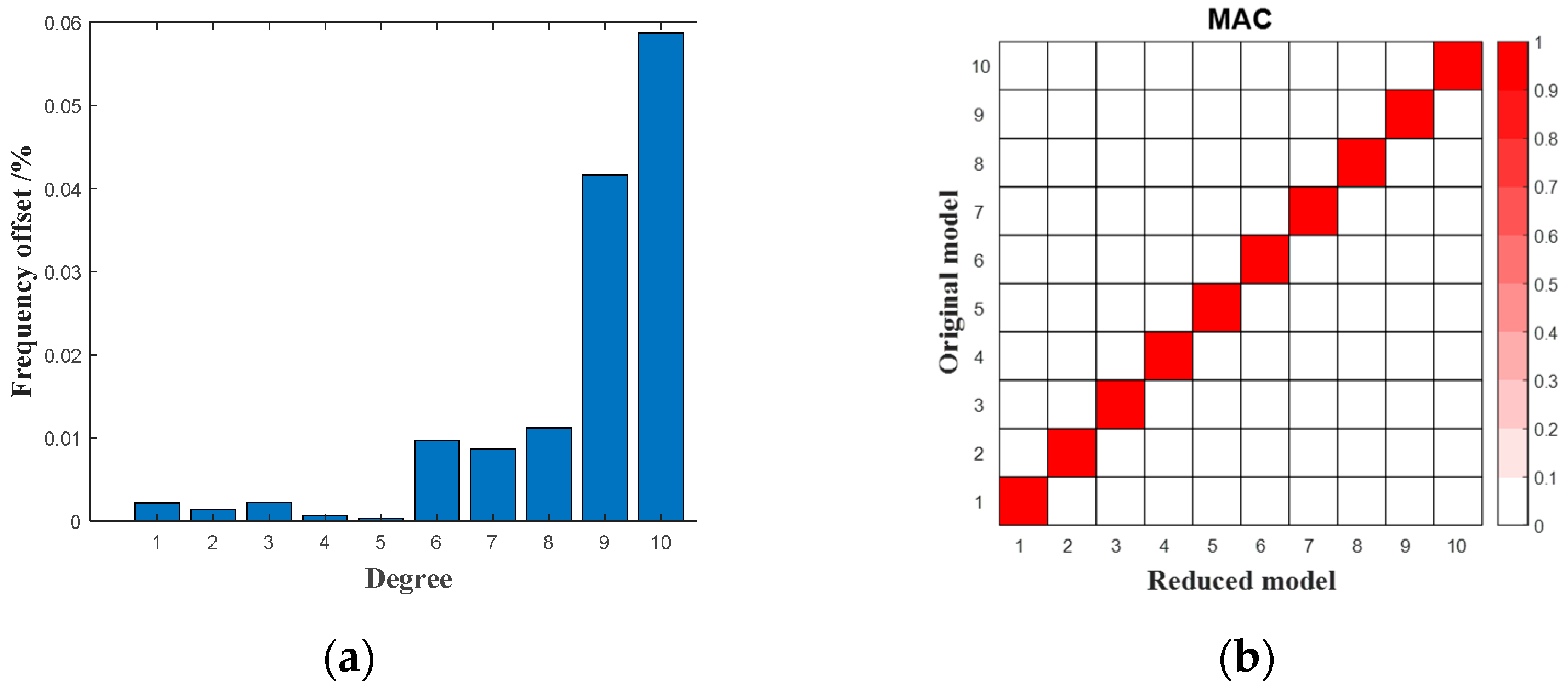
3.1. Three-Dimensional Variable Positive Pressure Hysteresis Coulomb Friction Contact Model
- (1)
- The velocity of the friction damper along the u and v directions is zero;
- (2)
- The velocity of the friction damper along the u direction is zero, and the velocity along the v direction is not zero;
- (3)
- The velocity of the friction damper along the v direction is zero, and the velocity along the u direction is not zero;
- (4)
- The velocity of the friction damper along the u and v directions is not zero.
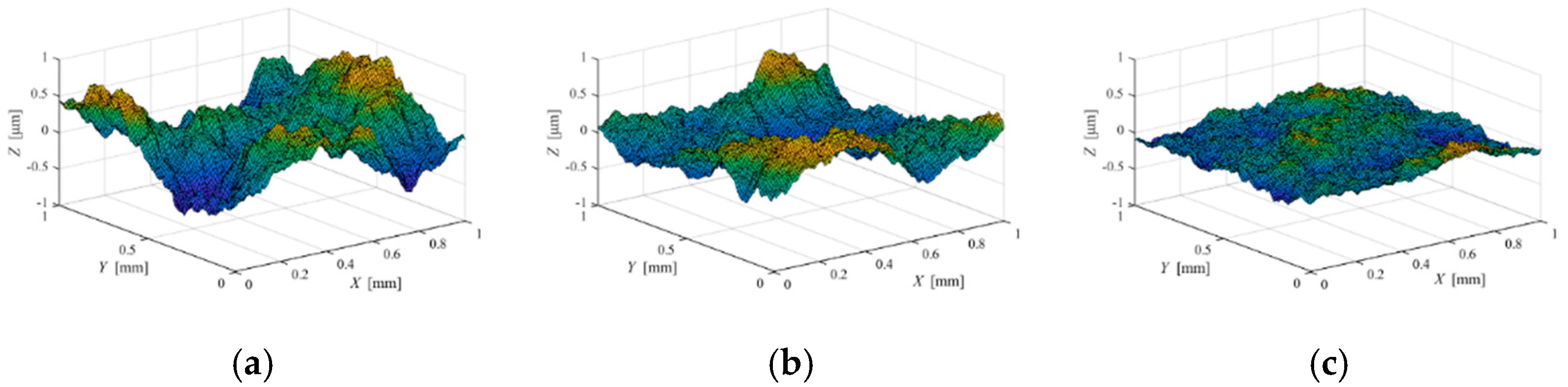
3.2. Simulation of Roughness Characteristics of Three-Dimensional Contact Surface Based on Fractal Geometry Theory
3.3. Calculation Model of Contact Stiffness of Complex Contact Surface
4. Nonlinear Dynamic Response Calculation Method
5. Vibration Response Analysis of Blade with Under-Platform Damper
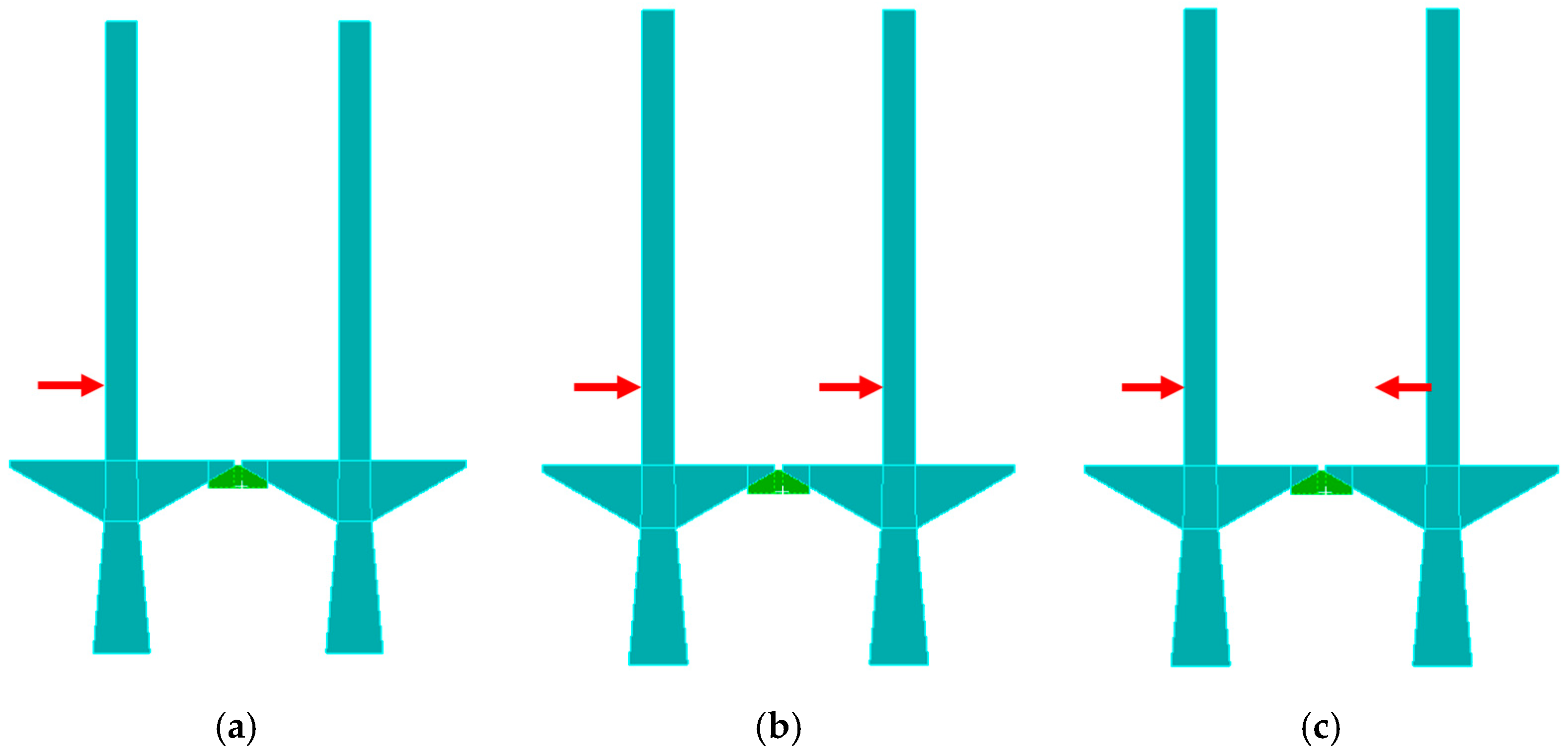
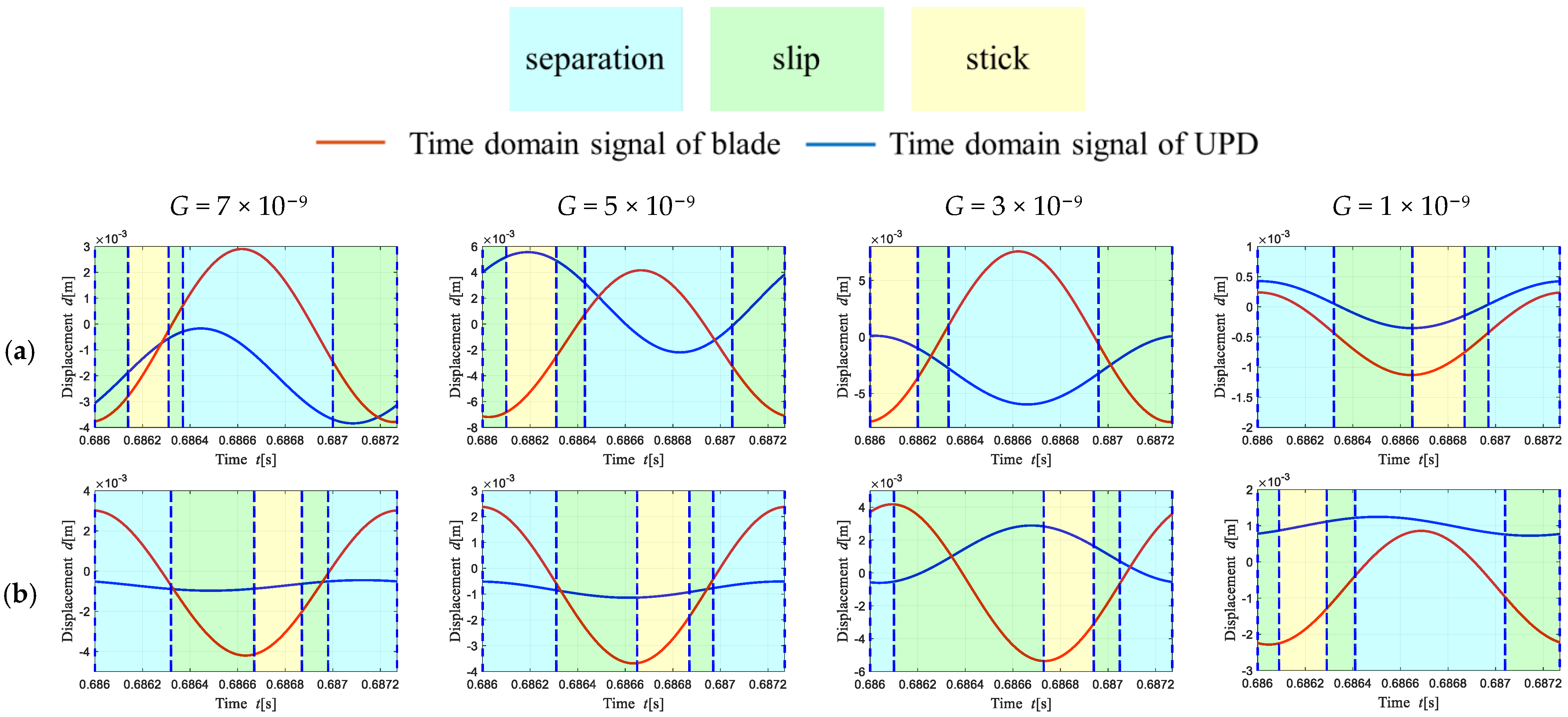
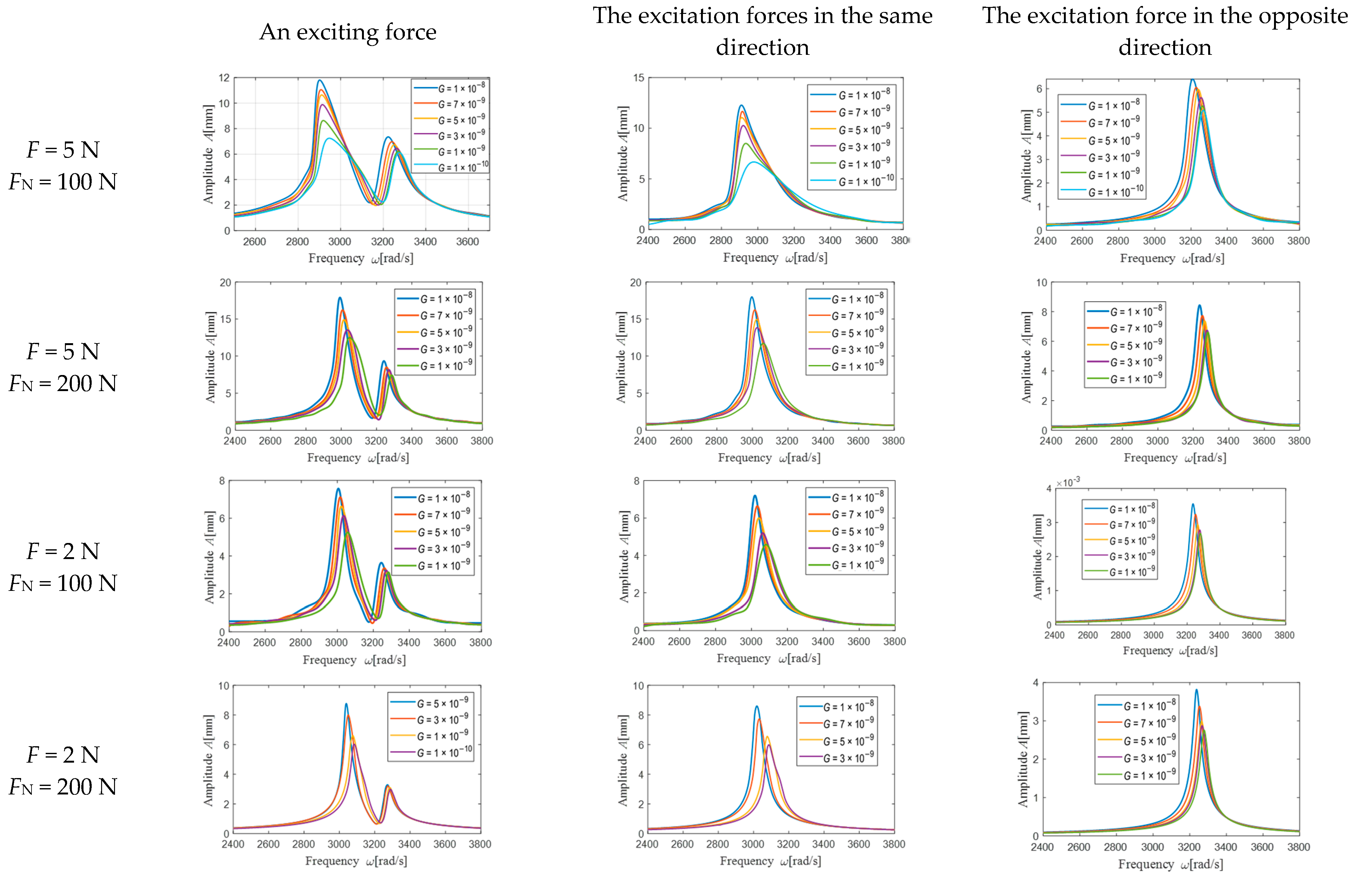
5.1. Time Domain Signals of Co-Directional and Reverse Excitation Force
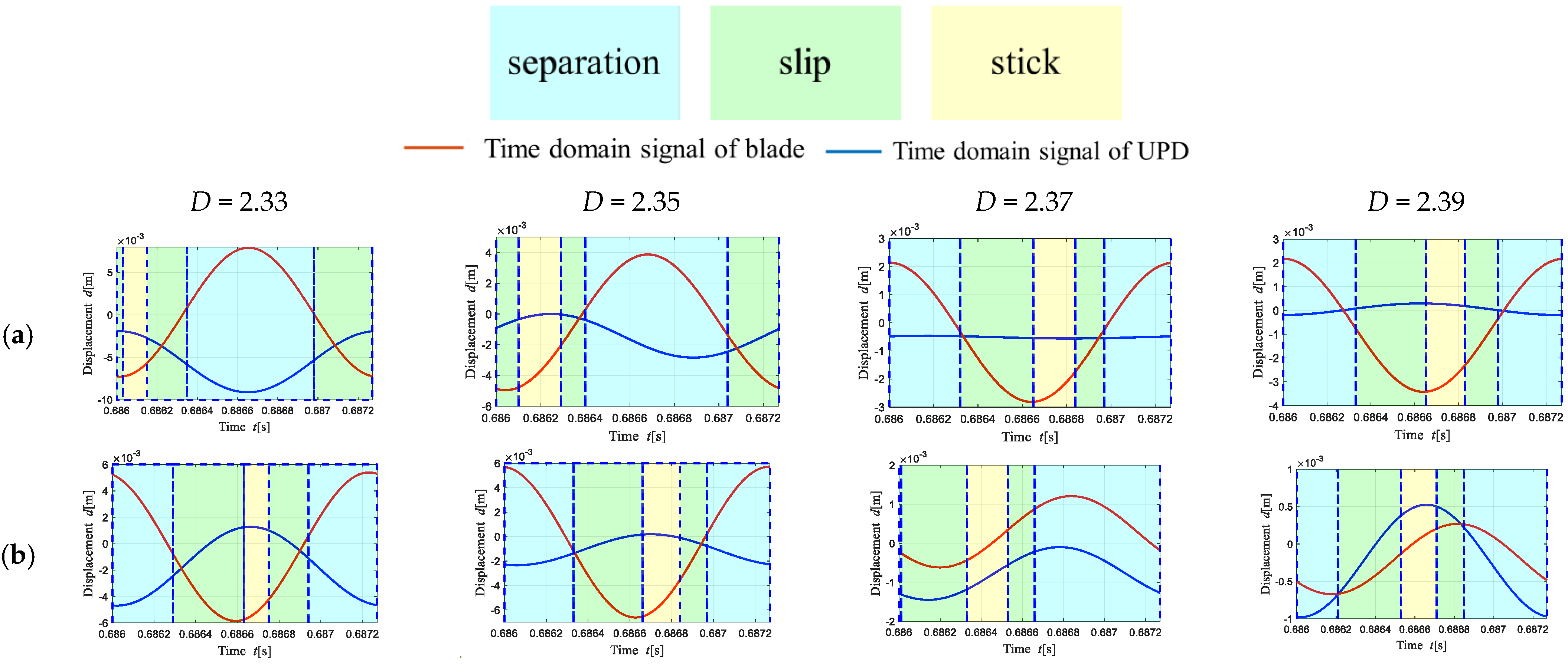
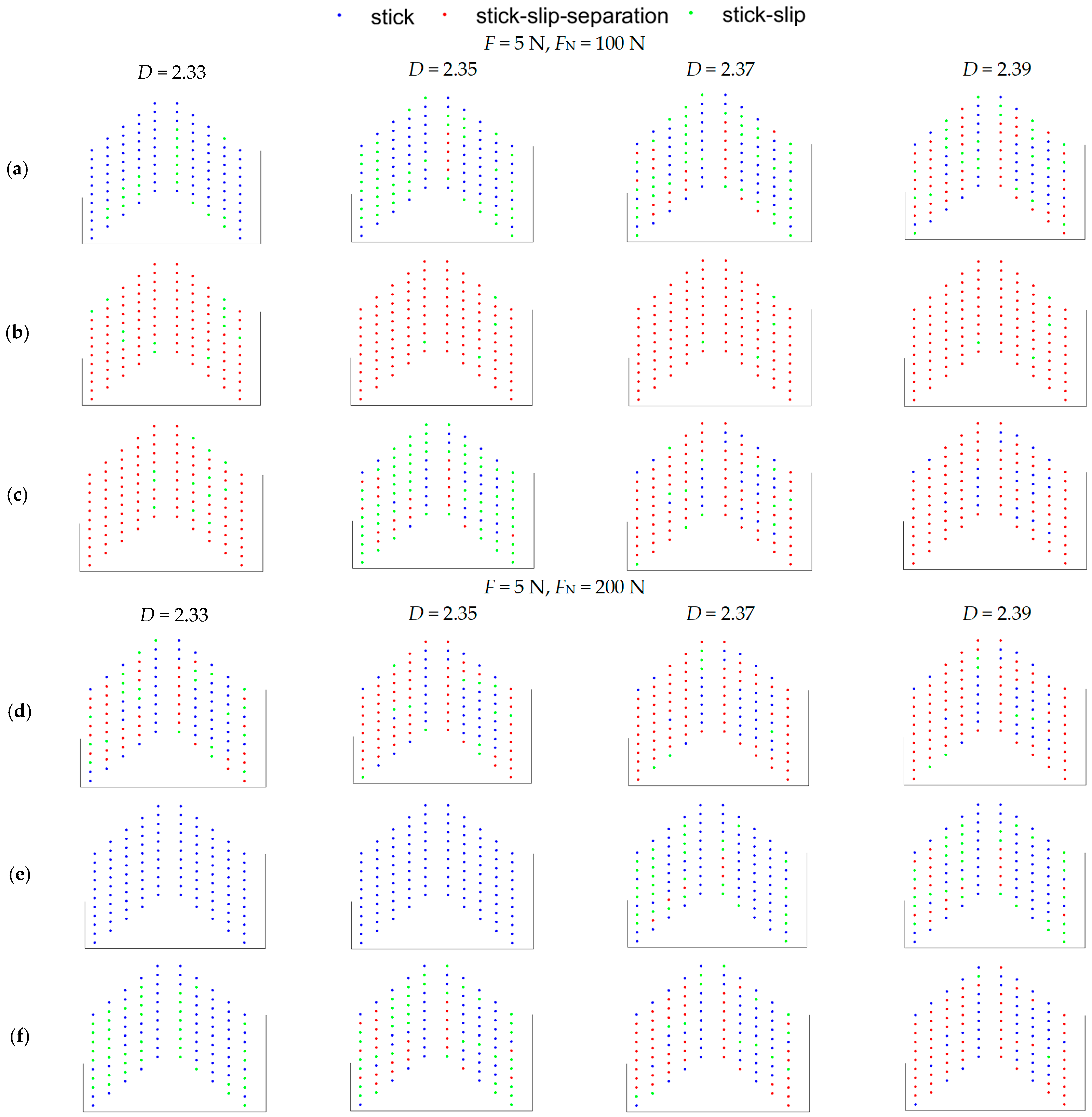
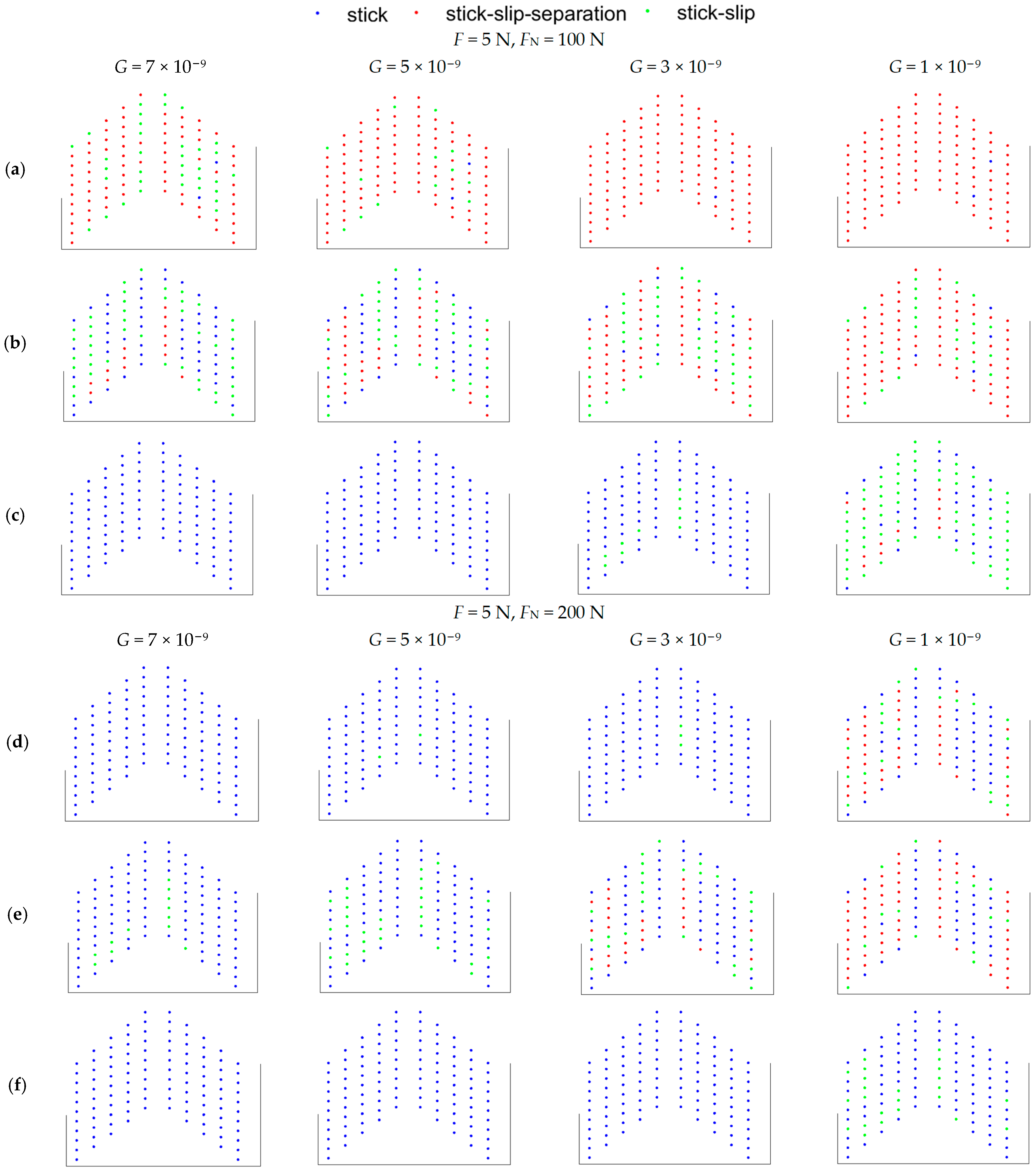
5.2. Influence of the Contact Surface Roughness on the Contact State of the Contact Surface of the Under-Platform Damper
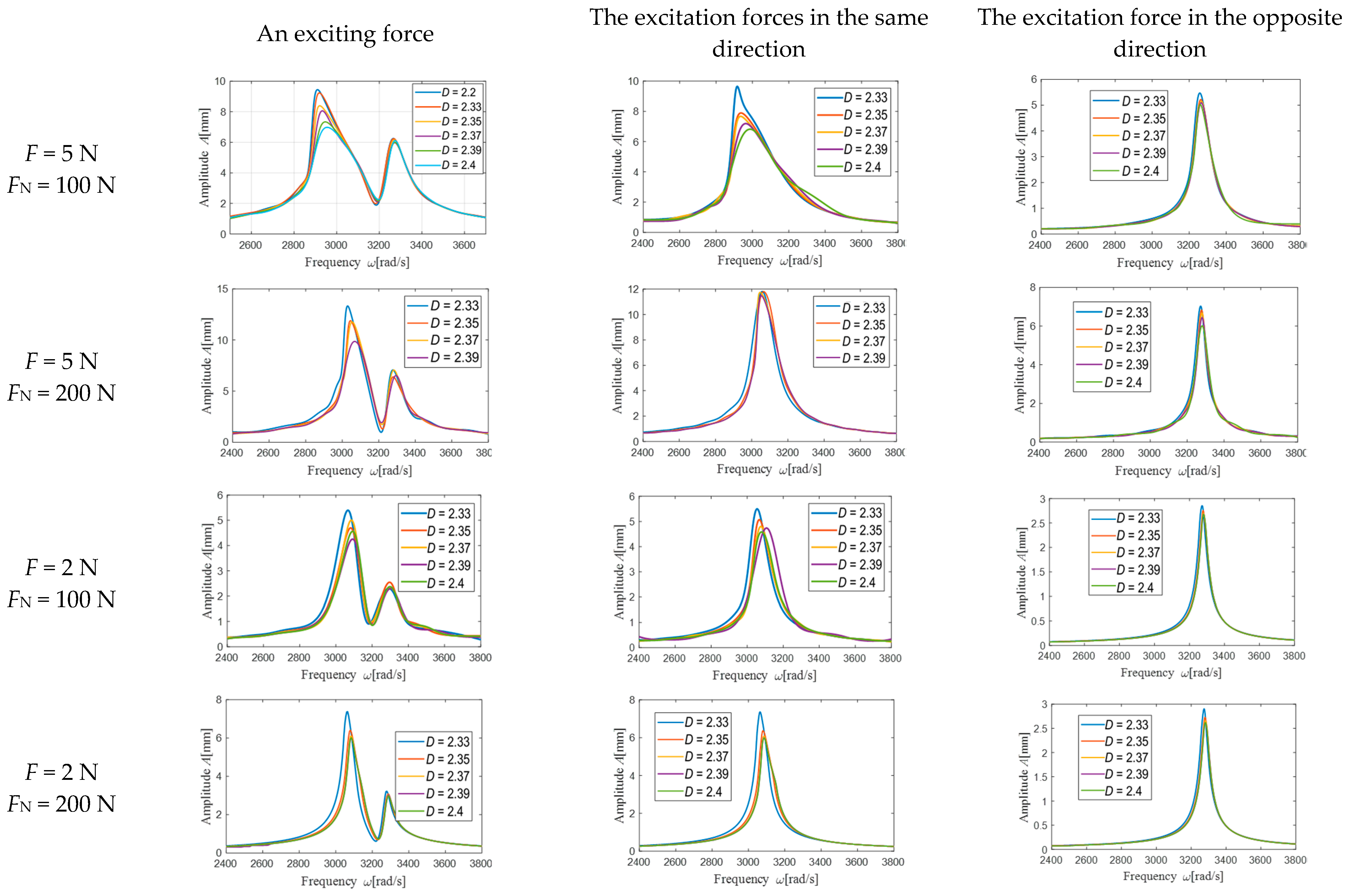
5.3. Influence of Contact Surface Roughness on Vibration Reduction Characteristics of Blades
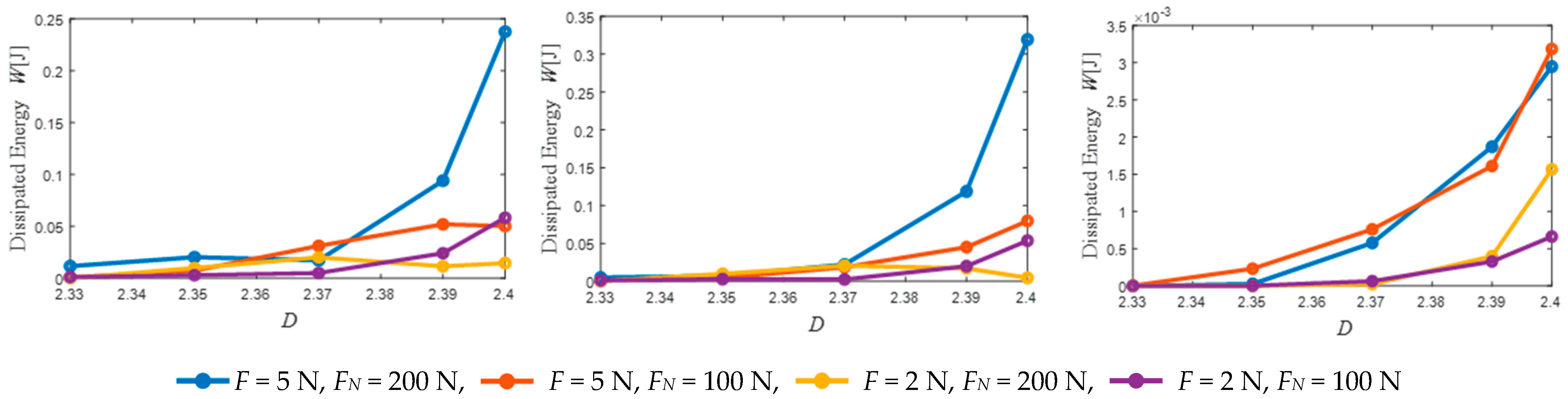
5.3.1. Influence of D on the Vibration Reduction Characteristics of UPD
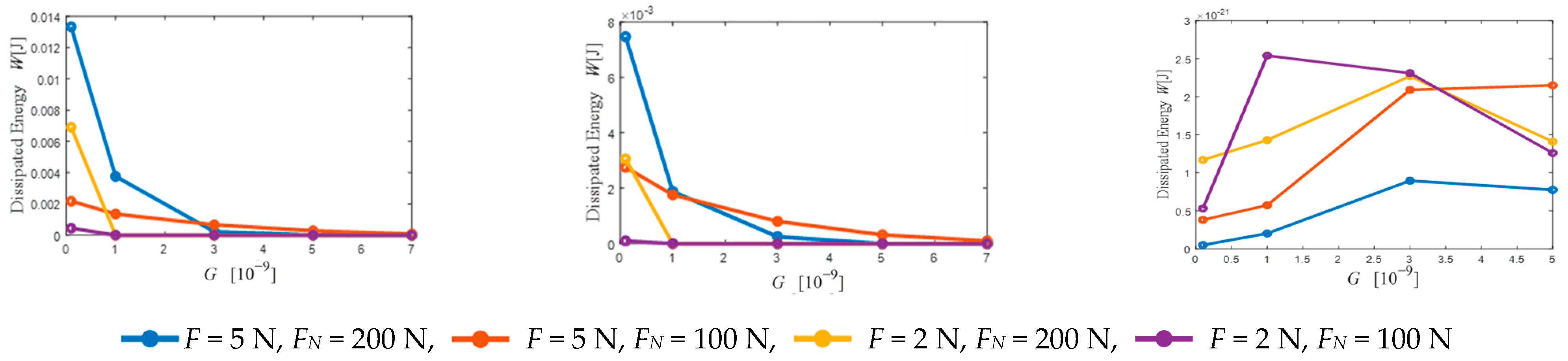
5.3.2. Influence of G on the Vibration Reduction Characteristics of UPD
6. Conclusions
- (1)
- Under excitation forces in the same direction, the UPD appeared to undergo translational motion, whereas under the opposite excitation force, rotation appeared. Under excitation forces in different directions, the contact state of the UPD between the blades appeared to have viscous slip separation at different times, which led to different nonlinear phenomena in the vibration process;
- (2)
- When the centrifugal force of the under-platform damper was small, there were more nodes on the contact surface of the under-platform damper, which led to a strong nonlinear phenomenon. With the increase in the centrifugal force, the contact nodes that were in a complete stick state gradually increased, while the nonlinear phenomena and vibration suppression performance weakened;
- (3)
- When the two blades were subjected to the same excitation force, there were more nodes in the slip state of the contact surface of the under-platform damper, which led to a strong nonlinear phenomenon, and the contact surface produced more dissipated energy. When the two blades were subjected to a single excitation force or a reverse excitation force, the contact nodes in a complete stick state increased, the nonlinear phenomenon weakened, the contact surface produced less dissipation energy, and the vibration suppression performance weakened.
- (4)
- The fractal dimension D determined the contribution of the high- and low-frequency components to the surface profile. Additionally, the fractal roughness G refers to a height-scaling parameter independent of the frequency. As the contact surface of the shock absorber under the platform became rougher, the D increased, whereas the G decreased. The number of nodes in the sliding state of the contact surface of the under-platform damper increased, which presents a strong nonlinear phenomenon. Moreover, the dissipation energy generated by the contact surface increased, the maximum response corresponding to the resonance frequency was reduced, and the vibration suppression performance was enhanced.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| N0 | normal initial positive pressure |
| su(t), sv(t) | displacements of the mass in two directions |
| ku, kv | shear spring stiffness in two directions |
| kn | normal spring stiffness |
| wu(t), wv(t) | displacements of the friction damper in two directions |
| Qu and Qv | external excitations along two directions |
| Qn | normal external excitation |
| μ | friction coefficient |
| N | pressure |
| n | distance of the normal motion of the mass block |
| f | total friction force |
| D | fractal dimension |
| G | fractal roughness parameter |
| M | overlapping ridge number |
| Φm,n | assumed phase |
| γ | fixed value equal to 1.5 |
| E1, E2 | Young’s modulus |
| v1, v2 | Poisson’s ratio |
| P | total contact load |
| A | actual contact area |
| δ | asperity interference |
| ΔFe | elastic force |
| Kn, Kt | normal and tangential contact stiffness |
| kni, kti | stiffness of each contact pair |
| M, K, C | mass, stiffness, damping matrix |
| Nh | truncated harmonic order |
| ω | external excitation frequency |
| U0, Uck, Usk | Fourier series corresponding to the 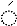 -order harmonic -order harmonic |
| Nd | degree of freedom of the whole system |
| f(t) | nonlinear force |
| fnl | external excitation force |
| P(ω) | dynamic stiffness matrix |
Abbreviations
| UPD | under-platform damper |
| FGT | fractal geometry theory |
| CB | Craig–Bampton |
References
- Petrov, E.P.; Zachariadis, Z.I.; Beretta, A.; Elliott, R. A study of nonlinear vibrations in a frictionally damped turbine bladed disk with comprehensive modeling of aerodynamic effects. J. Eng. Gas Turbine Power 2013, 135, 032504. [Google Scholar] [CrossRef]
- Panagiotopoulos, P.D.; Panagouli, O.K.; Mistakidis, E.S. Fractal geometry in structures. Numerical methods for convex energy problems. Int. J. Solids Struct. 1994, 31, 2211–2228. [Google Scholar] [CrossRef]
- Komvopoulos, K. Finite Element Analysis of a Layered Elastic Solid in Normal Contact with a Rigid Surface. J. Tribol. 1988, 110, 477–485. [Google Scholar] [CrossRef]
- Willner, K. Elasto-Plastic Normal Contact of Three-Dimensional Fractal Surfaces Using Halfspace Theory. J. Tribol. 2004, 126, 28–33. [Google Scholar] [CrossRef]
- Streator, J.L. Dynamic contact of a rigid sphere with an elastic half-space: A numerical simulation. J. Tribol. 2003, 125, 25–32. [Google Scholar] [CrossRef]
- Yang, B.D.; Menq, C.H. Characterization of Contact Kinematics and Application to the Design of Wedge Dampers in Turbomachinery Blading: Part II—Prediction of Forced Response and Experimental Verification//Turbo Expo: Power for Land, Sea, and Air. Am. Soc. Mech. Eng. 1997, 78712, V004T14A008. [Google Scholar]
- Sanliturk, K.Y.; Ewins, D.J.; Stanbridge, A.B. Underplatform dampers for turbine blades: Theoretical modeling, analysis, and comparison with experimental data. J. Eng. Gas Turbine Power 2001, 123, 919–929. [Google Scholar] [CrossRef]
- Schwingshackl, C.W.; Petrov, E.P.; Ewins, D.J. Effects of contact interface parameters on vibration of turbine bladed disks with underplatform dampers. J. Eng. Gas Turbine Power 2012, 134, 032507. [Google Scholar] [CrossRef]
- Panning, L.; Sextro, W.; Popp, K. Spatial dynamics of tuned and mistuned bladed disks with cylindrical and wedge-shaped friction dampers. Int. J. Rotating Mach. 2003, 9, 219–228. [Google Scholar] [CrossRef]
- Petrov, E.P. Explicit finite element models of friction dampers in forced response analysis of bladed disks. J. Eng. Gas. Turbine Power 2008, 130, 022502. [Google Scholar] [CrossRef]
- Goerke, D.; Willner, K. Normal contact of fractal surfaces—Experimental and numerical investigations. Wear 2008, 264, 589–598. [Google Scholar] [CrossRef]
- Iwan, W.D. On a Class of Models for the yielding behavior of continuous and composite systems. Int. J. Appl. Mech. 1967, 34, 612–617. [Google Scholar] [CrossRef]
- Niu, C.; Chen, J.; Yang, F.; Liu, Q.; Lei, H.; Wu, Y.; Wu, Y.; Rong, M. Investigation of the electrical rolling contact degradation based on fractal theory. Eng. Fail. Anal. 2020, 113, 104559. [Google Scholar] [CrossRef]
- Pesaresi, L.; Salles, L.; Jones, A.; Green, J.S.; Schwingshackl, C.W. Modelling the nonlinear behaviour of an underplatform damper test rig for turbine applications. Mech. Syst. Signal Process. 2017, 85, 662–679. [Google Scholar] [CrossRef]
- Pesaresi, L.; Armand, J.; Schwingshackl, C.W.; Salles, L.; Wong, C. An advanced underplatform damper modelling approach based on a microslip contact model. J. Sound Vib. 2018, 436, 327–340. [Google Scholar] [CrossRef]
- Qu, Z.; Hu, D.; Chen, Z. Contact nonlinear analysis for the under-platform dampers of blade based on a frictional energy dissipation model. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 30, pp. 146–155. [Google Scholar]
- He, S.; Jia, W.; Yang, Z.; He, B.; Zhao, J. Dynamics of a Turbine Blade with an Under-Platform Damper Considering the Bladed Disc’s Rotation. Appl. Sci. 2019, 9, 4181. [Google Scholar] [CrossRef]
- He, B.; Ouyang, H.; Ren, X.; He, S. Dynamic response of a simplified turbine blade model with under-platform dry friction dampers considering normal load variation. Appl. Sci. 2017, 7, 228. [Google Scholar] [CrossRef]
- Pařík, P.; Kim, J.-G.; Isoz, M.; Ahn, C.-U. A Parallel Approach of the Enhanced Craig–Bampton Method. Mathematics 2021, 9, 3278. [Google Scholar] [CrossRef]
- Borisenko, V.; Leoro, J.; Didenko, A. Main rotor blade modeling approaches comparison. Finite element and Craig-Bampton methods. J. Phys. Conf. Ser. 2021, 2131, 032096. [Google Scholar] [CrossRef]
- Kantar, E.; Hvidsten, S.; Mauseth, F.; Ildstad, E. A stochastic model for contact surfaces at polymer interfaces subjected to an electrical field. Tribol. Int. 2018, 127, 361–371. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, Y.; Zhu, H. A contact stiffness model of machined plane joint based on fractal geometry theory. J. Tribol. 2010, 132, 011401. [Google Scholar] [CrossRef]
- Liu, Y.; Shangguan, B.; Xu, Z. A friction contact stiffness model of fractal geometry in forced response analysis of a shrouded blade. Nonlinear Dyn. 2012, 70, 2247–2257. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, Y.; Han, H.; Ma, H.; Wang, H.; Li, Z. Meshing Characteristics of Spur Gears Considering Three-Dimensional Fractal Rough Surface Under Elastohydrodynamic Lubrication. Machines 2022, 10, 705. [Google Scholar] [CrossRef]
- Huangfu, Y.; Chen, K.; Ma, H.; Li, X.; Han, H.; Zhao, Z. An improved model for meshing characteristics analysis of spur gears considering fractal surface contact and friction. Mech. Mach. Theory 2021, 158, 104219. [Google Scholar]
- She, H.; Li, C.; Tang, Q.; Ma, H.; Wen, B. Computation and investigation of mode characteristics in nonlinear system with tuned/mistuned contact interface. Front. Mech. Eng. 2019, 15, 133–150. [Google Scholar] [CrossRef]
- Krack, M.; Gross, J. Harmonic Balance for Nonlinear Vibration Problems; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Urabe, M. Galerkin’s Procedure for Nonlinear Periodic Systems; Wisconsin University Madison Mathematics Research Center: Madison, WI, USA, 1964. [Google Scholar]
- Cardona, A.; Coune, T.; Lerusse, A.; Geradin, M. A multiharmonic method for non-linear vibration analysis. Int. J. Numer. Methods Eng. 1994, 37, 1593–1608. [Google Scholar] [CrossRef]
- Pierre, C.; Ferri, A.A.; Dowell, E.H. Multi-harmonic analysis of dry friction damped systems using an incremental harmonic bal- 524 ance method. Int. J. Appl. Mech. 1985, 52, 958–964. [Google Scholar] [CrossRef]
- Chan, T.F.C.; Keller, H.B. Arc-length continuation and multigrid techniques for nonlinear elliptic eigenvalue problems. SISC 1982, 3, 173–194. [Google Scholar] [CrossRef]
- He, J.H. A modified Newton–Raphson method. Commun. Numer. Meth. Eng. 2004, 20, 801–805. [Google Scholar] [CrossRef]
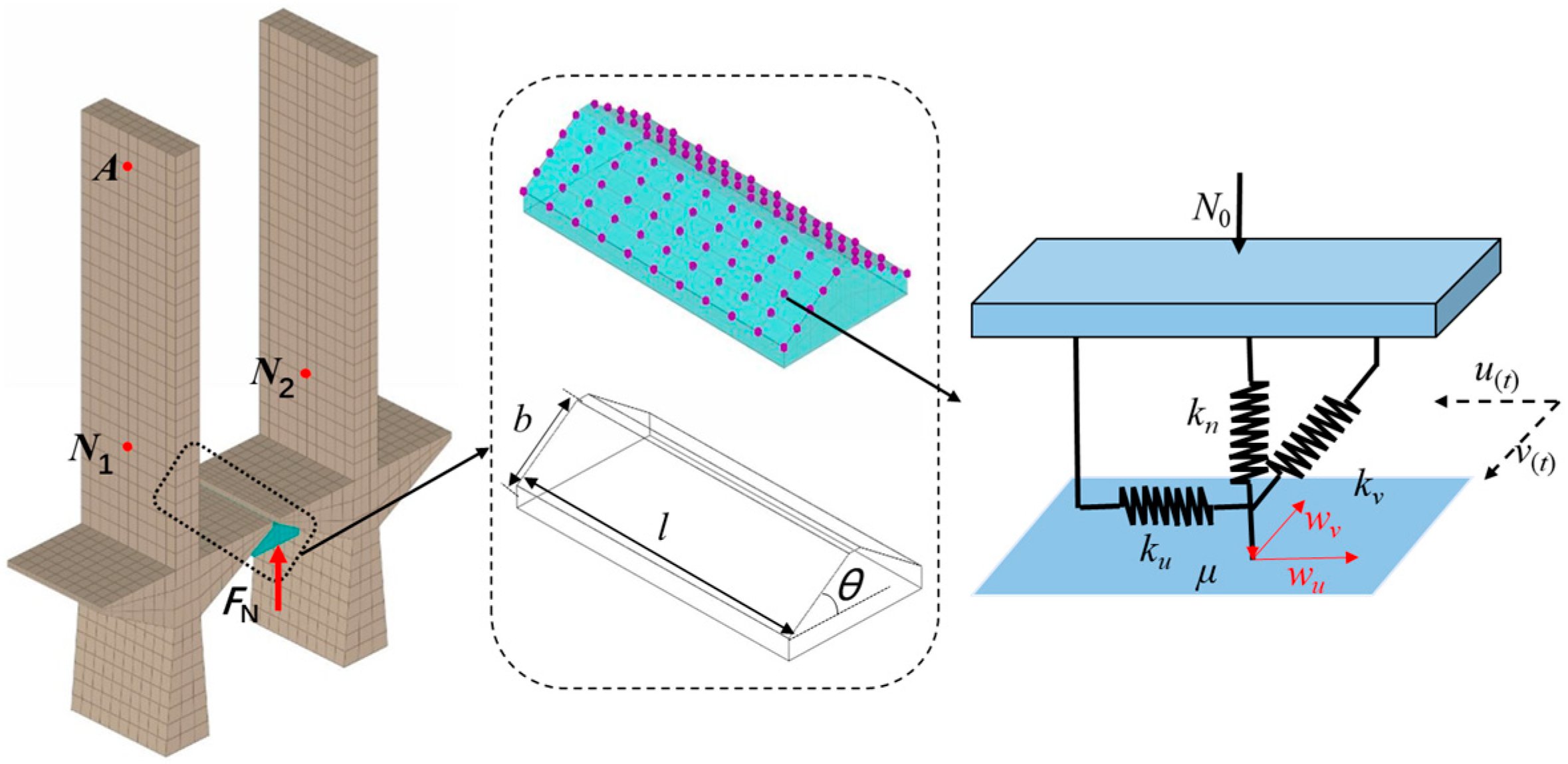
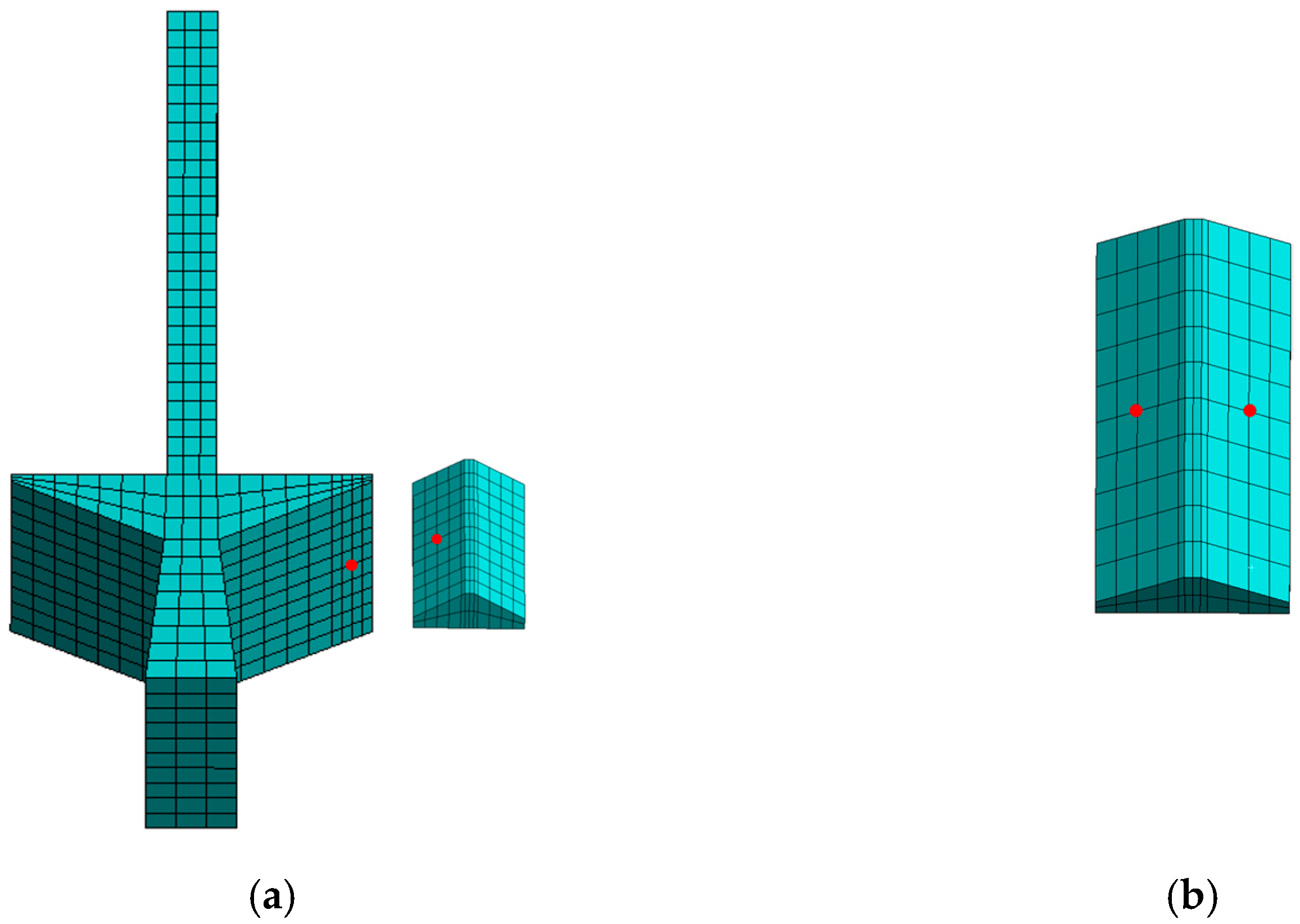

| Model | Total Degree of Freedom | Nonlinear Degree of Freedom |
|---|---|---|
| Original model | 15,279 | 660 |
| CB reduction model | 762 | 660 |
| Mode Order | Original Model Frequency/Hz | Reduced Model Frequency/Hz | Frequency Difference/% | MAC |
|---|---|---|---|---|
| 1 | 506.83 | 506.83 | 2.17 × 10−3 | 0.99 |
| 2 | 526.37 | 526.37 | 1.42 × 10−3 | 0.99 |
| 3 | 1230.70 | 1230.68 | 2.28 × 10−3 | 0.99 |
| 4 | 1325.70 | 1325.72 | 6.11 × 10−4 | 0.99 |
| 5 | 2567.10 | 2567.17 | 3.27 × 10−4 | 0.99 |
| 6 | 3206.60 | 3206.68 | 9.67 × 10−3 | 0.99 |
| 7 | 3559.80 | 3559.83 | 8.71 × 10−3 | 0.99 |
| 8 | 3575.50 | 3575.56 | 1.12 × 10−2 | 0.99 |
| 9 | 4802.10 | 4802.29 | 4.16 × 10−2 | 0.99 |
| 10 | 5449.50 | 5449.80 | 5.87 × 10−2 | 0.99 |
| Parameters | Blade Length | Blade Width | Blade Thickness | Density | Young’s Modulus | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| Value | 145 mm | 28 mm | 7 mm | 7.8 × 10−6 kg/mm3 | 197 GPa | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; She, H.; Yang, G.; Zang, C.; Li, C. The Influence of Interface Roughness on the Vibration Reduction Characteristics of an Under-Platform Damper. Appl. Sci. 2023, 13, 2128. https://doi.org/10.3390/app13042128
Hu S, She H, Yang G, Zang C, Li C. The Influence of Interface Roughness on the Vibration Reduction Characteristics of an Under-Platform Damper. Applied Sciences. 2023; 13(4):2128. https://doi.org/10.3390/app13042128
Chicago/Turabian StyleHu, Shijie, Houxin She, Guang Yang, Chaoping Zang, and Chaofeng Li. 2023. "The Influence of Interface Roughness on the Vibration Reduction Characteristics of an Under-Platform Damper" Applied Sciences 13, no. 4: 2128. https://doi.org/10.3390/app13042128
APA StyleHu, S., She, H., Yang, G., Zang, C., & Li, C. (2023). The Influence of Interface Roughness on the Vibration Reduction Characteristics of an Under-Platform Damper. Applied Sciences, 13(4), 2128. https://doi.org/10.3390/app13042128







