Parameter Study for Child Booster Seats in Frontal Collisions
Abstract
:1. Introduction
2. The Frontal Collision Simulation Model with a Child Booster Seat
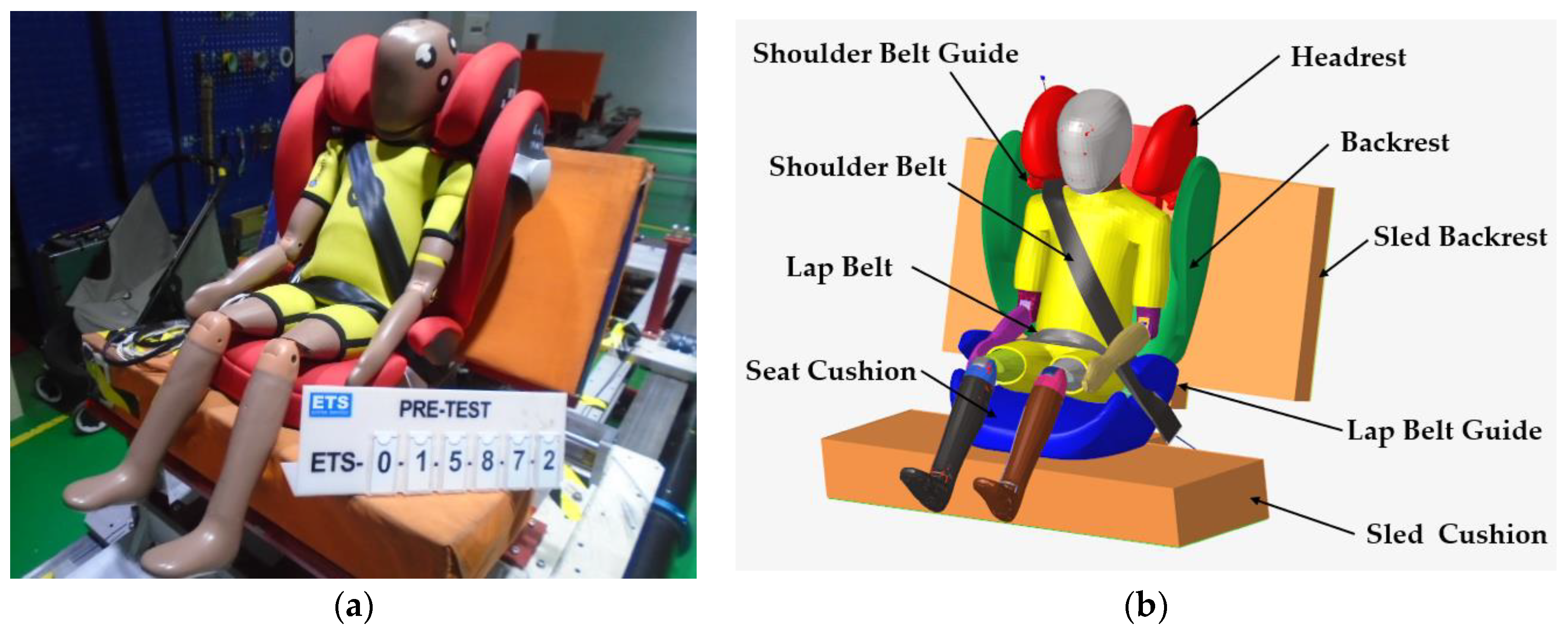
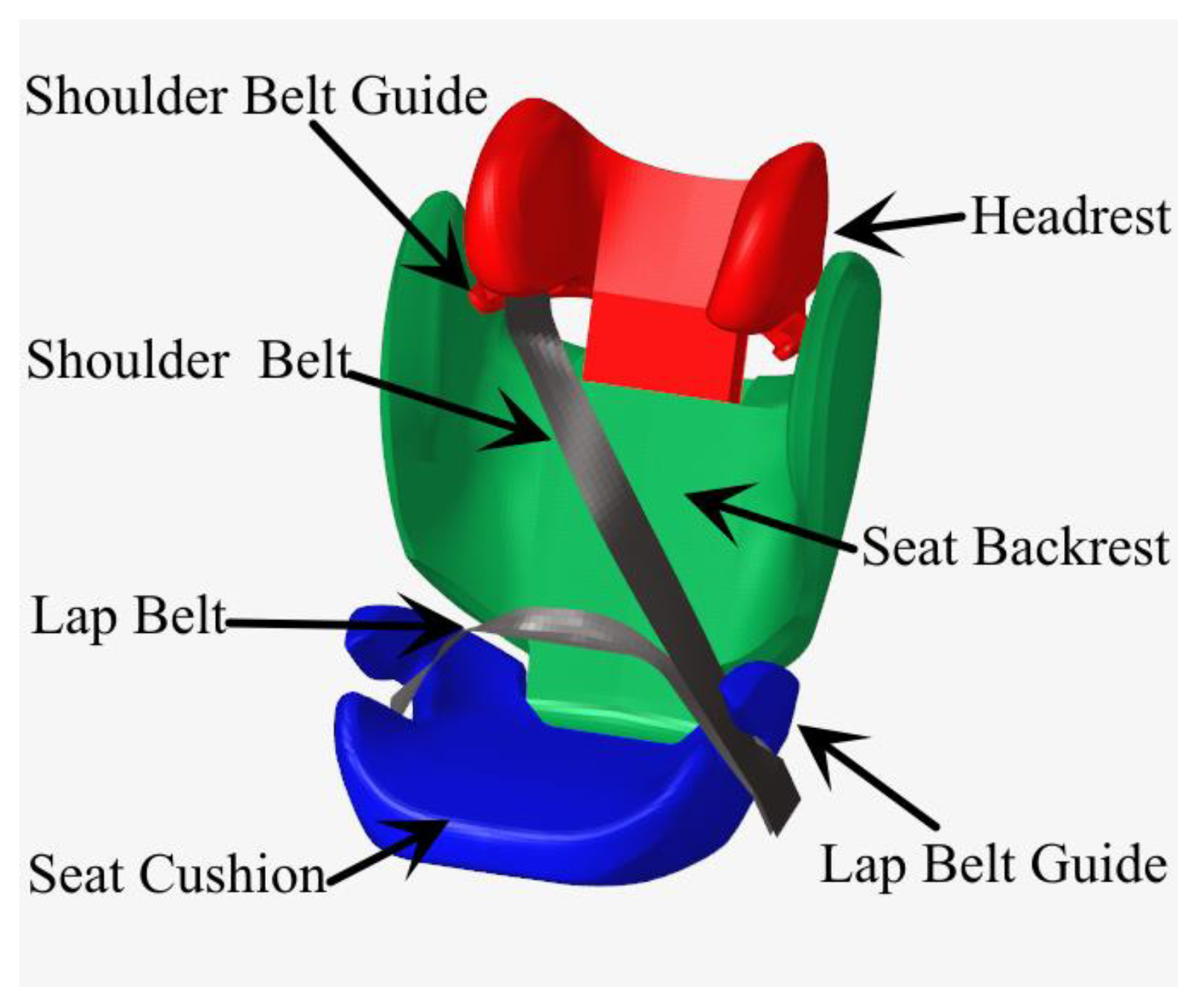
2.1. Establishment of the Simulation Model
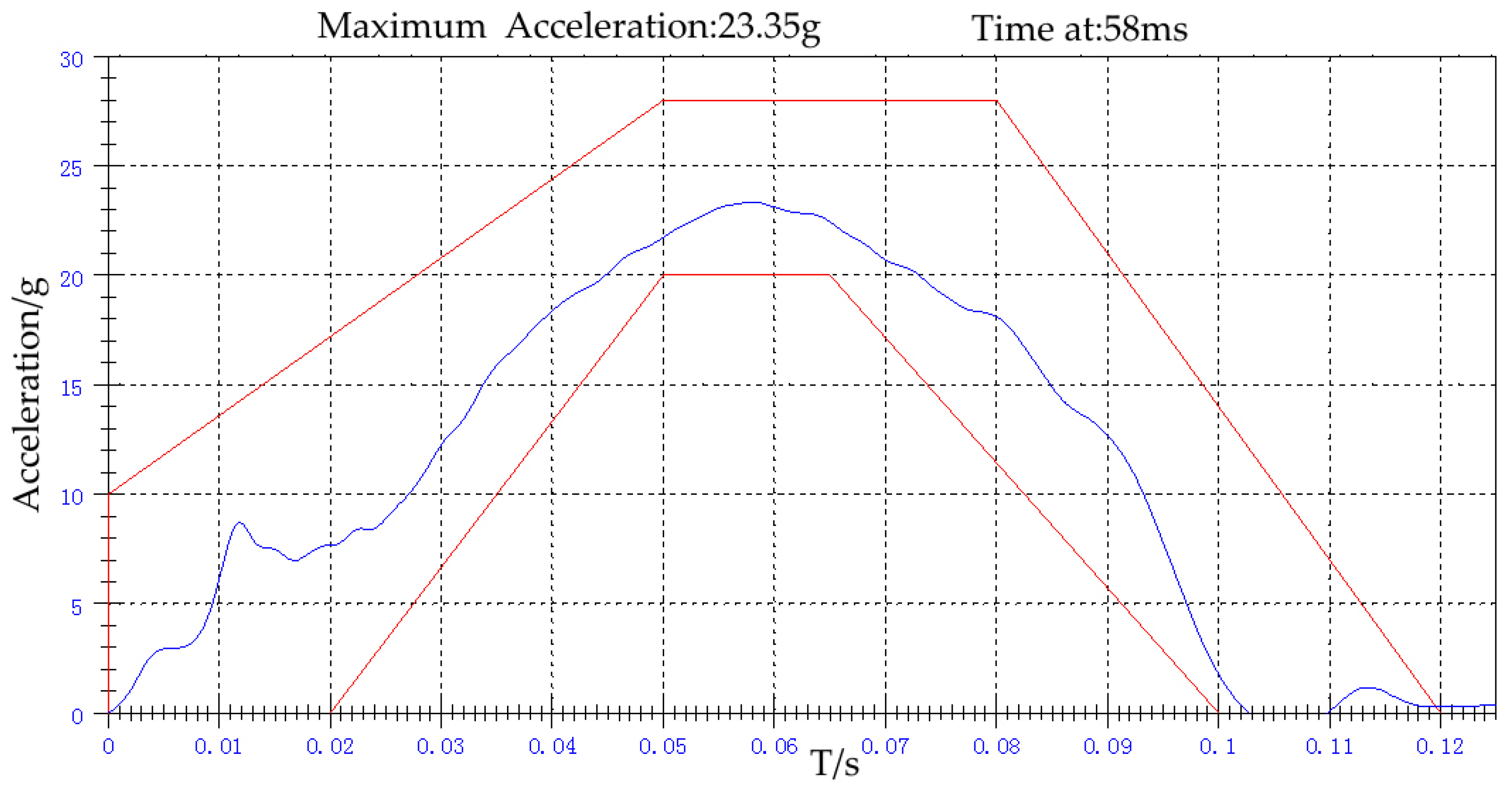
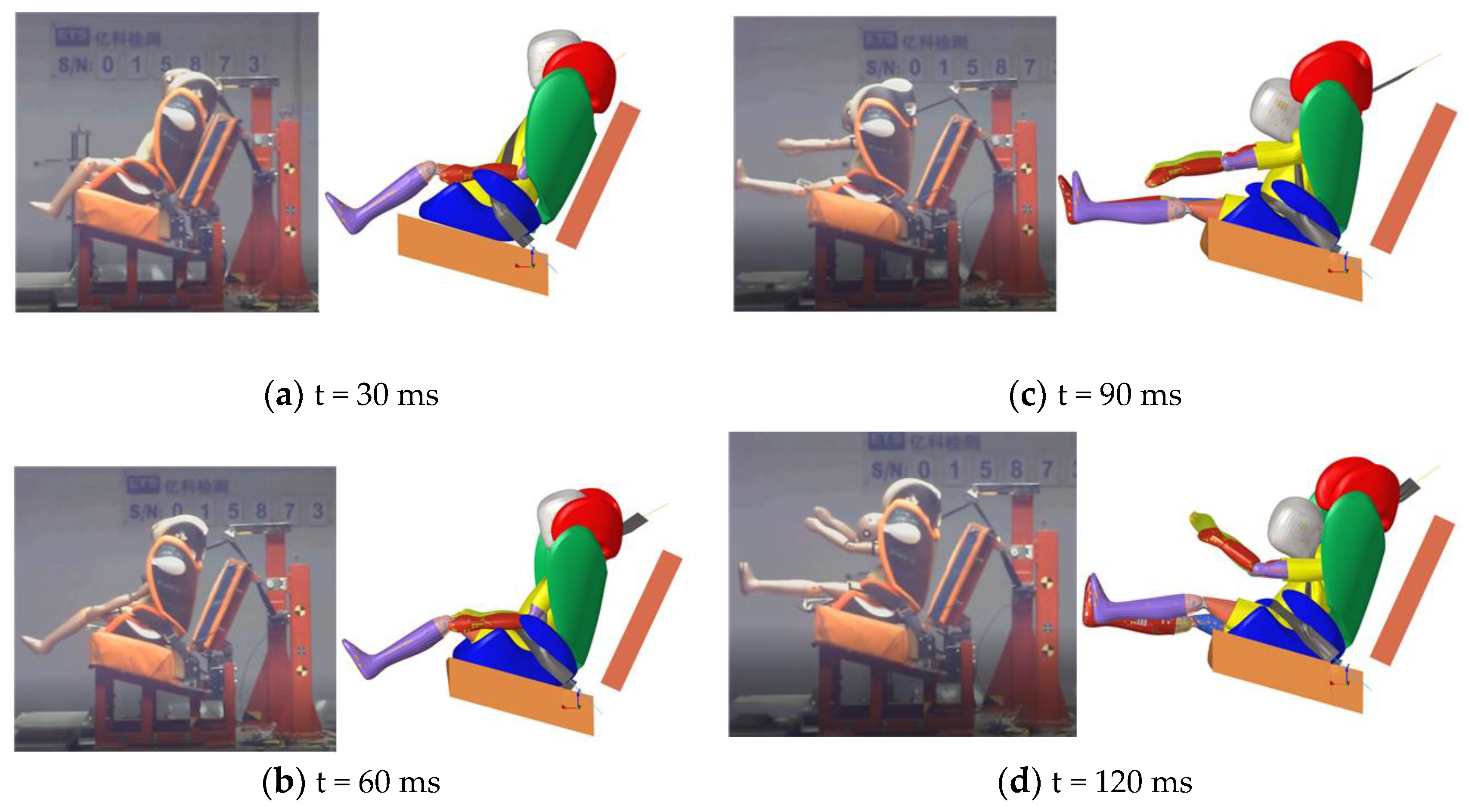
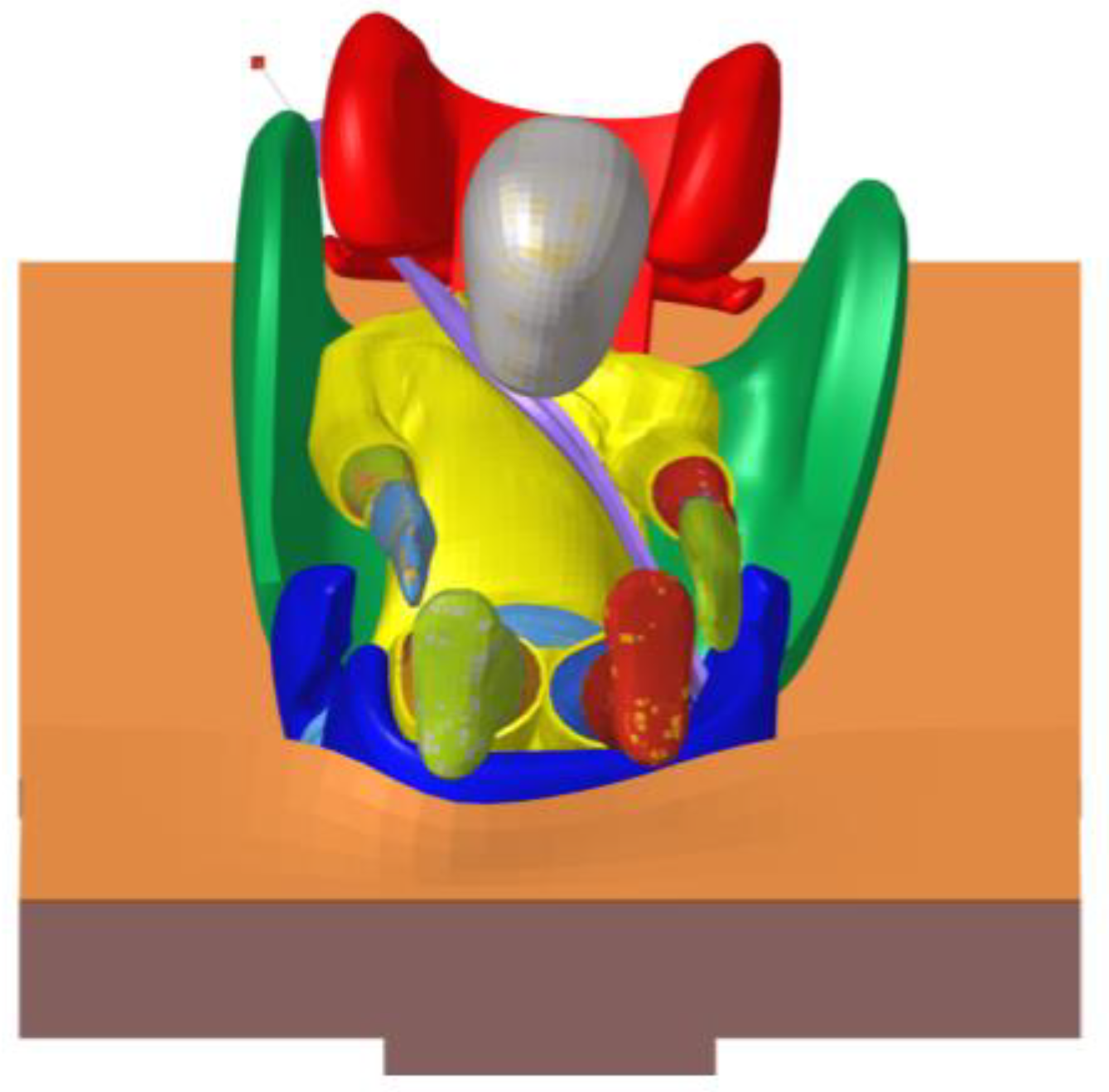
2.2. Validation of the Simulation Model
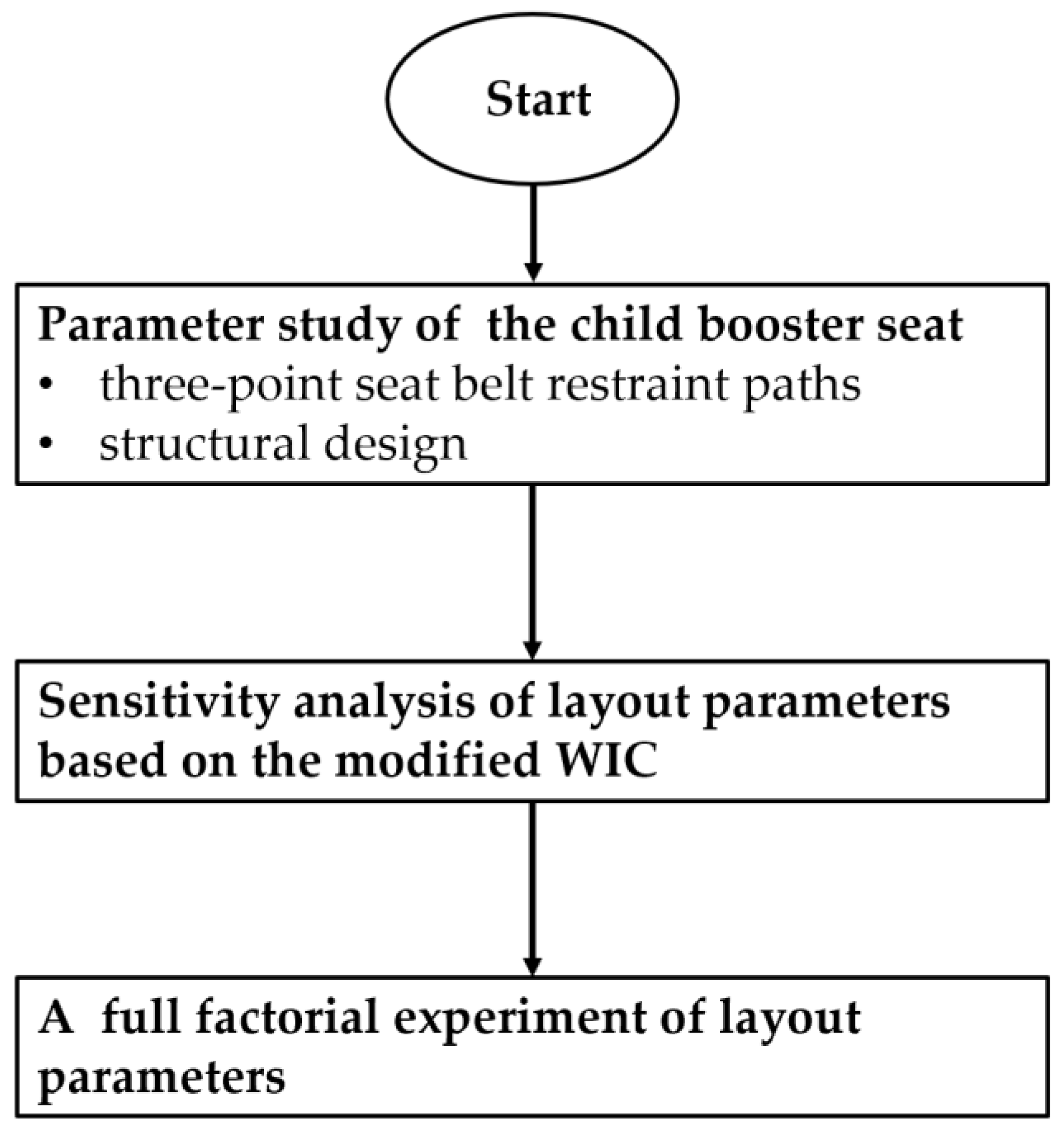
3. Design Framework
4. Parameter Study of Child Booster Seats
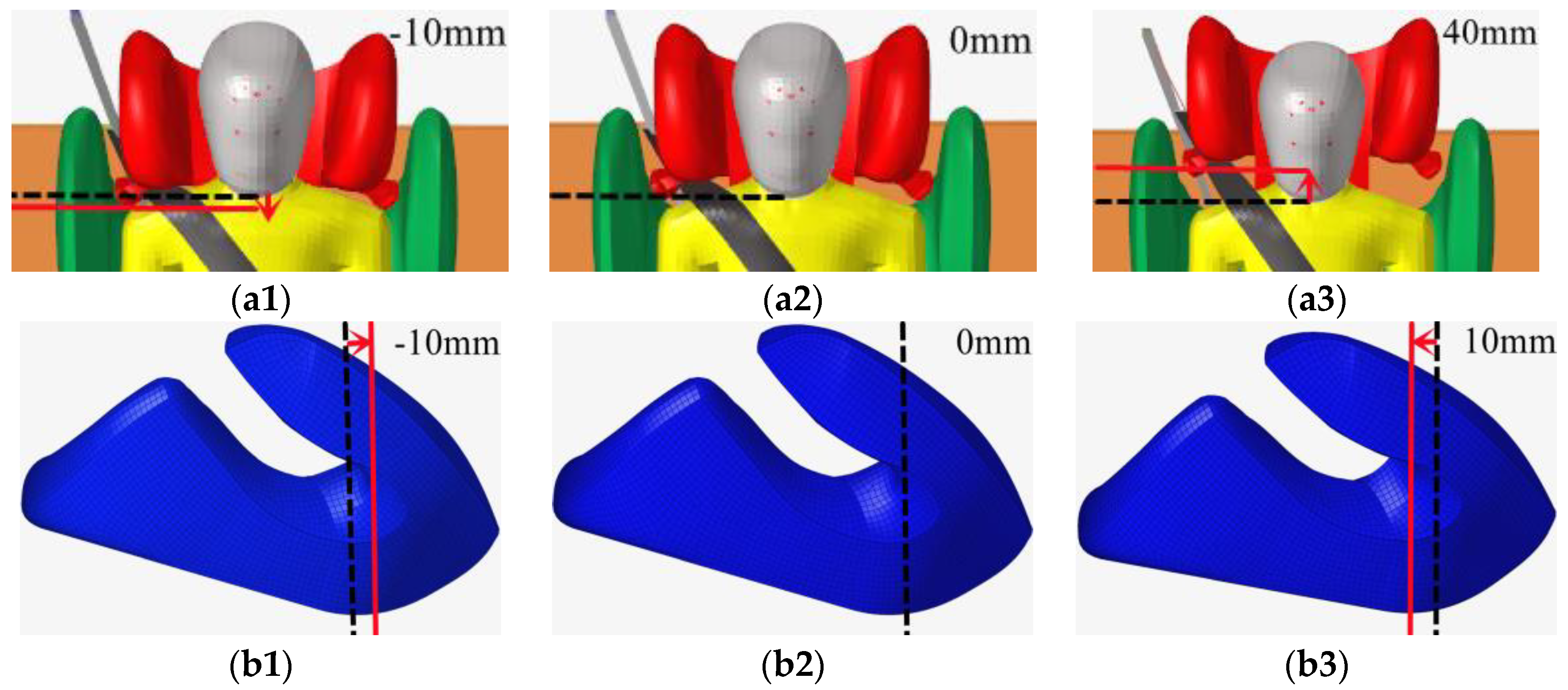
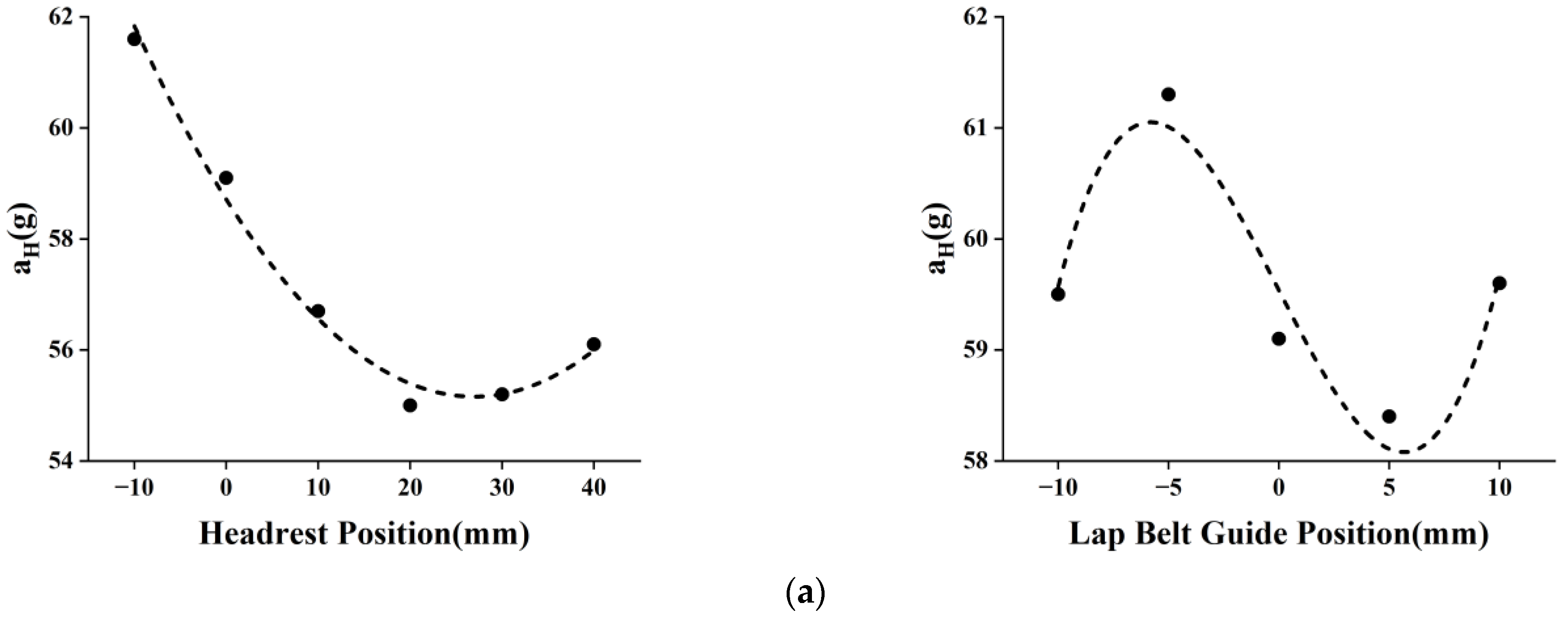
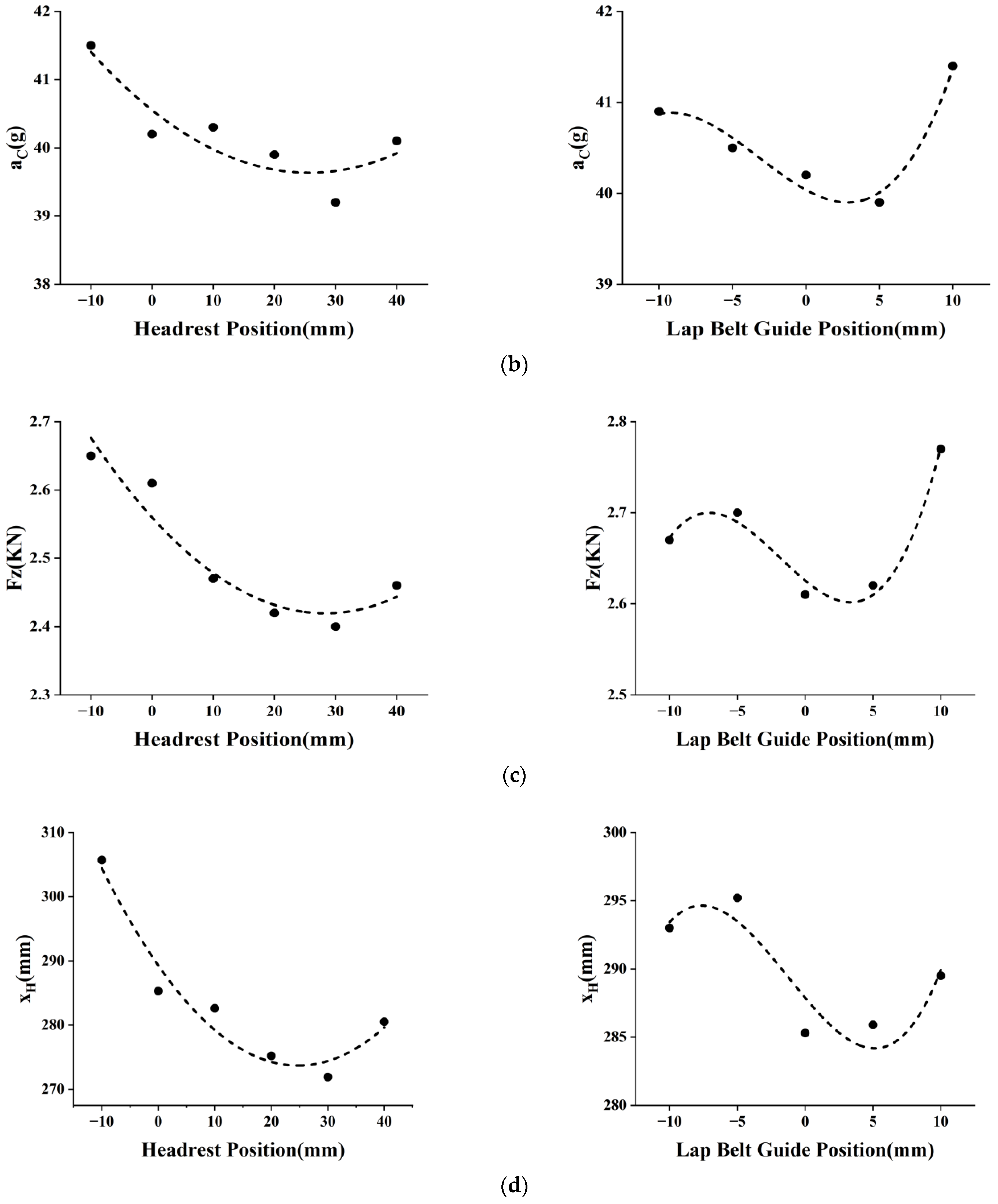
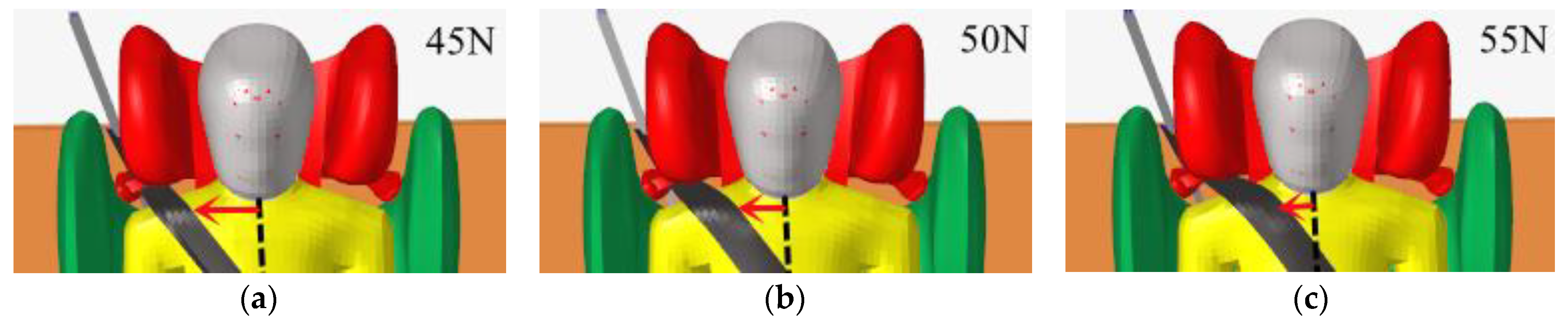
4.1. Parametric Study of Three-Point Seat Belt Restraint Path
4.2. Parameter Study of Structural Design
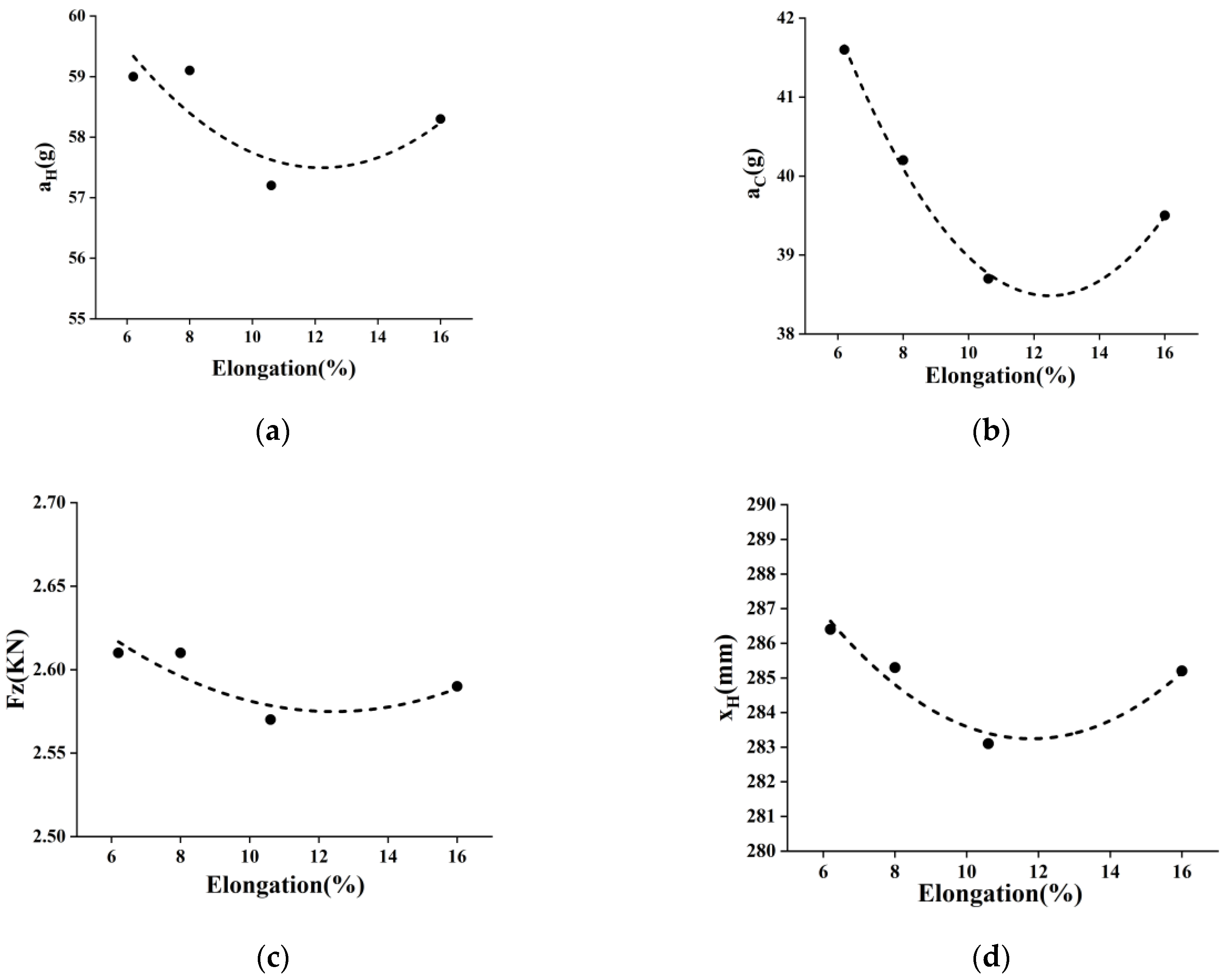
4.2.1. Webbing Stiffness
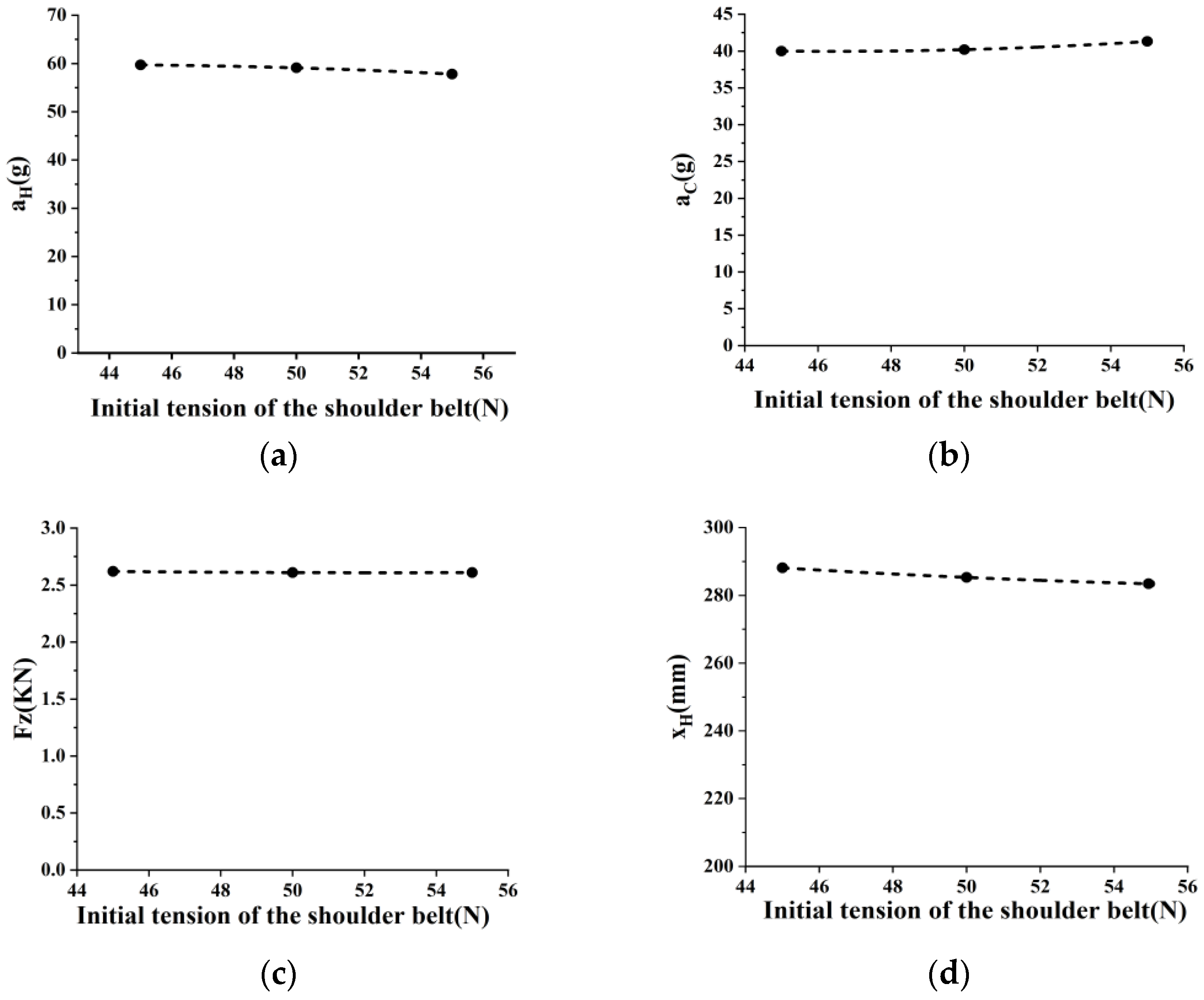
4.2.2. Initial Tension of the Shoulder Belt
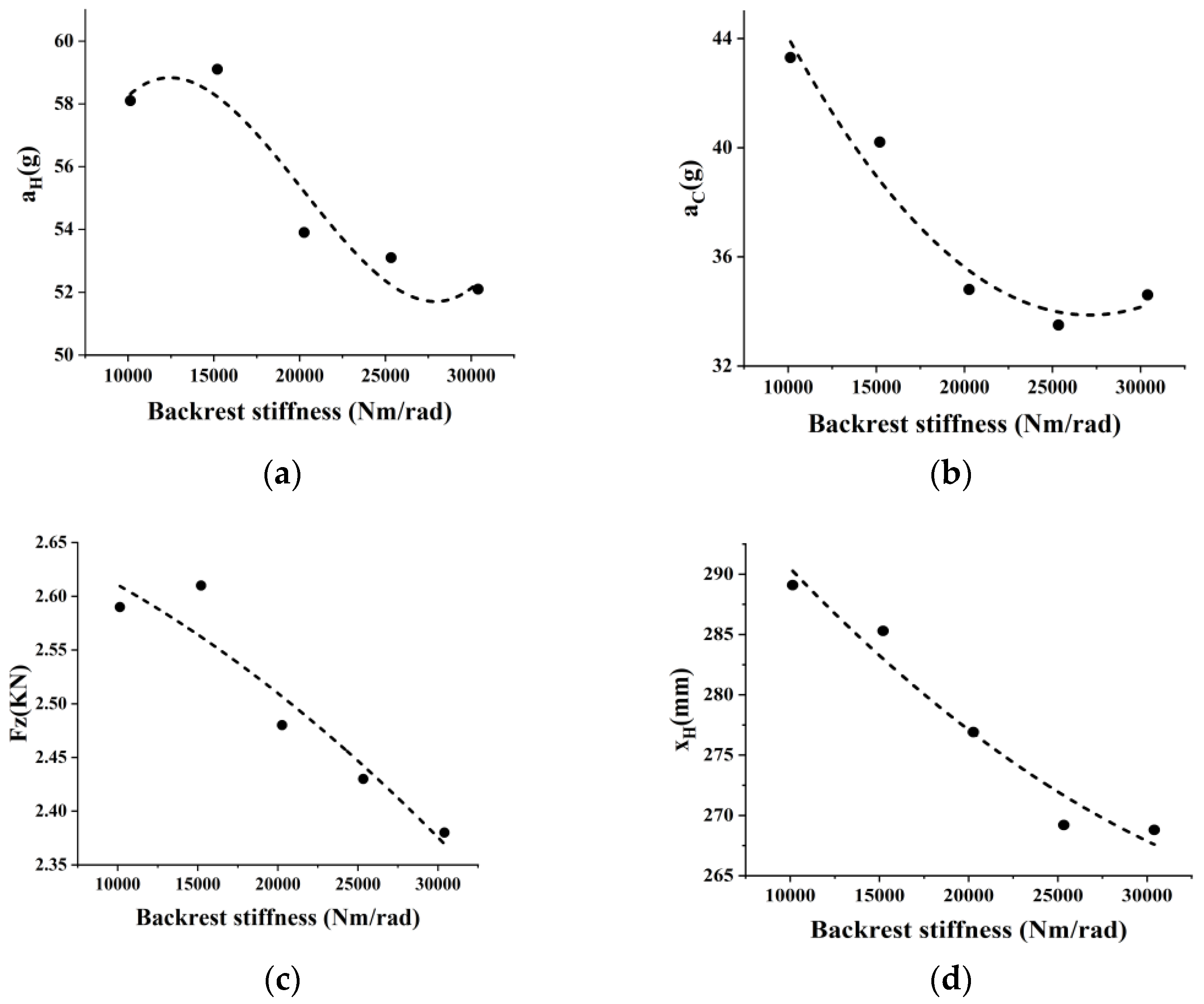
4.2.3. Seat Backrest Stiffness
4.2.4. Cushion Angle
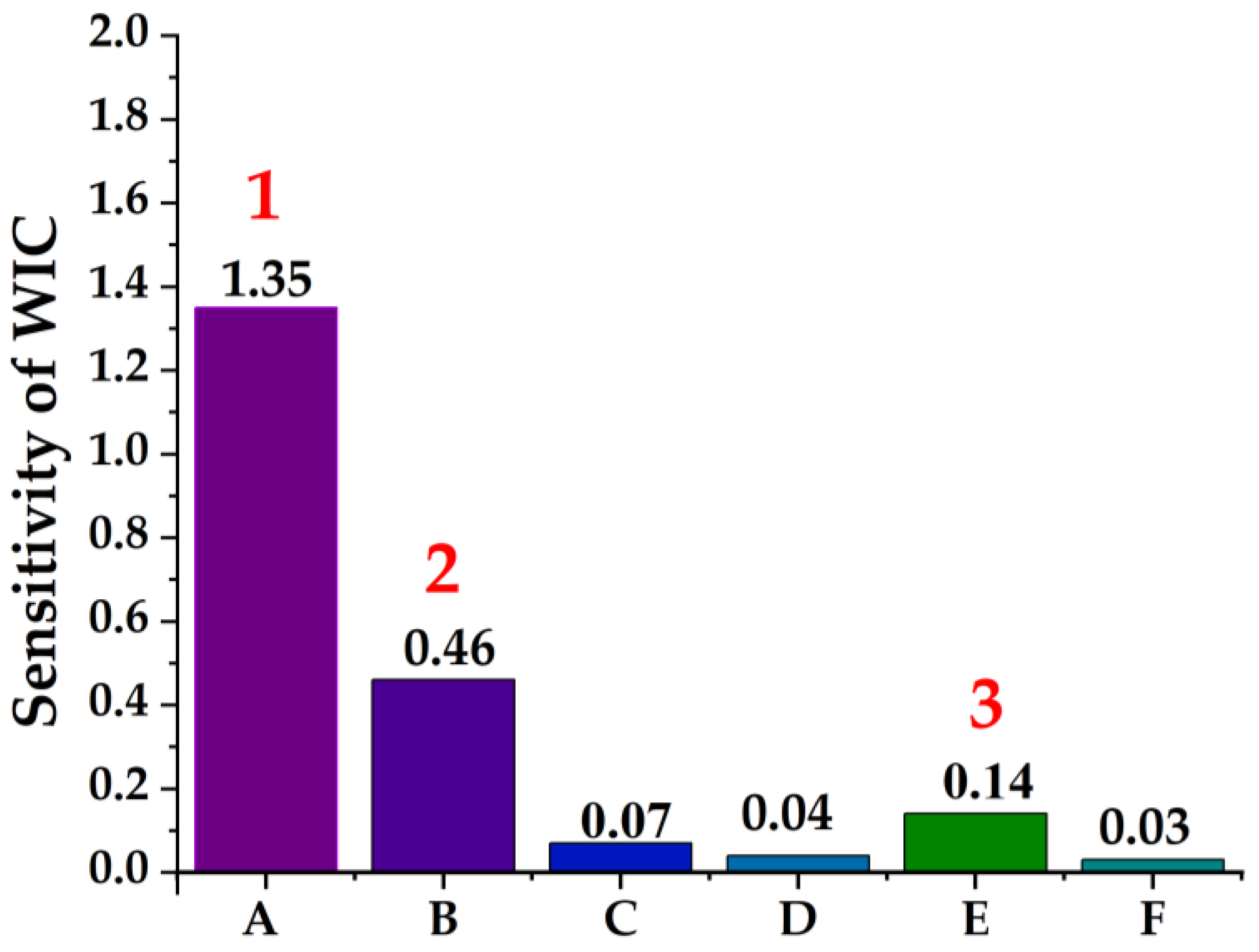
5. Parameter Sensitivity Analysis
6. Value Determination of the Selected Layout Parameters
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rosen, H.E.; Bari, I.; Paichadze, N.; Peden, M.; Khayesi, M.; Monclús, J.; Hyder, A.A. Global road safety 2010–18: An analysis of Global Status Reports. Injury 2022. [Google Scholar] [CrossRef] [PubMed]
- Jermakian, J.S.; Klinich, K.D.; Orton, N.R.; Flannagan, C.A.; Manary, M.A.; Malik, L.A.; Narayanaswamy, P. Factors affecting tether use and correct use in child restraint installations. J. Saf. Res. 2014, 51, 99–108. [Google Scholar] [CrossRef] [PubMed]
- Pitt, T.M.; Howard, A.W.; HubkaRao, T.; Hagel, B.E. The effectiveness of booster seat use in motor vehicle collisions. Accid. Anal. Prev. 2021, 159, 106296. [Google Scholar] [CrossRef]
- Anderson, D.M.; Carlson, L.L.; Rees, D.I. Booster seat effectiveness among older children: Evidence from Washington state. Am. J. Prev. Med. 2017, 53, 210–215. [Google Scholar] [CrossRef]
- Ma, X.; Griffin, R.; McGwin, G.; Allison, D.B.; Heymsfield, S.B.; He, W.; Zhu, S. Effectiveness of booster seats compared with no restraint or seat belt alone for crash injury prevention. Acad. Emerg. Med. 2013, 20, 880–887. [Google Scholar] [CrossRef] [PubMed]
- Visvikis, C.; Carrol, J.; Pitcher, M.; Waagmeester, K. Assessing Lap Belt Path and Submarining Risk in Booster Seats: Abdominal Pressure Twin Sensors vs. Anterior-superior Iliac Spine Load Cells. In Proceedings of the IRCOBI Conference, Athens, Greece, 12–14 September 2018; pp. 655–668. Available online: http://www.ircobi.org/wordpress/downloads/irc18/pdf-files/92.pdf (accessed on 13 November 2022).
- Baker, G.H.; Mansfield, J.A.; Hunter, R.L.; Bolte IV, J.H. Comparison of Child and ATD Static Belt Fit and Belt Torso Contact on Belt-Positioning Booster Seats. In Proceedings of the IRCOBI Conference, online, 8–10 September 2021; pp. 556–580. Available online: http://www.ircobi.org/wordpress/downloads/irc21/pdf-files/2160.pdf (accessed on 13 November 2022).
- Baker, G.H.; Mansfield, J.A.; Hunter, R.L.; Bolte IV, J.H. Evaluation of static belt fit and belt torso contact for children on belt-positioning booster seats. Traffic Inj. Prev. 2021, 22, S87–S92. [Google Scholar] [CrossRef]
- Cruz-Jaramillo, I.; Torres-San-Miguel, C.; Cortes-Vásquez, O.; Martínez-Sáez, L. Numerical low-back booster analysis on a 6-year-old infant during a frontal crash test. Appl. Bionics Biomech. 2018, 2018, 2359262. [Google Scholar] [CrossRef]
- Hu, J.; Wu, J.; Reed, M.P.; Klinich, K.D.; Cao, L. Rear seat restraint system optimization for older children in frontal crashes. Traffic Inj. Prev. 2013, 14, 614–622. [Google Scholar] [CrossRef]
- Gras, L.-L.; Stockman, I.; Brolin, K. Evaluation of 6 and 10 year-old child human body models in emergency events. PLoS ONE 2017, 12, e0170377. [Google Scholar] [CrossRef]
- Johansson, M.; Pipkorn, B.; Lövsund, P. Child safety in vehicles: Validation of a mathematical model and development of restraint system design guidelines for 3-year-olds through mathematical simulations. Traffic Inj. Prev. 2009, 10, 467–478. [Google Scholar] [CrossRef] [PubMed]
- Bing, J.A.; Agnew, A.M.; Bolte IV, J.H. Compatibility of booster seats and vehicles in the US market. Traffic Inj. Prev. 2018, 19, 385–390. [Google Scholar] [CrossRef] [PubMed]
- Xuerong, Z.; Wenqian, Y. Simulation and experimental study on influencing factors of child safety seat collision detection deviation. Automot. Eng. 2019, 41, 915–921. [Google Scholar] [CrossRef]
- Albanese, B.; Bohman, K.; Bilston, L.; Koppel, S.; Charlton, J.L.; Olivier, J.; Keay, L.; Brown, J. Influence of child restraint system design features on comfort, belt fit and posture. Saf. Sci. 2020, 128, 104707. [Google Scholar] [CrossRef]
- Gu, X.; Sun, G.; Li, G.; Huang, X.; Li, Y.; Li, Q. Multiobjective optimization design for vehicle occupant restraint system under frontal impact. Struct. Multidiscip. Optim. 2013, 47, 465–477. [Google Scholar] [CrossRef]
- Zhao, Y.; Alashmori, M.; Bi, F.; Wang, X. Parameter identification and robust vibration control of a truck driver’s seat system using multi-objective optimization and genetic algorithm. Appl. Acoust. 2021, 173, 107697. [Google Scholar] [CrossRef]
- Liang, R.; Liu, N.; Liu, X.; Tang, X.; Hu, Y.; Bastien, C.; Liu, X. Effectiveness analysis of a foldable booster safety seat with integrated seatbelt buckle for reducing children’s vehicle accident injury risk. Int. J. Crashworthiness 2022, 1–17. [Google Scholar] [CrossRef]
- Jiang, Y.; Wu, P.; Zeng, J.; Zhang, Y.; Zhang, Y.; Wang, S. Multi-parameter and multi-objective optimisation of articulated monorail vehicle system dynamics using genetic algorithm. Veh. Syst. Dyn. 2020, 58, 74–91. [Google Scholar] [CrossRef]
- Du, X.; Deng, Y.; Zhang, G.; Cao, L.; Zhu, F. Conceptual design and evaluation of a novel bilateral pretension seatbelt: A computational study. Int. J. Crashworthiness 2019, 25, 391–400. [Google Scholar] [CrossRef]
- Yang, X.; Shi, J.; Fu, Q.; Pu, S.; Pan, Z.; Lian, C.; Yin, Z.; Liu, S.; Wang, G. Optimization Design and Injury Analysis of Driver’s Restraint System in Sedan Small Offset Collision. Processes 2022, 10, 940. [Google Scholar] [CrossRef]
- Zhou, H.; Liao, J.; Zhang, Q.; Zhang, G.; Zhang, D. Injuries analysis of rear row occupants exposed to vehicle’s frontal oblique collision. Int. J. Automot. Technol. 2021, 22, 595–607. [Google Scholar] [CrossRef]
- Hongling, L.; Yude, D.; Changliang, C.; Chen, C. Combined with finite element analysis of car seat safety performance improvement. J. Mech. Sci. Technol. 2021, 35, 79–89. [Google Scholar] [CrossRef]
- Song, Z.; Cao, L.; Chou, C.C. Development of test equipment for pedestrian-automatic emergency braking based on C-NCAP (2018). Sensors 2020, 20, 6206. [Google Scholar] [CrossRef] [PubMed]
- Durbin, D.R.; Hoffman, B.D.; Agran, P.F.; Denny, S.A.; Hirsh, M.; Johnston, B.; Lee, L.K.; Monroe, K.; Schaechter, J.; Tenenbein, M. Child passenger safety. Pediatrics 2018, 142, e20182461. [Google Scholar] [CrossRef]
- Sybilski, K.; Mazurkiewicz, Ł.; Jurkojć, J.; Michnik, R. Evaluation of the effect of muscle forces implementation on the behavior of a dummy during a head-on collision. Acta Bioeng. Biomech. 2021, 23, 1–21. [Google Scholar] [CrossRef]
- Sybilski, K.; Małachowski, J. Impact of disabled driver’s mass center location on biomechanical parameters during crash. Appl. Sci. 2021, 11, 1427. [Google Scholar] [CrossRef]
- Baker, G.; Stockman, I.; Bohman, K.; Jakobsson, L.; Osvalder, A.-L.; Svensson, M.; Wimmerstedt, M. Kinematics and shoulder belt engagement of children on belt-positioning boosters during evasive steering maneuvers. Traffic Inj. Prev. 2018, 19, S131–S138. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, Y. Simulation and experiment study on the deviation influence factors of dynamic collision test for child safety seat. Int. J. Crashworthiness 2021, 26, 283–294. [Google Scholar] [CrossRef]
- Liu, Q.; Tong, N.; Han, X. A Global Sensitivity Analysis Method for Multi-Input Multi-Output System and Its Application in Structural Design. Int. J. Comput. Methods 2022, 19, 2141005. [Google Scholar] [CrossRef]
- Hong, L.; Liu, G. Optimal design of rear-seat restraint system based on new safety seat during frontal collisions. Proceedings of the Institution of Mechanical Engineers. Part D J. Automob. Eng. 2022, 09544070221076899. [Google Scholar] [CrossRef]
- Koc, K.; Ekmekcioğlu, Ö.; Gurgun, A.P. Integrating feature engineering, genetic algorithm and tree-based machine learning methods to predict the post-accident disability status of construction workers. Autom. Constr. 2021, 131, 103896. [Google Scholar] [CrossRef]
- Zhang, X.; Niu, Y. Research on general layout parameters of I-SIZE child safety seat in frontal impact. Int. J. Crashworthiness 2022, 27, 968–978. [Google Scholar] [CrossRef]
- Binhui, J.; Shuifang, D.; Haojie, M.; Jinhai, Y. Simulation study of thoracic injury criteria in children. Automot. Eng. 2015, 37, 897–903. [Google Scholar] [CrossRef]
- China Automotive Technology Research Center Co. C-NCAP Management Rules; 2021 ed.; Automotive Technology Research Center: Tianjin, China, 2020; Available online: https://www.c-ncap.org.cn/ (accessed on 13 November 2022).
- Shasthri, S.; Kausalyah, V.; Shah, Q.; Abdullah, K. Parametric study for head injury criteria response of three-year olds in a child restraint system in oblique and lateral intrusive side impact. Int. J. Crashworthiness 2015, 20, 1–11. [Google Scholar] [CrossRef]
- Sibilski, K.; Małachowski, J. Sensitivity study on seat belt system key factors in terms of disabled driver behavior during frontal crash. Acta Bioeng. Biomech. 2019, 21, 169–180. [Google Scholar] [CrossRef]
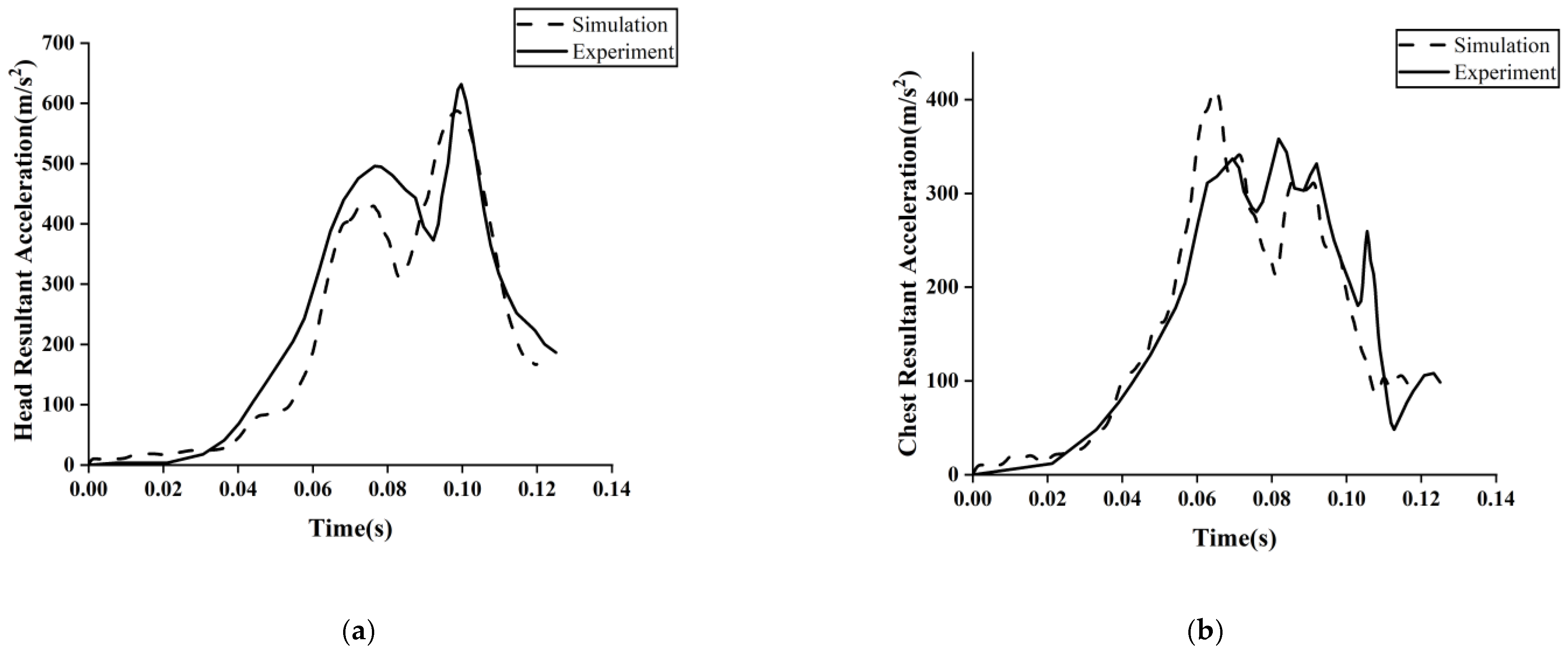


| Injury Evaluation Indices | Experiment | Simulation | Error (%) |
|---|---|---|---|
| 3 ms head resultant acceleration (g) | 64.8 | 59.1 | −8.7 |
| Head resultant acceleration peak (g) | 64.2 | 59.9 | −6.7 |
| 15 ms Head Injury Criterion | 403.7 | 371.1 | −8.1 |
| 3 ms chest resultant acceleration (g) | 35.3 | 40.2 | 13.9 |
| Chest resultant acceleration peak (g) | 36.6 | 41.9 | 14.5 |
| Number | (mm) | (Nm/rad) | (g) | (g) | (kN) | WIC |
|---|---|---|---|---|---|---|
| 1 | 20 | 20,267 | 51.4 | 34.4 | 2.2 | 0.6713 |
| 2 | 25 | 20,267 | 51.3 | 34.3 | 2.19 | 0.6693 |
| 3 | 30 | 20,267 | 51.2 | 34.8 | 2.18 | 0.6701 |
| 4 | 20 | 25,333 | 47.5 | 32.6 | 2.11 | 0.6308 |
| 5 | 25 | 25,333 | 47.6 | 32.5 | 2.10 | 0.6301 |
| 6 | 30 | 25,333 | 48.0 | 32.4 | 2.07 | 0.6295 |
| 7 | 20 | 30,400 | 47.3 | 32.5 | 2.12 | 0.6300 |
| 8 | 25 | 30,400 | 47.6 | 32.4 | 2.10 | 0.6296 |
| 9 | 30 | 30,400 | 47.9 | 32.2 | 2.08 | 0.6288 |
| Project | (g) | (g) | (kN) | (mm) | WIC |
|---|---|---|---|---|---|
| Original model | 59.1 | 40.2 | 2.61 | 285.3 | 0.7819 |
| Final design model | 47.9 | 32.2 | 2.08 | 256.6 | 0.6288 |
| Reduced injury (%) | 18.9 | 19.9 | 20.3 | 10.1 | 19.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Gao, J.; Tu, W. Parameter Study for Child Booster Seats in Frontal Collisions. Appl. Sci. 2023, 13, 2206. https://doi.org/10.3390/app13042206
Zhang X, Gao J, Tu W. Parameter Study for Child Booster Seats in Frontal Collisions. Applied Sciences. 2023; 13(4):2206. https://doi.org/10.3390/app13042206
Chicago/Turabian StyleZhang, Xuerong, Jing Gao, and Wenqiong Tu. 2023. "Parameter Study for Child Booster Seats in Frontal Collisions" Applied Sciences 13, no. 4: 2206. https://doi.org/10.3390/app13042206




