Humic Substances: From Supramolecular Aggregation to Fractal Conformation—Is There Time for a New Paradigm?
Abstract
:1. Introduction
2. Models of the Structure of Humic Substances
2.1. The Micellar Model
2.2. The Supramolecular Aggregate Model
3. Selected Methods and Experimental Approaches for Analysis of HS Structure
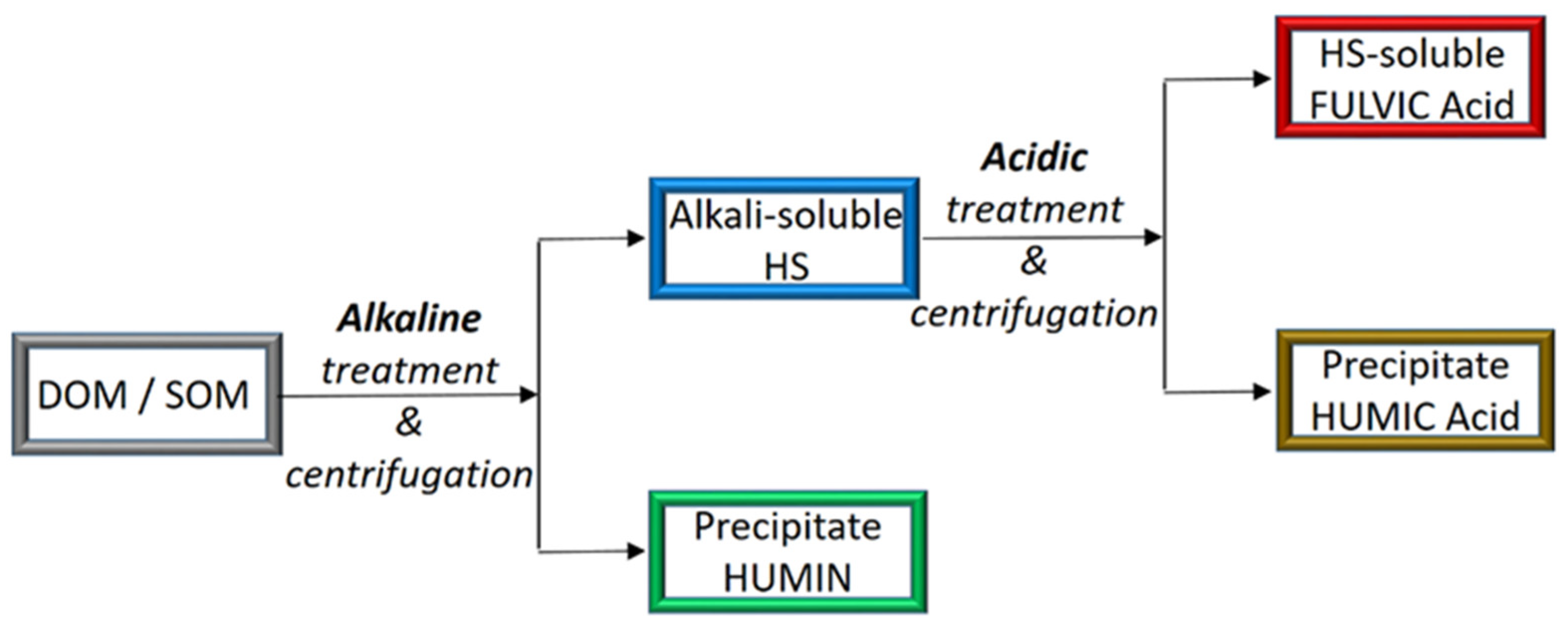
3.1. Extraction and Fractionation of Humic Substances
3.2. Solid State Investigations
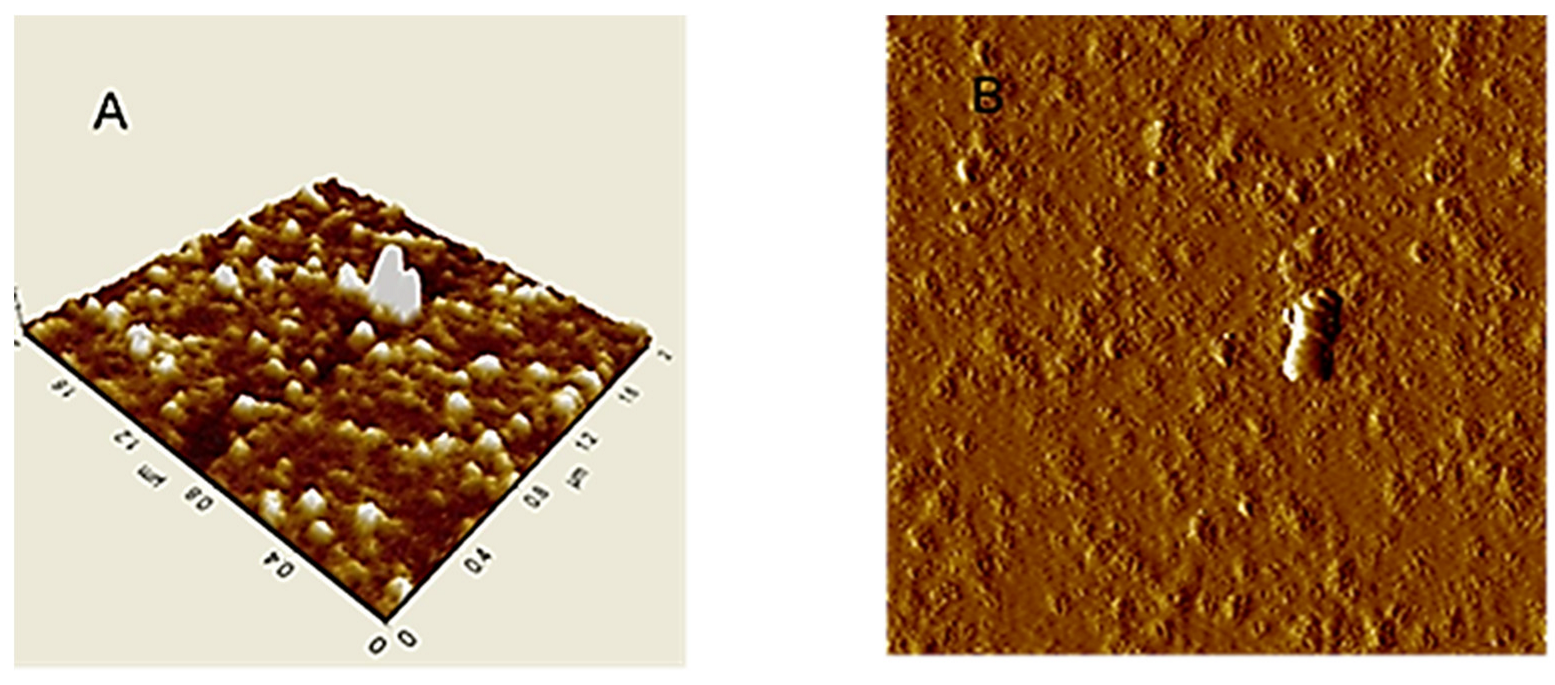
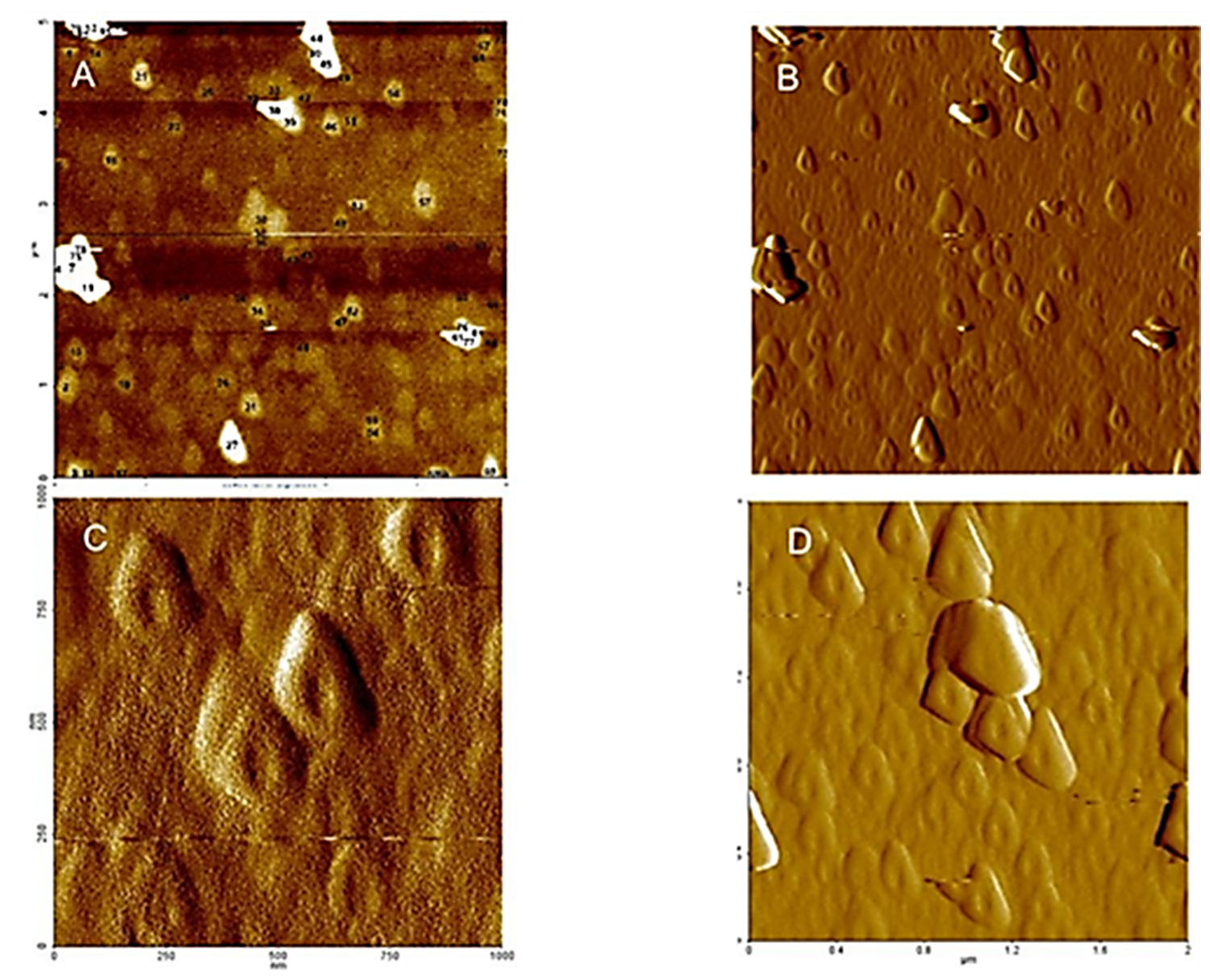
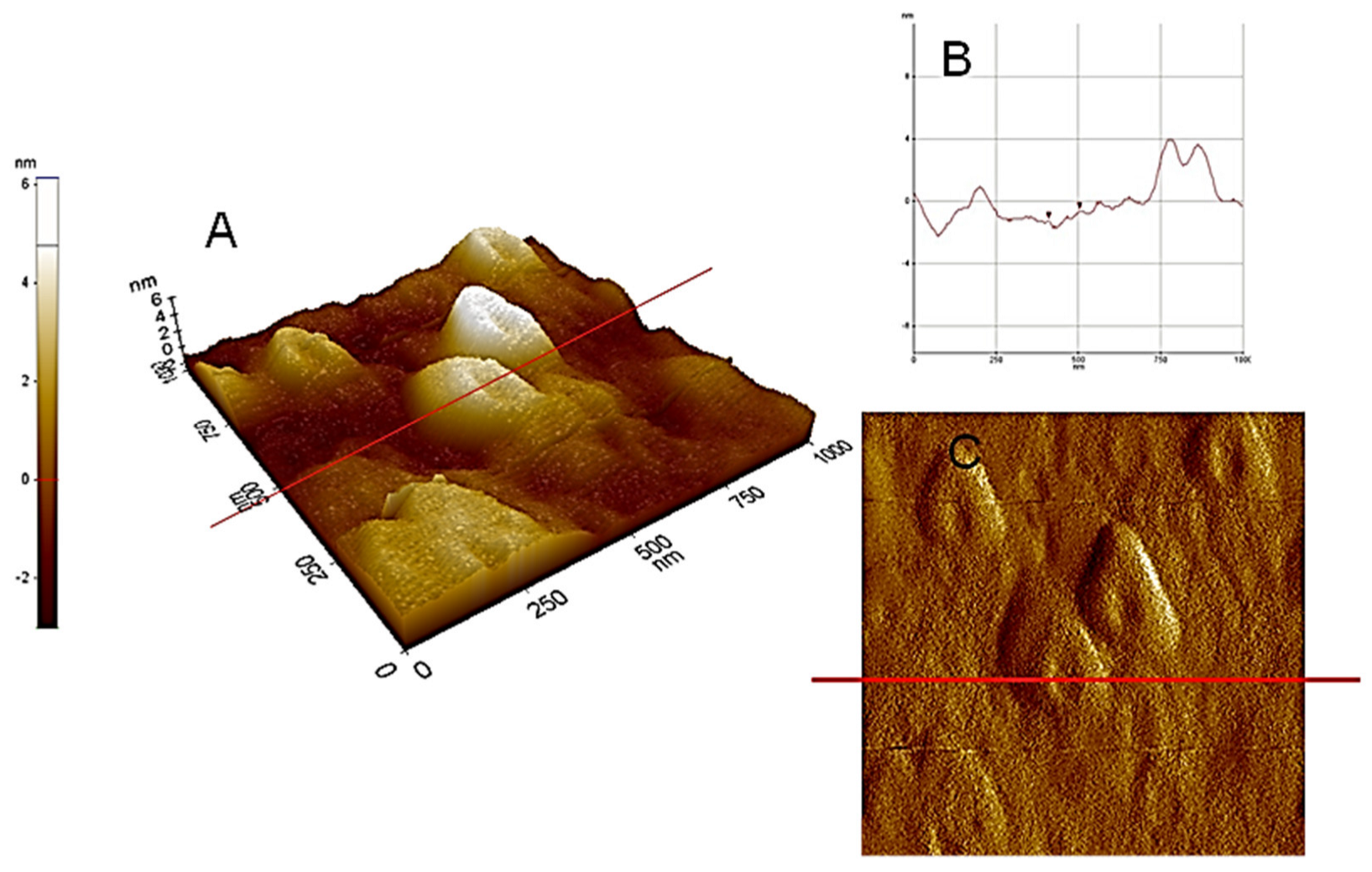
3.2.1. Microscopy Techniques: Scanning Electron Microscopy (SEM), Transmission Electron Microscopy (TEM), Atomic Force Microscopy AFM
3.2.2. Nuclear Magnetic Resonance Techniques
The Limits of the NMR Techniques in Humic Chemistry
NMR Results of Humic Substances
3.3. Liquid State Investigations
3.3.1. Scattering Techniques
Dynamic Light Scattering
Light/X-ray/Neutron Scattering Studies and Fractal Architecture of HS Aggregates
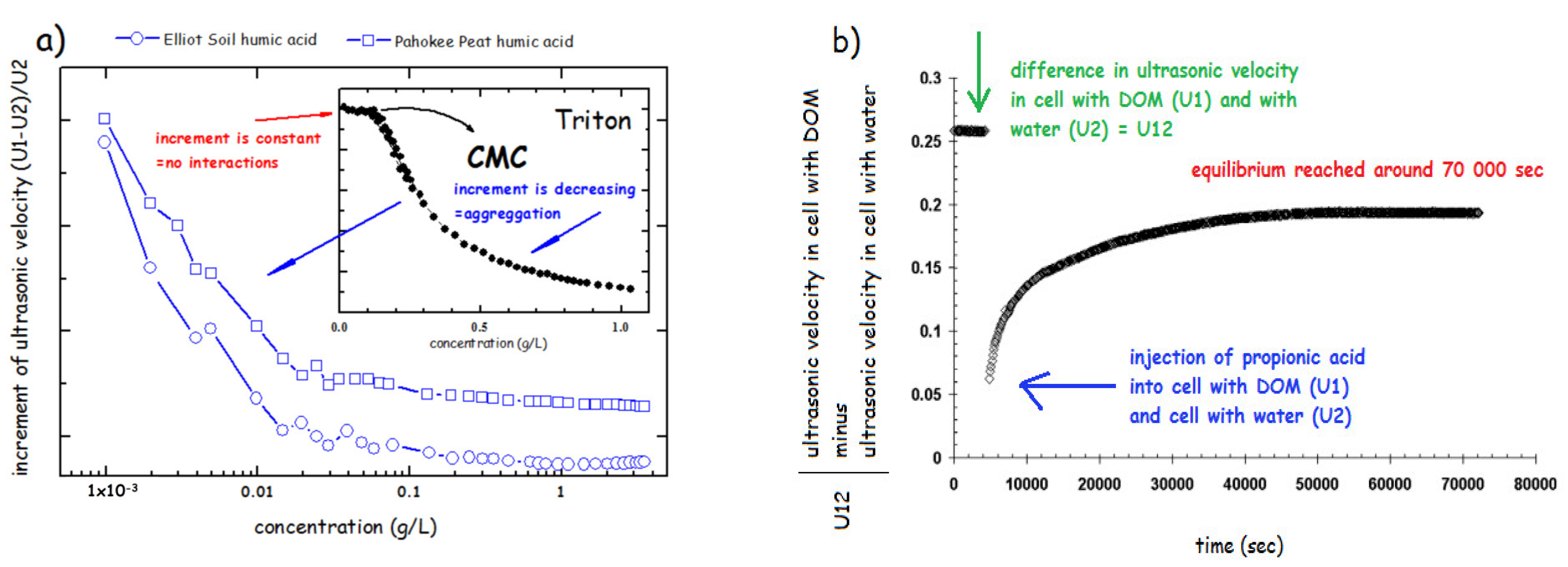
3.3.2. Ultrasonic Velocimetry
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AFM | Atomic Force Microscopy |
| AHA | Aldrich Humic Acid |
| CMC | Critical Micellar Concentration |
| CP | Cross Polarization |
| CZE | Capillary Zone Electrophoresis |
| df | fractal dimension |
| Dh | hydrodynamic particle diameter |
| DLS | Dynamic Light Scattering |
| DSC | Differential Scanning Calorimetry |
| DOC | Dissolved Organic Carbon |
| DOM | Dissolved Organic Matter |
| DOSY | Diffusion Ordered Spectroscopy |
| EHA | Elliot soil Humic Acid |
| FA | Fulvic Acid |
| FCS | Fluorescence Correlation Spectroscopy |
| FFC | Fast Field Cycling |
| GPC | Gel Permeation Chromatography |
| HA | Humic Acid |
| HPSEC | High-Performance Size Exclusion Chromatography |
| HRMAS | High-Resolution Magic Angle Spinning |
| HS | Humic Substances |
| IHSS | International Humic Substances Society |
| LDE | Laser Doppler Electrophoresis |
| MALLS | Multi-Angle Laser Light Scattering |
| MAOM | Mineral-Associated Organic Matter |
| MAS | Magic Angle Spinning |
| Mw | weight-averaged molar mass |
| NOM | Natural Organic Matter |
| NMR | Nuclear Magnetic Resonance |
| PCS | Photon Correlation Spectroscopy |
| PdI | Polydispersity Index |
| PSD | Particle Size Distribution |
| POM | Particulate Organic Matter |
| Rp | Particle Radius |
| Rg | Radius of gyration |
| RLHA | Rendzic Leptosol Humic Acid |
| SANS | Small-Angle Neutron Scattering |
| SAXS | Small-Angle X-ray Scattering |
| SEC | Size Exclusion Chromatography |
| SOM | Soil Organic Matter |
| SRHA | Suwannee River HA |
| SRFA | Suwannee River FA |
| TOC | Total Organic Carbon |
| UF | Ultrafiltration |
References
- Cambardella, C.A.; Elliott, E.T. Particulate Soil Organic-Matter Changes across a Grassland Cultivation Sequence. Soil Sci. Soc. Am. J. 1992, 56, 777–783. [Google Scholar] [CrossRef]
- Zsolnay, A. Dissolved organic matter: Artefacts, definitions, and functions. Geoderma 2003, 113, 187–209. [Google Scholar] [CrossRef]
- Dafner, E.V.; Wangersky, P.J. A brief overview of modern directions in marine DOC studies—Part I. Methodological aspects. J. Environ. Monit. 2002, 4, 48–54. [Google Scholar] [CrossRef] [PubMed]
- Bolan, N.S.; Adriano, D.C.; Kunhikrishnan, A.; James, T.; McDowell, R.; Senesi, N. Dissolved Organic Matter: Biogeochemistry, Dynamics, and Environmental Significance in Soils. Adv. Agron. 2011, 110, 1–75. [Google Scholar] [CrossRef]
- Blaser, P. The role of natural organic matter in the dynamics of metals in forest soils. In Humic Substances in the Global Environment and Implications on Human Health; Senesi, N., Miano, T.M., Eds.; Elsevier: Amsterdam, The Netherlands, 1994; pp. 943–960. [Google Scholar]
- Chiou, C.T.; Malcolm, R.L.; Brinton, T.I.; Kile, D.E. Water solubility enhancement of some organic pollutants and pesticides by dissolved humic and fulvic acids. Environ. Sci. Technol. 1986, 20, 502–508. [Google Scholar] [CrossRef]
- Quagliotto, P.; Montoneri, E.; Tambone, F.; Adani, F.; Gobetto, R.; Viscardi, G. Chemicals from wastes: Compost-derived humic acid-like matter as surfactant. Environ. Sci. Technol. 2006, 40, 1686–1692. [Google Scholar] [CrossRef]
- Guggenberger, G.; Kaiser, K. Dissolved organic matter in soil: Challenging the paradigm of sorptive preservation. Geoderma 2003, 113, 293–310. [Google Scholar] [CrossRef]
- Raulund-Rasmussen, K.; Borggaard, O.K.; Hansen, H.C.B.; Olsson, M. Effect of natural organic soil solutes on weathering rates of soil minerals. Eur. J. Soil Sci. 1998, 49, 397–406. [Google Scholar] [CrossRef]
- Lundström, U.S.; van Breemen, N.; Iongmans, A.G. Evidence for microbial decomposition of organic acids during podzolization. Eur. J. Soil Sci. 1995, 46, 489–496. [Google Scholar] [CrossRef]
- Lu, Y.H.; Wassmann, R.; Neue, H.U.; Huang, C.Y. Dynamics of dissolved organic carbon and methane emissions in a flooded rice soil. Soil Sci. Soc. Am. J. 2000, 64, 2011–2017. [Google Scholar] [CrossRef]
- McDowell, W.H. Dissolved organic matter in soils—Future directions and unanswered questions. Geoderma 2003, 113, 179–186. [Google Scholar] [CrossRef]
- Marschner, B.; Kalbitz, K. Controls of bioavailability and biodegradability of dissolved organic matter in soils. Geoderma 2003, 113, 211–235. [Google Scholar] [CrossRef]
- Kalbitz, K.; Solinger, S.; Park, J.H.; Michalzik, B.; Matzner, E. Controls on the dynamics of dissolved organic matter in soils: A review. Soil Sci. 2000, 165, 277–304. [Google Scholar] [CrossRef]
- Kleber, M.; Lehmann, J. Humic substances extracted by alkali are invalid proxies for the dynamics and functions of organic matter in terrestrial and aquatic ecosystems. J. Environ. Qual. 2019, 48, 207–216. [Google Scholar] [CrossRef]
- Schmidt, M.W.I.; Torn, M.S.; Abiven, S.; Dittmar, T.; Guggenberger, G.; Janssens, I.A.; Kleber, M.; Kögel-Knabner, I.; Lehmann, J.; Manning, D.A.; et al. Persistence of soil organic matter as an ecosystem property. Nature 2011, 478, 49–56. [Google Scholar] [CrossRef]
- Li, Y.; Fang, F.; Wei, J.; Wu, X.; Cui, R.; Li, G.; Zheng, F.; Tan, D. Humic acid fertilizer improved soil properties and soil microbial diversity of continuous cropping peanut: A three-year experiment. Sci. Rep. 2019, 9, 12014. [Google Scholar] [CrossRef]
- Rullkötter, J. Geochemistry Organic. In Encyclopedia of Physical Science and Technology; Meyers, R.A., Ed.; Academic Press: New York, NY, USA, 2003; pp. 549–574. [Google Scholar] [CrossRef]
- Knicker, H. How does fire affect the nature and stability of soil organic nitrogen and carbon? A review. Biogeochemistry 2007, 85, 91–118. [Google Scholar] [CrossRef]
- Gerke, J. Concepts and misconceptions of humic substances as the stable part of soil organic matter: A review. Agronomy 2018, 8, 76–91. [Google Scholar] [CrossRef]
- Di Iorio, E.; Circelli, L.; Angelico, R.; Torrent, J.; Tan, W.; Colombo, C. Environmental implications of interaction between humic substances and iron oxide nanoparticles: A review. Chemosphere 2022, 303, 135172–135183. [Google Scholar] [CrossRef]
- Cotrufo, M.F.; Ranalli, M.G.; Haddix, M.L.; Six, J.; Lugato, E. Soil carbon storage informed by particulate and mineral-associated organic matter. Nat. Geosci. 2019, 12, 989–994. [Google Scholar] [CrossRef]
- Sanderman, J.; Maddern, T.; Baldock, J. Similar composition but differential stability of mineral retained organic matter across four classes of clay minerals. Biogeochemistry 2014, 121, 409–424. [Google Scholar] [CrossRef]
- Lehmann, J.; Kinyangi, J.; Solomon, D. Organic matter stabilization in soil microaggregates: Implications from spatial heterogeneity of organic carbon contents and carbon forms. Biogeochemistry 2007, 85, 45–57. [Google Scholar] [CrossRef]
- Keiluweit, M.; Bougoure, J.J.; Nico, P.S.; Pett-Ridge, J.; Weber, P.K.; Kleber, M. Mineral protection of soil carbon counteracted by root exudates. Nat. Climate Change 2015, 5, 588–595. [Google Scholar] [CrossRef]
- Lehmann, J.; Kleber, M. The contentious nature of soil organic matter. Nature 2015, 528, 60–68. [Google Scholar] [CrossRef] [PubMed]
- Woolf, D.; Lehmann, J. Microbial models with minimal mineral protection can explain long-term soil organic carbon persistence. Sci. Rep. 2019, 9, 6522. [Google Scholar] [CrossRef]
- Baveye, P.C.; Wander, M. The (bio)chemistry of soil humus and humic substances: Why is the “new view” still considered novel after more than 80 years? Front. Environ. Sci. 2019, 7, 27–32. [Google Scholar] [CrossRef]
- Janzen, H. The Future of Humic Substances Research: Preface to a Debate. J. Environ. Qual. 2019, 48, 205–206. [Google Scholar] [CrossRef]
- Olk, D.C.; Bloom, P.R.; De Nobili, M.; Chen, Y.; McKnight, D.M.; Wells, M.J.M.; Weber, J. Using Humic Fractions to Understand Natural Organic Matter Processes in Soil and Water: Selected Studies and Applications. J. Environ. Qual. 2019, 48, 1633–1643. [Google Scholar] [CrossRef]
- Nobili, M.; Bravo, C.; Chen, Y. The spontaneous secondary synthesis of soil organic matter components: A critical examination of the soil continuum model theory. Appl. Soil Ecol. 2020, 154, 103655. [Google Scholar] [CrossRef]
- Ghosh, K.; Schnitzer, M. Macromolecular structures of humic substances. Soil Sci. 1980, 129, 266–276. [Google Scholar] [CrossRef]
- Marinsky, J.A.; Reddy, M.M. Vapor-pressure osmometric study of the molecular weight and aggregation tendency of a reference-soil fulvic acid. Anal. Chim. Acta 1990, 232, 123–130. [Google Scholar] [CrossRef]
- Swift, R.S.; Posner, A.M. Gel chromatography of humic acids. J. Soil Sci. 1971, 22, 237–249. [Google Scholar] [CrossRef]
- Swift, R.S. Macromolecular properties of soil humic substances: Fact, fiction, and opinion. Soil Sci. 1999, 164, 790–802. [Google Scholar] [CrossRef]
- Chin, W.C.; Orellana, M.; Verdugo, P. Spontaneous assembly of marine dissolved organic matter into polymer gels. Nature 1998, 391, 568–572. [Google Scholar] [CrossRef]
- Wershaw, R.L. A new model for humic materials and their interactions with hydrophobic organic chemicals in soil-water or sediment-water systems. J. Contam. Hydrol. 1986, 1, 29–45. [Google Scholar] [CrossRef]
- Wershaw, R.L. Model for humus in soils and sediments. Environ. Sci. Technol. 1993, 27, 814–817. [Google Scholar] [CrossRef]
- Wershaw, R.L. Molecular aggregation of humic substances. Soil Sci. 1999, 164, 803–813. [Google Scholar] [CrossRef]
- Guetzloff, T.F.; Rice, J.A. Does humic acid form a micelle? Sci. Tot. Environ. 1994, 152, 31–35. [Google Scholar] [CrossRef]
- Guetzloff, T.F.; Rice, J.A. Micellar nature of humic colloids. In Humic and Fulvic Acids: Isolation, Structure, and Environmental Role; Chapter 2; Gaffney, J.S., Marley, N.A., Clark, S.B., Eds.; ACS Symposium Series 651; American Chemical Society: Washington, DC, USA, 1996. [Google Scholar] [CrossRef]
- Engebretson, R.R.; von Wandruszka, R. Microorganization in dissolved humic acids. Environ. Sci. Technol. 1994, 28, 1934–1941. [Google Scholar] [CrossRef]
- Puchalskl, M.M.; Morra, M.J.; von Wandruszka, R. Fluorescence quenching of synthetic organic compounds by humic materials. Environ. Sci. Technol. 1992, 26, 1787–1792. [Google Scholar] [CrossRef]
- von Wandruszka, R.; Ragle, C.; Engebretson, R. The role of selected cations in the formation of pseudomicelles in aqueous humic acid. Talanta 1997, 44, 805–809. [Google Scholar] [CrossRef]
- von Wandruszka, R. The micellar model of humic acid: Evidence from pyrene fluorescence measurements. Soil Sci. 1998, 163, 921–930. [Google Scholar] [CrossRef]
- von Wandruszka, R.; Engebretson, R. Kinetics of humic acid associations. In Humic Substances and Chemical Contaminants; Clapp, C.E., Hayes, M.H.B., Senesi, N., Bloom, P.R., Jardine, P.M., Eds.; Soil Science Society of America: Madison, WI, USA, 2001. [Google Scholar] [CrossRef]
- Kučerík, J.; Šmejkalová, D.; Čechlovská, H.; Pekař, M. New insights into aggregation and conformational behaviour of humic substances: Application of high resolution ultrasonic spectroscopy. Org. Geochem. 2007, 38, 2098–2110. [Google Scholar] [CrossRef]
- Piccolo, A.; Nardi, S.; Concheri, G. Micelle-like conformation of humic substances as revealed by size exclusion chromatography. Chemosphere 1996, 33, 595–602. [Google Scholar] [CrossRef] [PubMed]
- Peuravuori, J.; Pihlaja, K. Molecular size distribution and spectroscopic properties of aquatic humic substances. Anal. Chim. Acta 1997, 337, 133–149. [Google Scholar] [CrossRef]
- Fetsch, D.; Hradilová, M.; Peña-Méndez, E.M.; Havel, J. Capillary zone electrophoresis study of humic substances aggregation. J. Chromatogr. A 1998, 817, 313–323. [Google Scholar] [CrossRef]
- Jones, M.N.; Bryan, N.D. Colloidal properties of humic substances. Adv. Colloid. Interface Sci. 1998, 78, 1–48. [Google Scholar] [CrossRef]
- Conte, P.; Piccolo, A. Conformational arrangement of dissolved humic substances. Influence of solution composition on association of humic molecules. Environ. Sci. Technol. 1999, 33, 1682–1690. [Google Scholar] [CrossRef]
- Piccolo, A.; Conte, P.; Cozzolino, A. Effects of mineral and monocarboxylic acids on the molecular association of dissolved humic substances. Eur. J. Soil Sci. 1999, 50, 687–694. [Google Scholar] [CrossRef]
- Varga, B.; Kiss, G.; Galambos, I.; Gelencser, A.; Hlavay, J.; Krivacsy, Z. Secondary structure of humic acids. Can micelle-like conformation be proved by aqueous size exclusion chromatography? Environ. Sci. Technol. 2000, 34, 3303–3306. [Google Scholar] [CrossRef]
- Young, C.; von Wandruszka, R. A comparison of aggregation behavior in aqueous humic acids. Geochem. Trans. 2001, 2, 16–20. [Google Scholar] [CrossRef]
- Piccolo, A. The supramolecular structure of humic substances. Soil Sci. 2001, 166, 810–832. [Google Scholar] [CrossRef]
- Sutton, R.; Sposito, G. Molecular structure in soil humic substances: The new view. Environ. Sci. Technol. 2005, 39, 9009–9015. [Google Scholar] [CrossRef]
- Yates, L.M.; von Wandruska, R. Effects of pH and metals on the surface tension of aqueous humic materials. J. Soil Sci. Soc. Am. 1999, 63, 1645–1649. [Google Scholar] [CrossRef]
- Senesi, N.; Lorusso, G.F.; Miano, T.M.; Maggipinto, G.; Rizzi, F.R.; Capozzi, V. The fractal dimension of humic substances as function of pH by turbidity measurements. In Humic Substances in the Global Environment and Implications on Human Health; Senesi, N., Miano, T.M., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1994; pp. 121–126. [Google Scholar]
- Piccolo, A. The supramolecular structure of humic substances: A novel understanding of humus chemistry and implications in soil science. Adv. Agron. 2002, 75, 57–133. [Google Scholar] [CrossRef]
- Piccolo, A. In memoriam Prof. F.J. Stevenson and the question of humic substances in soil. Chem. Biol. Technol. Agric. 2016, 3, 23–25. [Google Scholar] [CrossRef]
- Baigorri, R.; Fuentes, M.; González-Gaitano, G.; García-Mina, J.M. Analysis of molecular aggregation in humic substances in solution. Colloids Surf. A Physicochem. Eng. Asp. 2007, 302, 301–306. [Google Scholar] [CrossRef]
- Baigorri, R.; Fuentes, M.; González-Gaitano, G.; García-Mina, J.M. Simultaneous presence of diverse molecular patterns in humic substances in solution. J. Phys. Chem. B 2007, 111, 10577–10582. [Google Scholar] [CrossRef]
- Nebbioso, A.; Piccolo, A. Basis of a humeomics science: Chemical fractionation and molecular characterization of humic biosuprastructures. Biomacromolecules 2011, 12, 1187–1199. [Google Scholar] [CrossRef]
- Chilom, G.; Bruns, A.S.; Rice, J.A. Aggregation of humic acid in solution: Contributions of different fractions. Org. Geochem. 2009, 40, 455–460. [Google Scholar] [CrossRef]
- Chilom, G.; Rice, J.A. Structural organization of humic acid in the solid state. Langmuir 2009, 25, 9012–9015. [Google Scholar] [CrossRef] [PubMed]
- Chilom, G.; Baglieri, A.; Johnson-Edler, C.A.; Rice, J.A. Hierarchical self-assembling properties of natural organic matter’s components. Org. Geochem. 2013, 57, 119–126. [Google Scholar] [CrossRef]
- Zheng, G.; Price, W.S. Direct hydrodynamic radius measurement on dissolved organic matter in natural waters using diffusion NMR. Environ. Sci. Technol. 2012, 46, 1675–1680. [Google Scholar] [CrossRef] [PubMed]
- Drastík, M.; Novak, F.; Kučerík, J. Origin of heat-induced structural changes in dissolved organic matter. Chemosphere 2013, 90, 789–795. [Google Scholar] [CrossRef]
- Kučerík, J.; Čechlovská, H.; Bursáková, P.; Pekař, M. Lignite humic acids aggregates studied by high resolution ultrasonic spectroscopy: Thermodynamic stability and molecular feature. J. Therm. Anal. Calorim. 2009, 96, 637–643. [Google Scholar] [CrossRef]
- Conte, P.; Kučerík, J. Water dynamics and its role in structural hysteresis of dissolved organic matter. Environ. Sci. Technol. 2016, 50, 2210–2216. [Google Scholar] [CrossRef]
- Wells, M.J.M. Supramolecular answers to the organic matter controversy. J. Environ. Qual. 2019, 48, 1644–1651. [Google Scholar] [CrossRef]
- Wells, M.J.M.; Stretz, H.A. Supramolecular architectures of natural organic matter. Sci. Tot. Environ. 2019, 671, 1125–1133. [Google Scholar] [CrossRef]
- Esfahani, M.R.; Stretz, H.A.; Wells, M.J.M. Abiotic reversible self-assembly of fulvic and humic acid aggregates in low electrolytic conductivity solutions by dynamic light scattering and zeta potential investigation. Sci. Total Environ. 2015, 537, 81–92. [Google Scholar] [CrossRef]
- Stevenson, F.J. Humus Chemistry: Genesis, Composition, Reactions, 2nd ed.; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Wang, H.; Adeleye, A.S.; Huang, Y.; Li, F.; Keller, A.A. Heteroaggregation of nanoparticles with biocolloids and geocolloids. Adv. Colloid Interface Sci. 2015, 226, 24–36. [Google Scholar] [CrossRef]
- Leenheer, J.A.; Croué, J.-P. Peer reviewed: Characterizing aquatic dissolved organic matter. Environ. Sci. Technol. 2003, 37, 18A–26A. [Google Scholar] [CrossRef]
- Ohno, T.; Hess, N.J.; Qafoku, N.P. Current understanding of the use of alkaline extractions of soils to investigate soil organic matter and environmental processes. J. Environ. Qual. 2019, 48, 1561–1564. [Google Scholar] [CrossRef]
- Hatcher, P.G.; Waggoner, D.C.; Chen, H. Evidence for the existence of humic acids in peat soils based on solid-state 13C NMR. J. Environ. Qual. 2019, 48, 1571–1577. [Google Scholar] [CrossRef]
- Olk, D.C.; Bloom, P.R.; Perdue, E.M.; McKnight, D.M.; Chen, Y.; Farenhorst, A.; Senesi, N.; Chin, Y.-P.; Schmitt-Kopplin, P.; Hertkorn, N.; et al. Environmental and agricultural relevance of humic fractions extracted by alkali from soils and natural waters. J. Environ. Qual. 2019, 48, 217–232. [Google Scholar] [CrossRef]
- Seaman, J.C. Thin-foil SEM analysis of soil and groundwater colloids: Reducing instrument and operator bias. Environ. Sci. Tech. 2000, 34, 187–191. [Google Scholar] [CrossRef]
- Lead, J.R.; Muirhead, D.; Gibson, C.T. Characterization of freshwater natural aquatic colloids by Atomic Force Microscopy (AFM). Environ. Sci. Technol. 2005, 39, 6930–6936. [Google Scholar] [CrossRef]
- Chen, Y.; Schnitzer, M. Sizes and shapes of humic substances by electron microscopy. In Humic Substances II. In Search of Structure; Hayes, M.H.B., MacCarthy, P., Malcolm, R.L., Swift, R.S., Eds.; Wiley-Interscience: Chichester, UK, 1989; pp. 621–638. [Google Scholar]
- Senesi, N.; Rizzi, F.R.; Dellino, P.; Acquafredda, P. Fractal dimension of humic acids in aqueous suspension as a function of pH and time. J. Soil. Sci. Soc. Am. 1996, 60, 1773–1780. [Google Scholar] [CrossRef]
- Senesi, N.; Rizzi, F.R.; Dellino, P.; Acquafredda, P. Fractal humic acids in aqueous suspensions at various concentrations, ionic strengths, and pH values. Colloids Surf. A 1997, 127, 57–68. [Google Scholar] [CrossRef]
- Rizzi, F.R.; Stoll, S.; Senesi, N.; Buffle, J. A transmission electron microscopy study of the fractal properties and aggregation processes of humic acids. Soil Sci. 2004, 169, 765–775. [Google Scholar] [CrossRef]
- Shevchenko, S.M.; Bailey, G.W.; Akim, L.G. The conformational dynamics of humic polyanions in model organic and organo-mineral aggregates. J. Mol. Struct. 1999, 460, 179–190. [Google Scholar] [CrossRef]
- Chen, Y.; Schnitzer, M. Scanning electron microscopy of a humic acid and its metal and clay complexes. Soil Sci. Soc. Am. J. 1976, 40, 682–686. [Google Scholar] [CrossRef]
- Ikai, A.; Österberg, R. Atomic force microscopy of humic acids. Scanning Microsc. 1996, 10, 947–951. [Google Scholar]
- Baalousha, M.; Motelica-Heino, M.; Galaup, S.; Coustumer, P. Supramolecular structure of humic acids by TEM with improved sample preparation and staining. Microsc. Res. Tech. 2005, 66, 299–306. [Google Scholar] [CrossRef] [PubMed]
- Heath, G.R.; Scheuring, S. High-speed AFM height spectroscopy reveals μs-dynamics of unlabeled biomolecules. Nat. Commun. 2018, 9, 4983–4993. [Google Scholar] [CrossRef]
- Baalousha, M.; Prasad, A.; Lead, J.R. Quantitative measurement of the nanoparticle size and number concentration from liquid suspensions by atomic force microscopy. Environ. Sci. Processes Impacts 2014, 16, 1338–1347. [Google Scholar] [CrossRef]
- Heath, G.R.; Kots, E.; Robertson, J.L.; Lansky, S.; Khelashvili, G.; Weinstein, H.; Scheuring, S. Localization atomic force microscopy. Nature 2021, 594, 385–390. [Google Scholar] [CrossRef]
- Cheng, S.; Bryant, R.; Doerr, S.H.; Williams, P.R.; Wright, C.J. Application of atomic force microscopy to the study of natural and model soil particles. J. Microsc. 2008, 231, 384–394. [Google Scholar] [CrossRef]
- Copello, F.D.R.; Lizarraga, L.; Orsetti, S.; Molina, F.V. Swelling and aggregation of Leonardite upon pH change and Pb II binding: An AFM study. Environ. Chem. 2018, 15, 162–170. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Zhou, T.-T.; Wang, C.-l.; Liu, H.-Y.; Zhang, C.-T.; Hu, F.-N.; Zhao, S.-W.; Geng, Z.-C. Aggregation of polydisperse soil colloidal particles: Dependence of Hamaker constant on particle size. Geoderma 2020, 359, 113999–114007. [Google Scholar] [CrossRef]
- Colombo, C.; Palumbo, G.; Angelico, R.; Cho, H.G.; Francioso, O.; Ertani, A.; Nardi, S. Spontaneous aggregation of humic acid observed with AFM at different pH. Chemosphere 2015, 138, 821–828. [Google Scholar] [CrossRef]
- Balnois, E.; Wilkinson, K.J.; Lead, J.; Buffle, J. Atomic force microscopy of humic substances: Effects of pH and ionic strength. Environ. Sci. Technol. 1999, 33, 3911–3917. [Google Scholar] [CrossRef]
- Chen, C.L.; Wang, X.K.; Jiang, H.W.P.; Hu, W.P. Direct observation of macromolecular structures of humic acid by AFM and SEM. Colloid Surf. A 2007, 302, 121–125. [Google Scholar] [CrossRef]
- Liu, A.G.; Wu, R.C.; Eschenazi, E.; Papadopoulos, K. AFM on humic acid adsorption on mica. Colloid Surf. A Physicochem. Eng. Asp. 2000, 174, 245–252. [Google Scholar] [CrossRef]
- Schaumann, G.E.; Thiele-Bruhn, S. Molecular modeling of soil organic matter: Squaring the circle? Geoderma 2011, 166, 1–14. [Google Scholar] [CrossRef]
- Plaschke, M.; Römer, J.; Klenze, R.; Kim, J.I. In situ AFM study of sorbed humic acid colloids at different pH. Colloids Surf. A 1999, 160, 269–279. [Google Scholar] [CrossRef]
- Plaschke, M.; Romer, J.; Kim, J.I. Characterization of Gorleben groundwater colloids by atomic force microscopy. Environ. Sci. Technol. 2002, 36, 4483–4488. [Google Scholar] [CrossRef]
- Conte, P.; Spaccini, R.; Piccolo, A. State of the art of CPMAS 13C-NMR spectroscopy applied to natural organic matter. Prog. Nucl. Magn. Reson. Spectrosc. 2004, 44, 215–223. [Google Scholar] [CrossRef]
- Dais, P.; Spyros, A. Nuclear magnetic resonance. In Chemical Analysis of Food: Techniques and Applications; Picó, Y., Ed.; Academic Press-Elsevier: Waltham, MA, USA, 2012; pp. 91–115. [Google Scholar]
- Simpson, A.J.; Simpson, M.J.; Soong, R. Nuclear magnetic resonance spectroscopy and its key role in environmental research. Environ. Sci. Technol. 2012, 46, 11488–11496. [Google Scholar] [CrossRef]
- Farooq, H.; Courtier-Murias, D.; Soong, R.; Bermel, W.; Kingery, W.; Simpson, A. HR-MAS NMR spectroscopy: A practical guide for natural samples. Curr. Org. Chem. 2013, 17, 3013–3031. [Google Scholar] [CrossRef]
- Conte, P.; Lo Meo, P. Nuclear magnetic resonance with fast field-cycling setup: A valid tool for soil quality investigation. Agronomy 2020, 10, 1040–1072. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Oxford University Press: New York, NY, USA, 1983. [Google Scholar]
- Rinaldi, P.L. Three-dimensional solution NMR spectroscopy of complex structures and mixtures. Analyst 2004, 129, 687–699. [Google Scholar] [CrossRef] [PubMed]
- Fuloria, N.K.; Fuloria, S. Structural elucidation of small organic molecules by 1D, 2D and multi-dimensional-solution NMR spectroscopy. J. Anal. Bioanal. Tech. 2013, 4, 1–8. [Google Scholar] [CrossRef]
- Berns, A.E.; Conte, P. Effect of rf field inhomogeneity and sample restriction on spectral resolution of CP/MAS- 13C NMR spectra of natural organic matter. Open Magn. Reson. J. 2010, 3, 75–83. [Google Scholar] [CrossRef]
- Berns, A.E.; Conte, P. Effect of ramp size and sample spinning speed on CP/MAS- 13C NMR spectra of soil organic matter. Org. Geochem. 2011, 42, 926–935. [Google Scholar] [CrossRef]
- Borgia, G.C.; Brown, R.J.S.; Fantazzini, P. Uniform-penalty inversion of multiexponential decay data. J. Magn. Reson. 1998, 132, 65–77. [Google Scholar] [CrossRef]
- Borgia, G.C.; Brown, R.J.S.; Fantazzini, P. Uniform-penalty inversion of multiexponential decay data: II. Data spacing, T2 data, systematic data errors, and diagnostics. J. Magn. Reson. 2000, 147, 273–285. [Google Scholar] [CrossRef]
- Borgia, G.C.; Brown, R.J.S.; Fantazzini, P. Examples of marginal resolution of NMR relaxation peaks using UPEN and diagnostics. Magn. Reson. Imaging 2001, 19, 473–475. [Google Scholar] [CrossRef]
- Bortolotti, V.; Brown, R.J.S.; Fantazzini, P.; Landi, G.; Zama, F. Uniform Penalty inversion of two-dimensional NMR relaxation data. Inverse Probl. 2016, 33, 015003–015021. [Google Scholar] [CrossRef] [Green Version]
- Bortolotti, V.; Brown, R.J.S.; Fantazzini, P.; Landi, G.; Zama, F. I2DUPEN: Improved 2DUPEN algorithm for inversion of two-dimensional NMR data. Microporous Mesoporous Mater. 2018, 269, 195–198. [Google Scholar] [CrossRef]
- Conte, P. Applications of fast field cycling NMR relaxometry. Annu. Rep. NMR Spectrosc. 2021, 104, 141–188. [Google Scholar] [CrossRef]
- Anoardo, E.; Galli, G.; Ferrante, G. Fast-Field-Cycling NMR: Applications and Instrumentation. Appl. Magn. Reson. 2001, 20, 365–404. [Google Scholar] [CrossRef]
- Conte, P.; Piccolo, A.; van Lagen, B.; Buurman, P.; de Jager, P.A. Quantitative differences in evaluating soil humic substances by liquid- and solid-state 13C-NMR spectroscopy. Geoderma 1997, 80, 339–352. [Google Scholar] [CrossRef]
- Simpson, A.J.; Kingery, W.L.; Hayes, M.H.B.; Spraul, M.; Humpfer, E.; Dvortsak, P.; Kerssebaum, R.; Godejohann, M.; Hofman, M. Molecular structure and associations of humic substances in the terrestrial environment. Naturwissenschaften 2002, 89, 84–88. [Google Scholar] [CrossRef]
- Hakim, A.; Suzuki, T.; Kobayashi, M. Strength of humic acid aggregates: Effects of divalent cations and solution pH. ACS Omega 2019, 4, 8559−8567. [Google Scholar] [CrossRef]
- Mao, J.; Chen, N.; Cao, X. Characterization of humic substances by advanced solid state NMR spectroscopy: Demonstration of a systematic approach. Org. Geochem. 2011, 42, 891–902. [Google Scholar] [CrossRef]
- Conte, P.; Berns, A.E. Dynamics of cross polarization in solid state nuclear magnetic resonance experiments of amorphous and heterogeneous natural organic substances. Anal. Sci. 2008, 24, 1183–1188. [Google Scholar] [CrossRef]
- Simpson, A.J.; Simpson, M.J. Nuclear Magnetic Resonance Analysis of Natural Organic Matter. In Biophysico-Chemical Processes Involving Natural Nonliving Organic Matter in Environmental Systems; Senesi, N., Xing, B., Huang, P.M., Eds.; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2009; pp. 589–650. [Google Scholar]
- Hu, Y.F.; Cheng, K.; He, L.C.; Zhang, X.; Jiang, B.; Jiang, L.; Li, C.G.; Wang, G.; Yang, Y.H.; Liu, M.L. NMR-Based Methods for Protein Analysis. Anal. Chem. 2021, 93, 1866–1879. [Google Scholar] [CrossRef]
- Yao, H.Y.; Wang, J.Q.; Yin, J.Y.; Nie, S.P.; Xie, M.Y. A review of NMR analysis in polysaccharide structure and conformation: Progress, challenge and perspective. Food Res. Int. 2021, 143, 110290–110308. [Google Scholar] [CrossRef]
- Lehmann, J.; Solomon, D.; Kinyangi, J.; Dathe, L.; Wirick, S.; Jacobsen, C. Spatial complexity of soil organic matter forms at nanometre scales. Nat. Geosci. 2008, 1, 238–242. [Google Scholar] [CrossRef]
- Zhou, J.L. Sampling of humic and colloidal phases in liquid samples. In Comprehensive Sampling and Sample Preparation: Analytical Techniques for Scientists; Pawliszyn, J., Ed.; Academic Press: Waltham, MA, USA, 2012; Volume 1, pp. 335–348. [Google Scholar] [CrossRef]
- Goldburg, W.I. Dynamic light scattering. Am. J. Phys. 1999, 67, 1152–1160. [Google Scholar] [CrossRef]
- Braun, J.; Renggli, K.; Razumovitch, J.; Vebert, C. Dynamic light scattering in supramolecular materials chemistry. In Supramolecular Chemistry: From Molecules to Nanomaterials, 1st ed.; Gale, P.A., Steed, J.W., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2012; pp. 1–14. [Google Scholar] [CrossRef]
- Hassan, P.A.; Rana, S.; Verma, G. Making sense of Brownian motion: Colloid characterization by dynamic light scattering. Langmuir 2015, 31, 3–12. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, S. DLS and zeta potential—What they are and what they are not? J. Control. Release 2016, 235, 337–351. [Google Scholar] [CrossRef] [PubMed]
- Reid, P.M.; Wilkinson, A.E.; Tipping, E.; Jones, M.N. Aggregation of humic substances in aqueous media as determined by light-scattering methods. Soil Sci. 1991, 42, 259–270. [Google Scholar] [CrossRef]
- Pinheiro, J.P.; Mota, A.M.; d’Oliveira, J.M.R.; Martinho, J.M.G. Dynamic properties of humic matter by dynamic light scattering and voltammetry. Anal. Chim. Acta 1996, 329, 15–24. [Google Scholar] [CrossRef]
- Ren, S.-Z.; Tombàcz, E.; Rice, J.A. Dynamic light scattering from fractals in solution: Application of dynamic scaling theory to humic acid. Phys. Rev. E 1996, 53, 2980–2983. [Google Scholar] [CrossRef]
- Martin, J.E.; Leyvraz, F. Quasielastic-scattering linewidths and relaxation times for surface and mass fractals. Phys. Rev. A 1986, 34, 2346–2350. [Google Scholar] [CrossRef]
- International Humic Substances Society. IHSS. Available online: www.humicsubstances.org (accessed on 29 January 2023).
- Palmer, N.E.; von Wandruszka, R. Dynamic light scattering measurements of particle size development in aqueous humic materials. Fresenius J. Anal. Chem. 2001, 371, 951–954. [Google Scholar] [CrossRef]
- Hosse, M.; Wilkinson, K.J. Determination of electrophoretic mobilities and hydrodynamic radii of three humic substances as a function of pH and ionic Strength. Environ. Sci. Technol. 2001, 35, 4301–4306. [Google Scholar] [CrossRef]
- Avena, M.J.; Vermeer, A.W.P.; Koopal, L.K. Volume and structure of humic acids studied by viscometry pH and electrolyte concentration effects. Colloids Surf. A 1999, 151, 213–224. [Google Scholar] [CrossRef]
- Alvarez-Puebla, R.A.; Garrido, J. Effect of pH on the aggregation of a gray humic acid in colloidal and solid states. Chemosphere 2005, 59, 659–667. [Google Scholar] [CrossRef]
- Baalousha, M.; Motelica-Heino, M.; Coustumer, P.L. Conformation and size of humic substances: Effects of major cation concentration and type, pH, salinity, and residence time. Colloids Surf. A Physicochem. Eng. Asp. 2006, 272, 48–55. [Google Scholar] [CrossRef]
- Verdugo, P.; Santschi, P.H. Polymer dynamics of DOC networks and gel formation in seawater. Deep-Sea Res. II 2010, 57, 1486–1493. [Google Scholar] [CrossRef]
- Verdugo, P. Marine microgels. Annu. Rev. Mar. Sci. 2012, 4, 375–400. [Google Scholar] [CrossRef] [PubMed]
- Jovanović, U.D.; Marković, M.M.; Cupać, S.B.; Tomic, Z.P. Soil humic acid aggregation by dynamic light scattering and laser Doppler electrophoresis. J. Plant Nutr. Soil Sci. 2013, 176, 674–679. [Google Scholar] [CrossRef]
- Angelico, R.; Ceglie, A.; He, J.-Z.; Liu, Y.-R.; Palumbo, G.; Colombo, C. Particle size, charge and colloidal stability of humic acids coprecipitated with ferrihydrite. Chemosphere 2014, 99, 239–247. [Google Scholar] [CrossRef]
- Tarasevich, Y.I.; Tryfonova, M.Y.; Dolenko, S.A.; Aksenenko, E.V. Adsorption-based approach to determine the size and mass of humic acids molecules. Adsorpt. Sci. Technol. 2016, 34, 125–133. [Google Scholar] [CrossRef]
- Dolenko, S.A.; Trifonova, M.Y.; Tarasevich, Y.I. Aqueous solutions of humic acids as self-organizing dissipative systems. J. Water Chem. Technol. 2017, 39, 360–367. [Google Scholar] [CrossRef]
- Klučáková, M.; Kalina, M. Composition, particle size, charge and colloidal stability of pH-fractionated humic acids. J. Soil Sediment 2015, 15, 1900–1908. [Google Scholar] [CrossRef]
- Klučáková, M. Characterization of pH-fractionated humic acids with respect to their dissociation behaviour. Environ. Sci. Pollut. Res. 2016, 23, 7722–7731. [Google Scholar] [CrossRef]
- Klučáková, M.; Věžníková, K. The role of concentration and solvent character in the molecular organization of humic acids. Molecules 2016, 21, 1410–1418. [Google Scholar] [CrossRef]
- Klučáková, M.; Věžníková, K. Micro-organization of humic acids in aqueous solutions. J. Mol. Struct. 2017, 1144, 33–40. [Google Scholar] [CrossRef]
- Klučáková, M. Size and charge evaluation of standard humic and fulvic acids as crucial factors to determine their environmental behavior and impact. Front. Chem. 2018, 6, 235–242. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, R.; Tang, J.; Li, H. Specific ion effect of H+ on variably charged soil colloid aggregation. Pedosphere 2020, 30, 844–852. [Google Scholar] [CrossRef]
- Tian, R.; Liu, X.; Gao, X.; Li, R.; Li, H. Observation of specific ion effects in humus aggregation process. Pedosphere 2021, 31, 736–745. [Google Scholar] [CrossRef]
- Hu, F.; Li, H.; Liu, X.; Li, S.; Ding, W.; Xu, C.; Li, Y.; Zhu, L. Quantitative characterization of non-classic polarization of cations on clay aggregate stability. PLoS ONE 2015, 10, e0122460. [Google Scholar] [CrossRef]
- Meakin, P. Fractal aggregates in geophysics. Rev. Geophys. 1991, 29, 317–354. [Google Scholar] [CrossRef]
- Senesi, N. Aggregation patterns and macromolecular morphology of humic substances: Fractal approach. Soil Sci. 1999, 164, 841–856. [Google Scholar] [CrossRef]
- Chen, S.-H.; Teixeira, J. Structure and fractal dimension of protein-detergent complexes. Phys. Rev. Lett. 1986, 57, 2583–2586. [Google Scholar] [CrossRef]
- Anitas, E.M. Small-Angle Scattering (Neutrons, X-rays, Light) from Complex Systems; Springer Briefs in Physics; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Kawahigashi, M.; Fujitake, N.; Azuma, J.; Takahashi, T.; Kajiwara, K.; Urakawa, H. The shape of humic acid in solution as observed by small-angle X-ray scattering. Soil Sci. Plant Nutr. 1995, 41, 363–366. [Google Scholar] [CrossRef]
- Rice, J.A.; Tombàcz, E.; Malekani, K. Applications of light and X-ray scattering to characterize the fractal properties of soil organic matter. Geoderma 1999, 88, 251–264. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman: New York, NY, USA, 1982. [Google Scholar]
- Oh, C.; Sorensen, C. The Effect of Overlap between Monomers on the Determination of Fractal Cluster Morphology. J. Colloid Interface Sci. 1997, 193, 17–25. [Google Scholar] [CrossRef] [PubMed]
- Anitas, E.M. Small-angle scattering from fractals: Differentiating between various types of structures. Simmetry 2020, 12, 65–95. [Google Scholar] [CrossRef]
- Rice, J.A. Applications of fractals in the study of humic materials. In Biophysical Chemistry of Fractal Structures in Environmental Systems; Senesi, N., Wilkinson, K.J., Eds.; John Wiley & Sons: Chichester, UK, 2008; Volume 11, pp. 221–238. [Google Scholar]
- Rice, J.A.; Lin, J.S. Fractal nature of humic materials. Environ. Sci. Technol. 1993, 27, 413–414. [Google Scholar] [CrossRef]
- Österberg, R.; Mortensen, K. Fractal dimension of humic acids—A small angle neutron scattering study. Eur. Biophys. J. 1992, 21, 163–167. [Google Scholar] [CrossRef]
- Österberg, R.; Mortensen, K. The growth of fractal humic acids: Cluster correlation and gel formation. Radiat. Environ. Biophys. 1994, 33, 269–276. [Google Scholar] [CrossRef]
- Österberg, R.; Mortensen, K.; Ikai, A. Direct observation of humic acid clusters, a nonequilibrium system with a fractal structure. Naturwissenschaften 1995, 82, 137–139. [Google Scholar] [CrossRef]
- Wagoner, D.B.; Christman, R.F.; Cauchon, G.; Paulson, R. Molar mass and size of Suwannee river natural organic matter using multi-angle laser light scattering. Environ. Sci. Technol. 1997, 31, 937–941. [Google Scholar] [CrossRef]
- Tombàcz, E.; Rice, J.A.; Ren, S.-Z. Fractal structure of polydisperse humic acid particles in solution studied by scattering methods. ACH Models Chem. 1997, 134, 877–888. [Google Scholar]
- Manning, T.J.; Bennett, T.; Milton, D. Aggregation studies of humic acid using multiangle laser light scattering. Sci. Total Environ. 2000, 257, 171–176. [Google Scholar] [CrossRef]
- Myneni, S.C.B.; Brown, J.T.; Martinez, G.A.; Meyer-Ilse, W. Imaging of humic substance macromolecular structures in water and soils. Science 1999, 286, 1335–1337. [Google Scholar] [CrossRef]
- Pranzas, P.K.; Willumeit, R.; Gehrke, R.; Thieme, J.; Knöchel, A. Characterisation of structure and aggregation processes of aquatic humic substances using small-angle scattering and X-ray microscopy. Anal. Bioanal. Chem. 2003, 376, 618–625. [Google Scholar] [CrossRef]
- Diallo, M.S.; Glinka, C.J.; Goddard, W.A.; Johnson J.H., J.H., Jr. Characterization of nanoparticles and colloids in aquatic systems 1. Small angle neutron scattering investigations of Suwannee River fulvic acid aggregates in aqueous solutions. J. Nanoparticle Res. 2005, 7, 435–448. [Google Scholar] [CrossRef]
- Kučerík, J.; Drastík, M.; Zmeškal, O.; Čtvrtníčková, A. Ultrasonic spectroscopy and fractal analysis in the study on progressive aggregation of humic substances in diluted solutions. WSEAS Trans. Environ. Dev. 2009, 5, 705–715. [Google Scholar]
- Taylor, T.M.; Davidson, P.M.; Bruce, B.D.; Weiss, J. Ultrasonic spectroscopy and differential scanning calorimetry of liposomal-encapsulated nisin. J. Agric. Food Chem. 2005, 53, 8722–8728. [Google Scholar] [CrossRef]
- Buckin, V.; Kudryashov, E.; Morrissey, S. High resolution ultrasonic spectroscopy for analysis in biocolloids. Int. Labmate 2002, 27, 23–24. [Google Scholar]
- Sarvazyan, A.P. Ultrasonic velocity of biological compounds. Annu. Rev. Biophys. Biophys. Chem. 1991, 20, 321–342. [Google Scholar] [CrossRef]
- Chalikian, T.V.; Sarvazyan, A.P.; Funck, T.; Cain, C.A.; Breslauer, K.J. Partial Molar Characteristics of Glycine and Alanine in Aqueous-Solutions at High-Pressures Calculated from Ultrasonic Velocity Data. J. Phys. Chem. 1994, 98, 321–328. [Google Scholar] [CrossRef]
- Buckin, V.A. Hydration of nucleic bases in dilute aqueous solutions. Apparent molar adiabatic and isothermal compressibilities, apparent molar volumes and their temperature slopes at 25 degrees C. Biophys. Chem. 1988, 29, 283–292. [Google Scholar] [CrossRef]
- Taulier, N.; Chalikian, T.V. Compressibility of protein transitions. Biochim. Biophys. Acta Protein Struct. Mol. Enzymol. 2002, 1595, 48–70. [Google Scholar] [CrossRef]
- Sarvazyan, A.P. Development of methods of precise ultrasonic measurements in small volumes of liquids. Ultrasonics 1982, 20, 151–154. [Google Scholar] [CrossRef]
- Pavlovskaya, G.; McClements, D.J.; Povey, M.J.W. Ultrasonic investigation of aqueous solutions of a globular protein. Food Hydrocoll. 1992, 6, 253–262. [Google Scholar] [CrossRef]
- Klučáková, M.; Kargerová, A.; Nováčková, K. Conformational changes in humic acids in aqueous solutions. Chem. Pap. 2012, 66, 875–880. [Google Scholar] [CrossRef]
- Řezáčová, V.; Conte, P.; Komendová, R.; Novák, F.; Repková, M.; Kučerík, J. Factors influencing structural heat-induced structural relaxation of dissolved organic matter. Ecotoxicol. Environ. Saf. 2019, 167, 422–428. [Google Scholar] [CrossRef] [PubMed]
- Čtvrtníčková, A.; Drastík, M.; Vlčková, Z.; Kučerík, J. Surface tension of regenerated humic acids salts. Chem. List. 2008, 102, s1142–s1143. [Google Scholar]
- Drastík, M.; Čtvrtníčková, A.; Zmeskal, O.; Kučerík, J. Aggregation of humic and fulvic acids in diluted solutions. In Energy, Environment, Ecosystems, Development and Landscape Architecture; Mastorakis, N., Helmis, C., Papageorgiou, C.D., Bulucea, C.A., Panagopoulos, T., Eds.; WSEAS Press: Corfu, Greece, 2009; pp. 163–168. [Google Scholar]
- David, J.; Šmejkalová, D.; Hudecová, Š.; Zmeškal, O.; von Wandruszka, R.; Gregor, T.; Kučerík, J. The physico-chemical properties and biostimulative activities of humic substances regenerated from lignite. SpringerPlus 2014, 3, 156–171. [Google Scholar] [CrossRef]
- Kučerík, J.; Bursáková, P.; Průšová, A.; Grebíková, L.; Schaumann, G.E. Hydration of humic and fulvic acids studied by DSC. J. Therm. Anal. Calorim. 2012, 110, 451–459. [Google Scholar] [CrossRef]
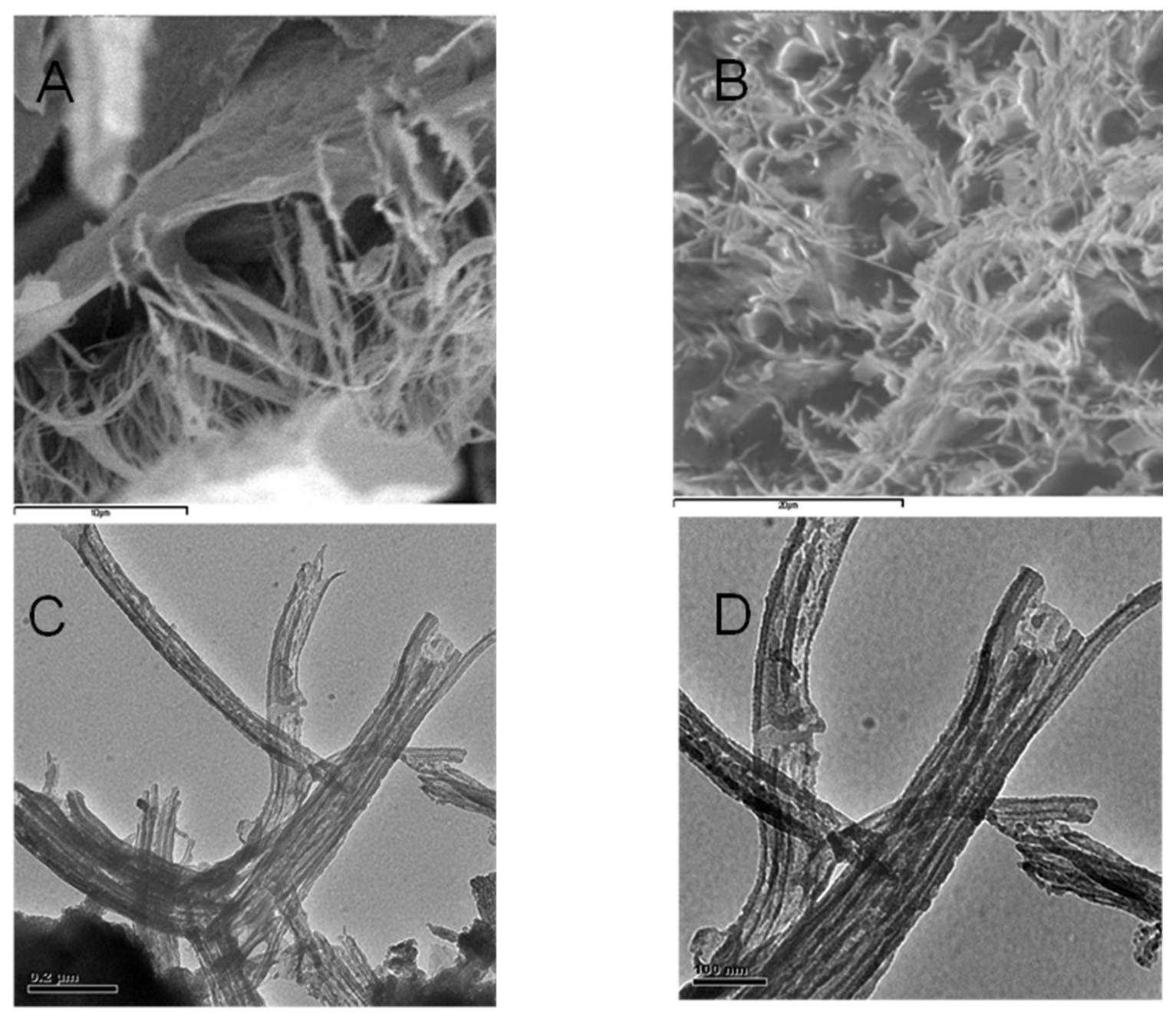



| Models | Methods | References |
|---|---|---|
| HS are flexible linear colloids at low concentrations while at high concentrations spherical colloids are stable | Surface pressure, viscosity, DLS, FCS | [32,140,141,142,143,144] |
| “two-phase” model | Vapor-pressure osmometry | [33] |
| biopolymer gels assembly from free polymeric DOM | DLS, flow cytometry | [36] |
| HS form ‘micelle-like’ aggregates or pseudo-micelles through non-covalent interactions (H-bonding, van der Waals and hydrophobic interactions). | Surface tension, SAXS, fluorescence spectroscopy, ultrasonic velocimetry, HPSEC, CZE, GPC, FFC NMR | [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,71] |
| In aqueous solutions HS exist as soluble macroligands or high molecular weight macromolecules that assume random coil conformations | HPSEC, MALLS | [34,35,75,174,176] |
| HS are non-covalently bonded aggregates of small molecules in aqu. solutions | DSC, DOSY, DLS, LDE, UF, CPMAS-NMR | [60,61,62,63,64,65,66,67,125,126,127,136,137,146,147,148,149,150,151,152,153,154,155,156,157,158] |
| HS form fractal aggregates in aqueous solutions | SAXS, SANS, SEM, TEM, DLS, turbidimetry, ultrasonic velocimetry | [59,85,86,87,140,161,164,166,169,170,171,172,173,175,179,188,192] |
| HS form aggregates and clusters of different sizes and shapes in aqueous solutions | In-situ X-ray microscopic imaging | [177,178] |
| HS form globular aggregates and ring-like structures | AFM | [97,98,102,103] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angelico, R.; Colombo, C.; Di Iorio, E.; Brtnický, M.; Fojt, J.; Conte, P. Humic Substances: From Supramolecular Aggregation to Fractal Conformation—Is There Time for a New Paradigm? Appl. Sci. 2023, 13, 2236. https://doi.org/10.3390/app13042236
Angelico R, Colombo C, Di Iorio E, Brtnický M, Fojt J, Conte P. Humic Substances: From Supramolecular Aggregation to Fractal Conformation—Is There Time for a New Paradigm? Applied Sciences. 2023; 13(4):2236. https://doi.org/10.3390/app13042236
Chicago/Turabian StyleAngelico, Ruggero, Claudio Colombo, Erika Di Iorio, Martin Brtnický, Jakub Fojt, and Pellegrino Conte. 2023. "Humic Substances: From Supramolecular Aggregation to Fractal Conformation—Is There Time for a New Paradigm?" Applied Sciences 13, no. 4: 2236. https://doi.org/10.3390/app13042236
APA StyleAngelico, R., Colombo, C., Di Iorio, E., Brtnický, M., Fojt, J., & Conte, P. (2023). Humic Substances: From Supramolecular Aggregation to Fractal Conformation—Is There Time for a New Paradigm? Applied Sciences, 13(4), 2236. https://doi.org/10.3390/app13042236








