A Multi-Objective Optimization Method of a Mobile Robot Milling System Construction for Large Cabins
Abstract
:Featured Application
Abstract
1. Introduction
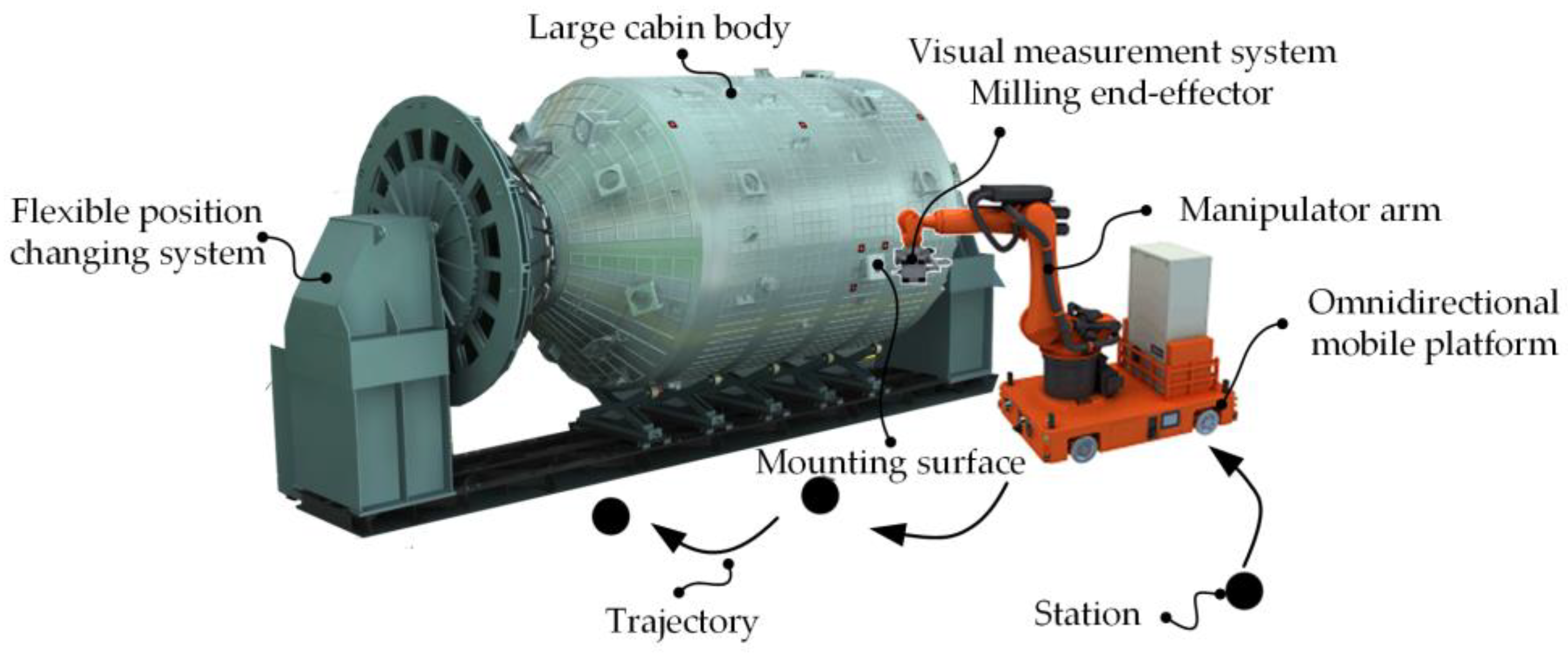
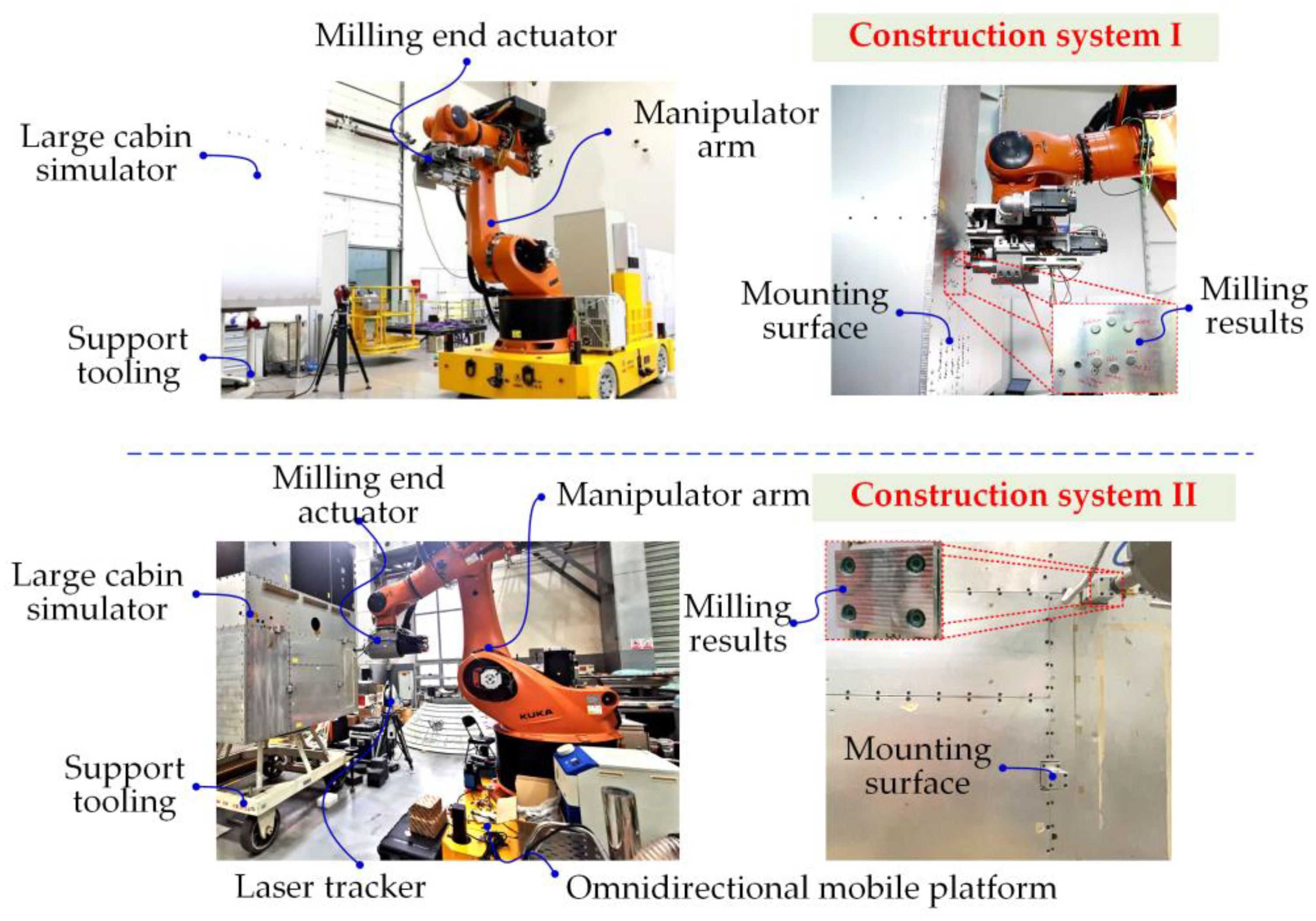
2. The Mobile Robot System
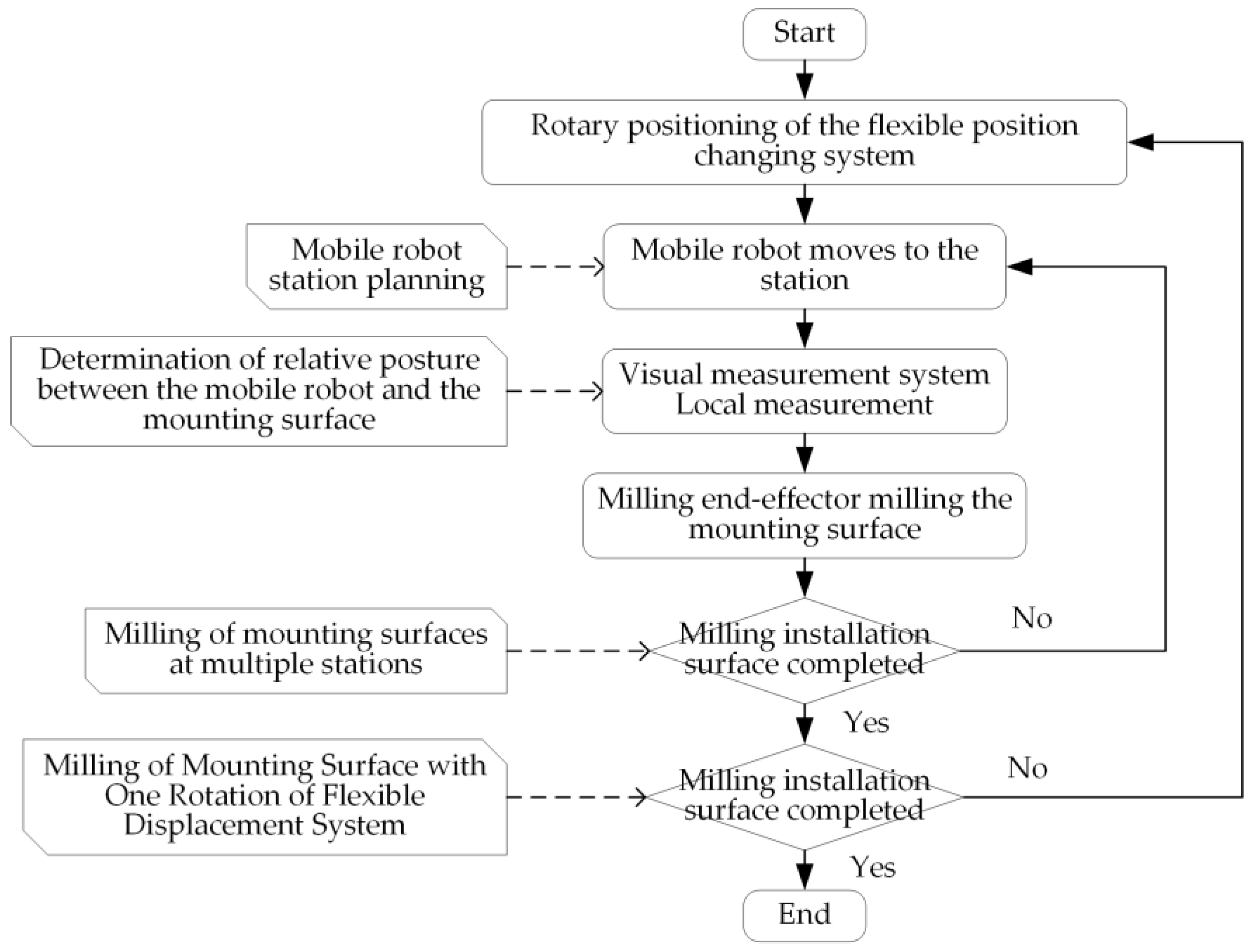
- (1)
- Rotary positioning of the flexible position changing system;
- (2)
- The mobile robot (omnidirectional mobile platform + manipulator + visual measurement system + milling end-effector) moves and positions along the trajectory according to the planned station position;
- (3)
- The visual measurement system corrects the relative posture between the mobile robot and the mounting surface by measuring the local target points on the large cabin body;
- (4)
- Milling end-effector milling the mounting surface according to the existing numerical control program;
- (5)
- Move the mobile robot to the lower station and repeat (2) to (5);
- (6)
- Rotary positioning of the flexible position changing system, repeat (2) to (6), until the installation surface has completed all milling processes.
3. Multi-Objective Optimization of System Construction
3.1. Characteristics of System Construction and Its Mathematical Description
- (1)
- The error accumulation of the constructed mobile robot system is minimal;
- (2)
- The total cost of the mobile robot system is the lowest;
- (3)
- The milling time of all the large cabin faces of the constructed mobile robot system is the shortest.
3.2. A Multi-Objective Optimization Method for System Construction Based on a Genetic Algorithm
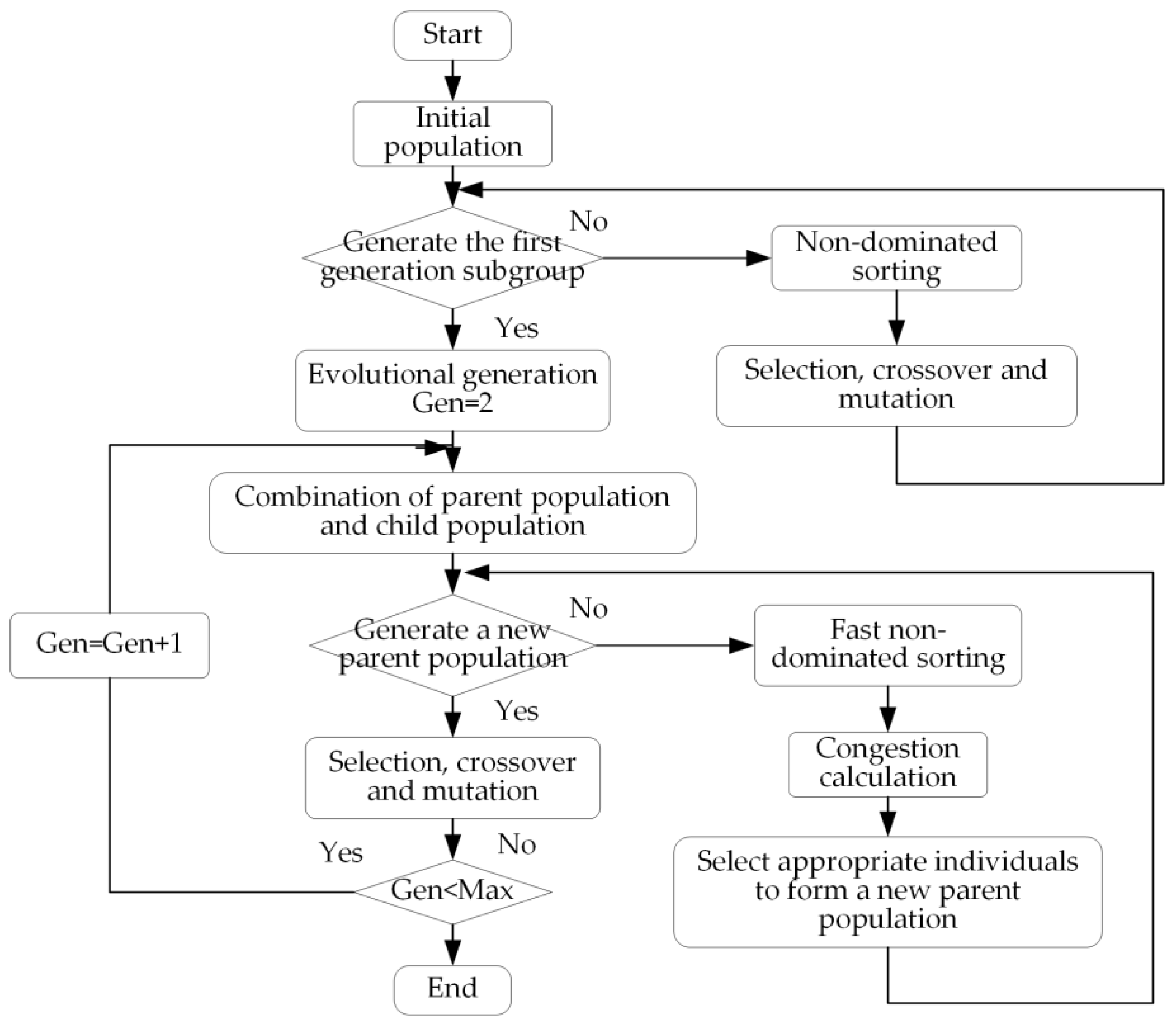
3.2.1. NSGA-II Algorithm
- (1)
- The initial population is randomly generated, and the size was N. The non-dominated queuing is performed on the initial population, and the selection, crossover and mutation operations are carried out on the initial population by the genetic algorithm to obtain the first-generation progeny population.
- (2)
- The combination of parent population and child population in the second generation, and the rapid non-dominant sequencing is carried out, and the crowding degree of individuals in each non-dominant layer is calculated, and the appropriate individuals are selected to form a new parent population according to the non-dominant relationship between individuals. Starting from the second generation, the following generations are treated in the same way.
- (3)
- The genetic algorithm is used to select, cross and mutate the parent population to generate a new offspring population.
- (4)
- Repeat steps (2) and (3) until the constraints of the algorithm are met.
3.2.2. Multi-Objective Optimization of Mobile Robot System Construction
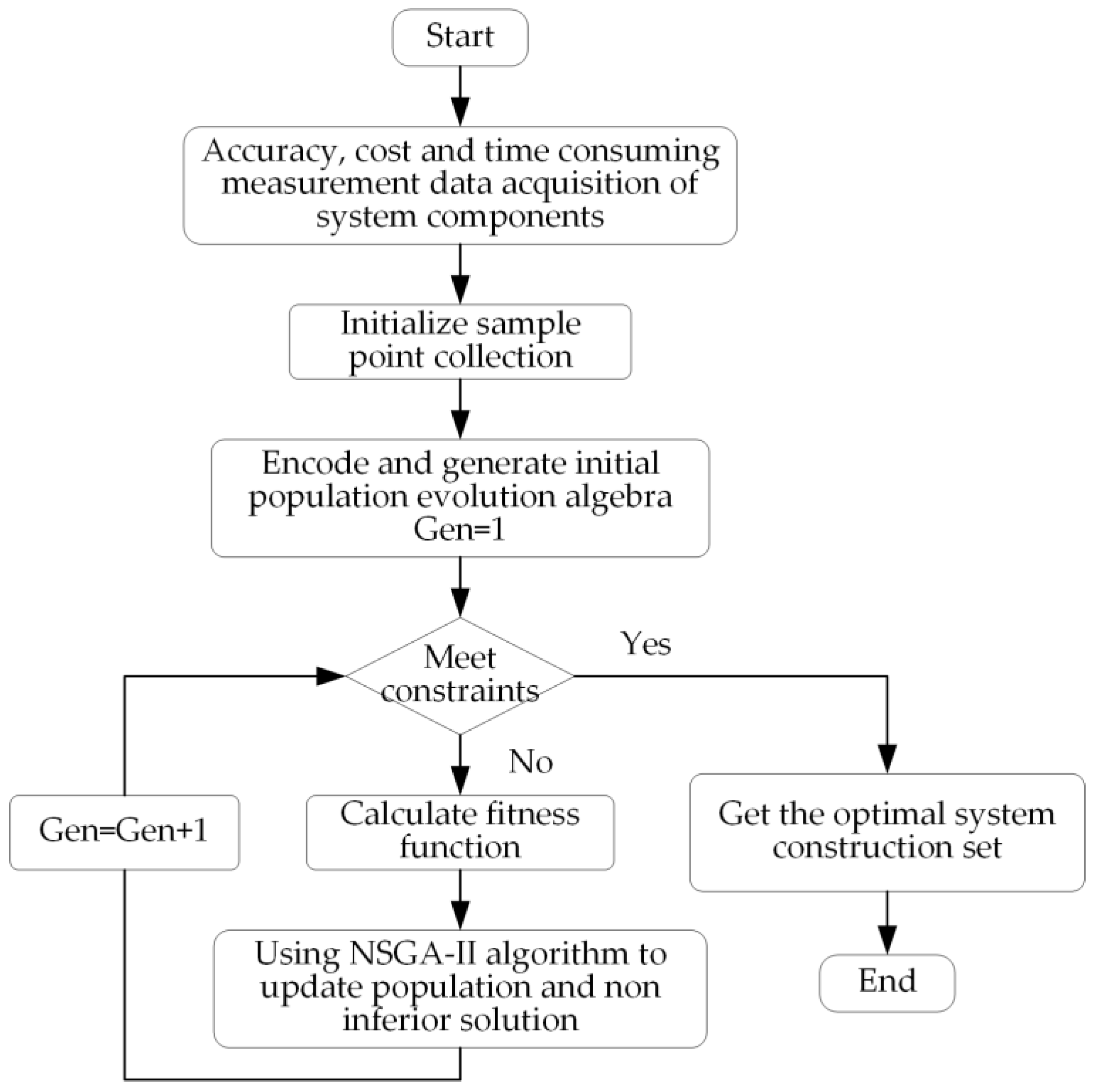
- (1)
- Measured data acquisition: the positioning accuracy of the omnidirectional mobile platform is related to the measurement method, and the positioning accuracy of laser navigation is generally 3 mm. Based on two-dimensional code visual measurement positioning, positioning accuracy is generally 1 mm. The navigation and positioning accuracy of a high precision spatial locator (iGPS) is generally 0.5 mm. Composite measurements can ensure higher positioning accuracy, but the cost is also higher. At the same time, the higher the precision, the longer the time to adjust and control. There are many ways to improve the positioning accuracy of the manipulator, such as correcting D-H parameters to improve the error compensation. The grating two-stage closed-loop is used to improve the joint angle accuracy and then the robot positioning accuracy. The higher the accuracy, the higher the cost, and the smaller the working space. The accuracy of the vision measurement system, milling end-effector and flexible position changing system are also positively correlated with the cost.
- (2)
- Initialize component set: According to step (1), components are classified and selected according to accuracy, cost and time, and multiple groups of actual data constitute the initial population of the genetic algorithm.
- (3)
- Coding and generating population: the number of system components is represented by m, and the number of specific components in the component is represented by n. Rows and columns of the matrix are used for coding, that is, columns represent m components and rows represent n specific components. Then the coding of the constructed system can be obtained and corresponds to the matrix of precision, cost and time.
- (4)
- Fitness calculation: there are three goals. The first goal is the sum of the error accumulation of each component in the milling process, the second goal is the sum of the cost of each component, and the third goal is the sum of the working time of each component. Its fitness function is shown in Equation (1).
- (5)
- Update population and non-inferior solution set: For the populations processed by the above steps, the non-inferior solution set constructed by the optimal system can be updated through the NSGA-II genetic algorithm operations such as fast non-dominant sorting, crowding calculation, selection, crossover and mutation, and the updated new population can be used for the next generation calculation.
- (6)
- Iterative optimization: Repeat steps (4)~(5) until the constraint condition (the set number of iterations) is satisfied, and the final non-inferior solution set of the optimal system can be obtained.
4. Verification and Analysis
4.1. Application of the Multi-Objective Optimization Method in Optimal System Construction
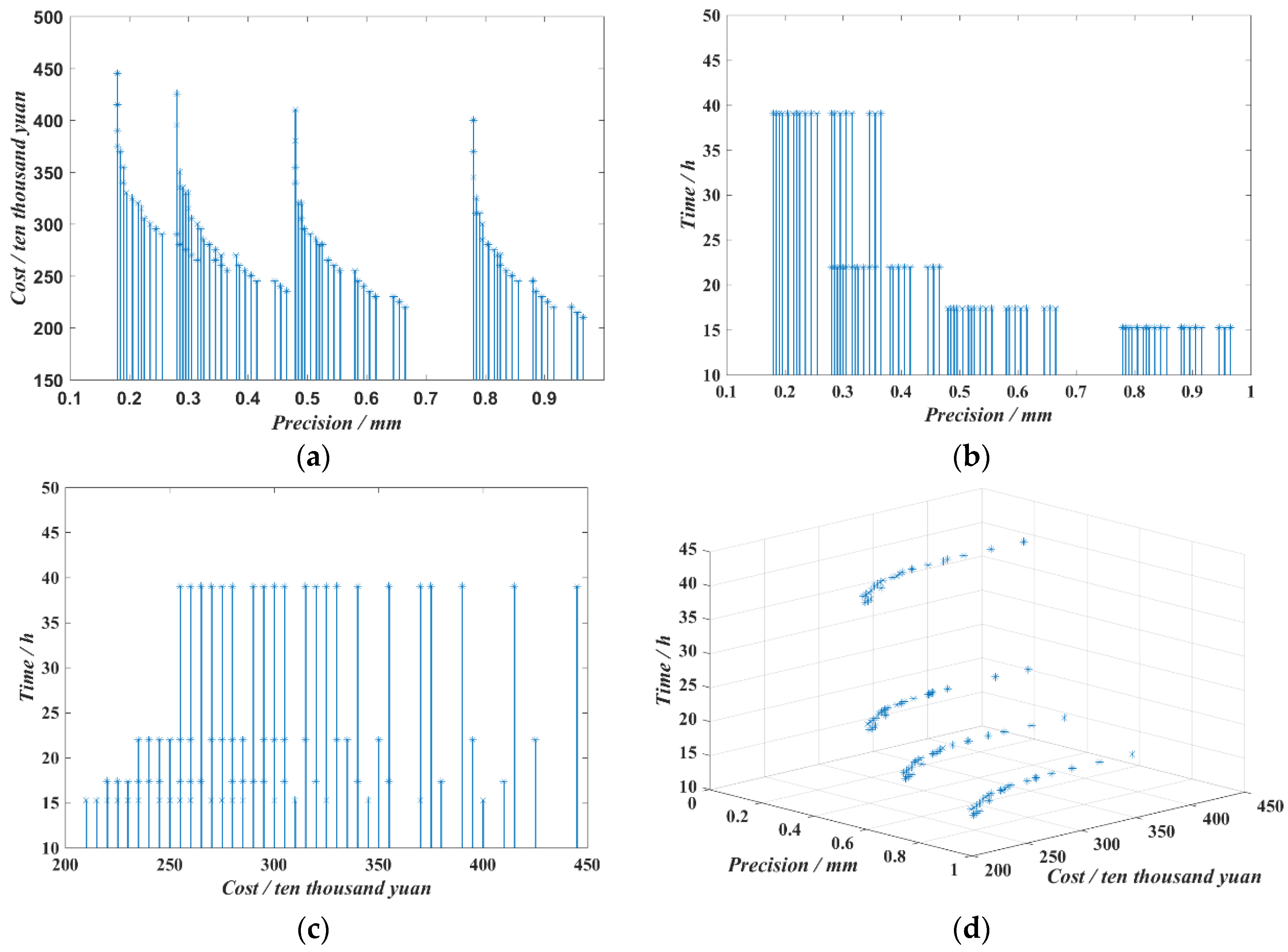
- (1)
- There is a significant negative correlation between the cumulative error and the sum of costs in Figure 6a, a significant negative correlation between the cumulative error and the milling time in Figure 6b, and a positive correlation between the sum of costs and the milling time in Figure 6c, indicating that the three objective functions are contradictory to each other;
- (2)
- Considering the actual design requirements, existing equipment status and subsequent support funds and other factors, the non-inferior solution set in Figure 6d can select the appropriate mobile robot system and determine the component requirements according to the corresponding code, which can ensure that the accuracy, cost and time of the system meet the construction requirements.
4.2. Validation of Optimization Methods for Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, F.G.; Mei, B.; Liu, X.J.; Zhang, J.B.; Yue, Y. Novel Mode and Equipment for Machining Large Complex Components. J. Me-Chanical Eng. 2020, 56, 70–78. [Google Scholar]
- Tao, B.; Zhao, X.; Li, R.; Ding, H. Research on robotic measurement-operation-machining technology and its application. China Mech. Eng. 2020, 31, 49–56. [Google Scholar]
- Verl, A.; Valente, A.; Melkote, S.; Brecher, C.; Ozturk, E.; Tunc, L.T. Robots in machining. CIRP Annals. 2019, 68, 799–822. [Google Scholar] [CrossRef]
- Möller, C.; Schmidt, H.C.; Koch, P.; Böhlmann, C.; Kothe, S.-M.; Wollnack, J.; Hintze, W. Machining of large scaled CFRP-Parts with mobile CNC-based robotic system in aerospace industry. Procedia Manuf. 2017, 14, 17–29. [Google Scholar] [CrossRef]
- Waurzyniak, P. Expanding the Horizons of Aerospace Automation. Manuf. Eng. 2016, 156, 59–67. [Google Scholar]
- Guo, Y.; Dong, H.; Wang, G.; Ke, Y. Vibration analysis and suppression in robotic boring process. Int. J. Mach. Tools Manuf. 2016, 101, 102–110. [Google Scholar] [CrossRef]
- Jackson, T. High-Accuracy Articulated Mobile Robots; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Logemann, T. Mobile Robot Assembly Cell (RACe) for Drilling and Fastening; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Susemihl, H.; Moeller, C.; Kothe, S.; Schmidt, H.C.; Shah, N.; Brillinger, C.; Wollnack, J.; Hintze, W. High Accuracy Mobile Robotic System for Machining of Large Aircraft Components. SAE Int. J. Aerosp. 2016, 9, 231–238. [Google Scholar] [CrossRef]
- Wen, K.; Zhang, J.B.; Yue, Y. Method for improving accuracy of NC-driven mobile milling robot. J. Mech. Eng. 2021, 57, 72–80. [Google Scholar]
- Chen, Q.-T.; Yin, S.; Zhang, J.-B.; Yue, Y.; Zhou, Y.-H.; Wen, K.; Yang, J.-Z.; Bai, X.-P. Pose Optimization of Industrial Robots Based on Stiffness for Milling Tasks. Robot 2021, 43, 90–100. [Google Scholar]
- Tao, B.; Zhao, X.; Ding, H. Mobile-robotic machining for large complex components: A review study. Sci. China Technol. Sci. 2019, 62, 1388–1400. [Google Scholar] [CrossRef]
- Susemihl, H.; Brillinger, C.; Stürmer, S.P.; Hansen, S.; Boehlmann, C.; Kothe, S.; Wollnack, J.; Hintze, W. Referencing Strategies for High Accuracy Machining of Large Aircraft Components with Mobile Robotic Systems; SAE Technical Paper; SAE: Warrendale, PA, USA, 2017. [Google Scholar]
- Zhou, Z.; Liu, W.; Wu, Q.; Wang, Y.; Yu, B.; Yue, Y.; Zhang, J. A Combined Measurement Method for Large-Size Aerospace Components. Sensors 2020, 20, 4843. [Google Scholar] [CrossRef] [PubMed]
- Ren, M.; Fu, L.; Xiao, G.; Chen, M.; Wang, X. Non-Lambertian photometric stereo vision algorithm based on a multi-scale convolution deep learning architecture. Sci. Sin. Technol. 2020, 50, 323–334. [Google Scholar] [CrossRef]
- Brillinger, C.; Susemihl, H.; Ehmke, F.; Staude, T.; Deutmarg, K.; Klemstein, M.; Boehlmann, C.; Hintze, W.; Wollnack, J. Mobile Laser Trackers for Aircraft Manufacturing: Increasing Accuracy and Productivity of Robotic Applications for Large Parts; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Tao, B.; Zhao, X.; Ding, H. Study on robotic mobile machining techniques for large complex components. Sci. Sin. Technol. 2018, 48, 1302–1312. [Google Scholar] [CrossRef]
- Chen, Y.-D.; Chang, S.-L.; Feng, Q.-G. Industrial robot system based on CPS approach. J. Beijing Univ. Aeronaut. Astronsutics 2018, 44, 931–938. [Google Scholar]
- Li, G.; Zhu, W.; Dong, H.; Ke, Y. Stiffness-oriented performance indices defined on two-dimensional manifold for 6-DOF in-dustrial robot. Robot. Comput. Integr. Manuf. 2021, 68, 102076. [Google Scholar] [CrossRef]
- Wu, M.; Dai, S.-L.; Yang, C. Mixed Reality Enhanced User Interactive Path Planning for Omnidirectional Mobile Robot. Appl. Sci. 2020, 10, 1135. [Google Scholar] [CrossRef]
- Wu, H.; Wang, Y.; Wei, X.; Zhu, D. Spatial Path Planning for Robotic Milling of Automotive Casting Components Based on Optimal Machining Posture. Metals 2022, 12, 1271. [Google Scholar] [CrossRef]
- Yang, B.; Guo, K.; Sun, J. Chatter Detection in Robotic Milling Using Entropy Features. Appl. Sci. 2022, 12, 8276. [Google Scholar] [CrossRef]

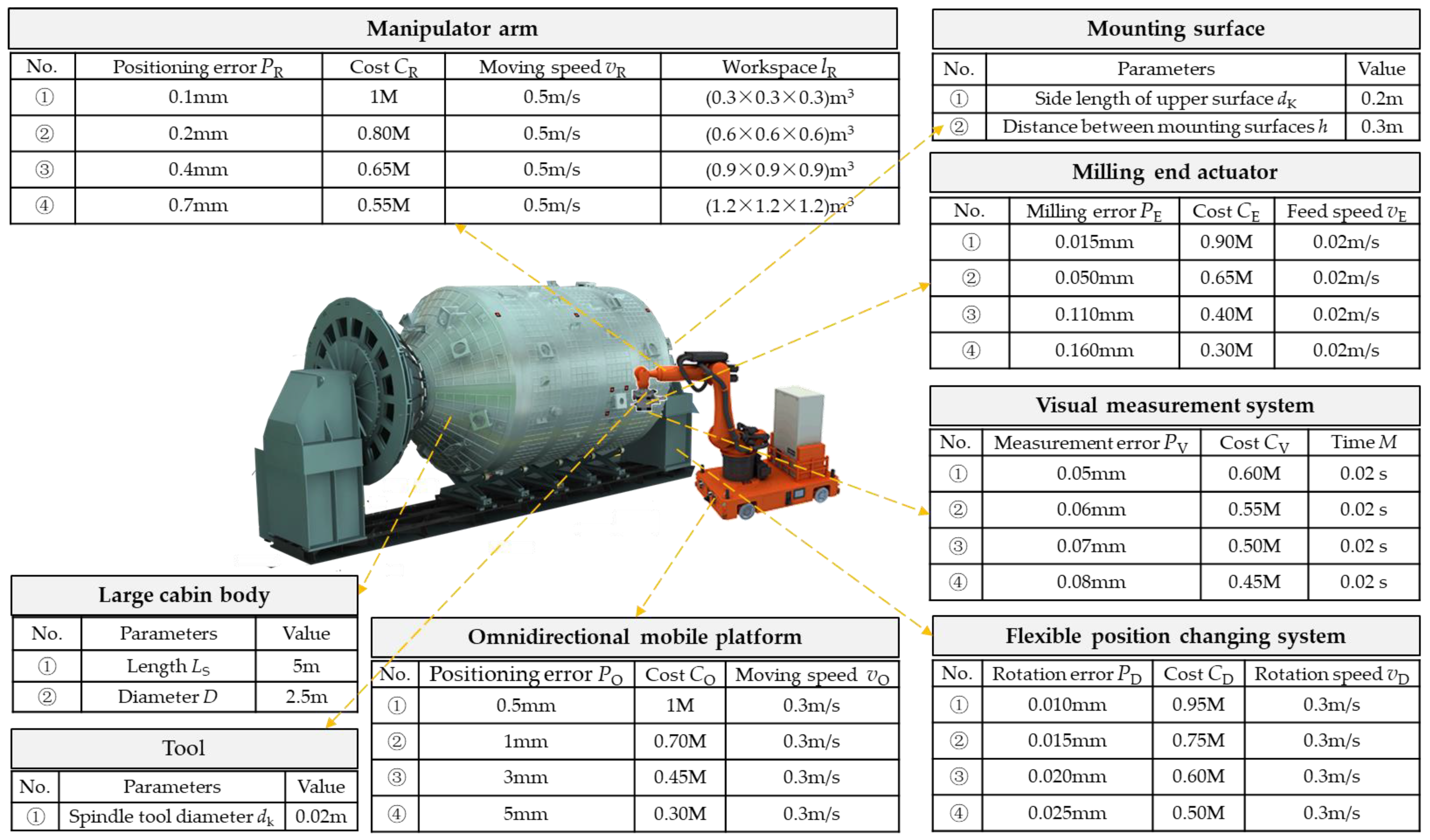
| Parameter | Meaning |
|---|---|
| PR | the positioning error of the manipulator |
| PV | the measurement error of the visual measurement system |
| PE | machining error of end effector in milling |
| PD | the rotation error of the flexible position changing system |
| CO | the market price (cost) of an omnidirectional mobile platform |
| CR | the market price of the mechanical arm |
| CV | the market price of a visual measurement system |
| CE | the market price of milling end-effector |
| CD | the market price of the flexible position changing system |
| TO | the time when the omnidirectional mobile platform participates in the milling process |
| TR | the time for the manipulator to participate in the milling process |
| TV | the time when the visual measurement system participates in the milling process |
| TE | the time that the end effector participates in the milling process |
| TD | the time that the flexible position changing system participates in the milling process |
| System | System 1 | System 2 | ||
|---|---|---|---|---|
| Scheme 1 | Scheme 2 | Scheme 1 | Scheme 2 | |
| Omnidirectional mobile platform | ④ | ④ | ④ | ④ |
| Arm of machinery | ① | ② | ① | ② |
| Visual measurement system | ② | ② | ② | ② |
| Milling end-effector | ④ | ④ | ② | ② |
| Flexible position changing system | ④ | ④ | ④ | ④ |
| Final milling error f1 (mm) | 0.345 | 0.445 | 0.235 | 0.335 |
| Total cost f2 (ten thousand Yuan) | 265 | 245 | 300 | 280 |
| Milling time f3 (hour) | 39.452 | 9.891 | 39.452 | 9.891 |
| Parameters | Final Milling Error f1 (mm) | Total Cost f2 (Ten Thousand Yuan) | Milling Time f3 (Hour) |
|---|---|---|---|
| Scheme 1 of System 1 | 0.384 | 265 | 0.615 |
| Scheme 2 of System 2 | 0.356 | 280 | 0.152 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, K.; Zhang, Z.; Zhang, J.; Zhang, X.; Chen, T.; Gao, X.; Zhang, W. A Multi-Objective Optimization Method of a Mobile Robot Milling System Construction for Large Cabins. Appl. Sci. 2023, 13, 2288. https://doi.org/10.3390/app13042288
Wen K, Zhang Z, Zhang J, Zhang X, Chen T, Gao X, Zhang W. A Multi-Objective Optimization Method of a Mobile Robot Milling System Construction for Large Cabins. Applied Sciences. 2023; 13(4):2288. https://doi.org/10.3390/app13042288
Chicago/Turabian StyleWen, Ke, Zhiqiang Zhang, Jiabo Zhang, Xiaohui Zhang, Tao Chen, Xin Gao, and Wen Zhang. 2023. "A Multi-Objective Optimization Method of a Mobile Robot Milling System Construction for Large Cabins" Applied Sciences 13, no. 4: 2288. https://doi.org/10.3390/app13042288
APA StyleWen, K., Zhang, Z., Zhang, J., Zhang, X., Chen, T., Gao, X., & Zhang, W. (2023). A Multi-Objective Optimization Method of a Mobile Robot Milling System Construction for Large Cabins. Applied Sciences, 13(4), 2288. https://doi.org/10.3390/app13042288





