Method and Experimental Study of Zeolite Crystal Manipulation Based in Hydrodynamic Forces for Single Crystal Assessment
Abstract
:1. Introduction
2. Materials and Methods
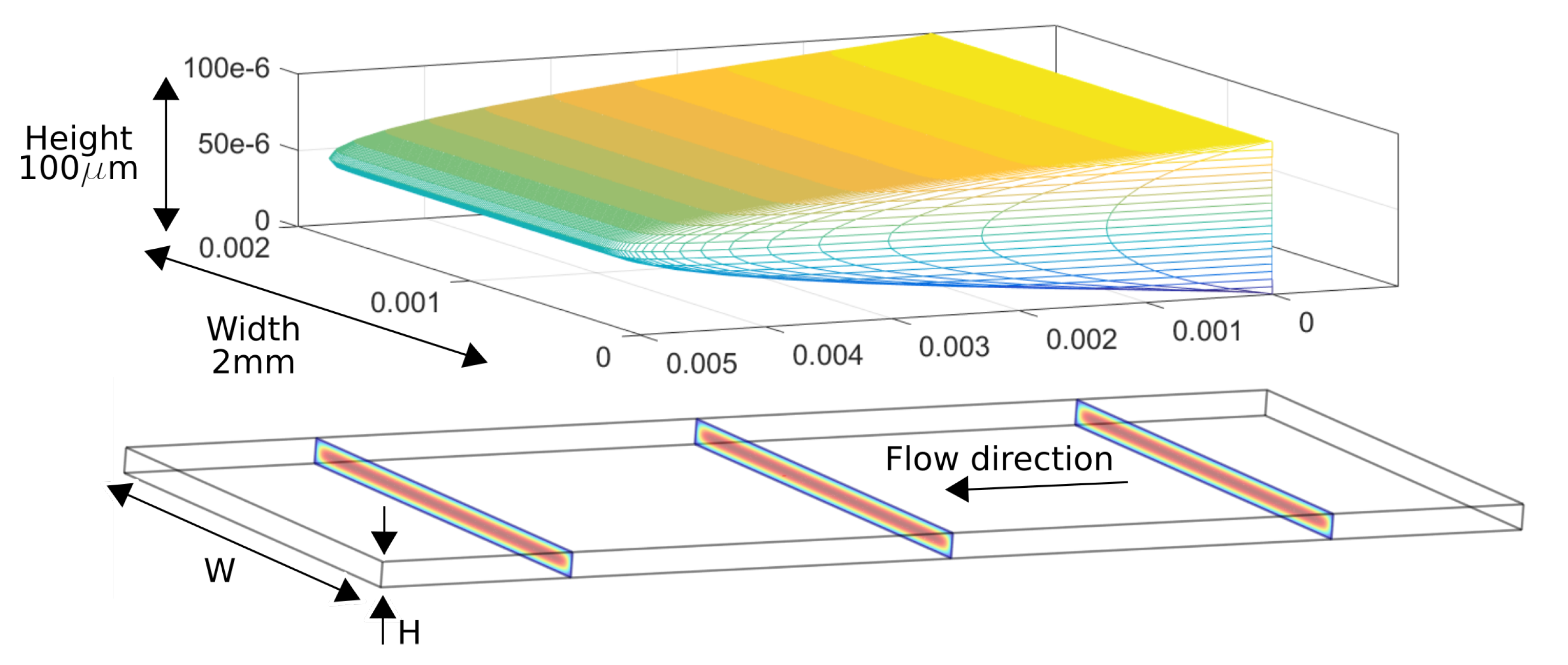
2.1. Microfluidic Channel
- The microchannel is prefilled with deionized water, leaving room for the sample of zeolite crystals in the selected input tubing.
- The sample of zeolite crystals/deionized water in the microcentrifuge tube is agitated.
- By using a 3-mL syringe 21 G × 32 mm (0.8 mm) (1-1/4”), 100 L of the sample is taken from the microcentrifugue tube, bringing down the needle to about of the fluid height.
- The needle of the syringe is inserted in the selected input tubing until it reaches the bottom wall of the microchannel, and the input tubing is filled with the syringe contents.
- The microchannel is rotated to vertical position, with the sample filled tubing upward, so gravity and drag forces convey the crystals in the channel.
- Immediately after the previous step, the microfluidic device is gently tapped on a soft surface and returned to original horizontal orientation.
- The microchannel is observed with the microscope looking for crystals. If they are not found, the previous step is repeated.
- Once the crystals are found in the microchannel, the two inputs are gently filled with deionized water in order to connect the microfluidic device with the syringe pump tubing.
2.2. Experimental Setup
2.3. Velocity Profile in the Microchannel
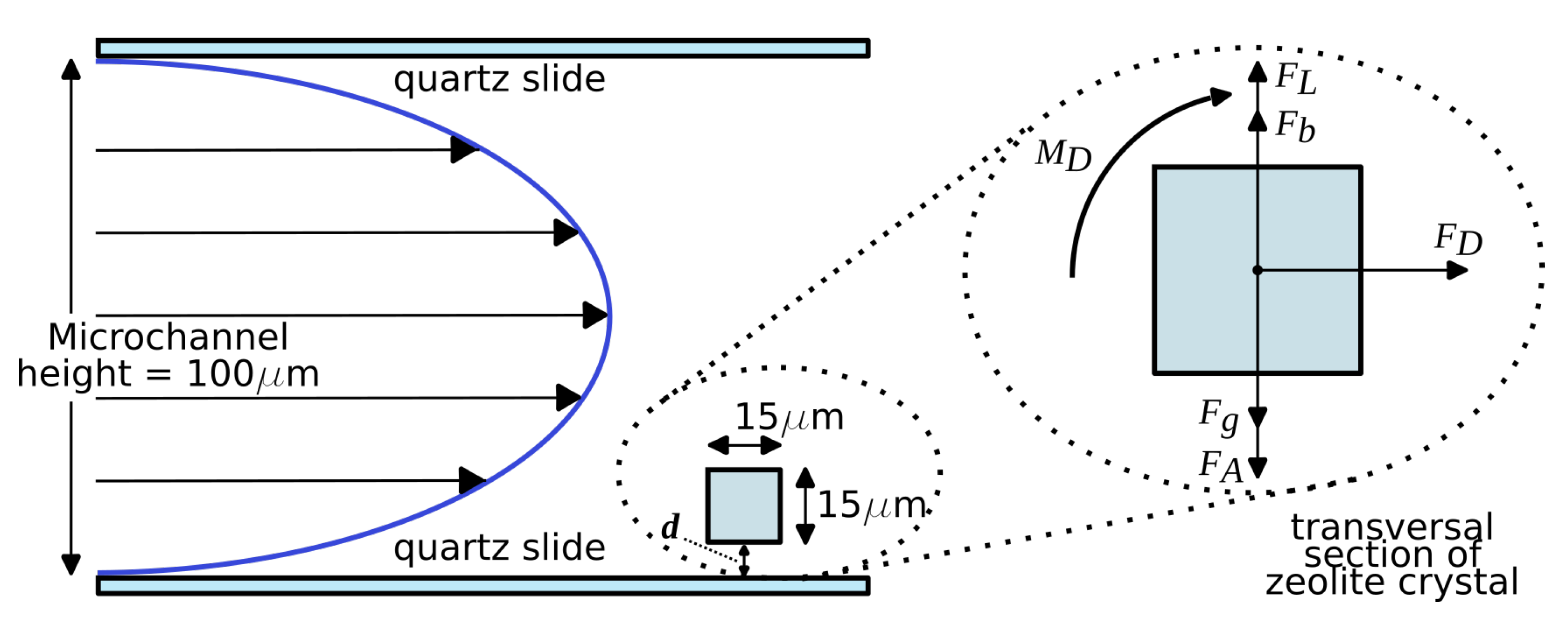
2.4. Force Balance Model
3. Results
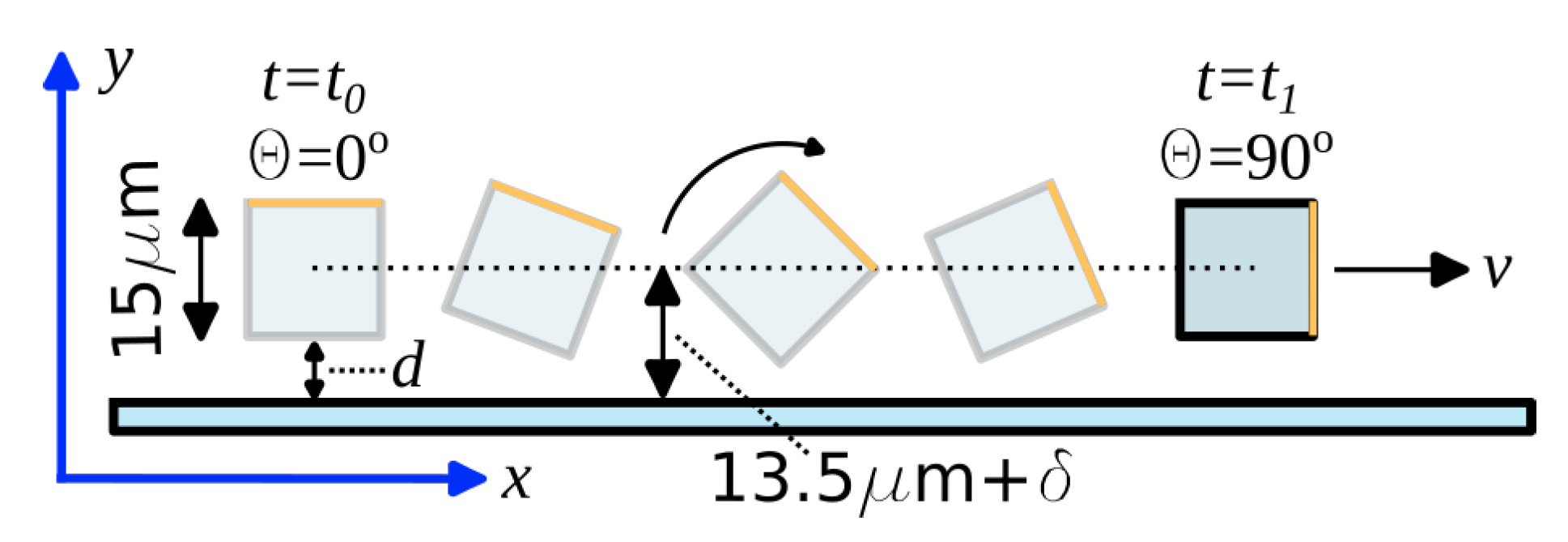
3.1. Time-Dependent Study
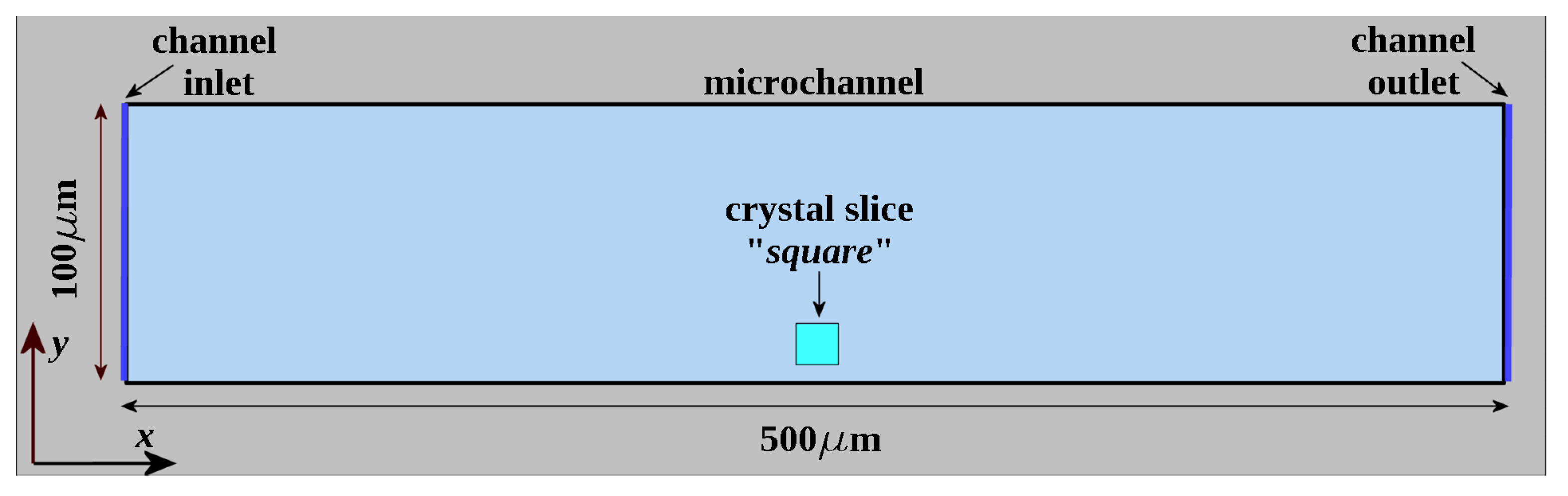
3.2. Stationary Study
3.3. Volumetric Force Estimation
3.4. Experimental Crystal Manipulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ZSM-5 | Zeolite Socony Mobil-5 |
| CFD | Computational Fluid Dynamics |
| PDMS | polydimethylsiloxane |
| FSI | Fluid-Solid Interaction |
| PTFE | Polytetrafluoroethylene |
| OD | Outer Diameter |
| ID | Inner Diameter |
References
- Hendriks, F.C.; Schmidt, J.E.; Rombouts, J.A.; Lammertsma, K.; Bruijnincx, P.C.A.; Weckhuysen, B.M. Probing Zeolite Crystal Architecture and Structural Imperfections Using Differently Sized Fluorescent Organic Probe Molecules. Chem. Eur. J. 2017, 23, 6305–6314. [Google Scholar] [CrossRef] [PubMed]
- Roeffaers, M.B.J.; Sels, B.F.; Uji-i, H.; De Schryver, F.C.; Jacobs, P.A.; De Vos, D.E.; Hofkens, J. Spatially Resolved Observation of Crystal-Face-Dependent Catalysis by Single Turnover Counting. Nature 2006, 439, 572–575. [Google Scholar] [CrossRef] [PubMed]
- Roeffaers, M.B.J.; Hofkens, J.; De Cremer, G.; De Schryver, F.C.; Jacobs, P.A.; De Vos, D.E.; Sels, B.F. Fluorescence Microscopy: Bridging the Phase Gap in Catalysis. Catal. Today 2007, 126, 44–53. [Google Scholar] [CrossRef]
- Kayani, A.A.; Khoshmanesh, K.; Ward, S.A.; Mitchell, A.; Kalantar-zadeh, K. Optofluidics Incorporating Actively Controlled Micro- and Nano-Particles. Biomicrofluidics 2012, 6, 031501. [Google Scholar] [CrossRef] [PubMed]
- Bruus, H. Theoretical Microfluidics; OUP: Oxford, UK, 2008; 346p, ISBN 9780199235087. [Google Scholar]
- Monat, C.; Domachuk, P.; Grillet, C.; Collins, M.; Eggleton, B.J.; Cronin-Golomb, M.; Mutzenich, S.; Mahmud, T.; Rosengarten, G.; Mitchell, A. Optofluidics: A Novel Generation of Reconfigurable and Adaptive Compact Architectures. Microfluid. Nanofluidics 2008, 4, 81–95. [Google Scholar] [CrossRef]
- Hamdallah, S.I.; Zoqlam, R.; Erfle, P.; Blyth, M.; Alkilany, A.M.; Dietzel, A.; Qi, S. Microfluidics for Pharmaceutical Nanoparticle Fabrication: The Truth and the Myth. Int. J. Pharm. 2020, 584, 119408. [Google Scholar] [CrossRef] [PubMed]
- Torino, S.; Iodice, M.; Rendina, I.; Coppola, G.; Schonbrun, E. A Microfluidic Approach for Inducing Cell Rotation by Means of Hydrodynamic Forces. Sensors 2016, 16, 1326. [Google Scholar] [CrossRef] [PubMed]
- Suo, J.; Edwards, E.E.; Anilkumar, A.; Sulchek, T.; Giddens, D.P.; Thomas, S.N. Force and Torque on Spherical Particles in Micro-Channel Flows Using Computational Fluid Dynamics. R. Soc. Open Sci. 2016, 3, 160298. [Google Scholar] [CrossRef] [PubMed]
- Shukla, N.; Henthorn, K.H. Effect of Relative Particle Size on Large Particle Detachment from a Microchannel. Microfluid. Nanofluidics 2009, 6, 521–527. [Google Scholar] [CrossRef]
- Hahn, P.; Lamprecht, A.; Dual, J. Numerical Simulation of Micro-Particle Rotation by the Acoustic Viscous Torque. Lab Chip 2016, 16, 4581–4594. [Google Scholar] [CrossRef] [PubMed]
- Stone, H.A. Introduction to Fluid Dynamics for Microfluidic Flows. In CMOS Biotechnology; Lee, H., Westervelt, R.M., Ham, D., Eds.; Series on Integrated Circuits and Systems; Springer: New York, NY, USA, 2007; ISBN 978-0-387-68913-5. [Google Scholar]
- Ahmad, T.; Hassan, I. Experimental Analysis of Microchannel Entrance Length Characteristics Using Microparticle Image Velocimetry. J. Fluids Eng. Trans. ASME 2010, 132, 0411021–04110213. [Google Scholar] [CrossRef]
- Burdick, G.M.; Berman, N.S.; Beaudoin, S.P. Describing Hydrodynamic Particle Removal from Surfaces Using the Particle Reynolds Number. J. Nanopart. Res. 2001, 3, 455–467. [Google Scholar] [CrossRef]
- Xu, X.; Li, Z.; Nehorai, A. Finite Element Simulations of Hydrodynamic Trapping in Microfluidic Particle-Trap Array Systems. Biomicrofluidics 2013, 7, 054108. [Google Scholar] [CrossRef] [PubMed]




| Flow Rate Q [L/min] | Translational Velocity [m/s] | Drag Force [N] | Angular Velocity [/s] | Torque [Nm] |
|---|---|---|---|---|
| 40 | 1717.7 | 457.6 | 3400 | 177.1 |
| 60 | 2591.1 | 64.9 | 5045 | 530.5 |
| 80 | 3428.9 | 4.2 | 6624 | −156.6 |
| Flow Rate Q (L/min) | Flow Velocity (m/s) | Drag Force (N) | Torque (Nm) |
|---|---|---|---|
| 40 | 3.33 | 2.13 | 6.49 |
| 60 | 5 | 3.2 | 9.75 |
| 80 | 6.67 | 4.27 | 13.01 |
| Simulation | 1 Event of Experimental Data | ||||||
|---|---|---|---|---|---|---|---|
| Flow Rate Q [L/min] | Velocity [m/s] | Opposing Force 1 [N] | Est. Opposing Force 2 [N] | Force Error 3 [%] | Velocity [m/s] | Velocity Error 4 [%] | Angular Velocity [/s] |
| 40 | 318 | −2.16 | 324.8 | −2.9 | 900 | ||
| 60 | 411.9 | −2.85 | 415 | −1.15 | 1351 | ||
| 80 | 589.7 | −4.38 | 599.4 | −1.61 | 1621 | ||
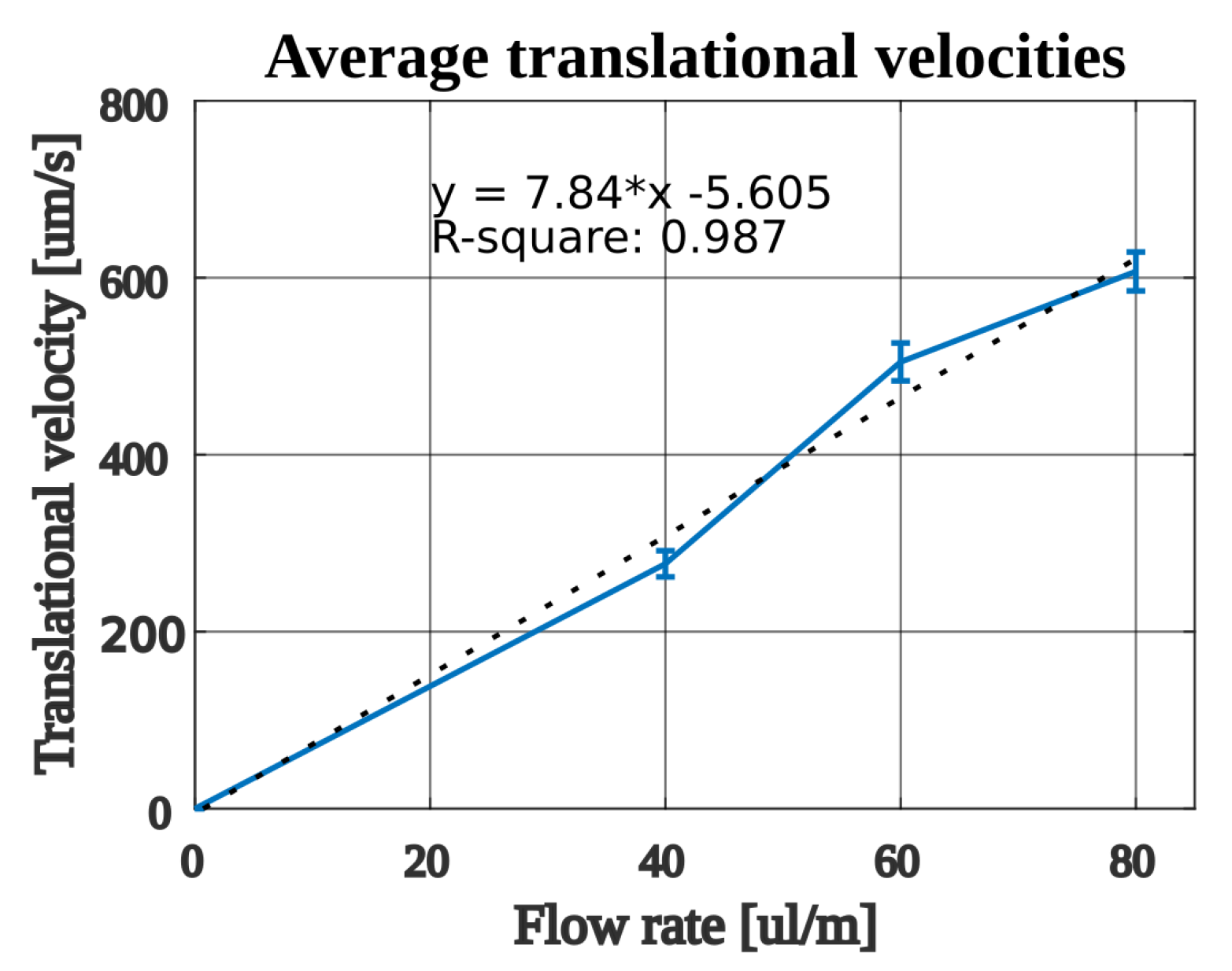
| Flow Rate [L/min] | Average Velocity [m/s] | Standard Error of the Mean [m/s] | Estimated Opposing Force [nN] |
|---|---|---|---|
| 40 | 276.7 | 14.8 | 1.79 |
| 60 | 504.9 | 21.37 | 2.59 |
| 80 | 607.1 | 21.98 | 3.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De la Torre, D.; Garcés-Chávez, V.; Sanchez-Lopez, J.D.D.; O’Donnell, K.A.; Nieto-Hipólito, J.I.; Yocupicio-Gaxiola, R.I. Method and Experimental Study of Zeolite Crystal Manipulation Based in Hydrodynamic Forces for Single Crystal Assessment. Appl. Sci. 2023, 13, 2699. https://doi.org/10.3390/app13042699
De la Torre D, Garcés-Chávez V, Sanchez-Lopez JDD, O’Donnell KA, Nieto-Hipólito JI, Yocupicio-Gaxiola RI. Method and Experimental Study of Zeolite Crystal Manipulation Based in Hydrodynamic Forces for Single Crystal Assessment. Applied Sciences. 2023; 13(4):2699. https://doi.org/10.3390/app13042699
Chicago/Turabian StyleDe la Torre, Dann, Veneranda Garcés-Chávez, Juan De Dios Sanchez-Lopez, Kevin A. O’Donnell, Juan Ivan Nieto-Hipólito, and Rosario Isidro Yocupicio-Gaxiola. 2023. "Method and Experimental Study of Zeolite Crystal Manipulation Based in Hydrodynamic Forces for Single Crystal Assessment" Applied Sciences 13, no. 4: 2699. https://doi.org/10.3390/app13042699
APA StyleDe la Torre, D., Garcés-Chávez, V., Sanchez-Lopez, J. D. D., O’Donnell, K. A., Nieto-Hipólito, J. I., & Yocupicio-Gaxiola, R. I. (2023). Method and Experimental Study of Zeolite Crystal Manipulation Based in Hydrodynamic Forces for Single Crystal Assessment. Applied Sciences, 13(4), 2699. https://doi.org/10.3390/app13042699






