1. Introduction
Fires in tunnels can cause considerable material and environmental damage and loss of life and health of tunnel users. Road tunnels belong to such capital-intensive construction projects, which often contribute to solving acute traffic problems in the region, protecting the environment and reducing the number of road accidents. They are considered as ecological structures protecting nature and original habitats, as they do not negatively affect the migration of animals. Tunnels are often part of supra-regional or transnational transport corridors and national critical infrastructures. A fire in a tunnel is considered to be one of the most destructive events that can cause significant secondary damage with a transnational impact due to a long-term interruption, or operation disruptions during tunnel closures. Therefore, special attention is paid to fire prevention, safe operation and resilience of the tunnel, as well as to readiness for firefighting and rescue work. The tunnel is considered as an intelligent structure that is equipped with many safety installations, such as traffic control system, emergency ventilation, camera monitoring system, emergency lighting, emergency power supply, measurement of physical quantities, etc. These installations are used by the central control system (CCS) for autonomous fire detection, ensuring conditions inside the tunnel suitable for safe self-rescue and evacuation, to prevent entry into the affected tunnel tube and to provide the necessary information for the escape of people until the arrival of firefighters and rescuers. This CCS effort is supported by tunnel control operators who continuously monitor the situation inside the tunnel and can also participate in fire detection and localization using fire detection and camera monitoring systems. One of the key tasks of the CCS in the event of a fire is to monitor the airflow velocity inside the tunnel and to regulate it using emergency ventilation to create and to maintain conditions suitable for smoke stratification in the upper part of the tunnel. The proper functioning of all tunnel safety systems and the readiness of tunnel control operators, firefighters and rescuers is critical for mitigating damage and preventing the loss of lives. For various possible fire scenarios, for each tunnel, there are pre-prepared and tested automatic responses of the tunnel to fire, which include various emergency ventilation operation strategies. These ventilation tests are conducted in the tunnel even before it is put into operation.
Computer simulation of fires is, at present, considered to be an effective means of preventing fires, increasing preparedness to deal with them and mitigating their consequences. Considerable efforts towards more accurate and reliable mathematical and physical fire models have led to the development of advanced simulation systems for modeling fires in a variety of important environments. Experimental investigation of fire behavior outside the laboratory is expensive and allows only a limited number of fire scenarios to be investigated. Such an experiment often leads to the destruction of the tested structure. The goal is therefore to develop such a software environment that will enable to reliably simulate the behavior of a real fire in a given structure using 3D visualization. Such a simulation makes it possible to flexibly change the parameters of the fire scenario according to the user’s requirements at present, and to test different extinguishing strategies and their effectiveness.
Computational Fluid Dynamics (CFD) techniques are at present often used to design and test ventilation systems and to simulate fire and smoke. The two most popular software tools are Fire Dynamics Simulator (FDS) and ANSYS Fluent. FDS is primarily used to simulate fire development [
1,
2] and ANSYS Fluent is a multi-purpose package that can be used for any fluid and heat flow problem [
3]. However, designing a simulation using both systems requires making certain design decisions, taking into account all relevant approximations and simplifications of the models and justifying them thoroughly [
4].
FDS [
5] is a CFD solver widely used for various applications, not only for solving practical problems in fire protection technology, but also for studying basic fire dynamics. It is an open-source code developed at NIST (National Institute of Standards and Technology, USA), which simulates basic physical and chemical processes related to fire, such as combustion, pyrolysis, thermal radiation, air circulation dynamics, airflows induced by fire, turbulence, fire suppression, etc. Some of the major features of the FDS code are the low-Mach large-eddy simulation, explicit second-order kinetic-energy-conserving numerics, Deardorff eddy viscosity, gray gas radiation, etc. These features have been widely used and validated for over two decades. FDS enables various types of 2D and 3D visualizations of fire courses and parameters. The complex dynamics of fire processes requires detailed resolution of the numerical mesh and a short time step to achieve sufficient calculation accuracy, which is demanding on computer performance and memory. FDS enables the simulation to be conducted in parallel on various platforms of high-performance computers to date.
There is extensive literature describing the various aspects of modeling fire and toxic smoke spread using FDS, modeling the course and effects of a fire and also modeling evacuation during a fire. Most researchers use laboratory-obtained data from small-scale models to validate simulations. Although there are a high number of practical applications in which FDS is used, there are not many papers in the literature dealing with the validation of tunnel fire simulation using data from large-scale experiments [
6,
7,
8,
9,
10], or such studies remain unpublished. The first validation study related to the FDS simulation of ventilation in a tunnel used a full-scale fire experiment conducted as part of the Massachusetts Highway Department Memorial Tunnel Fire Ventilation Test Program [
6]. The test consisted of a single-point supply of fresh air through a 28 m
2 opening in a 135 m tunnel. In [
7], a coupled hybrid (1D/3D-CFD) modeling methodology using the FDS 6 (version 6.7.5) was validated by full-scale fire tests in the 1600 m long Runehamar tunnel. For 6, 66 and 119 MW fires, temperature profiles, centerline velocity, backlayering lengths and maximum temperatures upstream and downstream from the fire source were investigated. The study [
8] examined three evacuation scenarios after a 20 MW fire accident in a 1500 m long railway tunnel with longitudinal ventilation and different ventilation activation times. The fire characteristics simulated by FDS were compared with empirical formulae based on small- and full-scale fire experiments. To investigate the effectiveness of water spray in blocking smoke and heat in a short underground belt transport tunnel in a mine with mechanical ventilation and a water curtain system, a full-scale fire test was conducted measuring selected fire characteristics [
9]. FDS (version 6.0.1) was then used to simulate smoke-spread characteristics, temperature distribution, visibility profiles and CO distribution. In [
10], a series of full-scale experiments with 1.35, 3 and 3.8 MW fires conducted in a short metro tunnel with mechanical ventilation system was described and then simulated by FDS (version 5.5). The smoke temperature and decay rate of the temperature distribution under the tunnel ceiling were investigated.
There are not many papers related to the validation of an airflow generated by emergency ventilation in a real tunnel (even without fire). However, the accurate reproduction of tunnel airflow is a key issue in modeling the operation of the tunnel ventilation system at any mode or fire development and smoke propagation in the event of fire [
4,
11]. To increase the confidence of practitioners and researchers in the ability of FDS to capture tunnel airflow, the average airflow velocity and velocity profile in the Dartford Tunnel (UK) were simulated using FDS 6 and then compared with in situ measurements [
12]. The tunnel is 1430 m long with a circular cross-section with a diameter of 8.5 m. Although it was modeled as a tunnel with a square cross-section, the results correlate well with the measurements. This research demonstrates the ability of FDS to simulate jet fans and the airflow they create. In [
13,
14], the airflow generated by jet fans with a relatively small diameter, which are popular in car park ventilation systems, was investigated. The suitability of different implementations of the turbulence model in the FDS 6 system for simulating such airflow was also discussed. The research confirmed the FDS 6’s ability to simulate airflow velocities generated by jet fans in larger enclosures. An important issue related to the modeling of airflow in the tunnel is the effect of reducing the thrust efficiency of the jet fan. This effect was experimentally studied in [
15,
16]. According to [
17], such losses due to momentum transfer and high shear stress of the wall can reach up to 20–30%. Installing the jet fans close to walls causes increased wall shear stress around the jet. In [
17], the results of two full-scale measurements of different jet fan installations were investigated in order to analyze the efficiency of the installation. These measurements were used to design and validate a numerical model.
In [
18], an FDS 6 model of the 898 m long Polana tunnel (Slovakia) was developed and its ability to simulate airflow generated by emergency ventilation was tested. The model was validated using a full-scale in situ ventilation test. A method of adjusting the parameters of the tunnel walls was proposed, reflecting the effect of the reduction in the thrust efficiency of the jet fans and the FDS limitations related to the resolution and type of the numerical mesh. One of the three tested ventilation operation modes was used to set up the model, and then the data from the entire ventilation test were used to validate the model with respect to time-averaged steady-state airflow velocities. A comparison with the experimental data confirmed the very good accuracy of the simulation results of the time-averaged velocity measured by a grid of anemometers located in the tunnel cross-section, but pointed to a relatively lower accuracy of the simulation for the tunnel anemometers.
In this paper, we analyze the simulation results presented in [
18], propose an improved representation of tunnel anemometers and contribute to a better validation of the model. A substantial improvement in the modeling accuracy of the airflow velocity determined by tunnel anemometers is demonstrated. The data from the ventilation test are used to validate the improved model with respect to the average velocity and the time-averaged velocity of the steady-state ventilation-generated airflow measured by grid and tunnel anemometers.
3. Results and Discussion
The simulation described above was performed on the Intel(R) Core(TM) i7-8700K CPU@3.7 GHz computer (6 cores, 64 GB RAM). In this section, the simulation results are compared with the ones reported in [
18], where the results were validated in regard of the time-averaged airflow velocities within selected time intervals where the airflow velocity was considered to be stabilized. In [
18], a very good agreement of simulated and experimental results was reported for the velocities measured by the grid anemometers; however, a relatively lower accuracy was observed for velocities measured by the tunnel anemometers. The improved model and validation procedure described in this paper can be characterized as follows:
The analysis focused on the airflows generated by the three operation modes of ventilation operation (modes 1–3) during which the ventilation relatively soon created a stabilized airflow, the velocity of which was measured by the grid and tunnel anemometers. The average airflow and time-averaged airflow velocities at selected time intervals, where the airflow velocity was considered to be stabilized, were calculated. For the three individual ventilation modes, the 6 min time intervals 900–1260, 2760–3120 and 5390–5750 s were considered. We noted that although the Mode 1 ventilation scenario was used to set up the model’s parameters, in the following section, we include it when evaluating the simulation results as well, due to completeness.
3.1. Modeling Average Airflow Velocity Measured by the Grid Anemometers
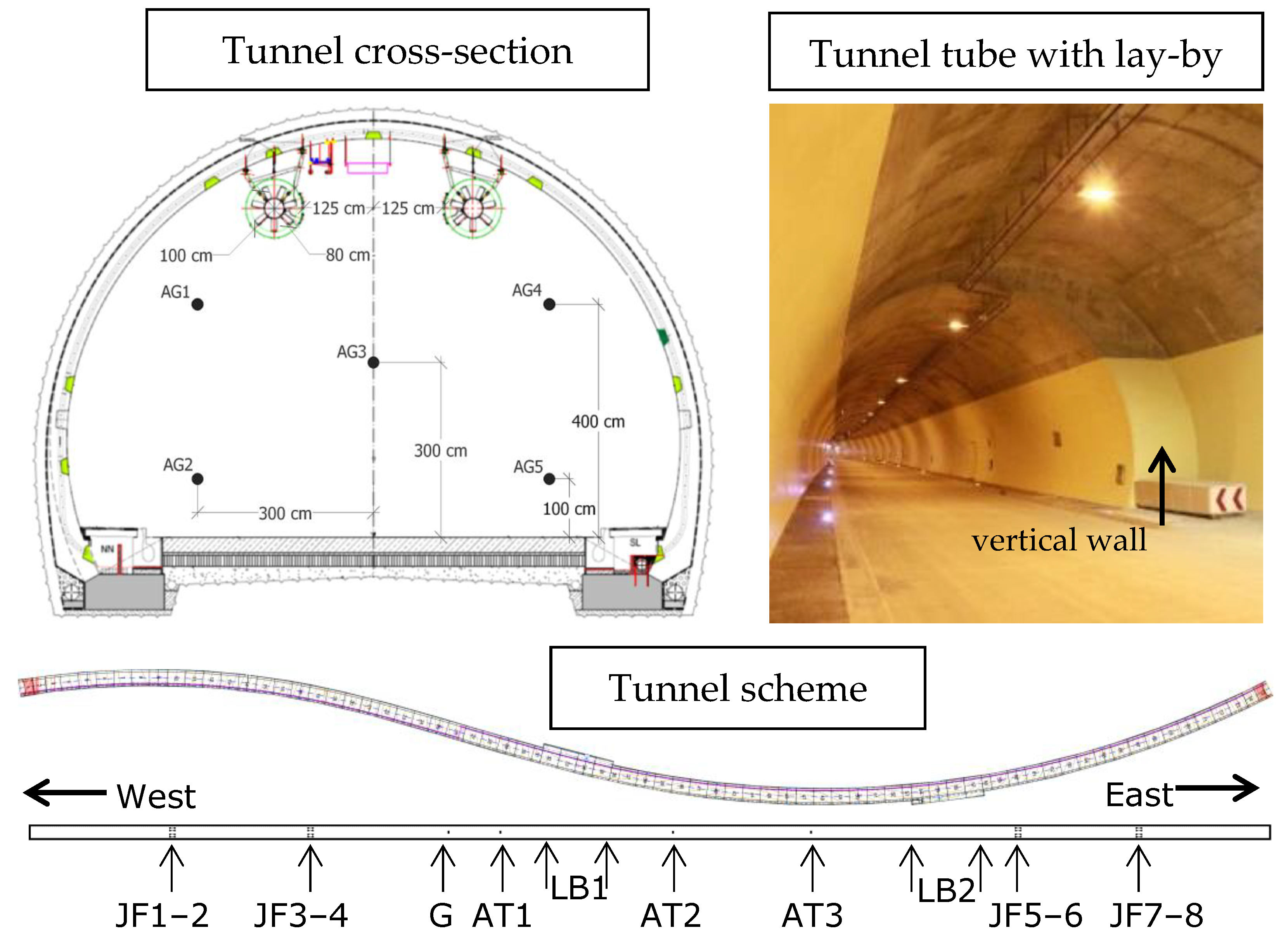
In
Figure 4, the values of the average airflow velocities in the experiment (represented by the black curve) and simulation (represented by the red curve) are shown. They were calculated as an arithmetic mean of the airflow velocities measured by the grid anemometers (AG1–5) for all the three ventilation modes measured at the considered time intervals by the grid anemometers. Relatively small differences between the experimental and simulation data can be observed. In
Figure 5 and
Figure 6, absolute and relative differences between the average airflow velocities obtained by the experiment and the simulation are illustrated for all the three ventilation modes. The maximal values of the differences are shown in
Table 3. The results indicate that the average velocities measured by the grid anemometers in the simulation differ from the experimental data by values lower (or in exceptional cases by relatively very close values) than the measurement accuracy of the grid anemometers (0.3 m/s). This evaluation indicates a relatively very good accuracy of average airflow velocity modeling using grid anemometers compared to the measurement accuracy of the grid anemometers.
3.2. Modeling Time-Averaged Airflow Velocity Measured by the Grid Anemometers
In this section, we followed the evaluation presented in [
18] in regard to the values of the time-averaged airflow velocities measured at selected time intervals by the grid anemometers (AG1–5). The comparison of the velocity values calculated by the procedure described here and the one reported in [
18] is shown in
Table 4,
Table 5 and
Table 6. The results indicate that the time-averaged airflow velocities obtained by both procedures differ from the experimental data by values significantly lower than the measurement accuracy of grid anemometers (0.3 m/s) for all the ventilation modes. This points to the high accuracy of the airflow velocity modeling by the grid measurement compared to the measurement accuracy of the grid anemometers.
3.3. Modeling Average Velocity Measured by the Tunnel Anemometers
In
Figure 7, the average airflow velocities measured by the tunnel anemometers AT1–3 in the experiment and in both simulations in the considered time intervals are illustrated. The figure indicates that the improved representation of the tunnel anemometers in the simulation (represented by the red color) presents significantly less differences in the simulation results from the experimental data (represented by the black color), while the simulation results reported in [
18] (represented by the yellow curve) relatively significantly overestimate the values of the average airflow velocity in Mode 1 and underestimate the values of the average airflow velocity in both the other tested modes of ventilation operation (modes 2–3). In
Figure 8 and
Figure 9, the absolute and relative differences between the average airflow velocities obtained by both the considered simulations and experimental data are illustrated. In
Table 7, the maximum and minimum differences between experimental and simulated average airflow velocities are shown. The curves indicate that the result’s accuracy corresponding to the simulation presented here is much better than the one corresponding to the simulation from [
18]. The average airflow velocities measured by the tunnel anemometers in both the simulations differ from the experimental data by values greater than the measurement accuracy of the tunnel anemometers (in the case of Mode 2 in the simulation presented in this paper by slightly higher values). However, the difference in the accuracy of the considered simulations is noticeable (
Table 7).
3.4. Modeling Average Velocity Measured by the Tunnel Anemometers: Moving Average
When evaluating the simulation results, we to date considered the velocity values measured by tunnel anemometers, which tend to slightly fluctuate, even though in practice it is customary to consider several velocity values when monitoring and evaluating the airflow velocity at a given time. Therefore, in
Figure 10,
Figure 11 and
Figure 12 we present a 5-point moving average of the corresponding velocity values to illustrate the underlying trends of the measured velocity in the experimental data and in both the simulations. In this way, we eliminated to some extent the tendency of the velocity values to fluctuate slightly, similarly to what the tunnel’s CCS does. In
Table 8, the maximum and minimum differences between experimental and simulated average airflow velocities determined by moving average are shown. The illustrations confirm the large difference between the results’ accuracies of the simulation presented in this paper and in [
18]. Relatively sufficient (although less) accuracy with respect to the measurement accuracy of the tunnel anemometers it can be observed for modes 2 and 3. The accuracy for model 1 is lower, but can still be considered sufficient for practical purposes. However, relatively high inaccuracies in the simulation results presented in [
18] are observed. From this analysis, it can be concluded that the improved representation of the tunnel anemometers significantly increased the accuracy of the simulation, and the achieved accuracy appears to be sufficient for the practical use.
3.5. Modeling Time-Averaged Airflow Velocity Measured by the Tunnel Anemometers
In this section, we again followed the evaluation presented in [
18] to illustrate the significant improvement in the accuracy of the results presented here related to the accuracy of measurement of the value of the stable airflow velocity generated by the ventilation.
In
Table 9,
Table 10 and
Table 11, the time-averaged airflow velocities measured by the tunnel anemometers AT1–3 in the considered time intervals in the experiment and in both simulations and their comparison are shown. The tables indicate that the time-averaged velocity obtained based on measurements by tunnel anemometers in the simulation reported in [
18] differs from the time-averaged velocity obtained from experimental data from the tunnel anemometers by significantly more than the accuracy value of the grid anemometers (0.3 m/s), which points to the insufficient accuracy of the used representation of the measurement by tunnel anemometers. The results of the simulation presented in this paper indicate a significant increase in the accuracy of modeling the measurement by the tunnel anemometers, while the deviations from experimentally obtained values are less than the accuracy of the grid anemometers (0.3 m/s), but in the case of modes 1 and 3, slightly higher than the accuracy of the tunnel anemometers (0.1 m/s). However, such accuracy of modeling can be considered sufficient for practical applications of the model.