The Spatio-Temporal Evolution of Rock Failure Due to Blasting under High Stress
Abstract
1. Introduction
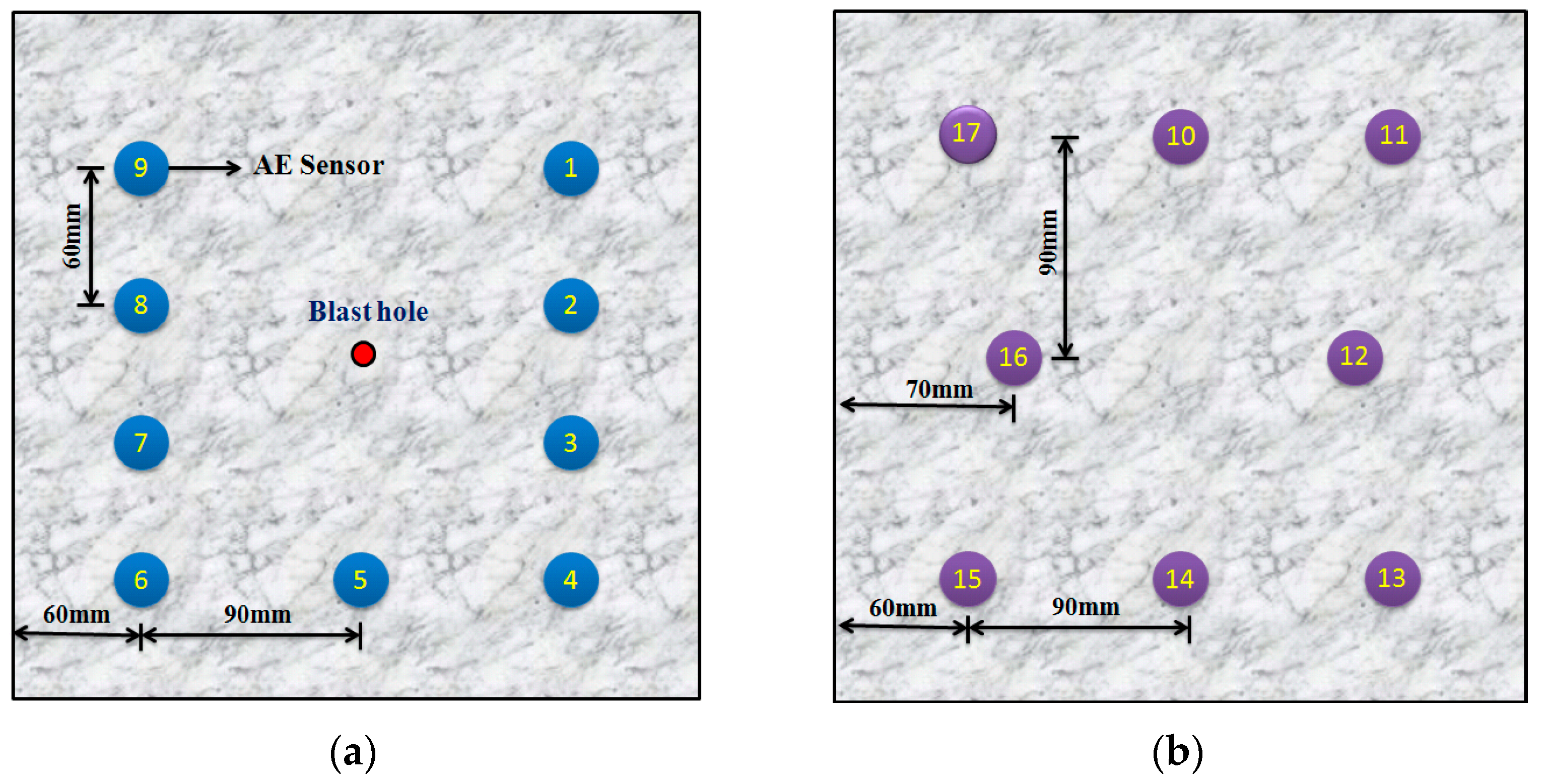
2. Test Schemes
3. AE Location Method and Verification of Its Accuracy
4. Features of AE Time Series for Rock Fracture under the Effect of Blasting
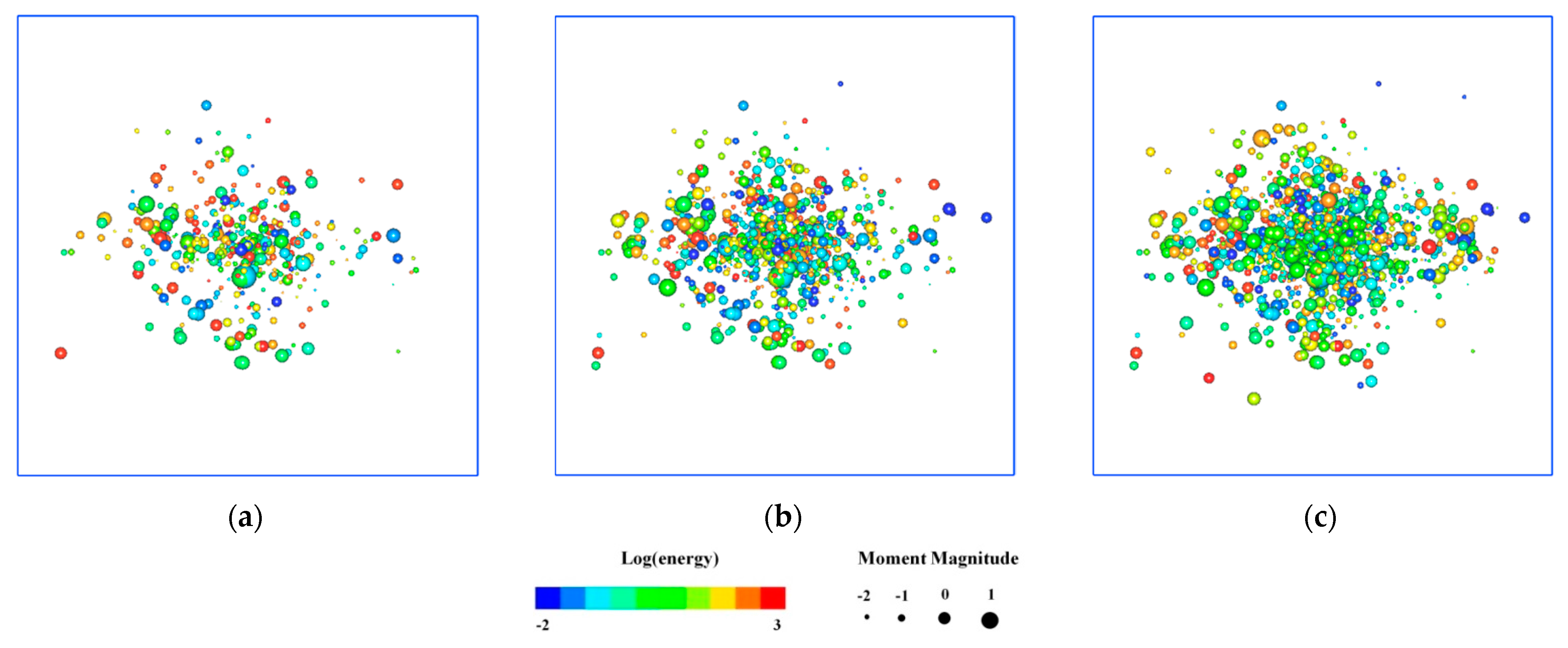
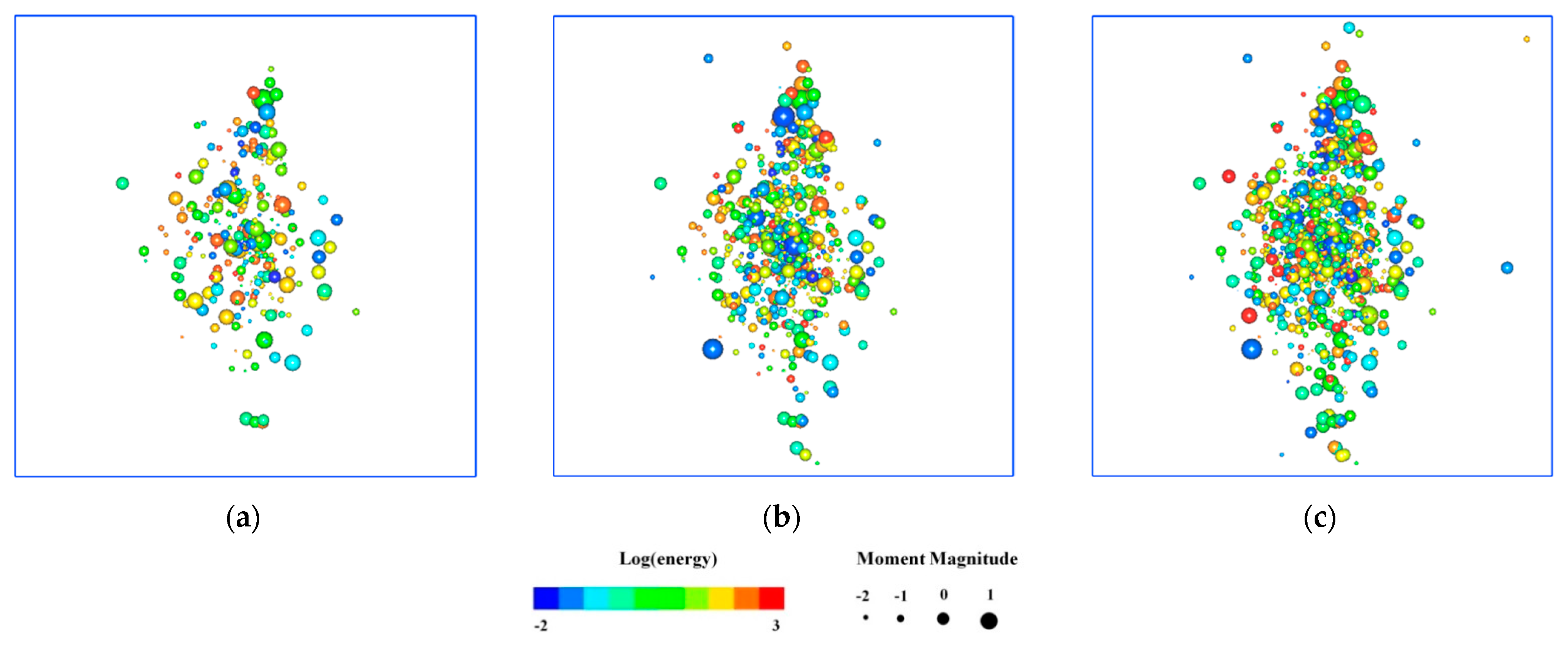
5. Spatial Evolution of AE for Rock Fracture under the Effect of Blasting
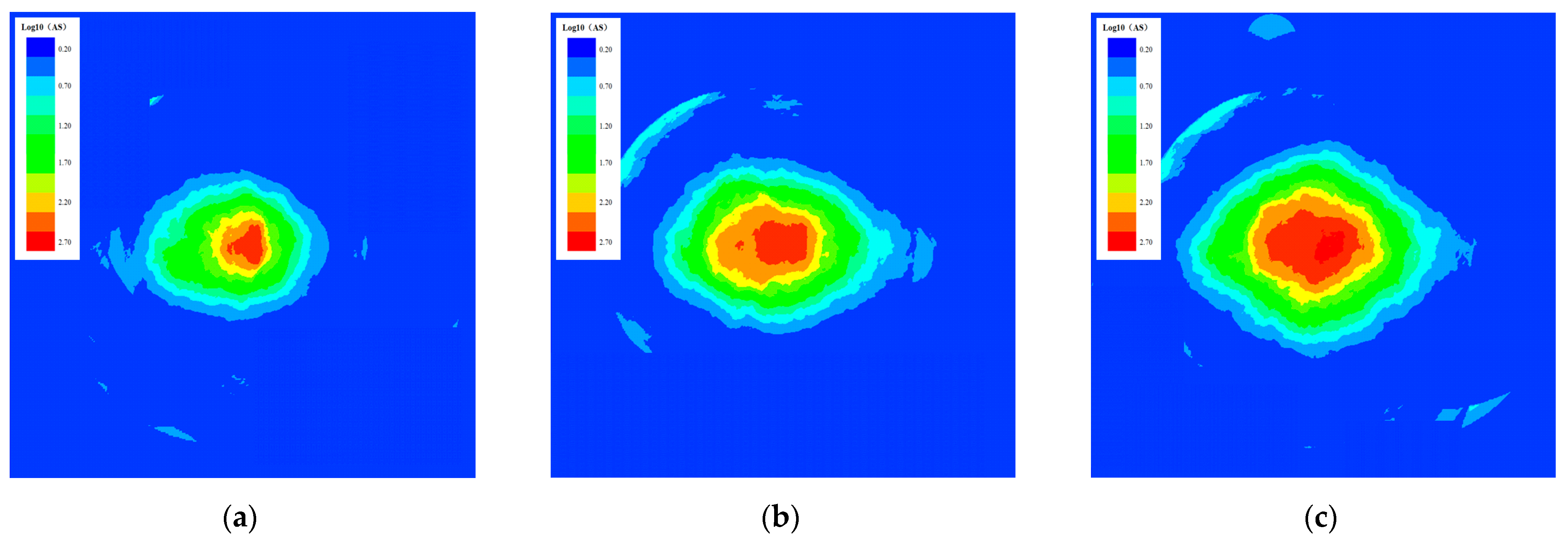
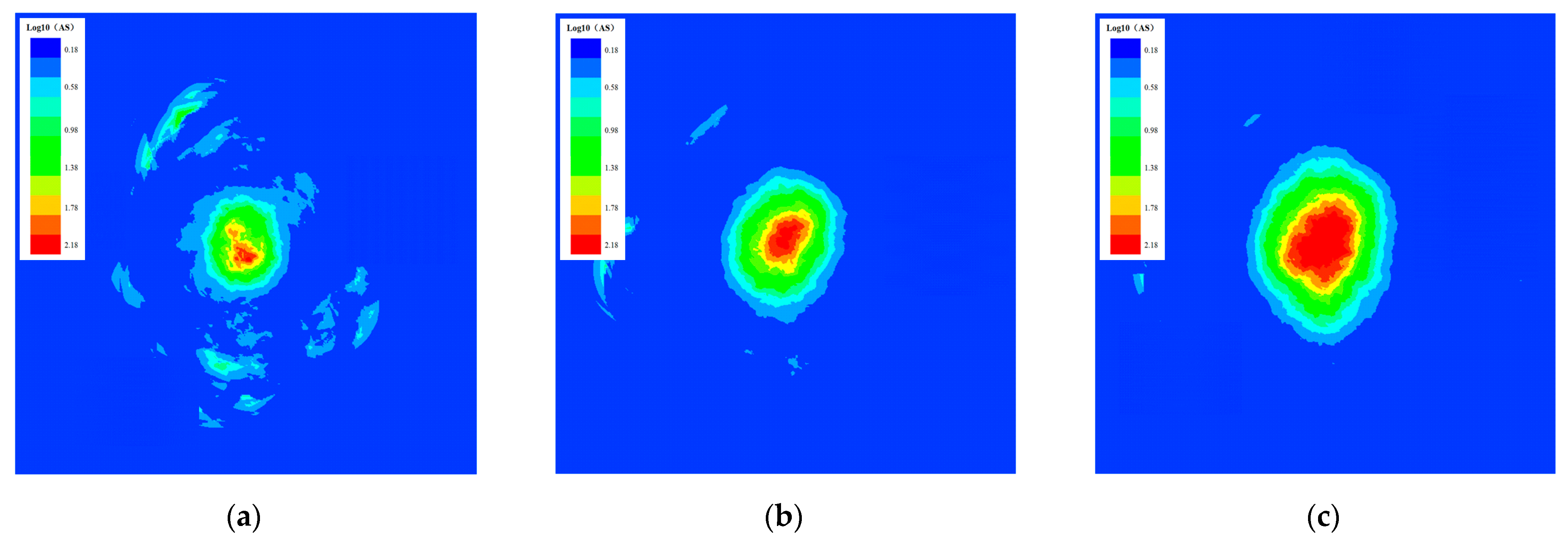
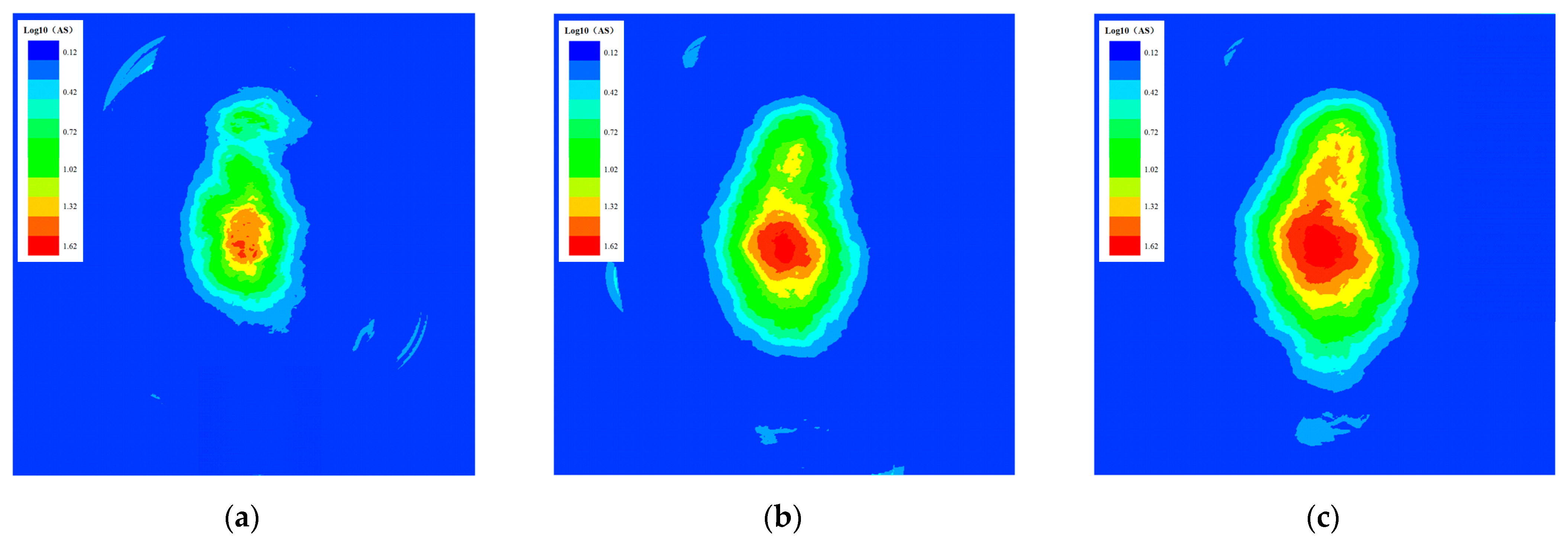
6. Distribution of the Apparent Stress Field under the Effect of Blasting
7. Numerical Simulation of the Blasting-Induced Damage in Rock
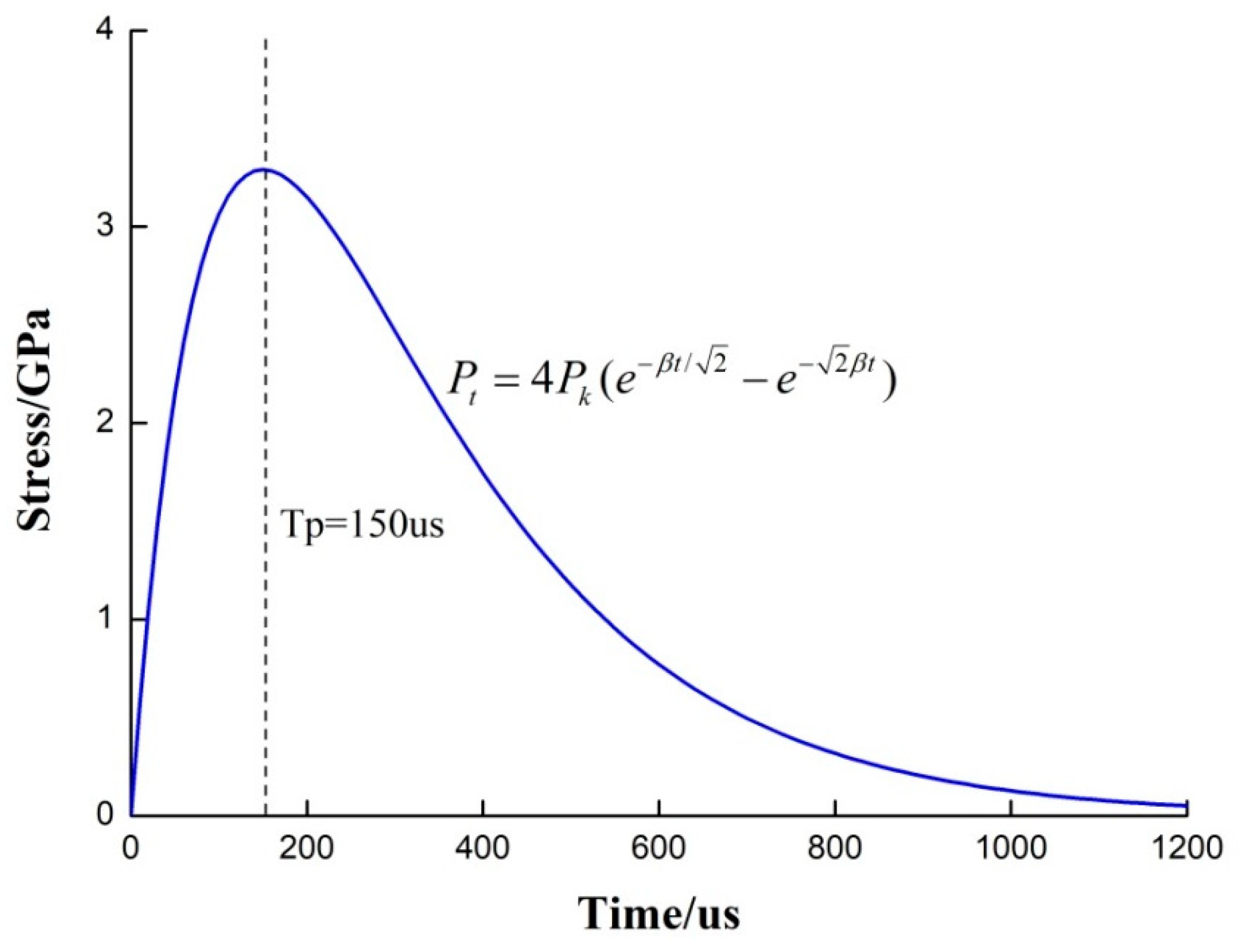
7.1. Design of the Test Schemes
7.2. Analysis of Test Results
8. Conclusions
- (1)
- Both stress loading and blasting disturbance will cause damage and destruction in the specimen, stress loading has the greatest contribution to specimen failure. The single sample test shows that the proportion of AE signal generated by explosion disturbance increases with the increase of explosion times. The test results of different groups of samples show that the higher the stress level of rock mass is, the higher the AE signal ratio generated by blasting disturbance is, and the blasting disturbance is more likely to damage and destroy the rock mass in high stress state.
- (2)
- The spatial distribution of AE events shows that the maximum principal stress plays a remarkable role of directional guidance in the generation and propagation of blasting-induced cracks. The strain energy stored in different zones of the samples differs greatly due to different initial stress environments and the elastic energy stored in the samples is gradually released during blasting. Therefore, the AE events in the direction of the maximum principal stress of the sample after blasting are significantly increased.
- (3)
- The results of numerical simulation reveal that the damage zone induced by blasting gradually extends due to the effect of dynamic loads before the blasting-induced stress waves reach the peak stress. The presence of the initial stress field influences the propagation of explosive detonation waves, thus playing an obvious role of directional guidance in the development of the tensile failure zones. The direction of development of the damage zones is consistent with the direction of the maximum principal stress.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, K.; Pan, H.; Zhang, T.; Wang, H. Experimental study on the radial vibration characteristics of a coal briquette in each stage of its life cycle under the action of CO2 gas explosion. Fuel 2022, 320, 123922. [Google Scholar] [CrossRef]
- Du, K.; Liu, M.; Yang, C.; Tao, M.; Feng, F.; Wang, S. Mechanical and Acoustic Emission (AE) characteristics of rocks under biaxial confinements. Appl. Sci. 2021, 11, 769. [Google Scholar] [CrossRef]
- Lin, X.; Li, B.; Li, P.; Ding, Q.; Huang, M. Study of the evolution characteristics of Microseismic Events during the excavation of underground caverns under high geostress. Appl. Sci. 2022, 12, 12145. [Google Scholar] [CrossRef]
- Huo, X.; Shi, X.; Qiu, X.; Chen, H.; Zhou, J.; Zhang, S.; Rao, D. Study on rock damage mechanism for lateral blasting under high in situ stresses. Appl. Sci. 2021, 11, 4992. [Google Scholar] [CrossRef]
- Gong, F.; Hao, Y.; Yong, L. The Effect of High Loading Rate on the Behaviour and Mechanical Properties of Coal-Rock Combined Body. Shock. Vib. 2018, 2018, 4374530. [Google Scholar] [CrossRef]
- Li, J.C.; Rong, L.F.; Li, H.B.; Hong, S.N. An SHPB Test Study on Stress Wave Energy Attenuation in Jointed Rock Masses. Rock Mech. Rock Eng. 2018, 2018, 403–420. [Google Scholar] [CrossRef]
- Sun, C.; Li, C.; Wei, X. Research on seismic wave quality factor of marble jointed rock mass under SHPB impact. Appl. Sci. 2022, 12, 10875. [Google Scholar] [CrossRef]
- Christensen, R.; Swanson, S.; Brown, W. Split-Hopkinson-bar tests on rock under confining pressure. Exp. Mech. 1972, 12, 508–513. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Z.; Lok, T.S.; Hong, L.; Yin, T. Innovative testing technique of rock subjected to coupled static and dynamic loads. Int. J. Rock Mech. Min. Sci. 2008, 45, 739–748. [Google Scholar] [CrossRef]
- Li, Y.; Peng, J.; Zhang, F.; Qiu, Z. Cracking behavior and mechanism of sandstone containing a pre-cut hole under combined static and dynamic loading. Eng. Geol. 2016, 213, 64–73. [Google Scholar] [CrossRef]
- He, C.; Yang, J.; Qi, Y. Laboratory study on the dynamic response of rock under blast loading with active confining pressure. Int. J. Rock Mech. Min. Sci. 2018, 102, 101–108. [Google Scholar] [CrossRef]
- Zhu, W.C.; Gai, D.; Wei, C.H.; Li, S.G. High-pressure air blasting experiments on concrete and implications for enhanced coal gas drainage. J. Nat. Gas Sci. Eng. 2016, 36, 1253–1263. [Google Scholar] [CrossRef]
- Zhang, F.; Peng, J.; Qiu, Z.; Chen, Q.; Li, Y.; Liu, J. Rock-like brittle material fragmentation under coupled static stress and spherical charge explosion. Eng. Geol. 2017, 220, 266–273. [Google Scholar] [CrossRef]
- Yi, C.; Johansson, D.; Greberg, J. Effects of in-situ stresses on the fracturing of rock by blasting. Comput. Geotech. 2017, 104, 321–330. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, W.; Chen, M.; Yan, P.; Zhang, Y. Numerical simulation of the complete rock blasting response by SPH–DAM–FEM approach. Simul. Model. Pract. Theory 2015, 56, 55–68. [Google Scholar] [CrossRef]
- Ma, G.W.; An, X.M. Numerical simulation of blasting-induced rock fractures. Int. J. Rock Mech. Min. Sci. 2008, 45, 966–975. [Google Scholar] [CrossRef]
- Jian-po, L.; Chang-yin, Z.; Ying-tao, S.; Ren, W.; Gang, L.; Shi-da, X. Temporal-spatial evolution of acoustic emission during progressive fracture processes around tunnel triggered by blast-induced disturbances under uniaxial and biaxial compression. Tunn. Undergr. Space Technol. 2020, 96, 103229. [Google Scholar] [CrossRef]
- Long, Y.; Liu, J.P.; Lei, G.; Si, Y.T.; Zhang, C.Y.; Wei, D.C.; Shi, H.X. Progressive fracture processes around tunnel triggered by blast disturbances under biaxial compression with different lateral pressure coefficients. Trans. Nonferrous Met. Soc. China 2020, 30, 2518–2535. [Google Scholar] [CrossRef]
- Yuan-hui, L.; Gang, L.; Shi-da, X.; Da-wei, W. The spatial-temporal evolution law of microseismic activities in the failure process of deep rock masses. J. Appl. Geophys. 2018, 154, 1–10. [Google Scholar] [CrossRef]
- Choy, G.L.; Boatwright, J.L. Global patterns of radiated seismic energy and apparent stress. J. Geophys. Res. Solid Earth. 1995, 100, 18205–18228. [Google Scholar] [CrossRef]
- Lasocki, S.; Orlecka-Sikora, B. Seismic hazard assessment under complex source size distribution of mining-induced seismicity. Tectonophysics 2008, 456, 28–37. [Google Scholar] [CrossRef]
- Newman, A.V.; Okal, E.A. Teleseismic estimates of radiated seismic energy: The E/M 0 discriminant for tsunami earthquakes. J. Geophys. Res. Solid Earth. 1998, 103, 26885–26898. [Google Scholar] [CrossRef]
- Brune, J.N.; Brune, J.N. Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys. Res. 1970, 75, 4997–5009. [Google Scholar] [CrossRef]
- Archuleta, R.J.; Cranswick, E.; Mueller, C.; Spudich, P. Source parameters of the 1980 Mammoth Lakes, California earthquake sequence. J. Geophys. Res. Solid Earth. 1982, 87, 4595–4607. [Google Scholar] [CrossRef]
- Li, J.C.; Li, H.B.; Ma, G.W.; Zhou, Y.X. Assessment of underground tunnel stability to adjacent tunnel explosion. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2013, 35, 227–234. [Google Scholar] [CrossRef]
- Eissa, E.; Kazi, A. Relation between static and dynamic Young’s moduli of rocks. Int. J. Rock Mech. Min. Geomech. Abstr. 1988, 25, 479–482. [Google Scholar] [CrossRef]
- Yilmaz, O.; Unlu, T. Three dimensional numerical rock damage analysis under blasting load. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2013, 38, 266–278. [Google Scholar] [CrossRef]







 No damage
No damage  Shear failure
Shear failure  Tensile failure.
Tensile failure.
 No damage
No damage  Shear failure
Shear failure  Tensile failure.
Tensile failure.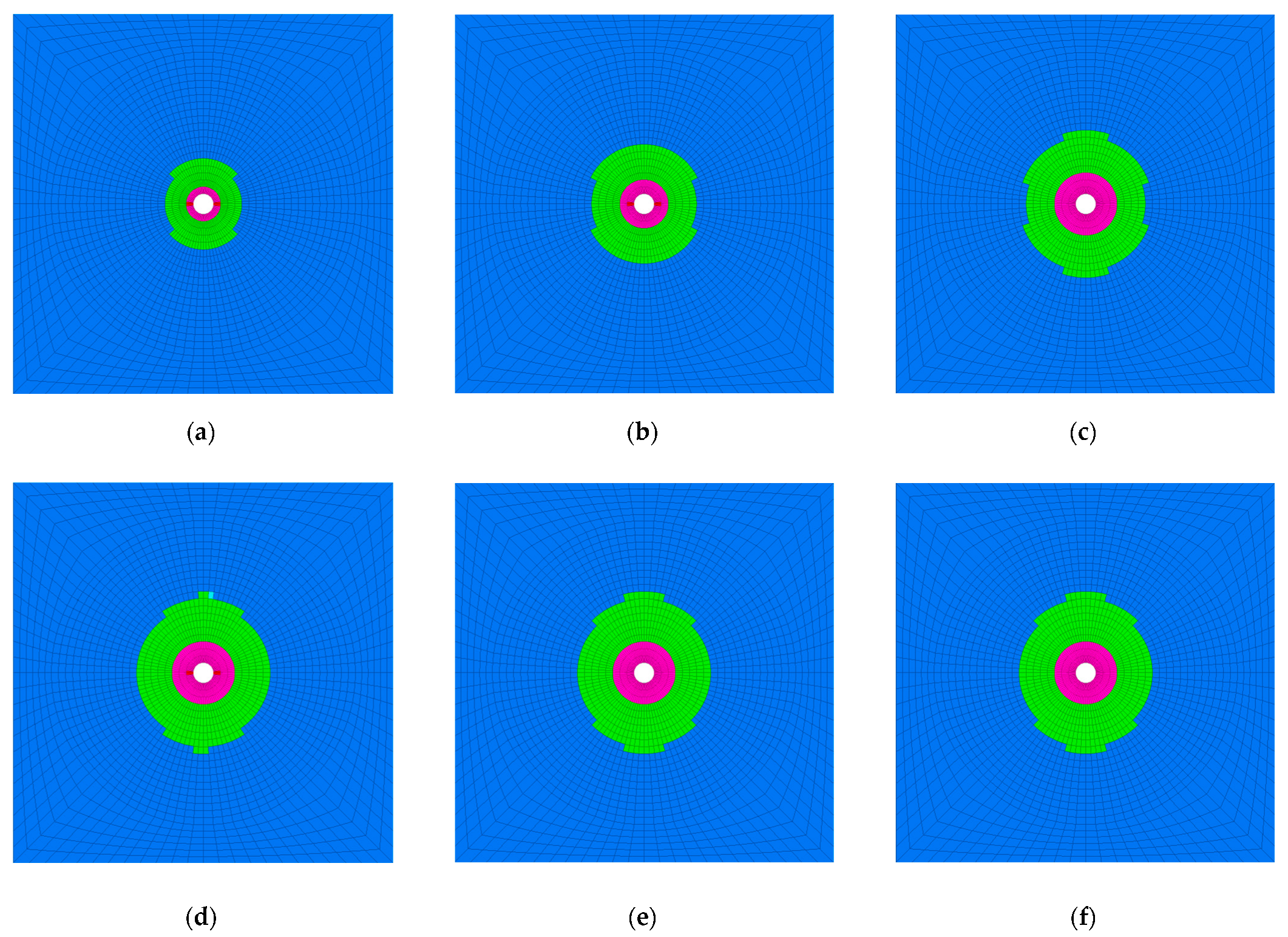
 No damage;
No damage;  Shear failure;
Shear failure;  Tensile failure.
Tensile failure.
 No damage;
No damage;  Shear failure;
Shear failure;  Tensile failure.
Tensile failure.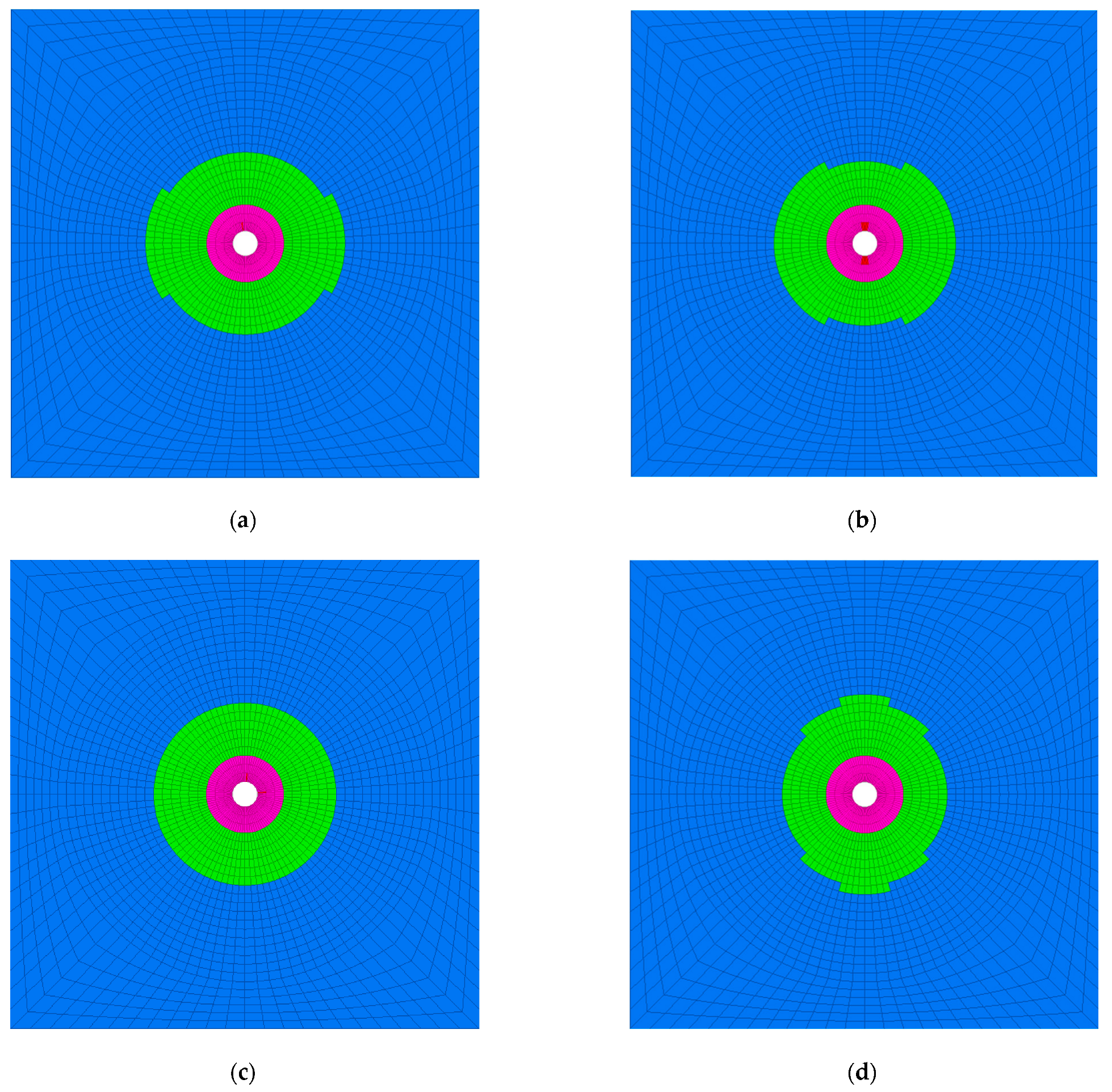
| Test Plan | Model Number | P2/MPa | P1/MPa | Number of Blasting Operations | Mass of Charge/g | Lateral Pressure Coefficient |
|---|---|---|---|---|---|---|
| 1 | N1–1, N1–2 and N1–3 | 16 | 32 | 6 | 1 | 2.0 |
| 2 | N2–1, N2–2 and N2–3 | 16 | 24 | 6 | 1 | 1.5 |
| 3 | N3–1, N3–2 and N3–3 | 16 | 16 | 6 | 1 | 1.0 |
| 4 | N4–1, N4–2 and N4–3 | 16 | 8 | 6 | 1 | 0.5 |
| Test Plan | Model Number | P2/MPa | P1/MPa | Blast Number | Lateral Pressure Coefficient |
|---|---|---|---|---|---|
| 1 | M1–1 | 20 | 40 | 1 | 2.0 |
| 2 | M2–1 | 20 | 30 | 1 | 1.5 |
| 3 | M3–1 | 20 | 20 | 1 | 1.0 |
| 4 | M4–1 | 20 | 10 | 1 | 0.5 |
| Conditions | Shear Modulus (GPa) | Bulk Modulus (GPa) | Tensile Strength (MPa) | Friction Angle (°) | Cohesion (MPa) |
|---|---|---|---|---|---|
| Static | 33.6 | 56 | 3.92 | 44.19 | 20.1 |
| Dynamic | 42.2 | 70.3 | 33.8 | 44.19 | 173 |
| Explosive Type | The Density (kg/m3) | The Propagation Velocity (m/s) of Detonation Waves | Rise-Time to Peak Pressure (μs) |
|---|---|---|---|
| Emulsion explosives | 1250 | 5582 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, G.; Zhu, S.; Shi, X.; Wu, D. The Spatio-Temporal Evolution of Rock Failure Due to Blasting under High Stress. Appl. Sci. 2023, 13, 2781. https://doi.org/10.3390/app13052781
Lei G, Zhu S, Shi X, Wu D. The Spatio-Temporal Evolution of Rock Failure Due to Blasting under High Stress. Applied Sciences. 2023; 13(5):2781. https://doi.org/10.3390/app13052781
Chicago/Turabian StyleLei, Gang, Shengyan Zhu, Xiaozhang Shi, and Dawei Wu. 2023. "The Spatio-Temporal Evolution of Rock Failure Due to Blasting under High Stress" Applied Sciences 13, no. 5: 2781. https://doi.org/10.3390/app13052781
APA StyleLei, G., Zhu, S., Shi, X., & Wu, D. (2023). The Spatio-Temporal Evolution of Rock Failure Due to Blasting under High Stress. Applied Sciences, 13(5), 2781. https://doi.org/10.3390/app13052781




