Numerical Analysis of Seismic Pounding between Adjacent Buildings Accounting for SSI
Abstract
:1. Introduction
2. Theoretical Model Framework
2.1. Equation of Motion
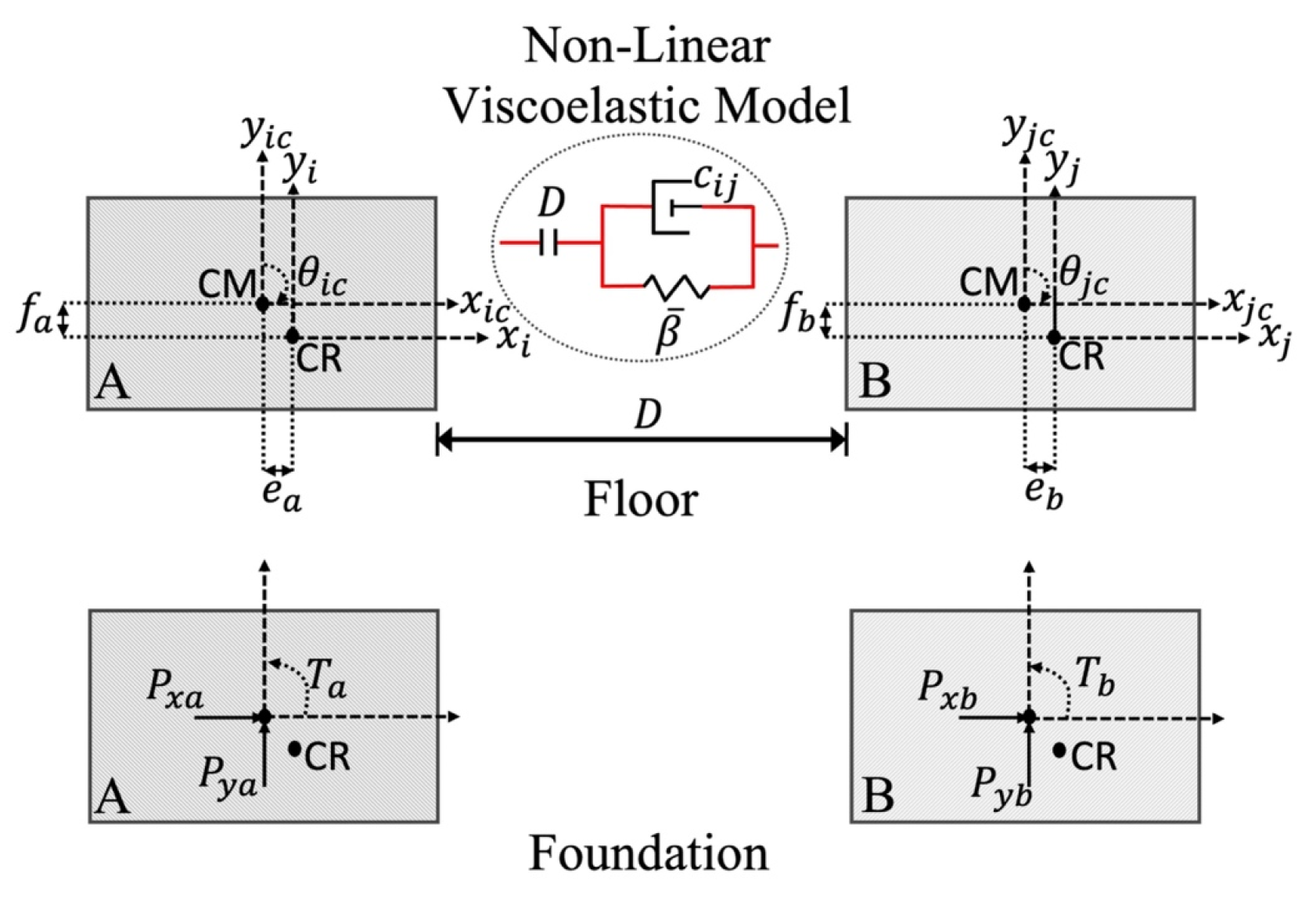
2.2. Pounding Forces
2.3. Approximate Normal Modes of Adjacent Buildings
2.4. Equation of Motion for SSI System
3. Numerical Study
3.1. Structure Properties
3.2. Response Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notations
| symbolized Building A | |
| dimensionless frequency | |
| symbolized Building B | |
| , | mass ratios for sliding, rocking, and torsion |
| damping matrices of the SSI system for each building | |
| submatrices of damping in x- and y-axis for Building A | |
| ith floor damping coefficient in the longitudinal and transverse directions for Building A | |
| jth floor damping coefficient in the longitudinal and transverse directions for Building B | |
| damping of impact element | |
| CM, CR | center of mass and resistance |
| torsional damping matrices of Building A in relation to CR and CM | |
| , | damping of soil dashpots |
| distance between buildings | |
| , | damping ratio of soil dashpots |
| coefficient of restitution | |
| , | eccentricity in x-direction of Buildings A and B |
| , | column vector with all elements equal to , |
| pounding force vector | |
| , | pounding force influence coefficient vectors in longitudinal, transverse, and vertical directions |
| , | shear force matrices of SSI system for each building |
| shear force of ith floor | |
| , | yield strength of ith floor |
| eccentricity in y-direction of Buildings A and B | |
| column vector with all elements equal to | |
| maximum wave frequency | |
| shear modulus of soil | |
| , | height of ith and jth floor level |
| , | column vector composed of story heights |
| , | moments of inertia of ith and jth floors |
| , , , | moments of inertia of the base for each building |
| , | polar moment of inertia and moment of inertia for rocking of each building |
| , | stiffness matrices of SSI system for each building |
| submatrices of stiffness in x- and y-axis for Building A | |
| ith floor stiffness coefficient in longitudinal and transverse directions for Building A | |
| jth floor stiffness coefficient in longitudinal and transverse directions for Building B | |
| torsional stiffness matrices of Building A in relation to CR and CM | |
| , | stiffness of soil springs |
| , | generalized mass matrix of SSI systems of each building |
| mass of related building | |
| mass matrix of superstructure | |
| mass at ith floor of Building A | |
| mass at jth floor of Building B | |
| , | foundation masse |
| N | number of stories of Building A |
| , | loading vector of SSI system |
| SSI forces | |
| SSI moments | |
| , | radius of gyration in relation to mass center |
| radius of a circle having same area as building plan | |
| S | number of stories of Building B |
| , | SSI torques of buildings |
| t | time variable |
| , | deformation vector of Buildings A and B |
| shear wave velocity of soil | |
| x- and y-directional displacement vectors of buildings with SSI effects | |
| x- and y-directional displacement vectors of buildings without SSI effects | |
| , , , | total displacement vectors of center mass of floors |
| , | x- and y-directional displacements of foundations of buildings |
| , | ground acceleration records |
| constant for determining classical damping | |
| impact stiffness parameter | |
| , | rotational vector of building with and without SSI effects |
| relative displacement influence coefficient with respect to ground | |
| relative velocity influence coefficient with respect to ground | |
| time step | |
| damping ratio related to e | |
| friction coefficient during collision | |
| circular frequency of applied excitation | |
| or column vector with all elements equal to 1 | |
| vector of zeros |
References
- Zembaty, Z.; Cholewicki, A.; Jankowski, R.; Szulc, J. Trzęsienia ziemi 21 września 2004 r. w Polsce północno-wschodniej oraz ich wpływ na obiekty budowlane (Earthquakes of September 21, 2004 in north-eastern Poland and their effects on structures). Inżynieria I Bud. 2005, 61, 3–9. (In Polish) [Google Scholar]
- Zembaty, Z.; Jankowski, R.; Cholewicki, A.; Szulc, J. Trzęsienie ziemi 30 listopada 2004 r. na Podhalu oraz jego wpływ na obiekty budowlane (Earthquake of November 30, 2004 in Podhale and its effects on structures). Inżynieria I Bud. 2005, 61, 507–511. (In Polish) [Google Scholar]
- Kasai, K.; Maison, B.F. Building pounding damage during the 1989 Loma Prieta earthquake. Eng. Struct. 1997, 19, 195–207. [Google Scholar] [CrossRef]
- Vasiliadis, L.; Elenas, A. Performance of school buildings during the Athens earthquake of 7 September 1999. In Proceedings of the 12th European Conference on Earthquake Engineering, London, UK, 9–13 September 2002. [Google Scholar]
- Kamgar, R.; Tavakoli, R.; Rahgozar, P.; Jankowski, R. Application of discrete wavelet transform in seismic nonlinear analysis of soil–structure interaction problems. Earthq. Spectra 2021, 37, 1980–2012. [Google Scholar] [CrossRef]
- Karafagka, S.; Fotopoulou, S.; Pitilakis, D. Fragility assessment of non-ductile RC frame buildings exposed to combined ground shaking and soil liquefaction considering SSI. Eng. Struct. 2021, 229, 111629. [Google Scholar] [CrossRef]
- Duan, W.; Congress, S.S.C.; Cai, G.; Liu, S.; Dong, X.; Chen, R.; Liu, X. A hybrid GMDH neural network and logistic regression framework for state parameter–based liquefaction evaluation. Can. Geotech. J. 2021, 99, 1801–1811. [Google Scholar] [CrossRef]
- Özcebe, A.G.; Giretti, D.; Bozzoni, F.; Fioravante, V.; Lai, C.G. Centrifuge and numerical modelling of earthquake-induced soil liquefaction under free-field conditions and by considering soil-structure interaction. Bull. Earthq. Eng. 2021, 19, 47–75. [Google Scholar] [CrossRef]
- Duan, W.; Zhao, Z.; Cai, G.; Pu, S.; Liu, S.; Dong, X. Evaluating model uncertainty of an in situ state parameter-based simplified method for reliability analysis of liquefaction potential. Comput. Geotech. 2022, 151, 104957. [Google Scholar] [CrossRef]
- Madabhushi, G.S.P.; Garcia-Torres, S. Sustainable measures for protection of structures against earthquake induced liquefaction. Indian Geotech. J. 2021, 51, 467–481. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A. Pounding of buildings in series during earthquakes. Earthq. Eng. Struct. Dyn. 1988, 16, 443–456. [Google Scholar] [CrossRef]
- Flenga, M.G.; Favvata, M.J. Fragility Curves and Probabilistic Seismic Demand Models on the Seismic Assessment of RC Frames Subjected to Structural Pounding. Appl. Sci. 2021, 11, 8253. [Google Scholar] [CrossRef]
- Kazemi, F.; Mohebi, B.; Jankowski, R. Predicting the seismic collapse capacity of adjacent SMRFs retrofitted with fluid viscous dampers in pounding condition. Mech. Syst. Signal Process. 2021, 161, 107939. [Google Scholar] [CrossRef]
- Miari, M.; Jankowski, R. Incremental dynamic analysis and fragility assessment of buildings founded on different soil types experiencing structural pounding during earthquakes. Eng. Struct. 2022, 252, 113118. [Google Scholar] [CrossRef]
- Polycarpou, P.C.; Papaloizou, L.; Komodromos, P. An efficient methodology for simulating earthquake-induced 3D pounding of buildings. Earthq. Eng. Struct. Dyn. 2014, 43, 985–1003. [Google Scholar] [CrossRef]
- Chau, K.T.; Wei, X.X. Pounding of structures modelled as non-linear impacts of two oscillators. Earthq. Eng. Struct. Dyn. 2001, 30, 633–651. [Google Scholar] [CrossRef]
- Favvata Maria, J.; Karayannis Chris, G.; Liolios Asterios, A. Influence of exterior joint effect on the inter-story pounding interaction of structures. Struct. Eng. Mech. 2009, 33, 113–136. [Google Scholar] [CrossRef]
- Jing, H.-S.; Young, M. Impact interactions between two vibration systems under random excitation. Earthq. Eng. Struct. Dyn. 1991, 20, 667–681. [Google Scholar] [CrossRef]
- Kazemi, F.; Miari, M.; Jankowski, R. Investigating the effects of structural pounding on the seismic performance of adjacent RC and steel MRFs. Bull. Earthq. Eng. 2021, 19, 317–343. [Google Scholar] [CrossRef]
- Khatami, S.M.; Naderpour, H.; Barros, R.C.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Determination of Peak Impact Force for Buildings Exposed to Structural Pounding during Earthquakes. Geosciences 2020, 10, 18. [Google Scholar] [CrossRef] [Green Version]
- Balendra, T. A simplified model for lateral load analysis of asymmetrical buildings. Eng. Struct. 1983, 5, 154–162. [Google Scholar] [CrossRef]
- Novak, M.; Hifnawy, L.E. Effect of soil-structure interaction on damping of structures. Earthq. Eng. Struct. Dyn. 1983, 11, 595–621. [Google Scholar] [CrossRef]
- Sivakumaran, K.S.; Balendra, T. Seismic analysis of asymmetric multistorey buildings including foundation interaction and P-Δ effects. Eng. Struct. 1994, 16, 609–624. [Google Scholar] [CrossRef]
- Uz, M.E.; Hadi, M.N.S. Optimal design of semi active control for adjacent buildings connected by MR damper based on integrated fuzzy logic and multi-objective genetic algorithm. Eng. Struct. 2014, 69, 135–148. [Google Scholar] [CrossRef] [Green Version]
- Hadi, M.N.S.; Uz, M.E. Investigating the optimal passive and active vibration controls of adjacent buildings based on performance indices using genetic algorithms. Eng. Optim. 2015, 47, 265–286. [Google Scholar] [CrossRef] [Green Version]
- Miari, M.; Choong, K.K.; Jankowski, R. Seismic Pounding Between Bridge Segments: A State-of-the-Art Review. Arch. Comput. Methods Eng. 2021, 28, 495–504. [Google Scholar] [CrossRef]
- Chopra, A.K.; Gutierrez, J.A. Earthquake response analysis of multistorey buildings including foundation interaction. Earthq. Eng. Struct. Dyn. 1974, 3, 65–77. [Google Scholar] [CrossRef]
- Gupta, V.K.; Trifunac, M.D. Seismic response of multistoried buildings including the effects of soil-structure interaction. Soil Dyn. Earthq. Eng. 1991, 10, 414–422. [Google Scholar] [CrossRef]
- Veletsos, A.S.; Meek, J.W. Dynamic behaviour of building-foundation systems. Earthq. Eng. Struct. Dyn. 1974, 3, 121–138. [Google Scholar] [CrossRef]
- Richart, F.E.; Hall, J.R.; Woods, R.D. Vibrations of Soils and Foundations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1970. [Google Scholar]
- Goel, R.K. Simplified analysis of asymmetric structures with supplemental damping. Earthq. Eng. Struct. Dyn. 2001, 30, 1399–1416. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.-L.; Tsai, K.-C. Simplified seismic analysis of one-way asymmetric elastic systems with supplemental damping. Earthquake Eng. Struct. Dyn. 2007, 36, 783–800. [Google Scholar] [CrossRef]
- Uz, M.; Hadi, M.N. Investigating the effects of pouding for inelastic base isolated adjacent buildings under earthquake excitations. In Incorporating Sustainable Practice in Mechanics of Structures and Materials; Fragomeni, S., Venkatesan, S., Lam, N., Setunge, S., Eds.; CRC Press: Leiden, The Netherlands, 2011; pp. 329–334. [Google Scholar]
- Jankowski, R.; Mahmoud, S. Earthquake-Induced Structural Pounding; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Lin, J.-L.; Tsai, K.-C.; Miranda, E. Seismic History Analysis of Asymmetric Buildings with Soil–Structure Interaction. J. Struct. Eng. 2009, 135, 101–112. [Google Scholar] [CrossRef]
- Migda, W.; Szczepański, M.; Lasowicz, N.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Non-Linear Analysis of Inter-Story Pounding between Wood-Framed Buildings during Ground Motion. Geosciences 2019, 9, 488. [Google Scholar] [CrossRef] [Green Version]
- Favvata, M.J. Minimum required separation gap for adjacent RC frames with potential inter-story seismic pounding. Eng. Struct. 2017, 152, 643–659. [Google Scholar] [CrossRef]
- Abdel Raheem, S.E. Mitigation measures for earthquake induced pounding effects on seismic performance of adjacent buildings. Bull. Earthq. Eng. 2014, 12, 1705–1724. [Google Scholar] [CrossRef]
- Raheem, S.E.A.; Alazrak, T.M.A.; Shafy, A.G.A.A.; Ahmed, M.M.; Gamal, Y.A.S. Seismic pounding between adjacent buildings considering soil-structure interaction. Earthq. Struct. 2021, 20, 55–70. [Google Scholar] [CrossRef]
- Abdel Raheem, S.; Fooly, M.; Shafy, A.; Abbas, Y.; Omar, M.; Latif, M.; Mahmoud, S. Seismic Pounding Effects on Adjacent Buildings in Series with Different Alignment Configurations. Steel Compos. Struct. 2018, 28, 289–308. [Google Scholar] [CrossRef]
- Abdel Raheem, S.; Fooly, M.; Omar, M.; Abdel Zaher, A. Seismic pounding effects on the adjacent symmetric buildings with eccentric alignment. Earthq. Struct. 2019, 16, 715–726. [Google Scholar] [CrossRef]
- Balendra, T.; Tat, C.W.; Lee, S.-L. Modal damping for torsionally coupled buildings on elastic foundation. Earthq. Eng. Struct. Dyn. 1982, 10, 735–756. [Google Scholar] [CrossRef]
- Balendra, T.; Tat, C.W.; Lee, S.L. Vibration of Asymmetrical Building‐Foundation Systems. J. Eng. Mech. 1983, 109, 430–449. [Google Scholar] [CrossRef]
- Flenga, M.G.; Favvata, M.J. Probabilistic seismic assessment of the pounding risk based on the local demands of a multistory RC frame structure. Eng. Struct. 2021, 245, 112789. [Google Scholar] [CrossRef]
- Jankowski, R. Impact Force Spectrum for Damage Assessment of Earthquake-Induced Structural Pounding. Key Eng. Mater. 2005, 293–294, 711–718. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamics of Structures, 2nd ed.; McGraw-Hill Book Co., Inc.: New York, NY, USA, 1993. [Google Scholar]
- Jankowski, R. Theoretical and experimental assessment of parameters for the non-linear viscoelastic model of structural pounding. J. Theor. Appl. Mech. 2007, 45, 931–942. [Google Scholar]
- Hosseini, S.H.; Naderpour, H.; Vahdani, R.; Jankowski, R. Evaluation of pounding effects between reinforced concrete frames subjected to far-field earthquakes in terms of damage index. Bull. Earthq. Eng. 2022, 20, 1219–1245. [Google Scholar] [CrossRef]
- Hadi, M.N.S.; Uz, M.E. Inelastic Base Isolated Adjacent Buildings under Earthquake Excitation with the Effect of Pounding. In Proceedings of the 5th Civil Engineering Conference in the Asian Region and Australasian Structural Engineering Conference CECAR 5/ASEC 2010, Sydney, Australia, 8–12 August 2010; pp. 155–201. [Google Scholar]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure to estimate seismic demands for unsymmetric-plan buildings. Earthq. Eng. Struct. Dyn. 2004, 33, 903–927. [Google Scholar] [CrossRef] [Green Version]
- Cruz, C.; Miranda, E. Evaluation of the Rayleigh damping model for buildings. Eng. Struct. 2017, 138, 324–336. [Google Scholar] [CrossRef]
- Goldsmith, W. Impact: The Theory and Physical Behaviour of Colliding Solids; Edward Arnold: London, UK, 1960. [Google Scholar]
- Uz, M.E.; Hadi, M.N.S. Seismic history analysis of asymmetrical adjacent buildings with soil-structure interaction con-sideration. In Proceedings of the 8th World Conference on Earthquake Resistant Engineering Structures, Chianciano, Italy, 7–9 September 2011; pp. 225–236. [Google Scholar]
- Uz, M.E.; Hadi, M.N.S. Earthquake Resistant Design of Buildings, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Kan, C.L.; Chopra, A.K. Coupled Lateral Torsional Response of Buildings to Ground Motion; University of California: Berkeley, CA, USA, 1976. [Google Scholar]
- Abdel Raheem, S.E.; Ahmed, M.M.; Alazrak, T.M.A. Evaluation of soil–foundation–structure interaction effects on seismic response demands of multi-story MRF buildings on raft foundations. Int. J. Adv. Struct. Eng. 2015, 7, 11–30. [Google Scholar] [CrossRef] [Green Version]
- Sulistiawan, H.; Supriyadi; Yulianti, I. Shear wave velocity profiling analysis for site classification using microtremor single station method. AIP Conf. Proc. 2018, 2014, 020003. [Google Scholar] [CrossRef]
- Khatami, S.M.; Naderpour, H.; Razavi, S.M.N.; Barros, R.C.; Sołtysik, B.; Jankowski, R. An ANN-Based Approach for Prediction of Sufficient Seismic Gap between Adjacent Buildings Prone to Earthquake-Induced Pounding. Appl. Sci. 2020, 10, 3591. [Google Scholar] [CrossRef]
- Khatami, S.M.; Naderpour, H.; Barros, R.C.; Jankowski, R. Verification of Formulas for Periods of Adjacent Buildings Used to Assess Minimum Separation Gap Preventing Structural Pounding during Earthquakes. Adv. Civ. Eng. 2019, 2019, 9714939. [Google Scholar] [CrossRef]
- Abdel Raheem, S.E. Exploring Seismic Response of Bridges with Bidirectional Coupled Modelling of Base Isolation Bearings System. Arab. J. Sci. Eng. 2014, 39, 8669–8679. [Google Scholar] [CrossRef]








| Sliding | Torsion | Rocking | |
|---|---|---|---|
| Spring | |||
| Mass Ratio | |||
| Damping Ratio | |||
| Coefficient |
| Story No. | Story Height , | ||||
|---|---|---|---|---|---|
| 1F | 2.85 | 0.30 | 3.46 | 0.4065 | 5.06 |
| 2F | 5.7 | 0.30 | 3.46 | 0.4065 | 3.86 |
| 3F | 8.55 | 0.30 | 3.46 | 0.4065 | 3.86 |
| 4F | 11.4 | 0.30 | 3.46 | 0.4065 | 3.86 |
| 5F | 14.25 | 0.30 | 3.46 | - | - |
| Cases Frequency | Case I | Case I * | Case IV | Case IV * | RB | RB * | ||
|---|---|---|---|---|---|---|---|---|
| (Hz) | 0.698 | 0.685 | 0.788 | 0.787 | 0.794 | 0.792 | 0.865 | 0.994 |
| (Hz) | 0.783 | 0.787 | 0.932 | 0.931 | 0.941 | 0.940 | 0.837 | 0.990 |
| (Hz) | 1.120 | 1.107 | 1.224 | 1.222 | 1.233 | 1.231 | 0.899 | 0.993 |
| (Hz) | 1.896 | 1.874 | 1.942 | 1.937 | 1.943 | 1.941 | 0.965 | 0.998 |
| (Hz) | 2.227 | 2.175 | 2.301 | 2.297 | 2.306 | 2.303 | 0.944 | 0.997 |
| (Hz) | 2.905 | 2.795 | 3.013 | 3.007 | 3.019 | 3.015 | 0.927 | 0.997 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uz, M.E.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Numerical Analysis of Seismic Pounding between Adjacent Buildings Accounting for SSI. Appl. Sci. 2023, 13, 3092. https://doi.org/10.3390/app13053092
Uz ME, Jakubczyk-Gałczyńska A, Jankowski R. Numerical Analysis of Seismic Pounding between Adjacent Buildings Accounting for SSI. Applied Sciences. 2023; 13(5):3092. https://doi.org/10.3390/app13053092
Chicago/Turabian StyleUz, Mehmet Eren, Anna Jakubczyk-Gałczyńska, and Robert Jankowski. 2023. "Numerical Analysis of Seismic Pounding between Adjacent Buildings Accounting for SSI" Applied Sciences 13, no. 5: 3092. https://doi.org/10.3390/app13053092
APA StyleUz, M. E., Jakubczyk-Gałczyńska, A., & Jankowski, R. (2023). Numerical Analysis of Seismic Pounding between Adjacent Buildings Accounting for SSI. Applied Sciences, 13(5), 3092. https://doi.org/10.3390/app13053092






