Chemical-Physical Model of Gaseous Mercury Emissions from the Demolition Waste of an Abandoned Mercury Metallurgical Plant
Abstract
1. Introduction
2. Materials
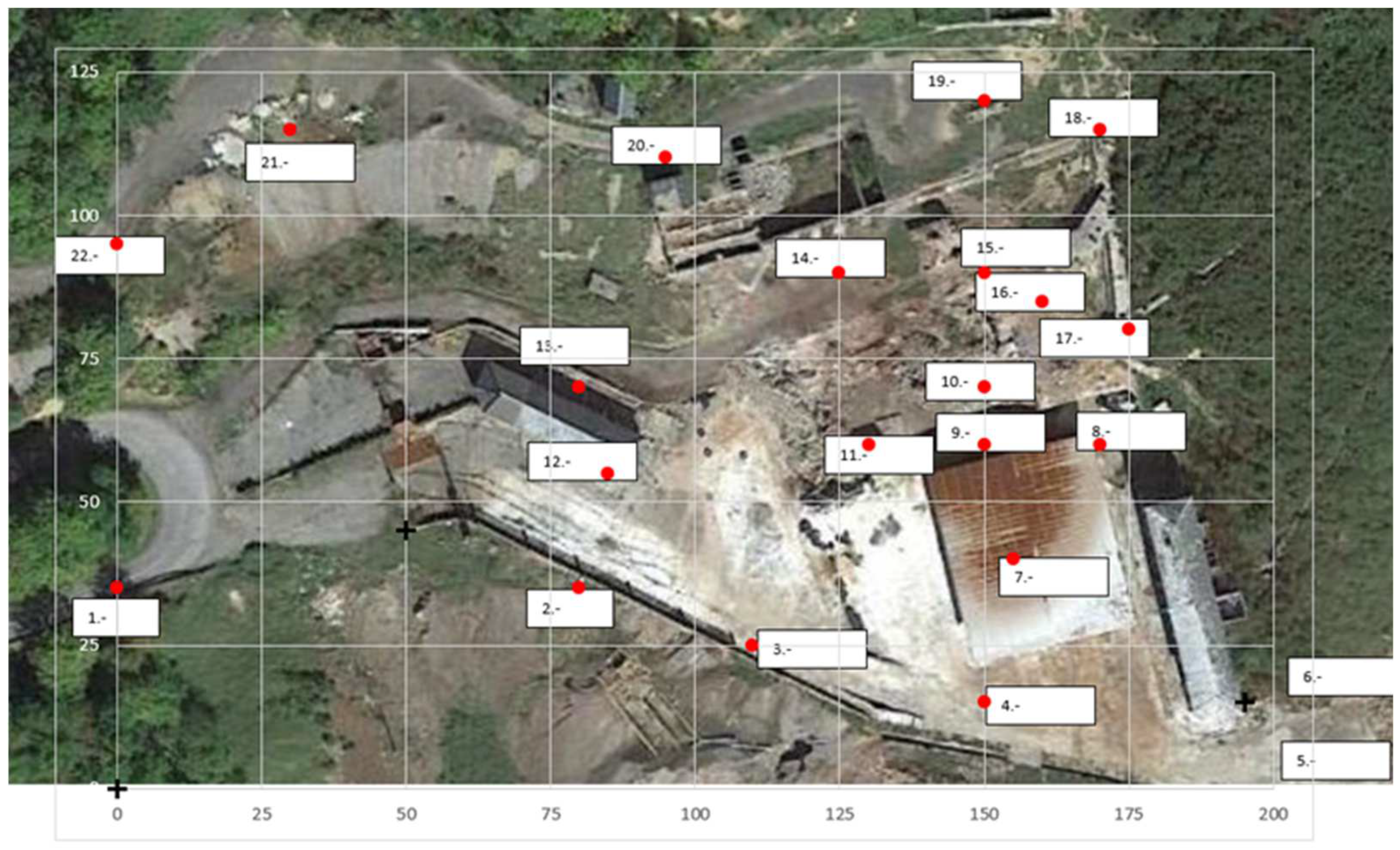
2.1. Site Description
2.2. Measurement of Gaseous Mercury
2.3. Empirical Models of Emission and Diffusion
3. Methods
3.1. Main Hypothesis Regarding Gaseous Hg Flux
- (a)
- A flat upward flow diffusion over the rubble area, in which the diffusion velocity decreases with distance from the emission plane.
- (b)
- A hemispherical radial flow diffusion, outside of the rubble area, in which the concentration will decrease with the inverse of the distance to the center of the rubble area.
- (a)
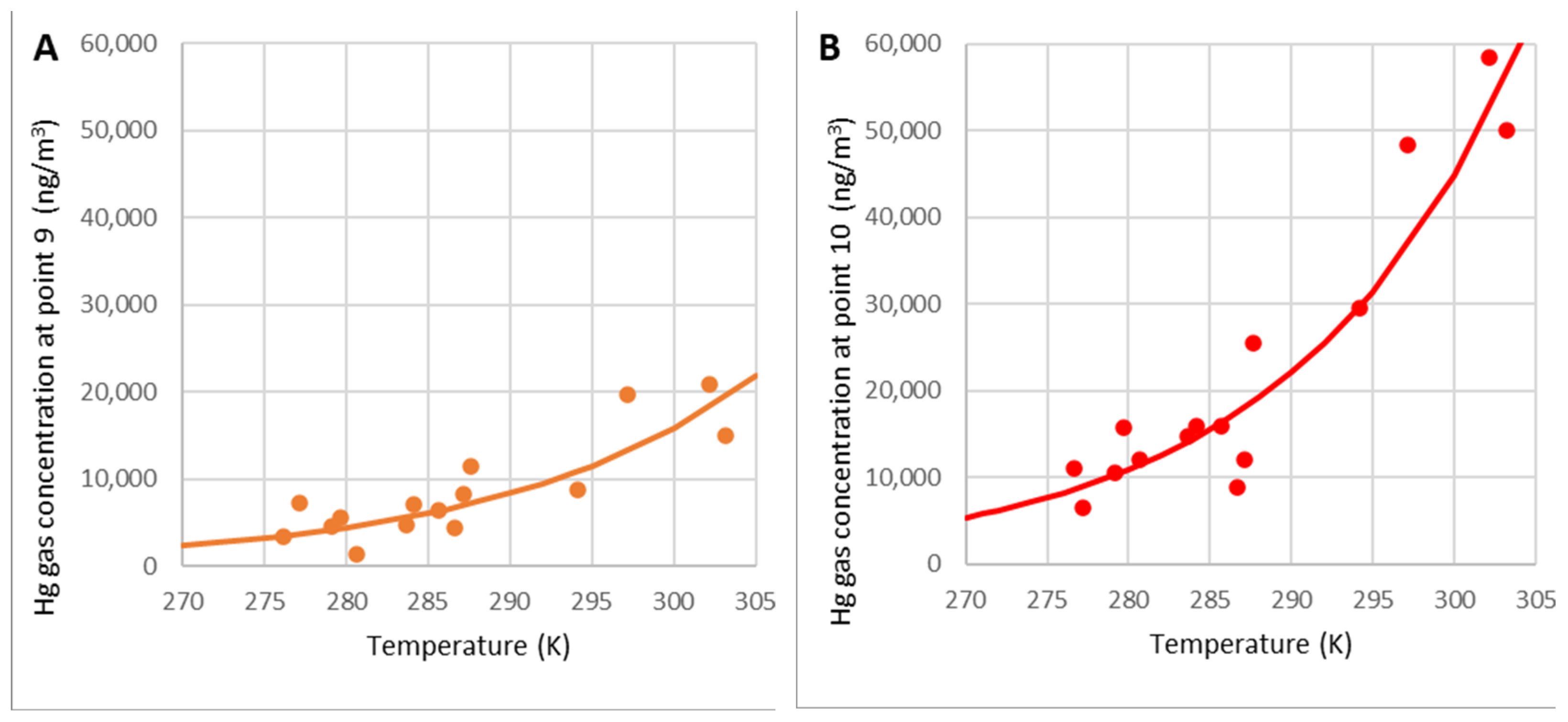
- Assuming the radial diffusion, the concentration measurements at the border of the debris area, point 9, makes it possible to determine the emission rate G (ng/s).
- (b)
- Assuming the flat diffusion near the debris surface, the concentration over the debris, point 10, makes it possible to determine the mass transfer coefficient K′ (m/s).
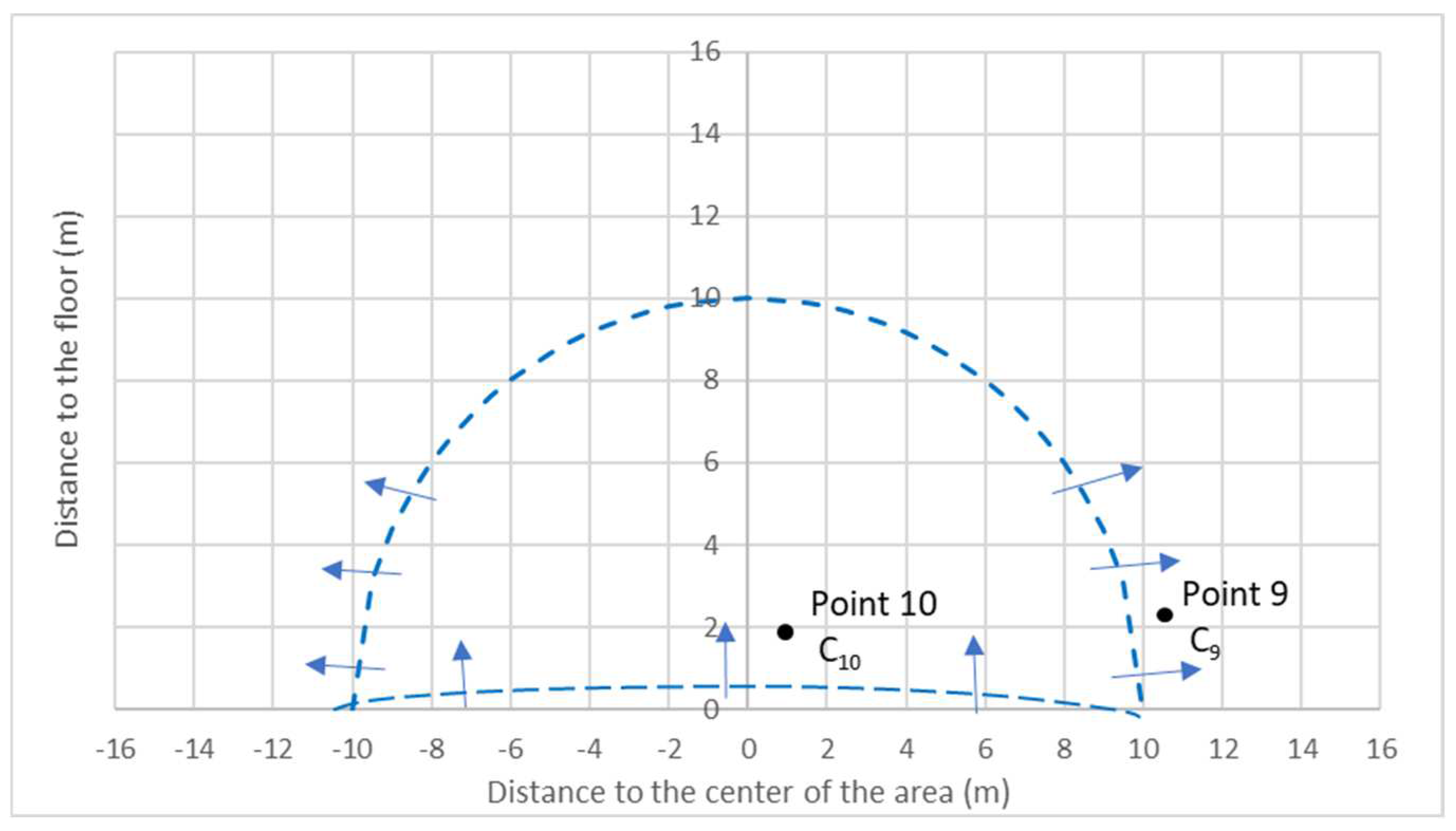
3.2. Models of Radial and Flat Diffusion Based on Fick’s Laws
3.2.1. Model of Radial Flow Diffusion and Determination of the Emission Rate G
3.2.2. Model of Flat Upward Flow Diffusion and Determination of Mass Transfer Coefficient K′
3.3. Models of Mercury Emission at the Focus
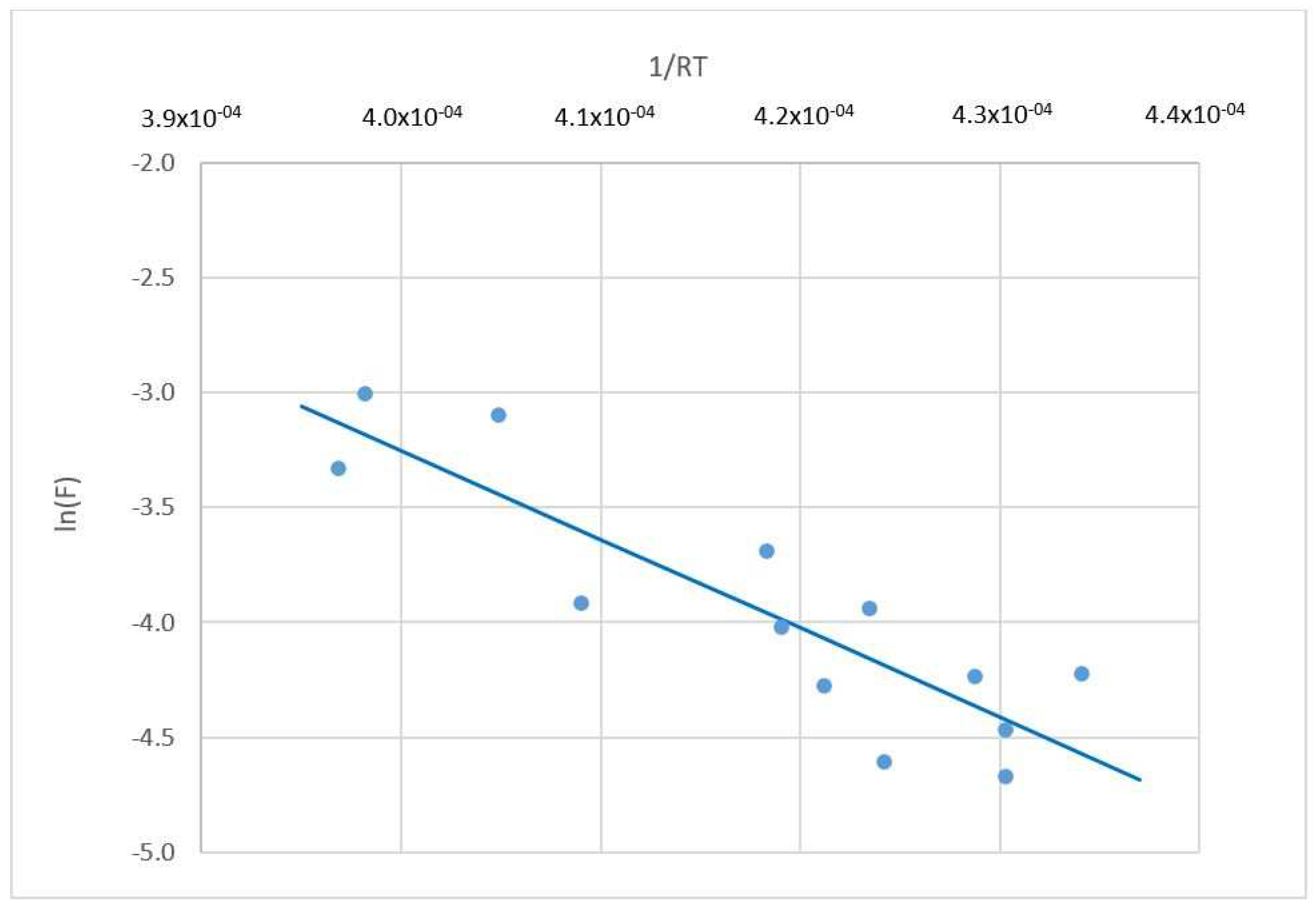
3.3.1. Model Based on Arrhenius Theory
Estimation of the Apparent Activation Energy Ea and the Coefficient cf
Validation of the Model Based on the Arrhenius Equation
3.3.2. Model Based on the Laws of Liquid Evaporation
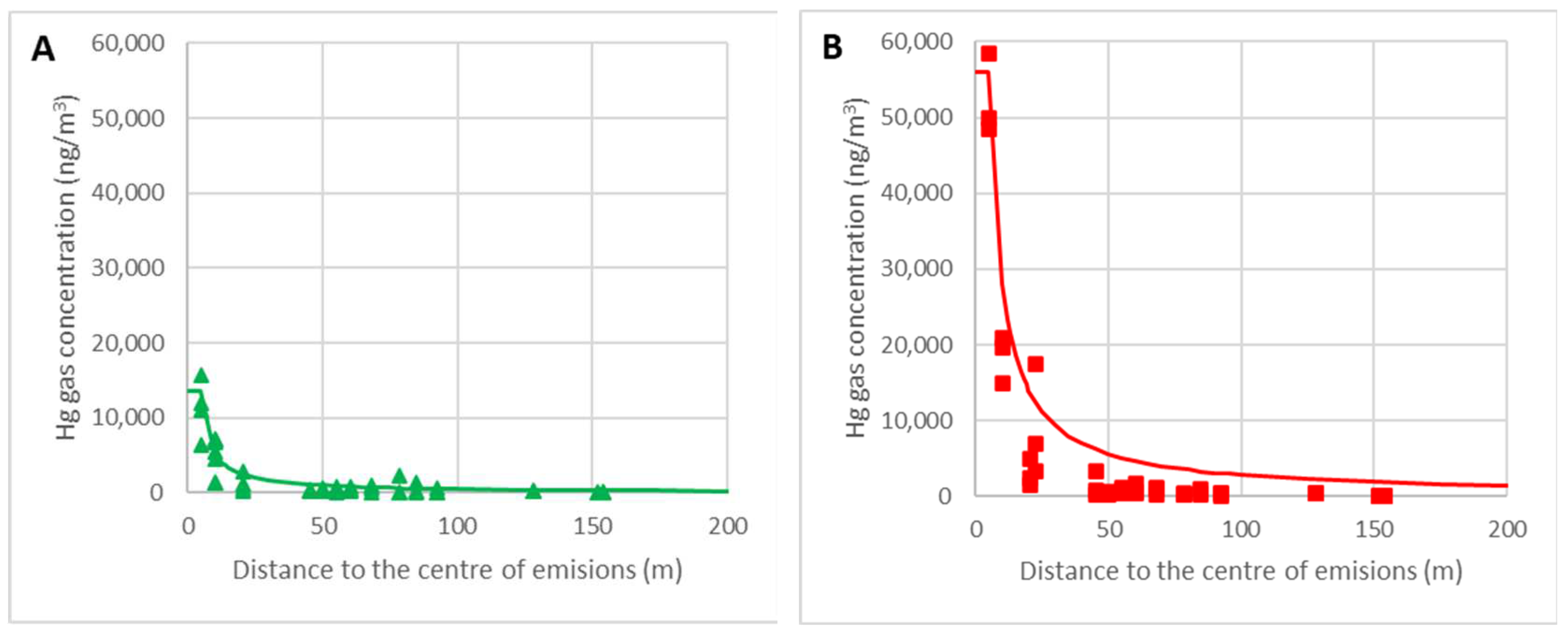
3.4. Model of Mercury Dispersion around the Focus
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gabriel, M.C.; Williamson, D.G. Principal biogeochemical factors affecting the speciation and transport of mercury through the terrestrial environment. Environ. Geochem. Health 2004, 26, 421–434. [Google Scholar] [CrossRef]
- Grigal, D.F. Inputs and outputs of mercury from terrestrial watersheds: A review. Environ. Rev. 2002, 10, 1–39. [Google Scholar] [CrossRef]
- Schroeder, W.H.; Munthe, J. Atmospheric mercury—An overview. Atmos. Environ. 1998, 32, 809–822. [Google Scholar] [CrossRef]
- Ebinghaus, R.; Kock, H.H.; Temme, C.; Einax, J.W.; Lowe, A.G.; Richter, A.; Burrows, J.P.; Schroeder, W.H. Antarctic Springtime Depletion of Atmospheric Mercury. Environ. Sci. Technol. 2002, 36, 1238–1244. [Google Scholar] [CrossRef]
- Fitzgerald, W.F. Is mercury increasing in the atmosphere? The need for an atmospheric mercury network (AMNET). Water Air Soil Pollut. 1995, 80, 245–254. [Google Scholar]
- Morse, J.W. Interactions of trace metals with authigenic sulfide minerals: Implications for their bioavailability. Mar. Chem. 1994, 46, 1–6. [Google Scholar] [CrossRef]
- Pacyna, E.G.; Pacyna, J.M.; Sundseth, K.; Munthe, J.; Kindbom, K.; Wilson, S.; Steenhuisen, F.; Maxson, P. Global emission of mercury to the atmosphere from anthropogenic sources in 2005 and projections to 2020. Atmos. Environ. 2010, 44, 2487–2499. [Google Scholar] [CrossRef]
- Gustin, M.S. Are mercury emissions from geologic sources significant? A status report. Sci. Total Environ. 2003, 304, 153–167. [Google Scholar] [CrossRef] [PubMed]
- Streets, D.G.; Hao, J.; Wu, Y.; Jiang, J.; Chan, M.; Tian, H.; Feng, X. Anthropogenic mercury emissions in China. Atmos. Environ. 2005, 39, 7789–7806. [Google Scholar] [CrossRef]
- Wang, S.; Feng, X.; Qiu, G.; Shang, L.; Li, P.; Wei, Z. Mercury concentrations and air/soil fluxes in Wuchuan mercury mining district, Guizhou province, China. Atmos. Environ. 2007, 41, 5984–5993. [Google Scholar]
- Poissant, L.; Casimir, A. Water-air and soil-air exchange rate of total gaseous mercury measured at background sites. Atmos. Environ. 1998, 32, 883–893. [Google Scholar] [CrossRef]
- Ferrara, R. Mercury mines in Europe: Assessment of emissions and environmental contamination. Mercury Contaminated Sites: Characterization, Risk Assessment and Remediation; Springer: Berlin/Heidelberg, Germany, 1999; pp. 51–72. [Google Scholar]
- Dory, A. Le mercure dans les Asturies. Rev. Univ. Mines Met. 1894, 32, 145–210. [Google Scholar]
- Fernández-Martínez, R.; Loredo, J.; Ordónez, A.; Rucandio, M.I. Distribution and mobility of mercury in soils from an old mining area in Mieres, Asturias (Spain). Sci. Total Environ. 2005, 346, 200–212. [Google Scholar] [CrossRef] [PubMed]
- Higueras, P.; Fernández-Martínez, R.; Esbrí, J.M.; Rucandio, I.; Loredo, J.; Ordónez, A.; Alvarez, R. Mercury soil pollution in Spain: A review. Environment, Energy and Climate Change I: Environmental Chemistry of Pollutants and Wastes; Springer: Berlin/Heidelberg, Germany, 2015; pp. 135–158. [Google Scholar]
- Loredo, J.; Soto, J.; Álvarez, R.; Ordóñez, A. Atmospheric monitoring at abandoned mercury mine sites in Asturias (NW Spain). Environ. Monit. Assess. 2007, 130, 201–214. [Google Scholar] [CrossRef]
- Garcia Gonzalez, H.; García-Ordiales, E.; Diez, R.R. Analysis of the airborne mercury and particulate arsenic levels close to an abandoned waste dump and buildings of a mercury mine and the potential risk of atmospheric pollution. SN Appl. Sci. 2022, 4, 76. [Google Scholar] [CrossRef]
- Rodríguez, R.; Garcia-Gonzalez, H.; García-Ordiales, E. Empirical Model of Gaseous Mercury Emissions for the Analysis of Working Conditions in Outdoor Highly Contaminated Sites. Sustainability 2022, 14, 13951. [Google Scholar] [CrossRef]
- Nagl, C.; Spangl, W.; Buxbaum, I. Sampling Points for Air Quality; Representativeness and Comparability of Measurement in Accordance with Directive 2008/50/EC on Ambient Air Quality and Cleaner Air for Europe; European Parliament: Luxembourg, 2019. [Google Scholar]
- McCarthy, J.H.; Vaughn, W.W.; Learned, R.E.; Meuschke, J.L. Mercury in Soil Gas and Air—A Potential Tool in Mineral Exploration (No. 609); US Geological Survey: Washington, DC, USA, 1969. [Google Scholar]
- Schroeder, W.H.; Munthe, J.; Lindqvist, O. Cycling of mercury between water, air, and soil compartments of the environment. Water Air Soil Pollut. 1989, 48, 337–347. [Google Scholar] [CrossRef]
- O’Connor, D.; Hou, D.; Ok, Y.S.; Mulder, J.; Duan, L.; Wu, Q.; Wang, S.; Tack, F.M.; Rinklebe, J. Mercury speciation, transformation, and transportation in soils, atmospheric flux, and implications for risk management: A critical review. Environ. Int. 2019, 126, 747–761. [Google Scholar] [CrossRef]
- Scholtz, M.T.; Van Heyst, B.J.; Schroeder, W.H. Modelling of mercury emissions from background soils. Sci. Total Environ. 2003, 304, 185–207. [Google Scholar] [CrossRef]
- Ci, Z.; Peng, F.; Xue, X.; Zhang, X. Air–surface exchange of gaseous mercury over permafrost soil: An investigation at a high-altitude (4700 m asl) and remote site in the central Qinghai–Tibet Plateau. Atmos. Chem. Phys. 2016, 16, 14741–14754. [Google Scholar] [CrossRef]
- Gačnik, J.; Živković, I.; Ribeiro Guevara, S.; Jaćimović, R.; Kotnik, J.; Horvat, M. Validating an evaporative calibrator for gaseous oxidized mercury. Sensors 2021, 21, 2501. [Google Scholar]
- Dunham-Cheatham, S.M.; Lyman, S.; Gustin, M.S. Comparison and calibration of methods for ambient reactive mercury quantification. Sci. Total Environ. 2023, 856, 159219. [Google Scholar] [CrossRef]
- Massman, W.J. Molecular diffusivities of Hg vapor in air, O2 and N2 near STP and the kinematic viscosity and thermal diffusivity of air near STP. Atmos. Environ. 1999, 33, 453–457. [Google Scholar] [CrossRef]
- Koster van Groos, P.G.; Esser, B.K.; Williams, R.W.; Hunt, J.R. Isotope effect of mercury diffusion in air. Environ. Sci. Technol. 2014, 48, 227–233. [Google Scholar] [CrossRef] [PubMed]
- Jeon, J.W.; Han, Y.J.; ChaJeon, S.H.; Kim, P.R.; Kim, Y.H.; Kim, H.; Seok, G.S.; Noh, S. Application of the passive sampler developed for atmospheric mercury and its limitation. Atmosphere 2019, 10, 678. [Google Scholar] [CrossRef]
- Cabassi, J.; Tassi, F.; Venturi, S.; Calabrese, S.; Capecchiacci, F.; D’Alessandro, W.; Vaselli, O. A new approach for the measurement of gaseous elemental mercury (GEM) and H2S in air from anthropogenic and natural sources: Examples from Mt. Amiata (Siena, Central Italy) and Solfatara Crater (Campi Flegrei, Southern Italy). J. Geochem. Explor. 2017, 175, 48–58. [Google Scholar] [CrossRef]
- Vaselli, O.; Nisi, B.; Rappuoli, D.; Cabassi, J.; Tassi, F. Gaseous elemental mercury and total and leached mercury in building materials from the former Hg-mining area of Abbadia San Salvatore (Central Italy). Int. J. Environ. Res. Public Health 2017, 14, 425. [Google Scholar] [CrossRef]
- Qiu, G.; Feng, X.; Meng, B.; Sommar, J.; Chunhao, G.Q. Environmental geochemistry of an active Hg mine in Xunyang, Shaanxi Province, China. Appl. Geochem. 2012, 27, 2280–2288. [Google Scholar] [CrossRef]
- Zhang, H.A.; Lindberg, S.E. Processes influencing the emission of mercury from soils: A conceptual model. J. Geophys. Res. Atmos. 1999, 104, 21889–21896. [Google Scholar]
- Zhu, W.; Li, Z.; Li, P.; Yu, B.; Lin, C.J.; Sommar, J.; Feng, X. Re-emission of legacy mercury from soil adjacent to closed point sources of Hg emission. Environ. Pollut. 2018, 242, 718–727. [Google Scholar] [CrossRef]
- Sommar, J.; Osterwalder, S.; Zhu, W. Recent advances in understanding and measurement of Hg in the environment: Surface-atmosphere exchange of gaseous elemental mercury (Hg0). Sci. Total Environ. 2020, 721, 137648. [Google Scholar] [CrossRef]
- Llanos, W.; Kocman, D.; Higueras, P.; Horvat, M. Mercury emission and dispersion models from soils contaminated by cinnabar mining and metallurgy. J. Environ. Monit. 2011, 13, 3460. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.; Hodges, J.T. Development of a high-resolution laser absorption spectroscopy method with application to the determination of absolute concentration of gaseous elemental mercury in air. Anal. Chem. 2018, 90, 6781–6788. [Google Scholar]
- Siegel, S.M.; Siegel, B.Z. Temperature determinants of plant-soil-air mercury relationships. Water Air Soil Pollut. 1988, 40, 443–448. [Google Scholar] [CrossRef]
- Zhang, H.; Lindberg, S.E.; Marsik, F.J.; Keeler, G.J. Mercury airy surface exchange kinetics of background soils of the Tahquamenon river watershed in the Michigan Upper Peninsula. Water Air Soil Pollut. 2001, 126, 151–169. [Google Scholar] [CrossRef]
- Yuan, W.; Wang, X.; Lin, C.J.; Sommar, J.; Lu, Z.; Feng, X. Process factors driving dynamic exchange of elemental mercury vapor over soil in broadleaf forest ecosystems. Atmos. Environ. 2019, 219, 117047. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Z.; Wang, C.; Zhang, X. The soil displacement measurement of mercury emission flux of the sewage irrigation farmlands in Northern China. Ecosyst. Health Sustain. 2019, 5, 169–180. [Google Scholar] [CrossRef]
- Choi, H.D.; Holsen, T.M. Gaseous mercury emissions from unsterilized and sterilized soils: The effect of temperature and UV radiation. Environ. Pollut. 2009, 157, 1673–1678. [Google Scholar] [CrossRef]
- Park, S.Y.; Holsen, T.M.; Kim, P.R.; Han, Y.J. Laboratory investigation of factors affecting mercury emissions from soils. Environ. Earth Sci. 2014, 72, 2711–2721. [Google Scholar] [CrossRef]
- Lindberg, S.E.; Kim, K.H.; Meyers, T.P.; Owens, J.G. Micrometeorological Gradient Approach for quantifying Air Surface Exchange of- Mercury Vapor: Tests over-Contaminated soils. Environ. Sci. Technol. 1995, 29, 126–135. [Google Scholar] [CrossRef]
- Kocman, D.; Horvat, M. A laboratory based experimental study of mercury emission from contaminated soils in the River Idrijca catchment. Atmos. Chem. Phys. Discuss. 2009, 9, 25159–25185. [Google Scholar] [CrossRef]
- Cizdziel, J.V.; Jiang, Y.; Nallamothu, D.; Brewer, J.S.; Gao, Z. Air/surface exchange of gaseous elemental mercury at different landscapes in Mississippi, USA. Atmosphere 2019, 10, 538. [Google Scholar] [CrossRef]
- EPA Contract 88-01-6065; Mathematical Models for Estimating Workplace Concentration Levels: A Literature Review. Clemens Associates Inc.: Santa Fe, NM, USA, 1981.
- Huber, M.L.; Laesecke, A.; Friend, D.G. Correlation for the Vapor Pressure of Mercury. Ind. Eng. Chem. Res. 2006, 45, 7351–7361. [Google Scholar] [CrossRef]

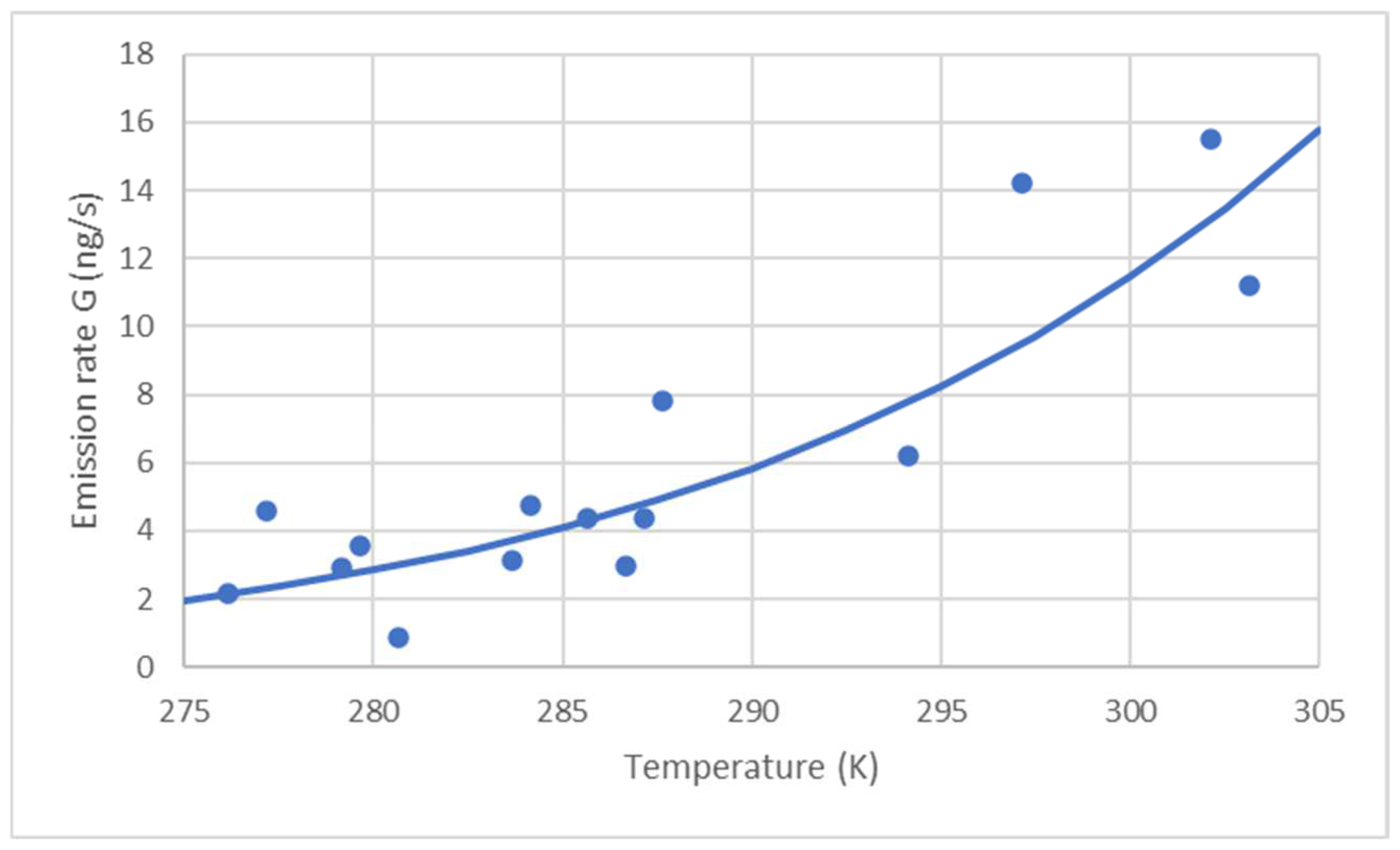
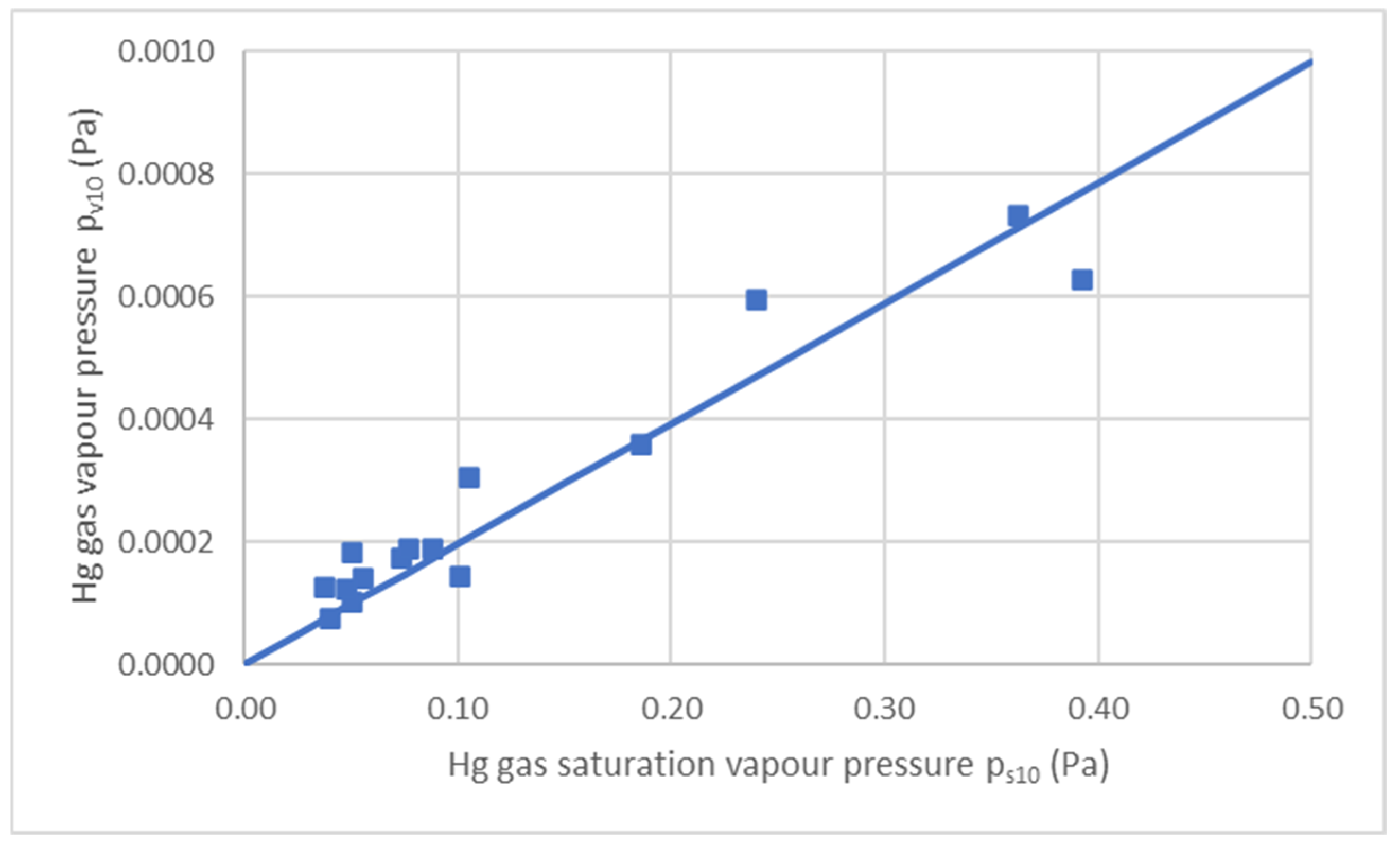
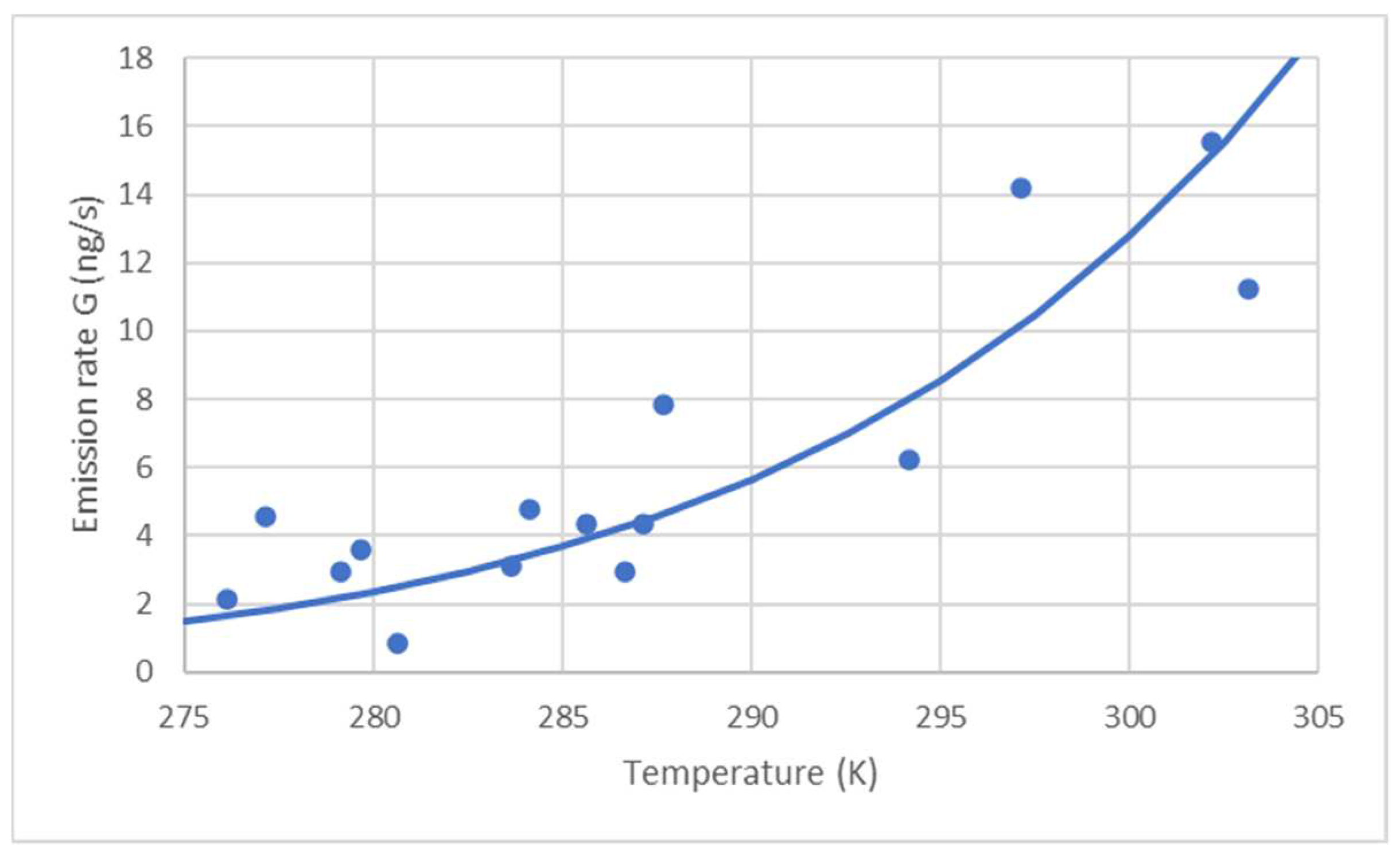

| θ (°C) | T (K) | A (m2) | C9 (ng/m3) | D (m2/s) | G (ng/s) | F (ng/s m2) | F (ng/m2 h) |
|---|---|---|---|---|---|---|---|
| 29 | 302 | 314 | 20,867 | 1.18 × 10−5 | 15.51 | 0.0494 | 177.8 |
| 30 | 303 | 314 | 15,000 | 1.19 × 10−5 | 11.22 | 0.0357 | 128.6 |
| 6.5 | 279.5 | 314 | 5524 | 1.03 × 10−5 | 3.57 | 0.0114 | 40.9 |
| 7.5 | 280.5 | 314 | 1330 | 1.04 × 10−5 | 4.53 | 0.0028 | 9.9 |
| 12.5 | 285.5 | 314 | 6488 | 1.07 × 10−5 | 4.36 | 0.0139 | 49.9 |
| 10.5 | 283.5 | 314 | 4689 | 1.06 × 10−5 | 3.11 | 0.0099 | 35.6 |
| 4 | 277 | 314 | 7205 | 1.01 × 10−5 | 4.58 | 0.0146 | 52.5 |
| 11 | 284 | 314 | 7153 | 1.06 × 10−5 | 6.06 | 0.0152 | 54.5 |
| 14 | 287 | 314 | 6426 | 1.08 × 10−5 | 5.62 | 0.0139 | 49.9 |
| 14.5 | 287.5 | 314 | 11,493 | 1.08 × 10−5 | 7.82 | 00249 | 89.6 |
| 24 | 297 | 314 | 19,681 | 1.15 × 10−5 | 14.19 | 0.0452 | 162.7 |
| 21 | 294 | 314 | 8785 | 1.13 × 10−5 | 6.22 | 0.0198 | 71.3 |
| 13.5 | 286.5 | 314 | 4387 | 1.08 × 10−5 | 2.96 | 0.0094 | 34.0 |
| 3 | 276 | 314 | 3402 | 1.01 × 10−5 | 2.15 | 0.0068 | 24.6 |
| 6 | 279 | 314 | 4538 | 1.03 × 10−5 | 2.92 | 0.0093 | 33.5 |
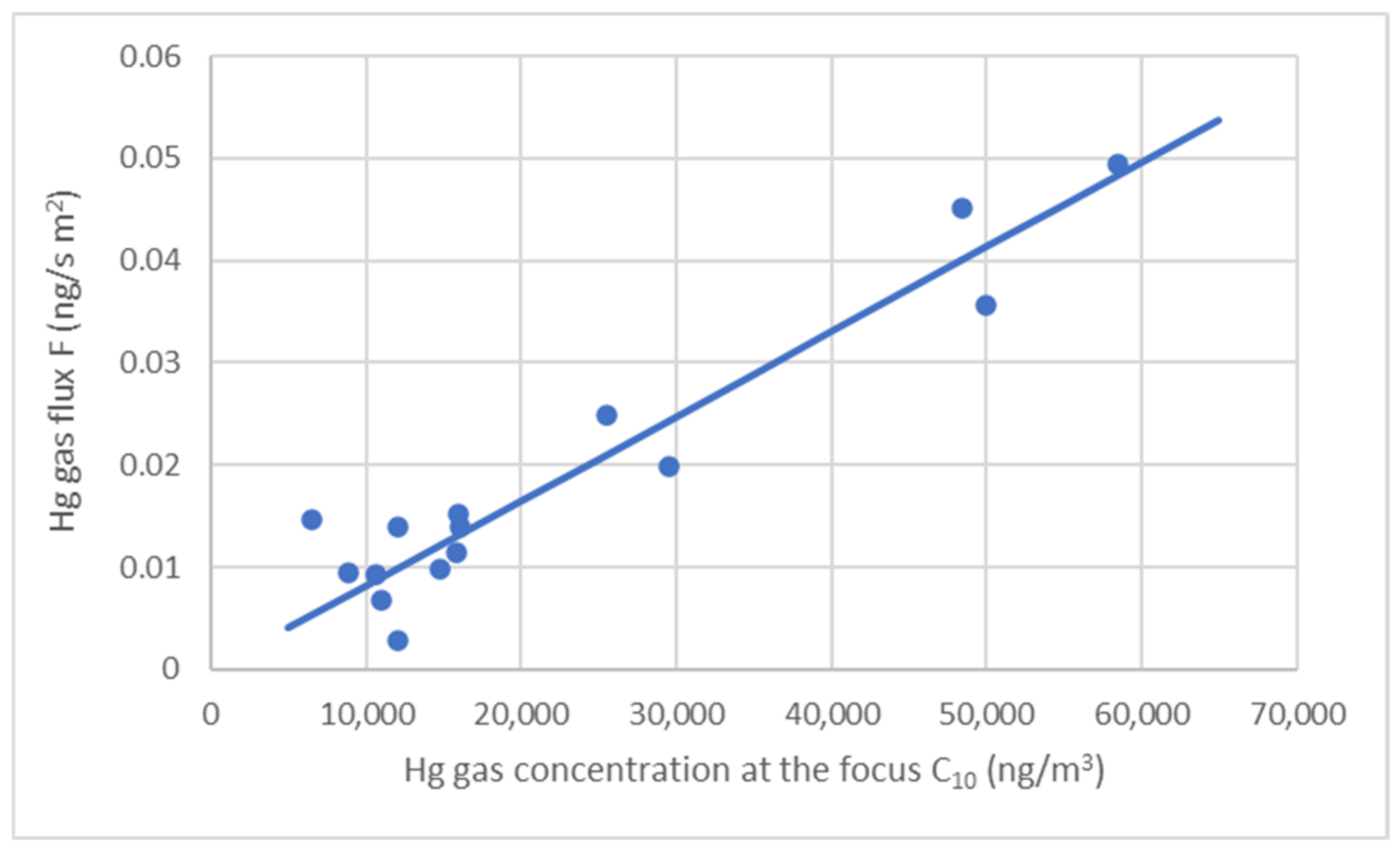
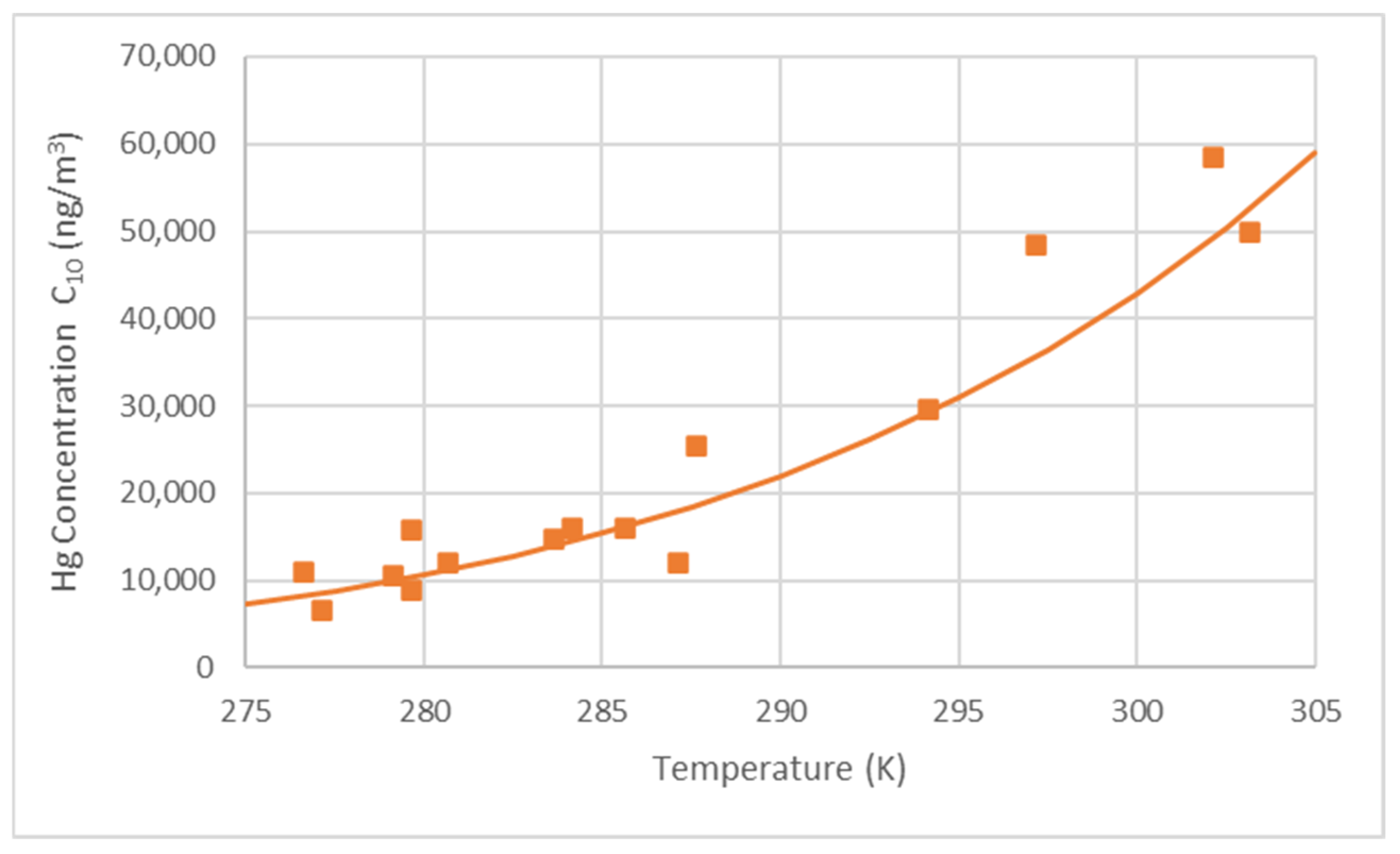
| θ (°C) | T (K) | C10 (ng/m3) | G (ng/s) | F (ng/sm2) | K′ (m/s) |
|---|---|---|---|---|---|
| 29 | 302 | 58,488 | 15.51 | 0.0494 | 8.45 × 10−7 |
| 30 | 303 | 50,000 | 11.22 | 0.0357 | 7.14 × 10−7 |
| 6.5 | 279.5 | 15,827 | 3.57 | 0.0114 | 7.18 × 10−7 |
| 7.5 | 280.5 | 12,028 | 4.53 | 0.0028 | 2.29 × 10−7 |
| 12.5 | 285.5 | 16,024 | 4.36 | 0.0139 | 8.66 × 10−7 |
| 10.5 | 283.5 | 14,757 | 3.11 | 0.0099 | 6.71 × 10−7 |
| 4 | 277 | 6512 | 4.58 | 0.0146 | 2.24 × 10−6 |
| 11 | 284 | 15,945 | 6.06 | 0.0152 | 9.50 × 10−7 |
| 14 | 287 | 12,089 | 5.62 | 0.0139 | 1.15 × 10−6 |
| 14.5 | 287.5 | 25,500 | 7.82 | 0.0249 | 9.76 × 10−7 |
| 24 | 297 | 48,397 | 14.19 | 0.0452 | 9.34 × 10−7 |
| 21 | 294 | 29,518 | 6.22 | 0.0198 | 6.71 × 10−7 |
| 13.5 | 286.5 | 8890 | 2.96 | 0.0094 | 1.06 × 10−6 |
| 3.5 | 276.5 | 11,011 | 2.15 | 0.0068 | 6.21 × 10−7 |
| 6 | 279 | 10,589 | 2.92 | 0.0093 | 8.79 × 10−7 |
| θ (°C) | T (K) | C10 (ng/m3) | C10 (mol/m3) | pv10 (Pa) | ps10 (Pa) | pv10/ps10 |
|---|---|---|---|---|---|---|
| 29 | 302 | 58,488 | 2.92 × 10−7 | 7.32 × 10−4 | 3.55 × 10−1 | 0.00206 |
| 30 | 303 | 50,000 | 2.49 × 10−7 | 6.28 × 10−4 | 3.85 × 10−1 | 0.00163 |
| 6.5 | 279.5 | 15,827 | 7.89 × 10−8 | 1.83 × 10−4 | 4.95 × 10−2 | 0.00371 |
| 7.5 | 280.5 | 12,028 | 6.00 × 10−8 | 1.40 × 10−4 | 5.43 × 10−2 | 0.00257 |
| 12.5 | 285.5 | 16,024 | 7.99 × 10−8 | 1.90 × 10−4 | 8.62 × 10−2 | 0.00220 |
| 10.5 | 283.5 | 14,757 | 7.36 × 10−8 | 1.73 × 10−4 | 7.18 × 10−2 | 0.00241 |
| 4 | 277 | 6512 | 3.25 × 10−8 | 7.48 × 10−5 | 3.89 × 10−2 | 0.00192 |
| 11 | 284 | 15,945 | 7.95 × 10−8 | 1.88 × 10−4 | 7.52 × 10−2 | 0.00250 |
| 14 | 287 | 12,089 | 6.03 × 10−8 | 1.44 × 10−4 | 9.87 × 10−2 | 0.00146 |
| 14.5 | 287.5 | 25,500 | 1.27 × 10−7 | 3.04 × 10−4 | 1.03 × 10−1 | 0.00294 |
| 24 | 297 | 48,397 | 2.41 × 10−7 | 5.96 × 10−4 | 2.35 × 10−1 | 0.00254 |
| 21 | 294 | 29,518 | 1.47 × 10−7 | 3.60 × 10−4 | 1.82 × 10−1 | 0.00197 |
| 13.5 | 279.5 | 8890 | 4.43 × 10−8 | 1.06 × 10−4 | 9.44 × 10−2 | 0.00112 |
| 3.5 | 276.5 | 11,011 | 5.49 × 10−8 | 1.26 × 10−4 | 3.71 × 10−2 | 0.00340 |
| 6 | 302 | 10,589 | 5.28 × 10−8 | 1.23 × 10−4 | 4.95 × 10−2 | 0.00248 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez, R.; Fernández, B.; Malagón, B.; Garcia-Ordiales, E. Chemical-Physical Model of Gaseous Mercury Emissions from the Demolition Waste of an Abandoned Mercury Metallurgical Plant. Appl. Sci. 2023, 13, 3149. https://doi.org/10.3390/app13053149
Rodríguez R, Fernández B, Malagón B, Garcia-Ordiales E. Chemical-Physical Model of Gaseous Mercury Emissions from the Demolition Waste of an Abandoned Mercury Metallurgical Plant. Applied Sciences. 2023; 13(5):3149. https://doi.org/10.3390/app13053149
Chicago/Turabian StyleRodríguez, Rafael, Begoña Fernández, Beatriz Malagón, and Efrén Garcia-Ordiales. 2023. "Chemical-Physical Model of Gaseous Mercury Emissions from the Demolition Waste of an Abandoned Mercury Metallurgical Plant" Applied Sciences 13, no. 5: 3149. https://doi.org/10.3390/app13053149
APA StyleRodríguez, R., Fernández, B., Malagón, B., & Garcia-Ordiales, E. (2023). Chemical-Physical Model of Gaseous Mercury Emissions from the Demolition Waste of an Abandoned Mercury Metallurgical Plant. Applied Sciences, 13(5), 3149. https://doi.org/10.3390/app13053149








