Review on Optimization Techniques of PV/Inverter Ratio for Grid-Tie PV Systems
Abstract
:1. Introduction
2. Literature Review
2.1. Derating Factor of PV Technology
2.2. PV Array to Inverter Sizing Strategies
- Manufacturers’ recommendations based on PV guidelines.
- DC/AC sizing ratio according to third-party publications.
2.2.1. Manufacturers’ Recommendations Based on PV Guidelines
2.2.2. DC/AC Sizing Ratio According to Third-Party Publications
2.2.3. A Climate Classification
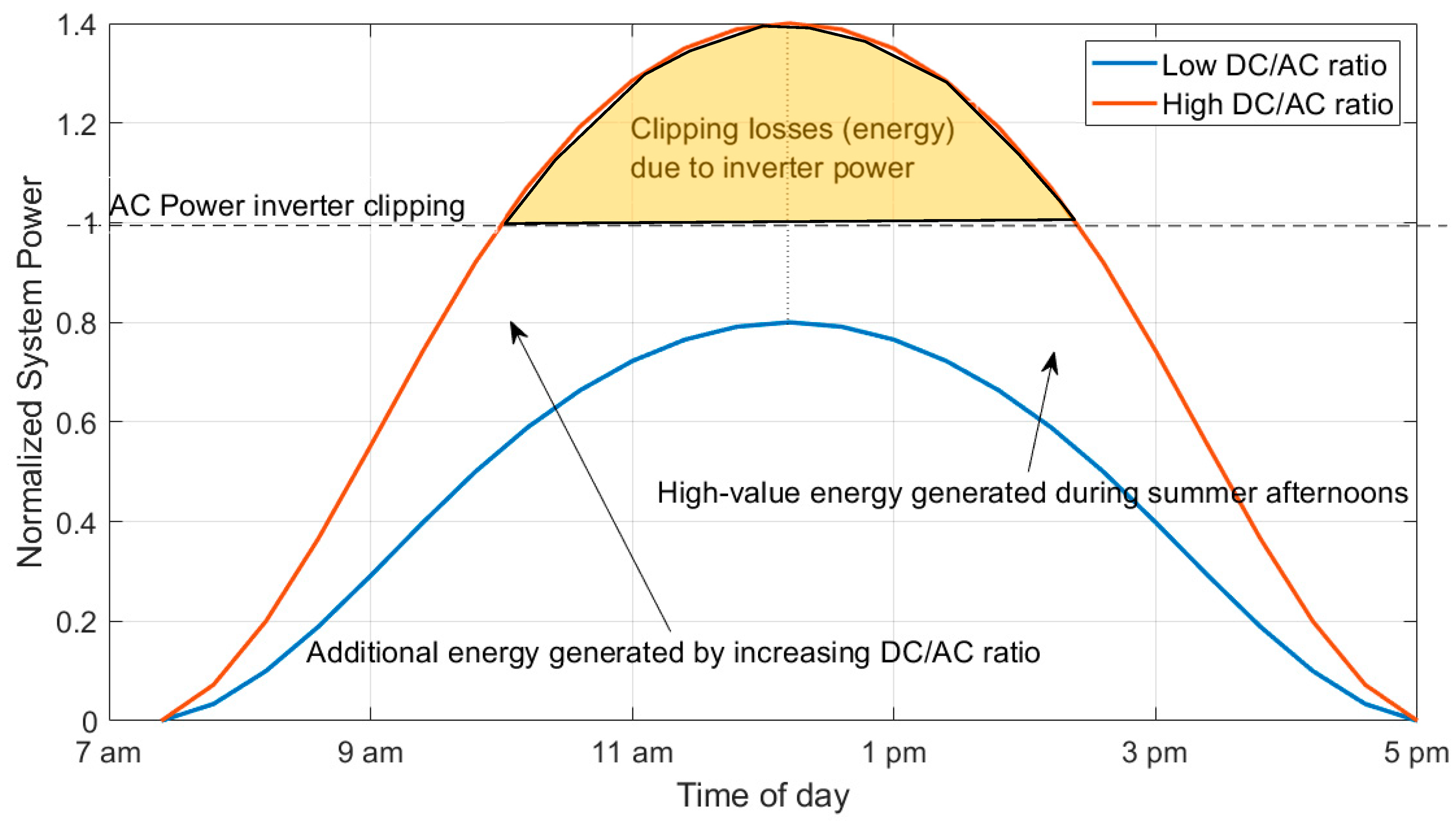
2.3. Analytical Methods Affect the Inverter in the PV Inverter
3. Recommended Deep Learning for Inverter Sizing
3.1. System Cost Consideration
3.2. Recommended Approach
3.3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pingel, S.; Frank, O.; Winkler, M.; Oaryan, S.; Geipel, T.; Hoehne, H.; Berghold, J. Potential induced degradation of solar cells and panels. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010. [Google Scholar] [CrossRef]
- Akcaoǧlu, S.C.; Martinopoulos, G.; Zafer, C. Experimental Analysis of the Potential Induced Degradation Effect on Organic Solar Cells. Int. J. Photoenergy 2017, 2017, 2101932. [Google Scholar] [CrossRef] [Green Version]
- Makhloufi, S.; Abdessemed, R. Type-2 fuzzy logic optimum PV/inverter sizing ratio for grid-connected PV systems: Application to selected Algerian locations. J. Electr. Eng. Technol. 2011, 6, 731–741. [Google Scholar] [CrossRef] [Green Version]
- Li, J. Optimal sizing of grid-connected photovoltaic battery systems for residential houses in Australia. Renew. Energy 2019, 136, 1245–1254. [Google Scholar] [CrossRef]
- Koutroulis, E.; Blaabjerg, F. Methods for the optimal design of grid-connected PV inverters. Int. J. Renew. Energy Res. 2011, 1, 54–64. [Google Scholar]
- Sulaiman, S.I.; Rahman, T.K.A.; Musirin, I.; Shaari, S.; Sopian, K. An intelligent method for sizing optimization in grid-connected photovoltaic system. Sol. Energy 2012, 86, 2067–2082. [Google Scholar] [CrossRef]
- Zhu, J.; Bründlinger, R.; Mühlberger, T.; Betts, T.R.; Gottschalg, R. Optimised inverter sizing for photovoltaic systems in high-latitude maritime climates. IET Renew. Power Gener. 2011, 5, 58–66. [Google Scholar] [CrossRef]
- King, B.H.; Granata, J.E.; Sandia, A.J.L.H. Systems Long Term Exposure program: Analysis of the first year of data. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Tampa Bay, FL, USA, 6–12 June 2013. [Google Scholar] [CrossRef] [Green Version]
- Riley, D.; Stein, J.; Kratochvil, J. Testing and characterization of PV modules with integrated microinverters. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Tampa Bay, FL, USA, 6–12 June 2013. [Google Scholar] [CrossRef]
- Hussin, M.Z. Design Impact of 6.08 kWp Grid-Connected Photovoltaic System at Malaysia Green Technology Corporation. Int. J. Electr. Electron. Syst. Res. 2012, 5, 1–10. [Google Scholar]
- Charki, A.; Logerais, P.O.; Bigaud, D.; Kébé, C.M.F.; Ndiaye, A. Lifetime assessment of a photovoltaic system using stochastic Petri nets. Int. J. Model. Simul. 2017, 37, 149–155. [Google Scholar] [CrossRef]
- He, J.; Sangwongwanich, A.; Yang, Y.; Iannuzzo, F. Lifetime Evaluation of Three-Level Inverters for 1500-V Photovoltaic Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4285–4298. [Google Scholar] [CrossRef]
- Durand, S.J. Attaining a 30-year photovoltaic system lifetime: The BOS issues. Prog. Photovolta. Res. Appl. 1994, 2, 107–113. [Google Scholar] [CrossRef]
- Chen, S.; Li, P.; Brady, D.; Lehman, B. Determining the optimum grid-connected photovoltaic inverter size. Sol. Energy 2013, 87, 96–116. [Google Scholar] [CrossRef]
- Burger, B.; Rüther, R. Inverter sizing of grid-connected photovoltaic systems in the light of local solar resource distribution characteristics and temperature. Sol. Energy 2006, 80, 32–45. [Google Scholar] [CrossRef]
- Macêdo, W.N.; Zilles, R. Operational results of grid-connected photovoltaic system with different Inverter’s Sizing Factors (ISF). Prog. Photovolta. Res. Appl. 2007, 15, 337–352. [Google Scholar] [CrossRef]
- Camps, X.; Velasco, G.; de la Hoz, J.; Martín, H. Contribution to the PV-to-inverter sizing ratio determination using a custom flexible experimental setup. Appl. Energy 2015, 149, 35–45. [Google Scholar] [CrossRef]
- Luoma, J.; Kleissl, J.; Murray, K. Optimal inverter sizing considering cloud enhancement. Sol. Energy 2012, 86, 421–429. [Google Scholar] [CrossRef]
- Wang, H.X.; Muñoz-García, M.A.; Moreda, G.P.; Alonso-García, M.C. Optimum inverter sizing of grid-connected photovoltaic systems based on energetic and economic considerations. Renew. Energy 2018, 118, 709–717. [Google Scholar] [CrossRef]
- Kratzenberg, M.G.; Deschamps, E.M.; Nascimento, L.; Rüther, R.; Zürn, H.H. Optimal photovoltaic inverter sizing considering different climate conditions and energy prices. Energy Procedia 2014, 57, 226–234. [Google Scholar] [CrossRef] [Green Version]
- Paiva, G.M.; Pimentel, S.P.; Marra, E.G.; Alvarenga, B.P. Analysis of inverter sizing ratio for PV systems considering local climate data in central Brazil. IET Renew. Power Gener. 2017, 11, 1364–1370. [Google Scholar] [CrossRef]
- Pérez-Higueras, P.J.; Almonacid, F.M.; Rodrigo, P.M.; Fernández, E.F. Optimum sizing of the inverter for maximizing the energy yield in state-of-the-art high-concentrator photovoltaic systems. Sol. Energy 2018, 171, 728–739. [Google Scholar] [CrossRef]
- Hussin, M.Z.; Omar, A.M.; Shaari, S.; Sin, N.D.M. Review of state-of-the-art: Inverter-to-array power ratio for thin—Film sizing technique. Renew. Sustain. Energy Rev. 2017, 74, 265–277. [Google Scholar] [CrossRef]
- Good, J.; Johnson, J.X. Impact of inverter loading ratio on solar photovoltaic system performance. Appl. Energy 2016, 177, 475–486. [Google Scholar] [CrossRef]
- Wright, D. Levelized Cost of Electricity. In Solarnomics; Routledge: Oxford, UK, 2022. [Google Scholar] [CrossRef]
- Gilman, P.; Dobos, A.; DiOrio, N.; Freeman, J.; Janzou, S.; Ryberg, D. System Advisor Model (SAM) Photovoltaic Model Technical Reference Update; National Renewable Energy Laboratory: Golden, CO, USA, 2018. [Google Scholar]
- Martins Deschamps, E.; Rüther, R. Optimization of inverter loading ratio for grid connected photovoltaic systems. Sol. Energy 2019, 179, 106–118. [Google Scholar] [CrossRef]
- Nurunnabi, M.; Roy, N.K.; Pota, H.R. Optimal sizing of grid-tied hybrid renewable energy systems considering inverter to PV ratio—A case study. J. Renew. Sustain. Energy 2019, 11, 013505. [Google Scholar] [CrossRef]
- Luoma, J.; Kleissl, J. Optimal inverter sizing considering cloud enhancement. In Proceedings of the 40th ASES National Solar Conference 2011, Raleigh, NC, USA, 17–20 May 2011. [Google Scholar]
- Nasiri, R.; Khayamy, M.; Rashidi, M.; Nasiri, A.; Bhavaraju, V. Optimal Solar PV Sizing for Inverters Based on Specific Local Climate. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition, Portland, OR, USA, 23–27 September 2018. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef] [PubMed]
- Khatib, T.; Mohamed, A.; Sopian, K. A review of photovoltaic systems size optimization techniques. Renew. Sustain. Energy Rev. 2013, 22, 454–465. [Google Scholar] [CrossRef]
- Malamaki, K.N. Analytical and Detailed Evaluation of Power and Energy Losses in PV Plants Aiming at Their Integration in Future Ancillary Services Markets. 2020. Available online: http://ikee.lib.auth.gr/record/332342/files/GRI-2021-31027.pdf (accessed on 1 January 2023).
- Faccio, M.; Gamberi, M.; Bortolini, M.; Nedaei, M. State-of-art review of the optimization methods to design the configuration of hybrid renewable energy systems (HRESs). Front. Energy 2018, 12, 591–622. [Google Scholar] [CrossRef]
- Fouad, M.M.; Shihata, L.A.; Morgan, E.S.I. An integrated review of factors influencing the performance of photovoltaic panels. Renew. Sustain. Energy Rev. 2017, 80, 1499–1511. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Hiendro, A.; Sedraoui, K.; Twaha, S. Optimal sizing of grid-connected photovoltaic energy system in Saudi Arabia. Renew. Energy 2015, 75, 489–495. [Google Scholar] [CrossRef]
- Ustun, T.S.; Aoto, Y.; Hashimoto, J.; Otani, K. Optimal PV-INV Capacity Ratio for Residential Smart Inverters Operating under Different Control Modes. IEEE Access 2020, 8, 116078–116089. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Wang, T.; Zhao, Y. Highly Stable Inorganic Lead Halide Perovskite toward Efficient Photovoltaics. Acc. Chem. Res. 2021, 54, 3452–3461. [Google Scholar] [CrossRef]
- Baschel, S.; Koubli, E.; Roy, J.; Gottschalg, R. Impact of component reliability on large scale photovoltaic systems’ Performance. Energies 2018, 11, 1579. [Google Scholar] [CrossRef] [Green Version]
- Touzani, S.; Prakash, A.K.; Wang, Z.; Agarwal, S.; Pritoni, M.; Kiran, M.; Brown, R.; Granderson, J. Controlling distributed energy resources via deep reinforcement learning for load flexibility and energy efficiency. Appl. Energy 2021, 304, 117733. [Google Scholar] [CrossRef]
- Aghaei, M.; Kumar, N.M.; Eskandari, A.; Ahmed, H.; de Oliveira, A.K.V.; Chopra, S.S. Solar PV systems design and monitoring. In Photovoltaic Solar Energy Conversion; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar] [CrossRef]
- Clean Energy Council. Grid-Connected Solar PV Systems: Design Guidelines for Accredited Installers; Clean Energy Council: Melbourne, Australia, 2013; pp. 1–18. [Google Scholar]
- Best Practice Needed to Keep Pace with Increase in Renewable Energy Uptake—APVI. Available online: https://apvi.org.au/best-practice-needed-to-keep-pace-with-increase-in-renewable-energy-uptake/ (accessed on 14 January 2023).
- Arora, K.; Diu, S.; Roper, J.; Coonick, C.; Fraser, P.; Macdonald-Brown, J.; Mawbey, J.; Noble, R.; Pocock, S.; Roper, J.; et al. Solar PV on Commercial Buildings: A Guide for Owners and Developers; BRE National Solar Centre: Watford, UK, 2016. [Google Scholar]
- Saha, K. Planning and installing photovoltaic system: A guide for installers, architects and engineers. Int. J. Environ. Stud. 2014, 71, 887–888. [Google Scholar] [CrossRef]
- Schaeffer, G.J. Energy sector in transformation, trends and prospects. Procedia Comput. Sci. 2015, 52, 866–875. [Google Scholar] [CrossRef] [Green Version]
- Zeppel, H. Carbon mitigation actions by peri-urban and regional cities in Queensland. In Proceedings of the 6th State of Australian Cities Conference, Sydney, Australia, 26–29 November 2013. [Google Scholar]
- Brooks, B.; Xenergy, K.; Whitaker, C. Guideline for the use of the Performance Test Protocol for Evaluating Inverters Used in Grid-Connected Photovoltaic Systems; Sandia National Laboratories: Albuquerque, NM, USA, 2005. [Google Scholar]
- Kumar, K.; Sharma, S.; Jain, L.; Khaimah, R. Al Standalone Photovoltaic (PV) Module Outdoor Testing Facility for UAE Climate; CSEM-UAE Innovation Center LLC: Ras Al Khaimah, United Arab Emirates, 2007. [Google Scholar]
- ManualsLib. Pv Inverter Selection—Dupont Apollo Installation Manualline. Available online: https://www.manualslib.com/manual/1907236/Dupont-Apollo.html?page=20 (accessed on 13 January 2023).
- Baoding Tianwei Solarfilms Solar Panels Review. Available online: https://www.solarquotes.com.au/panels/baoding-tianwei-solarfilms-review.html (accessed on 13 January 2023).
- “Solarex Foresees A New Era For Energy—The Washington Post”. Available online: https://www.washingtonpost.com/archive/business/1999/05/24/solarex-foresees-a-new-era-for-energy/e1b8adfe-43ac-4e23-ba58-e48b4a479b84/ (accessed on 24 February 2023).
- Kefale, H.A.; Getie, E.M.; Eshetie, K.G. Optimal Design of Grid-Connected Solar Photovoltaic System Using Selective Particle Swarm Optimization. Int. J. Photoenergy 2021, 2021, 6632859. [Google Scholar] [CrossRef]
- “Solar inverters | Danfoss”. Available online: https://www.danfoss.com/en/markets/energy-and-natural-resources/dsp/solar-inverters/ (accessed on 14 January 2023).
- PDF4PRO. Technical Application Papers No. 10 Photovoltaic. Available online: https://pdf4pro.com/tag/65550/technical-application-papers-no.html (accessed on 13 January 2023).
- KACO New Energy. Inverters for Solar PV Systems + Battery Storage. Available online: https://kaco-newenergy.com/home/ (accessed on 14 January 2023).
- Power-One, Inc. Encyclopedia.com. Available online: https://www.encyclopedia.com/books/politics-and-business-magazines/power-one-inc (accessed on 14 January 2023).
- Leonics Co., Ltd. Solar Components. Thailand. Available online: https://www.enfsolar.com/leonics (accessed on 14 January 2023).
- PV Powered Inverters. AE Inverters. Available online: https://www.solarelectricsupply.com/solar-inverter/pv-powered (accessed on 14 January 2023).
- Solar Inverters. SMA Solar. Available online: https://www.sma.de/en/products/solar-inverters (accessed on 14 January 2023).
- Energy, P.S.; Staffelstein, B.; Engineering, M.S. Sputnik Engineering presents MaxTalk 2 and enhances the flexibility of its SolarMax-MT inverter. In Proceedings of the 26th Photovoltaic Symposium, Bad Staffelstein, Germany, 2–4 March 2011. [Google Scholar]
- Hussin, M.Z.; Yaacob, A.; Zain, Z.M.; Shaari, S.; Omar, A.M. Status of a grid-connected MBIPV project in Malaysia. In Proceedings of the 3rd ISESEE 2011—International Symposium and Exhibition in Sustainable Energy and Environment, Malacca, Malaysia, 1–3 June 2011. [Google Scholar]
- Zhang, S.; Tang, Y. Optimal schedule of grid-connected residential PV generation systems with battery storages under time-of-use and step tariffs. J. Energy Storage 2019, 23, 175–182. [Google Scholar] [CrossRef]
- Sick, F.; Erge, T. Photovoltaics in Buildings a Design Handbook for Architects and Engineers; Routledge: Oxford, UK, 2013; Available online: https://www.routledge.com/Photovoltaics-in-Buildings-A-Design-Handbook-for-Architects-and-Engineers/Erge-Sick/p/book/9781849711920 (accessed on 13 January 2023).
- Utility Scale Solar Power Plants: A Guide for Developers and Investors. Available online: https://www.ifc.org/wps/wcm/connect/topics_ext_content/ifc_external_corporate_site/sustainability-at-ifc/publications/publications_handbook_solarpowerplants (accessed on 13 January 2023).
- Young, W.R. Solar on schools designed for emergency shelters: 39th IEEE photovoltaic specialist conference. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Tampa Bay, FL, USA, 16–21 June 2013. [Google Scholar] [CrossRef]
- Emmanuel, M.; Akinyele, D.; Rayudu, R. Techno-economic analysis of a 10 kWp utility interactive photovoltaic system at Maungaraki school, Wellington, New Zealand. Energy 2016, 120, 573–583. [Google Scholar] [CrossRef]
- Notton, G.; Lazarov, V.; Stoyanov, L. Optimal sizing of a grid-connected PV system for various PV module technologies and inclinations, inverter efficiency characteristics and locations. Renew. Energy 2010, 35, 541–554. [Google Scholar] [CrossRef]
- Mondol, J.D.; Yohanis, Y.G.; Norton, B. The impact of array inclination and orientation on the performance of a grid-connected photovoltaic system. Renew. Energy 2007, 32, 118–140. [Google Scholar] [CrossRef]
- Mondol, J. Sizing of Grid-Connected Photovoltaic Systems; SPIE Newsroom: Bellingham, WA, USA, 2007. [Google Scholar] [CrossRef]
- Chen, S.; Li, P.; Brady, D.; Lehman, B. The impact of irradiance time behaviors on inverter sizing and design. In Proceedings of the 2010 IEEE 12th Workshop on Control and Modeling for Power Electronics, Boulder, CO, USA, 28–30 June 2010. [Google Scholar] [CrossRef]
- Hernandez, J.; Arredondo, C.A.; Vallejo, W.; Gordillo, G. Comparison of two grid connected photovoltaic systems GCPVS with different dimensioning factor DF during three years operation in Bogotá—Colombia. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Tampa, FL, USA, 3–8 June 2012. [Google Scholar] [CrossRef]
- Väisänen, J.; Kosonen, A.; Ahola, J.; Sallinen, T.; Hannula, T. Optimal sizing ratio of a solar PV inverter for minimizing the levelized cost of electricity in Finnish irradiation conditions. Sol. Energy 2019, 185, 350–362. [Google Scholar] [CrossRef]
- Lappalainen, K.; Valkealahti, S. Analysis of the operation of PV strings at the MPP closest to the nominal MPP voltage instead of the global MPP based on measured current-voltage curves. EPJ Photovolt. 2022, 13, 4. [Google Scholar] [CrossRef]
- Ksentini, A.; Azzag, E.; Bensalem, A. Sizing and optimisation of a photovoltaic pumping system. Int. J. Energy Technol. Policy 2019, 15, 71. [Google Scholar] [CrossRef]
- Tasghat, F.; Bensenouci, A.; Fathi, M.; Belkhiri, Y. PVsyst Sizing of a PV System for a Water Supply of an Agricultural Farm in an Isolated Area Using Pivot Technique. In Lecture Notes in Networks and Systems; Springer International Publishing: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Chaib, A.; Kesraoui, M.; Aklouche, M. Sizing a PV pumping system for an Algerian remote site. In Proceedings of the 2015 6th International Renewable Energy Congress, Sousse, Tunisia, 24–26 March 2015. [Google Scholar] [CrossRef]
- Freitas, S.; Serra, F.; Brito, M.C. Multi-objective genetic algorithm for the optimization of a PV system arrangement. In Proceedings of the ISES Solar World Congress 2015, Daegu, Republic of Korea, 8–12 November 2015. [Google Scholar] [CrossRef]
- Marcos, J.; Storkël, O.; Marroyo, L.; Garcia, M.; Lorenzo, E. Storage requirements for PV power ramp-rate control. Sol. Energy 2014, 99, 28–35. [Google Scholar] [CrossRef] [Green Version]
- Aristizábal, A.J.; Habib, A.; Ospina, D.; Castaneda, M.; Zapata, S.; Banguero, E. RenPower: Software for sizing renewable energy microgrids for academic teaching. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019. [Google Scholar] [CrossRef]
- Schepel, V.; Tozzi, A.; Klement, M.; Ziar, H.; Isabella, O.; Zeman, M. The Dutch PV portal 2.0: An online photovoltaic performance modeling environment for the Netherlands. Renew. Energy 2020, 154, 175–186. [Google Scholar] [CrossRef]
- Munzke, N.; Büchle, F.; Smith, A.; Hiller, M. Influence of efficiency, aging and charging strategy on the economic viability and dimensioning of photovoltaic home storage systems. Energies 2021, 14, 7673. [Google Scholar] [CrossRef]
- Beck, T.; Kondziella, H.; Huard, G.; Bruckner, T. Assessing the influence of the temporal resolution of electrical load and PV generation profiles on self-consumption and sizing of PV-battery systems. Appl. Energy 2016, 173, 331–342. [Google Scholar] [CrossRef]
- Eicker, U. Grid-Connected Photovoltaic Systems. In Solar Technologies for Buildings; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef] [Green Version]
- Masrur, H.; Gamil, M.M.; Islam, M.R.; Muttaqi, K.M.; Lipu, M.S.H.; Senjyu, T. An Optimized and Outage-Resilient Energy Management Framework for Multicarrier Energy Microgrids Integrating Demand Response. IEEE Trans. Ind. Appl. 2022, 58, 4171–4180. [Google Scholar] [CrossRef]
- Ketjoy, N.; Chamsa-ard, W.; Mensin, P. Analysis of factors affecting efficiency of inverters: Case study grid-connected PV systems in lower northern region of Thailand. Energy Rep. 2021, 7, 3857–3868. [Google Scholar] [CrossRef]
- Strand, T.; Mrig, L.; Hansen, R.; Emery, K. Technical evaluation of a dual-junction same-band-gap amorphous silicon photovoltaic system. Sol. Energy Mater. Sol. Cells 1996, 41–42, 617–628. [Google Scholar] [CrossRef]
- Alenezi, F.Q.; Sykulski, J.K.; Rotaru, M. Grid-connected photovoltaic module and array sizing based on an iterative approach. Int. J. Smart Grid Clean Energy 2014, 3, 247–254. [Google Scholar] [CrossRef] [Green Version]
- Toreti Scarabelot, L.; Arns Rampinelli, G.; Rambo, C.R. Overirradiance effect on the electrical performance of photovoltaic systems of different inverter sizing factors. Sol. Energy 2021, 225, 561–568. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Sopian, K.; Mahmoud, M. An iterative method for calculating the optimum size of inverter in PV systems for Malaysia. Electr. Rev. 2012, 88, 281–284. [Google Scholar]
- Ibrahim, M. Straight forward technique for sizing standalone PV hybrid systems. In Proceedings of the 20th—EU-PVSEC, Barcelona, Spain, 6–10 June 2005. [Google Scholar]
- Omer, S.A.; Wilson, R.; Riffat, S.B. Monitoring results of two examples of building integrated PV (BIPV) systems in the UK. Renew. Energy 2003, 28, 1387–1399. [Google Scholar] [CrossRef]
- Tinoco, S.; Reyes Duke, A.M. Cost-benefit analysis of the implementation of off-grid photovoltaic systems in the Northwest residential sector of San Pedro Sula, Honduras. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Surakarta, Indonesia, 24–25 August 2021. [Google Scholar] [CrossRef]
- Brito, E.M.D.S.; Cupertino, A.F.; Pereira, H.A.; Mendes, V.F. Reliability-based trade-off analysis of reactive power capability in PV inverters under different sizing ratio. Int. J. Electr. Power Energy Syst. 2022, 136, 107677. [Google Scholar] [CrossRef]
- Rodrigo, P.M.; Velázquez, R.; Fernández, E.F. DC/AC conversion efficiency of grid-connected photovoltaic inverters in central Mexico. Sol. Energy 2016, 139, 650–665. [Google Scholar] [CrossRef]
- Karimi, M.; Mokhlis, H.; Naidu, K.; Uddin, S.; Bakar, A.H.A. Photovoltaic penetration issues and impacts in distribution network—A review. Renew. Sustain. Energy Rev. 2016, 53, 594–605. [Google Scholar] [CrossRef]
- Demoulias, C. A new simple analytical method for calculating the optimum inverter size in grid-connected PV plants. Electr. Power Syst. Res. 2010, 80, 1197–1204. [Google Scholar] [CrossRef]
- Malamaki, K.N.D.; Demoulias, C.S. Minimization of electrical losses in two-axis tracking pv systems. IEEE Trans. Power Deliv. 2013, 28, 2445–2455. [Google Scholar] [CrossRef]
- Malamaki, K.N.D.; Demoulias, C.S. Estimation of additional pv converter losses operating under pf ≠ 1 based on manufacturer’s data at pf = 1. IEEE Trans. Energy Convers. 2019, 34, 540–553. [Google Scholar] [CrossRef]
- Wang, Y.; Das, R.; Putrus, G.; Kotter, R. Economic evaluation of photovoltaic and energy storage technologies for future domestic energy systems—A case study of the UK. Energy 2020, 203, 117826. [Google Scholar] [CrossRef]
- Ye, L.C.; Rodrigues, J.F.D.; Lin, H.X. Analysis of feed-in tariff policies for solar photovoltaic in China 2011–2016. Appl. Energy 2017, 203, 496–505. [Google Scholar] [CrossRef]
- Marino, C.; Nucara, A.; Panzera, M.F.; Pietrafesa, M.; Pudano, A. Economic comparison between a stand-alone and a grid connected PV system vs. Grid distance. Energies 2020, 13, 3846. [Google Scholar] [CrossRef]
- Najafi Ashtiani, M.; Toopshekan, A.; Razi Astaraei, F.; Yousefi, H.; Maleki, A. Techno-economic analysis of a grid-connected PV/battery system using the teaching-learning-based optimization algorithm. Sol. Energy 2020, 203, 69–82. [Google Scholar] [CrossRef]
- Brenna, M.; Foiadelli, F.; Longo, M.; Zaninelli, D. Energy Storage Control for Dispatching Photovoltaic Power. IEEE Trans. Smart Grid 2018, 9, 2419–2428. [Google Scholar] [CrossRef]
- Ciocia, A.; Amato, A.; Di Leo, P.; Fichera, S.; Malgaroli, G.; Spertino, F.; Tzanova, S. Self-Consumption and Self-Sufficiency in Photovoltaic Systems: Effect of Grid Limitation and Storage Installation. Energies 2021, 14, 1591. [Google Scholar] [CrossRef]
- Kumar, A.; Rizwan, M.; Nangia, U. A hybrid optimization technique for proficient energy management in smart grid environment. Int. J. Hydrogen Energy 2022, 47, 5564–5576. [Google Scholar] [CrossRef]
- Herteleer, B.; Cappelle, J.; Driesen, J. An autonomous photovoltaic system sizing program for office applications in Africa. Renew. Energy Power Qual. J. 2012, 1, 728–733. [Google Scholar] [CrossRef] [Green Version]
- Wen, S.; Zhao, T.; Tang, Y.; Xu, Y.; Zhu, M.; Huang, Y. A Joint Photovoltaic-Dependent Navigation Routing and Energy Storage System Sizing Scheme for More Efficient All-Electric Ships. IEEE Trans. Transp. Electrif. 2020, 6, 1279–1289. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Sabah, S.; Abbas, R.; Hossain, M.J.; Fahed, H. A novel sizing method of a standalone photovoltaic system for powering a mobile network base station using a multi-objective wind driven optimization algorithm. Energy Convers. Manag. 2021, 238, 114179. [Google Scholar] [CrossRef]
- Mohandes, B.; Wahbah, M.; El Moursi, M.S.; El-Fouly, T.H.M. Renewable energy management system: Optimum design and hourly dispatch. IEEE Trans. Sustain. Energy 2021, 12, 1615–1628. [Google Scholar] [CrossRef]
- SAM. Home—System Advisor Model (SAM). Nrel. 2020. Available online: https://sam.nrel.gov/ (accessed on 13 January 2023).
- NASA POWER. Prediction of Worldwide Energy Resources. Available online: https://power.larc.nasa.gov/ (accessed on 4 June 2022).







| Ref. | Range of Discussion on DC/AC Sizing and Cost | Literature Focus | Related Analysis and Results | Inverter Undersizing | Proposing System | Date Publish |
|---|---|---|---|---|---|---|
| [32] | Extensive | sizing optimization issues, hybrid PV/wind/diesel generator systems, hybrid PV/wind systems, hybrid PV/diesel generator, and standalone PV systems | No | Limited | No | 2013 |
| [33] | Limited | Power and Energy Losses in PV Plants in Future Ancillary Services Markets | Limited | No | No | 2020 |
| [34] | Limited | Optimization goals, utilized optimization methods, grid type as well as the investigated technology | Yes, statistical results | No | No | 2018 |
| [35] | Limited to PV system installed | Environmental, PV system, installation, cost factors as well as other miscellaneous factors | Limited | No | No | 2017 |
| This work | Extensive | DC/AC ratio optimization techniques | Yes, main results | yes | Yes | 2023 |
| Ref. | PV/Inverter Ratio | Company/Country | Recommendations |
|---|---|---|---|
| [56] | 0.88–1.1 | KACO New Energy | Power Ratio = PVGEN/PAC,INV |
| [57] | 0.7–1.0 | Power-One Inc. | PV Power @ STC/AC Power Nom. Max. of Inverter |
| [58] | 1.0 | Leonic Co., Ltd. | N/A |
| [54] | 0.8–1.2 | Danfoss Solar Inverters | Si PV = 0.94; Thin-Film = 0.94–0.90 and Thin–Film = 1.0 if Free-standing |
| [59] | 0.75–0.85 | AE PV-powered Inc | N/A |
| [60] | 0.8–1.2 | SMA Solar AG | PV/inverter power ratio (Vp) = input power inverter/peak power PV (0.9–1.0); Accepted Vp = 0.8–1.2 = (under extreme climate) |
| [61] | 0.8–1.1 | Energy, Staffelstein & Engineering | DF (Dimensioning factor) = Psolar/PWR,ACmax < 0.8:for DF = 0.8–1.15 = inverter too high; recommended for 35° inclination and south orientation; DF = (1.2–1.3): recommended facades (90° inclination), west or facing east; DF over 1.3: inverter too small; DF = (1.15 to 1.2): recommended to orient well to a very flat module under 15° inclinations or/and south (SW, SE). |
| [62] | 1.3–0.8 | Solar Photovoltaic Power: Designing Grid-Connected Systems, Malaysia | For Si PV = 0.80–0.75; for Thin–Film = 1.30–1.00 |
| [63] | 0.7–1.5 | UD, Delaware, US, Syllabus Book | Cost-effective and limited choice of inverter sizes to choose SF, even if overloaded occasionally. |
| [64] | 0.7–1.0 | Europe | Southern Europe (35–45° N) = 1.0–0.85; Central Europe (45–55° N) = 0.9–0.75; Northern Europe (55–70° N) = 0.8–0.7; |
| [65] | 0.8–1.2 | India | N/A |
| [66] | 0.7–0.65 | United States | N/A |
| [45] | 1–0.8 | United Kingdom | PV array-to-inverter ratio must be sized between 1:0.8 to 1:1 |
| [67] | 0.75 | Guideline/Standard Australia | The nominal AC output power of the inverter cannot be under 75% of the peak power of the PV array. |
| Climate Classification | Country/Territory with the Weather |
|---|---|
| Dfb | Humid continental climate, warm summer; at least four months averaging above 10 °C, all months with average temperatures below 22 °C, and coldest month averaging below 0 °C (or −3 °C). |
| Csb | Mediterranean climate, warm summer; the driest month of summer receives less than 40 mm, at least three times as much precipitation in the wettest month of winter as in the driest month of summer, all months with average temperatures below 22 °C, at least four months averaging above 10 °C, and coldest month averaging above 0 °C (or −3 °C). |
| Csa | Mediterranean climate, hot summer; the driest month of summer receives less than 40 mm, at least three times as much precipitation in the wettest month of winter as in the driest month of summer, at least four months averaging above 10 °C, at least one month’s average temperature above 22 °C, and coldest month averaging above 0 °C (or −3 °C). |
| Cfb | Subtropical highland climate or temperate oceanic climate; at least four months averaging above 10 °C, all months with average temperatures below 22 °C, and coldest month averaging above 0 °C (or −3 °C). |
| Cfa | No dry months in the summer. No significant precipitation difference between seasons. Humid subtropical climate; at least four months averaging above 10 °C (50 °F), at least one month’s average temperature above 22 °C (71.6 °F),and coldest month averaging above 0 °C (32 °F) (or −3 °C (27 °F)). |
| BSk | Cold semi-arid climate |
| BWh | The hot desert climate, and no month with an average temperature greater than 10 °C. |
| Cwa | Monsoon-influenced humid subtropical climate; at least ten times as much rain in the wettest month of summer as in the driest month of winter, at least four months averaging above 10 °C, at least one month’s average temperature above 22 °C, and coldest month averaging above 0 °C (or −3 °C). |
| Af | The average precipitation of at least 60 mm every month (tropical rainforest climate) |
| Aw | The driest month has a precipitation of less than 60 mm (tropical savanna or dry and wet climate). |
| Optimal Power Ratio | Method/Relation | Recommendation | Climate Classification | Country/Group | Ref. |
|---|---|---|---|---|---|
| 1.50–1.00 | SI; r = 1.5 medium efficiency inverter, r = 1.2 high-efficiency inverter. HSI; r = 1.10 medium and low-efficiency inverter, r = 1.00 high and medium efficiency inverter. | Dfb | Finland | [73,74] | |
| 0.71 | 0.71 | Csb | Eugene, OR, USA | [14] | |
| 0.71 | 0.71 | Csa | Sacramento, CA, USA | [14] | |
| 1.291–1.204 | β = 60° (1.204), β = 45° (1.291) | Csa | Batna, Algeria | [75,76] | |
| 1.220–1.153 | β = 60° (1.153), β = 45° (1.220) | Csa | Algiers, Algeria | [77] | |
| 0.67 | NA | 0.67 | Csa | Portugal | [78,79] |
| 1.00–0.80 | 0.85 | Cfb | Bogota, Colombia | [80] | |
| 0.65 | NA | 0.65 | Cfb | The Netherlands | [81] |
| 1.20–0.75 | v = 0.90 (Germany) | Cfb | Germany | [82] | |
| 0.95–0.85 | NA | Cfb | Freiburg, Germany | [83] | |
| 1.30–1.15 | 1.15 | Cfb | Nottingham, UK | [15] | |
| 0.90–0.70 | TF = 1.3, Overcast sky = 0.9–0.7 | Cfb | Northern Ireland, UK | [84] | |
| 1.10–1.50 | Low Eff. Inv; LSI = 1.4–1.5; HIS = 1.2–1.3, High Eff. Inv; LSI = 1.3–1.4; HIS = 1.1–1.2, | Cfb | Loughborough, UK | [7] | |
| 1.25 | 1.10–1.40 | Cfb | Oak ridge, TN, USA | [85] | |
| 1.25 | 1.10–1.40 | Cfb | Northern Ireland, UK | [7] | |
| 1.25 | TF = 1.10–1.15 | Cfb | Loughborough, UK | [86] | |
| NA | 0.69 | Cfa | Oak ridge, TN, USA | [14] | |
| 1.30–1.20 | Si PV = 1.30–1.20; Thin-Film < 1.00 | Cfa | UFSC, Florianópolis, South Brazil | [15] | |
| 0.83–0.78 | Thin-Film Fall = 0.82; Thin-Film Summer = 0.83; Thin-Film Spring = 0.82; Thin-Film Winter = 0.78; | BSk | Golden, Colorado | [87] | |
| 1.00–0.60 | 1.22 | BSk | San Diego, California | [18,27] | |
| NA | 0.74 | BSk | Prewitt, NM, USA | [14] | |
| 0.85–0.65 | Sfmin = 0.65; Sfmax = 0.85 for Gulf Council Countries | BWh | Kuwait | [88] | |
| NA | 0.67 | BWh | Phoenix, AZ, USA | [14] | |
| NA | 1.00 | BWh | Las Vegas, NV, USA | [14] | |
| 1.02–0.55 | NA | Cwa | Sao Paulo, Brazil | [89] | |
| 1.321–1.210 | β = 45° (1.321), β = 60° (1.210) | BWh | Adrar, Algeria | [3] | |
| 0.85–1.07 | Valid on all PV technologies | Af | Malaysia | # | |
| NA | 0.761 (Lanai)/0.741 (Oahu) | Aw | Lanai/Oahu, Hawaii, USA | [14] | |
| 1.43–1.21 | Valid on all PV technologies | Af | Kuala Lumpur, Kuching and Alor Setar, Johor Bharu, Ipoh, Malaysia | [90] | |
| 1.03–0.93 | Integrated (0.93), Flat surface (1.03) | Csa | Cadiz, Spain | [80] |
| Description | Dimensions |
|---|---|
| Minimum Batch Size | 128 |
| Initial Learning Rate | 0.0003 |
| Maximum Epochs | 15 |
| layers convolution 2d Layer 3 | 3 |
| batch Normalization Layer | 1 |
| relu Layer | 1 |
| Maximum Pooling 2d Layer 3, Stride = 2 | 3, 2 |
| convolution 2d Layer 3, 2 × Number of filters | 3, 2 × 12 |
| batch Normalization Layer | 1 |
| relu Layer | 1 |
| maximum Pooling 2d Layer 3, Stride = 2 | 3, 2 |
| convolution 2d Layer 3, 4 × Number of filters | 3, 4 × 12 |
| batch Normalization Layer | 1 |
| relu Layer | 1 |
| Maximum Pooling 2d Layer 3, Stride = 2 | 3, 2 |
| convolution 2d Layer 3, 4 × Number of filters | 3, 4 × 12 |
| batch Normalization Layer | 1 |
| relu Layer | 1 |
| convolution 2d Layer 3, 4 × Number of filters | 3, 4 × 12 |
| batch Normalization Layer | 1 |
| relu Layer | 1 |
| Maximum Pooling 2d Layer (time Pool Size 1) | 1 |
| dropout Layer | 1 |
| fully Connected Layer (12 = numClasses) | 12 |
| Soft-max Layer | 1 |
| classification Layer | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hazim, H.I.; Baharin, K.A.; Gan, C.K.; Sabry, A.H.; Humaidi, A.J. Review on Optimization Techniques of PV/Inverter Ratio for Grid-Tie PV Systems. Appl. Sci. 2023, 13, 3155. https://doi.org/10.3390/app13053155
Hazim HI, Baharin KA, Gan CK, Sabry AH, Humaidi AJ. Review on Optimization Techniques of PV/Inverter Ratio for Grid-Tie PV Systems. Applied Sciences. 2023; 13(5):3155. https://doi.org/10.3390/app13053155
Chicago/Turabian StyleHazim, Hazim Imad, Kyairul Azmi Baharin, Chin Kim Gan, Ahmad H. Sabry, and Amjad J. Humaidi. 2023. "Review on Optimization Techniques of PV/Inverter Ratio for Grid-Tie PV Systems" Applied Sciences 13, no. 5: 3155. https://doi.org/10.3390/app13053155
APA StyleHazim, H. I., Baharin, K. A., Gan, C. K., Sabry, A. H., & Humaidi, A. J. (2023). Review on Optimization Techniques of PV/Inverter Ratio for Grid-Tie PV Systems. Applied Sciences, 13(5), 3155. https://doi.org/10.3390/app13053155








