Optimization of Design Parameters Using SQP for an Agricultural Pipe Extraction Device
Abstract
:1. Introduction
2. Materials and Methods
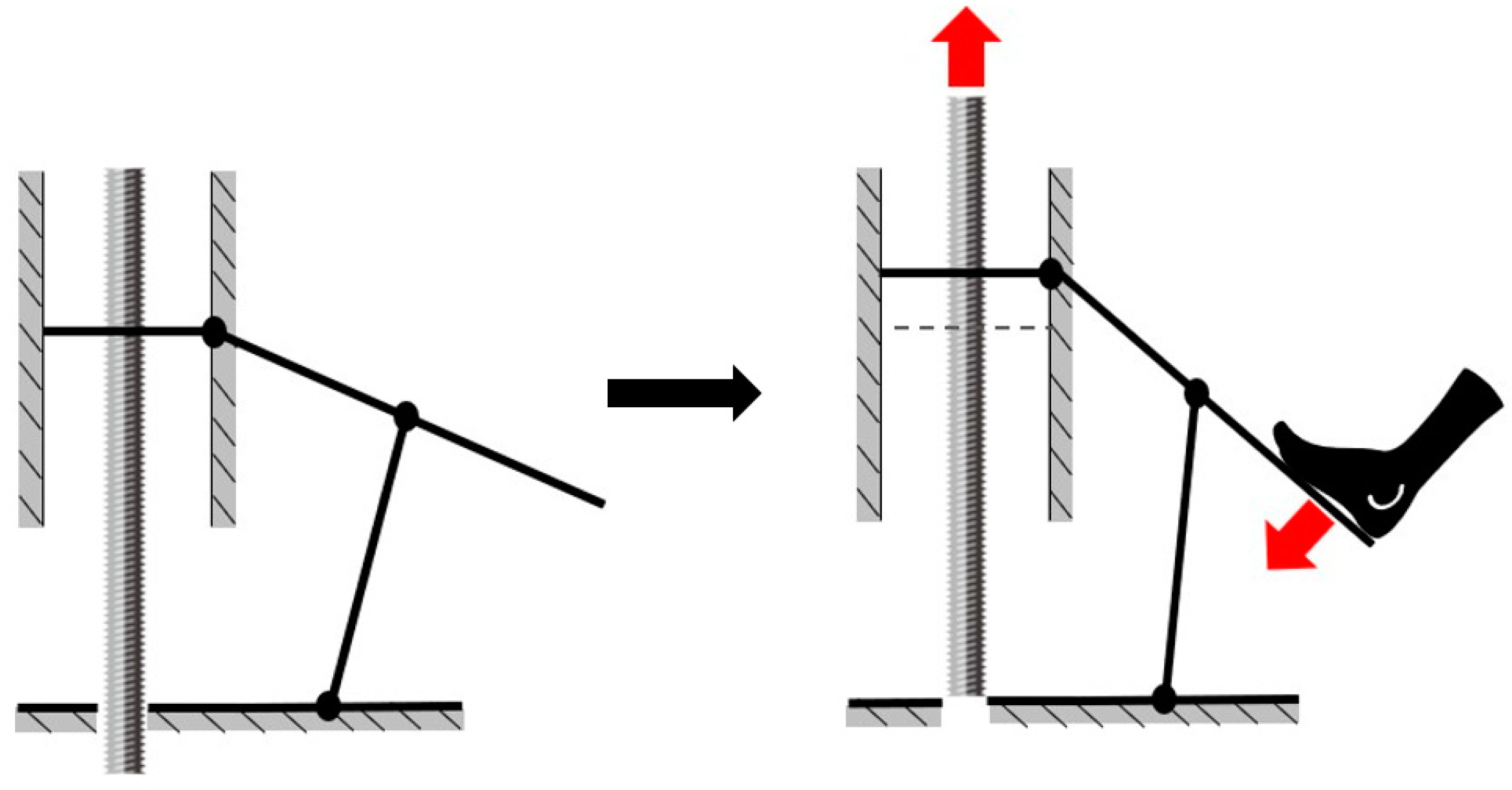
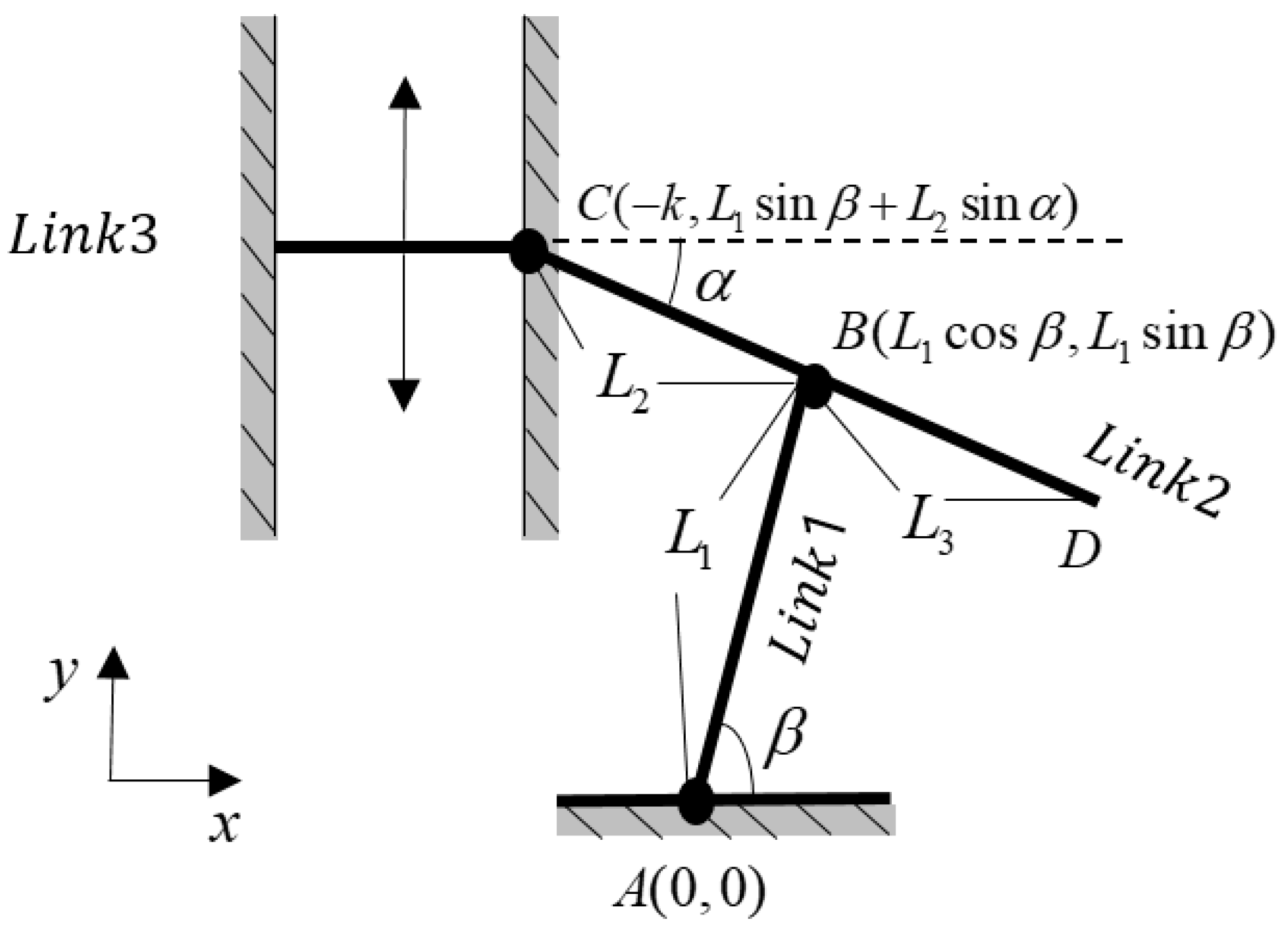
2.1. Extraction Device Modeling
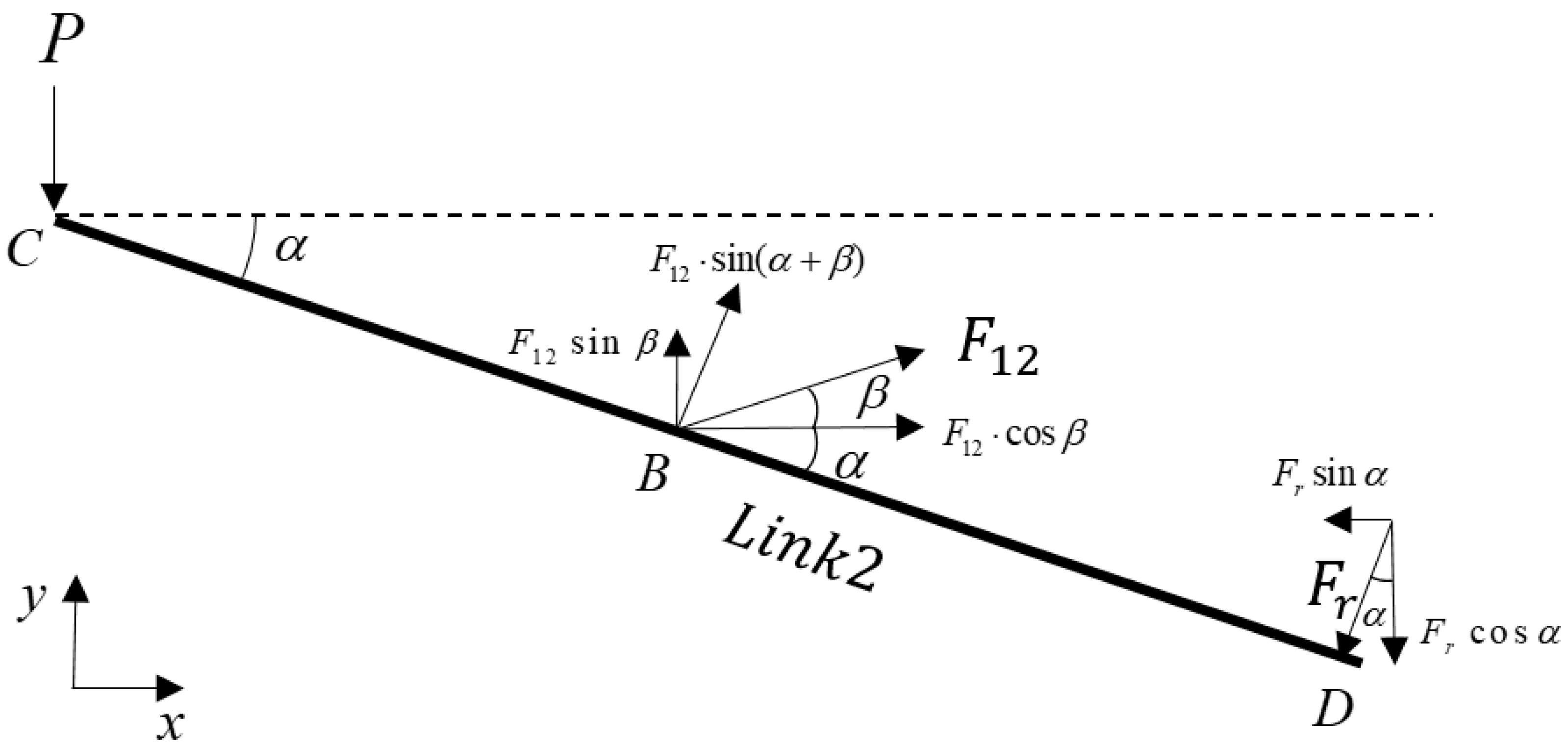
2.2. Objective Function for Optimization
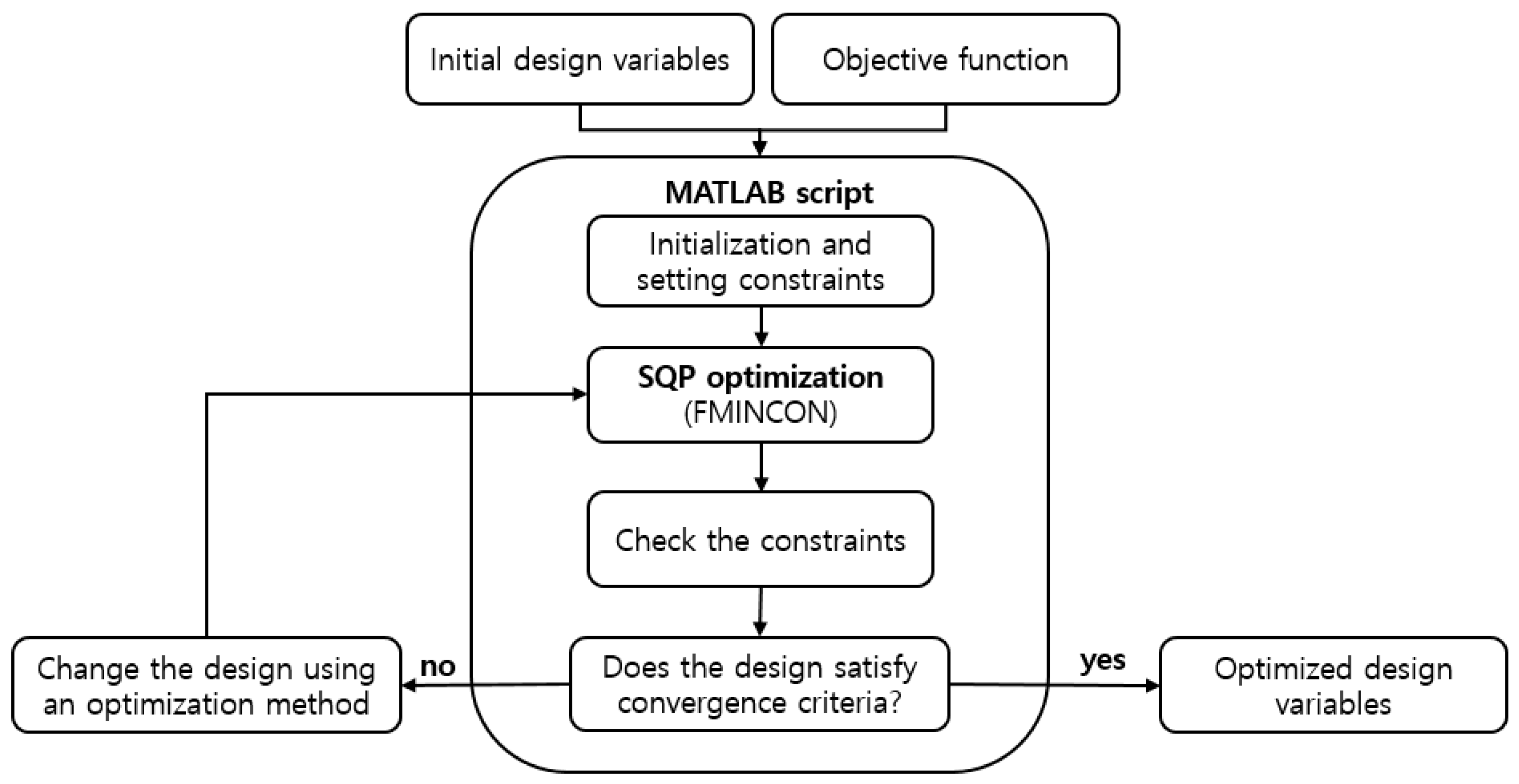
2.3. Optimal Design Method
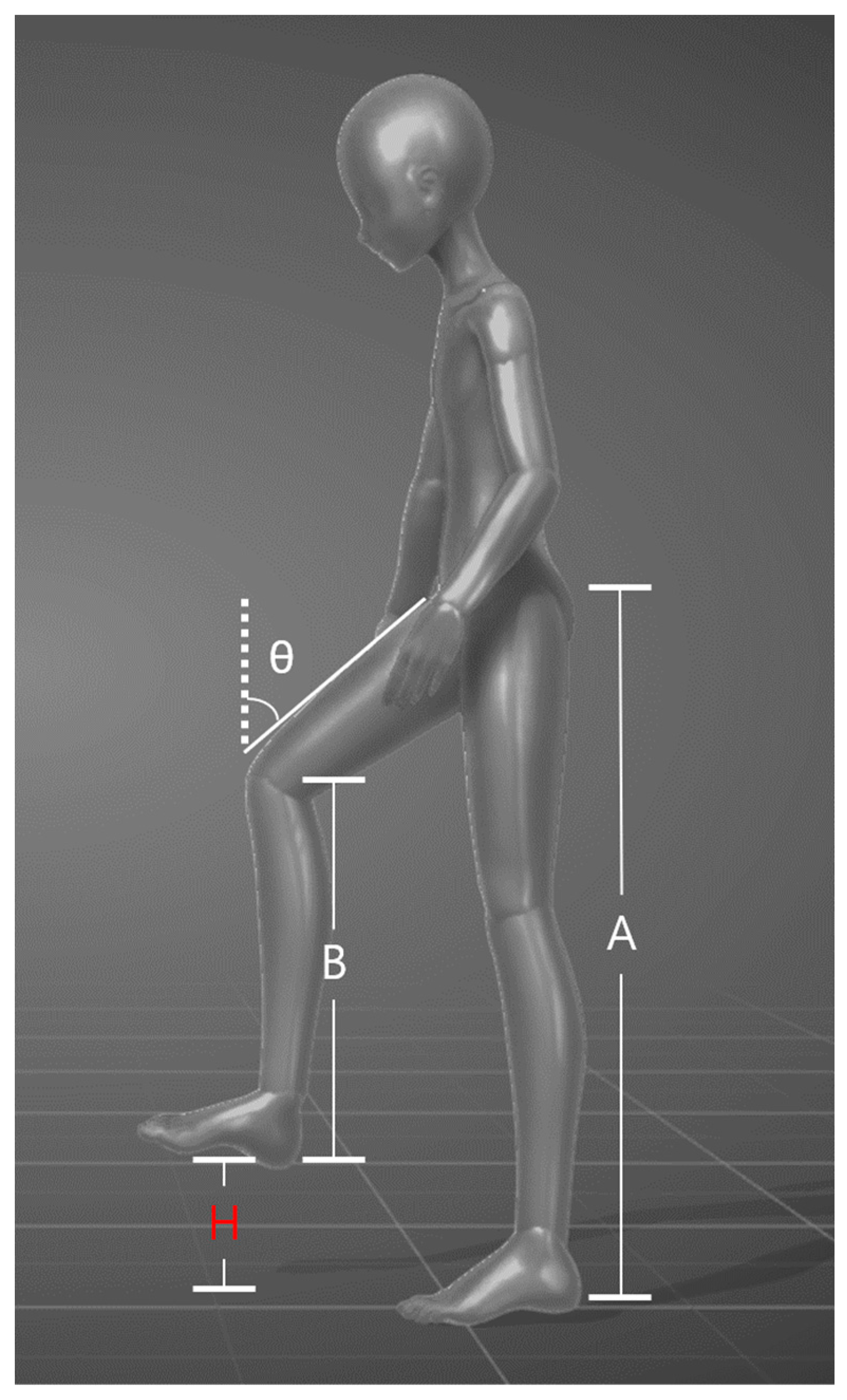
2.4. Constraints
2.5. Optimization Model Construction
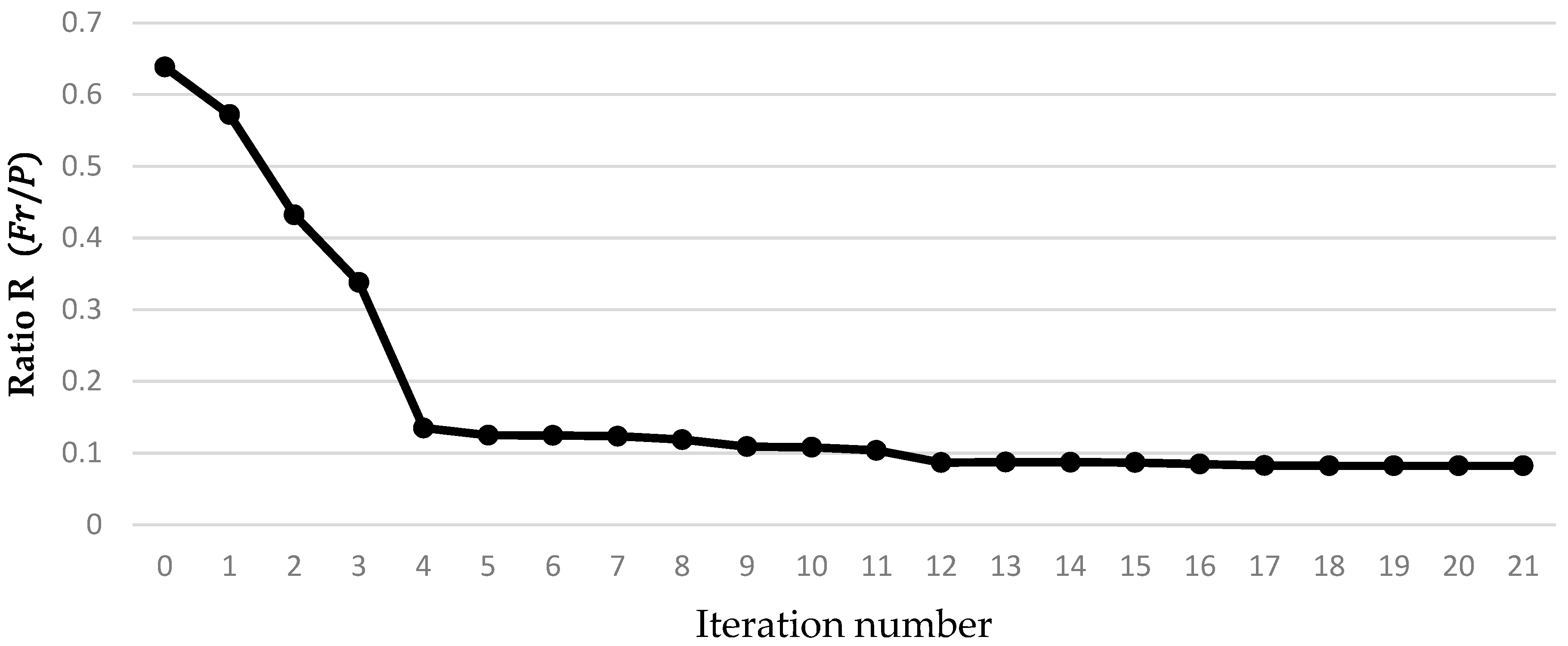
3. Results and Discussion
Optimal Design Result
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cho, H.-K.; Kim, K.-W.; Lee, I.-B. Design Optimization of Tractor Clutch Mechanism Systems by Using Feasible Direction Method. J. Biosyst. Eng. 2010, 35, 287–293. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.H.; Jin, S.-R.; Kim, J.-W.; Seo, T.-W.; Kim, J.-W. Optimal Design of a Four-bar Linkage Manipulator for Starfish-Capture Robot Platform. J. KICA 2013, 30, 961–968. [Google Scholar]
- Kim, S.-W.; Kim, D.-H. Design of Leg Length for a Legged Walking Robot Based on Theo Jansen Using PSO. J. Korean Inst. Intell. Syst. 2011, 21, 660–666. [Google Scholar] [CrossRef] [Green Version]
- Rahmanian-Koushkaki, H.; Mahmoodi-Eshkaftaki, M.; Azimi-Nejadian, H. Simulation of Draught Force during Chisel Ploughing Using Discrete Element Method. J. Biosyst. Eng. 2022, 47, 152–166. [Google Scholar] [CrossRef]
- Im, D.; Kim, J.-H.; Moon, D.-J.; Moon, T.I.; Yu, S.-H.; Park, Y.-J. Optimization of Bucket Size of Garlic Metering Device Using Multibody Dynamics Simulation. J. Biosyst. Eng. 2022, 47, 480–488. [Google Scholar] [CrossRef]
- Cha, H.K.; Jang, J.S.; Yoo, W.S.; Sohn, J.H. Optimum Design of Latch Position and Latch Length on Operating Mechanism of a Circuit Breaker using ADAMS and VisualDOC. Trans. Korean Soc. Mech. Eng. A 2014, 38, 1215–1220. [Google Scholar] [CrossRef]
- Kang, S.-H.; Im, B.-U.; Cho, H.-S.; Shin, S.-J. Cross-sectional Optimization of a Human-Powered Aircraft Main Spar using SQP and Geometrically Exact Beam Model. J. Comput. Struct. Eng. Inst. Korea 2018, 31, 183–190. [Google Scholar] [CrossRef]
- Bark, J. SQP Method for Optimal Design of Trusses Subject to Multiple Loading Conditions. JAIK 1998, 14, 21–28. [Google Scholar]
- Shin, S.-C.; Hur, S.-Y.; Choi, D. Optimal Design for Efficiency of 3K-Type Planetary Reducer Using Nonlinear Optimization. Trans. Korean Soc. Mech. Eng. A 2022, 46, 171–176. [Google Scholar] [CrossRef]
- Cha, M.-C.; Kim, S.-W.; Jeong, M.-S.; Lee, I.; Yoo, S.-J.; Park, C.-J. Thickness Optimization for Spar Cap of Composite Tidal Current Turbine Blade using SQP Method. Compos. Res. 2013, 26, 207–212. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.-H.; Chung, J.-H. Guidelines for the Elderly Housing considering Ergonomics and Context-Awareness. J. KICA 2016, 53, 138–145. [Google Scholar]
- KOSIS (Korean Statistical information Service). Farming Population by Age. 2021. Available online: https://kosis.kr/ (accessed on 1 May 2022).
- Hwang, I.-G.; Lee, H.-T.; Heo, B.-S.; Kim, Y.-J. The Effect of the Patellofemoral Pain Syndrome on EMG Activity during Step up Exercise. J. FISHRIES Mar. Sci. Educ. 2015, 27, 63–73. [Google Scholar] [CrossRef] [Green Version]
- Size Korea. The Eighth Anthropometric Survey of Koreans. Korean Agency for Technology and Standards. 2020. Available online: https://sizekorea.kr/ (accessed on 1 November 2022).
- Kim, J.-T.; Han, H.-W.; Oh, J.-S.; Chung, W.-J.; Cho, S.-J.; Park, Y.-J. Structural Design of Garlic Plants Footplate Considering Physical Characteristics of Elderly Women. J. Biosyst. Eng. 2020, 45, 16–23. [Google Scholar] [CrossRef]
- The Math Works, Inc. MATLAB (Version R2022a). 2022. Available online: https://www.mathworks.com/ (accessed on 1 November 2022).



| Name | Anterior Superior Iliac Spine (ASIS) | Tibiale |
|---|---|---|
| Definition | The most anterior palpable part of the iliac crest of the hip | At the top of the upper medial condyle of the tibia |
| Measuring instrument | Vertical ruler | |
| Design Variable | min | max | Initial |
|---|---|---|---|
| Angle between the extension line of Link3 and Link2 () [°] | 0 | 60 | 21.37 |
| Length of Link1 () [mm] | 30 | 500 | 218.19 |
| Length of Link2 from Point B to Point C () [mm] | 30 | 500 | 119.39 |
| Length of Link2 from Point B to Point D [mm] | 30 | 500 | 203.21 |
| Horizontal distance between Points A and C (k) [mm] | 0 | 50 | 27.84 |
| Optimization Results | |
| Angle between the extension line of Link3 and Link2 () [°] | 26.56 |
| Length of Link1 () [mm] | 287.52 |
| Length of Link2 from Point B to Point C () [mm] | 30 |
| Length of Link2 from Point B to Point D () [mm] | 305.41 |
| Horizontal distance between points A and C (k) [mm] | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-M.; Lee, S.-H.; Han, H.-W.; Oh, J.; Shim, S.-B. Optimization of Design Parameters Using SQP for an Agricultural Pipe Extraction Device. Appl. Sci. 2023, 13, 3167. https://doi.org/10.3390/app13053167
Lee S-M, Lee S-H, Han H-W, Oh J, Shim S-B. Optimization of Design Parameters Using SQP for an Agricultural Pipe Extraction Device. Applied Sciences. 2023; 13(5):3167. https://doi.org/10.3390/app13053167
Chicago/Turabian StyleLee, Su-Min, Sang-Hong Lee, Hyun-Woo Han, Jooseon Oh, and Sung-Bo Shim. 2023. "Optimization of Design Parameters Using SQP for an Agricultural Pipe Extraction Device" Applied Sciences 13, no. 5: 3167. https://doi.org/10.3390/app13053167
APA StyleLee, S.-M., Lee, S.-H., Han, H.-W., Oh, J., & Shim, S.-B. (2023). Optimization of Design Parameters Using SQP for an Agricultural Pipe Extraction Device. Applied Sciences, 13(5), 3167. https://doi.org/10.3390/app13053167






