Optimized Catenary Metasurface for Detecting Spin and Orbital Angular Momentum via Momentum Transformation
Abstract
:1. Introduction
2. Theory and Methods
3. Results
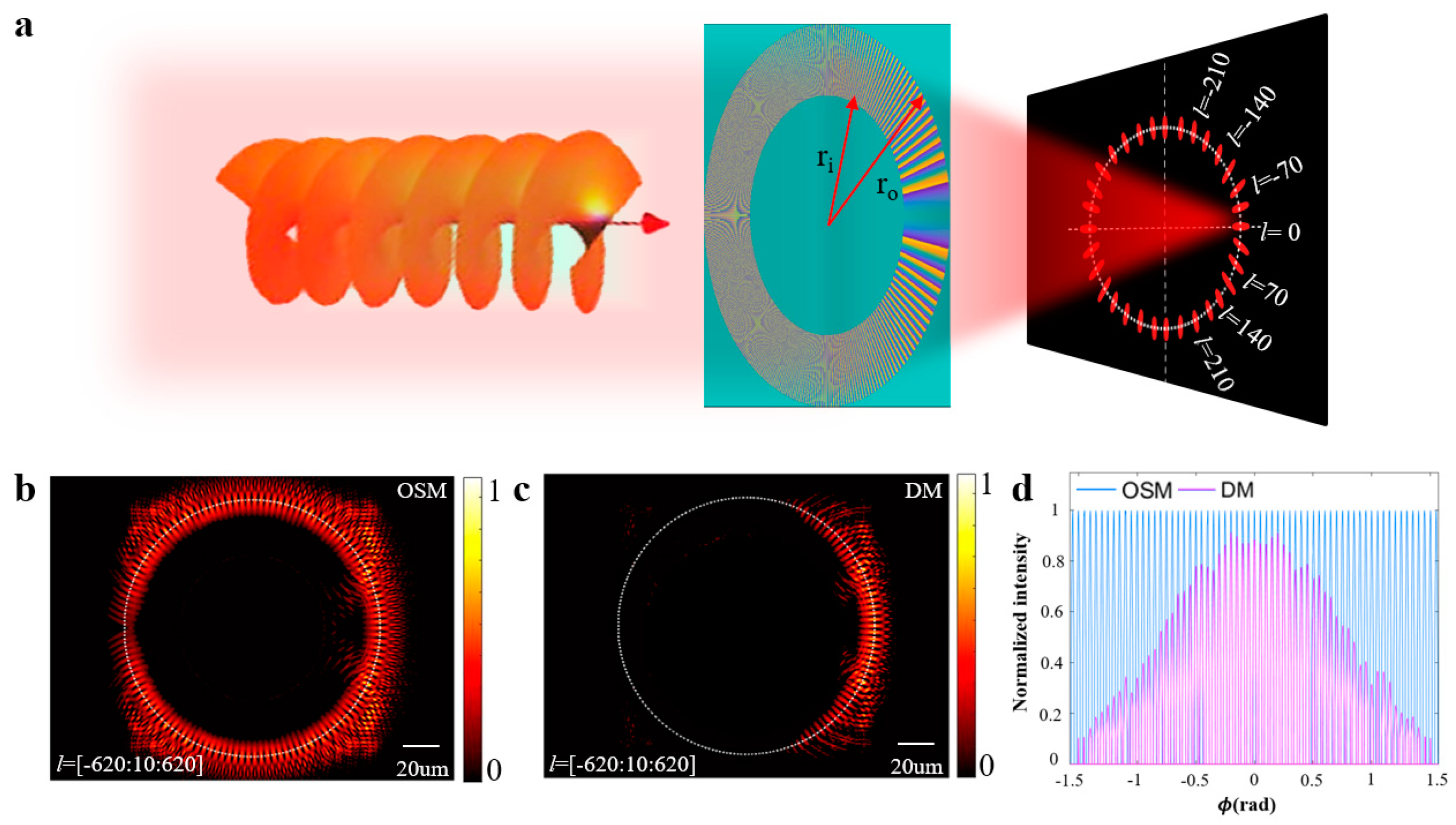
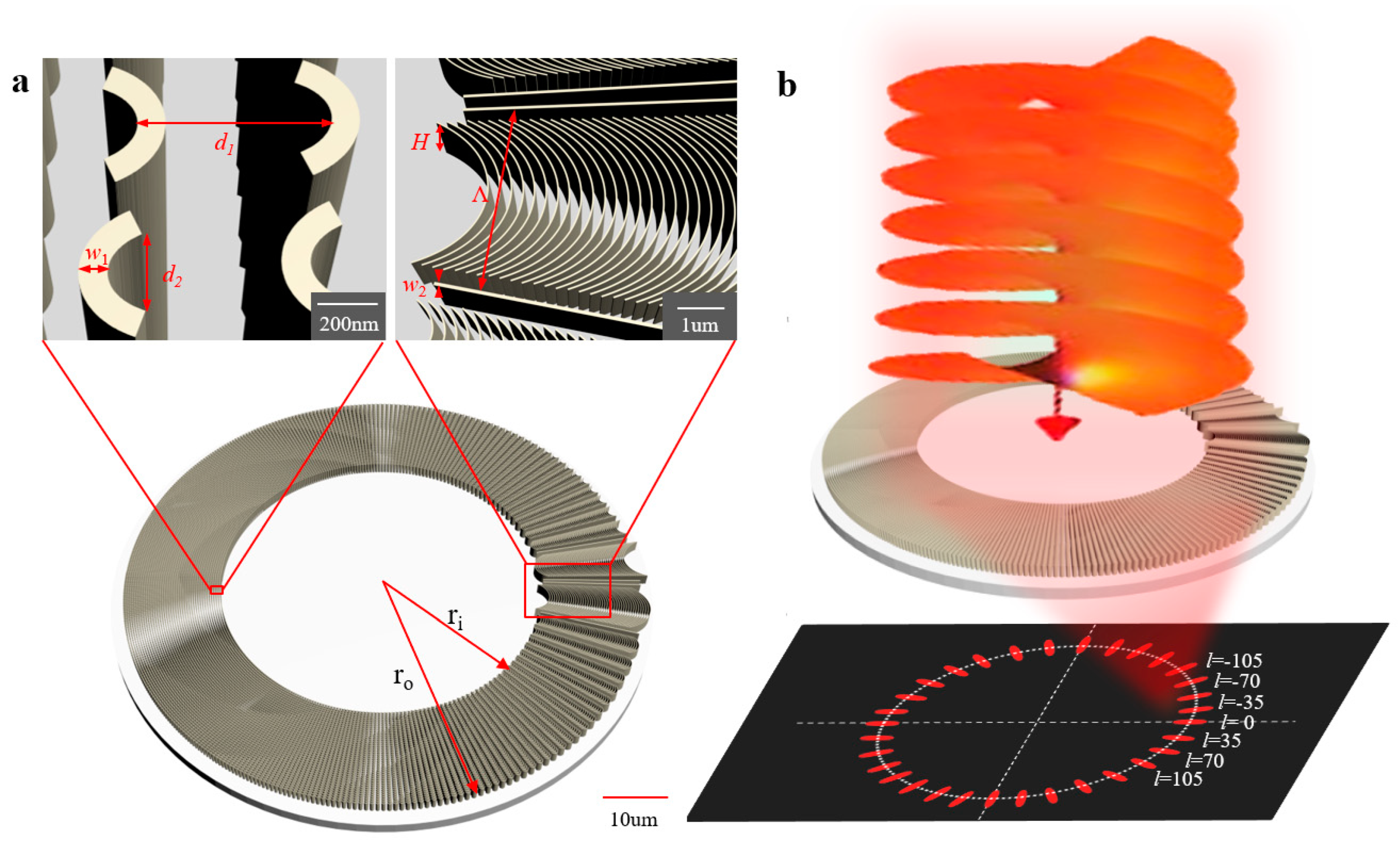
3.1. Analysis and Simulation
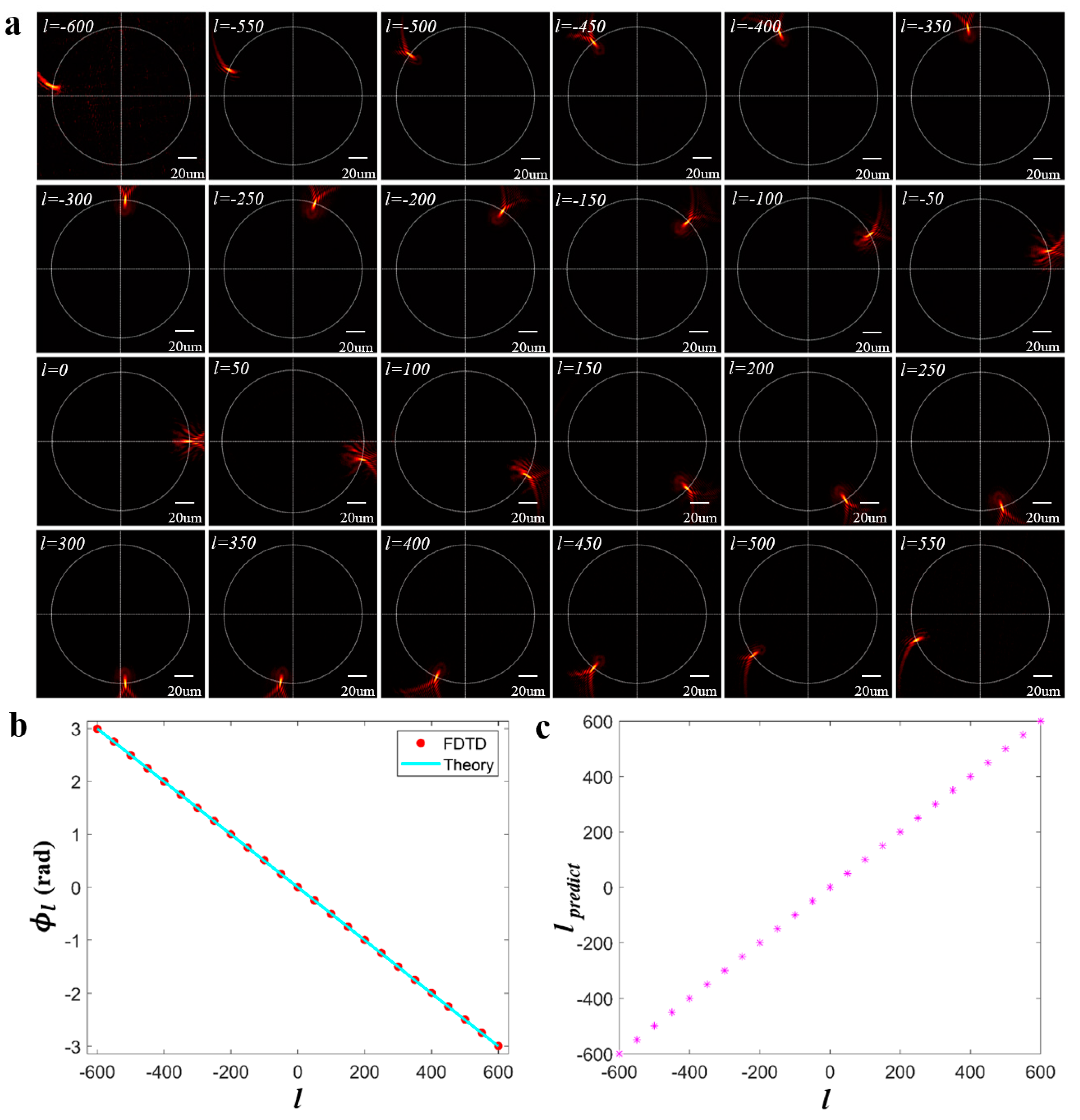
3.2. Model Establishment and Simulation
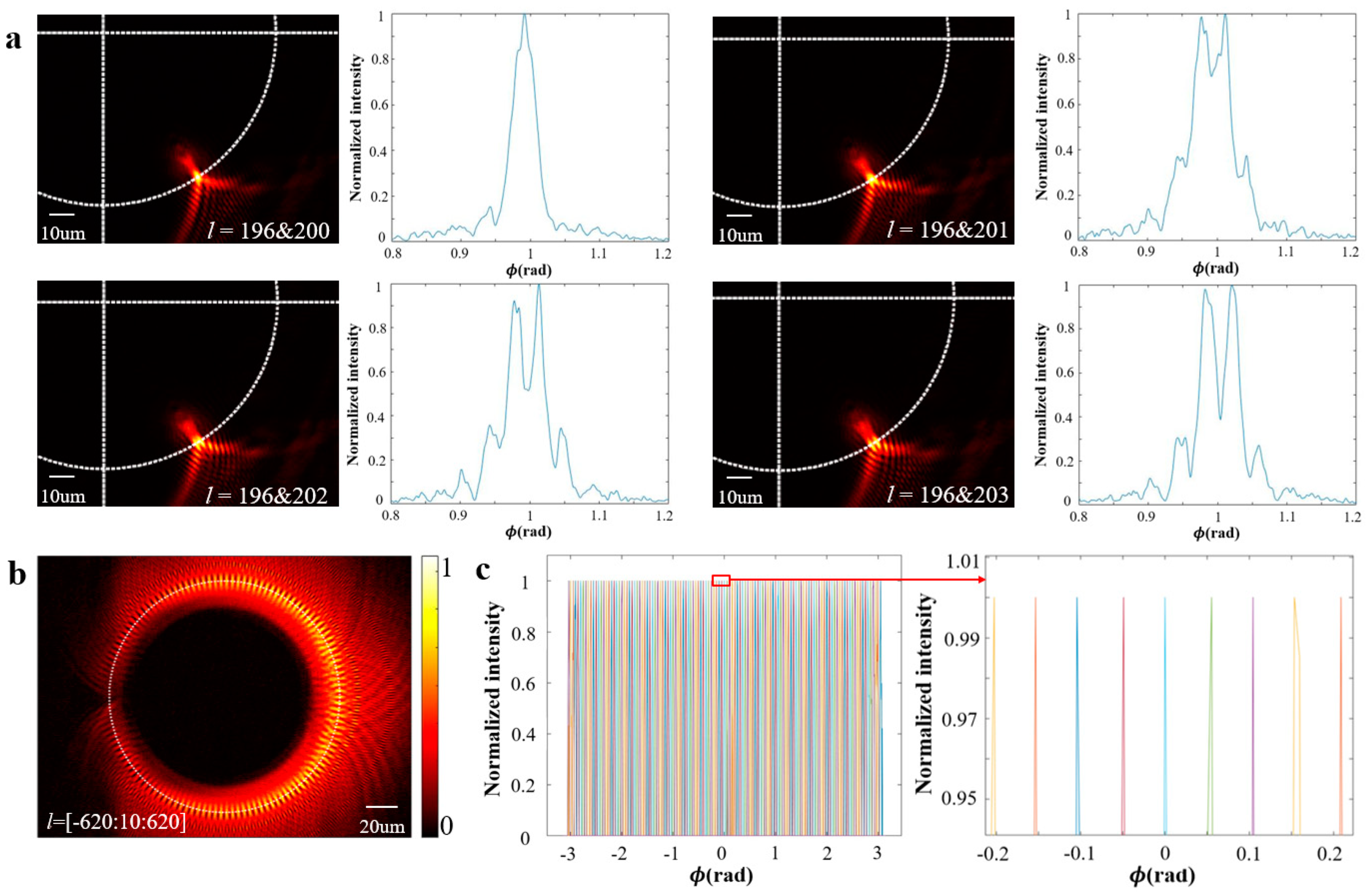
3.3. Resolution of Superimposed OAMs
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Poynting, J.H. The wave motion of a revolving shaft, and a suggestion as to the angular momentum in a beam of circularly polarised light. Proc. R. Soc. London Ser. A Contain. Pap. A Math. Phys. Character 1909, 82, 560–567. [Google Scholar]
- Beth, R.A. Mechanical Detection and Measurement of the Angular Momentum of Light. Phys. Rev. 1936, 50, 115–125. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photon 2011, 3, 161–204. [Google Scholar] [CrossRef] [Green Version]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Park, S.C.; Park, M.K.; Kang, M.G. Super-resolution image reconstruction: A technical overview. IEEE Signal Process. Mag. 2003, 20, 21–36. [Google Scholar] [CrossRef] [Green Version]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light. Sci. Appl. 2019, 8, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Phot. 2015, 7, 66–106. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high-security encryption. Nat. Photonics 2020, 14, 102–108. [Google Scholar] [CrossRef]
- Zhou, H.; Sain, B.; Wang, Y.; Schlickriede, C.; Zhao, R.; Zhang, X.; Wei, Q.; Li, X.; Huang, L.; Zentgraf, T. Polarization-encrypted orbital angular momentum multiplexed metasurface holography. ACS Nano 2020, 14, 5553–5559. [Google Scholar] [CrossRef] [PubMed]
- Ruffato, G.; Massari, M.; Romanato, F. Multiplication and division of the orbital angular momentum of light with diffractive transformation optics. Light. Sci. Appl. 2019, 8, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wen, Y.; Chremmos, I.; Chen, Y.; Zhang, Y.; Yu, S. Arbitrary Multiplication and Division of the Orbital Angular Momentum of Light. Phys. Rev. Lett. 2020, 124, 213901. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Kotlyar, V.V.; Shinkaryev, M.V.; Soi-Fer, V.A.; Uspleniev, G.V. The Phase Rotor Filter. J. Mod. Opt. 1992, 39, 1147–1154. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Coerwinkel, R.P.C.; Kristensen, M.; Woerdman, J.P. Helical-wavefront laser beams produced with a spiral phase plate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Bouchard, F.; Mand, H.; Mirhosseini, M.; Karimi, E.; Boyd, R.W. Achromatic orbital angular momentum generator. New J. Phys. 2014, 16, 123006. [Google Scholar] [CrossRef] [Green Version]
- Biener, G.; Niv, A.; Kleiner, V.; Hasman, E. Formation of helical beams by use of Pancharatnam–Berry phase optical elements. Opt. Lett. 2002, 27, 1875–1877. [Google Scholar] [CrossRef]
- Marrucci, L.; Manzo, C.; Paparo, D. Optical Spin-to-Orbital Angular Momentum Conversion in Inhomogeneous Anisotropic Media. Phys. Rev. Lett. 2006, 96, 163905. [Google Scholar] [CrossRef] [Green Version]
- Meng, W.; Hua, Y.; Cheng, K.; Li, B.; Liu, T.; Chen, Q.; Luan, H.; Gu, M.; Fang, X. 100 Hertz frame-rate switching three-dimensional orbital angular momentum multiplexing holography via cross convolution. Opto-Electronic Sci. 2022, 1, 220004. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, G.; Feng, D.; Zhou, L.; Guo, Y. Ultra-broadband metasurface holography via quasi-continuous nano-slits. J. Phys. D Appl. Phys. 2019, 53, 104002. [Google Scholar] [CrossRef]
- Yuan, X.; Xu, Q.; Lang, Y.; Jiang, X.; Xu, Y.; Chen, X.; Han, J.; Zhang, X.; Han, J.; Zhang, W. Tailoring spatiotemporal dynamics of plasmonic vortices. Opto-Electronic Adv. 2023, 220133. [Google Scholar] [CrossRef]
- Pu, M.; Li, X.; Ma, X.; Wang, Y.; Zhao, Z.; Wang, C.; Hu, C.; Gao, P.; Huang, C.; Ren, H.; et al. Catenary optics for achromatic generation of perfect optical angular momentum. Sci. Adv. 2015, 1, e1500396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Y.; Pu, M.; Zhao, Z.; Wang, Y.; Jin, J.; Gao, P.; Li, X.; Ma, X.; Luo, X. Merging Geometric Phase and Plasmon Retardation Phase in Continuously Shaped Metasurfaces for Arbitrary Orbital Angular Momentum Generation. ACS Photon. 2016, 3, 2022–2029. [Google Scholar] [CrossRef]
- Chen, J.; Wang, D.; Si, G.; Teo, S.L.; Wang, Q.; Lin, J. Planar peristrophic multiplexing metasurfaces. Opto-Electronic Adv. 2023, 220141. [Google Scholar] [CrossRef]
- Lv, Y.; Shang, Z.; Fu, S.; Huang, L.; Gao, L.; Gao, C. Sorting orbital angular momentum of photons through a multi-ring azimuthal-quadratic phase. Opt. Lett. 2022, 47, 5032. [Google Scholar] [CrossRef]
- Harris, M.; Hill, C.; Vaughan, J. Optical helices and spiral interference fringes. Opt. Commun. 1994, 106, 161–166. [Google Scholar] [CrossRef]
- Leach, J.; Padgett, M.; Barnett, S.; Franke-Arnold, S.; Courtial, J. Measuring the Orbital Angular Momentum of a Single Photon. Phys. Rev. Lett. 2002, 88, 257901. [Google Scholar] [CrossRef]
- de Araujo, L.E.E.; Anderson, M.E. Measuring vortex charge with a triangular aperture. Opt. Lett. 2011, 36, 787–789. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Gao, S.; Xiao, W.; Yang, J.; Huang, X.; Feng, Y.; Li, J.; Liu, W.; Li, Z. Measuring high-order optical orbital angular momentum with a hyperbolic gradually changing period pure-phase grating. Opt. Lett. 2018, 43, 3076–3079. [Google Scholar] [CrossRef]
- Estakhri, N.M.; Edwards, B.; Engheta, N. Inverse-designed metastructures that solve equations. Science 2019, 363, 1333–1338. [Google Scholar] [CrossRef]
- Lalegani, Z.; Ebrahimi, S.S.; Hamawandi, B.; La Spada, L.; Batili, H.; Toprak, M. Targeted dielectric coating of silver nanoparticles with silica to manipulate optical properties for metasurface applications. Mater. Chem. Phys. 2022, 287, 126250. [Google Scholar] [CrossRef]
- Akbari, M.; Shahbazzadeh, M.J.; La Spada, L.; Khajehzadeh, A. The Graphene Field Effect Transistor Modeling Based on an Optimized Ambipolar Virtual Source Model for DNA Detection. Appl. Sci. 2021, 11, 8114. [Google Scholar] [CrossRef]
- Greybush, N.J.; Pacheco-Peña, V.; Engheta, N.; Murray, C.B.; Kagan, C.R. Plasmonic Optical and Chiroptical Response of Self-Assembled Au Nanorod Equilateral Trimers. ACS Nano 2019, 13, 1617–1624. [Google Scholar] [CrossRef] [PubMed]
- Lincoln, R.L.; Scarpa, F.; Ting, V.P.; Trask, R.S. Multifunctional composites: A metamaterial perspective. Multifunct. Mater. 2019, 2, 043001. [Google Scholar] [CrossRef]
- Sahu, R.; Chaudhary, S.; Khare, K.; Bhattacharya, M.; Wanare, H.; Jha, A.K. Angular lens. Opt. Express 2018, 26, 8709–8718. [Google Scholar] [CrossRef]
- Pu, M.; Li, X.; Guo, Y.; Ma, X.; Luo, X. Nanoapertures with ordered rotations: Symmetry transformation and wide-angle flat lensing. Opt. Express 2017, 25, 31471–31477. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, S.; Pu, M.; He, Q.; Jin, J.; Xu, M.; Zhang, Y.; Gao, P.; Luo, X. Spin-decoupled metasurface for simultaneous detection of spin and orbital angular momenta via momentum transformation. Light. Sci. Appl. 2021, 10, 1–12. [Google Scholar] [CrossRef]
- Zhang, F.; Pu, M.; Li, X.; Ma, X.; Guo, Y.; Gao, P.; Yu, H.; Gu, M.; Luo, X. Extreme-Angle Silicon Infrared Optics Enabled by Streamlined Surfaces. Adv. Mater. 2021, 33, e2008157. [Google Scholar] [CrossRef]
- Luo, X.-G.; Pu, M.-B.; Li, X.; Ma, X.-L. Broadband spin Hall effect of light in single nanoapertures. Light. Sci. Appl. 2017, 6, e16276. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Hwang, Y.; Dai, Y.; Si, G.; Wei, S.; Choi, D.; Gómez, D.E.; Mitchell, A.; Lin, J.; Yuan, X. Broadband High-Efficiency Chiral Splitters and Holograms from Dielectric Nanoarc Metasurfaces. Small 2019, 15, e1900483. [Google Scholar] [CrossRef]
- Yin, X.; Ye, Z.; Rho, J.; Wang, Y.; Zhang, X. Photonic spin Hall effect at metasurfaces. Science 2013, 339, 1405–1407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Lin, P.; Huang, Y.-W.; Park, J.-S.; Chen, W.T.; Shi, Z.; Qiu, C.-W.; Cheng, J.-X.; Capasso, F. Meta-optics achieves RGB-achromatic focusing for virtual reality. Sci. Adv. 2021, 7, 4458. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, G.; Chen, S.; He, Q.; Xiong, L.; Wen, Y.; Zhang, F.; Lu, Y.; Guo, Y.; Pu, M.; Luo, X. Optimized Catenary Metasurface for Detecting Spin and Orbital Angular Momentum via Momentum Transformation. Appl. Sci. 2023, 13, 3237. https://doi.org/10.3390/app13053237
Fu G, Chen S, He Q, Xiong L, Wen Y, Zhang F, Lu Y, Guo Y, Pu M, Luo X. Optimized Catenary Metasurface for Detecting Spin and Orbital Angular Momentum via Momentum Transformation. Applied Sciences. 2023; 13(5):3237. https://doi.org/10.3390/app13053237
Chicago/Turabian StyleFu, Guoquan, Siran Chen, Qiong He, Lingxing Xiong, Yifeng Wen, Fei Zhang, Yuran Lu, Yinghui Guo, Mingbo Pu, and Xiangang Luo. 2023. "Optimized Catenary Metasurface for Detecting Spin and Orbital Angular Momentum via Momentum Transformation" Applied Sciences 13, no. 5: 3237. https://doi.org/10.3390/app13053237
APA StyleFu, G., Chen, S., He, Q., Xiong, L., Wen, Y., Zhang, F., Lu, Y., Guo, Y., Pu, M., & Luo, X. (2023). Optimized Catenary Metasurface for Detecting Spin and Orbital Angular Momentum via Momentum Transformation. Applied Sciences, 13(5), 3237. https://doi.org/10.3390/app13053237







