Analytical Prediction of Tunnel Deformation Beneath an Inclined Plane: Complex Potential Analysis
Abstract
:1. Introduction
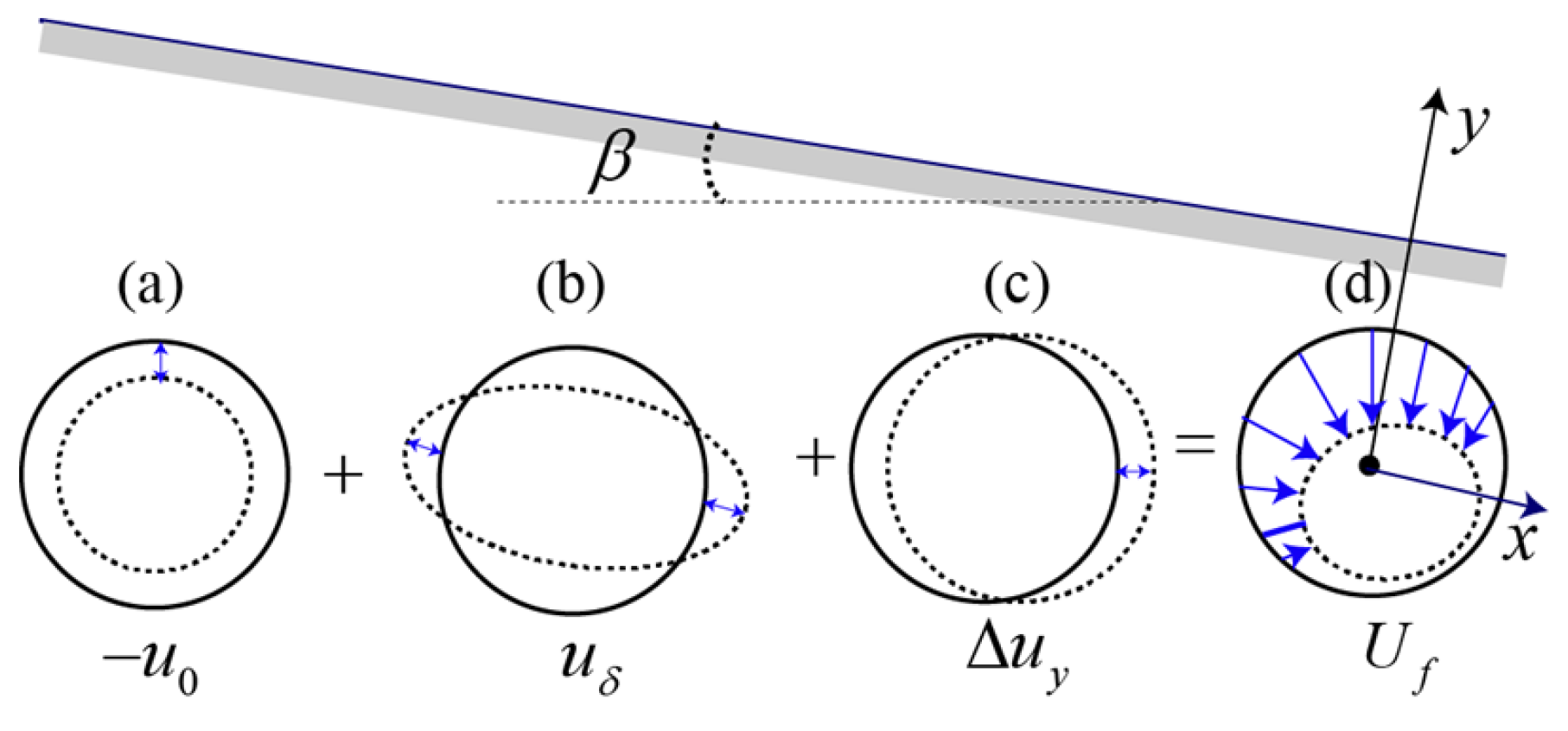
2. Tunnel Description Beneath a Slope
3. Mathematical Analysis
3.1. Asymmetric Stress around the Tunnel
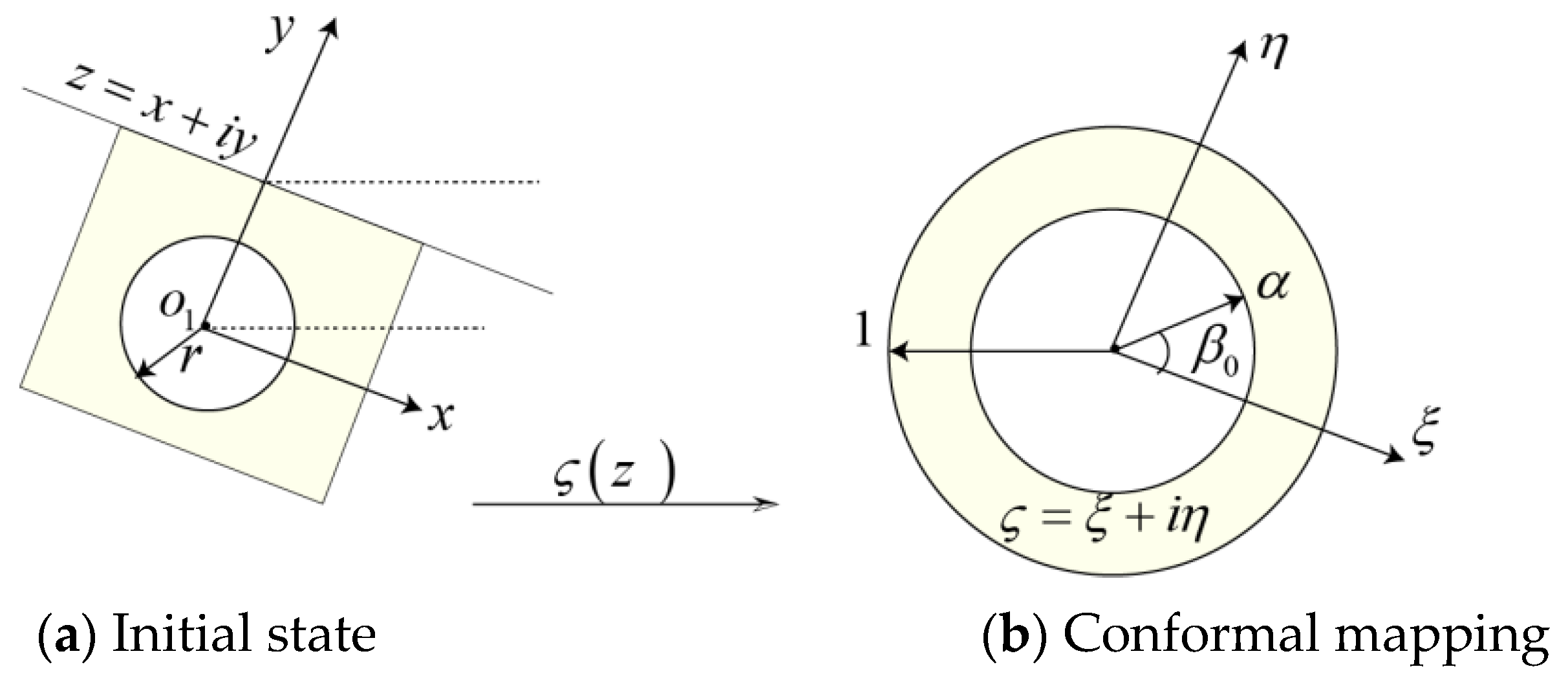
3.2. Complex Potential Analysis
3.2.1. Exact Solution
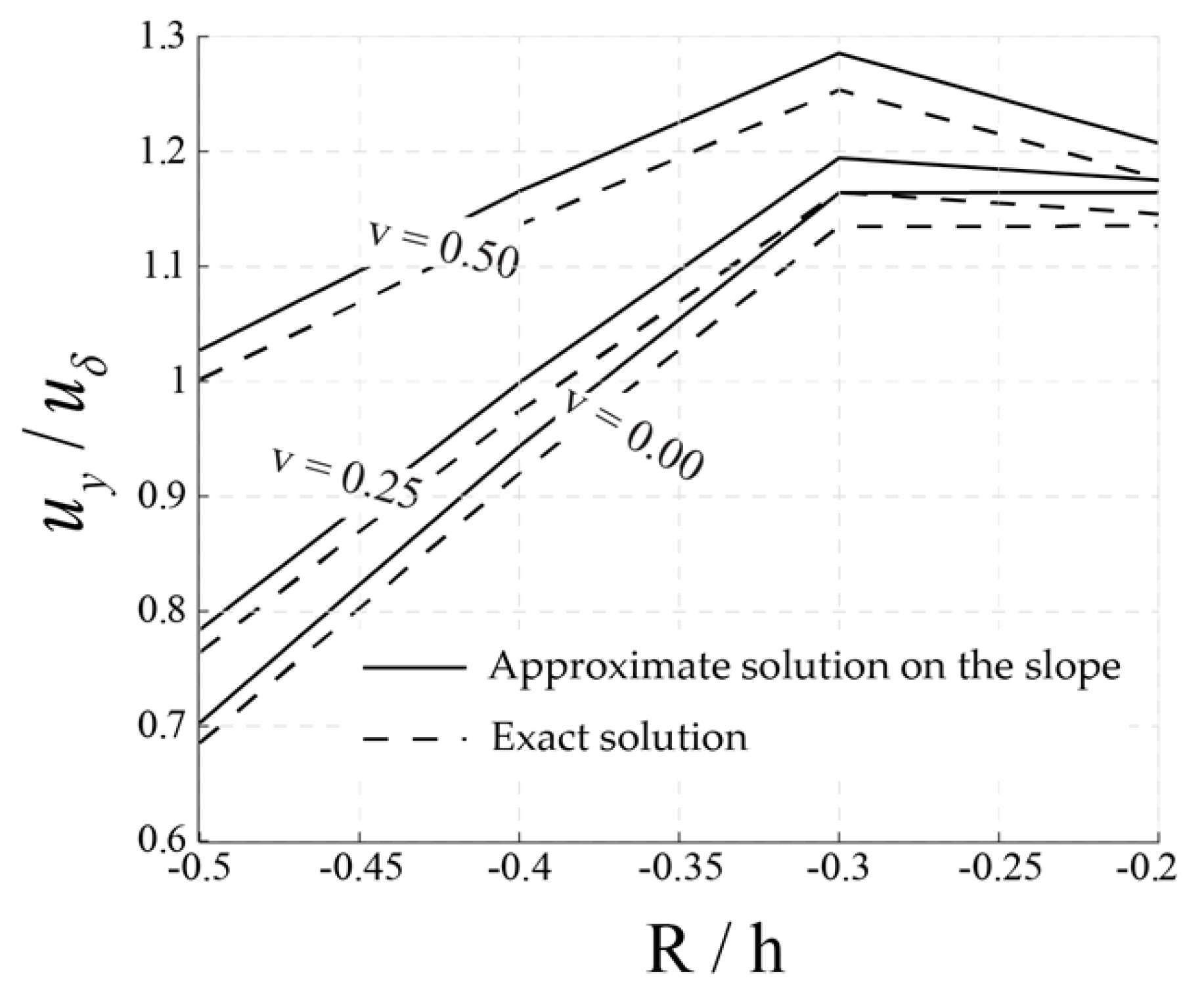
3.2.2. Approximate Analysis of the Tunnel Beneath the Slope
4. Verification of Analytical Formulas
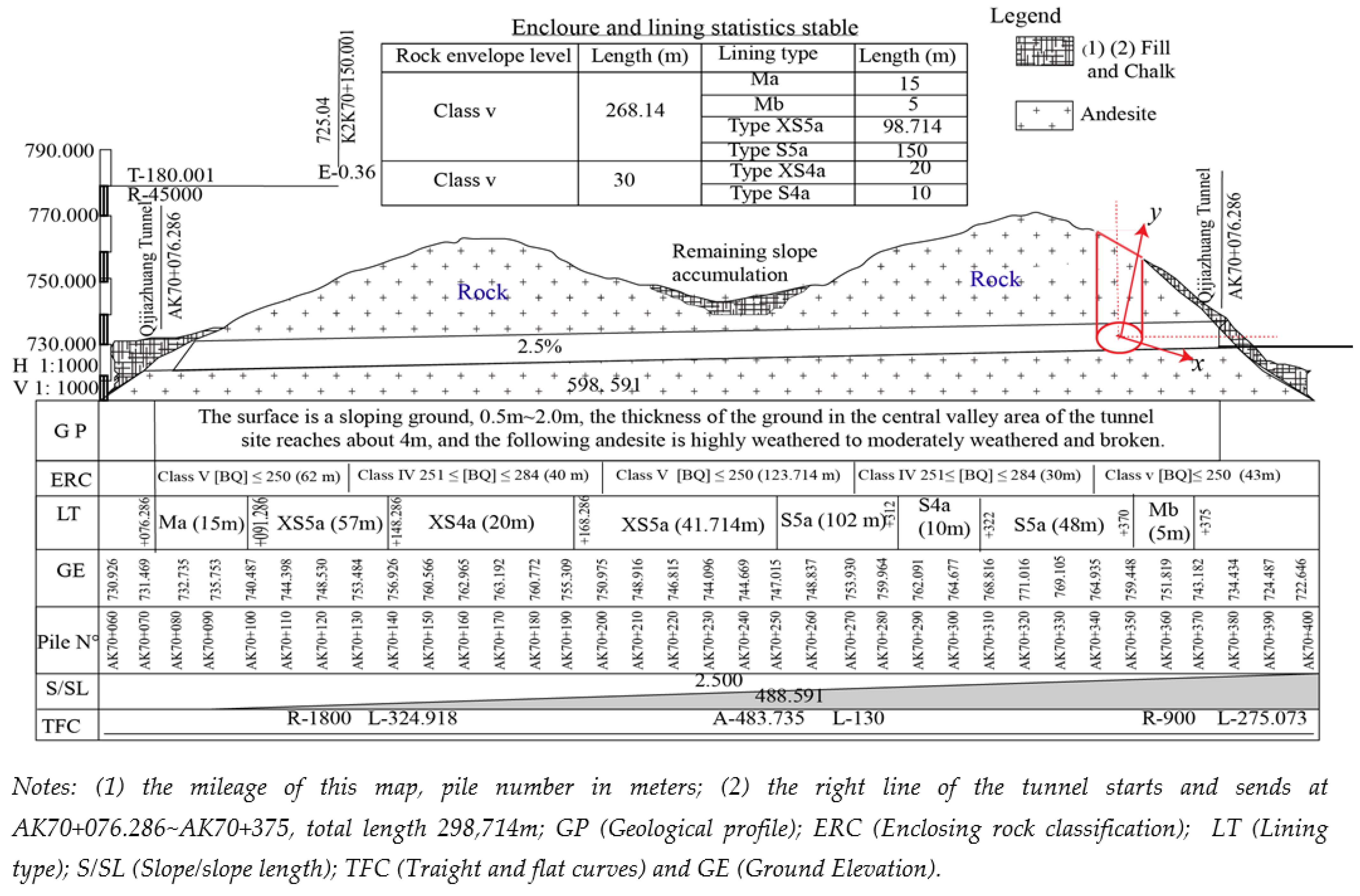
4.1. Presentation of Qijiazhuang Tunnel
4.2. Parametric Analysis of the Tunnel
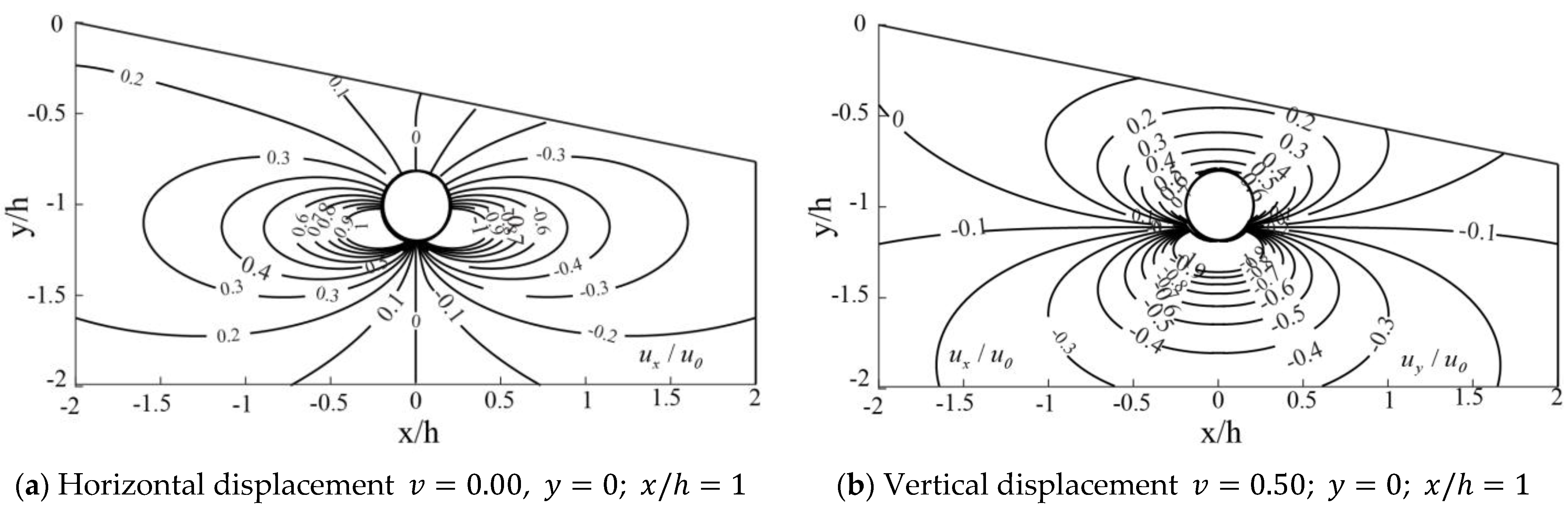
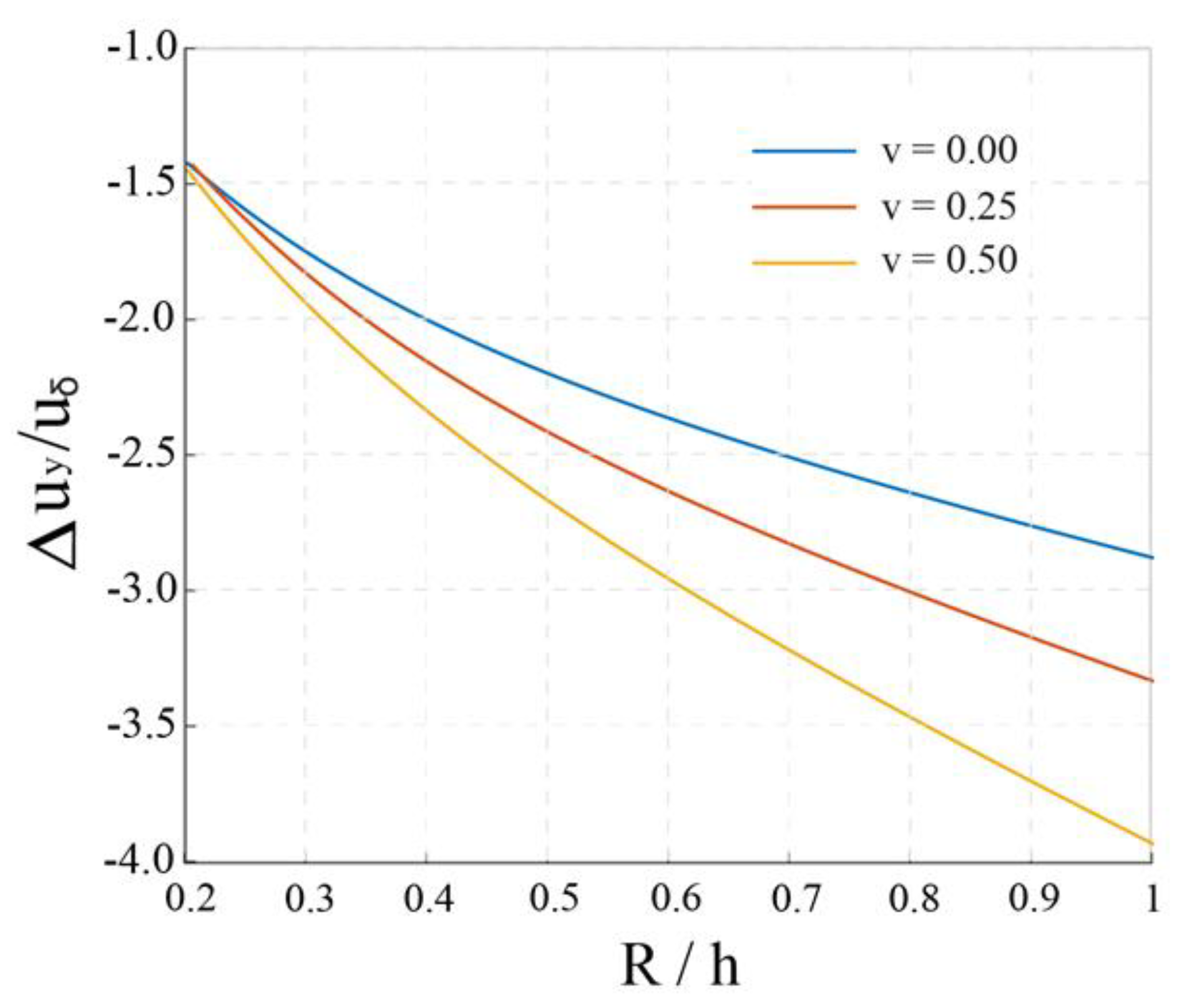
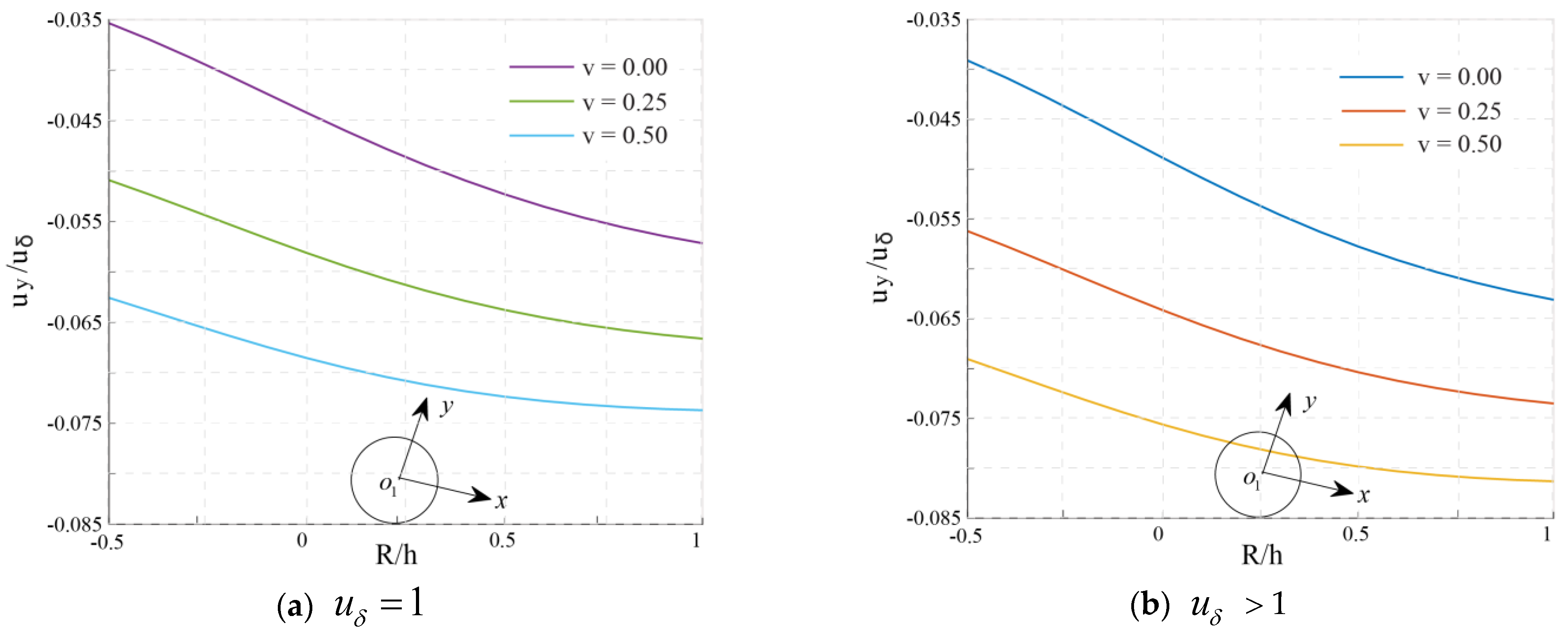
4.2.1. Effect of , and
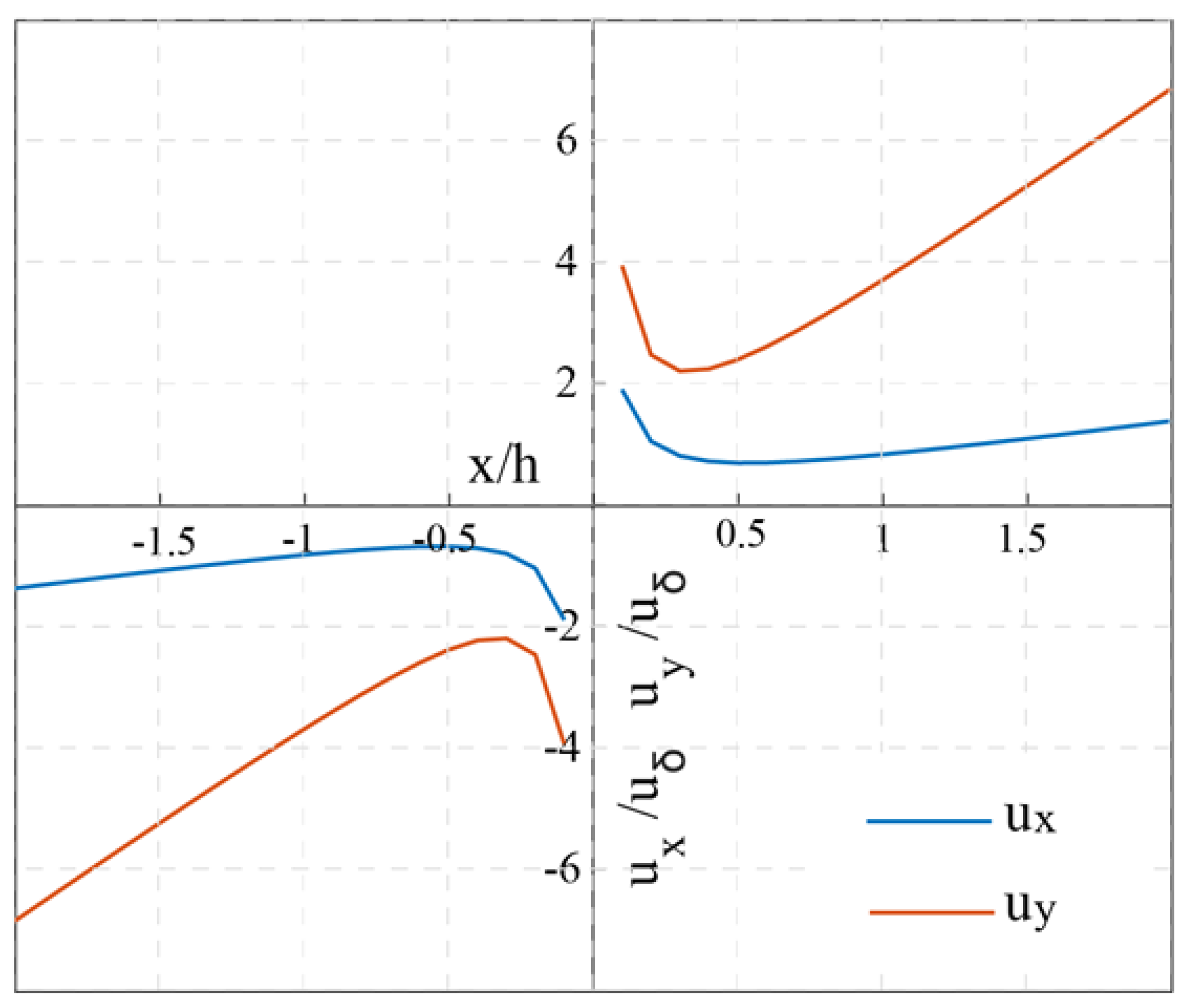
4.2.2. Effect of Tunnel Radius
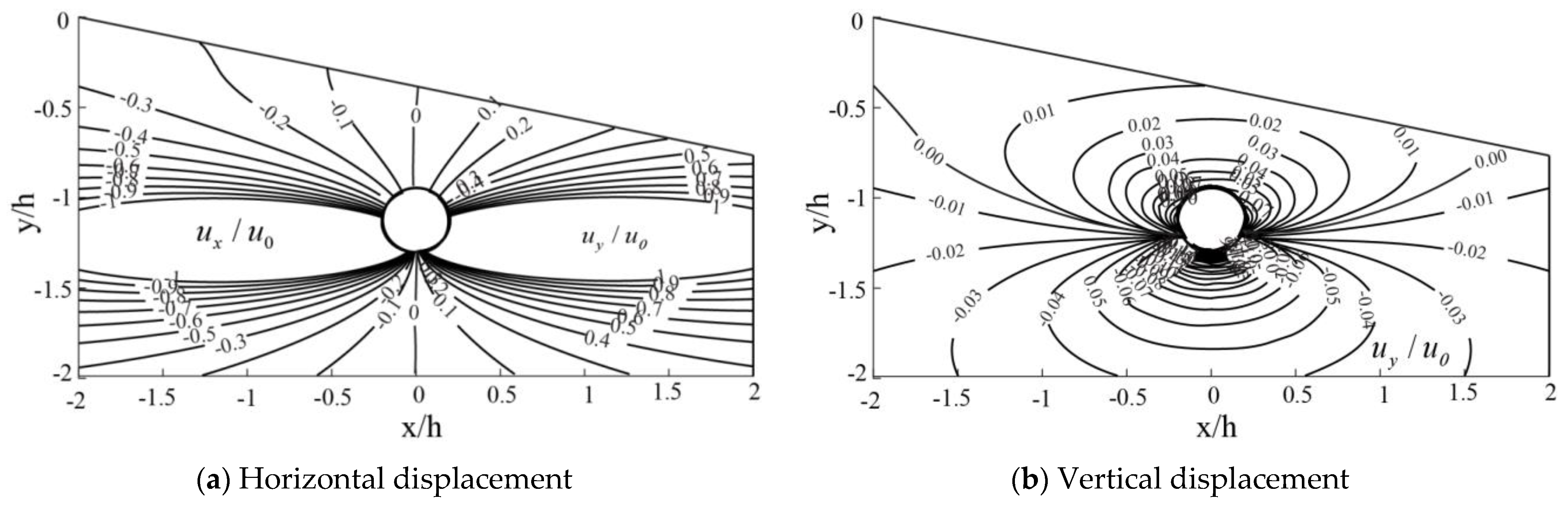
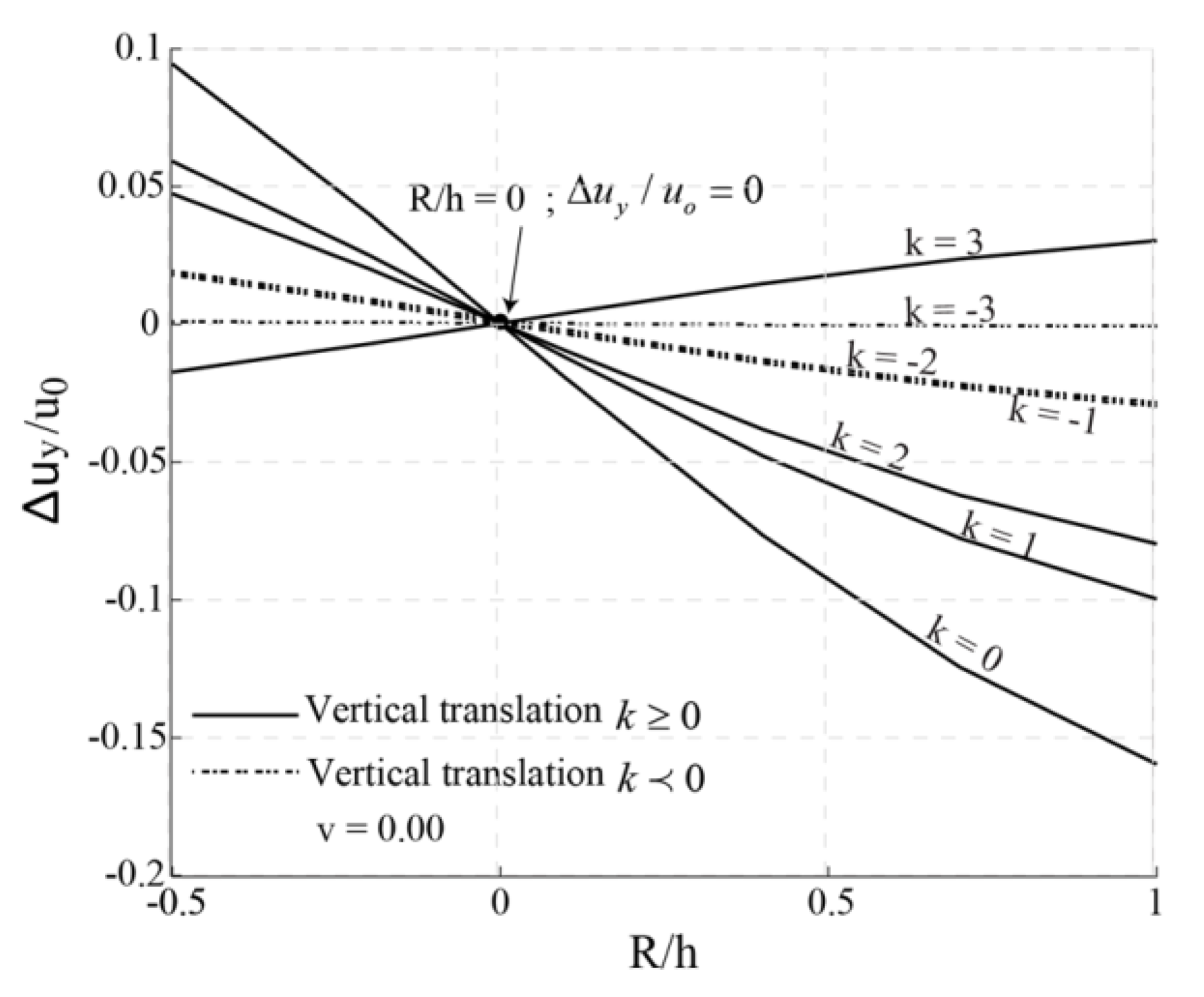
4.2.3. Effect of Contour Lines
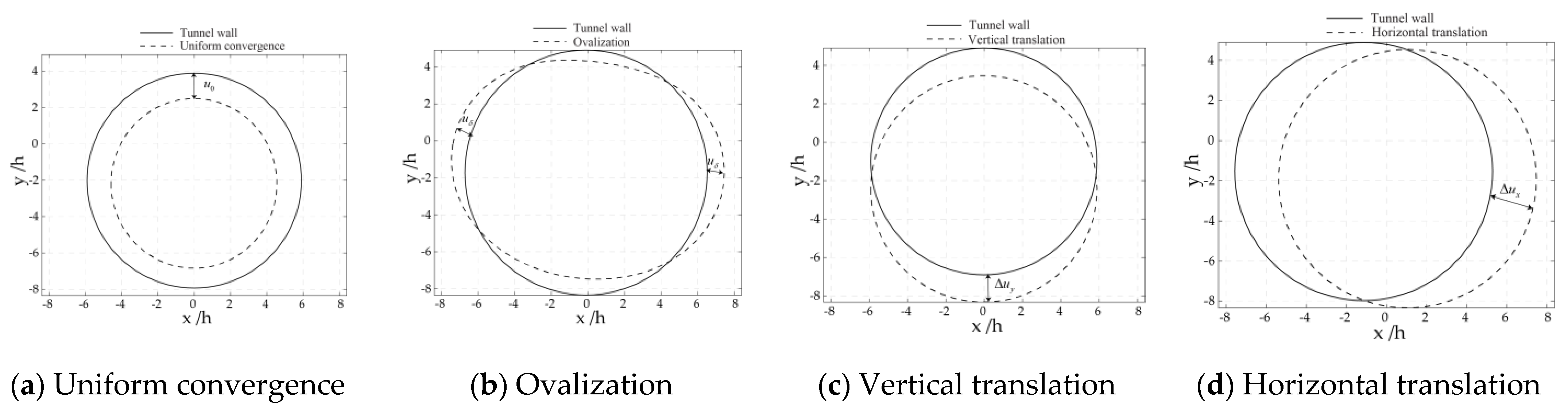
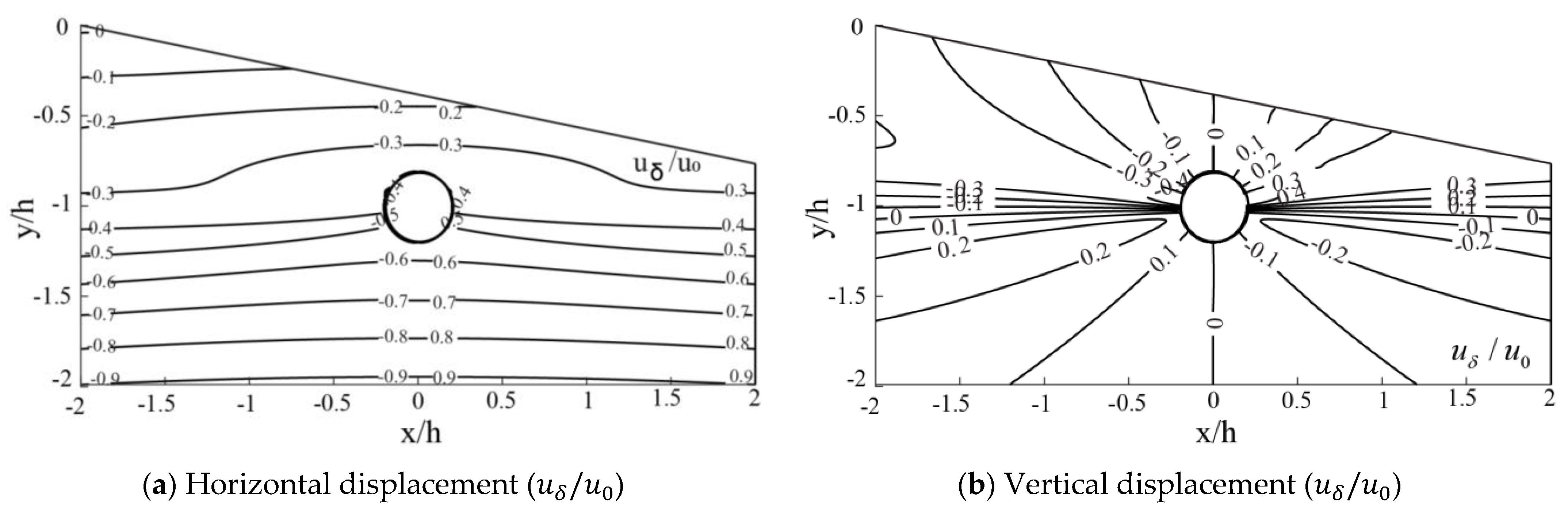
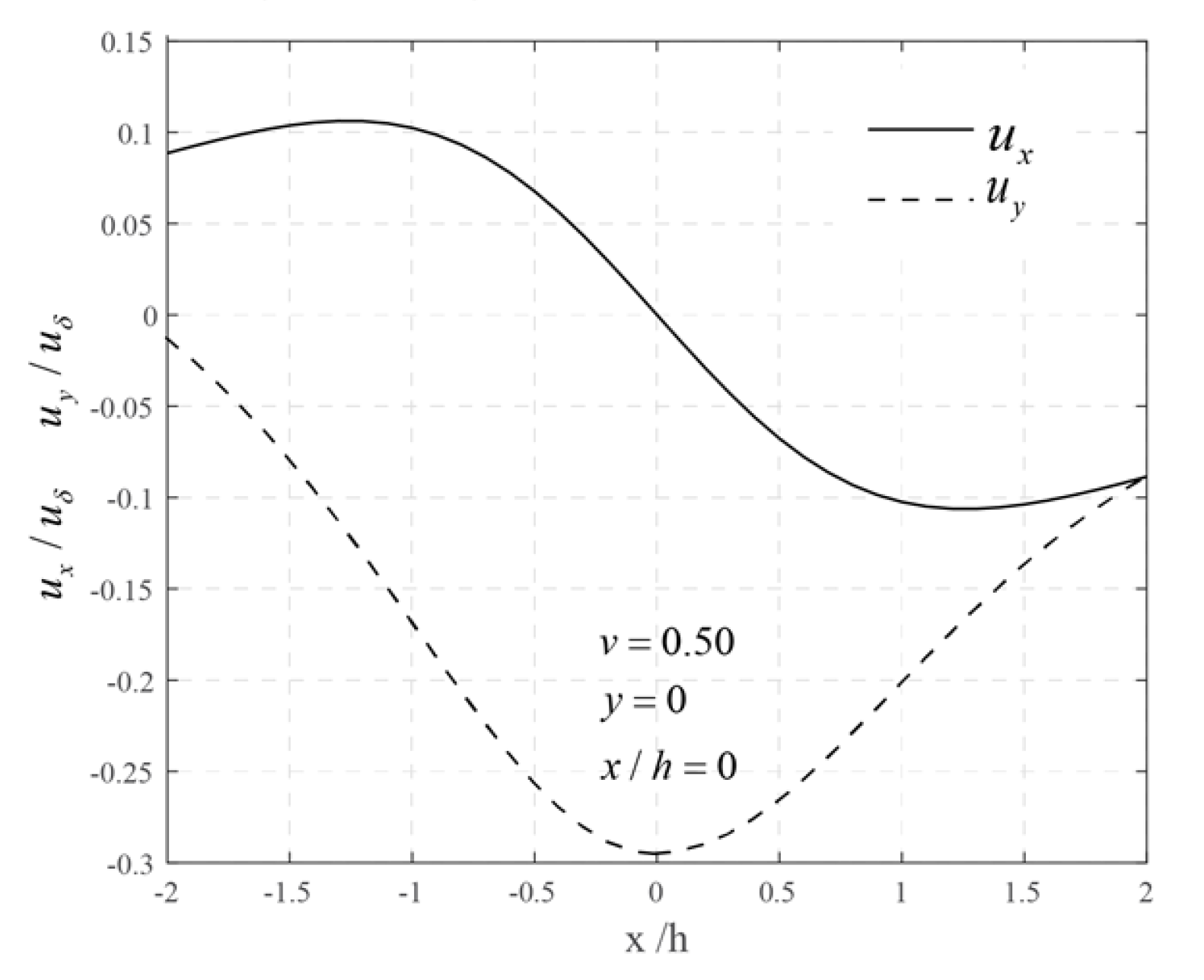
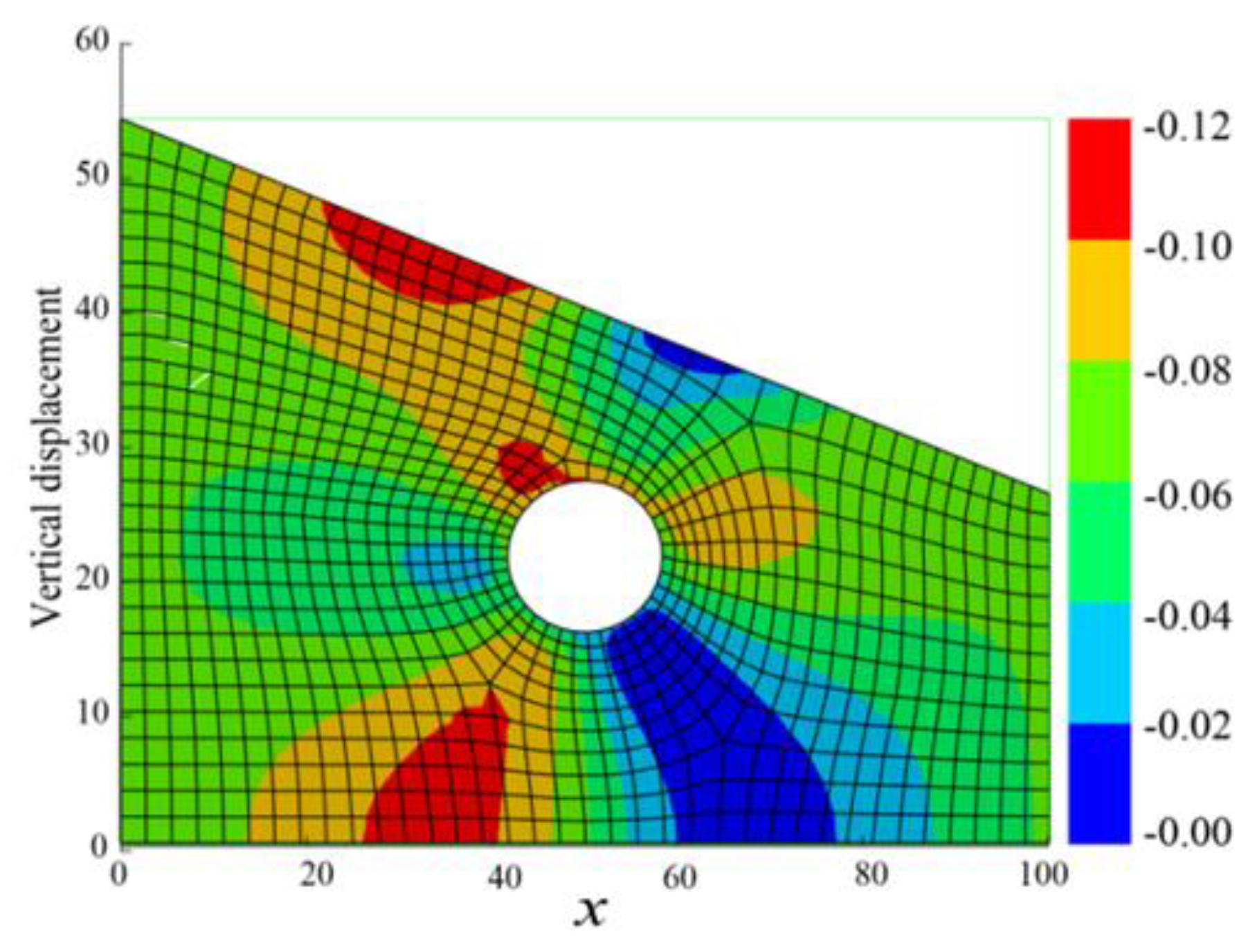
4.3. Analysis of the Deformation Parameters
4.3.1. Uniform Convergence
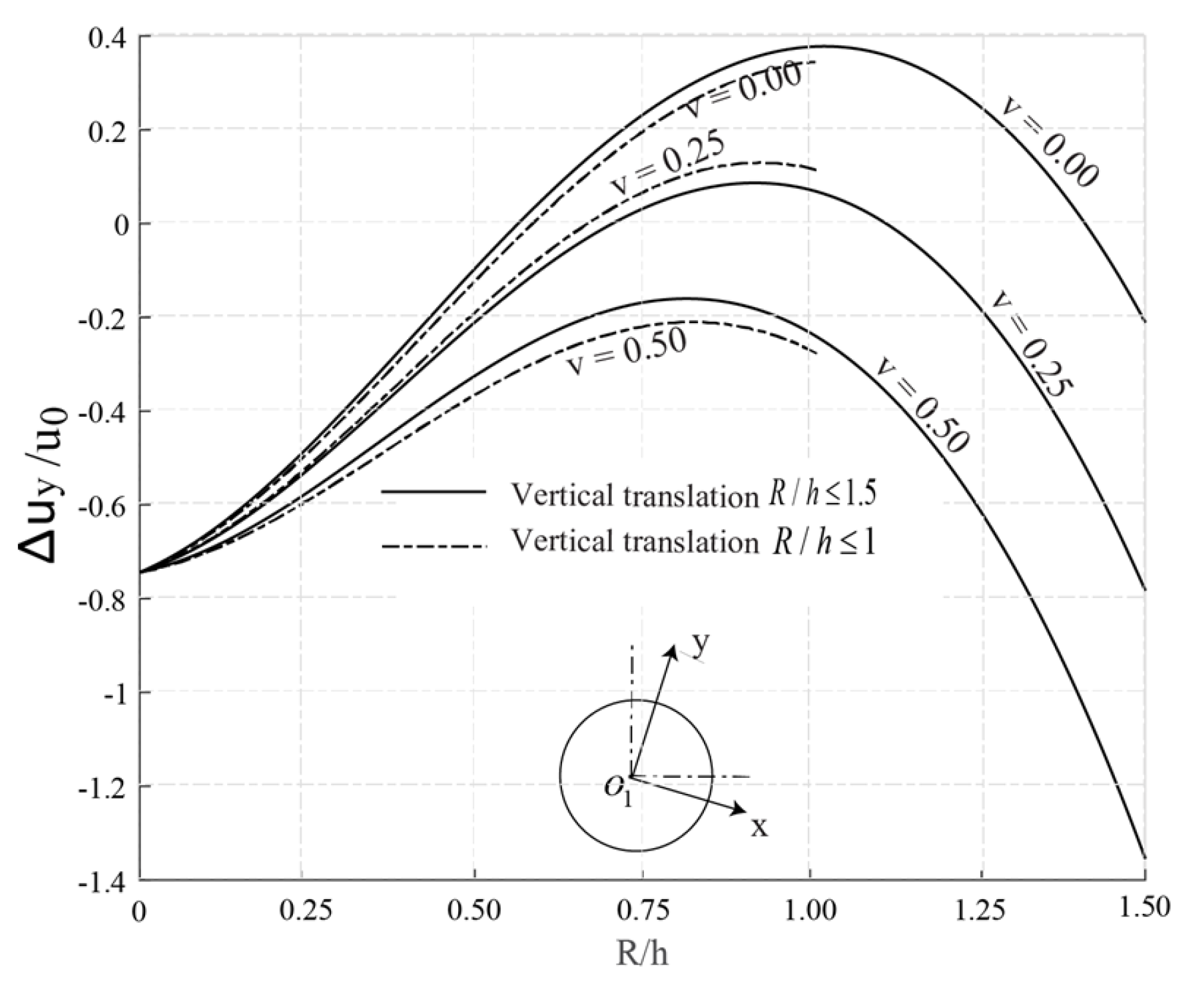
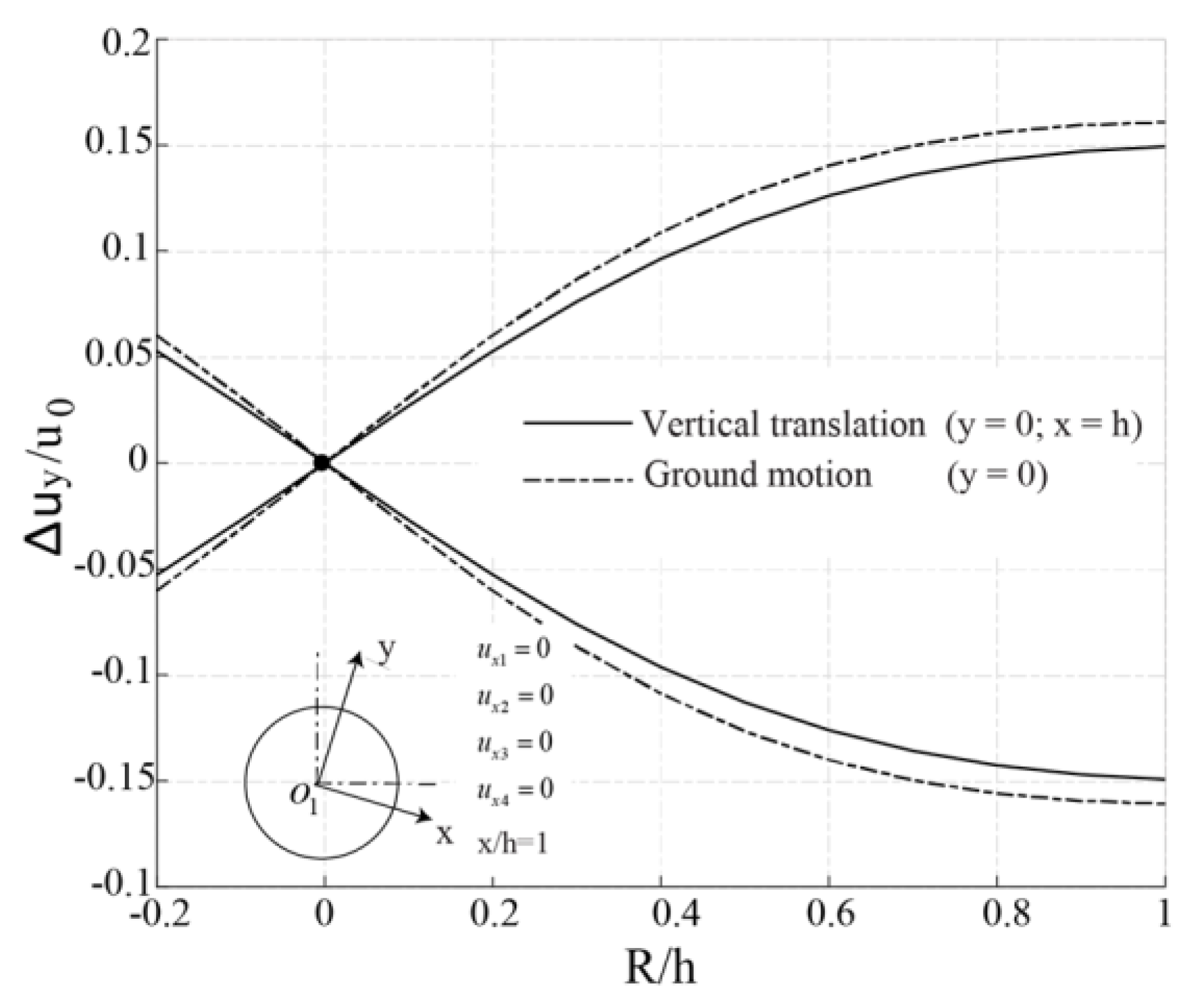
4.3.2. Ovalization Beneath the Slope
4.4. Stress Evaluation around the Tunnel
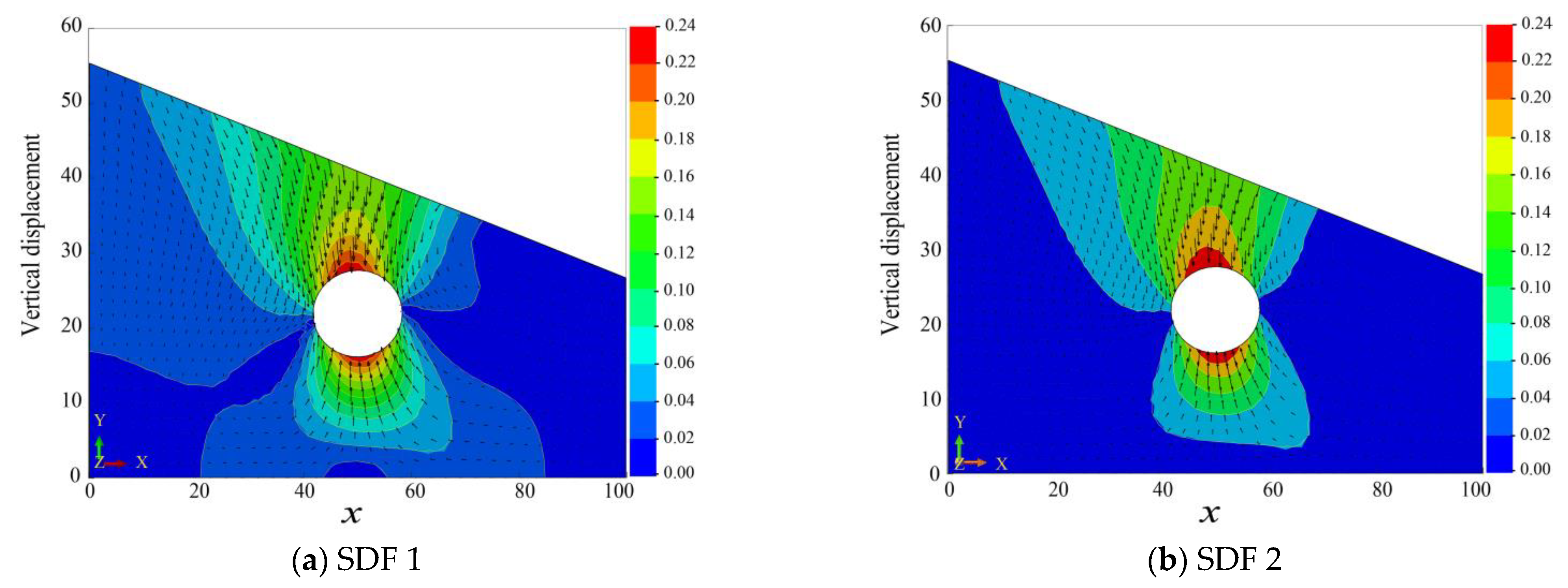
5. Application to Engineering Cases
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbols | Meaning |
| , | Cartesian coordinates |
| Angle of inclination | |
| Central axis of the tunnel | |
| and | Depth at left and right of tunnel |
| Central depth of the tunnel | |
| Radial distance from the tunnel axis | |
| Inner pressure | |
| Outer pressure | |
| Analytical function | |
| C, D | Real functions that satisfy the Cauchy–Riemann condition |
| Airy stress function | |
| Another analytical function of | |
| ,, | Harmonic function |
| Horizontal stress | |
| Vertical stress | |
| Shear stress | |
| , | Complex potential functions |
| Elastic constant | |
| Horizontal displacement | |
| Vertical displacement | |
| Shear modulus | |
| Mapped complex coordinate | |
| Embedment ratio parameter | |
| Constant | |
| Laurent series parameter | |
| Angular coordinate in the z-plane and -plane | |
| Uniform convergence | |
| First Lame coefficient | |
| Variable | |
| Tunnel radius | |
| Uniform convergence | |
| Maximum horizontal displacement | |
| Maximum vertical displacement | |
| Poisson ratio | |
| Ovalization parameter of the tunnel wall | |
| Distance between and | |
| Vertical translation | |
| Maximum vertical translation | |
| Final shape of displacement | |
| Maximum final shape of displacement | |
| SPO-SL | National Highway 109 of the Sixth Western Bypass Section |
Appendix A
Appendix B
Appendix C
References
- Fu, J.; Yang, J.; Klapperich, H.; Wang, S. Analytical Prediction of Ground Movements due to a Nonuniform Deforming Tunnel. Int. J. Geomech. 2015, 16, 04015089. [Google Scholar] [CrossRef]
- Peck, R.B. Deep excavations and tunneling in soft ground. In Sociedad Mexicana de Mecanica, Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City; International Society for Soil Mechanics and Geotechnical Engineering: London, UK, 1969; pp. 225–290. [Google Scholar]
- Mair, R.J.; Taylor, R.N.; Bracegirdle, A. Subsurface settlement profiles above tunnels in clays. Geotechnique 1993, 43, 315–320. [Google Scholar] [CrossRef]
- O’Reilly, M.P.; New, B.M. Settlements above tunnels in the United Kingdom—Their magnitude and prediction. PT 82 IMM. London 1982, 20005, 173–181. [Google Scholar] [CrossRef]
- Dyer, M.R.; Hutchinson, M.T.; Evans, N. Symposium on Geotechnical Aspects of Underground Constructions in Soft Ground Sudden Valley Sewer: A case history. In Proceedings—International London; Balkema: Rotterdam, The Netherland, 1996; pp. 671–676. [Google Scholar]
- Moh, Z.C.; Hwang, R.N.; Ju, D.H. Ground movements around tunnels in soft ground. In Geotechnical Aspects of Underground Construction in Soft Ground; Elshafie, M., Viggiani, G., Mair, R., Eds.; Balkema: Rotterdam, The Netherland, 1996; pp. 725–730. [Google Scholar]
- Wei, G.; Pang, S.; Zhang, S. Prediction of ground deformation induced by double parallel shield tunneling. Disaster Adv. 2013, 6, 91–98. [Google Scholar]
- Pinto, F.; Zymnis, D.M.; Whittle, A.J. Ground Movements due to Shallow Tunnels in Soft Ground. II: Analytical Interpretation and Prediction. J. Geotech. Geoenviron. Eng. 2014, 140, 04013041. [Google Scholar] [CrossRef] [Green Version]
- Amorosi, A.; Boldini, D.; De Felice, G.; Malena, M.; Sebastianelli, M. Tunneling-induced deformation and damage on historical masonry structures. Geotechnique 2014, 64, 118–130. [Google Scholar] [CrossRef]
- Hasanpour, R. Advance numerical simulation of tunneling by using a double shield TBM. Comput. Geotech. 2014, 57, 37–52. [Google Scholar] [CrossRef]
- Zheng, G.; Lu, P.; Diao, Y. Advance speed-based parametric study of greenfield deformation induced by EPBM tunneling in soft ground. Comput. Geotech. 2015, 65, 220–232. [Google Scholar] [CrossRef]
- Zheng, G.; Zhang, T.; Diao, Y. Mechanism and countermeasures of preceding tunnel distortion induced by succeeding EPBS tunneling in close proximity. Comput. Geotech. 2015, 66, 53–65. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M.; Zhang, M. Theoretical prediction of ground movements induced by tunnelling in multi-layered soils. Tunn. Undergr. Space Technol. 2011, 26, 345–355. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Huang, M.S.; Xi, X.G.; Yuan, X. Complex variable solutions for soil and liner deformation due to tunneling in clays. Int. J. Geomech. 2018, 18, 0001197. [Google Scholar] [CrossRef]
- Kong, F.; Lu, D.; Du, X.; Shen, C. Displacement analytical prediction of shallow tunnel based on unified displacement function under slope boundary. Int. J. Numer. Anal. Methods Geomech. 2018, 2018, 183–211. [Google Scholar] [CrossRef] [Green Version]
- Mindlin, R.D. Stress distribution around a tunnel. Trans. Am. Soc. Civil Eng. 1940, 195, 1117–1140. [Google Scholar] [CrossRef]
- Zymnis, D.M.; Whittle, A.J.; Chatzigiannelis, I. Effect of anisotropy in ground movements caused by tunneling. Geotechnique 2013, 63, 1083–1102. [Google Scholar] [CrossRef] [Green Version]
- Fang, Q.; Song, H.R.; Zhang, D.L. Complex variable analysis for stress distribution of an underwater tunnel in an elastic half plane. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 1821–1835. [Google Scholar] [CrossRef]
- Lu, A.Z.; Zeng, X.T.; Xu, Z. Solution for a circular cavity in an elastic half plane under gravity and arbitrary lateral stress. Int. J. Rock Mech. Min. Sci. 2016, 89, 34–42. [Google Scholar] [CrossRef]
- Lu, D.; Kong, F.; Du, X.; Shen, C.; Gong, Q.; Li, P. A unified displacement function to analytically predict ground deformation of shallow tunnel. Tunn. Undergr. Space Technol. 2019, 88, 129–143. [Google Scholar] [CrossRef]
- Wang, H.N.; Wu, L.; Jiang, M.J.; Song, F. Analytical stress and displacement due to twin tunneling in an elastic semi-infinite ground subjected to surcharge loads. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 809–828. [Google Scholar] [CrossRef]
- Mabe Fogang, P.; Liu, Y.; Zhao J, l.; Azeuda Ndonfack, K.I. Soil Deformation around a Cylindrical Cavity under Drained Conditions: Theoretical Analysis. Adv. Civ. Eng. 2022, 2022, 4127660. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, C.; Min, B.; Chen, W. Complex variable solution for tunneling-induced ground deformation considering the gravity effect and a cavern in the strata. Comput. Geotech. 2021, 135, 104154. [Google Scholar] [CrossRef]
- Mindlin, R.D. Stress distribution around a hole near the edge of a plate under tension. PSESA 1948, 5, 56–68. [Google Scholar]
- Sagaseta, C. Analysis of undrained soil deformation due to ground loss. Geotechnique 1987, 37, 301–320. [Google Scholar] [CrossRef]
- Verruijt, A.; Booker, J.R. Surface Settlements Due to Deformation of A Tunnel in an Elastic Half Plane. Geotechnique 1996, 46, 753–756. [Google Scholar] [CrossRef]
- Verruijt, A. A complex variable solution for a deforming circular tunnel in an elastic half-plane. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 77–89. [Google Scholar] [CrossRef]
- Loganathan, N.; Poulos, H.G. Analytical Prediction for Tunneling-Induced Ground Movements in Clays. J. Geotech. Geoenviron. Eng. 1998, 124, 846–856. [Google Scholar] [CrossRef]
- Verruijt, A. Deformations of an elastic half plane with a circular cavity. Int. J. Solids Struct. 1998, 35, 2795–2804. [Google Scholar] [CrossRef]
- Massinas, S.A.; Sakellariou, M.G. Closed-form solution for plastic zone formation around a circular tunnel in half-space obeying Mohr-Coulomb criterion. Geotechnique 2009, 59, 691–701. [Google Scholar] [CrossRef]
- Wang, L.-Z.; Li, L.-L.; Lv, X.-J. Complex Variable Solutions for Tunneling-Induced Ground Movement. Int. J. Geomech. 2009, 9, 63–72. [Google Scholar] [CrossRef]
- Boussinesq, J. Essai Sur La Théorie Des Eaux Courantes; Institut National de France: Paris, France, 1877. [Google Scholar]
- Jong, Y.G.; Liu, Y.; Zixuan Chen, Z.; Mabe Fogang, P. Hypoplastic Interface Model considering Plane Strain Condition and Surface Roughness. Adv. Civ. Eng. 2021, 2021, 1473181. [Google Scholar] [CrossRef]
- Lee, K.M.; Rowe, R.K.; Lo, K.Y. Subsidence owing to tunnelling. I. Estimating the gap parameter. Can. Geotech. J. 1992, 29, 929–940. [Google Scholar] [CrossRef]
- Gonzalez, C.; Sagaseta, C. Patterns of soil deformations around tunnels. Application to the extension of Madrid Metro. Comput. Geotech. 2001, 28, 445–468. [Google Scholar] [CrossRef]
- Park, K.H. Elastic solution for tunneling-induced ground movement in clays. Int. J. Geomech. 2004, 310–318. [Google Scholar] [CrossRef]
- Park, K.H. Analytical solution for tunnelling-induced ground movement in clays. Tunn. Undergr. Space Technol. 2005, 20, 249–261. [Google Scholar] [CrossRef]
- Vasiliev, V.V.; Lurie, S.A.; Salov, V.A. On the Flamant problem for a half-plane loaded with a concentrated force. Acta Mech. 2021, 232, 1761–1771. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; P. Noordhoff Ltd.: Groningen, The Netherlands, 1963. [Google Scholar]
- Mitchell, L.H. Stress-concentration factors at a doubly-symmetric hole. Aeronaut. Quart. 1966, 17, 177–186. [Google Scholar] [CrossRef]
- Exadaktylos, G.E.; Liolios, P.A.; Stavropoulou, M.C. A semi-analytical elastic stress–displacement solution for notched circular openings in rocks. Int. J. Solids Struct. 2003, 40, 1165–1187. [Google Scholar] [CrossRef]
- Verruijt, A.; Strack, O.E. Buoyancy of tunnels in soft soils. Geotechnique 2008, 58, 513–515. [Google Scholar] [CrossRef]
- Fu, J.Y.; Yang, J.S.; Yan, L.; Abbas, S.M. An analytical solution for deforming twin-parallel tunnels in an elastic half plane. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 524–538. [Google Scholar] [CrossRef]
- Strack, O.E.; Verruijt, A. A complex variable solution for a deforming buoyant tunnel in a heavy elastic half-plane. Int. J. Numer. Anal. Methods Geomech. 2022, 26, 1235–1252. [Google Scholar] [CrossRef]





| N° | Materials | E(GPa) | ϕ(°) | c(MPa) | ||
|---|---|---|---|---|---|---|
| 1 | soil | 21 × 10-3 | 0.50 | 22 | 18 × 10-3 | 18 |
| 2 | rock (highly weathered) | 1.9 | 0.35 | 27 | 0.15 | 19 |
| 3 | rock (moderately weathered) | 1.95 | 0.35 | 29 | 0.25 | 19.5 |
| 4 | rock (slightly weathered) | 2.1 | 0.35 | 29 | 0.25 | 19.5 |
| 5 | lining | 35 | 0.25 | — | — | 25 |
| 6 | Bolt and grout | 11.0 | 0.25 | 30 | 1.35 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mabe Fogang, P.; Liu, Y.; Zhao, J.-L.; Ka, T.A.; Xu, S. Analytical Prediction of Tunnel Deformation Beneath an Inclined Plane: Complex Potential Analysis. Appl. Sci. 2023, 13, 3252. https://doi.org/10.3390/app13053252
Mabe Fogang P, Liu Y, Zhao J-L, Ka TA, Xu S. Analytical Prediction of Tunnel Deformation Beneath an Inclined Plane: Complex Potential Analysis. Applied Sciences. 2023; 13(5):3252. https://doi.org/10.3390/app13053252
Chicago/Turabian StyleMabe Fogang, Pieride, Yang Liu, Jia-Le Zhao, Thierno Aliou Ka, and Shuo Xu. 2023. "Analytical Prediction of Tunnel Deformation Beneath an Inclined Plane: Complex Potential Analysis" Applied Sciences 13, no. 5: 3252. https://doi.org/10.3390/app13053252






