Toward the Utilization of 3D Blading in the Cantilevered Stator from Highly Loaded Compressors
Abstract
1. Introduction
2. Research Object and Investigation Methodology
2.1. Geometric Definition of the 3D Blading
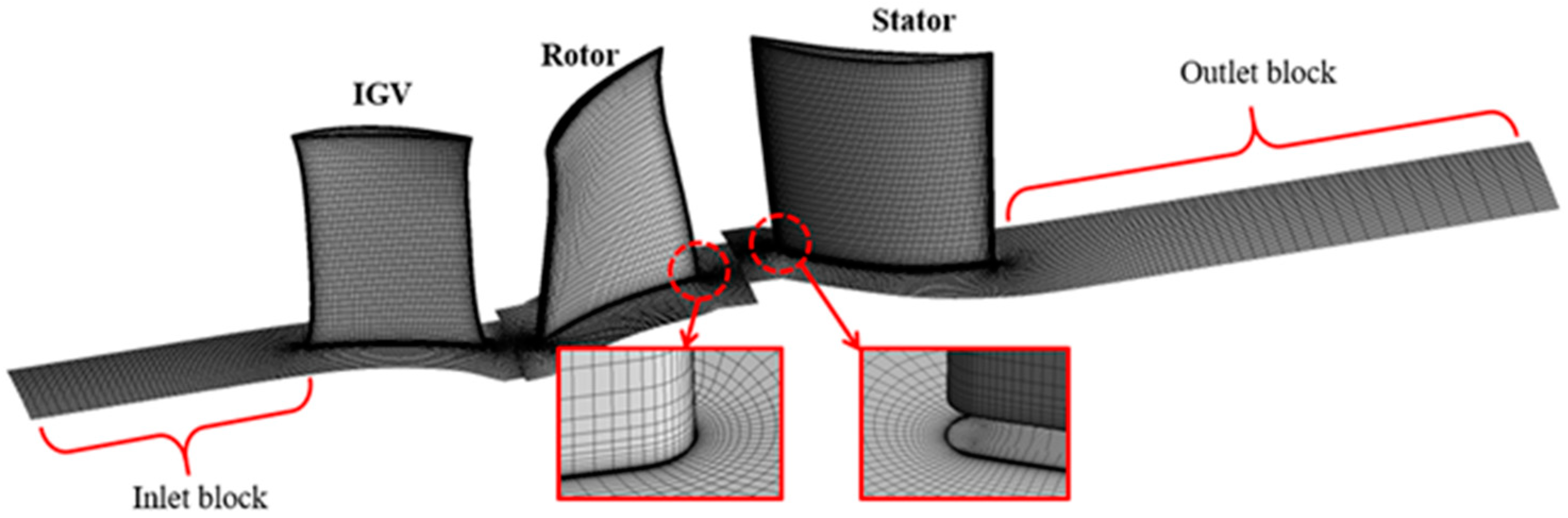
2.2. Numerical Simulation Method
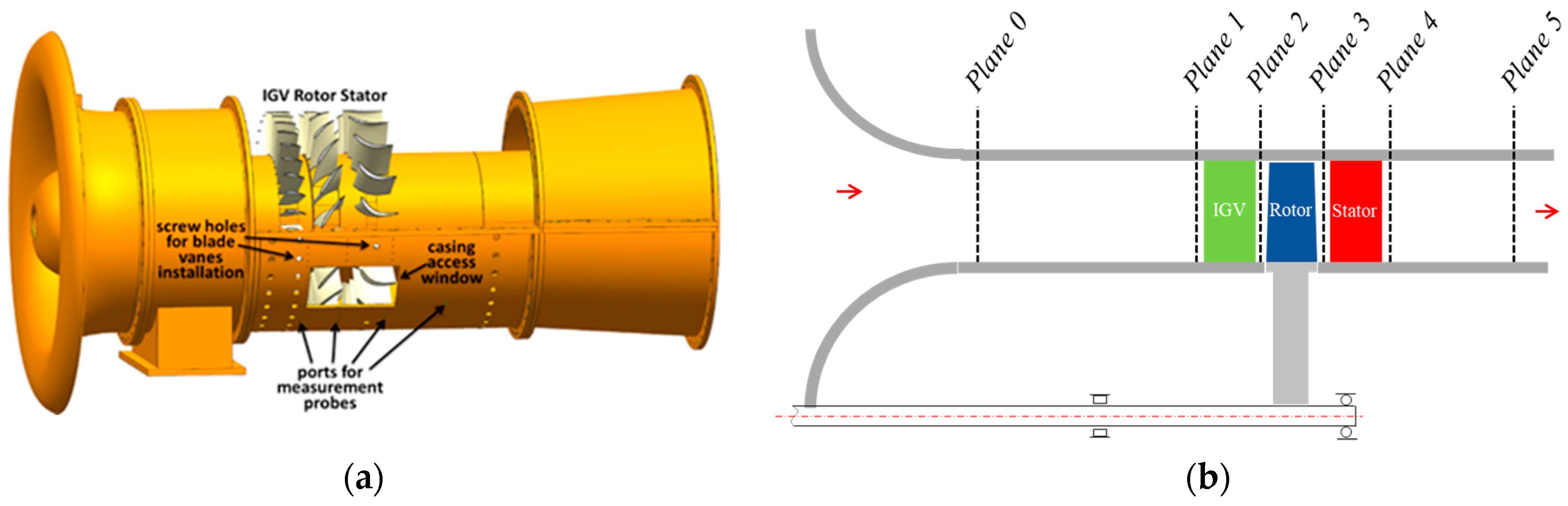
2.3. Experimental Method
3. Effects of 3D Blading on the Cantilevered Stator
3.1. Effects of the Blade Sweep
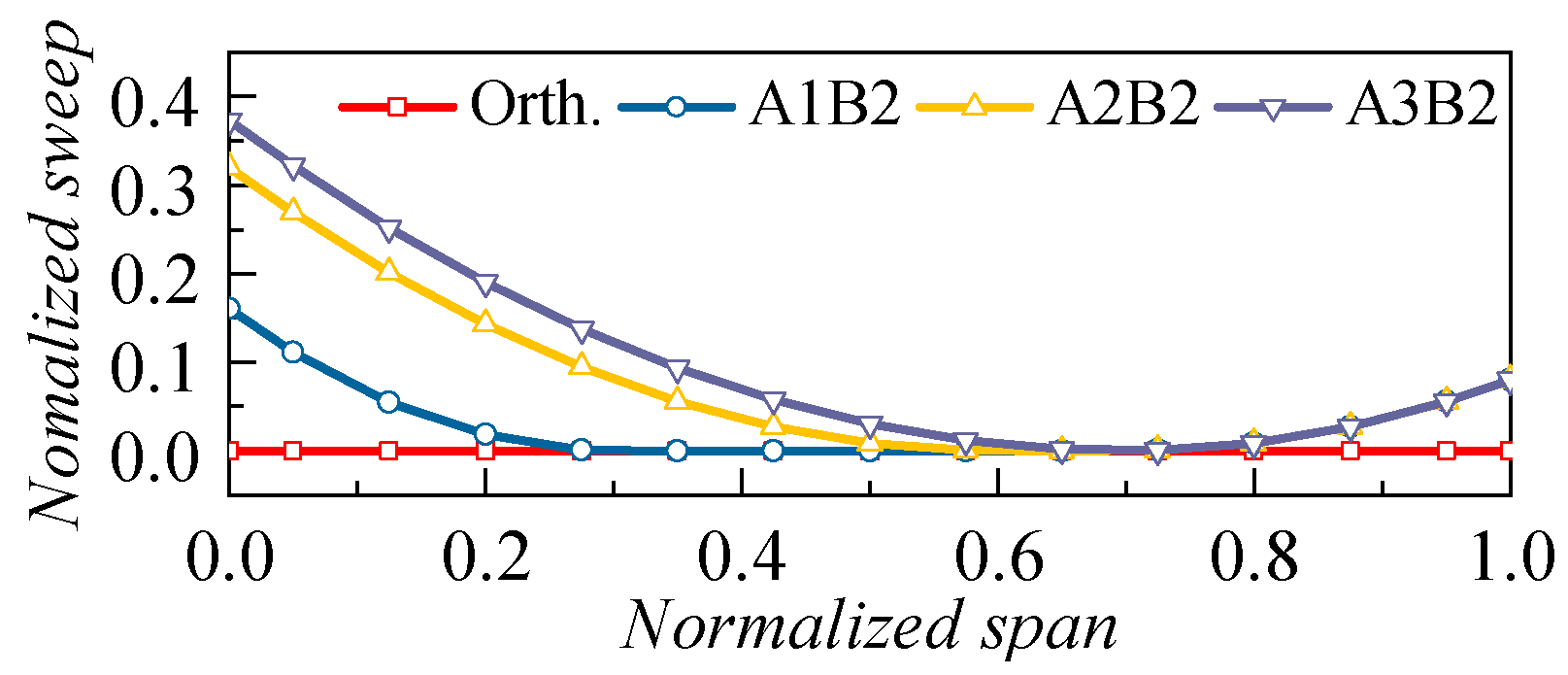
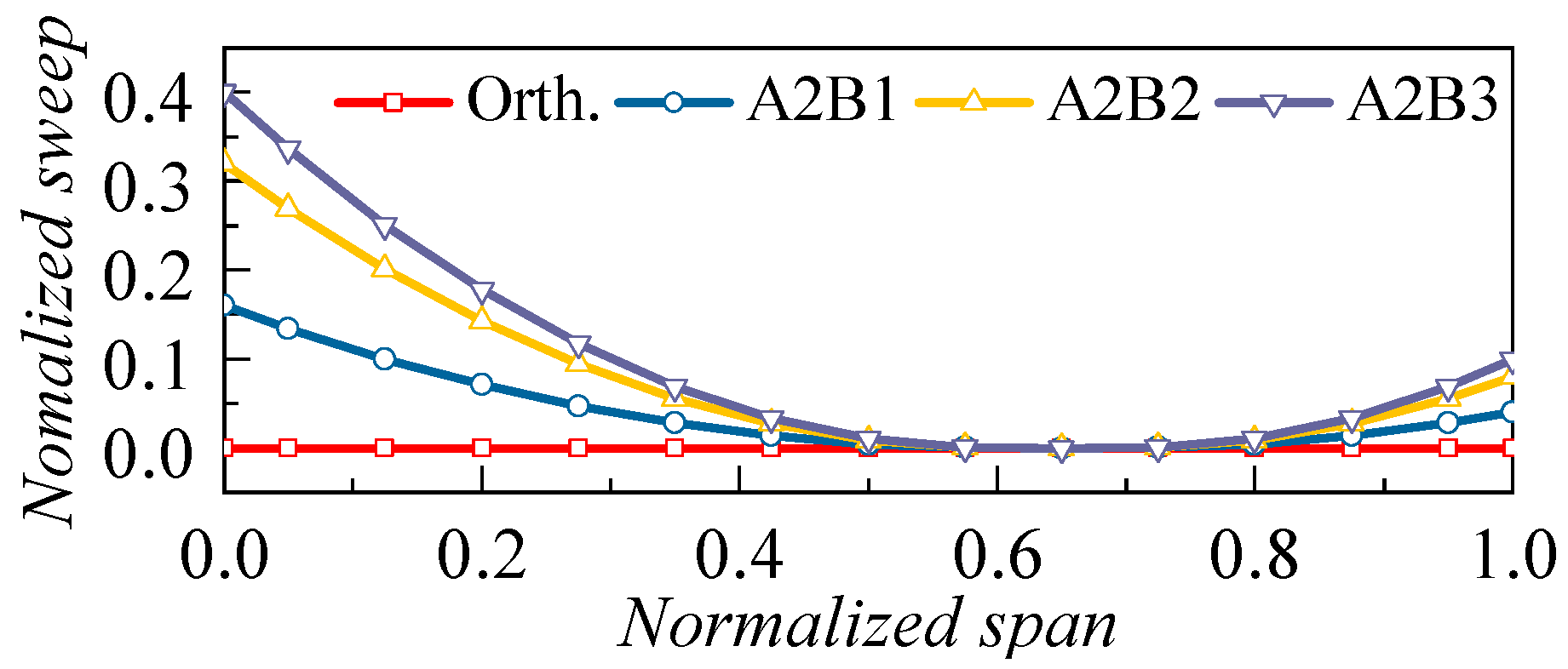
3.1.1. Effects of the Sweep Height
3.1.2. Effects of the Sweep Angle
3.2. Effects of the Blade Dihedral
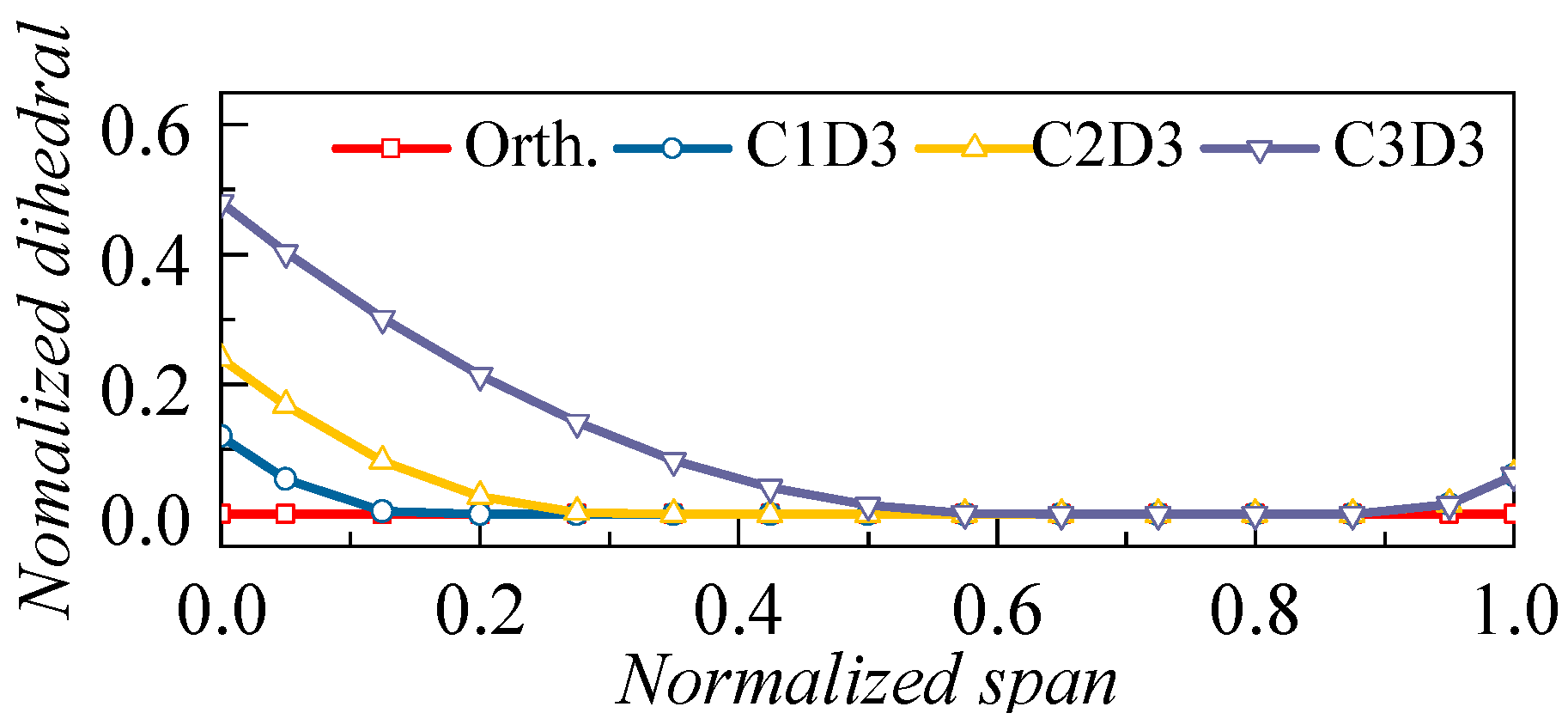
3.2.1. Effects of the Dihedral Height
3.2.2. Effects of the Dihedral Angle
3.3. Effects of the Compound Sweep and Dihedral
4. Application of 3D Blading in a Cantilevered Stator
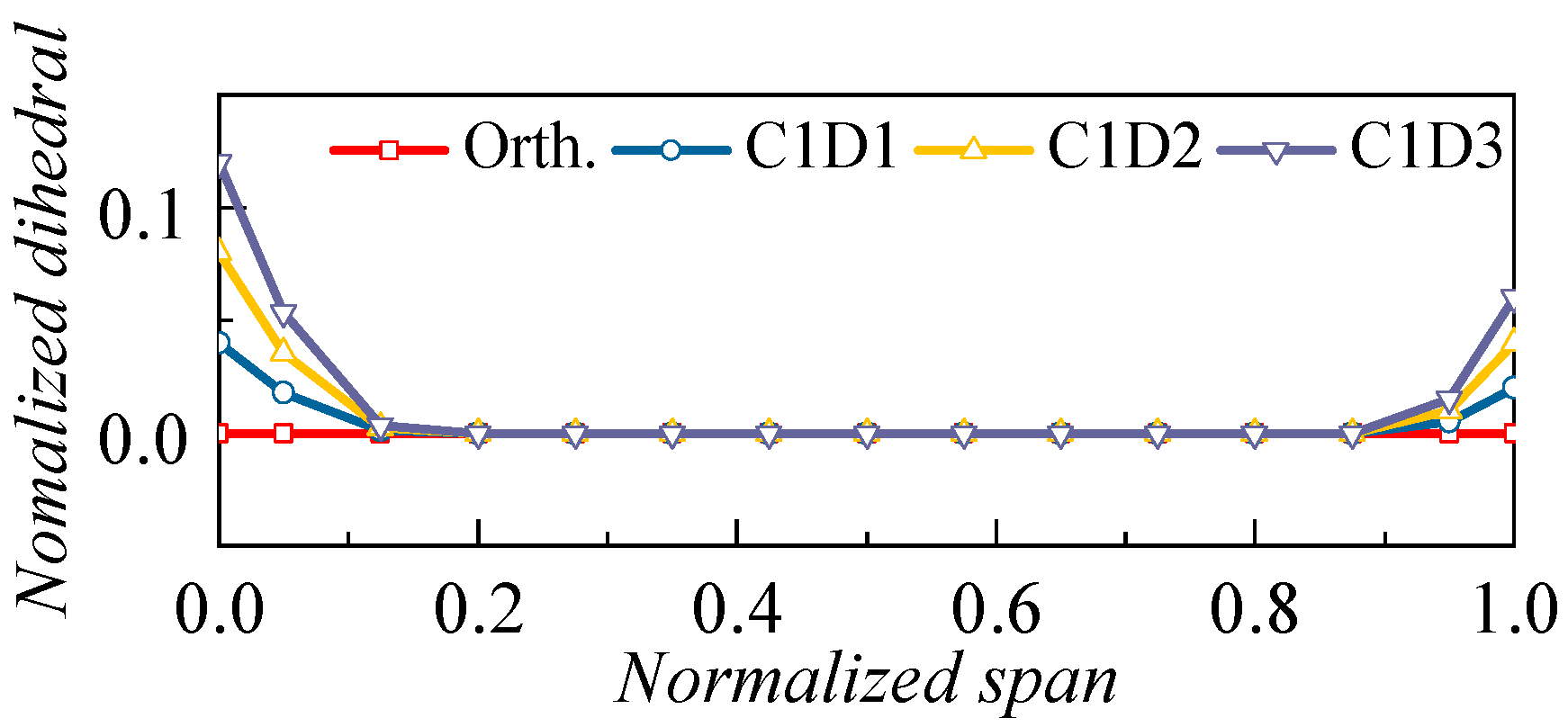
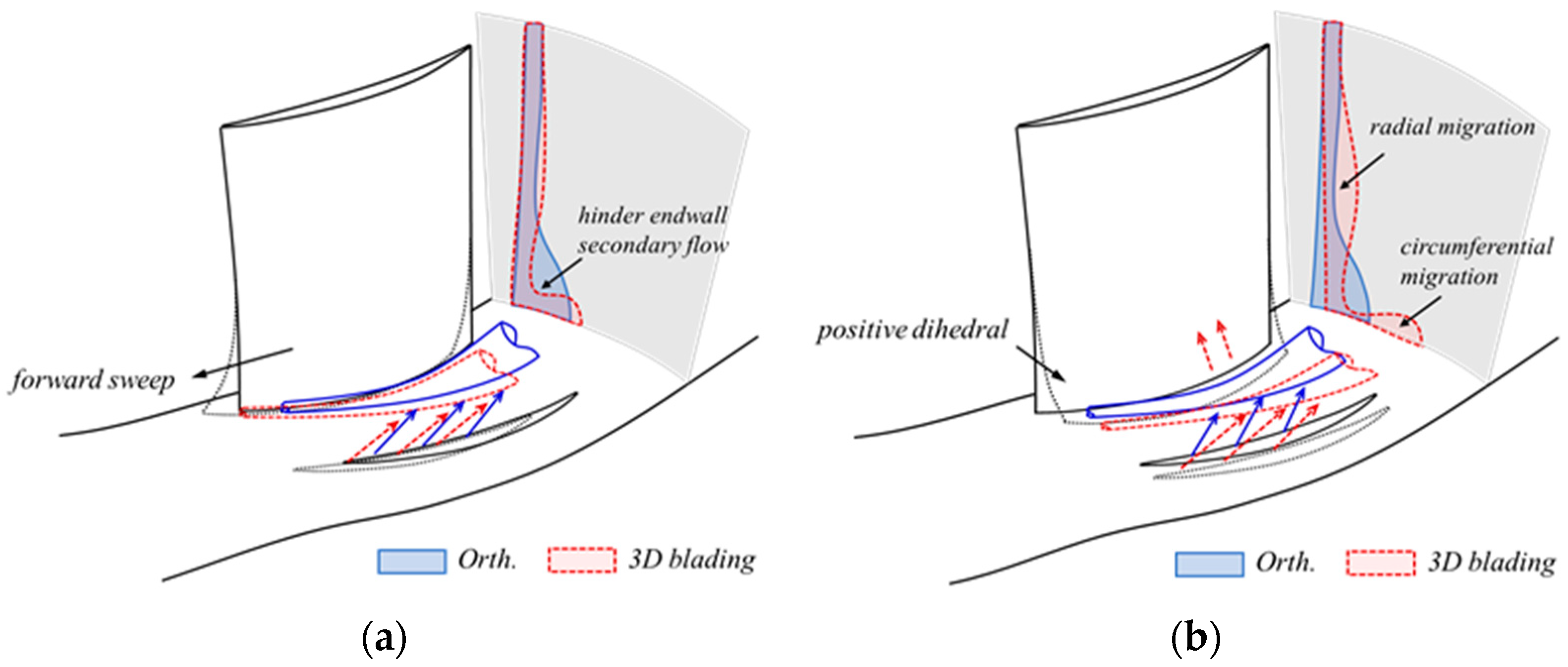
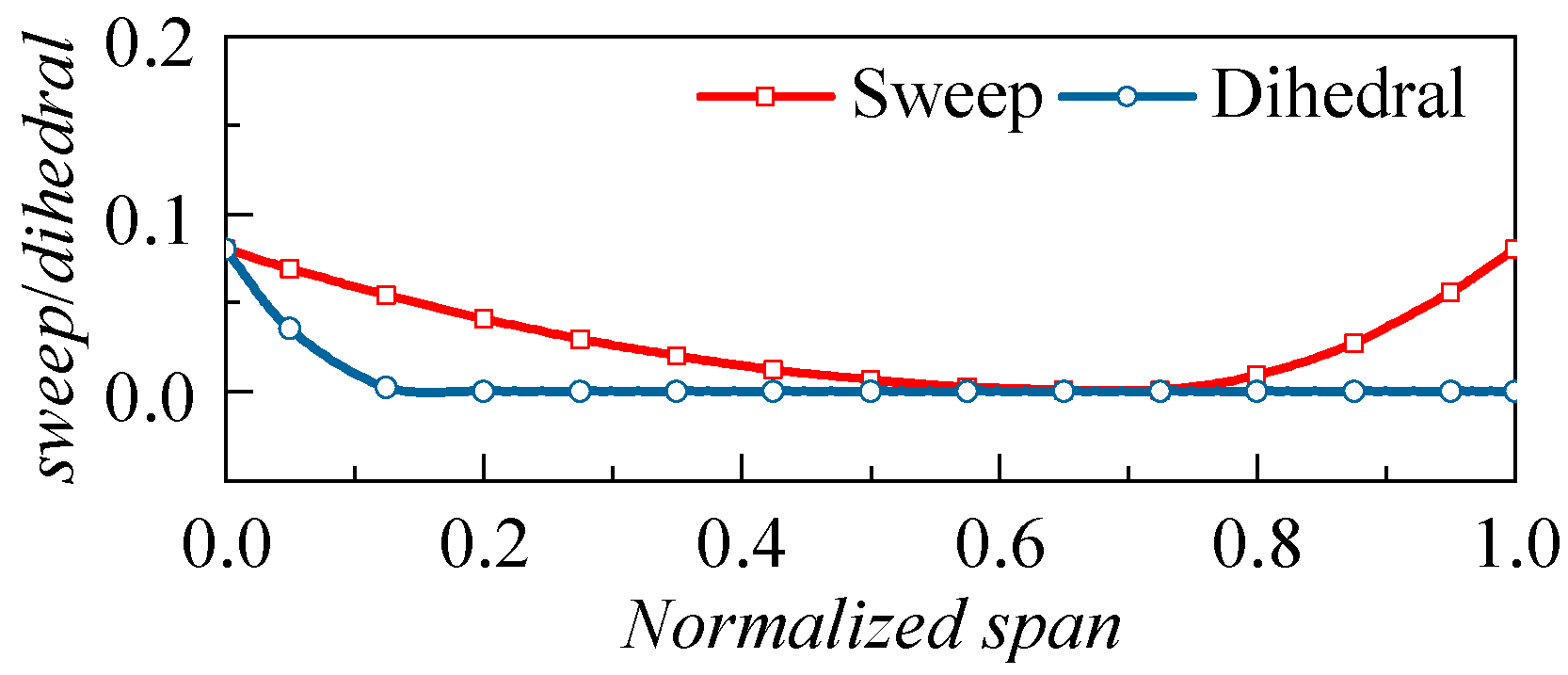
4.1. The Redesign of the Cantilevered Stator
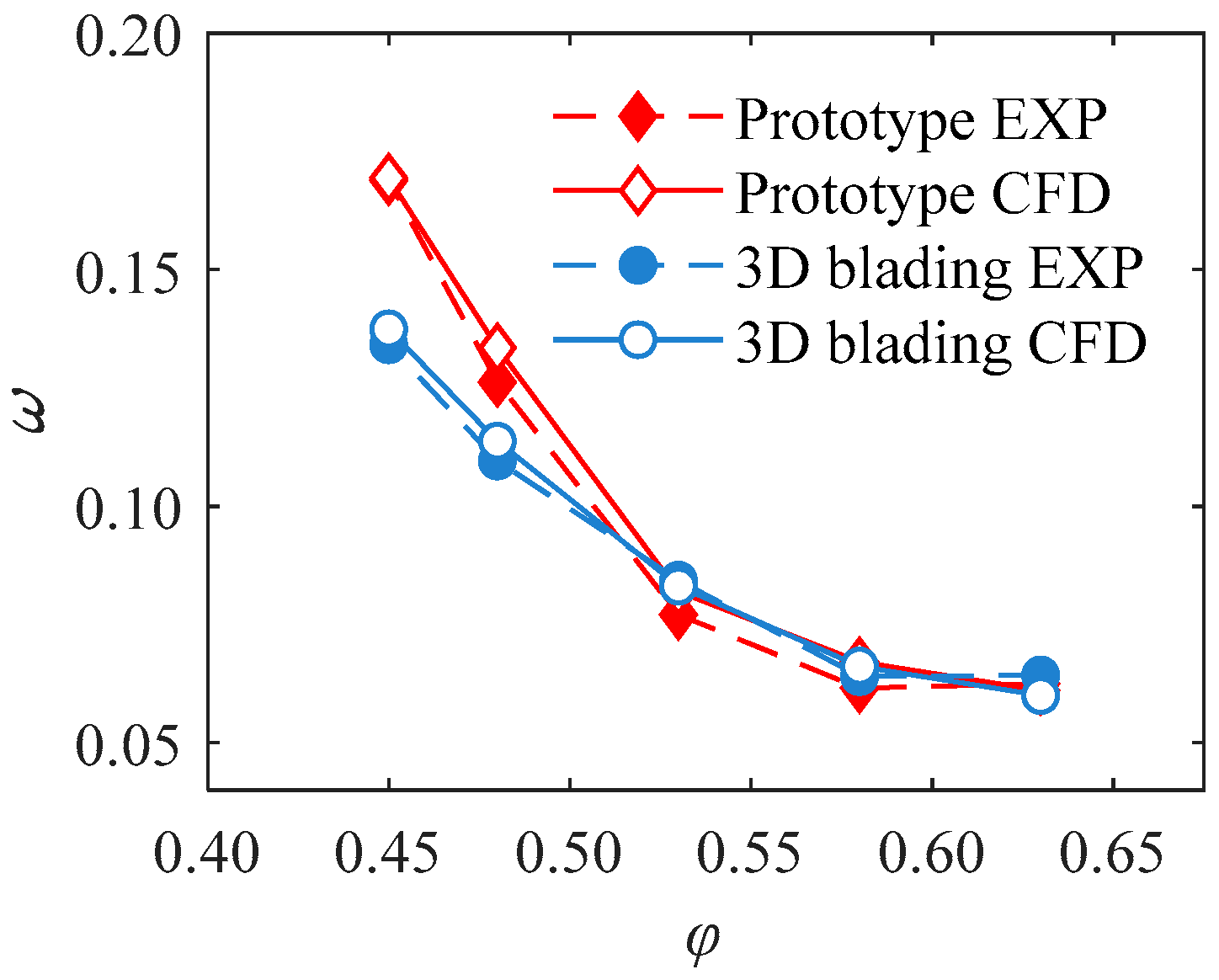
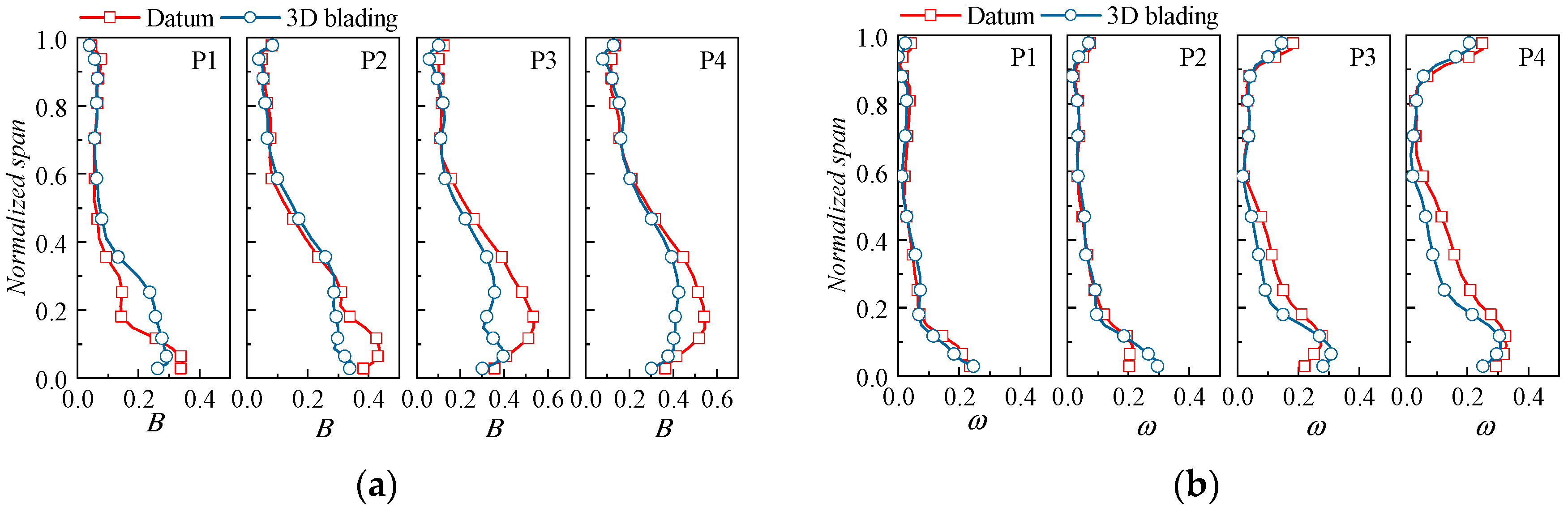
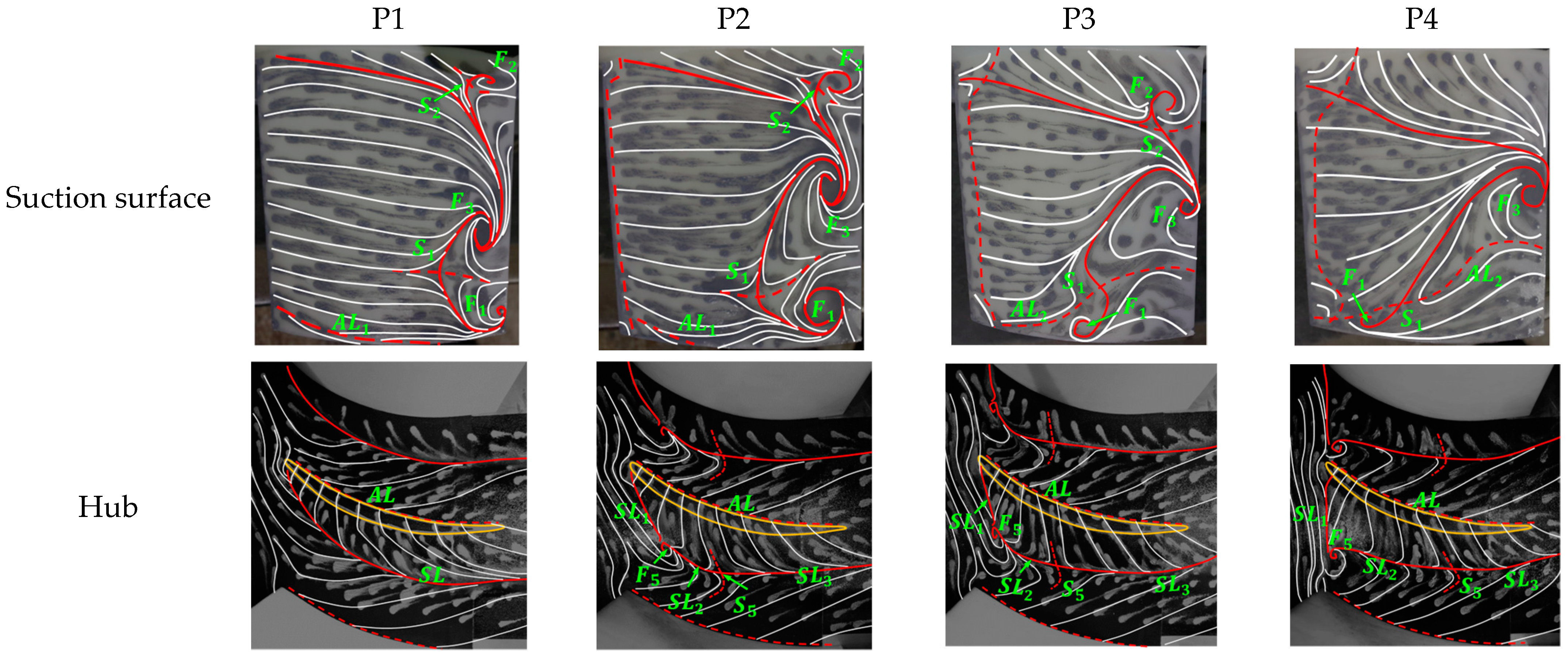
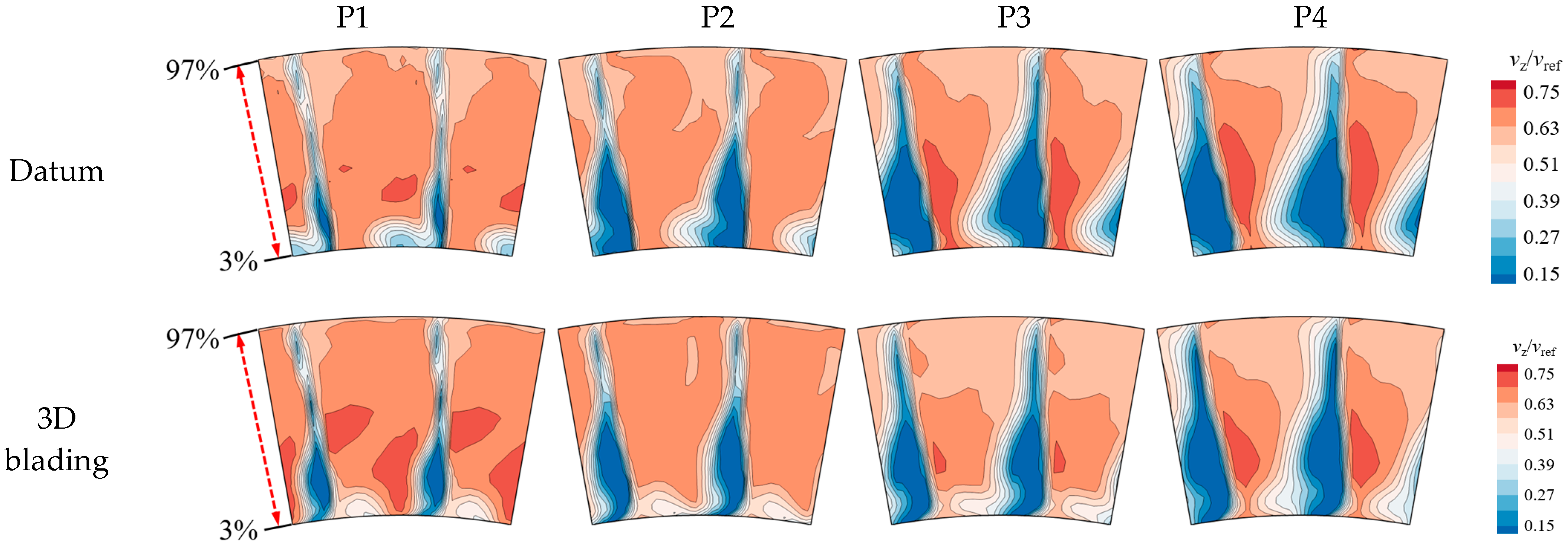
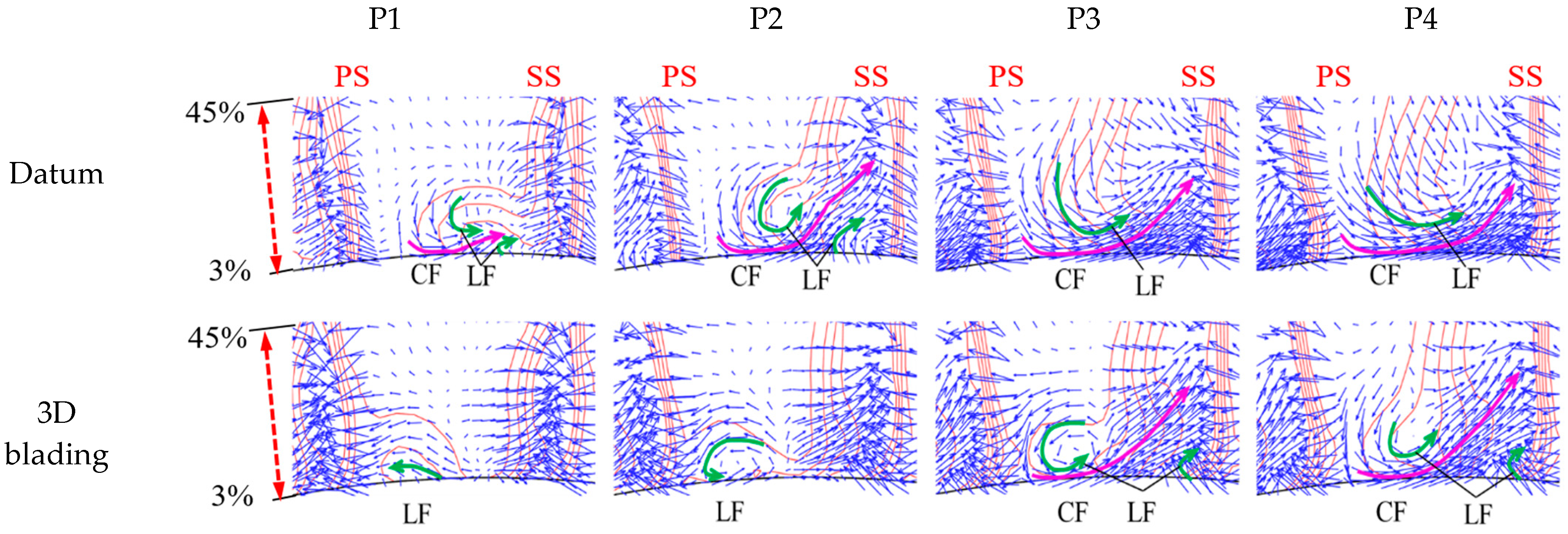
4.2. Discussion of the Experimental Results
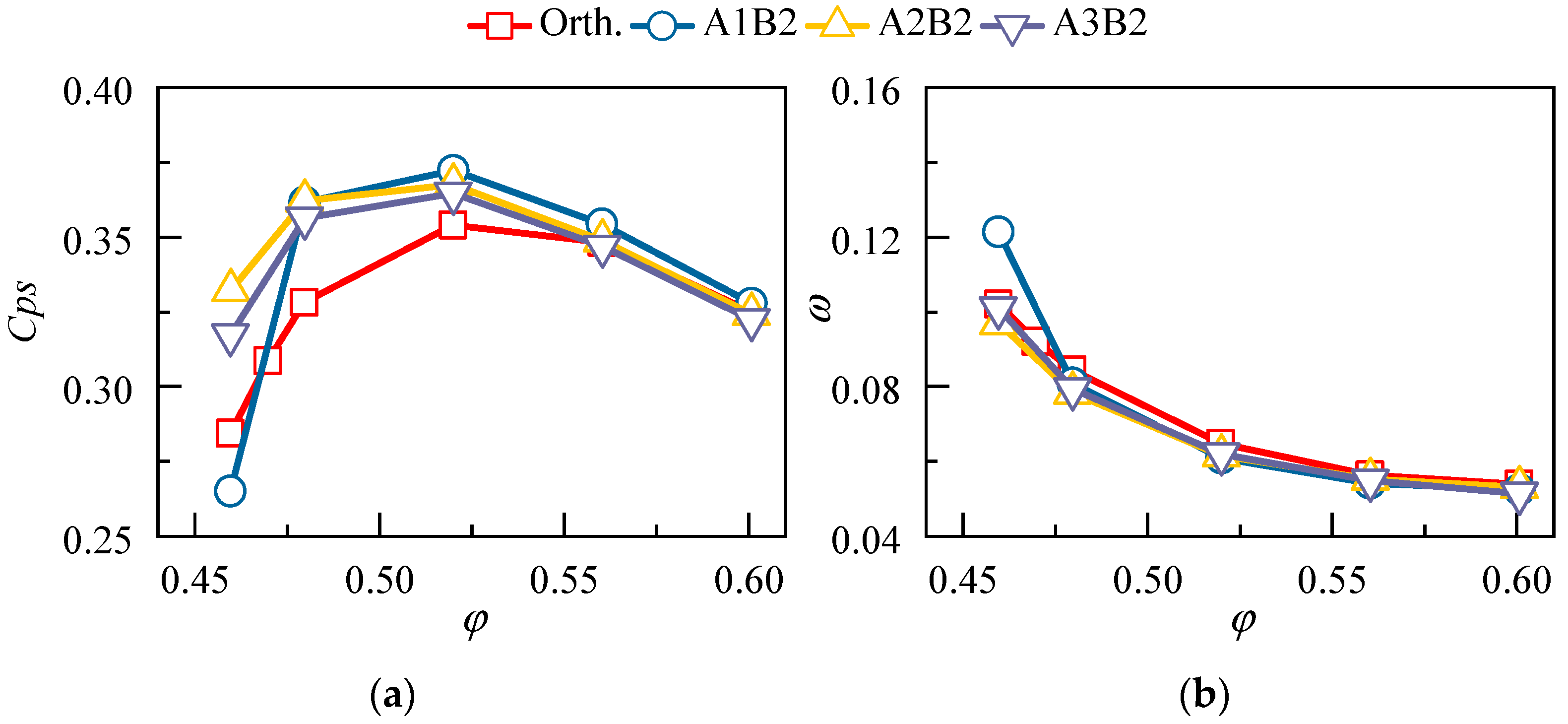
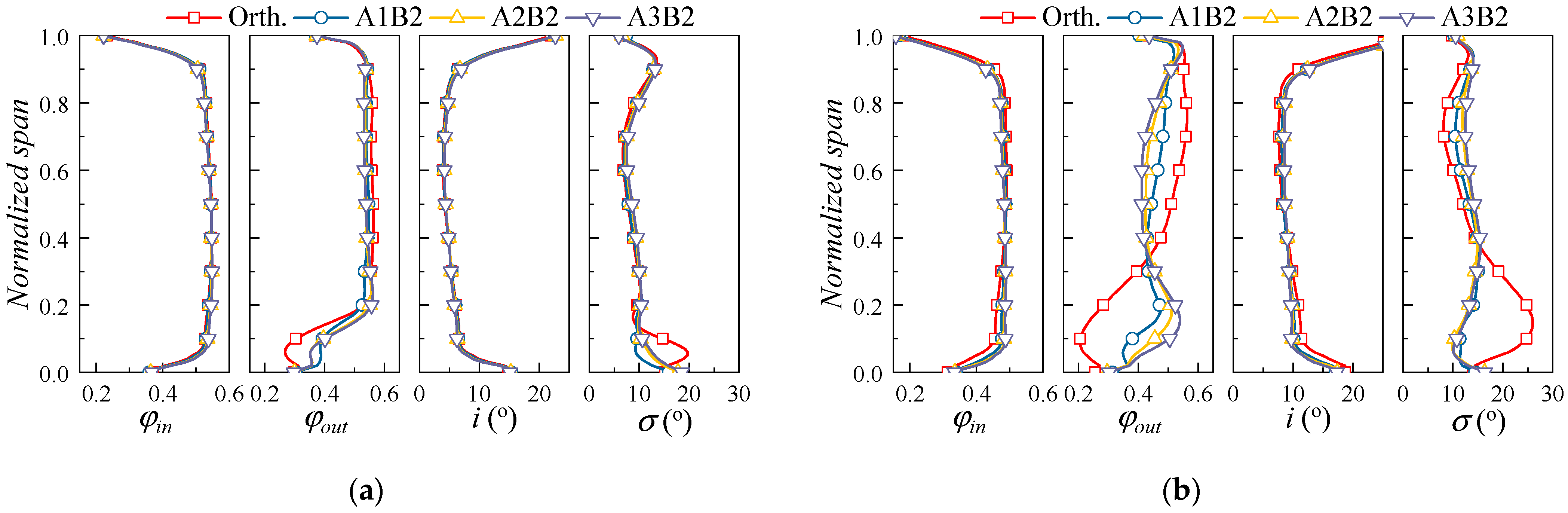
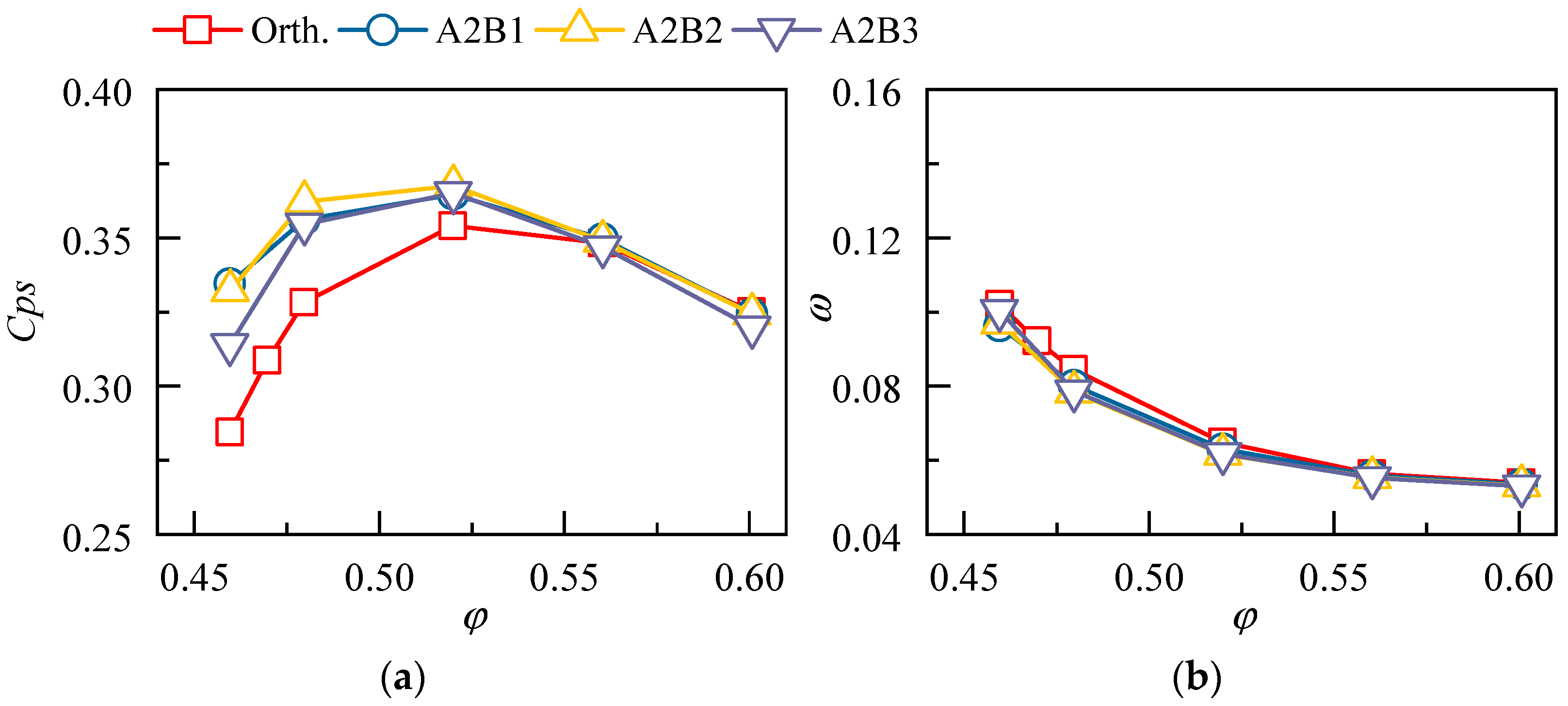
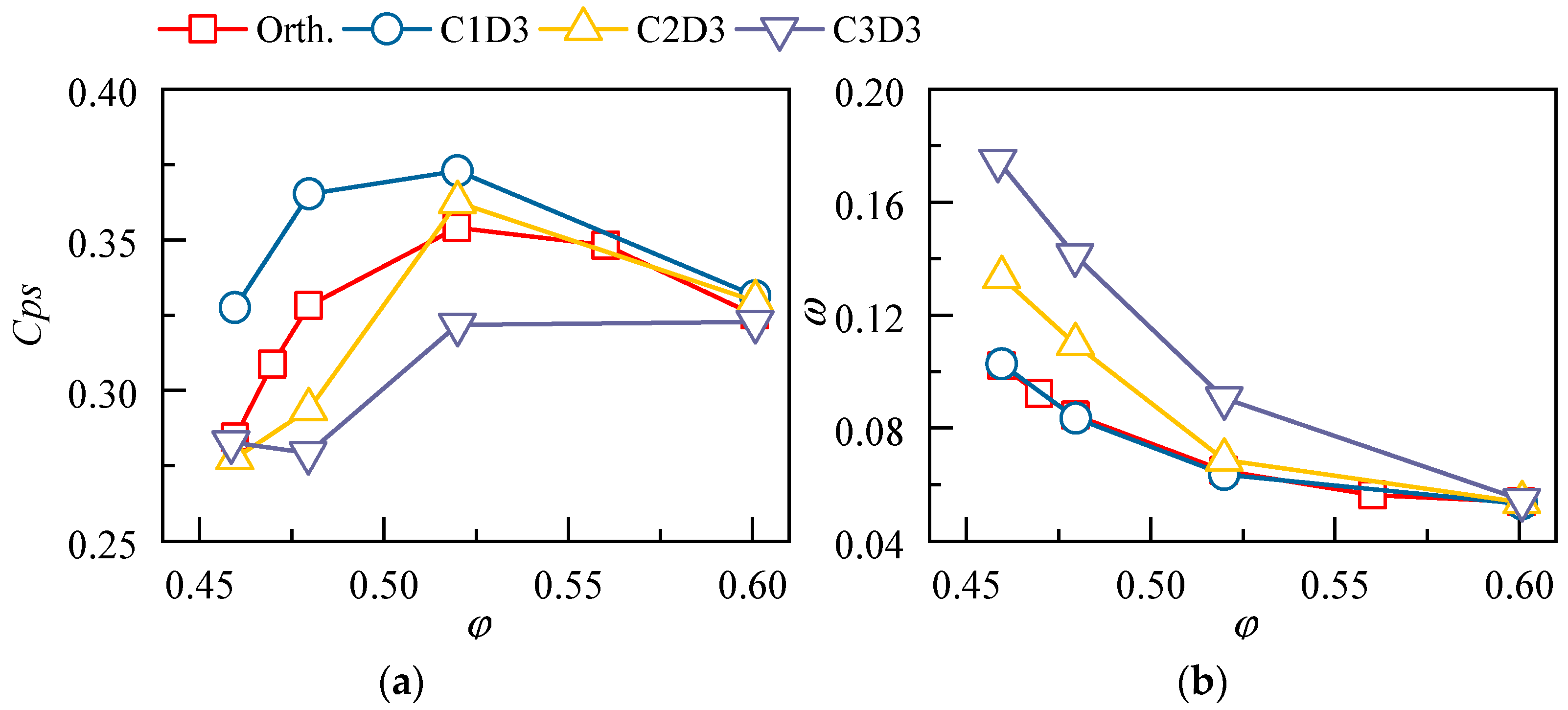
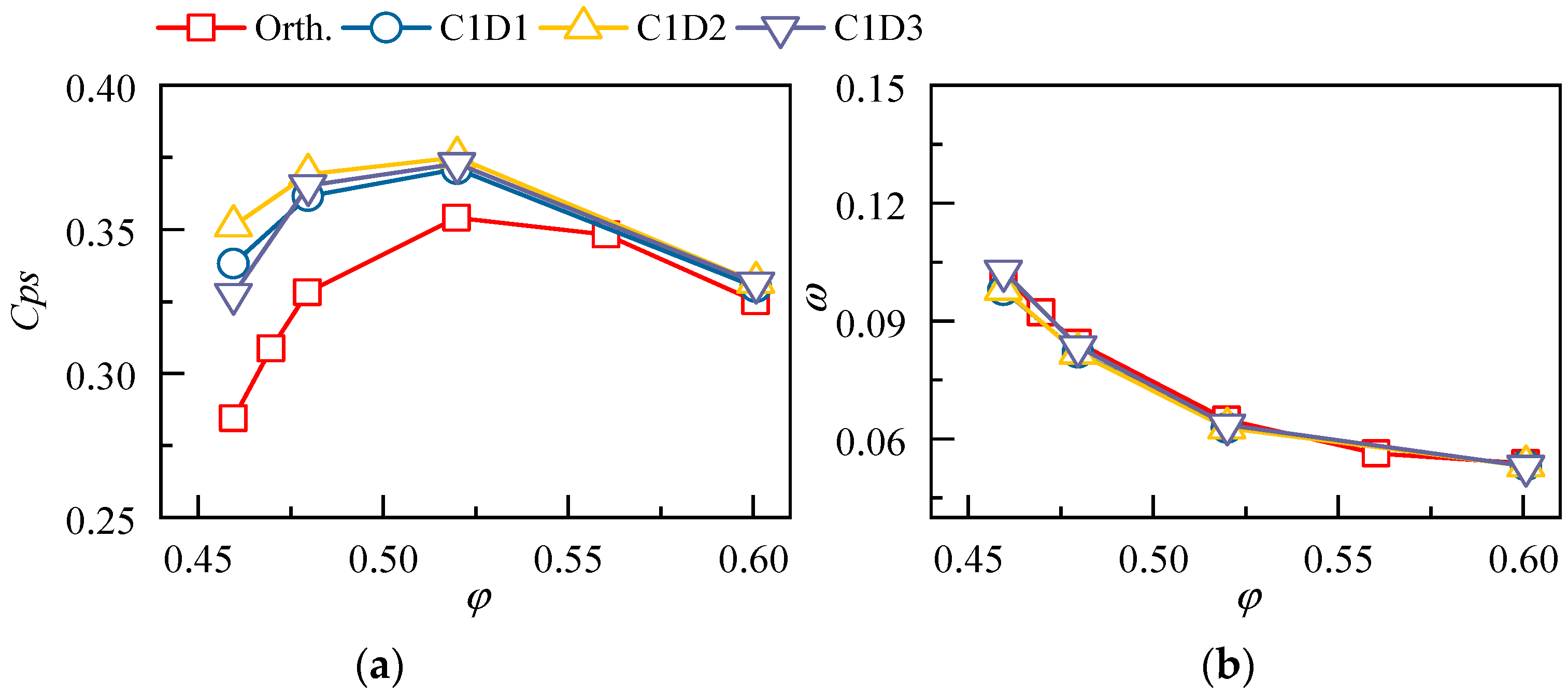
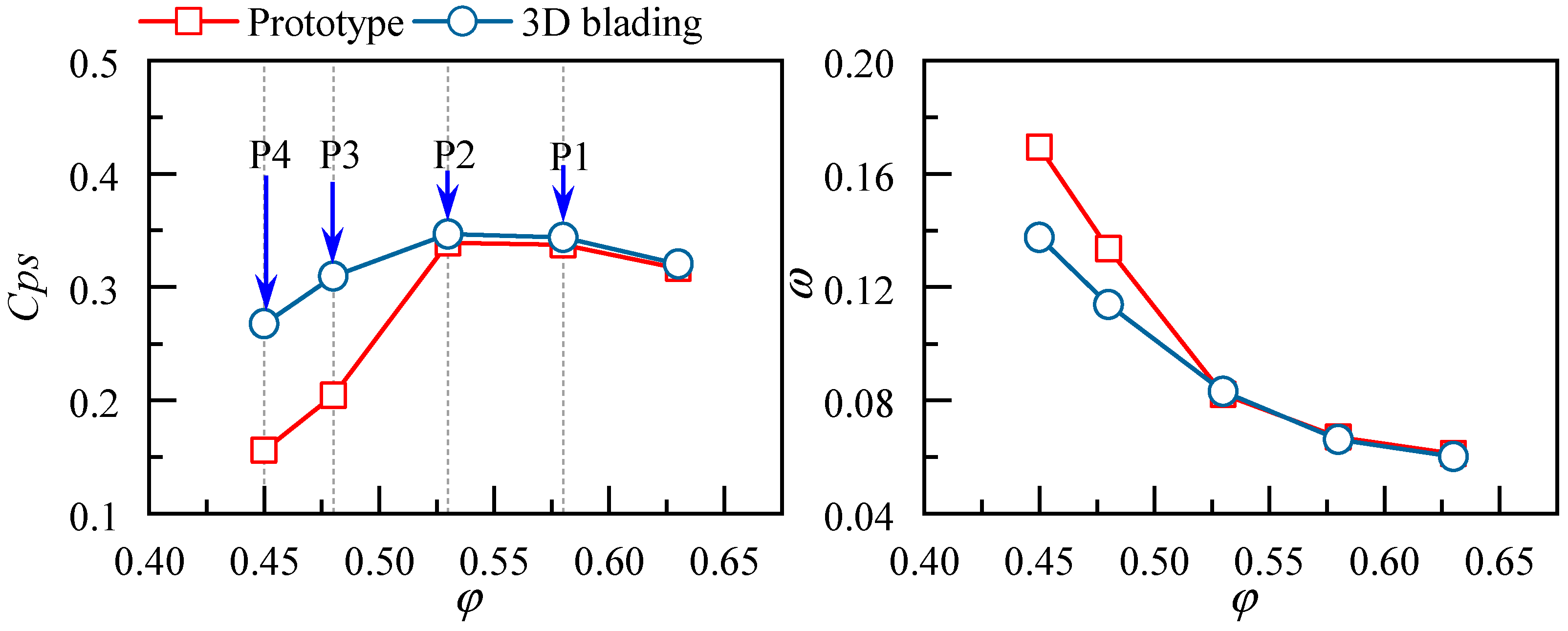
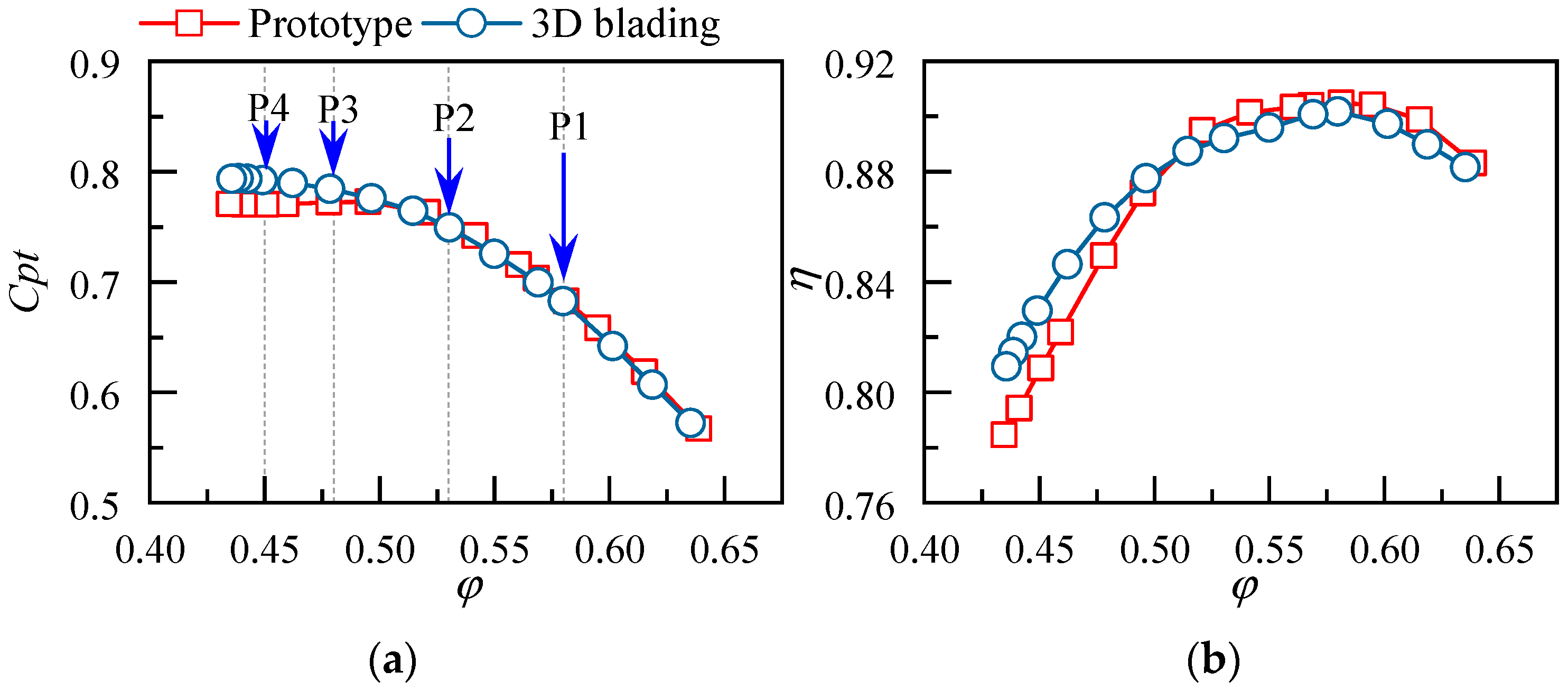
4.2.1. Effect of 3D Blading on the Aerodynamic Performance
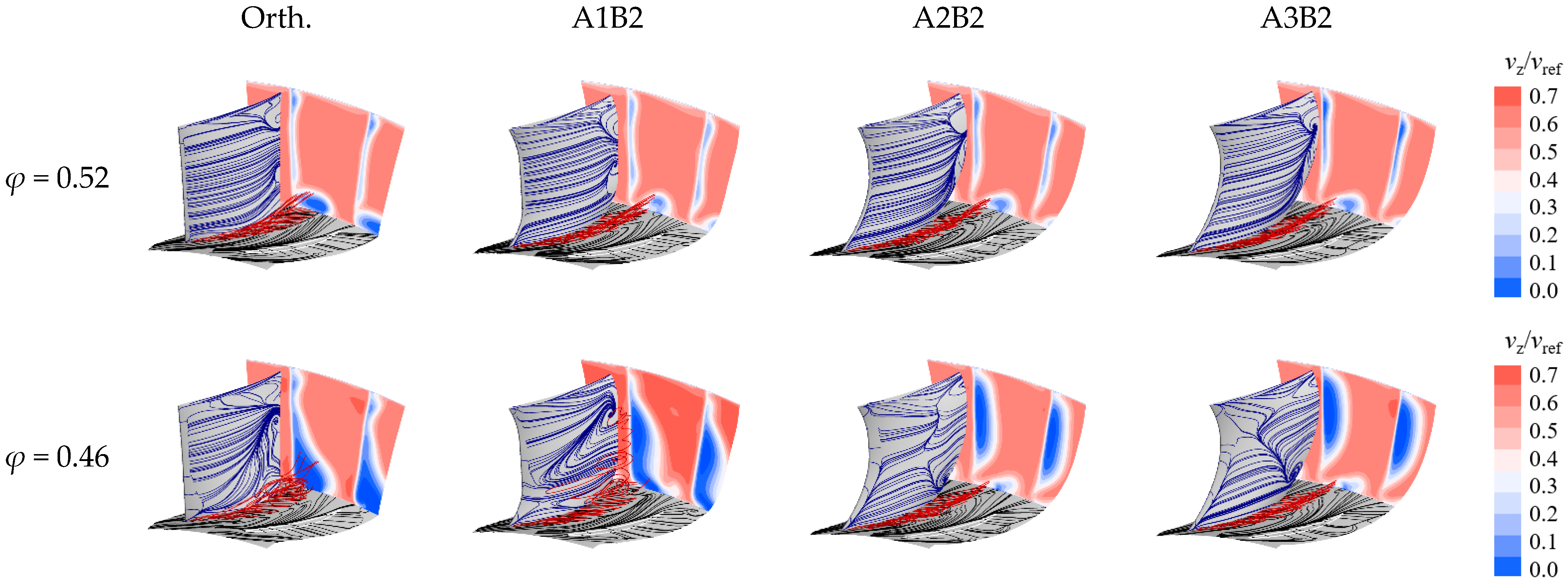
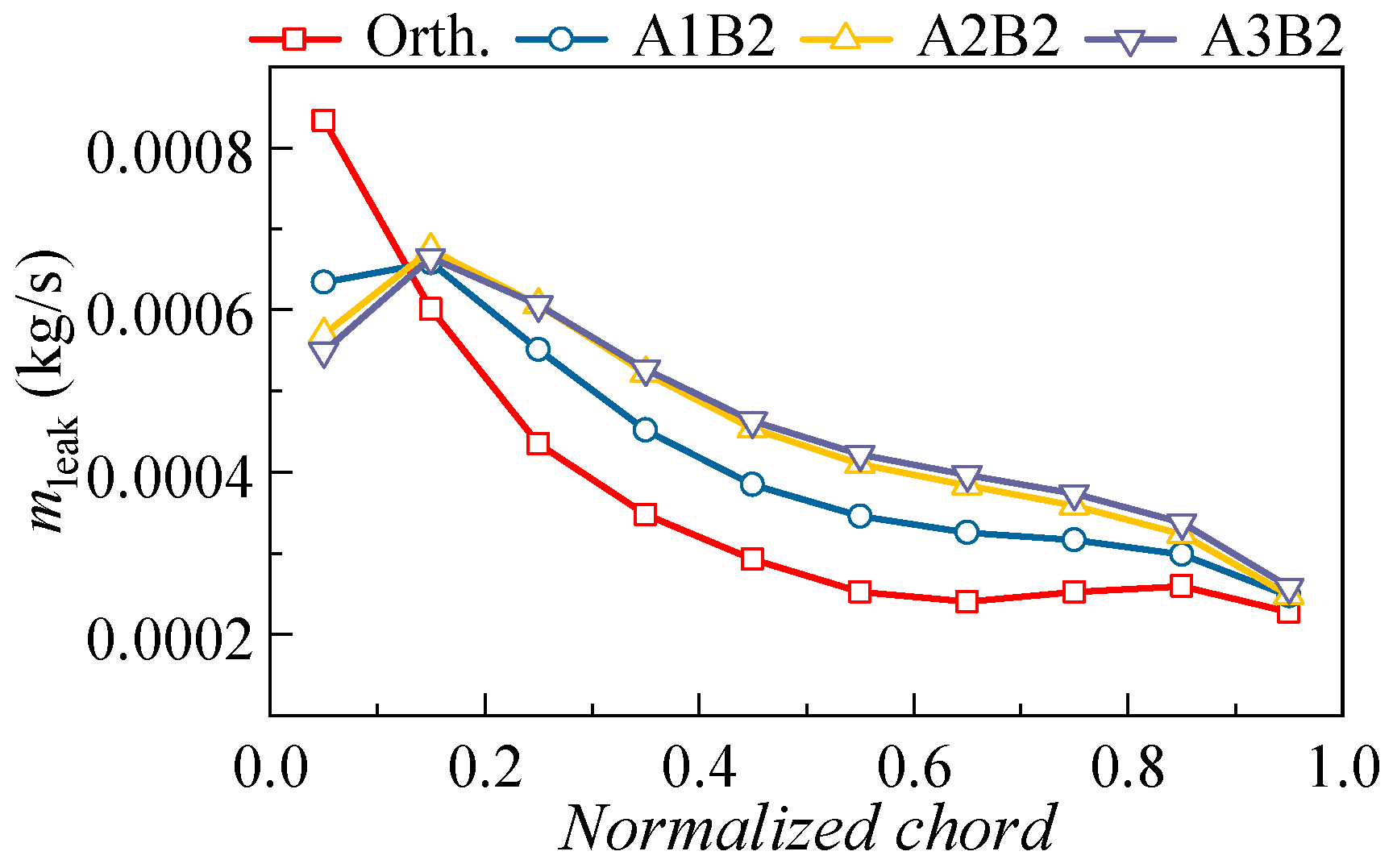
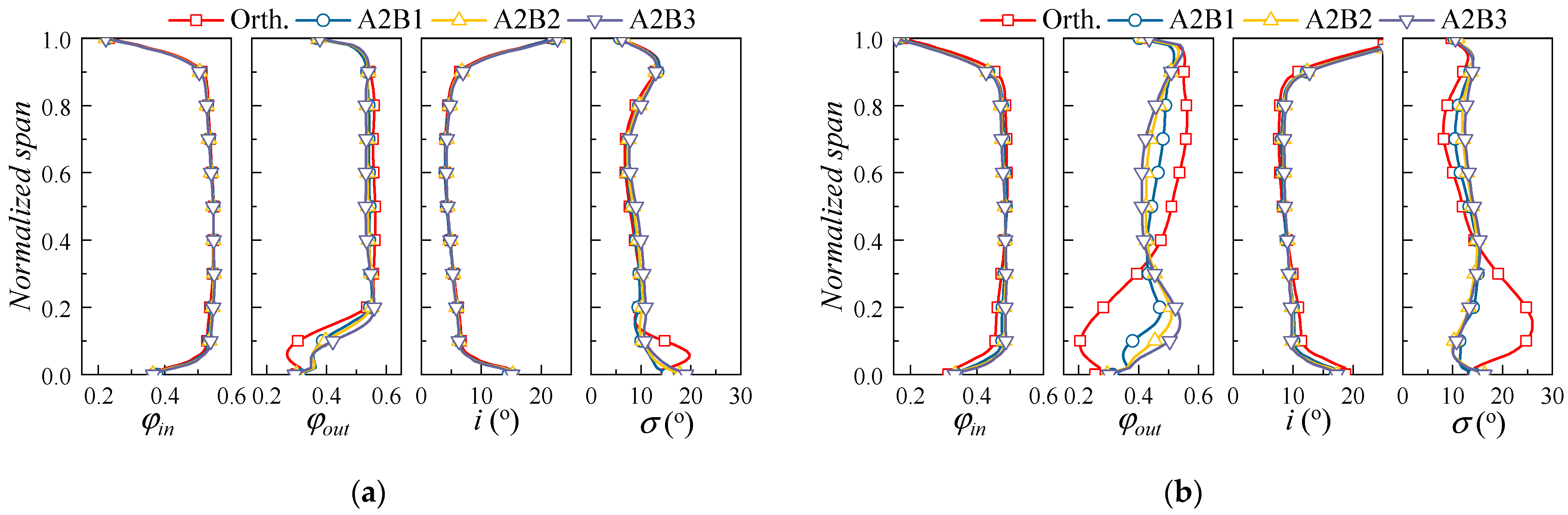
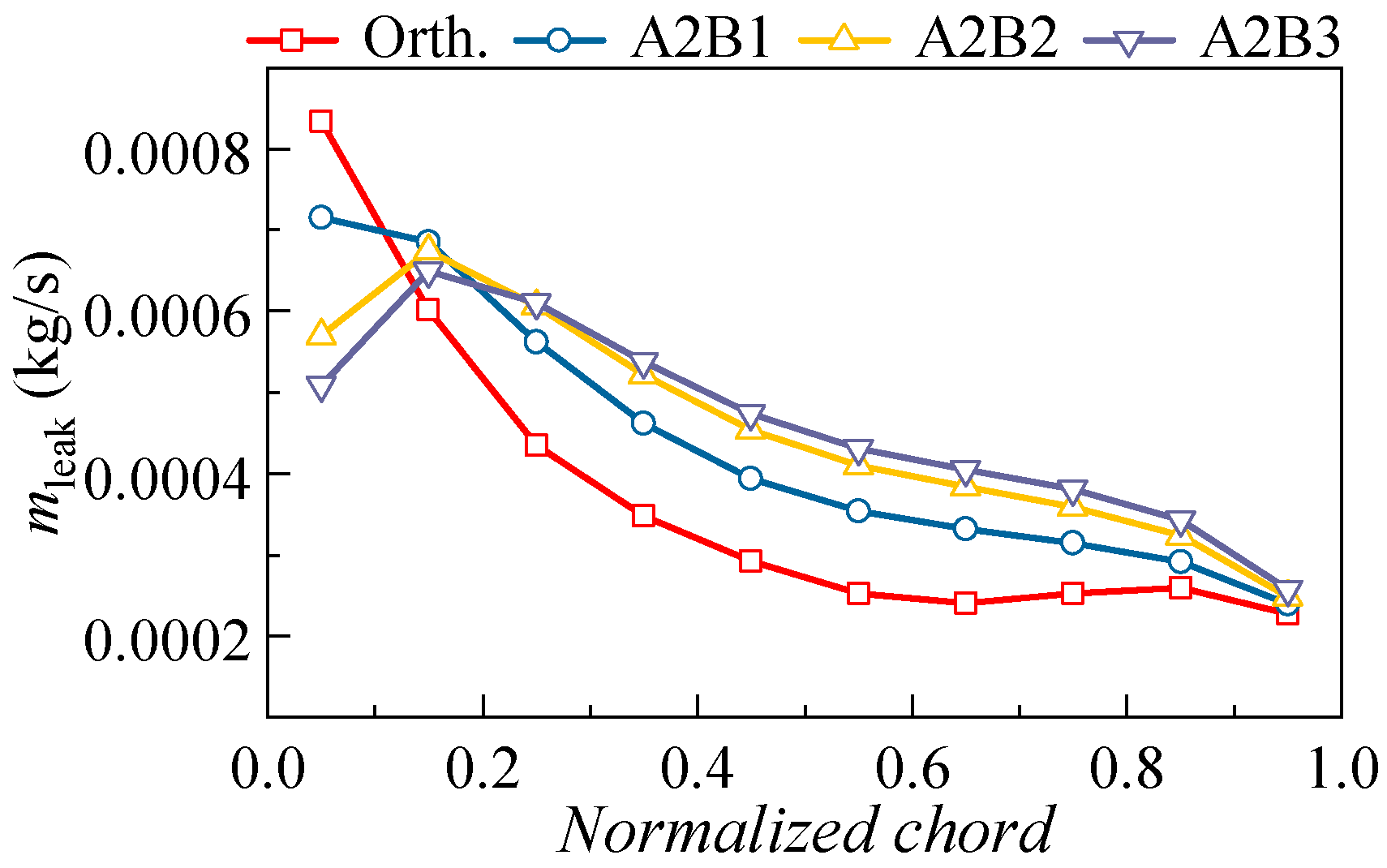
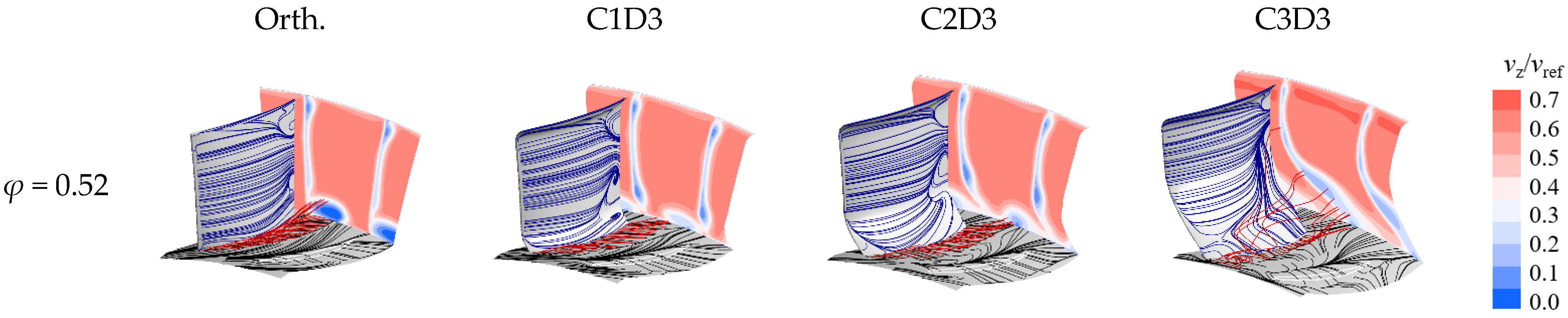
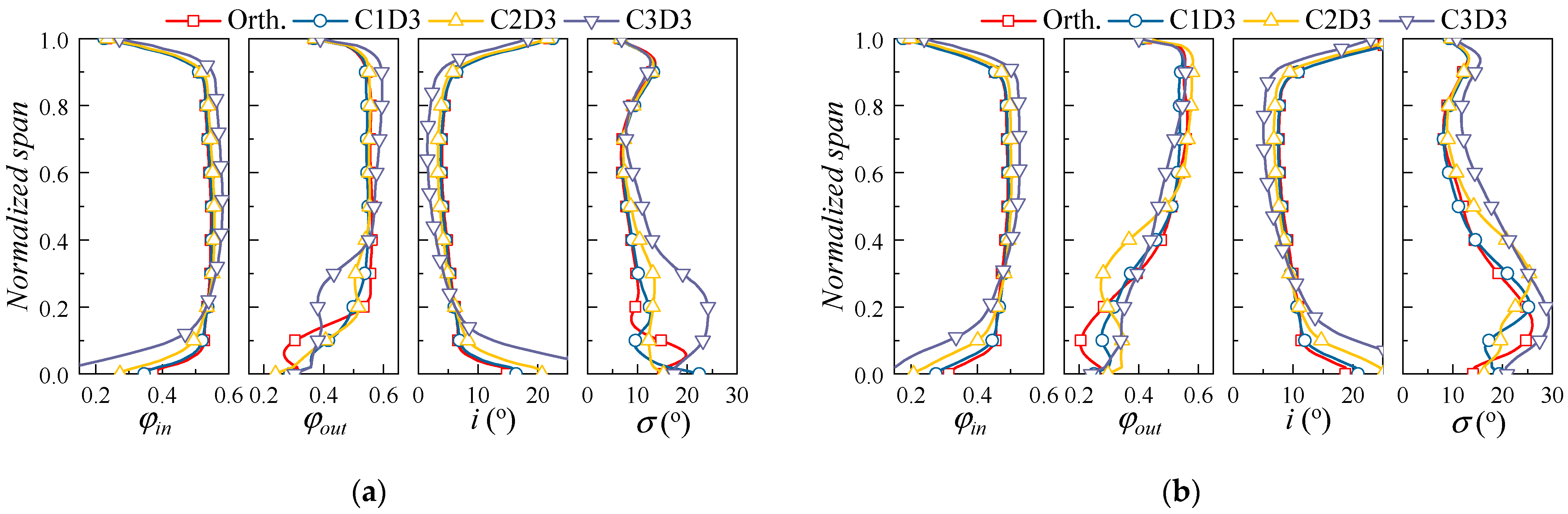
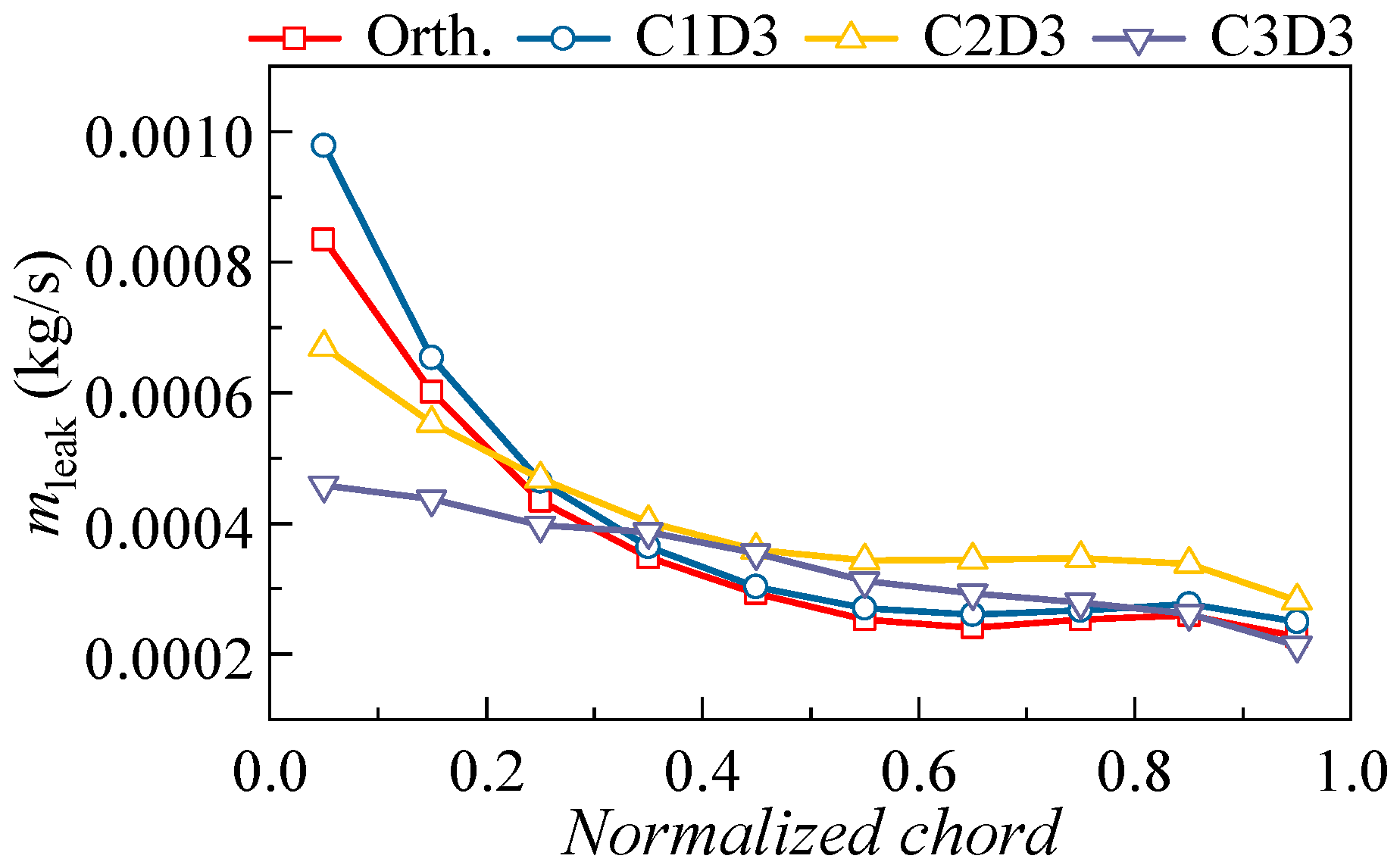
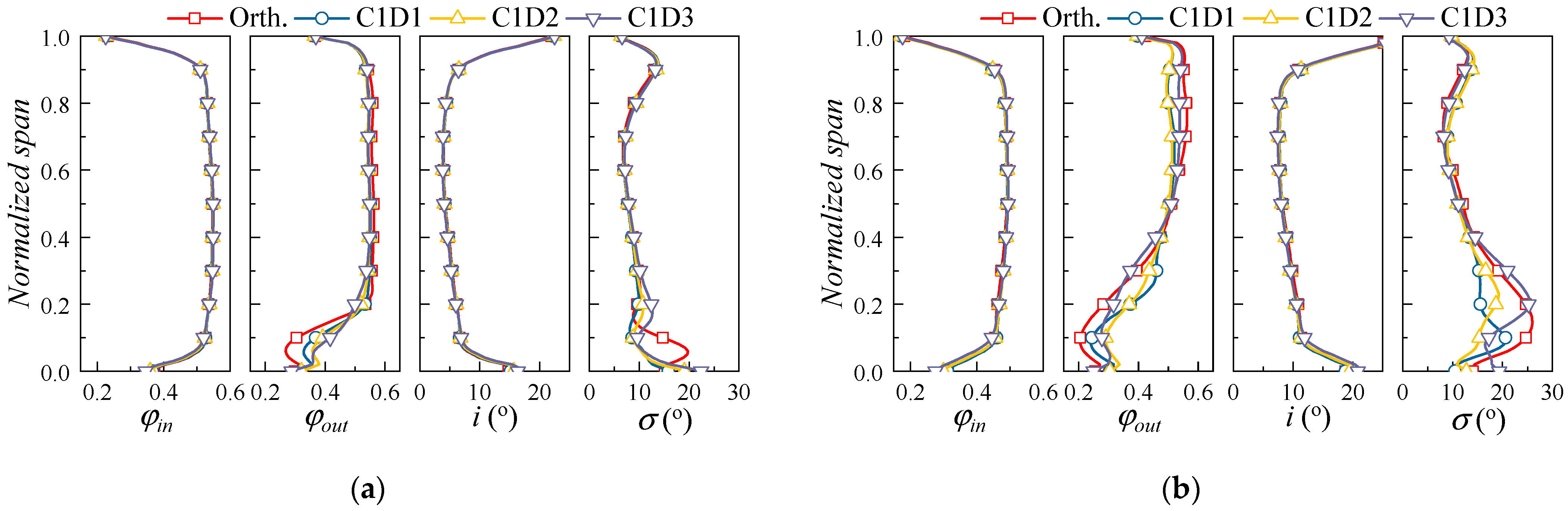
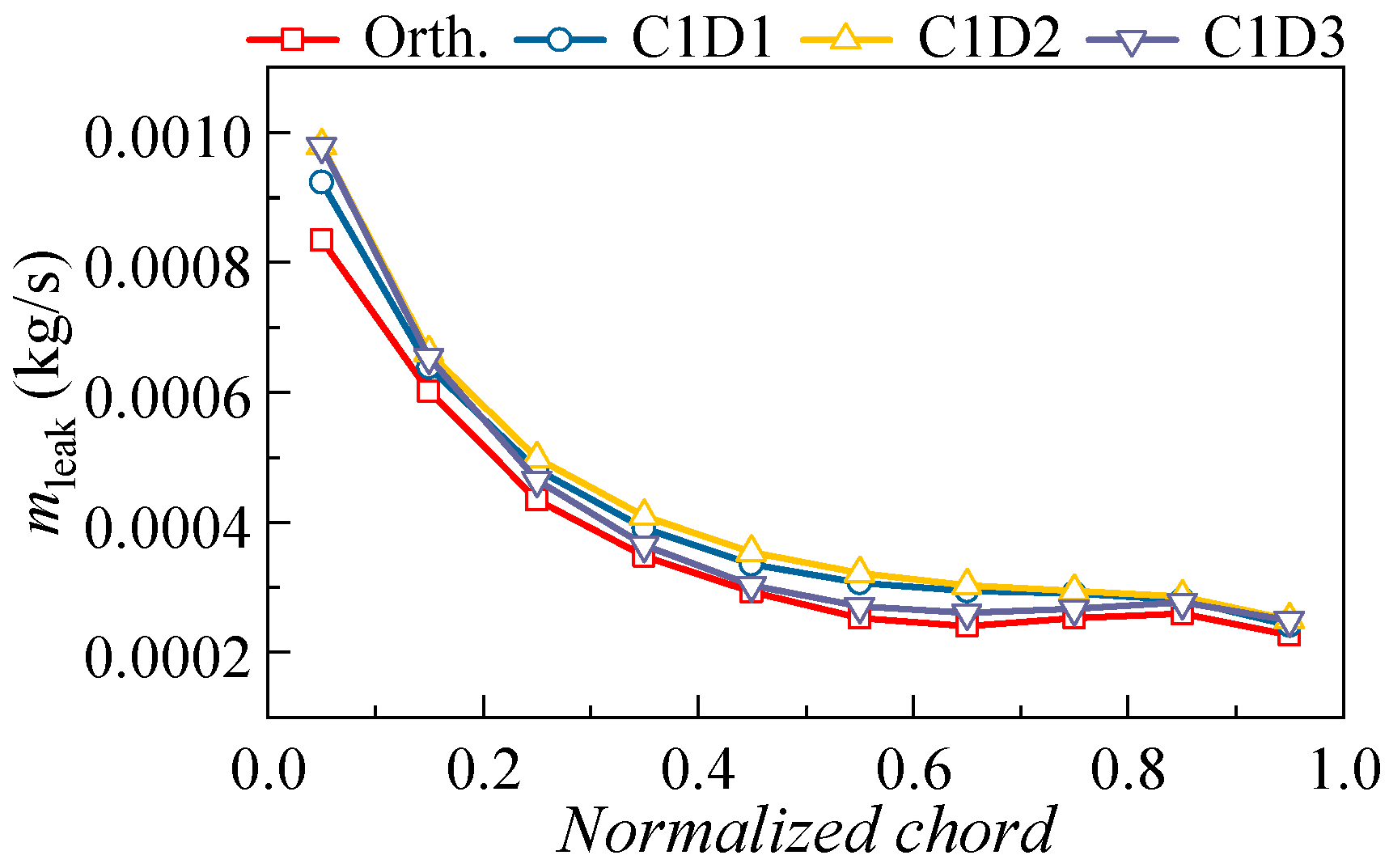
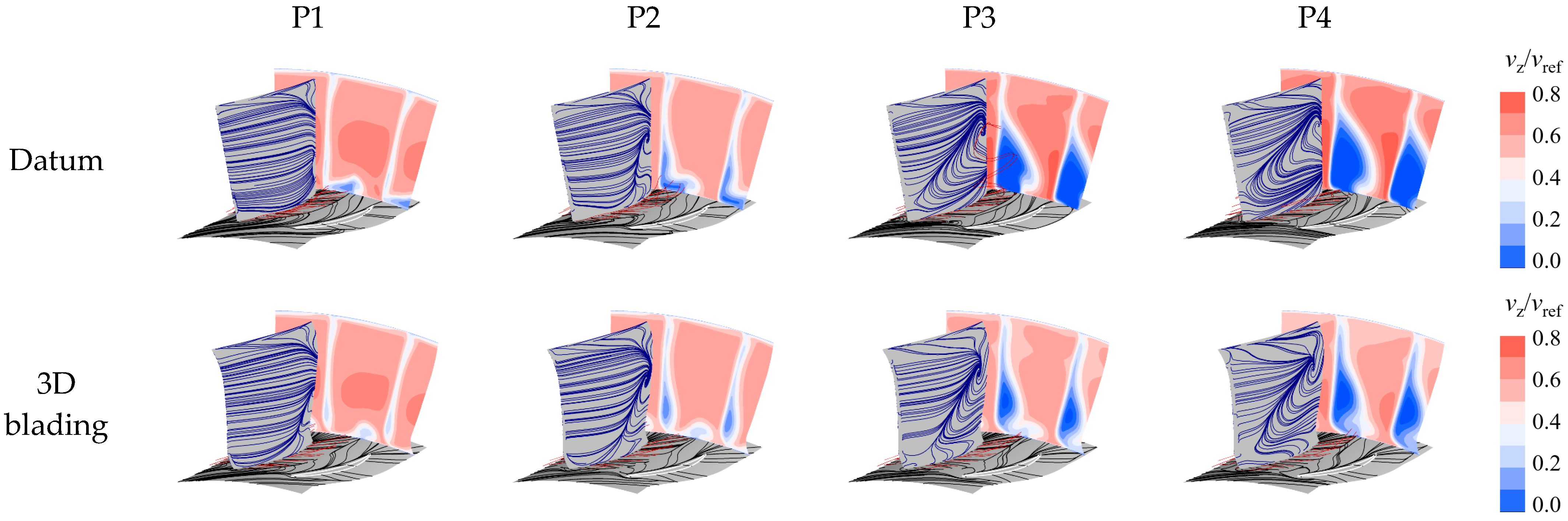
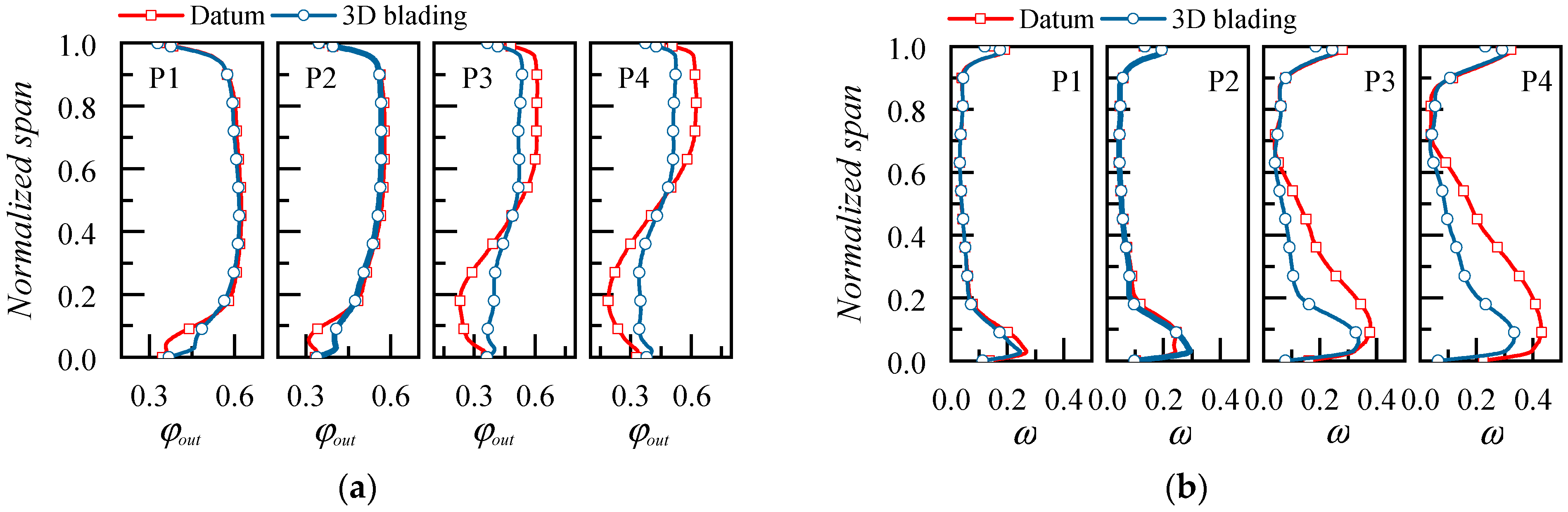
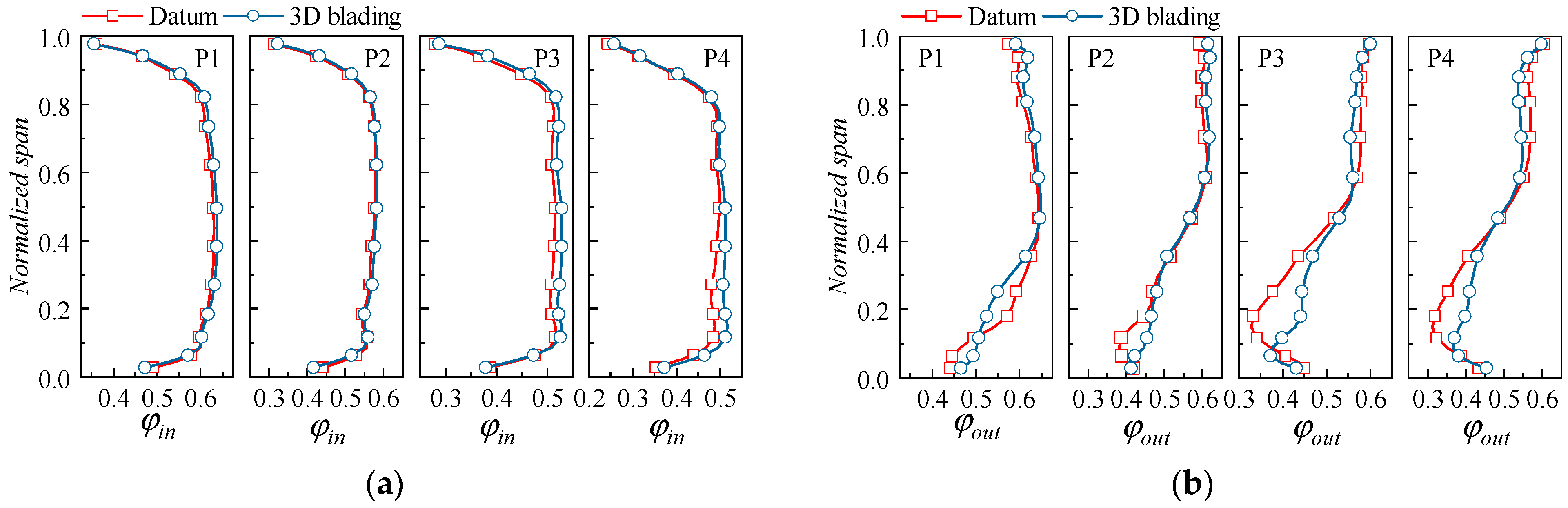
4.2.2. Effect of 3D Blading on the Flow Field Distribution
5. Conclusions
- The forward sweep can inhibit the transverse flow near the hub endwall and alleviate the flow separation at the corner region, while flow separation on the blade suction side was exaggerated slightly. Increasing the sweep height facilitates a uniform separation along the span without changing the endwall flow significantly, whereas excessively large sweep angles lead to a large-scale separation on the blade suction surface and harm the total effect;
- The positive dihedral not only pushes the trajectory of the leakage vortex away from the blade suction surface but also promotes the radial migration of the low-energy fluid at the hub corner. The utilization of large dihedral heights elongates the blade wake and induces the radial transportation of the leakage flow, while the excessive dihedral angle damages the performance at the midspan;
- The compound forward sweep and positive dihedral can combine the advantages of both strategies and provide better aerodynamic performance for the cantilevered stator, the benefit extends over the whole operating range and is more significant at lower mass flow ratios. In comparison to the orthogonal stator, the static pressure rise coefficient and the total pressure loss coefficient of the 3D bladed stator are increased and decreased by 25.5% and 11.1%, respectively;
- The compound sweep and dihedral were utilized to redesign a cantilevered stator in a low-speed compressor test facility. Experimental results demonstrate that the total pressure loss of the 3D cantilevered stator is reduced by 20.5% at the near-stall point, thus proving the effectiveness of the 3D blading technique. The advantage of 3D blading is more pronounced at small mass flow coefficients;
- The performance enhancement of the 3D blading stems mainly from the hub and lower span areas. At large mass flow ratios, the leakage flow leaks into the adjacent blade channel and causes secondary loss, yet at small mass flow rates, the inhibition of the leakage flow to the endwall secondary flow is not strong enough; hence, the corner separation needs further elimination. The design of the 3D cantilevered stator needs to optimize the evolution of corner flow structures over the operating range.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dean, R.C. Secondary Flow in Axial Compressors. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1954. [Google Scholar]
- Lakshminarayana, B. Methods of Predicting the Tip Clearance Effects in Axial Flow Turbomachinery. J. Basic Eng. 1970, 92, 467–480. [Google Scholar] [CrossRef]
- Lakshminarayana, B.; Horlock, J. Tip-Clearance Flow and Losses for an Isolated Compressor Blade; Her Majesty’s Stationery Office: London, UK, 1962. [Google Scholar]
- Lakshminarayana, B.; Horlock, J. Leakage and Secondary Flows in Compressor Cascades; Her Majesty’s Stationery Office: London, UK, 1967. [Google Scholar]
- George, K.K.; Agnimitra Sunkara, S.N.; George, J.T.; Joseph, M.; Pradeep, A.M.; Roy, B. Investigations on Stator Hub End Losses and its Control in an Axial Flow Compressor. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Dusseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Singh, U.K.; Ginder, R.B. The Effect of Hub Leakage Flow in a Transonic Compressor Stator. In Proceedings of the ASME 1998 International Gas Turbine and Aeroengine Congress and Exhibition, Stockholm, Sweden, 2–5 June 1998; p. V001T001A099. [Google Scholar]
- Lee, C.; Song, J.; Lee, S.; Hong, D. Effect of a Gap Between Inner Casing and Stator Blade on Axial Compressor Performance. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; pp. 203–210. [Google Scholar]
- Gbadebo, S.A.; Cumpsty, N.A.; Hynes, T.P. Three-Dimensional Separations in Axial Compressors. J. Turbomach. 2005, 127, 331–339. [Google Scholar] [CrossRef]
- Dong, Y.; Gallimore, S.J.; Hodson, H.P. Three-Dimensional Flows and Loss Reduction in Axial Compressors. J. Turbomach. 1987, 109, 354–361. [Google Scholar] [CrossRef]
- Wennerstrom, A.J. Experimental Study of a High-Throughflow Transonic Axial Compressor Stage. J. Eng. Gas Turbines Power 1984, 106, 552–560. [Google Scholar] [CrossRef]
- McDougall, N. A Comparison Between the Design Point and Near-Stall Performance of an Axial Compressor. J. Turbomach. 1990, 112, 109–115. [Google Scholar] [CrossRef]
- An, G.; Fan, Z.; Qiu, Y.; Wang, R.; Yu, X.; Liu, B. Numerical Investigation of the Effect of Hub Gaps on the 3D Flows Inside the Stator of a Highly Loaded Axial Compressor Stage. Energies 2022, 15, 6993. [Google Scholar] [CrossRef]
- Gbadebo, S.A.; Cumpsty, N.A.; Hynes, T.P. Interaction of Tip Clearance Flow and Three-Dimensional Separations in Axial Compressors. J. Turbomach. 2007, 129, 679–685. [Google Scholar] [CrossRef]
- Singh Tanwar, B.P.; Singh, A.; Mistry, C.S. Numerical Investigations on Application of Cantilever Stator on Aerodynamic Performance of Tandem Bladed Axial-Flow Compressor. In Proceedings of the ASME Turbo Expo 2021: Turbomachinery Technical Conference and Exposition, Online, 7–11 June 2021. [Google Scholar]
- Horlock, J.H.; Louis, J.F.; Percival, P.M.E.; Lakshminarayana, B. Wall Stall in Compressor Cascades. J. Basic Eng. 1966, 88, 637–648. [Google Scholar] [CrossRef]
- Peacock, R.E. A review of turbomachinery tip gap effects: Part 1: Cascades. Int. J. Heat Fluid Flow 1982, 3, 185–193. [Google Scholar] [CrossRef]
- Peacock, R.E. A review of turbomachinery tip gap effects: Part 2: Rotating machinery. Int. J. Heat Fluid Flow 1983, 4, 3–16. [Google Scholar] [CrossRef]
- Tweedt, D.L.; Okiishi, T.H.; Hathaway, M.D. Stator Endwall Leading-Edge Sweep and Hub Shroud Influence on Compressor Performance. J. Turbomach. 1986, 108, 224–232. [Google Scholar] [CrossRef]
- Storer, J.A.; Cumpsty, N.A. Tip Leakage Flow in Axial Compressors. J. Turbomach. 1991, 113, 252–259. [Google Scholar] [CrossRef]
- Yamaguchi, N.; Tominaga, T.; Hattori, S.; Mitsuhashi, T. IGTC-8 Secondary-loss reduction by forward-skewing of axial compressor rotor blading. In Proceedings of the 1991 Yokohama International Gas turbine Congress, Yokohama, Japan, 27 October–1 November 1991; pp. 61–68. [Google Scholar]
- Breugelmans, F.; Carels, Y.; Demuth, M.N. Influence Of Dihedral on the Secondary Flow in a Two-Dimensional Compressor Cascade. J. Eng. Gas Turbines Power 1984, 106, 578–584. [Google Scholar] [CrossRef]
- Weingold, H.D.; Neubert, R.J.; Behlke, R.F.; Potter, G.E. Bowed Stators: An Example of CFD Applied to Improve Multistage Compressor Efficiency. J. Turbomach. 1997, 119, 161–168. [Google Scholar] [CrossRef]
- Sasaki, T.; Breugelmans, F. Comparison of Sweep and Dihedral Effects on Compressor Cascade Performance. J. Turbomach. 1998, 120, 454–463. [Google Scholar] [CrossRef]
- Vad, J. Aerodynamic effects of blade sweep and skew in low-speed axial flow rotors at the design flow rate: An overview. Proc. Inst. Mech. Eng. 2008, 222, 69–85. [Google Scholar] [CrossRef]
- Xu, P.; Yu, X.; Liu, B. The Effects of Blade 3D Designs in Different Orthogonal Coordinates on the Performance of Compressor Cascades. Int. J. Turbo Jet-Engines 2014, 31, 329–345. [Google Scholar] [CrossRef]
- Lange, M.; Vogeler, K.; Mailach, R.; Gomez, S.E. An experimental verification of a new design for cantilevered stators with large hub clearances. J. Turbomach. 2013, 135, 041022. [Google Scholar] [CrossRef]
- Lu, H.; Li, Q.; Pan, T. Using forward end-sweep to reduce transonic cantilevered stator losses to improve compressor performance. Eng. Appl. Comput. Fluid Mech. 2018, 12, 293–307. [Google Scholar] [CrossRef]
- Gunn, E.J.; Hall, C.A. Nonaxisymmetric Stator Design for Boundary Layer Ingesting Fans. J. Turbomach. 2019, 141, 071010. [Google Scholar] [CrossRef]
- Gallimore, S.J.; Bolger, J.J.; Cumpsty, N.A.; Taylor, M.J.; Wright, P.I.; Place, J.M.M. The Use of Sweep and Dihedral in Multistage Axial Flow Compressor Blading—Part I: University Research and Methods Development. J. Turbomach. 2002, 124, 521–532. [Google Scholar] [CrossRef]
- Pullan, G.; Harvey, N.W. Influence of Sweep on Axial Flow Turbine Aerodynamics at Midspan. J. Turbomach. 2007, 129, 591–598. [Google Scholar] [CrossRef]
- An, G. Studies of the Unsteady Flow Behaviors for the Tip Leakage Flow and the Modeling of the Flow Blockage and Loss. Ph.D. Thesis, Beihang University, Beijing, China, 2016. [Google Scholar]
- Fu, D. Theoretical and Experimental Study on the Highly Loaded Compressor with Tandem Blades. Ph.D. Thesis, Beihang University, Beijing, China, 2019. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Liu, B.; An, G.; Yu, X. Assessment of curvature correction and reattachment modification into the shear stress transport model within the subsonic axial compressor simulations. Proc. Inst. Mech. Eng. 2015, 229, 910–927. [Google Scholar] [CrossRef]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Liu, B.; Qiu, Y.; An, G.; Yu, X. Utilization of Zonal Method for Five-Hole Probe Measurements of Complex Axial Compressor Flows. J. Fluids Eng. 2020, 142, 061504. [Google Scholar] [CrossRef]
- Liu, B.; Qiu, Y.; An, G.; Yu, X. Experimental Investigation of the Flow Mechanisms and the Performance Change of a Highly Loaded Axial Compressor Stage with/without Stator Hub Clearance. Appl. Sci. 2019, 9, 5134. [Google Scholar] [CrossRef]
- Lei, V.M.; Spakovszky, Z.S.; Greitzer, E.M. A Criterion for Axial Compressor Hub-Corner Stall. J. Turbomach. 2008, 130, 031006. [Google Scholar] [CrossRef]
- Taylor, J.V.; Miller, R.J. Competing Three-Dimensional Mechanisms in Compressor Flows. J. Turbomach. 2016, 139, 021009. [Google Scholar] [CrossRef]






| Parameter Type | 1 | 2 | 3 |
|---|---|---|---|
| A: Sweep height | 30% span | 60% span | 70% span |
| B: Sweep angle | 120° | 135° | 150° |
| Parameter Type | 1 | 2 | 3 |
|---|---|---|---|
| C: Dihedral height | 20% span | 40% span | 60% span |
| D: Dihedral angle | 120° | 135° | 150° |
| Hub | Midspan | Tip | |
|---|---|---|---|
| Diffusion factor (-) | 0.58 | 0.33 | 0.35 |
| Incidence (°) | 8 | 1 | 0 |
| Solidity (-) | 1.75 | 1.6 | 1.5 |
| Stagger angle (°) | 18 | 22 | 25 |
| Turning angle (°) | 49 | 45 | 42 |
| Hub-tip ratio (-) | 0.75 | ||
| Aspect ratio (-) | 1 | ||
| Hub clearance (% span) | 1% | ||
| Blade profile type | CDA | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Wang, R.; Yu, X.; An, G.; Qiu, Y.; Liu, B. Toward the Utilization of 3D Blading in the Cantilevered Stator from Highly Loaded Compressors. Appl. Sci. 2023, 13, 3335. https://doi.org/10.3390/app13053335
Xu X, Wang R, Yu X, An G, Qiu Y, Liu B. Toward the Utilization of 3D Blading in the Cantilevered Stator from Highly Loaded Compressors. Applied Sciences. 2023; 13(5):3335. https://doi.org/10.3390/app13053335
Chicago/Turabian StyleXu, Xiaobin, Ruoyu Wang, Xianjun Yu, Guangfeng An, Ying Qiu, and Baojie Liu. 2023. "Toward the Utilization of 3D Blading in the Cantilevered Stator from Highly Loaded Compressors" Applied Sciences 13, no. 5: 3335. https://doi.org/10.3390/app13053335
APA StyleXu, X., Wang, R., Yu, X., An, G., Qiu, Y., & Liu, B. (2023). Toward the Utilization of 3D Blading in the Cantilevered Stator from Highly Loaded Compressors. Applied Sciences, 13(5), 3335. https://doi.org/10.3390/app13053335






