Effectiveness of High-Damping Rubber (HDR) Damper and Tuned Mass—HDR Damper in Suppressing Stay-Cable Vibration

Abstract

High-damping rubber (HDR) dampers have the advantages of convenience for various shapes of pressure blocks, aesthetic installation, easy maintenance, temperature stability, etc.; thus, they present good application prospects in the vibration reduction of stay cables. Hence, a model of a taut cable equipped with two types of HDR damper—i.e., HDR damper and tuned mass–high-damping rubber damper (TM-HDR-D)—is established herein. Then, based on this theoretical model, the effect of each damper acting alone and in combination on the cable’s additional modal damping is studied. Finally, an actual cable of a cable-stayed bridge is used to study the effectiveness of two dampers for practical engineering. The results show that, when the TM-HDR-D has a small mass, the total additional modal damping of the cable approximates the superposition of the respective effects of the two dampers. The damping effect of HDR mainly depends on its stiffness and installation position; meanwhile, the damping contribution of TM-HDR-D is mainly related to its tuning frequency and installation position. In practical engineering, the smaller installation mass of TM-HDR-D can make up for the lack of damping enhancement of the cable-end HDR damper.

1. Introduction

In recent years, with the construction of a large number of high-rise buildings and long-span bridges, the civil engineering structure has become more flexible, and the structural vibration problem has become more prominent [1,2,3]. Cable-stayed bridges and other cable-supported bridges use a large number of cables as force transmission components [1]. However, cables, as lightweight, high-transverse-flexibility, and low-intrinsic-damping structural components [3], are prone to vibrations induced by environmental disturbances, such as wind, rain, live load, etc. [4,5,6,7]. Long-term large-amplitude vibration may lead to local fatigue damage of cables and can even affect the safety of the whole bridge. To reduce cable vibrations, there are many countermeasures that have been used in practical engineering, such as attaching dampers between cables and the bridge deck or tower, or installing cross-ties between adjacent cables, among others [8,9,10,11,12,13]. In terms of current practical engineering applications, installing dampers is the most widely used measure worldwide [10,11].

Dampers installed on the cable can enhance the cable system’s modal damping and, thus, suppress various types of vibration of the cable. Several different kinds of mechanical dampers have been successfully used in practice—for example, oil dampers were used in the Sutong Bridge [11] and the Fred Hartman Bridge [14]; viscous-shear dampers were used in the Sutong Bridge [11]; magnetorheological dampers were successfully installed on Dongting Lake Bridge [15] and Binzhou Yellow River Bridge [16]; friction dampers were also used in Uddevalla Bridge [17]; and high-damping rubber (HDR) dampers were applied in the Tatara Bridge [18]. Among them, viscous dampers and viscous-shear dampers are the most commonly used cable dampers. However, in practice, these two types of dampers also have oil leakage problems, especially for the viscous dampers [19]. Moreover, the cable modal damping obtained from viscous-shear dampers is heavily dependent on the ambient temperature and vibration frequency; for this reason, this type of damper is mostly used for suppressing vibrations of short cables. The friction damper is insensitive to the micro-amplitude vibration of the cable owing to the large static friction force [20], and the MR damper requires long-term power supply and regular maintenance [21].

Today, with the development of material science, HDR dampers have become a kind of damper with bright application prospects, because the HDR damper has no liquid leakage problem and has a long service life. Cables with HDR damper systems have been studied in many papers. Nakamura et al. [22] explored the damping characteristics of HDR dampers and verified their good damping performance via testing. To maximize the cable’s modal damping, Yoneda et al. [23] devised an empirical formula for optimizing the HDR damper parameters. Nakamura et al. [22] proposed a numerical method to study the cable–HDR damper system. Fujino and Hoang established a sagged cable–HDR damper system model by taking the flexibility of damper support into account and derived asymptotic formulae for the cable’s modal damping [24]. In previous studies, the damping contributed to the cable by the damper was related to its installation height. With the increase in cable length, it is difficult for a single damper to provide sufficient damping, because the damper can only be installed near the cable’s end. Hoang and Fujino [25] studied the combined damping effect of a cable equipped with two dampers—i.e., a viscous damper and a HDR damper—installed near the two ends of the cable. A taut cable with two HDR dampers was investigated by Cu et al. [26]. Di et al. [27] studied the combined damping effect of a viscous damper and an HDR damper installed on a shallow cable through theoretical and experimental methods. To mitigate the cable’s high-mode vortex-induced vibration, Di et al. [28] proposed the vibration reduction measures of installing double dampers (i.e., HDR damper and viscous damper) on the cable and carried out research on the system. Recently, Nguyen et al. [29] established a cable–two-HDR-damper system model by considering the cable’s bending stiffness, and they analyzed the combined influence of two HDR dampers on the cable’s first modal damping ratio. Compared with the damper installed on the cable end with support, tuned mass dampers (TMDs) or similar unsupported absorbers have better application prospects. Cu and Han [30] investigated a system of a taut cable with two dampers, i.e., a viscous damper and a TMD, and they found that using two dampers on the cable can improve the modal damping of the cable system, compared with using only one of the dampers.

Existing studies show that, for long cables, a single cable-end damper may no longer be able to provide enough modal damping for cable vibration control. In addition, there are also vibration-prone modes with lower damping, such as the first mode due to the influence of sag [31]. Therefore, a cable with more dampers at different positions is a feasible solution to improve the cable’s multimode damping. At the same time, the tuned mass–high-damping rubber damper (TM-HDR-D), as a TMD-type device, provides a great effect in cable vibration reduction. The damping of this type of TMD device is provided by high-damping rubber; the damper does not have problems such as oil leakage, making it especially suitable for practical engineering. To study the combined control effect of the two dampers on the vibration of the cable, the model of a cable with an HDR damper and a TM-HDR-D system is first established in this paper. Then, based on typical systems—i.e., a cable with only an HDR damper, a cable with only a TM-HDR-D, and a cable with two dampers—the cable vibration reduction analysis is carried out. Based on an actual cable of a real-world cable-stayed bridge, the parameter design process of the HDR damper and TM-HDR-D is presented, and the practical feasibility of the combined vibration reduction measures of the two dampers is verified.

2. Formulation of the Cable—HDR Damper—TM-HDR-D System

A taut cable with an HDR damper and a TM-HDR-D is depicted in Figure 1. The cable length is denoted by $L$, the cable mass per unit length is denoted by $m$, and the cable tension is denoted by $T$. $K_1$ indicates the HDR damper’s stiffness, and $\phi$ denotes the HDR damper’s loss factor. For the TM-HDR-D, $K_2$, $\phi$, and $M$ denote its stiffness, loss factor, and mass, respectively. The coordinate system is defined as shown in Figure 1, where the position coordinate axis x starts from the left cable end and points horizontally to the right end of the cable, and the direction of the $x^{*}$ axis is opposite to the $x$ axis; v(x, t) and $u_{\mathrm{tmd}}$ are the vertical dynamic displacement of the cable and the mass of the TM-HDR-D, respectively. The HDR damper and TM-HDR-D are at locations $x_1$ and $x_2$, respectively, and $x_2^{*}=L-x_2$. The cable sag, bending stiffness, and inherent damping are not considered in the model, due to their influence being so small that they can be ignored [32].

The motion equation of the cable damper system can be given by the following formula [32]:

$$T\frac{{\partial }^{2}v}{\partial x^2}-m\frac{{\partial }^{2}v}{\partial t^2}=f_{\mathrm{hdr}}\left(t\right)\delta \left(x-x_1\right)+f_{\mathrm{tmd}}\left(t\right)\delta \left(x-x_2\right)$$

(1)

where $\delta \left(·\right)$ denotes the delta function—that is, the two concentrated damping forces provided by the dampers acting on the cable, where $f_{\mathrm{hdr}}\left(t\right)$ located at $x=x_1$ and $f_{\mathrm{tmd}}\left(t\right)$ located at $x=x_2$.

Considering the free vibration of the cable system, the transverse displacement of the cable and the damping forces of two dampers have the following expressions:

$$v\left(x,t\right)=\tilde{v}\left(x\right)e^{\mathrm{i}\omega t}, f_{\mathrm{hdr}}\left(t\right)={\tilde{f}}_{\mathrm{hdr}}{e}^{\mathrm{i}\omega t} \mathrm{and} f_{\mathrm{tmd}}\left(t\right)={\tilde{f}}_{\mathrm{tmd}}{e}^{\mathrm{i}\omega t}$$

(2)

where $\mathrm{i}=\sqrt{-1}$, $\mathsf{\omega }$ denotes the cable’s complex angular frequency, and $\tilde{v},{\widetilde{ f}}_{\mathrm{hdr}}, \mathrm{and} {\tilde{f}}_{\mathrm{tmd}}$ denote the amplitude of the corresponding time-dependent variables. For a cable with two dampers, the cable displacement $\tilde{v}$ can be written as follows [25]:

$$\tilde{v}\left(x\right)=\{\begin{array}{c}{\tilde{v}}_{\mathrm{hdr}}\frac{\sin \left(\beta x\right)}{\sin \left(\beta x_1\right)}, 0\le x\le x_1\\ {\tilde{v}}_{\mathrm{hdr}}\frac{\sin \left[\beta \left(x_2-x\right)\right]}{\sin \left[\beta \left(x_2-x_1\right)\right]}+{\tilde{v}}_{\mathrm{tmd}}\frac{\sin \left[\beta \left(x-x_1\right)\right]}{\sin \left[\beta \left(x_2-x_1\right)\right]}, x_1\le x\le x_2\\ {\tilde{v}}_{\mathrm{tmd}}\frac{\sin \left(\beta x_2^{*}\right)}{\sin \left(\beta x^{*}\right)}, 0\le x^{*}\le x_2^{*}\end{array}$$

(3)

where $\beta =\omega \sqrt{m/T}$ = the complex wavenumber; ${\tilde{v}}_{\mathrm{hdr}}$ and ${\tilde{v}}_{\mathrm{tmd}}$ denote the cable amplitude at the HDR damper and the TM-HDR-D installation points, respectively. According to the vertical force equilibrium condition at the damper installation position, one finds

$$T\left(\frac{\partial v}{\partial x}|x_j^{+}-\frac{\partial v}{\partial x}|x_j^{-}\right)=f_j\left(t\right), j=1,2$$

(4)

Note that $f_1\left(t\right)=f_{\mathrm{hdr}}\left(t\right)$ and $f_2\left(t\right)=f_{\mathrm{tmd}}\left(t\right)$.

Then, substituting Equation (3) into Equation (4), one obtains

$$\{\begin{array}{c}\cot \left(\beta x_1\right)+\cot \left[\beta \left(x_2-x_1\right)\right]-\frac{{\tilde{v}}_{\mathrm{tmd}}}{{\tilde{v}}_{\mathrm{hdr}}}\frac{1}{\sin \left[\beta \left(x_2-x_1\right)\right]}=-\frac{{\tilde{f}}_{\mathrm{hdr}}/T}{\beta {\tilde{v}}_{\mathrm{hdr}}}\\ -\frac{{\tilde{v}}_{\mathrm{hdr}}}{{\tilde{v}}_{\mathrm{tmd}}}\frac{1}{\sin \left[\beta \left(x_2-x_1\right)\right]}+\cot \left[\beta \left(x_2-x_1\right)\right]+\cot \left(\beta x_2^{*}\right)=-\frac{{\tilde{f}}_{\mathrm{tmd}}/T}{\beta {\tilde{v}}_{\mathrm{tmd}}}\end{array}$$

(5)

where

$${\tilde{f}}_{\mathrm{hdr}}=K_1\left(1+\mathrm{i}\phi \right){\tilde{v}}_{\mathrm{hdr}}, {\tilde{f}}_{\mathrm{tmd}}=K_2\left(1+\mathrm{i}\phi \right)\left({\tilde{v}}_{\mathrm{tmd}}-{\tilde{u}}_{\mathrm{tmd}}\right)$$

(6)

The equilibrium equation of the TM-HDR-D has the following expression:

$$K_2\left(1+\mathrm{i}\phi \right)\left({\tilde{v}}_{\mathrm{tmd}}-{\tilde{u}}_{\mathrm{tmd}}\right)+{\omega }^{2}M{\tilde{u}}_{\mathrm{tmd}}=0$$

(7)

Let $\alpha ={\tilde{u}}_{\mathrm{tmd}}/{\tilde{v}}_{\mathrm{tmd}}$; ${\omega }_{\mathrm{tmd}}$ denotes the circular angular frequency of the TM-HDR-D, and ${\omega }_{\mathrm{tmd}}=\sqrt{K_2/M}$. Let $\rho ={\omega }_1^0/{\omega }_{\mathrm{tmd}}$; $s=\omega /{\omega }_1^0$, where ${\omega }_1^0$ is the cable’s fundamental circular frequency. Then, using Equation (7), we can derive $\alpha$ as follows:

$$\alpha =\frac{1+\mathrm{i}\phi }{1+\mathrm{i}\phi -{\rho }^2{s}^2}$$

(8)

Then, the damping force of the TM-HDR-D is rewritten as follows:

$${\tilde{f}}_{\mathrm{tmd}}=-\alpha {\omega }^{2}M{\tilde{v}}_{\mathrm{tmd}}$$

(9)

The characteristic equation of the cable system can be obtained by using Equation (5), as follows:

$$\left[\cot \left(\beta x_1\right)+\frac{{\tilde{f}}_{\mathrm{hdr}}}{T\beta {\tilde{v}}_{\mathrm{hdr}}}\right]\left[\cot \left(\beta x_2^{*}\right)+\frac{{\tilde{f}}_{\mathrm{tmd}}}{T\beta {\tilde{v}}_{\mathrm{tmd}}}\right]+\left[\cot \left(\beta x_1\right)+\frac{{\tilde{f}}_{\mathrm{hdr}}}{T\beta {\tilde{v}}_{\mathrm{hdr}}}+\cot \left(\beta x_2^{*}\right)+\frac{{\tilde{f}}_{\mathrm{tmd}}}{T\beta {\tilde{v}}_{\mathrm{tmd}}}\right]\cot \left[\beta \left(x_2-x_1\right)\right]=1$$

(10)

Some dimensionless parameters are defined as follows:

$${\overline{K}}_1=\frac{K_{1}L}{T},\mu =\frac{M}{mL}$$

(11)

The complex wavenumber can be obtained by numerically solving Equation (10). Finally, the formula of the cable’s modal damping ratio is as follows [32]:

$${\zeta }_n=\frac{\mathrm{Im}\left({\beta }_n\right)}{\left|{\beta }_n\right|}, n=1,2,\cdots$$

(12)

3. Numerical Parametric Study

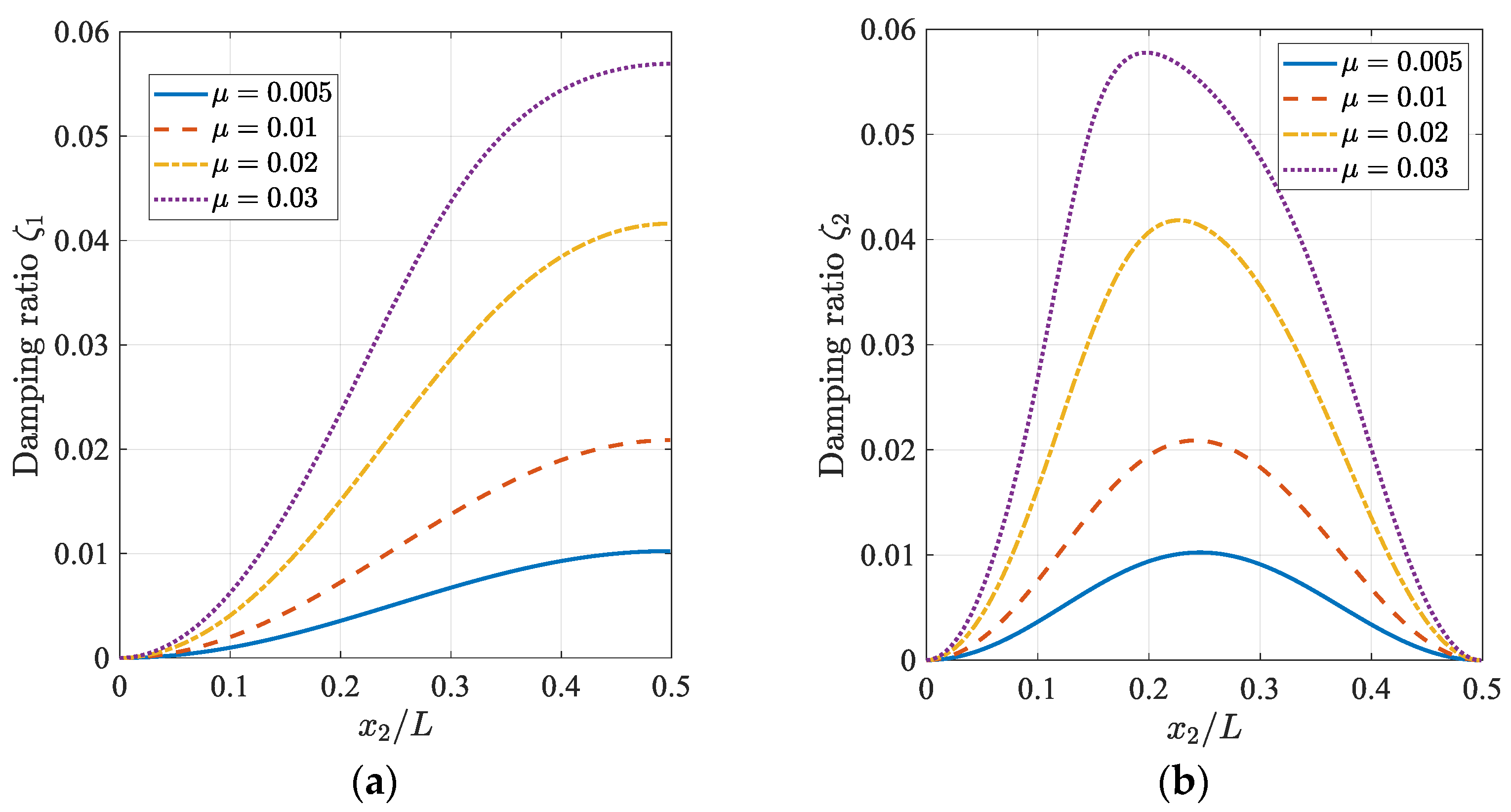
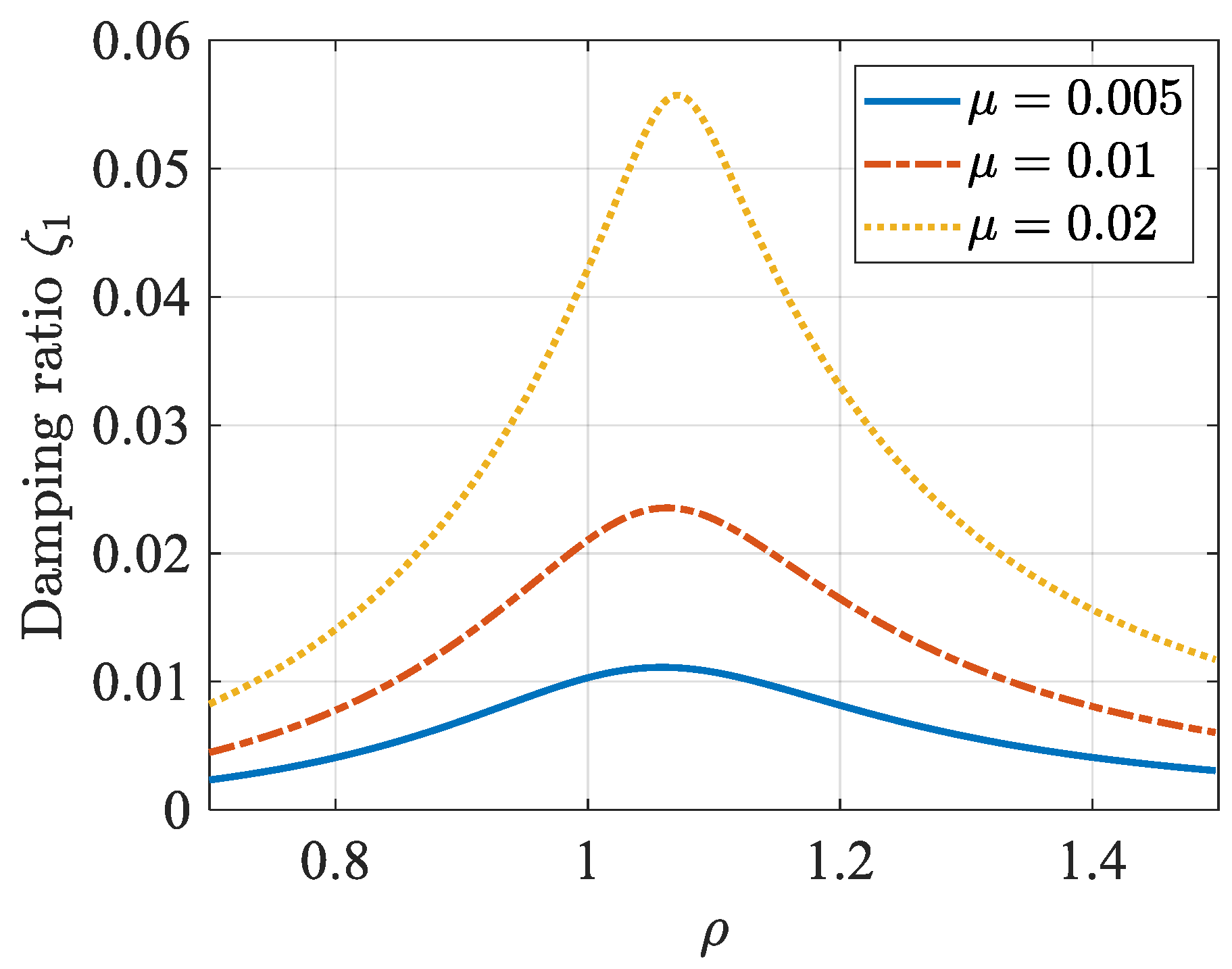
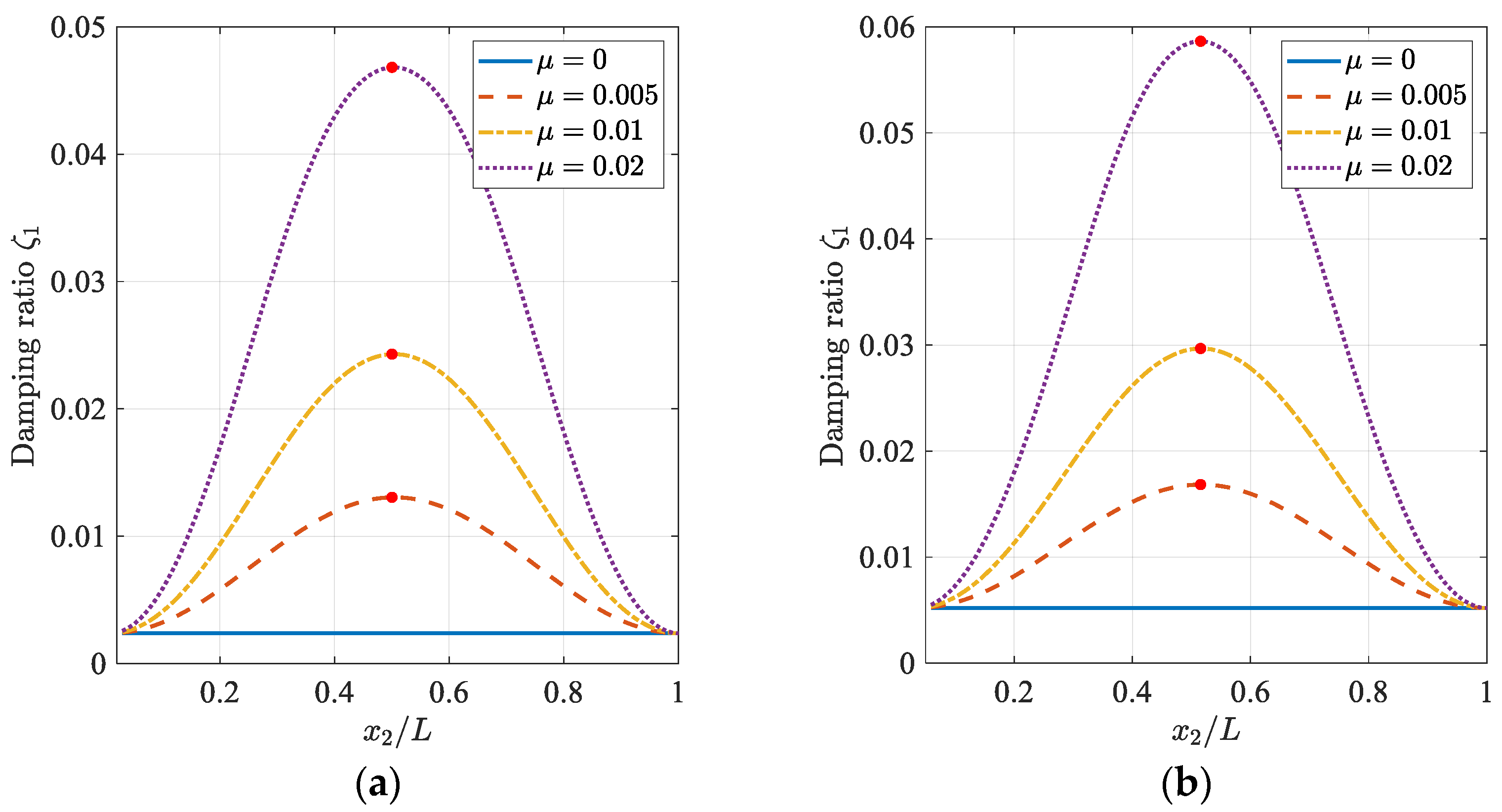
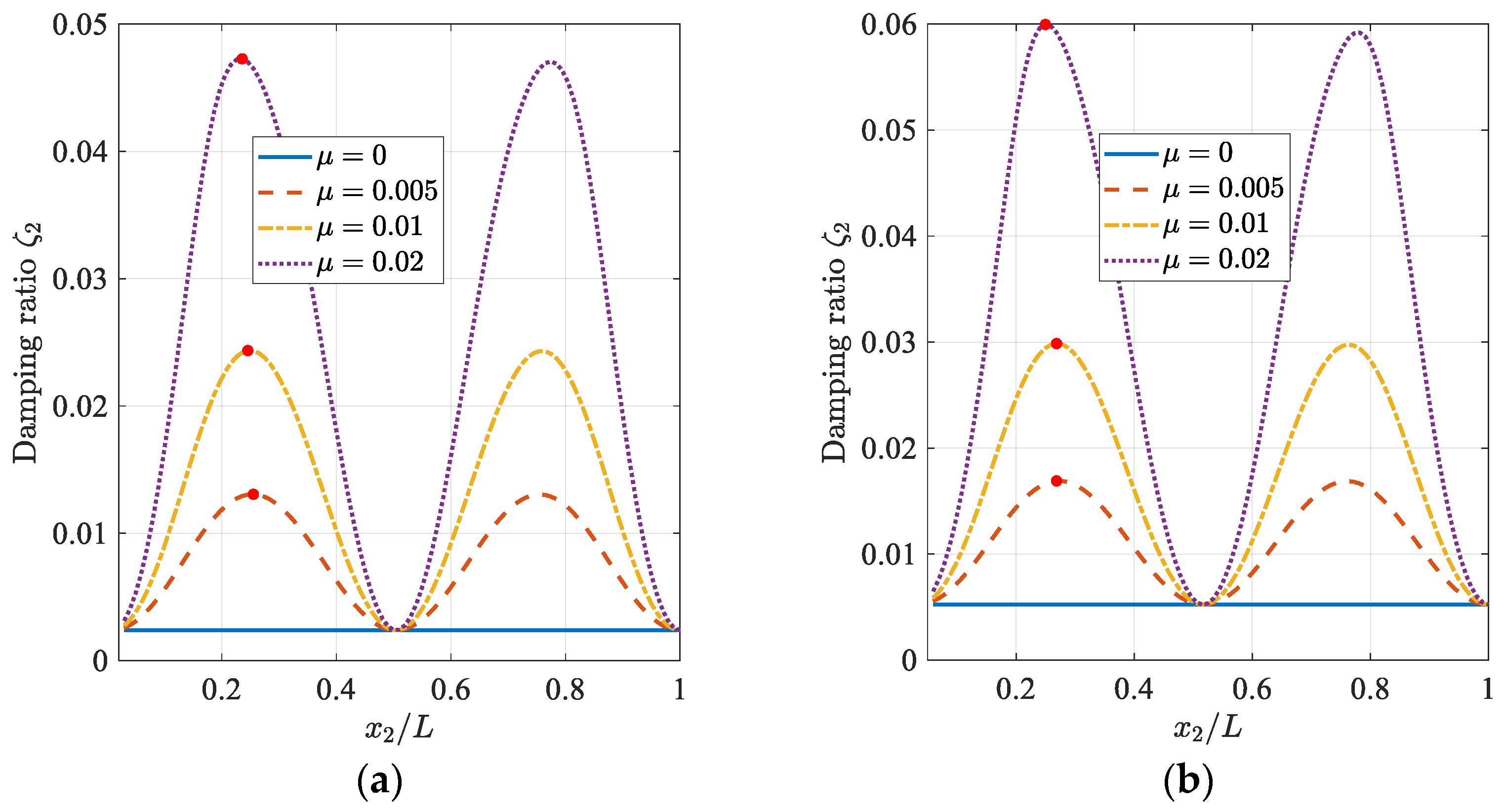
3.1. Cable with a Single HDR Damper

When the cable has a single HDR damper attached, the characteristic Equation (10) can be simplified to

$$\sin \left(\beta L\right)+\sin \left(\beta x_1\right)\sin \beta \left(L-x_1\right)\frac{{\overline{K}}_1\left(1+\mathrm{i}\phi \right)}{\beta L}=0$$

(13)

Then, the modal damping ratio of the cable is calculated by using Equation (12) after solving the complex wavenumber ${\beta }_n$ from Equation (13).

Figure 2a,b show the relationship curves between the cable’s modal damping ratio and the stiffness ${\overline{K}}_1$ of the HDR damper when the damper is installed with different loss factors and different installation locations, respectively.

Figure 2a indicates that there is an optimal HDR damper stiffness parameter value to maximize the modal damping; that is, the damping curves have peak points. Comparing the different curves illustrates that the HDR damper’s loss factor parameters have a significant impact on the cable’s modal damping. Specifically, with the HDR damper loss factor increased from 0.2 to 1.2, the maximum value of the cable’s modal damping ratio is enhanced by more than fourfold. It should be noted that the larger the loss factor, the lower the optimal stiffness of the damper. From Figure 2b, it can be seen that increasing the installation height of the HDR damper can effectively improve the cable’s modal damping. At the same time, the optimal stiffness parameter of the HDR damper decreases with the increase in the HDR damper’s installation height. Based on the preceding analysis, we can find that the maximum cable modal damping achieved by the HDR damper at the same installation height is smaller than that of the viscous damper commonly used in engineering. In order to further enhance the damping effect of the HDR damper, a feasible method is to increase the loss factor and installation height of the damper. However, at present, the maximum loss factor of the HDR damper can only reach about 1.2, and the installation height of the damper is also limited. Therefore, it is necessary to adopt multiple devices for cable vibration reduction.

3.2. Cable with a Single TM-HDR-D

For a cable–TM-HDR-D system, the characteristic Equation (10) can be simplified to

$$\sin \left(\beta L\right)-\sin \left(\beta x_2^{*}\right)\sin \left(\beta x_2\right)\alpha \mu \beta L=0$$

(14)

Then, the modal damping ratio of the system can be calculated via Equation (12) after solving the complex wavenumber ${\beta }_n$ from Equation (13).

Figure 3 shows the 1st and 2nd modal damping curves with the dependence of the installation location of the TM-HDR-D, with $\mu =0.005$, 0.01, 0.02, and 0.03.

When the cable is equipped with a single TM-HDR-D, as the damper is located near the middle of the cable span, the first modal damping ratio gradually increases and reaches the maximum value. Moreover, increasing the damper mass will significantly enhance its damping effect, as depicted in Figure 3a. When the damper’s installation mass is relatively small, in order to maximize the cable’s 2nd modal damping ratio, the optimal damper location is near the cable’s quarter point. However, when the damper’s mass is larger, i.e., $\mu =0.03$, the optimal damper location is closer to the cable’s anchor point, as illustrated in Figure 3b. The main reason for this phenomenon is that the larger mass of the damper causes obvious changes to the modal shape of the cable.

Similarly, for the enhancement of cable’s modal damping, it is efficient to increase the TM-HDR-D’s mass. Therefore, considering the convenience of installation and maintenance of the TM-HDR-D, it is feasible to select a damper with a large mass to be installed near the cable’s anchor point to ensure the damping effect.

Figure 4 shows the relationship between the cable’s first modal damping ratio and the tuning frequency ratio $\rho$ of the TM-HDR-D for different mass ratios ($\mu$). Note that the TM-HDR-D is located at $x_2/L=0.5$ with $\phi =0.5$.

As can be seen from Figure 4, the TM-HDR-D, as a kind of TMD-type device, is also sensitive to frequency. The best frequency tuning condition is about $\rho =1.06$. By comparing the curves under different mass ratios, it can be seen that the damper’s mass has a great influence on the modal damping and leads a small change in the best tuning frequency ratio $\rho$. In practice, in order to improve the robustness of the TM-HDR-D, the damper’s mass should be increased reasonably.

3.3. Cable with HDR Damper and TM-HDR-D

This section focuses a system of a cable with two dampers, and the cable’s modal damping is obtained via Equation (12) by numerically solving Equation (10).

Figure 5 depicts the cable’s first modal damping ratio with respect to the HDR damper’s stiffness with four TM-HDR-D mass ratios, i.e., $\mu =0, 0.005, 0.01, \mathrm{and} 0.02$. Note that the loss factor $\phi$ of both the HDR damper and the TM-HDR-D is set to $0.5$. The TM-HDR-D tunes to the cable’s first vibration mode; thus, the frequency ratio is determined as $\rho =1$. In this situation, the location of the TM-HDR-D is $0.5L$. Figure 5a,b show the first modal damping ratio curves of the cable with two dampers, where an HDR damper is located at $x_1/L$ = 0.02 and 0.05, respectively.

Figure 5 illustrates that the cable’s modal damping enhances greatly with the increase in the HDR damper’s installation height. Compared with the HDR damper, the TM-HDR-D can provide a greater damping contribution because it is not limited by its installation position. Increasing the TM-HDR-D’s installation mass further improves the modal damping of the cable system. Interestingly, when the TM-HDR-D has a small mass, the corresponding cable damping curves are approximately parallel to that of the HDR damper only, which indicates that the modal damping contribution of the TM-HDR-D and the HDR damper is approximately the linear superposition of their respective damping effects. However, when the mass of the TM-HDR-D is large, e.g., $\mu =0.02$, the curves are not parallel. In this situation, there is a certain coupling effect between the two dampers, and the combined damping effect is no longer subject to superposition. Figure 6 shows the typical modal shapes of a cable with a single HDR damper and of a cable with an HDR damper and a TM-HDR-D, corresponding to points (i) and (ii) in Figure 5b, respectively. Note that the solid line corresponds to the first modal shape of the cable without any dampers. Figure 6 shows that the cable-end HDR damper causes considerable changes in the modal shape of the cable system. Meanwhile, adding a TM-HDR-D to the cable–HDR damper system will continue to change the system’s modal shape, although not significantly. This also leads to the coupling effect of the two dampers, and the effect of the two dampers on the system’s damping is not a simple linear superposition.

Figure 7 depicts the second modal damping ratio versus the HDR damper stiffness, with $\mu =0, 0.005, 0.01, \mathrm{and} 0.2$. The TM-HDR-D herein is tuned to the second mode, i.e., $\rho =0.5$, and installed at $x_2/L$ = 0.25.

Figure 7 indicates that, with the TM-HDR-D tuned to the cable’s second mode, the cable’s damping can be significantly improved. When the TM-HDR-D has a small mass, the combined damping effect of both dampers is approximately the linear superposition of their respective effects, which is in accordance with the analysis results shown in Figure 5.

Figure 8 and Figure 9 investigate the effect of the installation location of the TM-HDR-D on the system’s modal damping ratios in the first and second modes, respectively. In Figure 8, the TM-HDR-D is tuned to the cable’s first vibration mode, i.e., the frequency ratio is $\rho =1$. Note that the parameters of the HDR damper are $\phi =0.5$ and ${\overline{K}}_1=40$. Figure 8 demonstrates that adding a TM-HDR-D to a cable–HDR damper system will greatly improve the system’s modal damping ratio. The damping effect is closely related to the installation mass and location of the TM-HDR-D. Specifically, the increase in the system’s modal damping ratio is proportional to the damper’s mass. Meanwhile, with the TM-HDR-D close to the cable’s middle point, the damping is increased the most in the first mode, as depicted in Figure 8.

Figure 9 shows the system damping ratio of a cable with two dampers versus the TM-HDR-D location. Let the TM-HDR-D loss factor $\phi$ be 0.5 and the frequency tuning ratio $\rho =0.5$. In addition, let the HDR damper’s loss factor $\phi$ be 0.5, and the location parameter $x_1/L$ is 0.02 and 0.05 in Figure 9a,b, respectively.

From Figure 9, it can be seen that the optimal TM-HDR-D installation location for the cable’s second modal damping is near the location $L/4$—especially closer to the quarter point of the HDR damper. The maximum point is marked with a solid circle in Figure 9. It should be noted that when the TM-HDR-D is close to the cable’s midpoint, the damping contribution of the TM-HDR-D is almost zero. Therefore, the TM-HDR-D should not be installed at the node of the cable’s modal shape in practical applications.

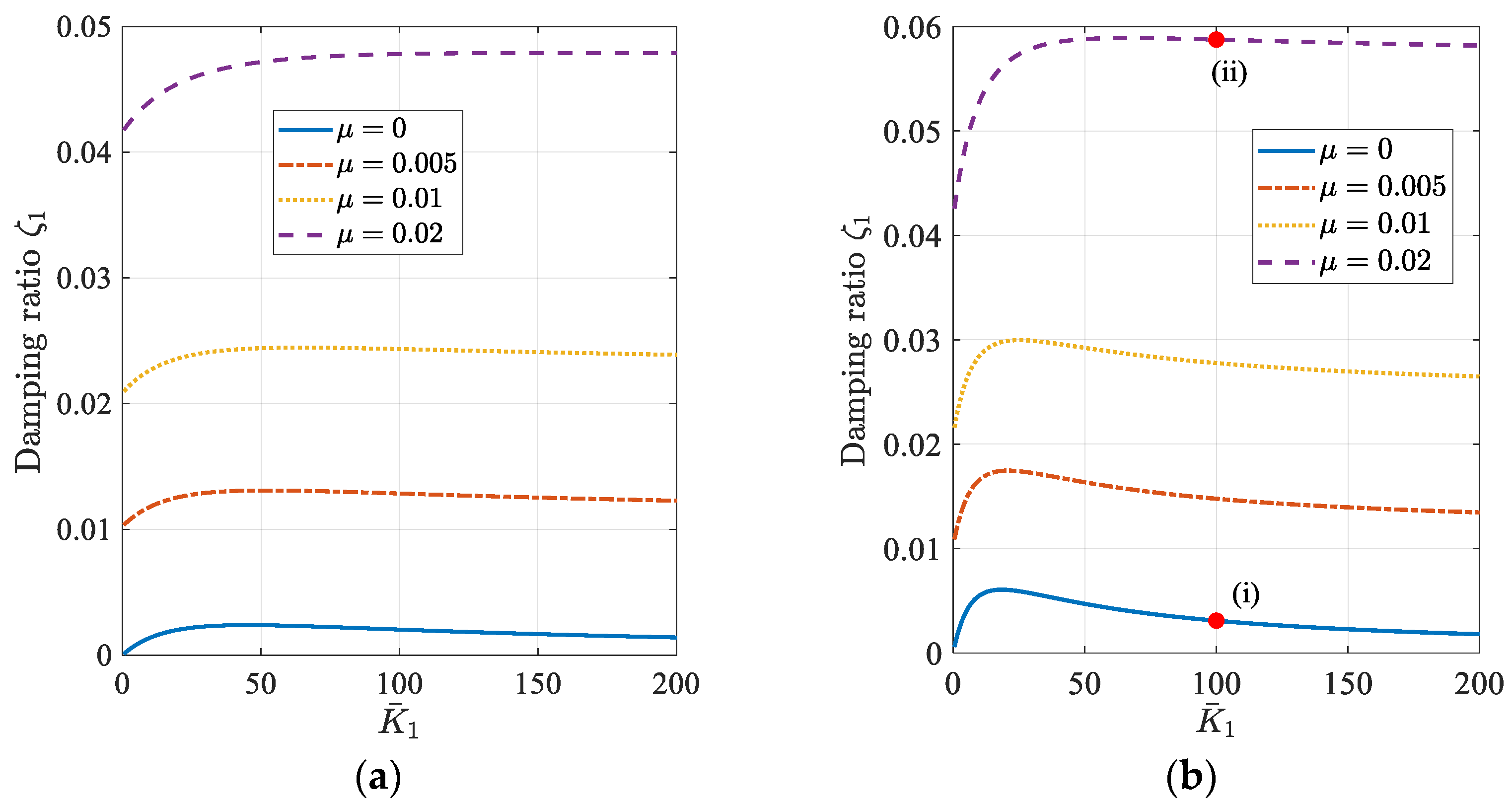
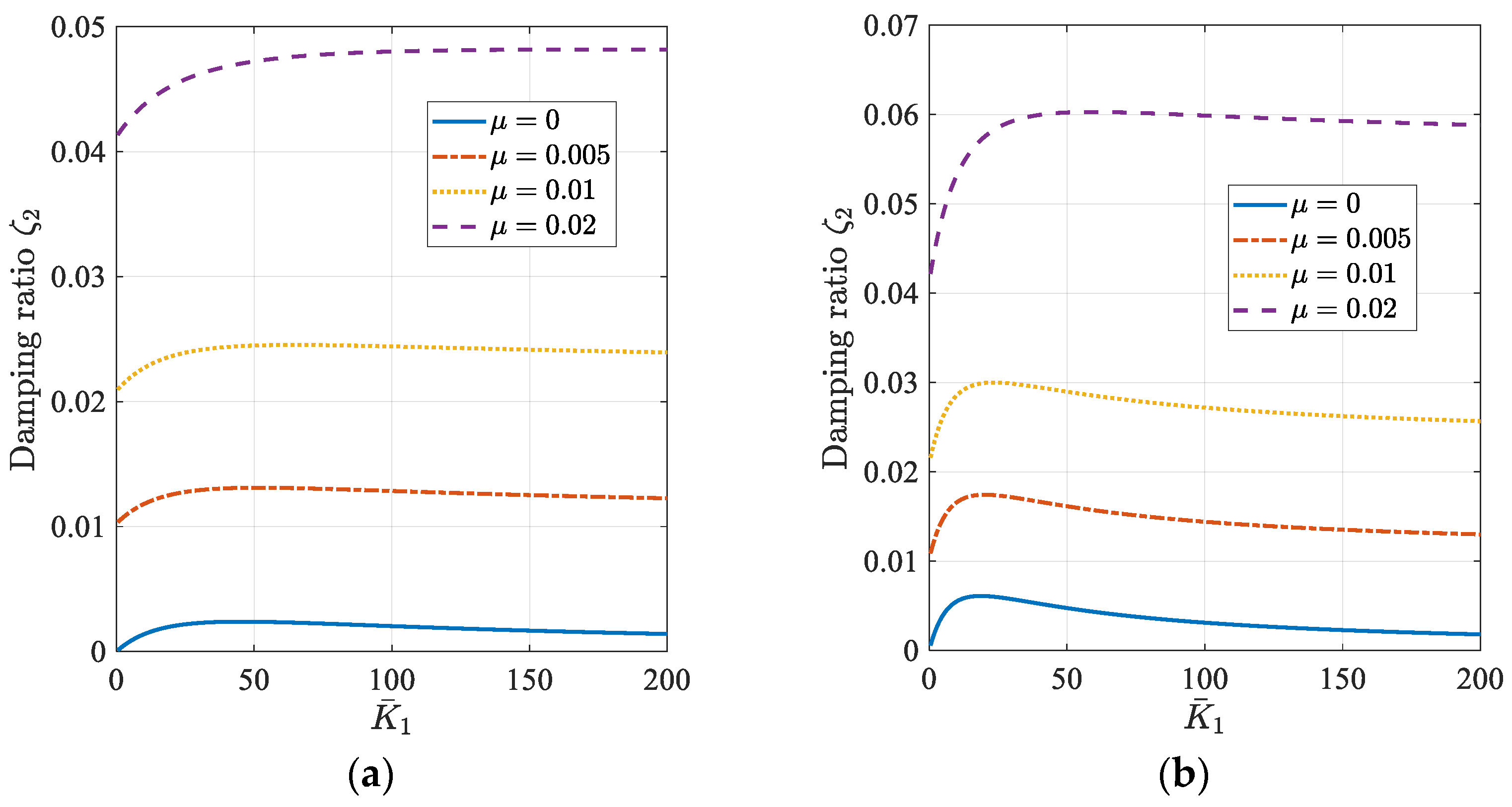
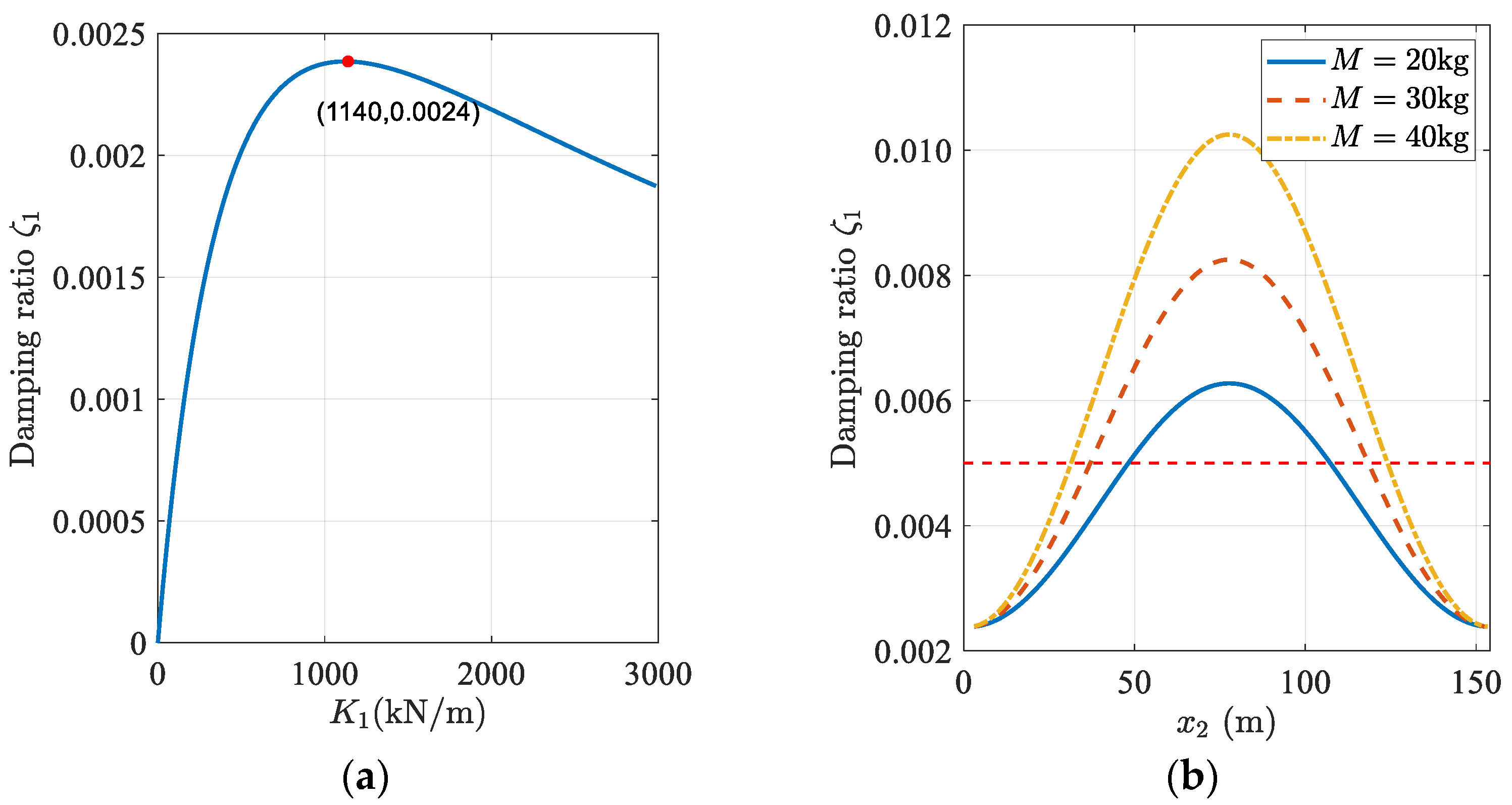
4. Example for Damper Design

In real-world bridge engineering, cables usually experience vibrations with more than one mode. The vibration mitigation device needs to suppress cable vibration for multiple modes. In this section, a real cable is used for damper design by considering the cable’s single-mode vibration and two-mode vibration. The cable parameters are given in

Table 1. Parameters of the cable for the present study.

Length L (m)	Tension T (kN)	Mass m (kg/m)	Fundamental Frequency (Hz)
154.08	3831	70.1	0.759

.

4.1. Targeting for a Single Mode

The parameters of the HDR damper and the TM-HDR-D are designed for mitigating the cable’s first mode of vibration, assuming that the installation position of the HDR damper is $x_1/L=0.02$, and the TM-HDR-D targets the cable’s first vibration mode, i.e., $\rho =1$. The loss factor of high-damping rubber is set to $\phi =0.5$ for both the HDR damper and the TM-HDR-D. Figure 10 shows the dampers’ design process by considering the cable’s first vibration mode.

For the HDR damper, there is an optimal stiffness parameter when the installation location and loss factor are determined. As shown in Figure 10a, the optimal damper stiffness is 1140 kN/m, and the maximum modal damping ratio is 0.0024. Note that the required cable damping ratio for suppressing rain- and wind-induced vibrations is about 0.005 [33]. Therefore, in this case, a single HDR damper cannot meet the vibration reduction requirements. In addition, an additional TM-HDR-D is used to make up for the deficiency of the damping contribution of a single HDR damper. Three different masses of TM-HDR-D, i.e., 20 kg, 30 kg, and 40 kg, are used to improve the first modal damping of the cable system, as depicted in Figure 10b. It can be seen that the effect of the TM-HDR-D on the system’s modal damping is very significant, and a small installation mass (such as 20 kg) can still meet the target damping requirements. At the same time, in order to reduce the TM-HDR-D’s installation height, its mass should be appropriately increased.

4.2. Targeting for Two Modes

The first two modes are taken into account for the dampers’ design in this section. An HDR damper is equipped near to the cable end, where $x_1/L=0.02$, and the stiffness parameter is 1140 kN/m. Let the HDR damper and the TM-HDR-D have the same loss factor $\phi =0.5$, and the TM-HDR-D’s mass is set to $M=70\mathrm{kg}$. Figure 11 depicts the system modal damping ratio of the first two modes versus the TM-HDR-D location for various frequency ratios ($\rho$). Figure 11a–c correspond to the first two modal damping curves when the TM-HDR-D tuning frequency ratio $\rho =0.7$, 0.8, and 0.9, respectively.

As mentioned in the above section, the TM-HDR-D device is sensitive to the cable vibration frequency, and the value of the tuning frequency ratio $\rho$ affects the distribution of the system’s modal damping in the first two cable modes. When $\rho$ is close to 1, its damping to the first cable mode is relatively large, and when the tuning frequency ratio is close to 0.5, its contribution to the system’s second modal damping ratio is relatively large, as depicted in Figure 11. More specifically, when the value of $\rho$ is 0.7 and 0.9, it is difficult for the system’s modal damping ratio to meet the requirements at the same time in first two modes—especially when the tuning frequency ratio is 0.9 (see Figure 11c). To make the first two modal damping ratios reach the design value, the tuning frequency ratio $\rho$ is suggested to be set to the intermediate value, e.g., 0.8, as depicted in Figure 11b. When the $\rho$ of the TM-HDR-D is $0.8$, to control the cable’s wind- and rain-induced vibration, the system’s damping level should be more than 0.005, and the TM-HDR-D should be attached to the cable at $x_2$= 38~48 m or 108~117 m.

4.3. Remarks

The actual HDR-type damper has amplitude–frequency dependence, but the theoretical analysis method in this paper can still be used to predict the modal damping of the system (see [33]). In addition, the cable-end HDR damper can be installed as an internal damper in the steel sleeve at the cable end near to the bridge deck or tower, without affecting the appearance of the bridge. For long cables, the HDR dampers can be installed at the two ends of the cable at the same time, which can further improve the damping contribution of the cable-end dampers [27]. For the high-order vortex-induced vibration of the cable–damper system reported in the current literature [28], a TM-HDR-D can also be added to control this type of vibration.

5. Conclusions

The theoretical model of a taut cable with two HDR-type dampers, i.e., an HDR damper and a TM-HDR-D, was established via the complex analysis method. Based on the theoretical model, the effects of the HDR damper and the TM-HDR-D on the cable vibration reduction under the individual and combined actions were studied. Finally, taking a real-world cable as an example, the combined design of two dampers was carried out. The following conclusions can be drawn:

• As a cable-end damper, the effectiveness of the HDR damper mainly depends on the damper’s stiffness, loss factor, and location. In practice, the damper’s stiffness needs to be optimized to achieve the best damping contribution to the cable system. The TM-HDR-D can be installed at any position of the cable, and through precise frequency tuning it can supplement the damping contribution of the cable-end HDR damper.
• When the TM-HDR-D has a small mass, the combined damping effect of the HDR damper and the TM-HDR-D approximates a linear superposition of their respective effects.
• In practice, a TM-HDR-D can be co-designed with an HDR damper to achieve multimodal damping improvement. The TM-HDR-D can make up for the deficiency of the HDR damper and achieve the multimode vibration control of the cable.