Abstract
Wireless covert communication is an emerging communication technique that prevents eavesdroppers. This paper presents a novel approach to wireless covert communication based on polar codes with dirty constellation polarization. The feasibility of dirty constellation polarization is analyzed, and the impact of covert transmission power on undetectability is investigated. We polarize the covert channel and decode the covert information using a successive-cancellation decoder. Simulation results demonstrate that polar codes can significantly improve the undetectability and reliability of covert communication when compared to BCH codes. Additionally, we find that polarized covert channels achieve better undetectability and reliability when using a successive-cancellation list decoder. The proposed algorithm shows significant improvement in the undetectability and reliability of wireless covert communication with dirty constellations. This research provides a promising direction for future development in the field of covert communication, with potential applications in secure communication systems.
1. Introduction
The proliferation of 5G and other wireless communication technologies has given rise to a broad range of multi-modal sensors, which have accelerated the process of social informatization [1,2]. However, the majority of IoT devices are susceptible to hacking and compromise. Given that eavesdroppers can intercept wireless communication signals, confidential information is at risk. This poses a significant threat to communication security. To ensure the privacy of user data, several approaches have been proposed to transmit noisy or incomplete data, which can impact the performance of some IoT applications [3]. As a result, it is crucial to transmitting information secretly without detection or interception, known as wireless covert communication.
Wireless covert channels, modern information-hiding technology in the wireless communication domain, conceal the transmission process of information that requires secrecy during typical wireless communication. Even if an eavesdropper intercepts the communication signal, it is impossible to differentiate it from standard wireless communication. The fundamental theory and performance limits of covert communication in AWGN channels are discussed in Ref. [4]. The authors established that a maximum of bits can be transmitted to the receiver reliably without being detected by the detector. Researchers have subsequently analyzed the covert communication capacity in multiple scenarios with unfavorable factors for eavesdroppers. These include the transmitter [5,6], receiver [7,8,9], and additional nodes [10,11]. Covert communication techniques include artificial additional signal noise, artificial coding domain error, and insertion of additional signal bands, among others. The research in this field has been extended to other communication scenarios, such as relay communication [12,13], multi-antenna [14,15], and broadcast communication [16,17,18], etc.
In the realm of covert communication, numerous techniques have been proposed to transmit confidential information without being detected [19] while some countermeasures to detect or localize covert communication entity has also been put forward [20]. However, achieving the theoretical covert rate of under detection remains a challenging task. With the growing demand for 5G, polar codes have emerged as a promising solution that can achieve the Shannon capacity for channel coding [21]. Therefore, it is imperative to investigate the potential of polar codes in the context of covert communication. To this end, our main contributions are listed as follows.
- We present a novel wireless covert channel that integrates polar code and dirty constellations, which, to the best of our knowledge, has not been proposed before.
- We employ two distinct decoding techniques, to enhance the reliability of the system and provide solutions for low-computational power scenarios.
- We conduct experiments on a wireless covert channel testbed to evaluate the performance of our proposals. The results show that the proposed wireless covert channel can obtain better reliability and undetectability.
The remainder of this paper is structured as follows. In Section 2, we present a summary of the system model and related works. The fundamental principles of our scheme are elaborated in Section 3. In Section 4, we provide a detailed description of our wireless covert channel. Section 5 presents the experimental results obtained from our proposed method. Lastly, in Section 6, we conclude this paper.
2. Background
2.1. System Model
The Alice-Bob model, as depicted in Figure 1, involves a transmitter, a receiver, and a detector commonly referred to as Alice, Bob, and Willie. The objective is to transmit information covertly between Alice and Bob while evading detection by Willie, who observes the wireless channel and determines whether covert communication is taking place or not. Willie’s probability of detection error comprises two components: the probability of missed detection and the probability of false alarm . However, due to the practicality of detection, Willie can only detect a finite number of samples. Our numerical analysis reveals that in the presence of noise uncertainty at Willie, there may exist an optimal number of samples that maximizes the communication rate subject to , where denotes the sum of (i.e., false positive rate) and (i.e., miss detection rate) at Willie. We consider an arbitrarily small number to be the maximum acceptable detection rate for Willie.
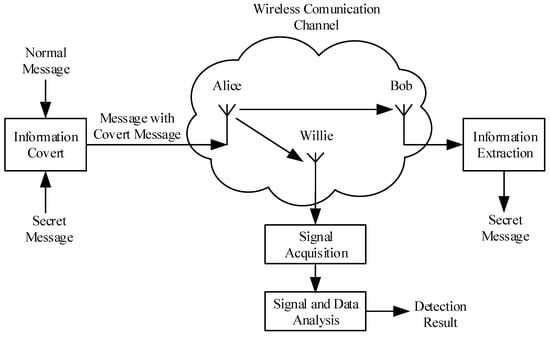
Figure 1.
The framework of wireless covert communication.
2.2. Wireless Covert Channels with Dirty Constellation
To reduce the probability of covert information being detected by potential eavesdroppers, we can convert the covert messages to constellation error of common signal, which is also called wireless covert communication with dirty constellation (WCC-DC).
The framework of WCC-DC is illustrated in Figure 2a. The premise of WCC-DC is wireless communication physical layer with OFDM structure. In order to reduce the statistical correlation, the transmitter can divide all OFDM subcarriers into secret subcarriers or normal subcarriers. The corresponding mapping sequence is also generated. The secret information will be modulated with QPSK to obtain covert signals. Covert signal and random noise signal are superposed on the subcarrier signal. To ameliorate the undetectability of covert communication, the covert constellation will be rotated at a certain angle, as shown in Figure 2b. The transmitter and receiver should share the mapping sequence before the covert communication starts. The receiver should demodulate the carrier message as normal first. Then, the carrier message should be modulated again to obtain the ideal carrier signal. The receiver subtracts the ideal carrier signal from the received signal to get residual signals, which is the covert signal with noise. The covert signal will be rotated in the opposite direction at a certain angle and demodulated with QPSK. The covert message will be extracted from modulated signal according to the mapping sequence. However, the wireless covert channel with dirty constellation has a high BLER (Block Error Rate) when the is small. When we increase the , the undetectability will deteriorate. Therefore, we plan to ameliorate the reliability of covert messages at low with polar codes.
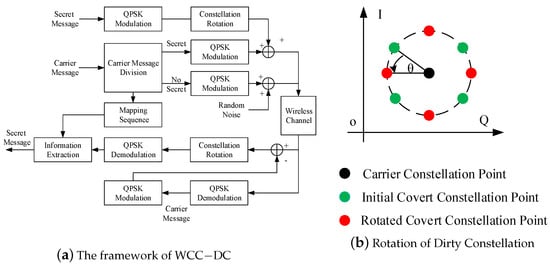
Figure 2.
The schematic diagram of wireless covert communication with dirty constellation.
3. Basis of Our Scheme
3.1. Binary Hypothesis Testing at Willie
According to the system model shown in Figure 1, the performance elements of the wireless covert channels mainly include two aspects: undetectability and reliability. In communication, Alice totally transmits n symbols to Bob. We denote the finite block as (), which consist of normal information and secret information . Willie’s task is to collect the messages transmitted by Alice and detect whether covert communication exists or not. Let the AWGN between Alice and Bob as . The signal received by Willie can be expressed as
Willie’s task is to detect whether covert communication exists. We define two hypotheses, and , to distinguish these two cases:
Let denotes that covert communication exists, denotes covert communication does not exist. In covert communication, the ultimate goal of Willie is to minimize the total error rate (i.e., ). Let T and F denote binary decisions that infer whether covert communication exists or not. The false positive rate and miss detection rate can be expressed as
Assuming Willie performs the optimal detection. Following Pinsker’s inequality [22,23], we can obtain
where relative entropy (also called K-L divergence) is defined as follows:
where n is the value range of x. Let denotes the distribution of sequence detected by Willie, and denotes the distribution of AWGN collected by Willie. Let P denote the transmit power. We can equivalently express Equation (5) as
It can be obtained that the K-L divergence deteriorates with the increase of transmit power P. We can ameliorate the value of K-L divergence by constraining the transmit power. Except for KL-divergence, we can also calculate the distance between distributions with the KS-Test (also called Kolmogorov–Smirnov statistic). The KS-distance [24] is defined as follows:
where , . Let and denote the cumulative distribution functions of and . and are both divided into K bins. The number of the elements in and are denoted by and , . We can express Equation (7) equivalently as
It can be obtained that we can also ameliorate the value of the KS test by constraining the transmit power. In summary, we can improve undetectability by constraining the power of covert communication. However, the BLER (Block Error Rate) would deteriorate with low transmit power. We can ameliorate the reliability of covert communication by encoding the covert messages with polar code.
3.2. Dirty Constellation Polarization
We always denote a binary discrete memoryless channel (B-DMC) W as with input alphabet X and output alphabet Y. The input alphabet X belongs to set, the output alphabet Y may be arbitrary. To measure the channel condition, Arıkan [21] mainly used two parameters: the symmetric capacity
and the Bhattacharyya parameter as
When the input alphabet is just 1 or 0, is an upper bound of the error probability of the maximum-likelihood (ML) decision. It is easy to see that and both take values in [0,1]. Intuitively, we will expect iff or iff .
In [25], Gallager proposed that the ensemble average probability of decoding error based on ML decoding satisfies
where
We denote the transition probability of discrete memoryless channel as , positive integer as N, and positive number as R. In the ensemble of block codes, every code is independently chosen with the probability assignment . Assuming , we can transform Equation (12) as
For binary symmetric channel, is maximized over Q by . For this Q, we have
The Equation (11) can be converted to
R in nats (that is, using ln) is the number of binary digits entering the encoder per transmitted per second. Thus, we use R in bits (that is, using log2) to interpret Equation (15), which is the number of binary digits entering the encoder per transmitted channel digit. It is known that , so we have
For any B-DMC, we have
When W is a symmetric channel, the symmetric capacity of W is equal to the Shannon capacity. Referring to Equation (17), it can be obtained that approaching 1 when . It shows that there exists a sequence of codes with the maximum probability of error when we encode the covert information in B-DMC.
The polarization code can realize by polarizing the channel. Channel polarization is an operation consisting of channel combining and channel splitting. With the length of block N trending to infinity, the symmetric capacity tends to be two-polar. Part of the symmetric capacity tends to be 1, the rest tends to be 0. If we polarize the covert channel in B-DMC, as the length of covert information blocks N becomes large, part of the covert information can be transmitted with the Shannon capacity. We can improve the undetectability by reducing the power of the covert signal without deteriorating the reliability of covert communication.
If the communication channel is AWGN (Additive White Gaussian Noise) channel, the transmit process of covert information can be expressed as . The signal received by Bob can be expressed as , . We denote the encoded covert information as . Assuming that each has the same probability, the probability of each is . We denote the BLER (Block Error Rate) based on maximum likelihood decoding as . The UUB (Union Upper Bound) of BLER (Block Error Rate) based on maximum likelihood decoding can be written as with
We use the standard notation , to denote the probability of error. We denote the Hamming distance and the codes with the same Hamming distance as d, .
4. Wireless Covert Channels with Polarized Dirty Constellation
To ameliorate the undetectability and reliability of WCC-DC, we proposed wireless covert communication method with polarized dirty constellation (WCC-PDC). The schematic diagram of the polarized dirty constellation is illustrated in Figure 3. Parts of the framework of WCC-PDC will be illustrated especially in the following chapters.
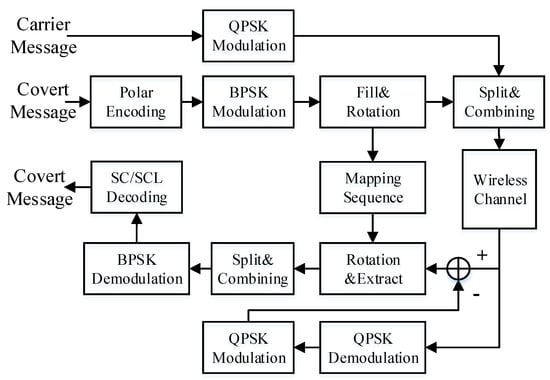
Figure 3.
The schematic diagram of wireless covert communication with polarization dirty constellation.
4.1. Polar Encoding
We use the standard notation to denote the encoding operation. is the conversion matrix consisting of various permutation operations. Erdal Arıkan provides a recursive formula as
Let denote the k-dimensional identity matrix for any positive integer k. We assume for positive integer n. It is simple to derive the recursive relationship as
With the identity , we can equivalently rewrite Equation (20) as
where is the n-dimensional Kronecker product of F matrix with F equals . is converted from the N-dimensional identity matrix, arranging the column vectors of the identity matrix in the order of odd first and then even. We can express as
where denotes the x-th column of matrix for positive integer . Let covert message be any vector over GF (2). We would obtain at output. Some preprocessing needs to be performed to combine polar code and dirty constellation.
4.2. Fill and Rotation
The size of the covert information block and the carrier information block are incompatible, the covert information needs to be filled with all 0 or all 1 bits as shown in Figure 4. For reducing the statistical relevance of covert information, our scheme will rotate the covert constellation point. If we modulate the covert information with BPSK, we see from Figure 4 the position of initial covert constellation points and carrier constellation points.
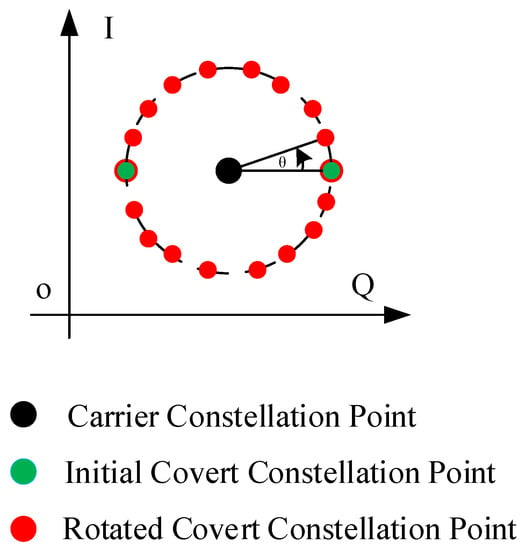
Figure 4.
Rotation of polarized covert constellation.
To improve the undetectability, we rotate the covert constellation point with degree with . Let us assume the coordinate of carrier constellation point is . The coordinate of covert constellation point is . When we rotate the covert constellation point, we can obtain
As we know, covert information is modulated with BPSK. Thus, we can express the covert constellation point as
When we receive the subcarrier signal, the received carrier information should be modulated again to obtain the residual signal. By reversing the rotation of the residual signal, we can obtain the covert signal. The covert information can be obtained via Log-Likehood Ratio(LLR) calculation.
4.3. Split and Combing
As we know, the length of the covert information N basing on polar code equals . Assuming covert communication is set on an 802.11a/g PHY layer. There are 48 subcarriers in a symbol in transmissions. The size of the covert information block and the carrier information block are incompatible, some all 0 or all 1 bits are filled in the first and the last symbol. As the length of the code block becomes large, the symmetric capacity terms tend towards 0 or 1. The length of the code block would be extended as much as possible. The number of filled bits k can be expressed as
The symbol construction of the subcarrier signal is illustrated in Figure 5. The black code blocks are filled bits that can also be used to judge the beginning and end of the covert information code block. The yellow code blocks are covert information code blocks. Finite covert code blocks would be split into multiple blocks and combined with the carrier information block.
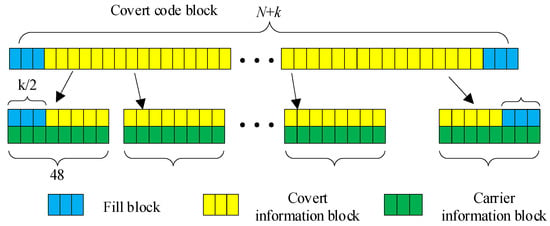
Figure 5.
Symbol construction of subcarrier signal.
When we receive the subcarrier signal, the subcarrier signal would be demodulated and modulated to obtain the residual signal. Then, the residual signal would be demodulated to obtain covert code blocks.
As illustrated in Figure 6, the covert information block would be extracted from the covert code block. Then, the covert information code block would be decoded by maximum likelihood decoding.
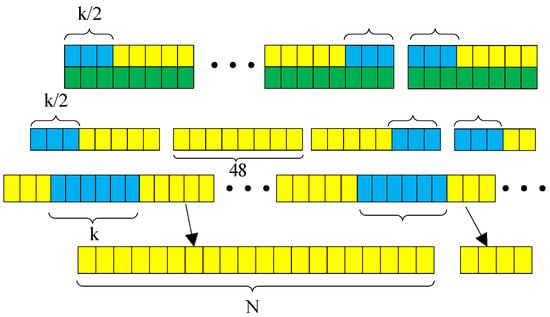
Figure 6.
Block extraction of covert information.
4.4. Maximum Likelihood Decoding
4.4.1. A Successive Cancellation (SC) Decoding
Polar code is a Gn-coset code with parameter where K is the code dimension and specifies the size of the information set A. Covert message would be encoded into , would be transmitted through the channel and Bob would receive . Thus, Bob needs a corresponding decoder that could generate an accurate estimate of with given knowledge of A, and . Because parts of the codewords are frozen bits, the decoder can directly set . The task is just to estimate of . Arıkan has given a specific successive cancellation (SC) decoder. The SC decoder can generate its estimate of with given parameter by computing
where and the decision functions are defined as
and the Log-Likelihood Ratio (LLR) can be expressed as
To calculate the LLR, we can use function f and function g
We can equivalently express the LLR as
Thus, the task of calculating an LLR at length N is converted to calculating two LLRs at length . This recursion can be continued down until the block length is 1, at which point the LLRs can be computed directly. To estimate the complexity of LLR calculations, we denote the Kolmogorov complexity of decoding over as . We have the complexity bound
where is the worst-case complexity of combining two LLRs at length into an LLR at length k. We can obtain the bound
We can obtain the overall decoder complexity
This overall complexity corresponds to a decoder whose DEs work privately. By sharing any partial results between DEs, the decoder could have a more efficient implementation with overall complexity .
4.4.2. A Successive Cancellation List (SCL) Decoding
Even though the code block length is comparable, the performance of polar codes is inferior to LDPC and turbo codes. To improve the performance of polar code, Ido [26] proposed a successive-cancellation list (SCL) decoder. In the SCL decoder, L decoding paths are considered concurrently at each decoding stage. By comparing the path metric (PM) of L results, the most likely estimate is selected as the decoder output. The path metric (PM) of path l() can be expressed as
where . For any two paths , when we have , we can equivalently obtain
We can obtain that the greater transition probability , the smaller the path metric . Then, Equation (34) can be expressed as
where and .
Assuming a decoding path of , the decoding process can be visualized through Figure 7, where the black paths represent the abandoned paths and the red paths indicate the adopted paths. At each node, the path metric is calculated, and the two paths with the smallest are chosen. This approach enables simultaneous maintenance of multiple code paths, thus ensuring the SCL code entry local best-generated code.
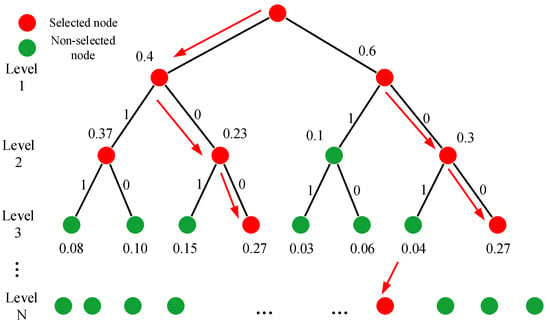
Figure 7.
Decoding process of SCL decoder.
5. Performance Evaluations
In this section, we first construct a wireless covert channel testbed and give the experiment settings in Section 5.1. Then, we evaluate the experiment results of WCC-PDC in Section 5.2. We finally verify the covert performance of the WCC-PDC compared with the WCC-DC.
5.1. Wireless Covert Channel Testbed
In this study, we constructed a small-scale experimental testbed, depicted in Figure 8, comprising four devices, including one covert transmitter (Alice), one receiver (Bob), one detector (Willie), and one normal communicator. Alice transmits covert messages to Bob, with the positions of Alice and Willie remaining fixed. Willie’s role is to detect the presence of covert communication, with patrols being conducted within the target area to increase the likelihood of detection. To simulate real-world communication scenarios, we designed one normal communicator who utilizes broadcast signals with varying power levels within the target area, thereby changing the signal-to-noise ratio for Bob. It should be noted that the communication activities of the normal communicator can also exert an impact on the detection results.
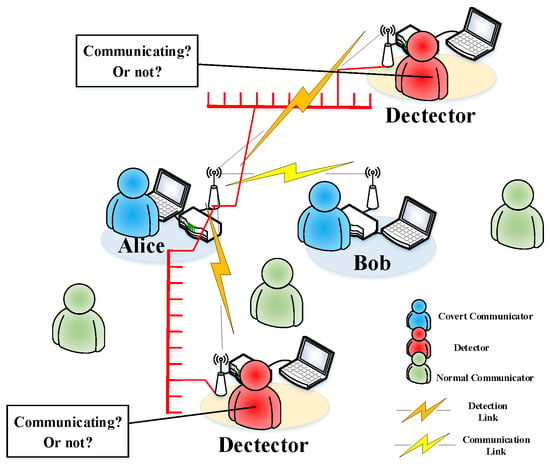
Figure 8.
Wireless covert channel testbed.
Within the testbed, we assume that Alice, Bob, and Willie are situated within an indoor line-of-sight (LOS) environment [27]. The distances between Alice and Bob, normal and Bob, and the normal communicator and detector are established as 2 m, 5 m, and 5 m, correspondingly. Furthermore, the distance between Alice and the detector is varied within the range of 1 m to 10 m. MATLAB is utilized to conduct diverse simulations on the covert communication simulation platform, with the goal of verifying the efficacy of Willie’s detection in the classical model of covert communication. The detection approach adopted by Willie is based on both KL divergence and KS tests. In some simulations, WCC-DC with the BCH code is chosen for comparison.
5.2. Experiment Results
5.2.1. Reliability
In this chapter, we investigate the reliability comparison of two covert communication channels, namely WCC-DC and WCC-PDC. BCH codes are employed for encoding and decoding in WCC-DC, while polar codes are utilized for covert information encoding in WCC-PDC. The decoding process employs both SC and SCL decoders. In order to examine the reliability of different covert signal transmission rates, we establish a comparison between two code rates, namely 0.5 and 0.2. To accurately replicate the diverse environmental noise conditions that exist in practical scenarios, we set two distinct carrier-secret ratios (), namely = 10 dB and = 15 dB. In this work, the number L of SCL decoders is set to 8, the length of the BCH code block is 1023 bits, and the length of the polar code block is 1024 bits.
As depicted in Figure 9a, the BLER of the wireless covert channels decreases as the code rate decreases to 0.2. It is worth noting that the represents the ratio between the secret carrier signals and noise signals. WCC-PDC exhibits lower BLER compared to WCC-DC with BCH code. Specifically, at = 18 dB, which is a normal value, the BLER of WCC-PDC with SC decoder reaches 0.02, and the BLER of WCC-PDC with SCL decoder reaches 1 . Moreover, even at = 18 dB, a low BLER of 0.03 can still be obtained by utilizing WCC-PDC with SCL decoder.
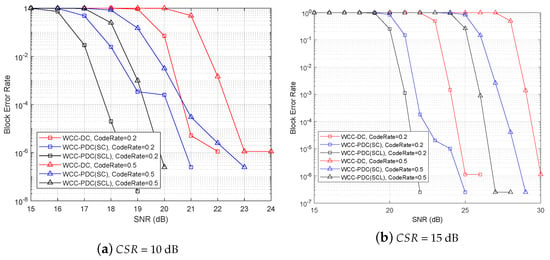
Figure 9.
Block error rate versus signal noise ratio.
Figure 9b illustrates the BLER of different wireless covert channels at = 15 dB. The figure shows that the BLER of the hidden channel decreases significantly as the increases. However, even at = 21 dB, a BLER of only 0.01 can be achieved using WCC-PDC and SCL decoder. This suggests that the reliability of the covert channel needs to be improved in low scenarios.
5.2.2. Undetectability
Undetectability is an important measure of wireless covert communication. It is typically assessed using measures such as ’KL divergence’ and ’KS Test’. The undetectability of I vectors, Q vectors, amplitude, and phases are detected with constellation errors.
In Figure 10a,b, we investigate the impact of the distance between Alice and Willie on undetectability. The of the received signal at Bob is kept at 20 dB, and the of the signal is set at 10 dB. As shown in Figure 10a, the KL divergence decreases with increasing distance between Alice and Willie. When the distance between Alice and Willie is greater than 5 m, the KL divergence of phase reaches a threshold and no longer changes, while the KL divergence of I vector, Q vector, and amplitude decrease with increasing distance. It can be observed that WCC-PDC can achieve better undetectability than WCC-DC, and our proposed WCC-PDC strategy can significantly improve the undetectability of covert communication.
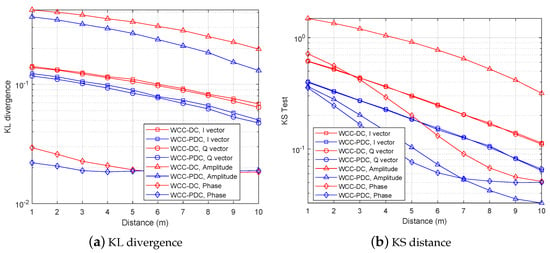
Figure 10.
Detection values versus detection distance.
In Figure 10b, the KL divergence decreases rapidly with increasing distance. It is important to note that the value of the KS test is generally higher than that of KL divergence at the same distance, which indicates that the KS test has better detection performance when the environmental noise is stable. However, when the noise power is uncertain, the KS test may have a high probability of detection error and may no longer be accurate, as we will confirm in the following simulation section.
In order to evaluate the undetectability of wireless covert communication, we analyzed the impact of Willie’s on undetectability using KL divergence and KS distance measures. Specifically, we conducted experiments shown in Figure 11a,b, where we investigated the case when the is set to 10 dB. Our findings suggest that when the of the secret carrier signal is 20 dB, the KL divergence reaches a critical value, beyond which higher values will be deemed as covert communication. However, when the is less than 20 dB, the KL divergence detection method cannot reliably detect the existence of covert communication. In this case, the results of the KS test are even worse than the KL divergence test, and a higher of 23 dB is required to detect the presence of covert communication. These observations indicate that the KL divergence test results are superior to the KS test when the ambient noise power is high.
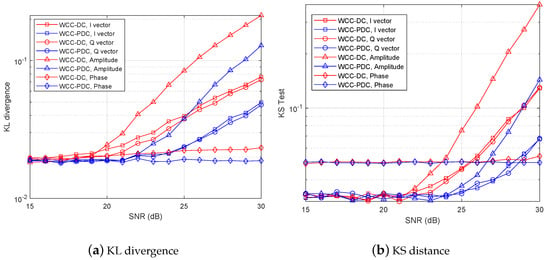
Figure 11.
Detection values versus signal noise ratio at Willie, and = 10 dB.
Furthermore, our experiments revealed that the wireless covert channel WCC-PDC, which we proposed, can achieve better undetectability compared to the wireless covert channel WCC-DC. This implies that under the same environment, WCC-PDC can utilize higher power than WCC-DC for covert communication without being detected. In summary, the results of our experiments suggest that WCC-PDC can provide better undetectability than WCC-DC, and the KL divergence test is a suitable method for detecting covert communication when the ambient noise power is high.
To evaluate the concealment performance of our proposed covert channel WCC-PDC at low power, we conducted experiments with a of 15 dB, which is the same as the experimental environment in Figure 9a. In Figure 12a, we observed that the KL divergence values at = 15 dB are smaller than those at = 10 dB, indicating better undetectability at low power. Additionally, the WCC-PDC cannot be detected when Willie’s is below 25 dB. This threshold is difficult to achieve in conventional communication and demonstrates that our proposed covert channel can achieve excellent concealment performance even at low power levels. In Figure 12b, we also observed that both wireless covert channels are virtually undetectable under KS test when Willie’s is below 25 dB. Furthermore, the WCC-PDC outperforms the WCC-DC in terms of undetectability, making covert communication nearly impossible to detect.
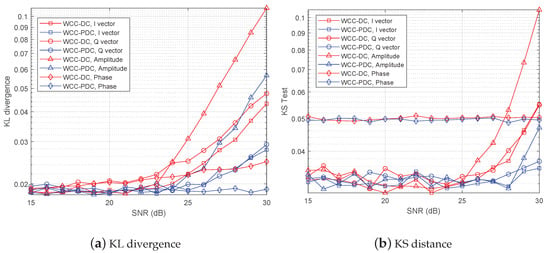
Figure 12.
Detection values versus signal noise ratio at Willie, and = 15 dB.
6. Conclusions
In this paper, we have proposed a novel scheme for wireless covert communication based on polar codes. By extending the polarization theory to wireless covert communication, we have demonstrated that a portion of covert information can be transmitted with Shannon capacity, provided that the length of the code block is sufficiently long. Specifically, we have polarized the dirty constellation in wireless covert communication and decoded the covert information using SC decoder and SCL decoder. Our simulation and analysis have revealed that we can achieve improved reliability and undetectability with the polarization of the dirty constellation.
Through experiments, we have shown that the WCC-PDC covert channel can achieve high reliability under low signal-to-noise ratio and better detection resistance compared to traditional WCC-DC covert channels when the bit error rate is not higher than 0.01. However, the WCC-PDC covert channel also has limitations, particularly its strong dependence on the code block length. Incomplete polarization of the code block may occur if the length of the concealed code block is insufficient, which may negatively affect both the reliability and concealment of the channel. In future research, we plan to explore the combination of MIMO channel optimization schemes to further enhance the performance of wireless covert communication.
Author Contributions
Conceptualization, M.H. and S.Q.; methodology, M.H. and S.Q.; software, M.H.; validation, S.Q. and X.J.; writing—original draft preparation, M.H. and S.Q.; writing—review and editing, X.J.; visualization, S.Q.; supervision, X.J.; funding acquisition, X.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China grant number U1836104, 61801073, 61931004, 62072250, National Key Research and Development Program of China grant number 2021QY0700, and The Startup Foundation for Introducing Talent of NUIST grant number 2021r039.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| IoT | Internet of Things |
| AWGN | Additive White Gaussian Noise |
| WCC-DC | Wireless Covert Communication with Dirty Constellation |
| OFDM | Linear dichroism |
| BPSK | Binary Phase Shift Keying |
| QPSK | Quadrature Phase Shift Keying |
| BLER | Block Error Rate |
| BLER | Block Error Rate |
| SNR | Signal Noise Ratio |
| B-DMC | Binary Discrete Memoryless Channel |
| ML | Maximum-Likehood |
| LLR | Log-Likehood Ratio |
| SC | Successive Cancellation |
| SCL | Successive Cancellation List |
References
- Dorri, A.; Kanhere, S.S.; Jurdak, R.; Gauravaram, P. Blockchain for IoT security and privacy: The case study of a smart home. In Proceedings of the 2017 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Big Island, HI, USA, 13–17 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 618–623. [Google Scholar]
- Gubbi, J.; Buyya, R.; Marusic, S.; Palaniswami, M. Internet of Things (IoT): A vision, architectural elements, and future directions. Future Gener. Comput. Syst. 2013, 29, 1645–1660. [Google Scholar] [CrossRef]
- Chakravorty, A.; Wlodarczyk, T.; Rong, C. Privacy preserving data analytics for smart homes. In Proceedings of the 2013 IEEE Security and Privacy Workshops, Berkeley, CA, USA, 19–22 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 23–27. [Google Scholar]
- Bash, B.A.; Goeckel, D.; Towsley, D. Limits of reliable communication with low probability of detection on AWGN channels. IEEE J. Sel. Areas Commun. 2013, 31, 1921–1930. [Google Scholar] [CrossRef]
- Wang, H.M.; Zhang, Y.; Zhang, X.; Li, Z. Secrecy and covert communications against UAV surveillance via multi-hop networks. IEEE Trans. Commun. 2019, 68, 389–401. [Google Scholar] [CrossRef]
- Soltani, R.; Bash, B.; Goeckel, D.; Guha, S.; Towsley, D. Covert single-hop communication in a wireless network with distributed artificial noise generation. In Proceedings of the 2014 52nd Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA., 30 September–3 October 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1078–1085. [Google Scholar]
- Shahzad, K.; Zhou, X.; Yan, S.; Hu, J.; Shu, F.; Li, J. Achieving covert wireless communications using a full-duplex receiver. IEEE Trans. Wirel. Commun. 2018, 17, 8517–8530. [Google Scholar] [CrossRef]
- Shu, F.; Xu, T.; Hu, J.; Yan, S. Delay-constrained covert communications with a full-duplex receiver. IEEE Wirel. Commun. Lett. 2019, 8, 813–816. [Google Scholar] [CrossRef]
- Sobers, T.V.; Bash, B.A.; Goeckel, D.; Guha, S.; Towsley, D. Covert communication with the help of an uninformed jammer achieves positive rate. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 625–629. [Google Scholar]
- Li, K.; Kelly, P.A.; Goeckel, D. Optimal power adaptation in covert communication with an uninformed jammer. IEEE Trans. Wirel. Commun. 2020, 19, 3463–3473. [Google Scholar] [CrossRef]
- Forouzesh, M.; Azmi, P.; Kuhestani, A.; Yeoh, P.L. Covert communication and secure transmission over untrusted relaying networks in the presence of multiple wardens. IEEE Trans. Commun. 2020, 68, 3737–3749. [Google Scholar] [CrossRef]
- Shahzad, K. Relaying via cooperative jamming in covert wireless communications. In Proceedings of the 2018 12th International Conference on Signal Processing and Communication Systems (ICSPCS), Cairns, Australia, 17–19 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Hu, J.; Yan, S.; Shu, F.; Wang, J. Covert transmission with a self-sustained relay. IEEE Trans. Wirel. Commun. 2019, 18, 4089–4102. [Google Scholar] [CrossRef]
- Arumugam, K.S.K.; Bloch, M.R.; Wang, L. Covert communication over a physically degraded relay channel with non-colluding wardens. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 766–770. [Google Scholar]
- Abdelaziz, A.; Koksal, C.E. Fundamental limits of covert communication over MIMO AWGN channel. In Proceedings of the 2017 IEEE Conference on Communications and Network Security (CNS), Las Vegas, NV, USA, 9–11 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–9. [Google Scholar]
- Arumugam, K.S.K.; Bloch, M.R. Covert communication over broadcast channels. In Proceedings of the 2017 IEEE Information Theory Workshop (ITW), Kaohsiung, Taiwan, 6–10 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 299–303. [Google Scholar]
- Arumugam, K.S.K.; Bloch, M.R. Embedding covert information in broadcast communications. IEEE Trans. Inf. Forensics Secur. 2019, 14, 2787–2801. [Google Scholar] [CrossRef]
- Dutta, A.; Saha, D.; Grunwald, D.; Sicker, D. Secret agent radio: Covert communication through dirty constellations. In Proceedings of the International Workshop on Information Hiding, Berkeley, CA, USA, 18–20 July 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 160–175. [Google Scholar]
- Choi, H.; Park, S.; Lee, H.N. Covert Anti-Jamming Communication Based on Gaussian Coded Modulation. Appl. Sci. 2021, 11, 3759. [Google Scholar] [CrossRef]
- Wei, G.; Ding, S.; Yang, H.; Liu, W.; Yin, M.; Li, L. A Novel Localization Method of Wireless Covert Communication Entity for Post-Steganalysis. Appl. Sci. 2022, 12, 12224. [Google Scholar] [CrossRef]
- Arikan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Lehmann, E. Testing statistical hypotheses: The story of a book. In Selected Works of EL Lehmann; Springer: Boston, MA, USA, 2012; pp. 995–999. [Google Scholar]
- Lee, S.; Baxley, R.J.; McMahon, J.B.; Frazier, R.S. Achieving positive rate with undetectable communication over MIMO Rayleigh channels. In Proceedings of the 2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM), A Coruna, Spain, 22–25 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 257–260. [Google Scholar]
- Gallager, R.G. Information Theory and Reliable Communication; Springer: New York, NY, USA, 1968; Volume 2. [Google Scholar]
- Tal, I.; Vardy, A. List decoding of polar codes. IEEE Trans. Inf. Theory 2015, 61, 2213–2226. [Google Scholar] [CrossRef]
- ANSI/IEEE Std 802.11 Working Group. IEEE Std 802.11b-1999; IEEE Standard for Information Technology—Telecommunications and Information Exchange between Systems—Local and Metropolitan Networks—Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications: Higher-Speed Physical Layer Extension in the 2.4 GHz Band. IEEE: Piscataway, NJ, USA, 2000; pp. 1–96.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).