Analytical and Numerical Study of the Axial Stiffness of Fiber-Reinforced Elastomeric Isolators (FREIs) under Combined Axial and Shear Loads
Abstract
Featured Application
Abstract
1. Introduction
2. Review of the Analytical Solutions for the Vertical Response of FREIs
2.1. Vertical Stiffness and Effective Compressive Modulus
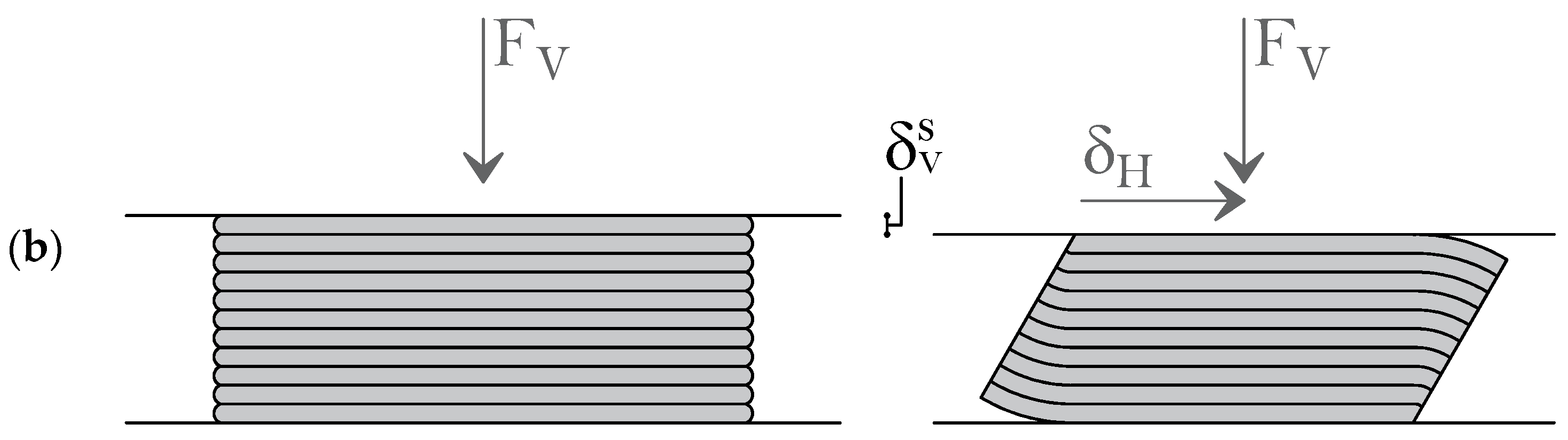
2.2. Axial Deformation under Vertical and Lateral Loads
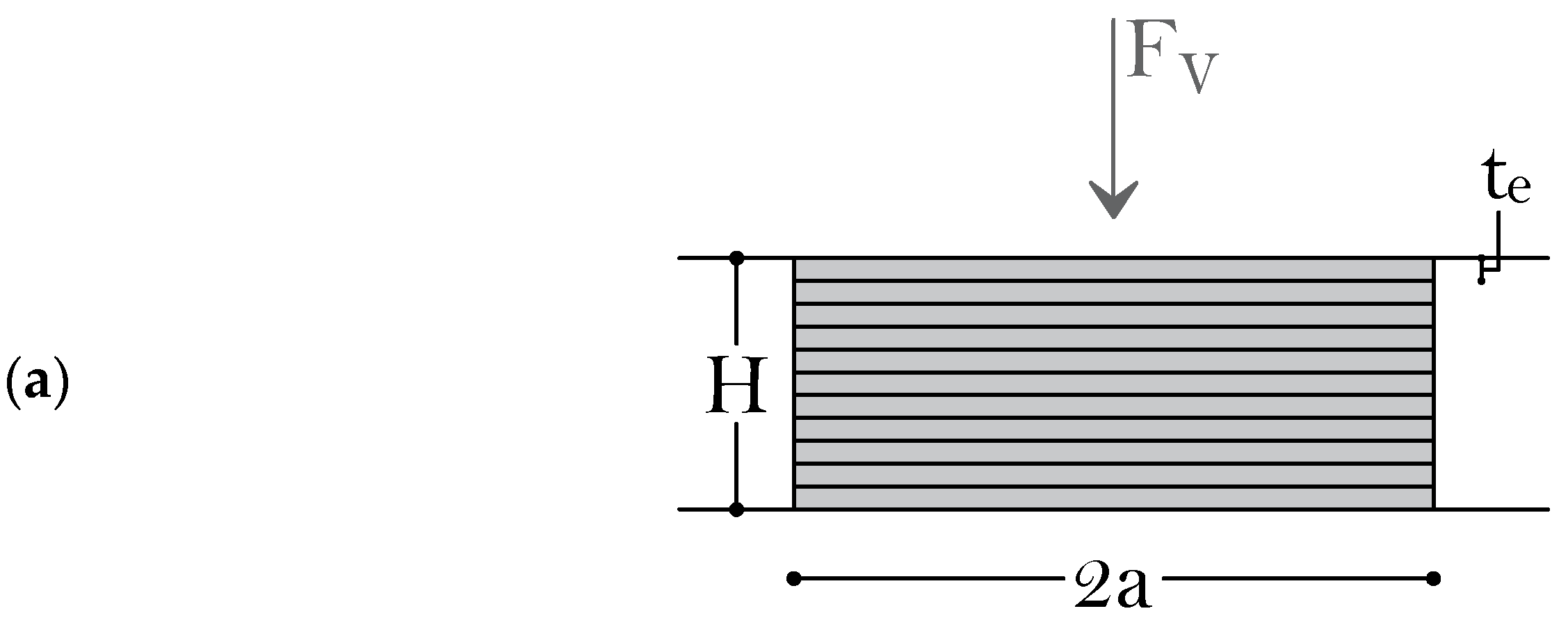
3. Vertical Stiffness and Effective Compressive Modulus under Axial and Shear Loads: Analytical Solution
3.1. Problem Setting
3.2. Analytical Formulation of the Function
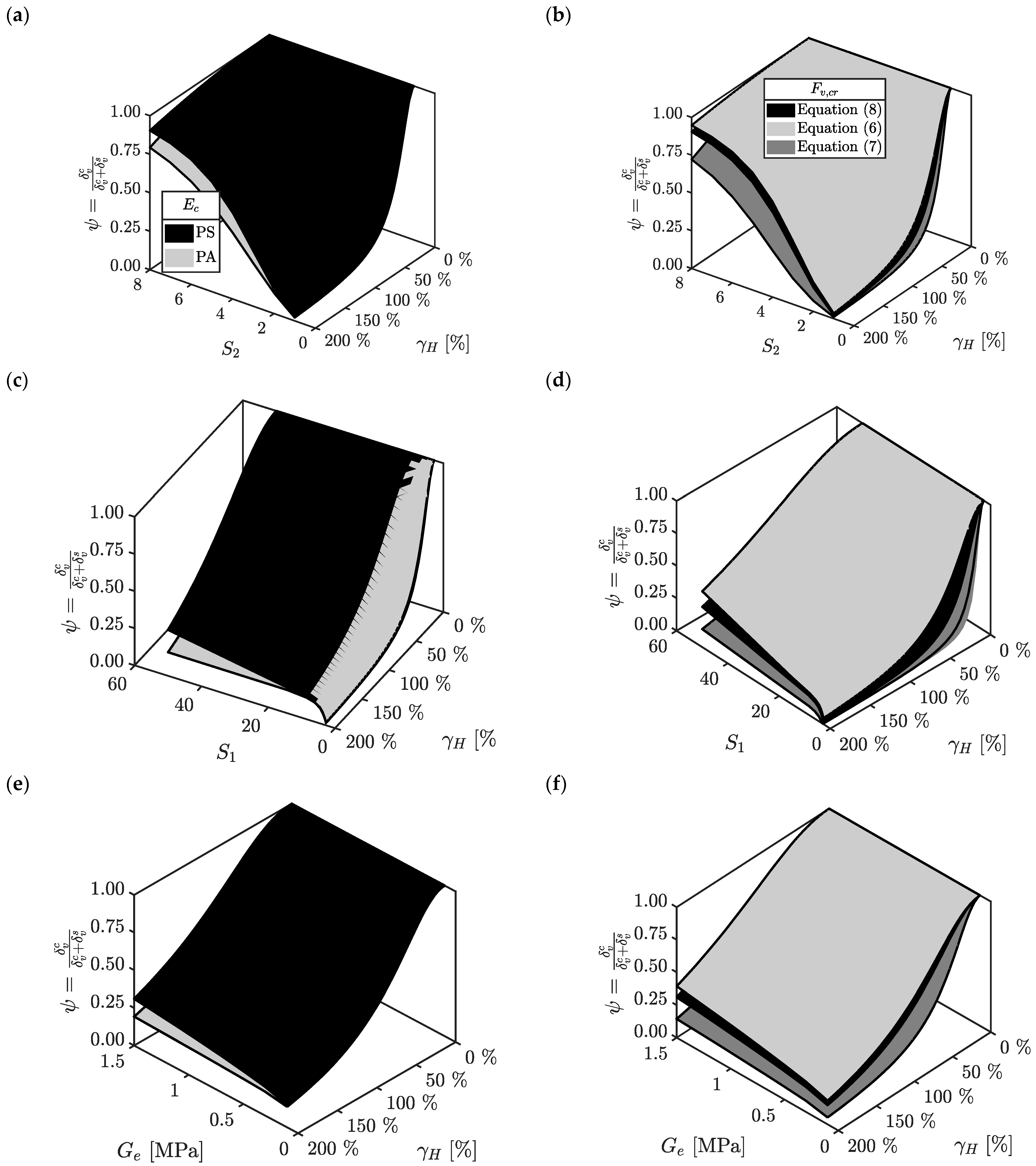
3.3. Variability of the Function
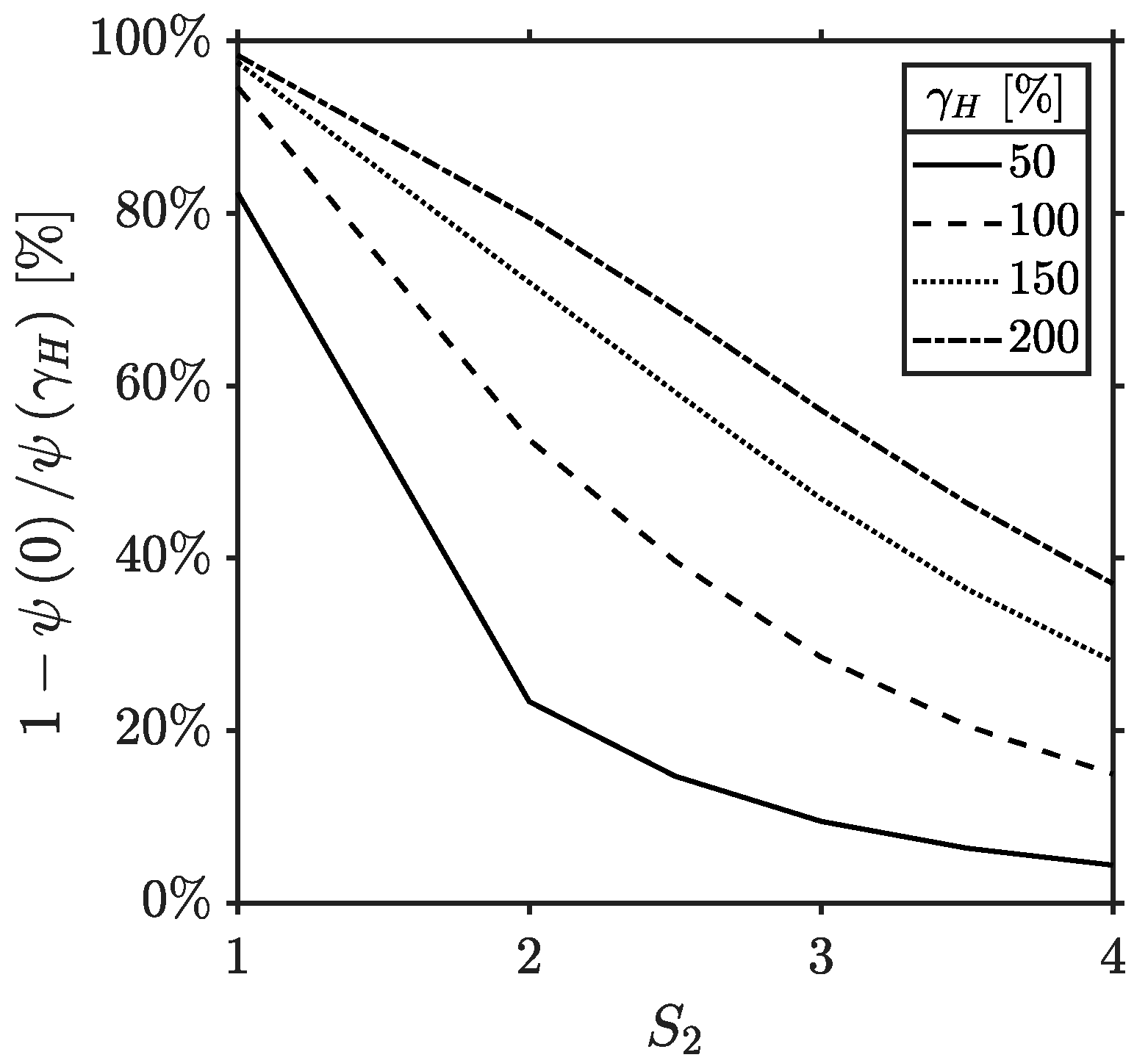
4. Finite Element Analyses
4.1. Description of the Finite Element Models
4.2. Numerical Modeling
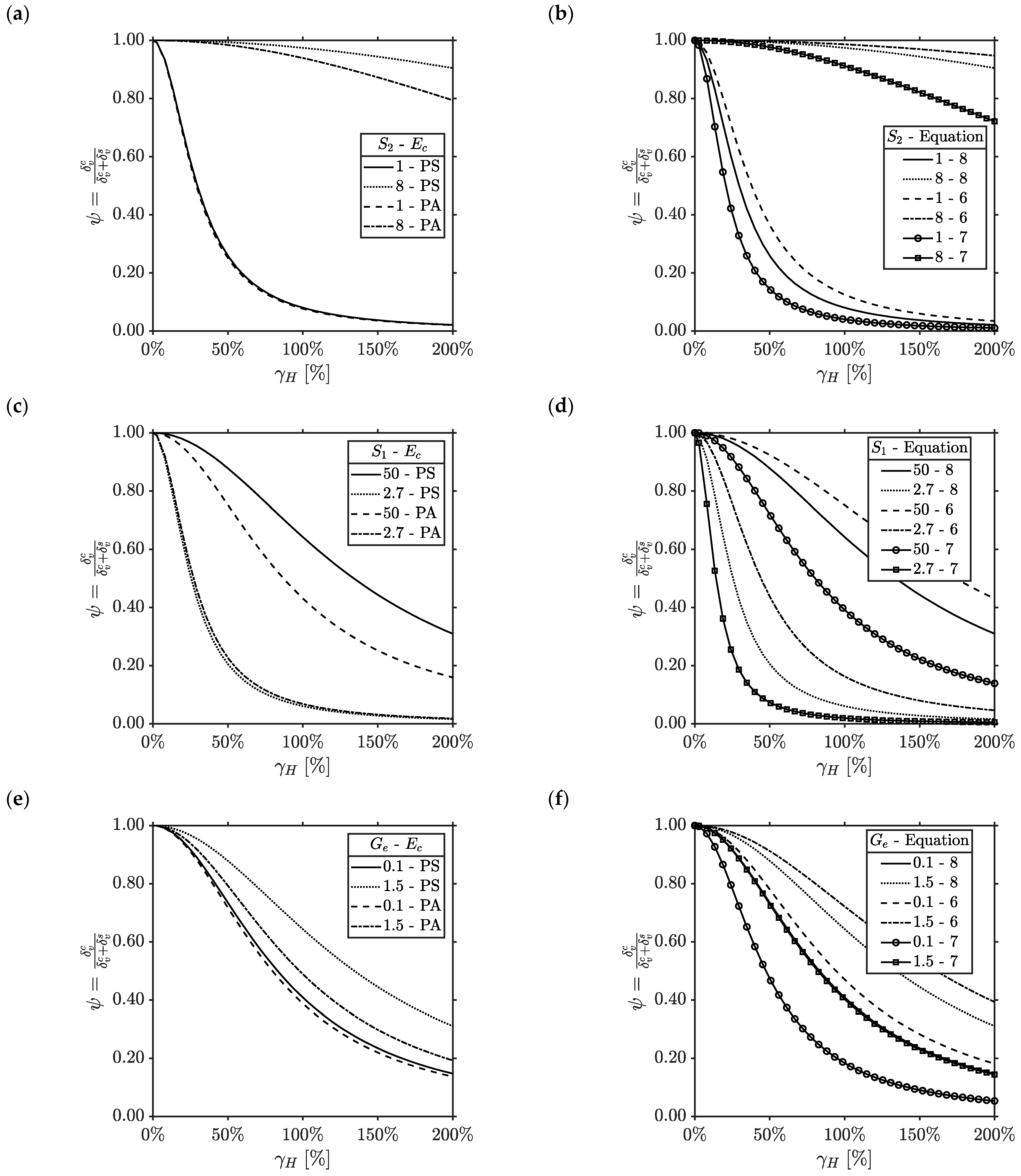
4.3. Numerical Results
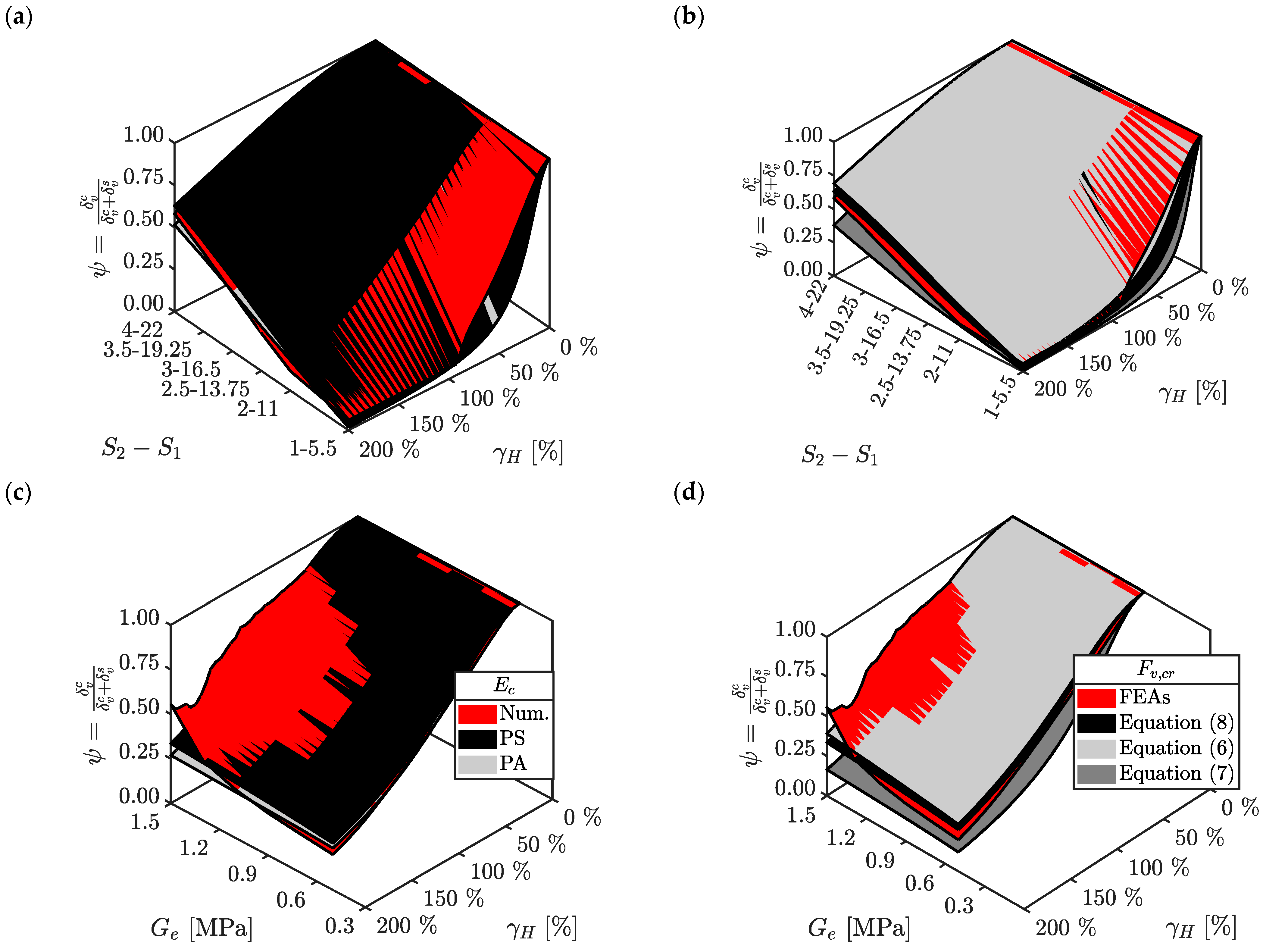
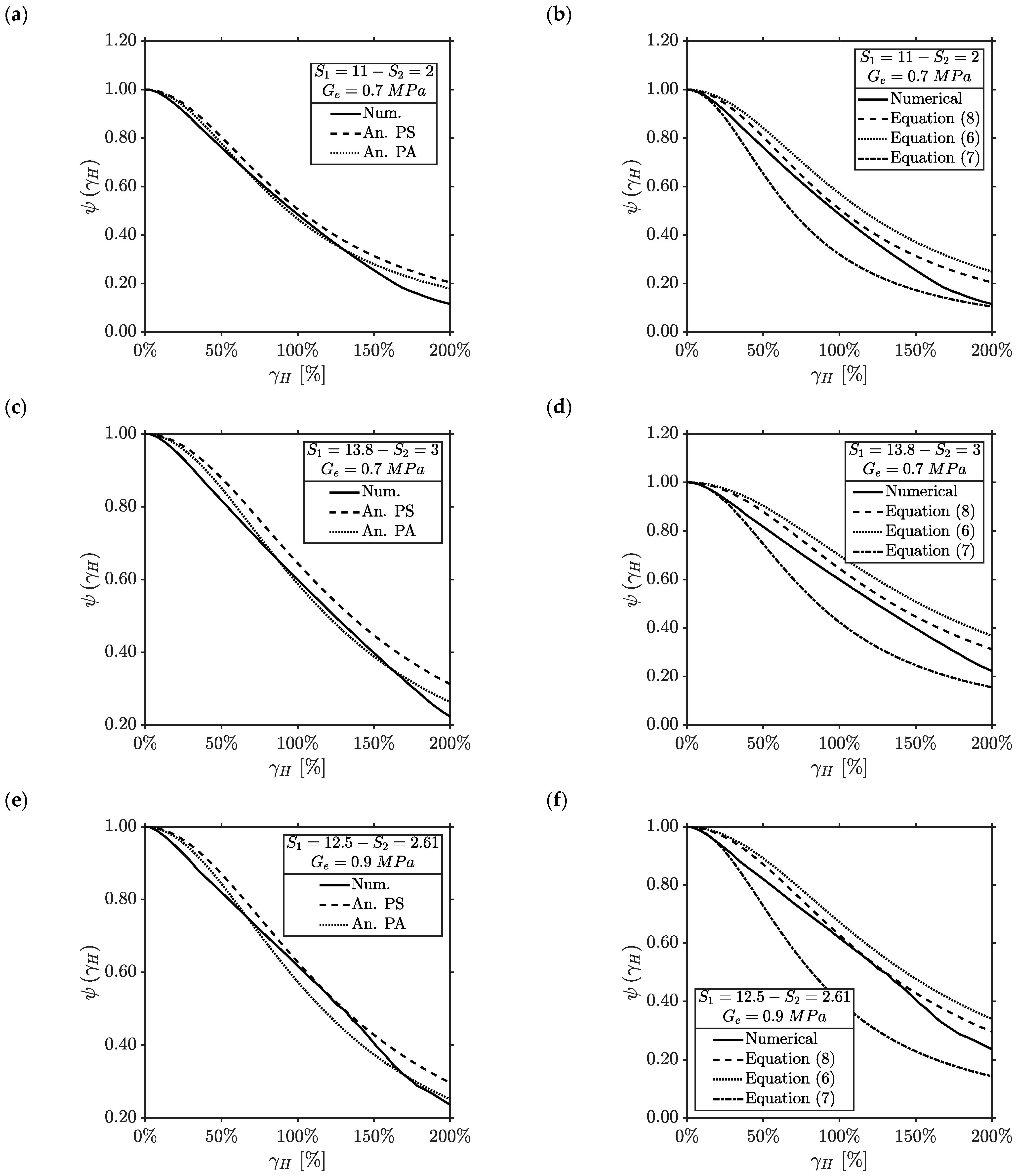
- Great reductions of with the horizontal deformation are related to smaller values of the primary and secondary shape factor (Figure 6a,b). When (), the function drops in a reduced range of shear strain (i.e., ), while for (), the minimum value of is around 0.5 at .
- The shear modulus of the rubber plays a minor role compared to the geometric parameters of the U-FREI (Figure 6c,d). A good agreement is found between numerical and analytical results, but for larger values of , the numerical trends return increasing values of . This is the effect of the full-rollover condition that is prominent for hard rather than soft compounds. Equation (15) does not take into account this phenomenon.
- : 36.3% (average on ) and 30.2% (average on );
- : 45.9% (average on ) and 28.3% (average on );
- : 57.0% (average on ) and 47.1% (average on );
- : 56.7% (average on ) and 48.4% (average on ).
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moon, B.Y.; Kang, G.J.; Kang, B.S.; Kelly, J.M. Design and manufacturing of fiber reinforced elastomeric isolator for seismic isolation. J. Mater. Process. Technol. 2002, 130, 145–150. [Google Scholar] [CrossRef]
- Crozier, W.F.; Stoker, J.R.; Martin, V.C.; Nordlin, E.F. A laboratory evaluation of full size elastomeric bridge baring pads. Transp. Res. Rec. 1975, 547, 55–58. [Google Scholar]
- Kelly, J.M. Analysis of fiber-reinforced elastomeric isolators. Int. J. Solids Struct. 1999, 2, 19–34. [Google Scholar]
- De Luca, A.; Guidi, L.G. State of art in the worldwide evolution of base isolation design. Soil Dyn. Earthq. Eng. 2019, 125, 105722. [Google Scholar] [CrossRef]
- Kelly, J.M. Analysis of the run-in effect in fiber-reinforced isolators under vertical load. J. Mech. Mater. Struct. 2008, 3, 1383–1401. [Google Scholar] [CrossRef]
- Ashkezari, G.D.; Aghakouchak, A.A.; Kokabi, M. Design, manufacturing and evaluation of the performance of steel like fiber reinforced elastomeric seismic isolators. J. Mater. Process. Technol. 2008, 197, 140–150. [Google Scholar] [CrossRef]
- Toopchi-Nezhad, H.; Tait, M.J.; Drysdale, R.G. Bonded versus unbonded strip fiber reinforced elastomeric isolators: Finite element analysis. Compos. Struct. 2011, 93, 850–859. [Google Scholar] [CrossRef]
- Kelly, J.M.; Konstantinidis, D.A. Mechanics of Rubber Bearings for Seismic and Vibration Isolation; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Toopchi-Nezhad, H.; Tait, M.J.; Drysdale, R.G. Testing and modeling of square carbon fiber-reinforced elastomeric seismic isolators. Struct. Control Health Monit. 2007, 15, 876–900. [Google Scholar] [CrossRef]
- Madera Sierra, I.E.; Losanno, D.; Strano, S.; Marulanda, J.; Thomson, P. Development and experimental behavior of HDR seismic isolators for low rise residential buildings. Eng. Struct. 2019, 183, 894–906. [Google Scholar] [CrossRef]
- Vaiana, N.; Losanno, D.; Ravichandran, N. A novel family of multiple springs models suitable for biaxial rate-independent hysteretic behavior. Comput. Struct. 2021, 244, 106403. [Google Scholar] [CrossRef]
- Vaiana, N.; Rosati, L. Classification and unified phenomenological modeling of complex uniaxial rate-independent hysteretic responses. Mech. Syst. Signal Process. 2023, 182, 109539. [Google Scholar] [CrossRef]
- Toopchi-Nezhad, H.; Tait, M.J.; Drysdale, R.G. Lateral Response Evaluation of Fiber-Reinforced Neoprene Seismic Isolators Utilized in an Unbonded Application. J. Struct. Eng. 2008, 134, 1627–1637. [Google Scholar] [CrossRef]
- Toopchi-Nezhad, H.; Drysdale, R.G.; Tait, M.J. Parametric Study on the Response of Stable Unbonded-Fiber Reinforced Elastomeric Isolators (SU-FREIs). J. Compos. Mater. 2009, 43, 1569–1587. [Google Scholar] [CrossRef]
- De Raaf, M.G.; Tait, M.J.; Toopchi-Nezhad, H. Stability of fiber-reinforced elastomeric bearings in an unbonded application. J. Compos. Mater. 2011, 45, 1873–1884. [Google Scholar] [CrossRef]
- UNI EN 1998-1:2013; Part 1: General Rules, Seismic Actions and Rules for Buildings. UNI Ente Italiano di Normazione: Milano, Italy, 2013.
- Galano, S.; Losanno, D.; Calabrese, A. Stability analysis of unbonded fiber reinforced isolators of square shape. Eng. Struct. 2021, 245, 112846. [Google Scholar] [CrossRef]
- Galano, S.; Calabrese, A.; Losanno, D. On the response of fiber reinforced elastomeric isolators (FREIs) under bidirectional shear loads. Structures 2021, 34, 2340–2354. [Google Scholar] [CrossRef]
- Galano, S.; Calabrese, A.; Losanno, D.; Serino, G.; Strano, S. Tuning the lateral response of unbonded fiber reinforced elastomeric isolators (U-FREIs) through horizontal holes: Experimental and numerical findings. Compos. Struct. 2022, 289, 115454. [Google Scholar] [CrossRef]
- Orfeo, A.; Tubaldi, E.; Muhr, A.H.; Losanno, D. Mechanical behaviour of rubber bearings with low shape factor. Eng. Struct. 2022, 266, 114532. [Google Scholar] [CrossRef]
- De Domenico, D.; Losanno, D.; Vaiana, N. Experimental tests and numerical modeling of full-scale unbonded fiber reinforced elastomeric isolators (UFREIs) under bidirectional excitation. Eng. Struct. 2023, 274, 115118. [Google Scholar] [CrossRef]
- Losanno, D.; De Domenico, D.; Madera-Sierra, I.E. Experimental testing of full-scale fiber reinforced elastomeric isolators (FREIs) in unbonded configuration. Eng. Struct. 2022, 260, 114234. [Google Scholar] [CrossRef]
- Losanno, D.; Ravichandran, N.; Parisi, F.; Calabrese, A.; Serino, G. Seismic performance of a Low-Cost base isolation system for unreinforced brick Masonry buildings in developing countries. Soil Dyn. Earthq. Eng. 2021, 141, 106501. [Google Scholar] [CrossRef]
- Losanno, D.; Ravichandran, R.; Parisi, F. Seismic fragility models for base-isolated unreinforced masonry buildings with fibre-reinforced elastomeric isolators. Earthq. Eng. Struct. Dyn. 2023, 52, 308–334. [Google Scholar] [CrossRef]
- Losanno, D.; Ravichandran, N.; Parisi, F. Seismic fragility of base-isolated single-storey unreinforced masonry buildings equipped with classical and recycled rubber bearings in Himalayan region. J. Build. Eng. 2022, 45, 103648. [Google Scholar] [CrossRef]
- Losanno, D.; Calabrese, A.; Madera-Sierra, I.E.; Spizzuoco, M.; Marulanda, J.; Thomson, P.; Serino, G. Recycled versus Natural-Rubber Fiber-Reinforced Bearings for Base Isolation: Review of the Experimental Findings. J. Earthq. Eng. 2020, 26, 1921–1940. [Google Scholar] [CrossRef]
- Cilento, F.; Losanno, D.; Piga, L. An experimental study on a novel reclaimed rubber compound for fiber-reinforced seismic isolators. Structures 2022, 45, 9–22. [Google Scholar] [CrossRef]
- Kelly, J.M. Earthquake-Resistant Design with Rubber; Springer: London, UK, 1996. [Google Scholar]
- Losanno, D.; Madera Sierra, I.E.; Spizzuoco, M.; Marulanda, J.; Thomson, P. Experimental assessment and analytical modeling of novel fiber-reinforced isolators in unbounded configuration. Compos. Struct. 2019, 212, 66–82. [Google Scholar] [CrossRef]
- Galano, S. Vertical response of unbonded fiber reinforced elastomeric isolators (U-FREIs) under bidirectional shear loading. Front. Built Environ. 2022, 8, 265. [Google Scholar] [CrossRef]
- Losanno, D.; Madera Sierra, I.E.; Spizzuoco, M.; Marulanda, J.; Thomson, P. Experimental performance of unbonded polyester and carbon fiber reinforced elastomeric isolators under bidirectional seismic excitation. Eng. Struct. 2022, 209, 110003. [Google Scholar] [CrossRef]
- Riascos, C.; Klopov, S.; Losanno, D.; Marulanda, J.; Thomson, P. Real-time hybrid simulations including rocking effects: The caso of a frame-structure with unbonded elastomeric isolators. Struct. Control Health Monit. 2022, 29, e2984. [Google Scholar] [CrossRef]
- Tsai, H.C.; Kelly, J.M. Stiffness Analysis of Fiber-Reinforced Elastomeric Isolators; PEER Report 05; Pacific Earthquake Engineering Research Center, College of Engineering, University of California Berkeley: Berkeley, CA, USA, 2001. [Google Scholar]
- Tsai, H.C. Compression stiffness of infinite-strip bearings of laminated elastic material interleaving with flexible reinforcements. Int. J. Solids Struct. 2004, 41, 6647–6660. [Google Scholar] [CrossRef]
- Tsai, H.C. Compression stiffness of circular bearings of laminated elastic material interleaving with flexible reinforcements. Int. J. Solids Struct. 2006, 43, 3484–3497. [Google Scholar] [CrossRef]
- Kelly, J.M.; Calabrese, A. Mechanics of Fiber Reinforced Bearings; PEER Report 101; Pacific Earthquake Engineering Research Center, College of Engineering, University of California Berkeley: Berkeley, CA, USA, 2012. [Google Scholar]
- Angeli, P.; Russo, G.; Paschini, A. Carbon fiber-reinforced rectangular isolators with compressible elastomer: Analytical solution for compression and bending. Int. J. Solids Struct. 2013, 50, 3519–3527. [Google Scholar] [CrossRef]
- Kelly, J.M.; Van Engelen, N.C. Single Series Solution for the Rectangular Fiber-Reinforced Elastomeric Isolator Compression Modulus; Headquarters at the University of California, Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2015. [Google Scholar]
- Pinarbasi, S.; Mengi, Y. Elastic layers bonded to flexible reinforcements. Int. J. Solids Struct. 2008, 45, 794–820. [Google Scholar] [CrossRef]
- Kelly, J.M. Tension Buckling in Multilayer Elastomeric Bearings. J. Eng. Mech. 2003, 129, 1363–1368. [Google Scholar] [CrossRef]
- Naeim, F.; Kelly, J.M. Design of Seismic Isolated Structures: From Theory to Practice; John Wiley & Sons, Inc.: New York, NY, USA, 1999. [Google Scholar]
- Kelly, J.M.; Marsico, M.R. Stability and post-buckling behavior in nonbolted elastomeric isolators. J. Anti-Seism. Syst. Int. Soc. 2010, 1, 41–54. [Google Scholar] [CrossRef]
- Calabrese, A.; Spizzuoco, M.; Galano, S.; Tran, N.; Strano, S.; Terzo, M. A parametric study on the stability of fiber reinforced rubber bearings under combined axial and shear loads. Eng. Struct. 2021, 2021, 111441. [Google Scholar] [CrossRef]
- Kelly, J.M.; Takhirov, S. Analytical and Numerical Study on Buckling of Elastomeric Bearings with Various Shape Factors; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2004. [Google Scholar]
- Tsai, H.H.; Kelly, J.M. Buckling load of seismic isolators affected by flexibility of reinforcement. Int. J. Solids Struct. 2005, 42, 255–269. [Google Scholar] [CrossRef]
- Tsai, H.H.; Kelly, J.M. Buckling of short beams with warping effect included. Int. J. Solids Struct. 2005, 42, 239–253. [Google Scholar] [CrossRef]
- Peng, T.B.; Li, J.Z.; Fan, L.C. Pilot Study on the Horizontal Shear Behavior of FRP Rubber Isolators; Asia-Pacific Conference on FRP in Structures (APFIS 2007); International Institute for FRP in Construction: Winnipeg, MB, Canada, 2007. [Google Scholar]
- Gerharer, U.; Strauss, A.; Bergmeister, K. Verbesserte Bemessungsrichtlinien für Bewehrte Elastomerlager. Bautechnik 2011, 88, 451–458. [Google Scholar] [CrossRef]
- Russo, G.; Pauletta, M.; Cortesia, A. A study on experimental shear behavior of fiber-reinforced elastomeric isolators with various fiber layouts, elastomers and aging conditions. Eng. Struct. 2013, 52, 422–433. [Google Scholar] [CrossRef]
- Toopchi-Nezhad, H. Horizontal stiffness solutions for unbonded fiber reinforced elastomeric bearings. Struct. Eng. Mech. 2014, 49, 395–410. [Google Scholar] [CrossRef]
- Van Engelen, N.C.; Tait, M.J.; Konstantinidis, D. Model of the Shear Behavior of Unbonded Fiber-Reinforced Elastomeric Isolators. J. Struct. Eng. 2015, 141, 04014169. [Google Scholar] [CrossRef]
- Van Ngo, T.; Dutta, A.; Deb, S.K. Evaluation of horizontal stiffness of fibre-reinforced elastomeric isolators. Earthq. Eng. Struct. Dyn. 2017, 46, 1747–1767. [Google Scholar] [CrossRef]
- Konstantinidis, D.; Kelly, J.M.; Makris, N. Experimental Investigations on the Seismic Response of Bridge Bearings; PEER Report 2008/02; Pacific Earthquake Engineering Research Center, College of Engineering, University of California Berkeley: Berkeley, CA, USA, 2008. [Google Scholar]
- UNI EN 15129:2018; Comité Européen de Normalisation TC 340, Anti-Seismic Devices. European Committee for Standardization CEN: Brussels, Belgium, 2018.
- Furinghetti, M.; Pavese, A. Equivalent Uniaxial Accelerogram for CSS-Based Isolation Systems Assessment under Two-Components Seismic Events. Mech. Based Des. Struct. Mach. 2017, 45, 282–295. [Google Scholar] [CrossRef]
- MSC. Software Corporation. MSC.Marc Mentat Release Guide; MSC. Software Corporation: Santa Ana, CA, USA, 2005. [Google Scholar]
- MSC. Software Corporation. MAR103 Experimental Elastomer Analysis; MSC. Software Corporation: Santa Ana, CA, USA, 2017. [Google Scholar]
- MSC. Software Corporation. Volume B: Element Library; MSC. Software Corporation: Santa Ana, CA, USA, 2017. [Google Scholar]
- Kelly, J.M.; Konstantinidis, D. Effect of Friction on Unbonded Elastomeric Bearings. J. Eng. Mech. 2009, 135, 953–960. [Google Scholar] [CrossRef]
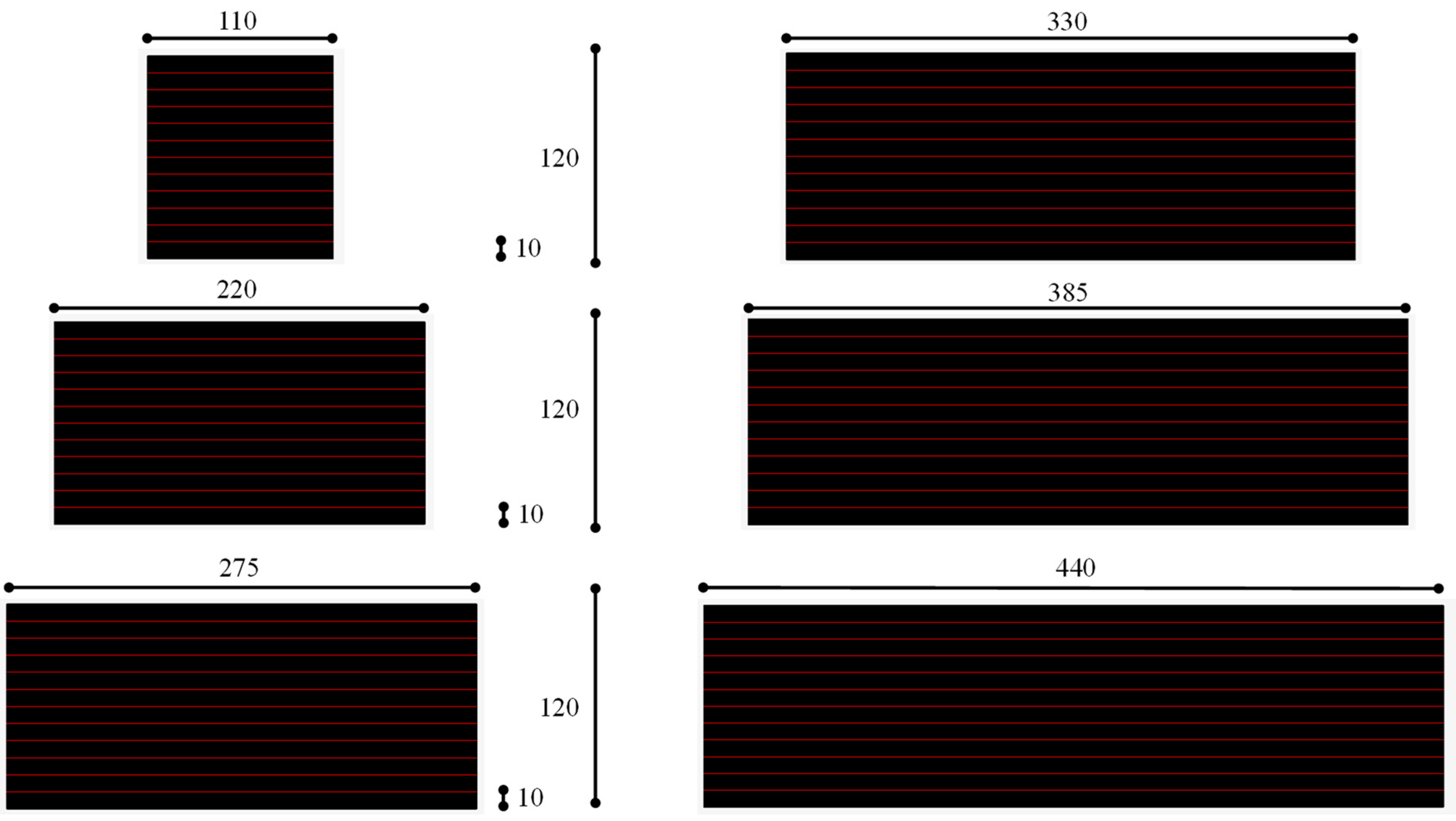

| 1 | 74.6% | 91.8% | 96.4% | 97.9% |
| 2 | 25.6% | 56.6% | 75.6% | 84.3% |
| 3 | 10.3% | 30.4% | 50.9% | 64.3% |
| 4 | 4.80% | 16.1% | 31.2% | 44.0% |
| 5 | 2.53% | 8.95% | 18.9% | 28.8% |
| 6 | 1.48% | 5.39% | 11.9% | 19.0% |
| 7 | 0.955% | 3.53% | 7.99% | 13.1% |
| 8 | 0.673% | 2.50% | 5.74% | 9.54% |
| 2.7 | 79.9% | 93.8% | 97.3% | 98.4% |
| 3.1 | 57.7% | 83.8% | 92.5% | 95.5% |
| 3.7 | 43.9% | 74.8% | 87.6% | 92.4% |
| 4.5 | 35.6% | 67.7% | 83.3% | 89.6% |
| 5.9 | 30.4% | 62.4% | 79.8% | 87.2% |
| 8.3 | 26.9% | 58.2% | 76.8% | 85.1% |
| 14 | 23.5% | 53.8% | 73.5% | 82.7% |
| 50 | 12.5% | 35.2% | 56.3% | 69.0% |
| 0.10 | 27.1% | 58.5% | 77.0% | 85.3% |
| 0.30 | 21.3% | 50.7% | 70.9% | 80.8% |
| 0.50 | 18.7% | 46.6% | 67.4% | 78.2% |
| 0.70 | 16.8% | 43.4% | 64.5% | 75.9% |
| 0.90 | 15.4% | 40.8% | 62.0% | 73.9% |
| 1.1 | 14.2% | 38.5% | 59.8% | 72.0% |
| 1.3 | 13.2% | 36.7% | 57.9% | 70.4% |
| 1.5 | 12.5% | 35.1% | 56.2% | 68.9% |
| 2a | H | |||||
|---|---|---|---|---|---|---|
| [mm] | [mm] | [mm] | [mm] | [-] | [-] | [MPa] |
| 110 | 120 | 10.0 | 1.00 | 5.500 | 1.00 | 0.500 |
| 220 | 11.00 | 2.00 | 0.700 | |||
| 275 | 13.75 | 2.50 | 0.900 | |||
| 330 | 16.50 | 3.00 | 1.10 | |||
| 385 | 19.25 | 3.50 | 1.30 | |||
| 440 | 22.00 | 4.00 | 1.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galano, S.; Calabrese, A. Analytical and Numerical Study of the Axial Stiffness of Fiber-Reinforced Elastomeric Isolators (FREIs) under Combined Axial and Shear Loads. Appl. Sci. 2023, 13, 3515. https://doi.org/10.3390/app13063515
Galano S, Calabrese A. Analytical and Numerical Study of the Axial Stiffness of Fiber-Reinforced Elastomeric Isolators (FREIs) under Combined Axial and Shear Loads. Applied Sciences. 2023; 13(6):3515. https://doi.org/10.3390/app13063515
Chicago/Turabian StyleGalano, Simone, and Andrea Calabrese. 2023. "Analytical and Numerical Study of the Axial Stiffness of Fiber-Reinforced Elastomeric Isolators (FREIs) under Combined Axial and Shear Loads" Applied Sciences 13, no. 6: 3515. https://doi.org/10.3390/app13063515
APA StyleGalano, S., & Calabrese, A. (2023). Analytical and Numerical Study of the Axial Stiffness of Fiber-Reinforced Elastomeric Isolators (FREIs) under Combined Axial and Shear Loads. Applied Sciences, 13(6), 3515. https://doi.org/10.3390/app13063515






