Uncertainty Analysis of Spherical Joint Three-Dimensional Rotation Angle Measurement
Abstract
:1. Introduction
2. Principle and Experiment
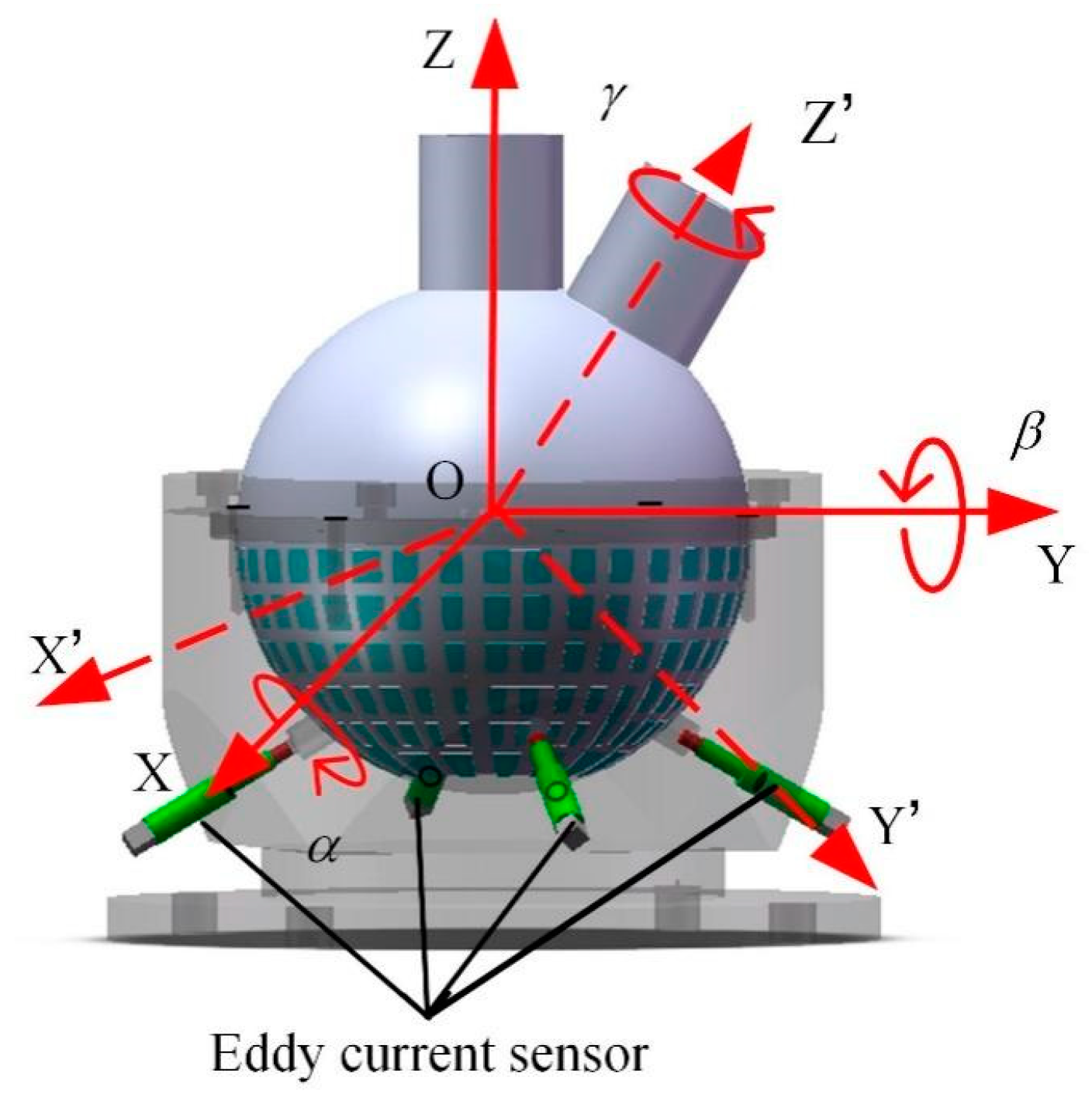
2.1. Principle
2.2. Measurement System and Data Acquisition
2.3. Generalized Regression Neural Network Data Processing
3. Uncertainty Analysis of Spherical Joint Space Rotation Measurement System
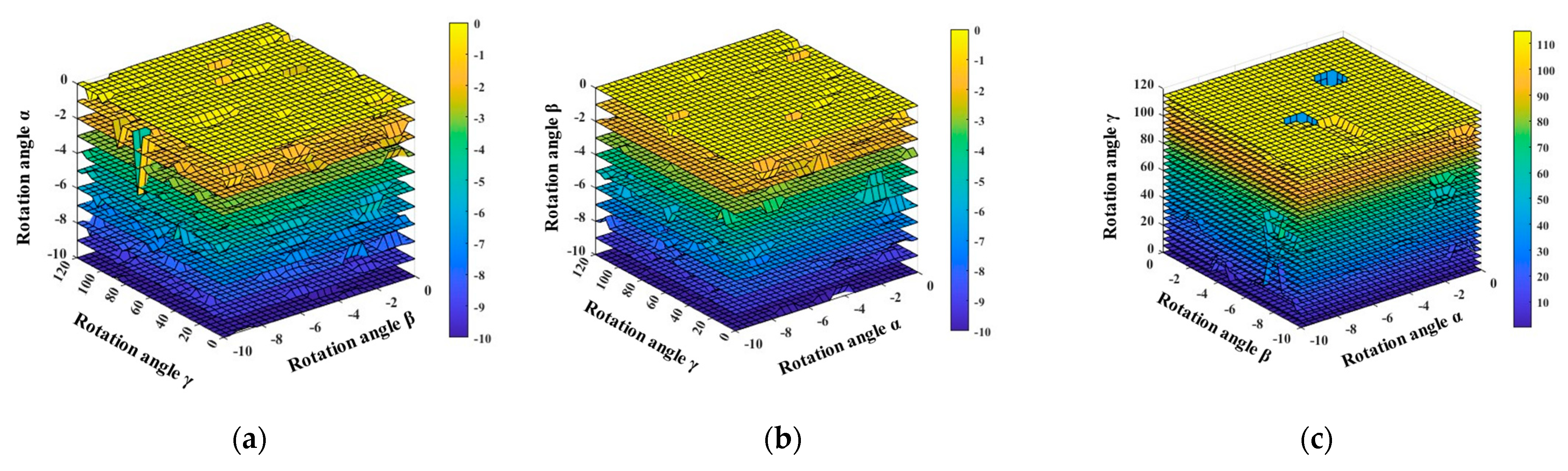
3.1. Source Analysis of Uncertainty under Specific Angle Measurement
- y—measurement results synthesized according to the uncertainty model;
- Y—results obtained through measurement model calculation;
- u1—the uncertainty component of the calibration platform rotation;
- u2—the uncertainty component of ball head eccentricity;
- u3—the uncertainty component of the sensor and neural network measurement model.
3.2. Uncertainty Caused by Calibration Platform Rotation Error
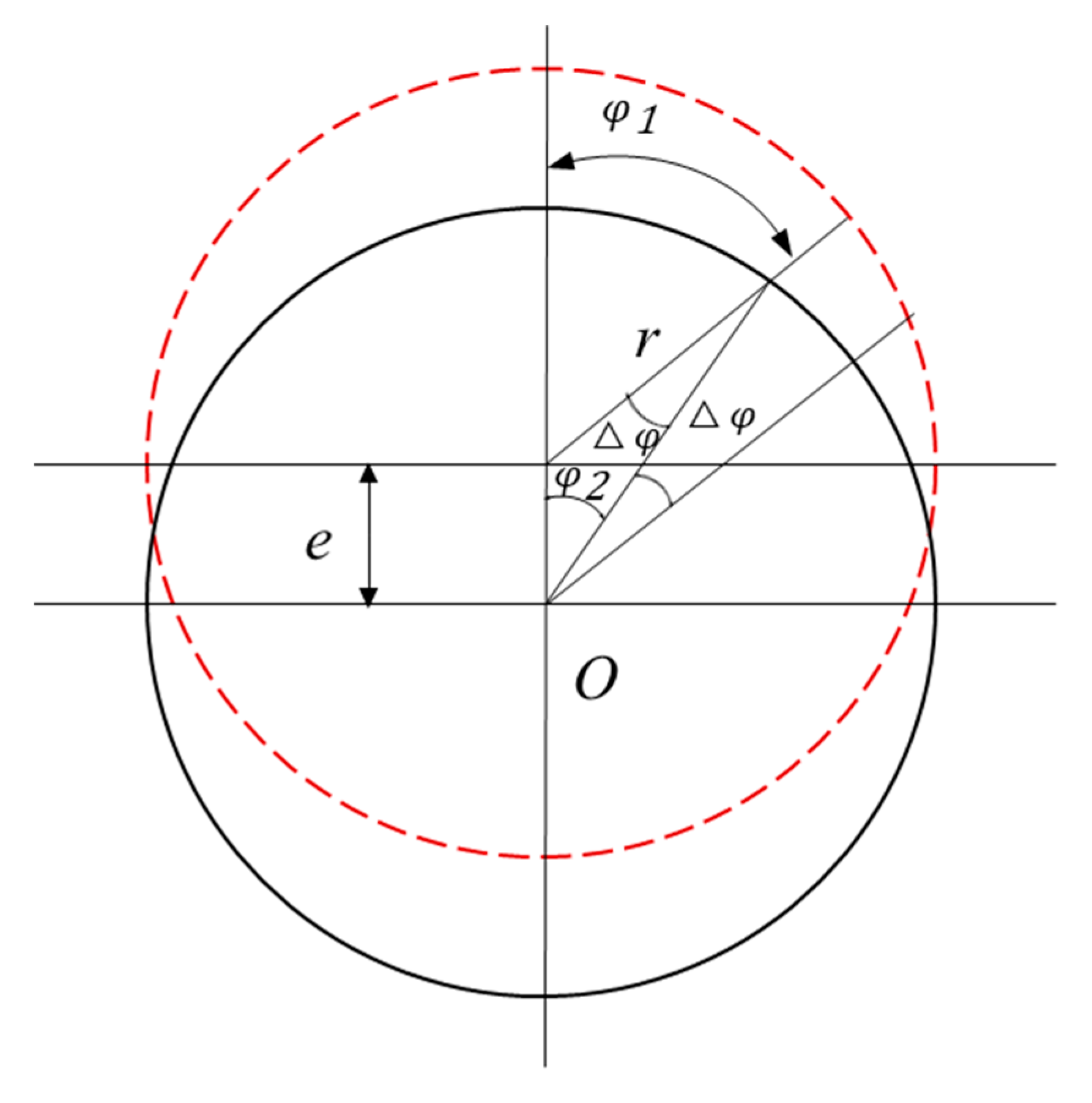
3.3. Uncertainty Caused by Ball Head Eccentricity
3.4. Uncertainty Caused by Network Model and Sensor
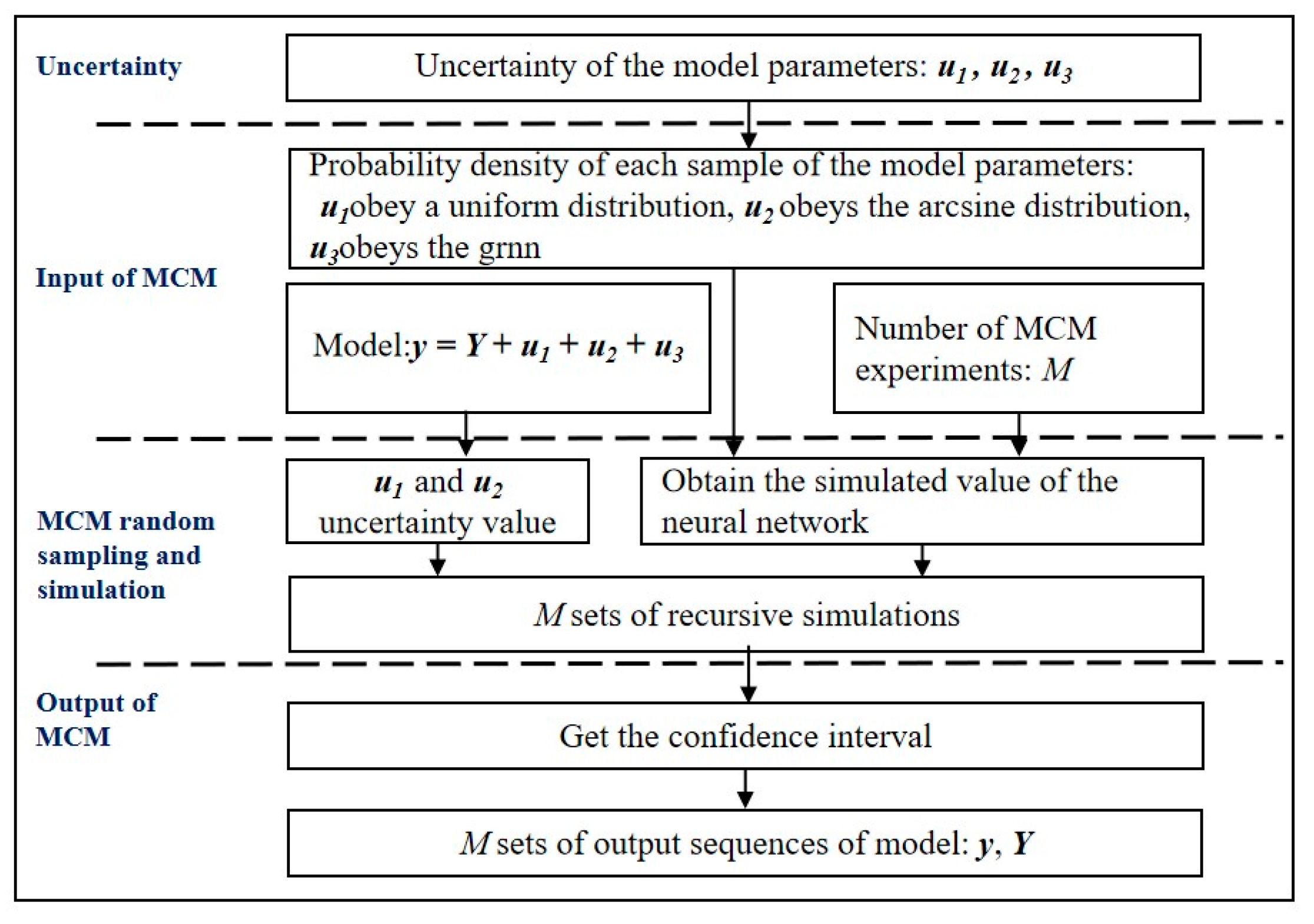
4. Evaluation of Measurement Uncertainty at Specific Angles
- (1)
- After optimizing the parameters of the measurement model based on GRNN, the ω value was determined, which was the optimal network measurement model.
- (2)
- The probability density function of each input value of the sensor array is determined as S1~N (−1.9587, 0.00102), the input S2~N (−1.6779, 0.00122), the input S3~N (2.4394, 0.00102), and the input S4~N (−3.5227, 0.00112).
- (3)
- When setting random sampling times, M = 106, S1, S2, S3, and S4 are randomly selected through random M number generation in MATLAB and put into a well-trained neural network measurement model to obtain M (α, β, and γ) sample values which contain both the sensor and the neural network’s own uncertainty.
- (4)
- The above two sections show that the rotation errors caused by the errors of the three-dimensional rotary calibration table are respectively subjected to U(−1″, 1″), subjected to U(−3.6″, 3.6″), and subjected to U(−2″, 2″). The rotation errors caused by the ball head eccentricity error are as follows: obeys the arcsine distribution (−2′41″, 2′41″), obeys the arcsine distribution (−2′37″, 2′37″), and obeys the arcsine distribution (−1′35″, 1′35″).
- (5)
- M random simulation samples are performed separately, assuming that the items are independent of each other, and are calculated according to Equation (5), with the sample values (α″, β″, γ″) of (α, β, and γ).
- (6)
- According to the algorithm steps of the Monte Carlo method, the final result of calculating the average of 106 simulation calculations yields α, β, γ at (−5°, −5°, 0°), the optimal estimate of the measured value at (−5°, −58′51″, −4°59′59″, 0°11′12″), at which point the standard uncertainty for each rotation angle is = 1′33″, = 1′31″, and = 39″.
- (7)
- The confidence probability p = 95% is set, and the sum and quantiles after numerical increments (α″, β″, γ″) are obtained. Thus, the inclusion intervals of α, β, and γ are α ϵ [−5°1′26″, −4°56′19″], β ϵ [−5°2′29″, −4°57′30″], and γ ϵ [10′8″, 12′17″], depending on (12):calculated for the extended uncertainty of each rotation angle, then α, β, and γ at (−5°, −5°, 0°) is measured as (−4°59′55″ ± 2′39″, −5°1″ ± 2′29″, 49″ ± 1′5″). Figure 10 shows the process of specific uncertainty assessment.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, C.; Lv, J. Geometrical deviation modeling and monitoring of 3D surface based on multi-output Gaussian process. Measurement 2022, 199, 111569. [Google Scholar] [CrossRef]
- Belagoune, S.; Bali, N. Deep learning through LSTM classification and regression for transmission line fault detection, diagnosis and location in large-scale multi-machine power systems. Measurement 2021, 177, 109330. [Google Scholar] [CrossRef]
- Nguyen, Q.; Chou, Y. Multiple-Inputs and Multiple-Output Wireless Power Combining and Delivery Systems. IEEE Trans. Power Electron. 2015, 30, 6254–6263. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J. Joint 2D-DOD, 2D-DOA, and Polarization Angles Estimation for Bistatic EMVS-MIMO Radar via PARAFAC Analysis. IEEE Trans. Veh. Technol. 2020, 69, 1626–1638. [Google Scholar] [CrossRef]
- Chau, E.; Kim, J.R. Engineering of a protein probe with multiple inputs and multiple outputs for evaluation of alpha synuclein aggregation states. Biochem. Eng. J. 2022, 178, 108292. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Wang, K. Real-time uncertainty estimation of stripe center extraction results using adaptive BP neural network. Measurement 2022, 194, 111022. [Google Scholar] [CrossRef]
- Zhang, K.; Cheng, G. Evaluation of roundness error uncertainty by a Bayesian dynamic model. Measurement 2020, 155, 107565. [Google Scholar] [CrossRef]
- Zhang, B.; Shin, Y.C. A probabilistic neural network for uncertainty prediction with applications to manufacturing process monitoring. Appl. Soft Comput. 2022, 124, 108995. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, Y. Prediction of short-term PV power output and uncertainty analysis. Appl. Energy 2018, 228, 700–711. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Z. Corn yield prediction and uncertainty analysis based on remotely sensed variables using Bayesian neural network approach. Remote Sens. Environ. 2021, 259, 112408. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, D. Measurement uncertainty evaluation in whiplash test model via neural network and support vector machine-based Monte Carlo method. Measurement 2018, 119, 229–245. [Google Scholar] [CrossRef]
- Antanasijević, D.; Pocajt, V. Modeling of dissolved oxygen in the Danube River using artificial neural networks and Monte Carlo Simulation uncertainty analysis. J. Hydrol. 2014, 519, 1895–1907. [Google Scholar] [CrossRef]
- Mou, J.; Su, J. Evaluation of Angle Measurement Uncertainty of Fiber Optic Gyroscope Based on Monte Carlo Method. IEEE Trans. Instrum. Meas. 2021, 70, 3080390. [Google Scholar] [CrossRef]
- Zhen-Ying, C.; Wen-Shu, J. Uncertainty evaluation for dynamic identification of a micro contact probe based on the signal transmission chain analysis method. Meas. Sci. Technol. 2020, 31, 125007. [Google Scholar] [CrossRef]
- Madsen, D.; Morel-Forster, A. A Closest Point Proposal for MCMC-based Probabilistic Surface Registration. In Computer Vision–ECCV 2020, Proceedings of the Part XVII 16 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 281–296. [Google Scholar]
- Zhang, K.; Su, K. Dynamic evaluation and analysis of the uncertainty of roundness error measurement by Markov Chain Monte Carlo method. Measurement 2022, 201, 111771. [Google Scholar] [CrossRef]
- Shim, H.-S.; Park, S.-N. Numerical Experiments on the Application of Markov Chain Monte Carlo for the Establishment of Calibration Intervals. IEEE Trans. Instrum. Meas. 2022, 71, 1000610. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z. Application of adaptive Monte Carlo method to evaluate pose uncertainty in monocular vision system. Opt. Eng. 2022, 61, 061413. [Google Scholar] [CrossRef]
- Hu, P.; Lu, Y. Measurement method of rotation angle and clearance in intelligent spherical hinge. Meas. Sci. Technol. 2018, 29, 064012. [Google Scholar] [CrossRef]
- Hu, P.; Tang, C. Research on Measurement Method of Spherical Joint Rotation Angle Based on ELM Artificial Neural Network and Eddy Current Sensor. IEEE Sens. J. 2021, 21, 12269–12275. [Google Scholar] [CrossRef]
- Hu, P.; Zhao, L. A New Method for Measuring the Rotational Angles of a Precision Spherical Joint Using Eddy Current Sensors. Sensors 2020, 20, 4020. [Google Scholar] [CrossRef]
- Yang, L.; Hu, P. A new method for measuring 3D rotation angle of spherical joint. Measurement 2022, 190, 110661. [Google Scholar] [CrossRef]
- Narender, K.; MadhusudhanRao, A. Thermo physical properties of wrought aluminum alloys 6061, 2219 and 2014 by gamma ray attenuation method. Thermochim. Acta 2013, 569, 90–96. [Google Scholar] [CrossRef]
- Qiu, Z. Precision Mechanical Design Basics; China Machine Press: Beijing, China, 2007; p. 227. [Google Scholar]
- Ruxton, G.D.; Wilkinson, D.M. Advice on testing the null hypothesis that a sample is drawn from a normal distribution. Anim. Behav. 2015, 107, 249–252. [Google Scholar] [CrossRef]



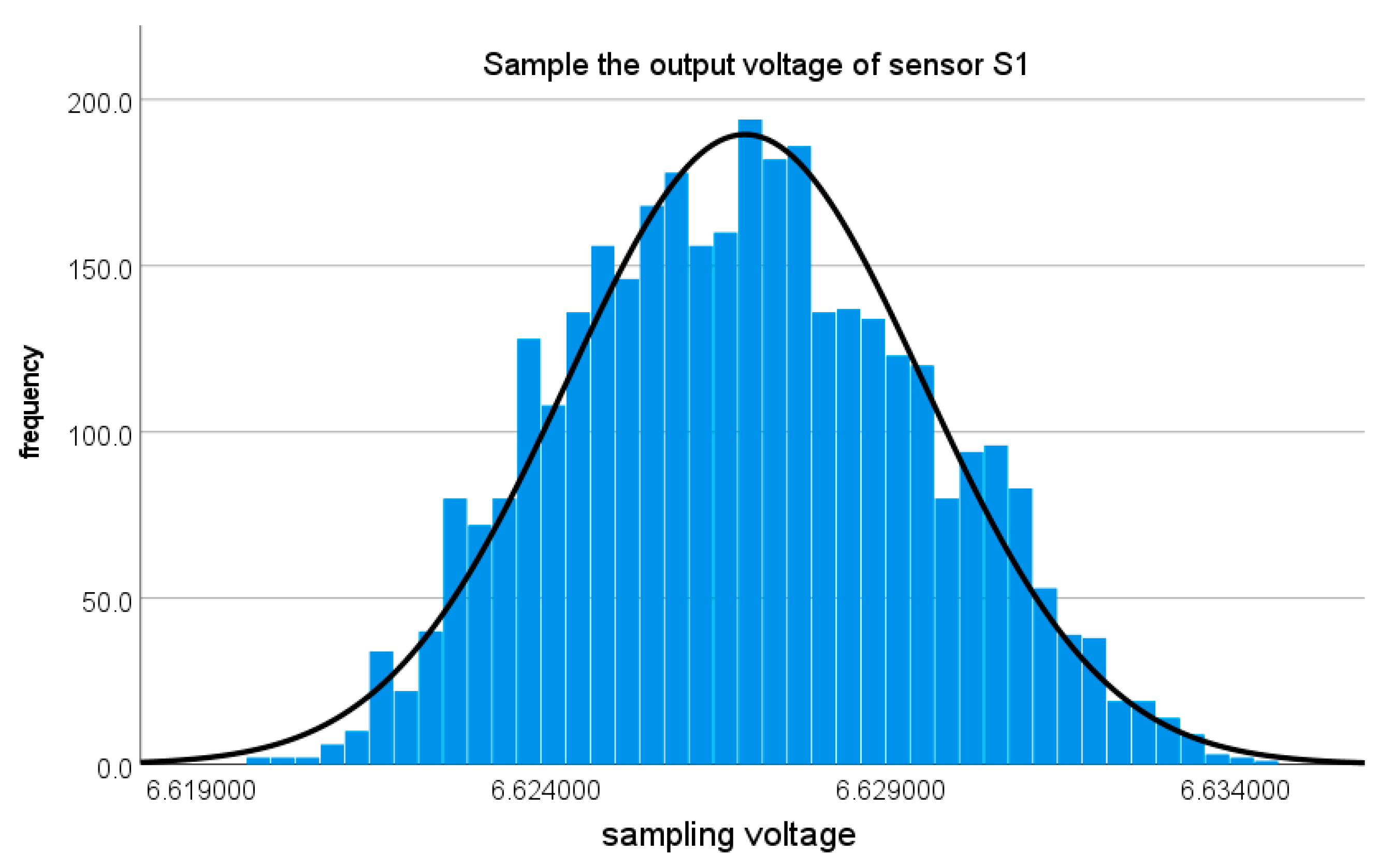
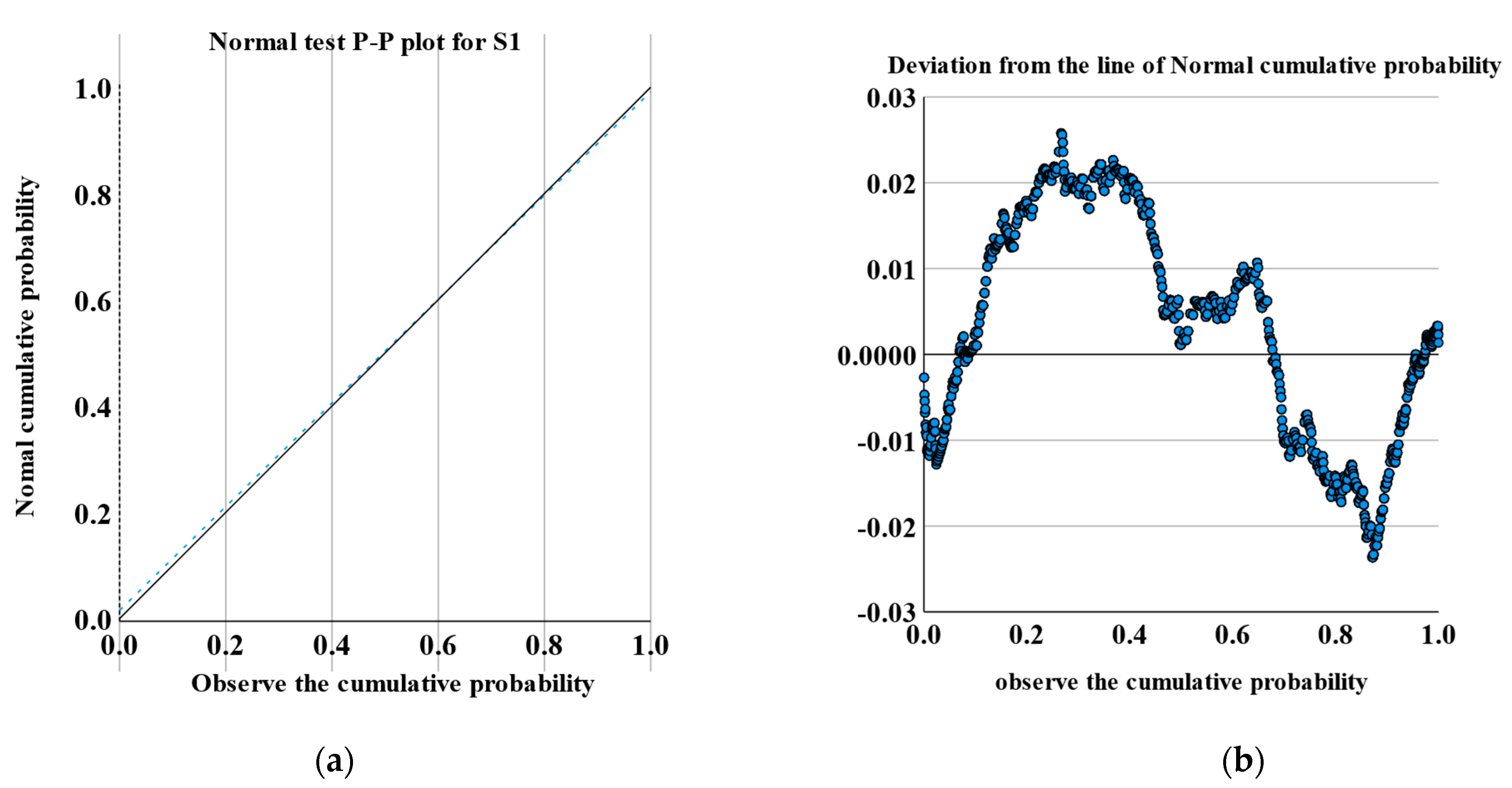

| Sensor Model | The Average | The Standard Deviation | Skewness | Kurtosis | S–W Test |
|---|---|---|---|---|---|
| S1 | 6.627 | 0.003 | 0.12 | −0.523 | 0.994 (0.000 ***) |
| S2 | 3.470 | 0.001 | 0.049 | 0.075 | 0.999 (0.010 **) |
| S3 | 2.190 | 0.001 | 0.146 | −0.085 | 0.998 (0.000 ***) |
| S4 | 6.098 | 0.001 | −0.085 | −0.207 | 0.997 (0.000 ***) |
| Sampling of S1 | Data 1 | Data 2 | Data 3 | Data 4 | Data 5 | Data 6 | Data 7 | Data 8 | Data 9 |
|---|---|---|---|---|---|---|---|---|---|
| Average (V) | 6.6246 | 6.6645 | 6.6697 | 6.6269 | 6.6277 | 6.6105 | 6.6282 | 6.6629 | 6.6613 |
| The SD(V) | 0.0063 | 0.0025 | 0.0059 | 0.0026 | 0.0014 | 0.0082 | 0.0012 | 0.0012 | 0.0034 |
| (α, β, γ) | Angle of Component | The Best Estimate | Standard Uncertainty | Interval | Extension Uncertainty |
|---|---|---|---|---|---|
| (−5°, −5°, 0°) | α | −4°59′55″ | 1′33″ | [−5°2′27″, −4°57′22″] | 2′39″ |
| β | −5°1″ | 1′31″ | [−5°2′29″, −4°57′31″] | 2′29″ | |
| γ | 49″ | 1′3″ | [−16″, 1′53″] | 1′5″ | |
| (−5°, 5°, 5°) | α | −5° | 1′33″ | [−5°2′33″, −4°57′27″] | 2′33″ |
| β | 5° | 1′30″ | [4°57′31″, 5°2′29″] | 2′29″ | |
| γ | 5°16″ | 42″ | [4°59′11″, 5°1′21″] | 1′6″ | |
| (5°, −5°, 0°) | α | 4°1″ | 1°1″ | [3°7′28″, 5°22′33″] | 1°7′33″ |
| β | −5°1″ | 1′31″ | [−5°2′30″, −4°57′31″] | 2′29″ | |
| γ | 56′59″ | 36′59″ | [44′45″, 2°38′44″] | 56′59″ | |
| (5°, 5°, 5°) | α | 4°47′20″ | 39′18″ | [4°33′40″, 6°21′52″] | 54′6″ |
| β | 5°19′17″ | 27′29″ | [4°28′4″, 5°36′26″] | 43′51″ | |
| γ | 5°33′18″ | 33′20″ | [4°30′44″, 5°55′51″] | 37′34″ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Yang, Q.; Yang, L.; Hu, P. Uncertainty Analysis of Spherical Joint Three-Dimensional Rotation Angle Measurement. Appl. Sci. 2023, 13, 3544. https://doi.org/10.3390/app13063544
Zhang J, Yang Q, Yang L, Hu P. Uncertainty Analysis of Spherical Joint Three-Dimensional Rotation Angle Measurement. Applied Sciences. 2023; 13(6):3544. https://doi.org/10.3390/app13063544
Chicago/Turabian StyleZhang, Jin, Qianyun Yang, Long Yang, and Penghao Hu. 2023. "Uncertainty Analysis of Spherical Joint Three-Dimensional Rotation Angle Measurement" Applied Sciences 13, no. 6: 3544. https://doi.org/10.3390/app13063544






