Simplified Calculation Model for Contact Resistance Based on Fractal Rough Surfaces Method
Abstract
:1. Introduction
2. Modeling
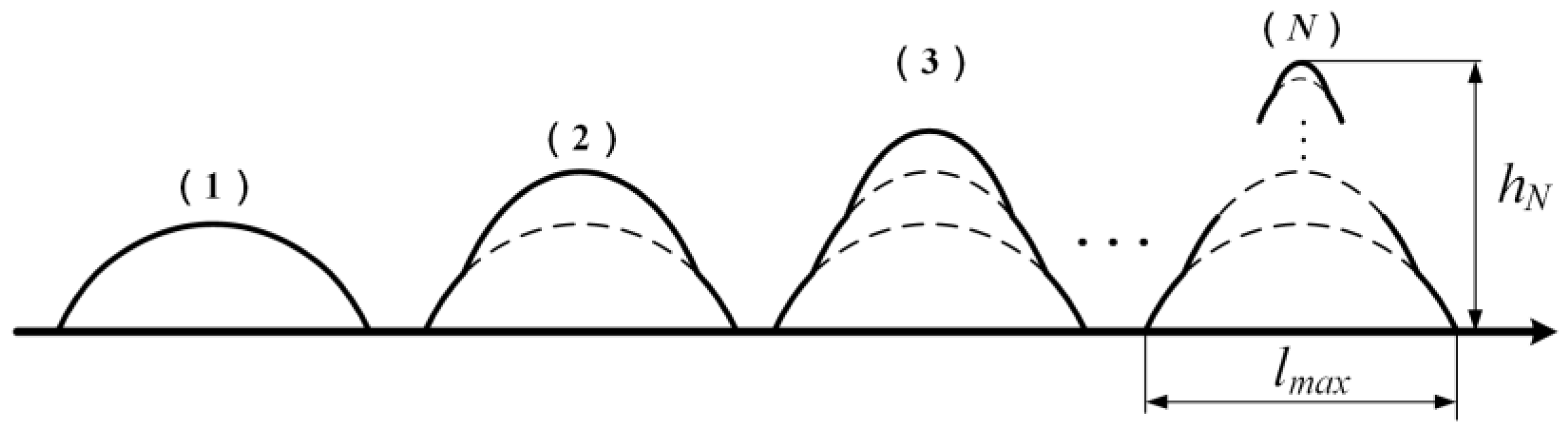
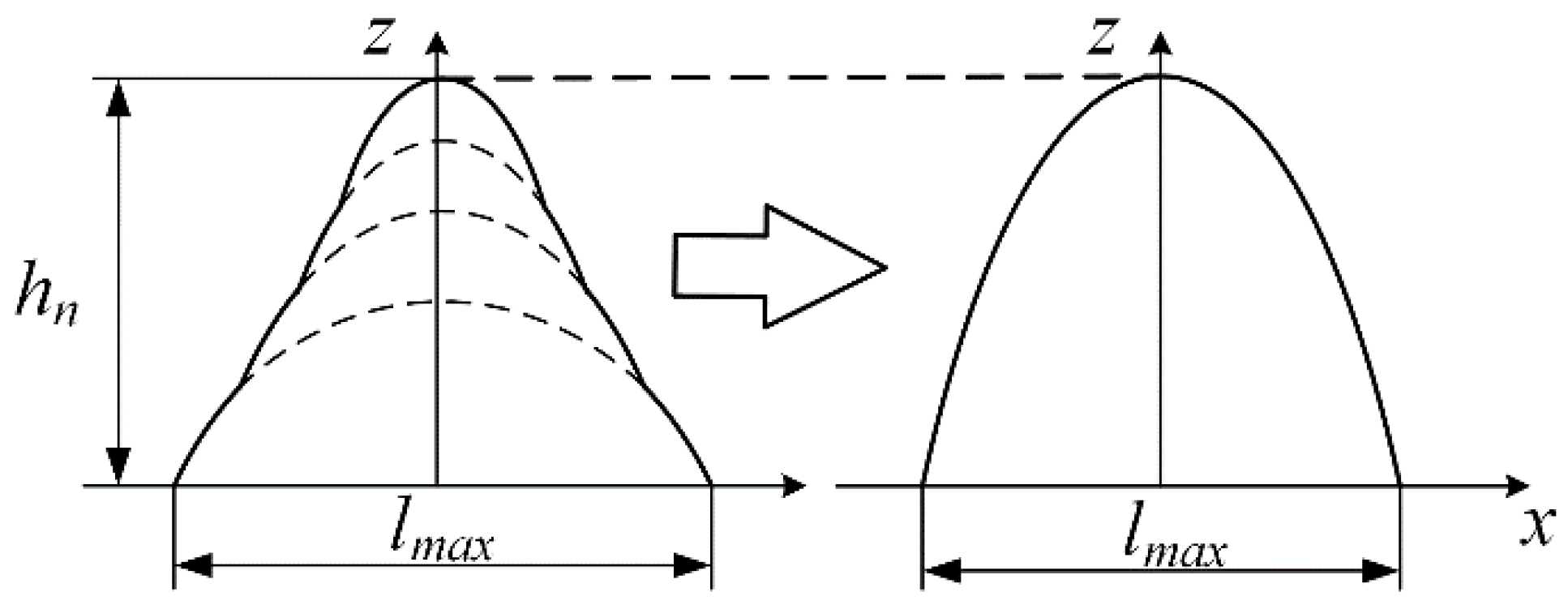
2.1. Rough Surface Morphology Structure
2.2. Contact Properties
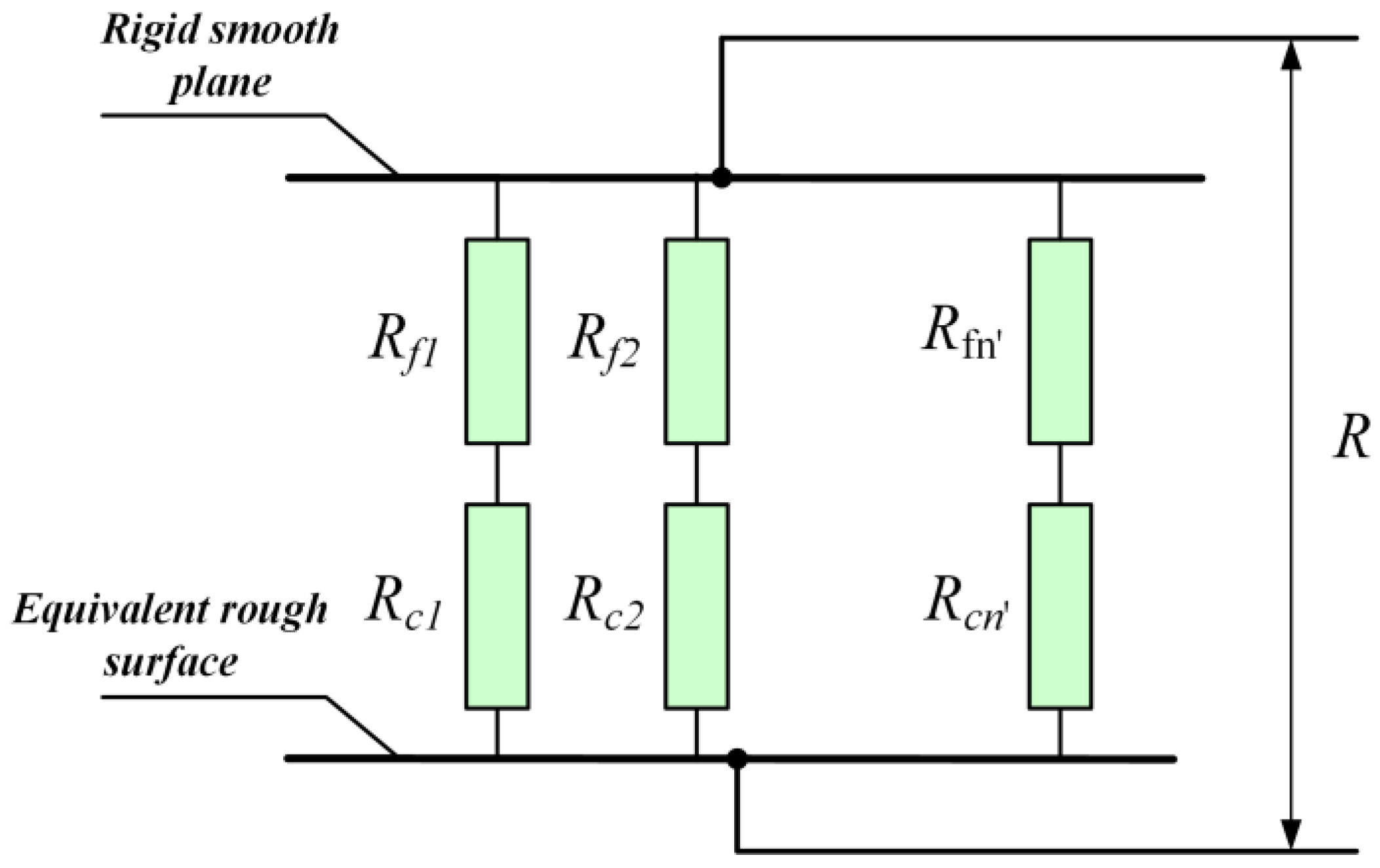
2.3. Contact Resistance Model
3. Results and Analysis
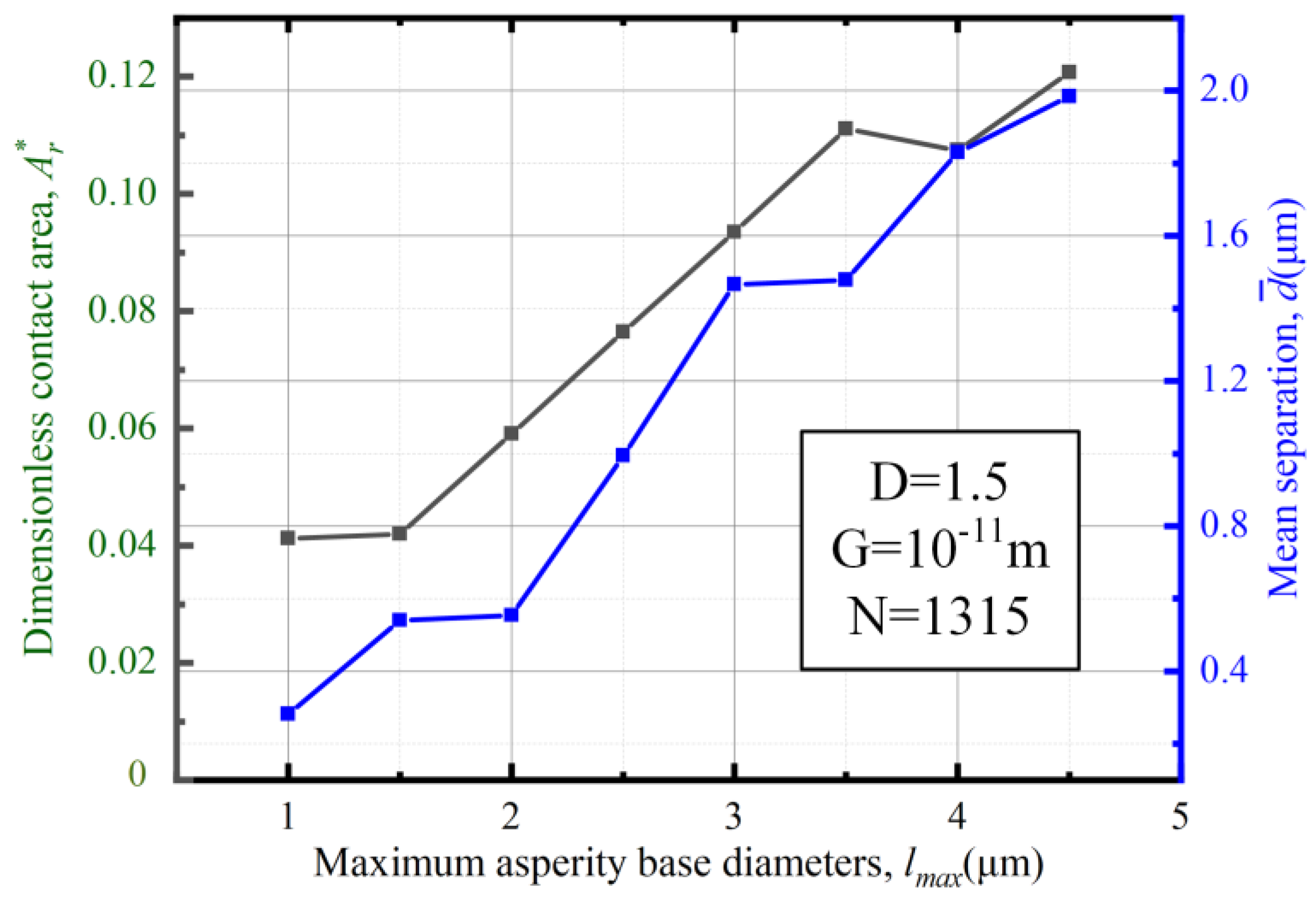
3.1. Surface Morphological Analysis
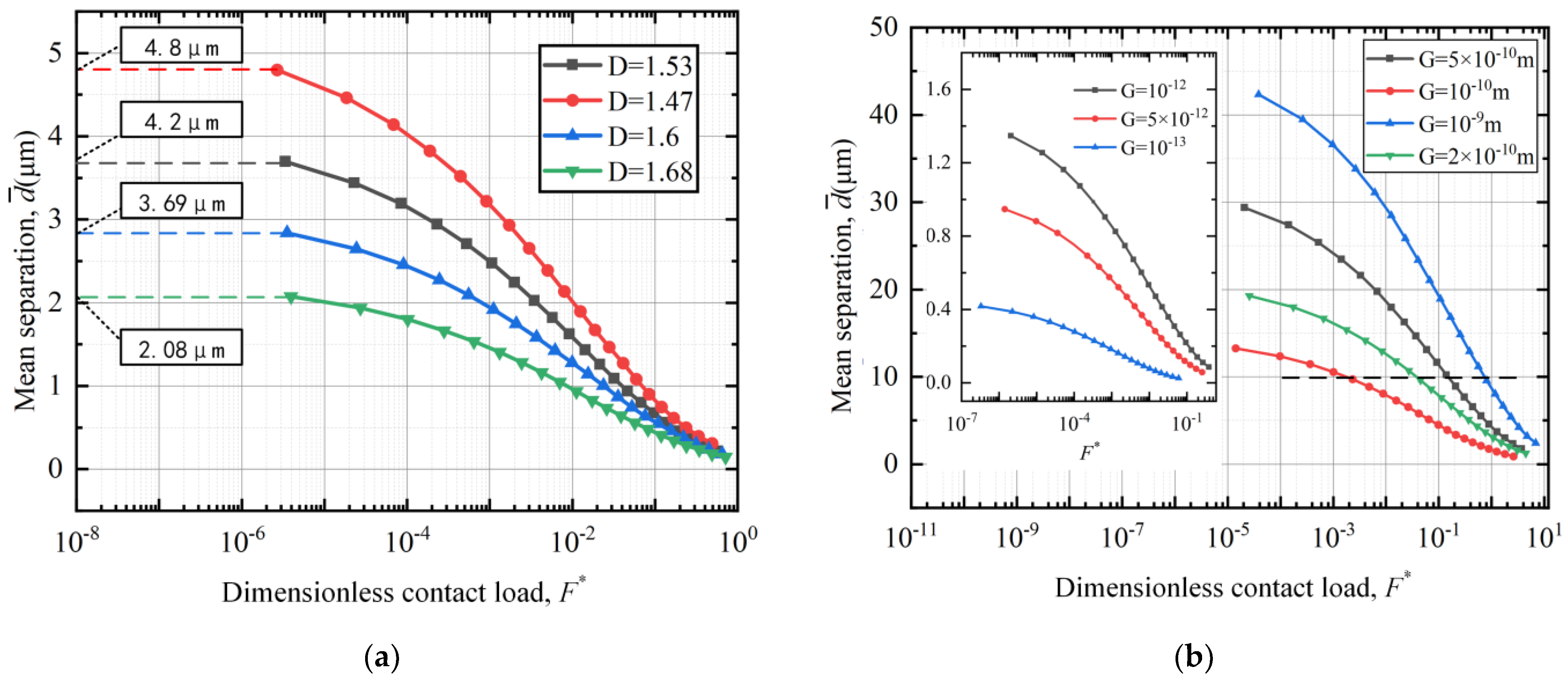
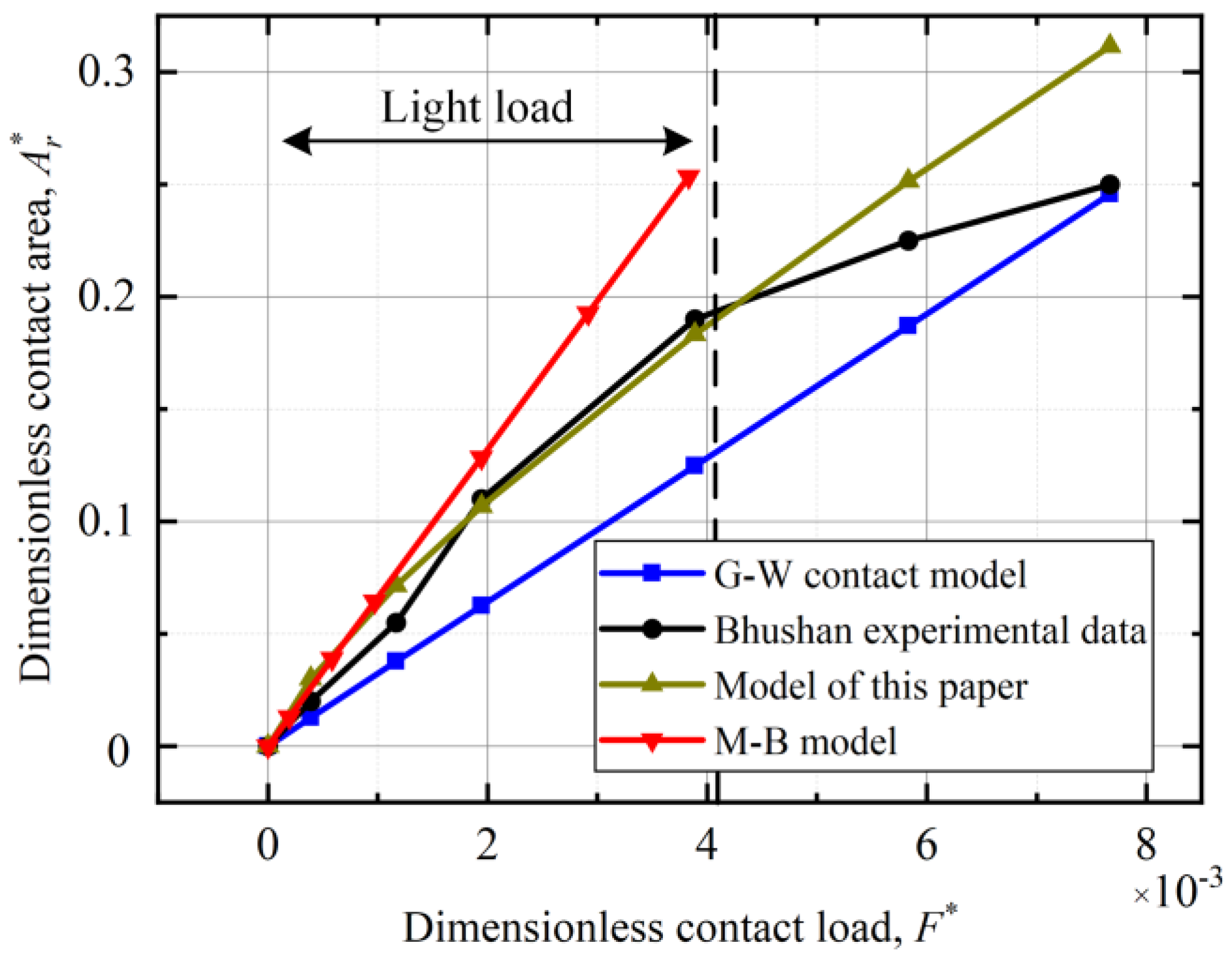
3.2. Contact Characteristics Analysis
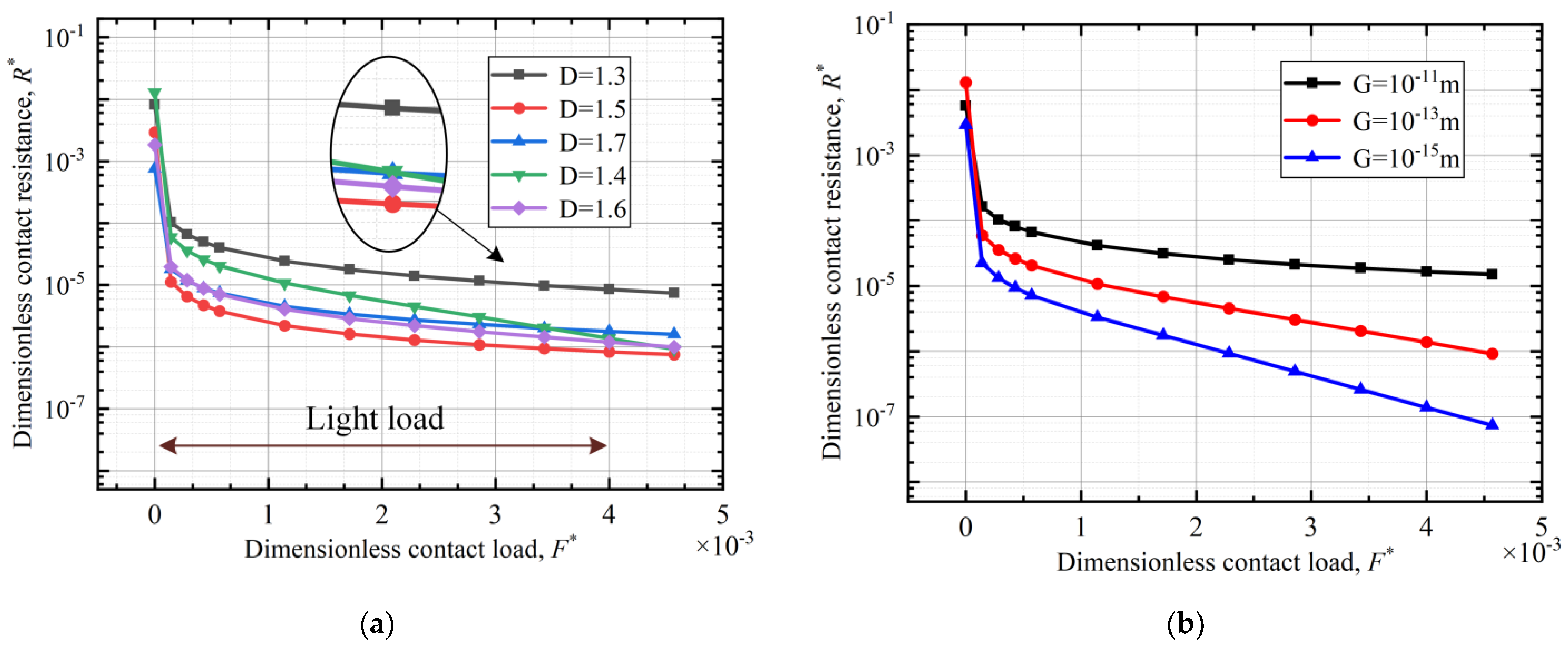
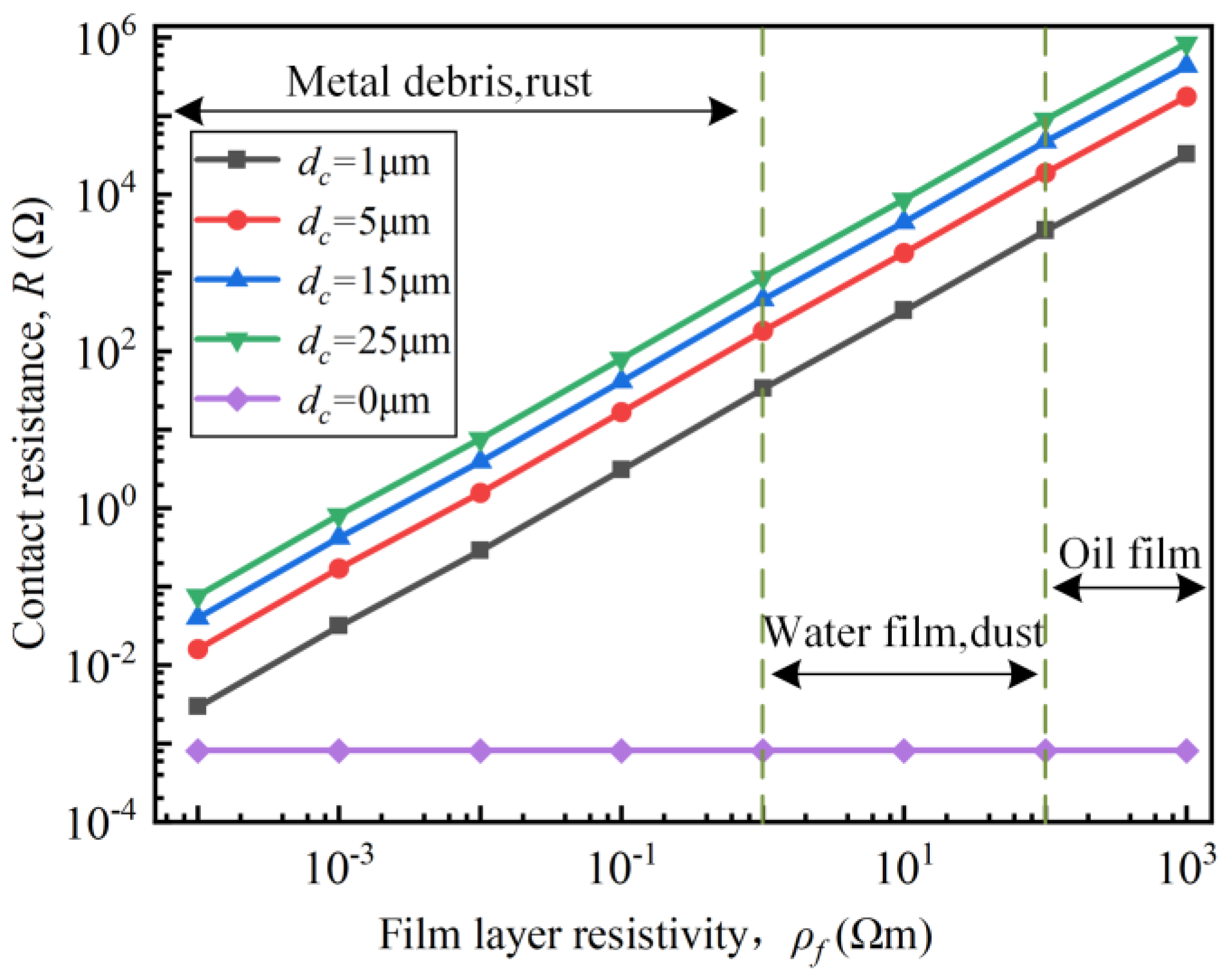
3.3. Contact Resistance Analysis and Finite Element Verification
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Whitehouse, D.J.; Archard, J.F. The properties of random surfaces of significance in their contact. A Math. Phys. Sci. 1970, 316, 97–121. [Google Scholar]
- Majumdar, A.; Bhushan, B. Fractal model of elastic-plastic contact between rough surfaces. J. Tribol.-Trans. Asme 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Ge, S.R. The fractal behavior and fractal characterization of rough surfaces. Tribology 1997, 17, 73–80. [Google Scholar]
- Thomas, T.R.; Rosén, B.-G.; Amini, N. Fractal characterization of the anisotropy of rough surfaces. Wear 1990, 232, 41–50. [Google Scholar] [CrossRef]
- Kang, M.C.; Kim, J.S.; Kim, K.H. Fractal dimension analysis of machined surface depending on coated tool wear. Surf. Coat. Technol. 2005, 193, 259–265. [Google Scholar] [CrossRef]
- Jackson, R.L. An Analytical Solution to an Archard-Type Fractal Rough Surface Contact Model. Tribol. Trans. 2010, 53, 543–553. [Google Scholar] [CrossRef]
- Chui, M.W.; Feng, Y.Q.; Wang, W.; Li, P.L. Numerical simulation method of 3D gaussian rough surface. Surf. Technol. 2013, 42, 63–65. [Google Scholar]
- Archard, J.F. Elastic deformation and the laws of friction. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1957, 243, 190–205. [Google Scholar]
- Greenwood, J.A.; Williamson, J.P.B. Contact of nominally flat surfaces. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]
- Zhang, X.L.; Chen, Y.H. The model of normal contact stiffness of joint interfaces incorporating elastoplastic deformation mechanism. J. Vib. Eng. 2015, 28, 91–99. [Google Scholar]
- Chen, Q.; Xu, F. Research on fractal model of normal contact stiffness between two spheroidal joint surfaces considering friction factor. Tribol. Int. 2016, 97, 253–264. [Google Scholar] [CrossRef]
- Song, Z.; Komvopoulos, K. Contact mechanics analysis of oscillatory sliding of a rigid fractal surface against an elastic–plastic half-space. Philos. Mag. 2014, 94, 3215–3233. [Google Scholar] [CrossRef]
- Fu, W.P.; Lou, L.T. Theoretical model for the contact stiffness and damping of mechanical joint surface. J. Mech. Eng. 2017, 53, 73–82. [Google Scholar] [CrossRef]
- Zhang, X.L.; Wen, S.H. Fractal model of tangential contact damping of plane joint interfaces with simulation. J. Xi’an Jiaotong Univ. 2011, 45, 74–213. [Google Scholar]
- Persson, B.N.J.; Bucher, F.; Chiaia, B. Elastic contact between randomly rough surfaces: Comparison of theory with numerical results. Phys. Rev. B 2002, 65, 184106. [Google Scholar] [CrossRef] [Green Version]
- Morag, Y.; Etsion, I. Resolving the contradiction of asperities plastic to elastic mode transition in current contact models of fractal rough surfaces. Wear 2007, 262, 624–629. [Google Scholar] [CrossRef]
- Yuan, Y.; Cheng, Y.; Liu, K.; Gan, L. A revised Majumdar and Bushan model of elastoplastic contact between rough surfaces. Appl. Surf. Sci. 2017, 425, 1138–1157. [Google Scholar] [CrossRef]
- Tong, Y.; Müller, M.; Ostermeyer, G.P. Investigations on the dynamic influence of the contact angle on frictional sliding processes between rough surfaces using NURBS and mortar-based augmented Lagrangian method. Tribol. Int. 2021, 158, 106889. [Google Scholar] [CrossRef]
- Hu, J.; Song, H.; Sandfeld, S.; Liu, X.; Wei, Y. Multiscale study of the dynamic friction coefficient due to asperity plowing. Friction 2021, 9, 822–839. [Google Scholar] [CrossRef]
- Berman, D.; Walker, M.J.; Krim, J. Contact voltage-induced softening of RF microelectromechanical system gold-on-gold contacts at cryogenic temperatures. J. Appl. Phys. 2010, 108, 044307. [Google Scholar] [CrossRef]
- Brown, C.; Rezvanian, O.; Zikry, M.A.; Krim, J. Temperature dependence of asperity contact and contact resistance in gold RF MEMS switches. J. Micromech. Microeng. 2009, 19, 025006. [Google Scholar] [CrossRef] [Green Version]
- Broue, A.; Fourcade, T.; Dhennin, J. Validation of bending tests by nanoindentation for micro-contact analysis of MEMS switches. J. Micromech. Microeng. 2010, 20, 085025. [Google Scholar] [CrossRef]
- Zhou, M.Q.; Yu, B. A Monte Carlo method for simulating fractal surfaces. Phys. A Stat. Mech. Its Appl. 2007, 386, 176–186. [Google Scholar] [CrossRef]
- Krithivasan, V.; Jackson, R.L. An analysis of three-dimensional elasto-plastic sinusoidal contact. Tribol. Lett. 2007, 27, 31–43. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.Q.; Yu, B. Fractal model for thermal contact conductance. J. Heat Transf. 2008, 130, 101301. [Google Scholar] [CrossRef]
- Lau, Y.Y.; Yang, W. A higher dimensional theory of electrical contact resistance. J. Appl. Phys. 2009, 105, 124902. [Google Scholar] [CrossRef]
- Bhushan, B. The real area of contact in polymeric magnetic media—II: Experimental data and analysis. ASLE Trans. 1985, 28, 181–197. [Google Scholar] [CrossRef]
- Ross, R.B. Metallic Materials Specification Handbook; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]








| Parameters | Range of Values | Parameters | Range of Values |
|---|---|---|---|
| D | 1.3~1.7 | G/m | 10−9~10−15 |
| lmax/m | 10−6~5 × 10−6 | lmin/m | 10−8~5 × 10−8 |
| L/m | 5 × 10−4 | E*/Pa | 5.064 × 1010 |
| ρ/(Ωm) | 4.317 × 10−8 | ρf/(Ωm) | 10−4~103 |
| dc/μm | 0.1~25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Yu, B.; Li, Y.; Yang, Q. Simplified Calculation Model for Contact Resistance Based on Fractal Rough Surfaces Method. Appl. Sci. 2023, 13, 3648. https://doi.org/10.3390/app13063648
Zhang C, Yu B, Li Y, Yang Q. Simplified Calculation Model for Contact Resistance Based on Fractal Rough Surfaces Method. Applied Sciences. 2023; 13(6):3648. https://doi.org/10.3390/app13063648
Chicago/Turabian StyleZhang, Changgeng, Baichuan Yu, Yongjian Li, and Qingxin Yang. 2023. "Simplified Calculation Model for Contact Resistance Based on Fractal Rough Surfaces Method" Applied Sciences 13, no. 6: 3648. https://doi.org/10.3390/app13063648
APA StyleZhang, C., Yu, B., Li, Y., & Yang, Q. (2023). Simplified Calculation Model for Contact Resistance Based on Fractal Rough Surfaces Method. Applied Sciences, 13(6), 3648. https://doi.org/10.3390/app13063648






