An Identification Method for the “Effective Coupling Loss Factor” Based on the Hybrid FE-SEA Model
Abstract
:1. Introduction
2. Basic Theoretical Parameters of the FE-SEA Method
2.1. Modal Density
2.1.1. Lateral Vibration Modal Density of a One-Dimensional Beam
2.1.2. Modal Density of Two-Dimensional Plates
- (1)
- When the system frequency ratio meets the condition :
- (2)
- When the system frequency ratio meets the condition :
- (3)
- When the system frequency ratio meets the condition :
2.1.3. Sound Mode Density
2.2. Internal Loss Factor
2.2.1. Internal Loss Factor of the Structure
2.2.2. Intracavitary Loss Factor
2.3. Coupling Loss Factor
2.3.1. Coupling Loss Factor between Structures
2.3.2. Coupling Loss Factor between Sound Cavity and Structure
2.3.3. Coupling Loss Factor between Cavity and Cavity
3. Hybrid FE-SEA Modeling Parameter Identification Algorithm
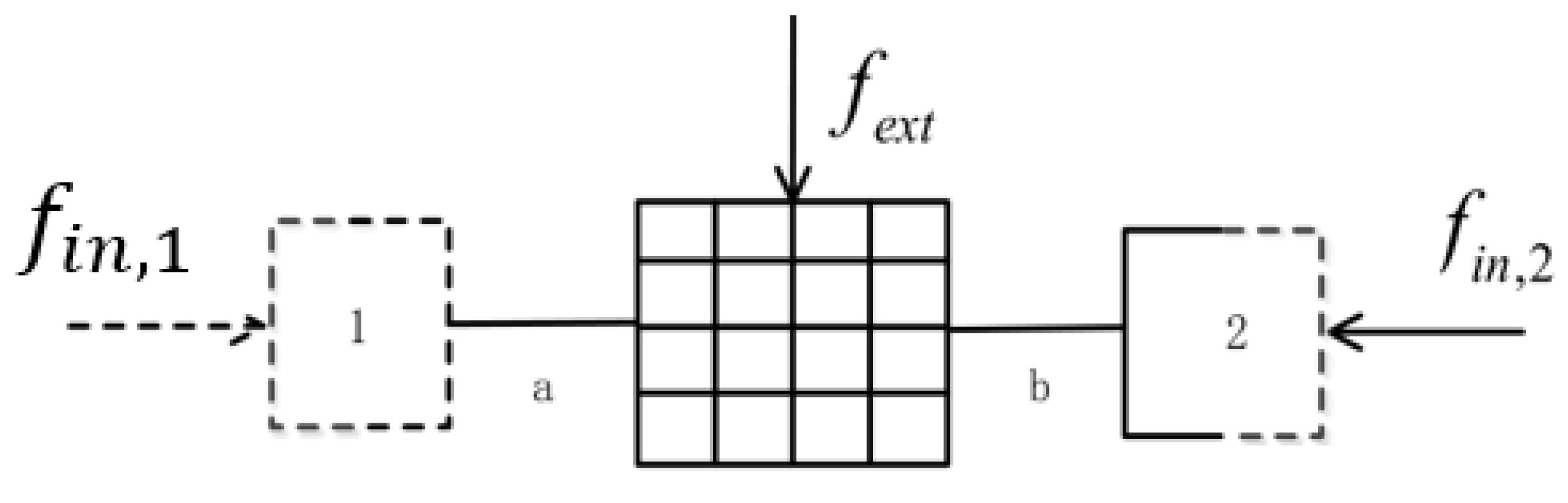
3.1. Deterministic Subsystem Response Derivation of Three-Coupled Systems
- (1)
- The displacement response of the deterministic subsystem obtained by this method is based on the overall average response, and the response of a certain position cannot be predicted.
- (2)
- One of the derivation conditions of the equation is that the random subsystems in the system conform to the reciprocity relation of the diffusion field, and the interaction between the random subsystems can be ignored.
- (3)
- The premise of formula derivation is the energy density () of the random subsystem, so whether the prediction of the deterministic subsystem response cross spectrum () is accurate is affected by the accuracy of the random subsystem K energy response ().
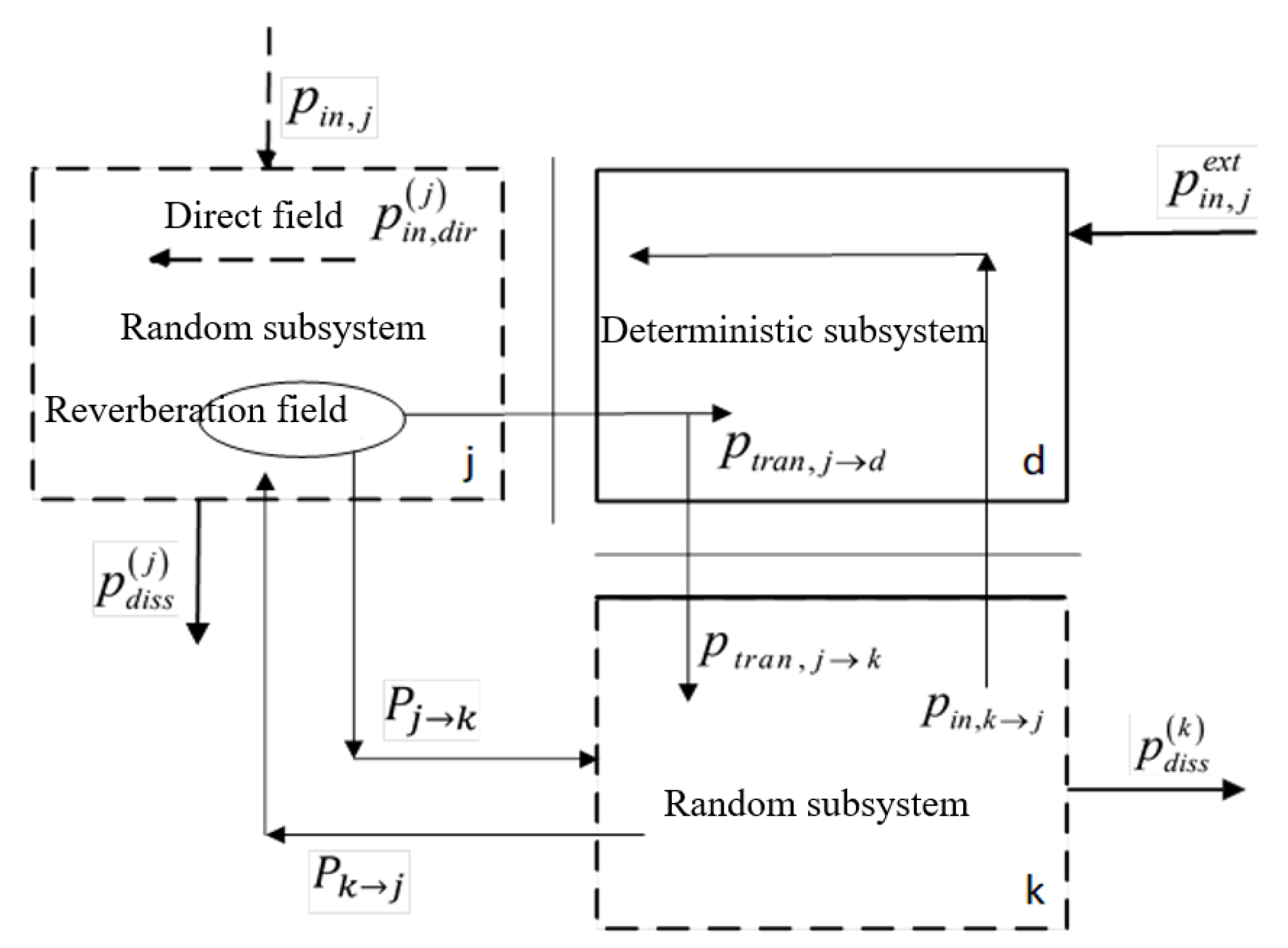
3.2. Derivation of the Energy Response of Random Subsystems of Three-Coupled Systems
3.2.1. Random Subsystem Energy Response of Three-Coupled Systems
3.2.2. Energy Response of Multiple Coupled Random Subsystems Considering Power Flow
3.3. Derivation of Energy Response of a Random Subsystem in a Multi-Coupled System
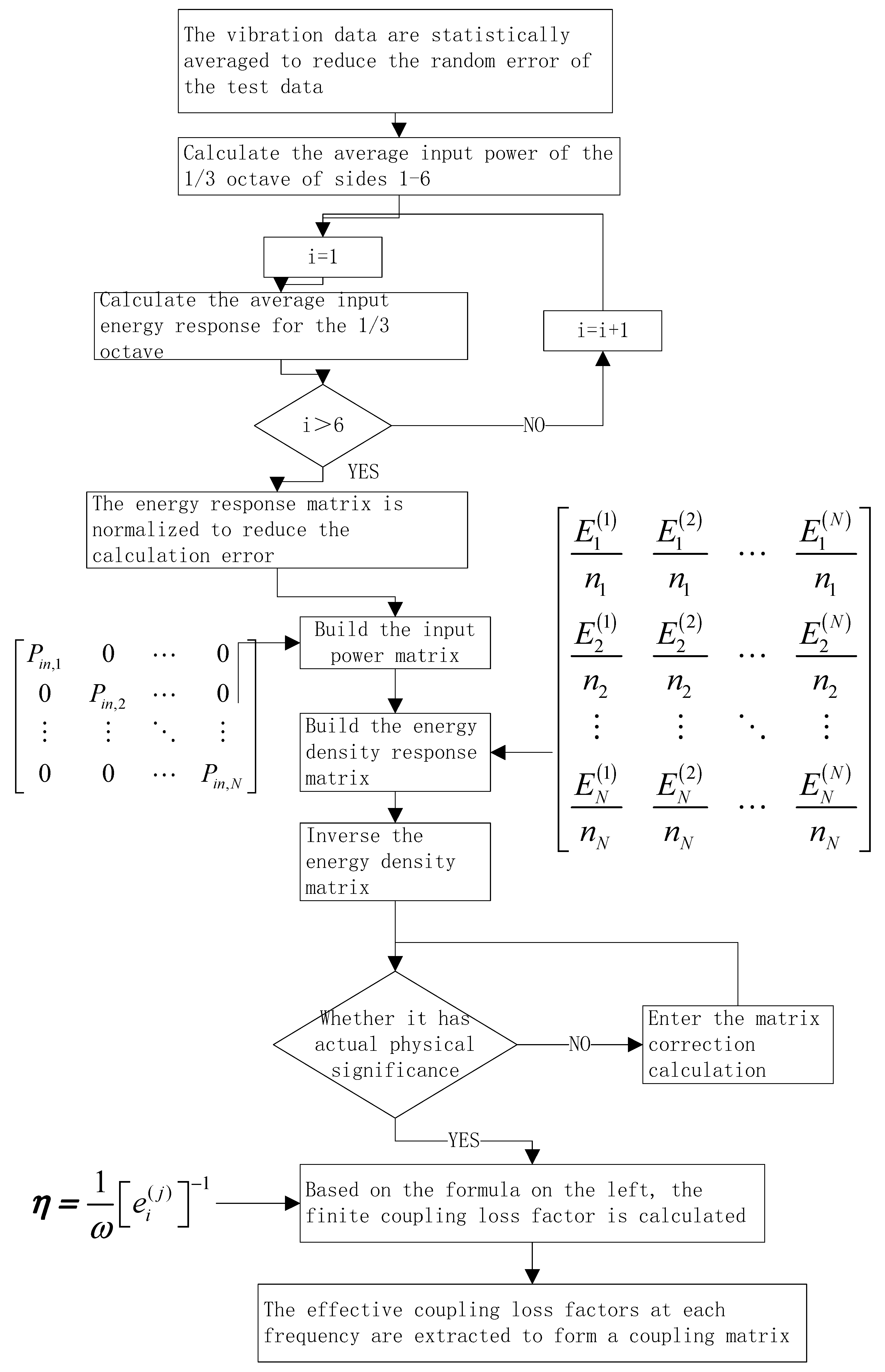
3.4. Coupling Matrix Solution of the Multi-System Coupling Model
3.5. Iterative Improvement of Ill-Conditioned Matrix Parameters
- (1)
- Select matrix C and transform matrix AX = B to ACy = B.
- (2)
- Select factor α. Then, select the initial point value and use the decomposition method to solve to obtain the value of .
- (3)
- Iterate into the loop and calculate .
- (4)
- Solve .
- (5)
- Solve .
- (6)
- When , the iterative cycle ends and the solution vector y is obtained.
- (7)
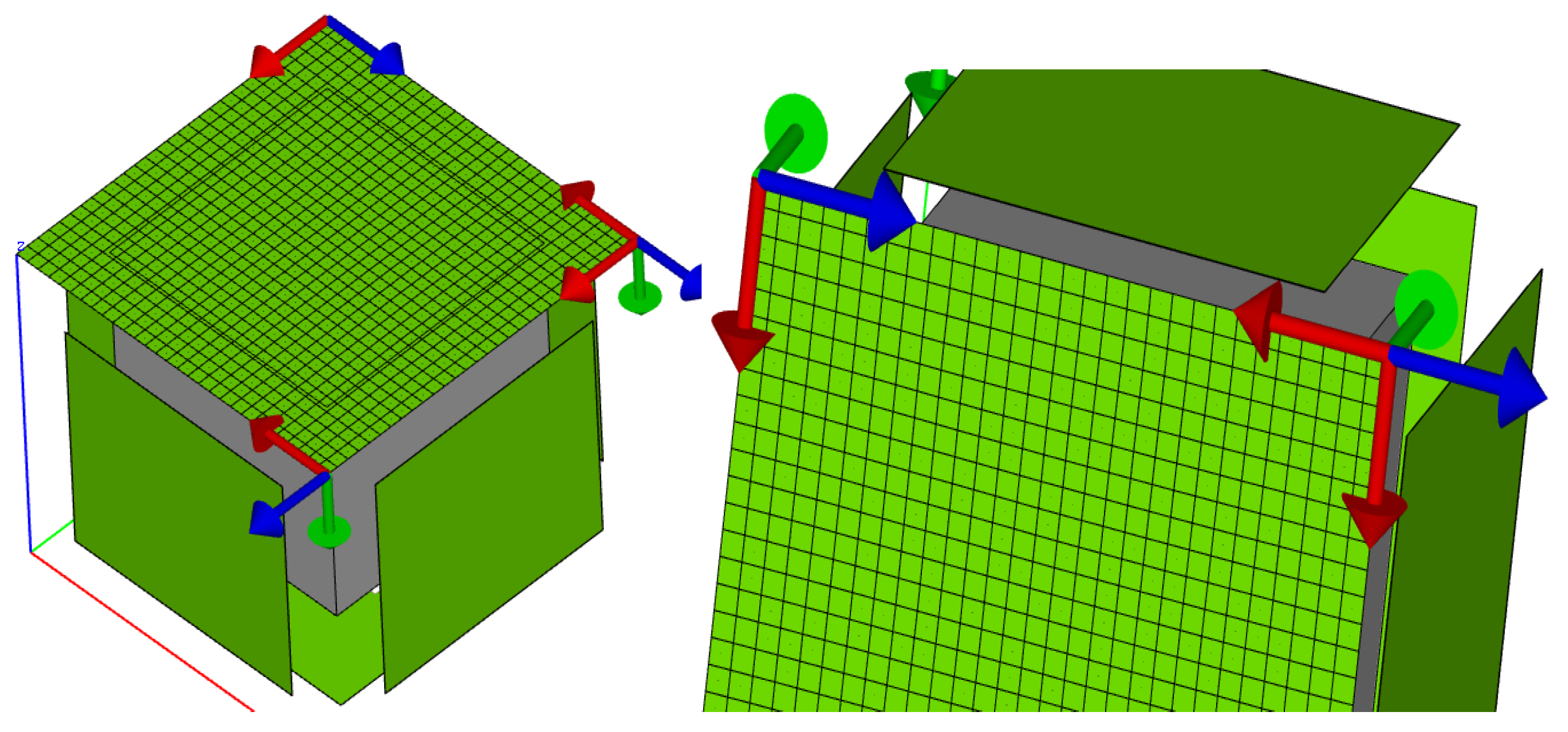
3.6. The Algorithm of a Case Analysis
3.6.1. Numerical Example
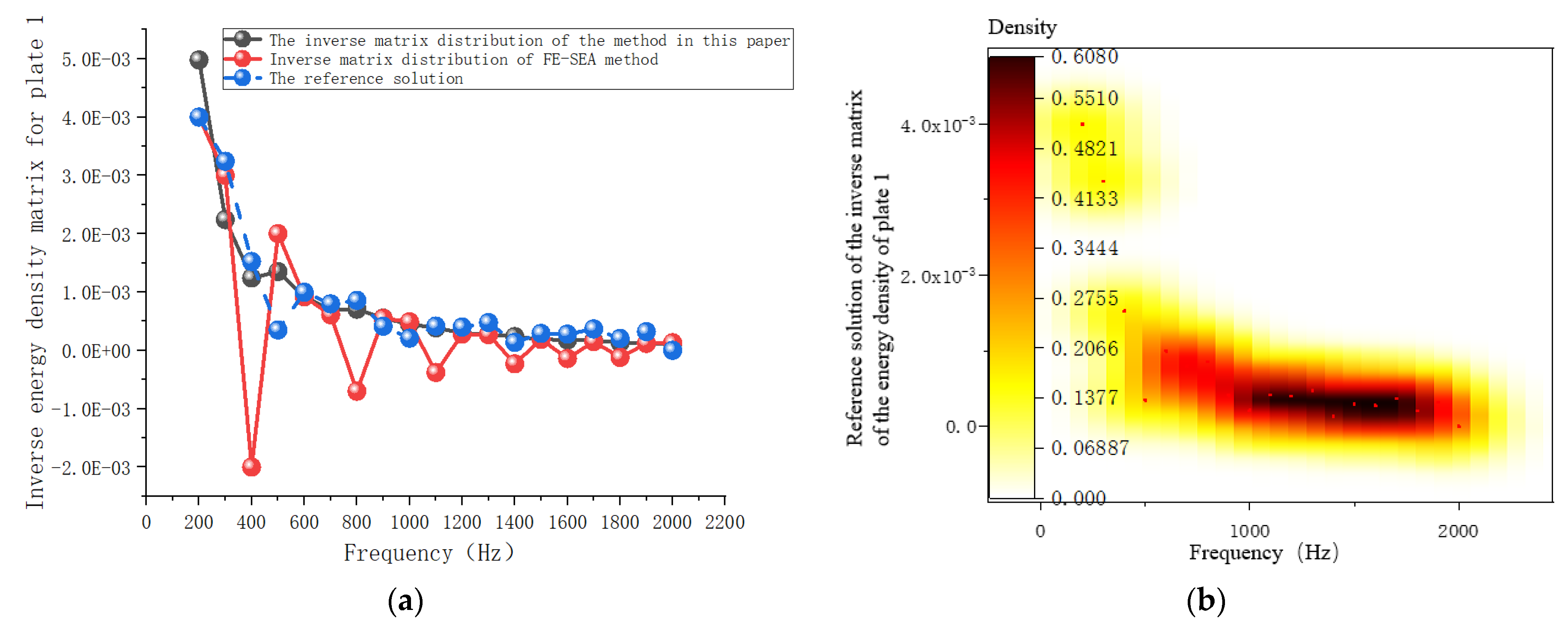
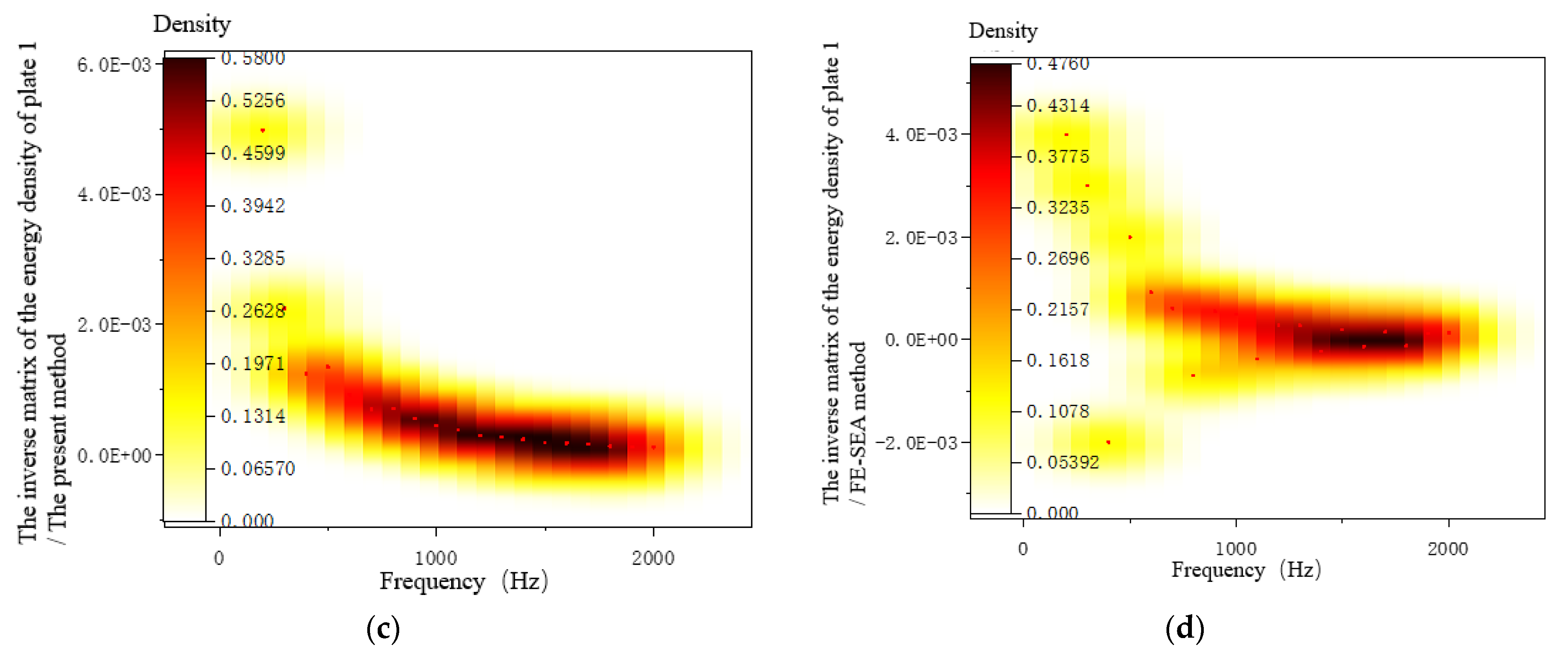
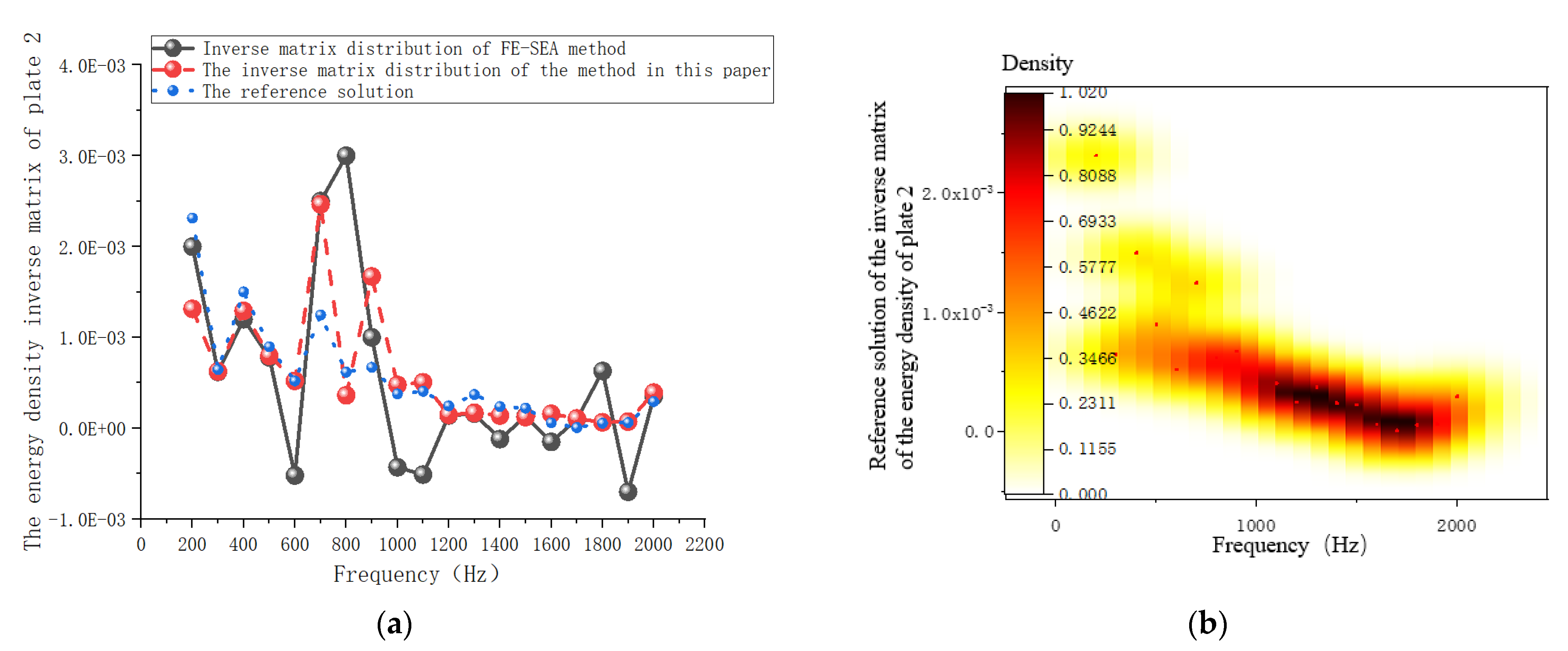
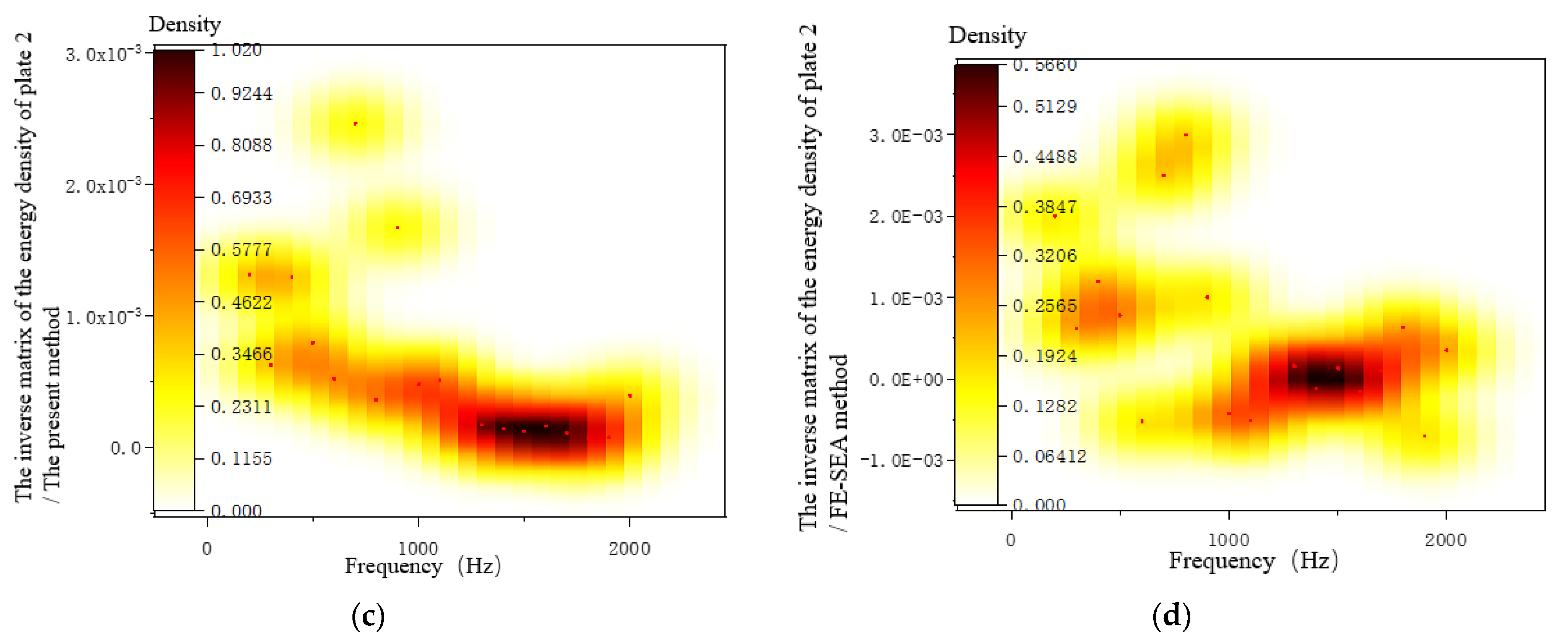
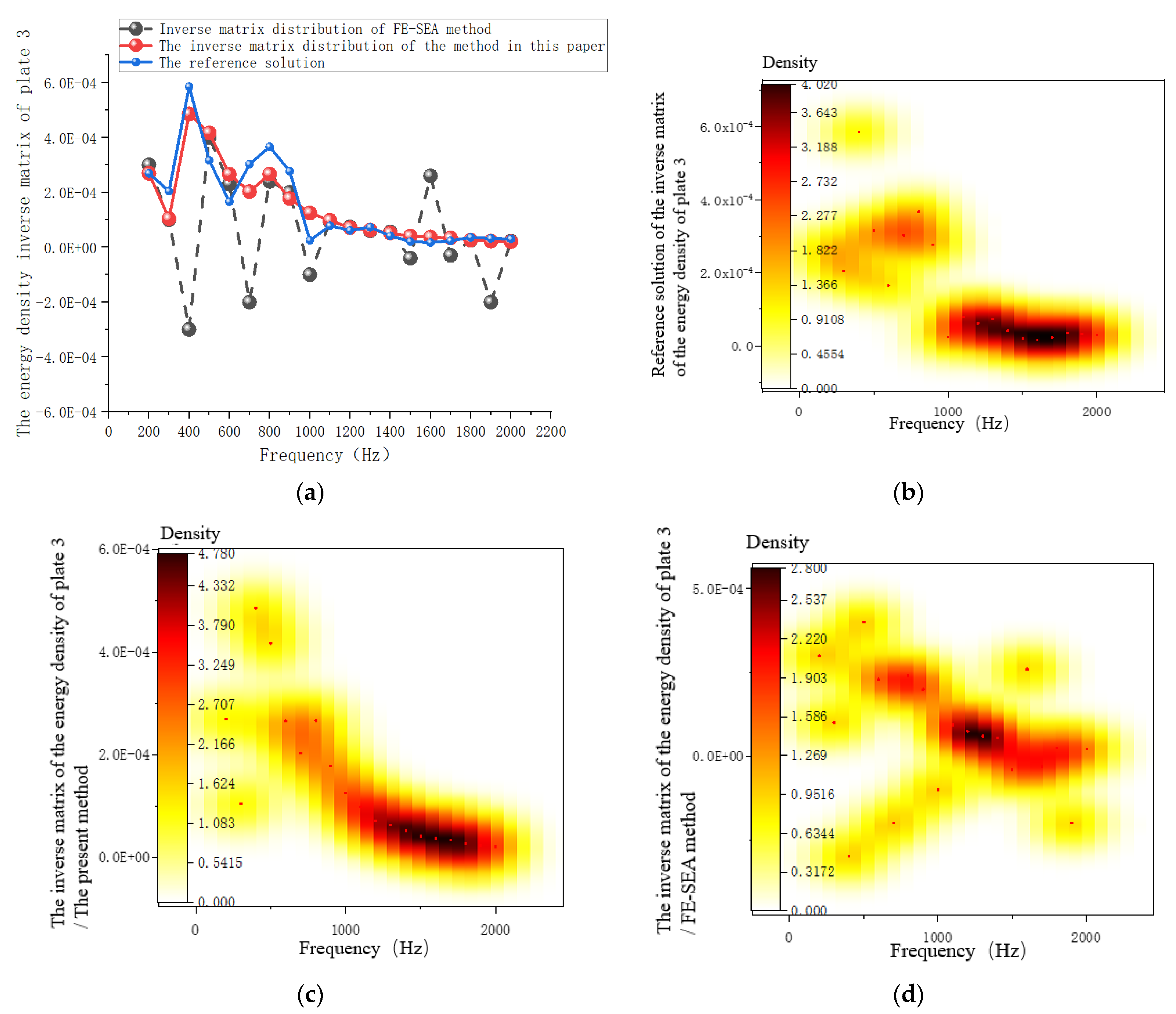
3.6.2. System Response Analysis
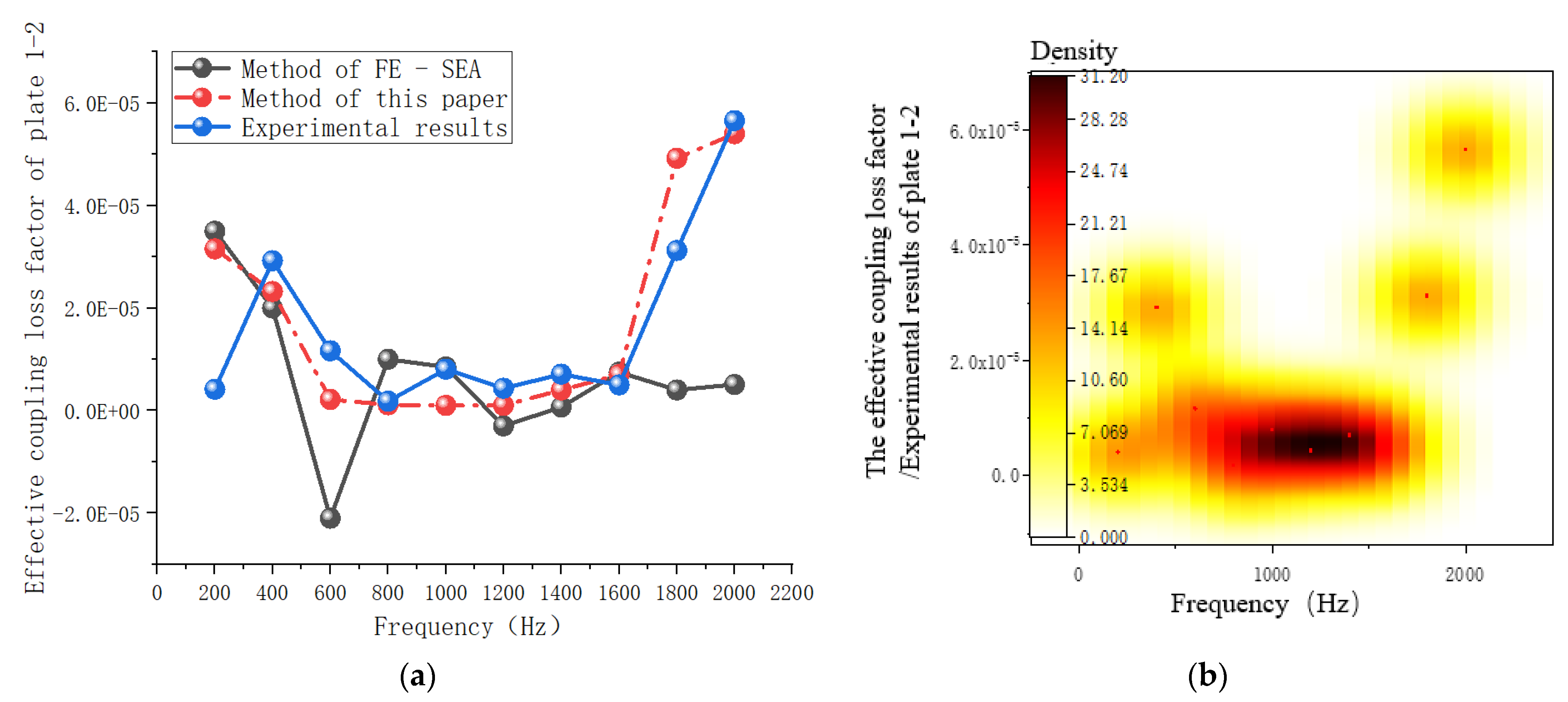
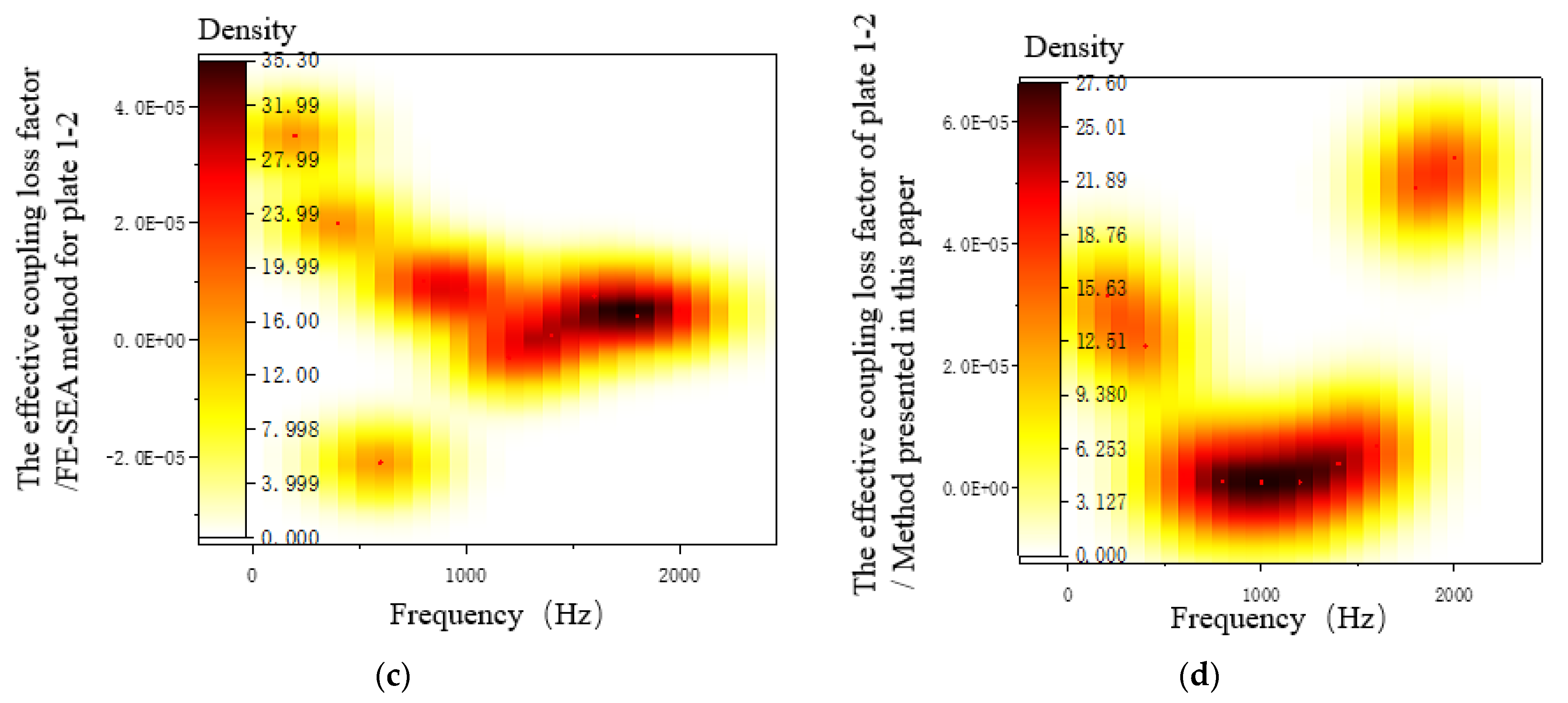
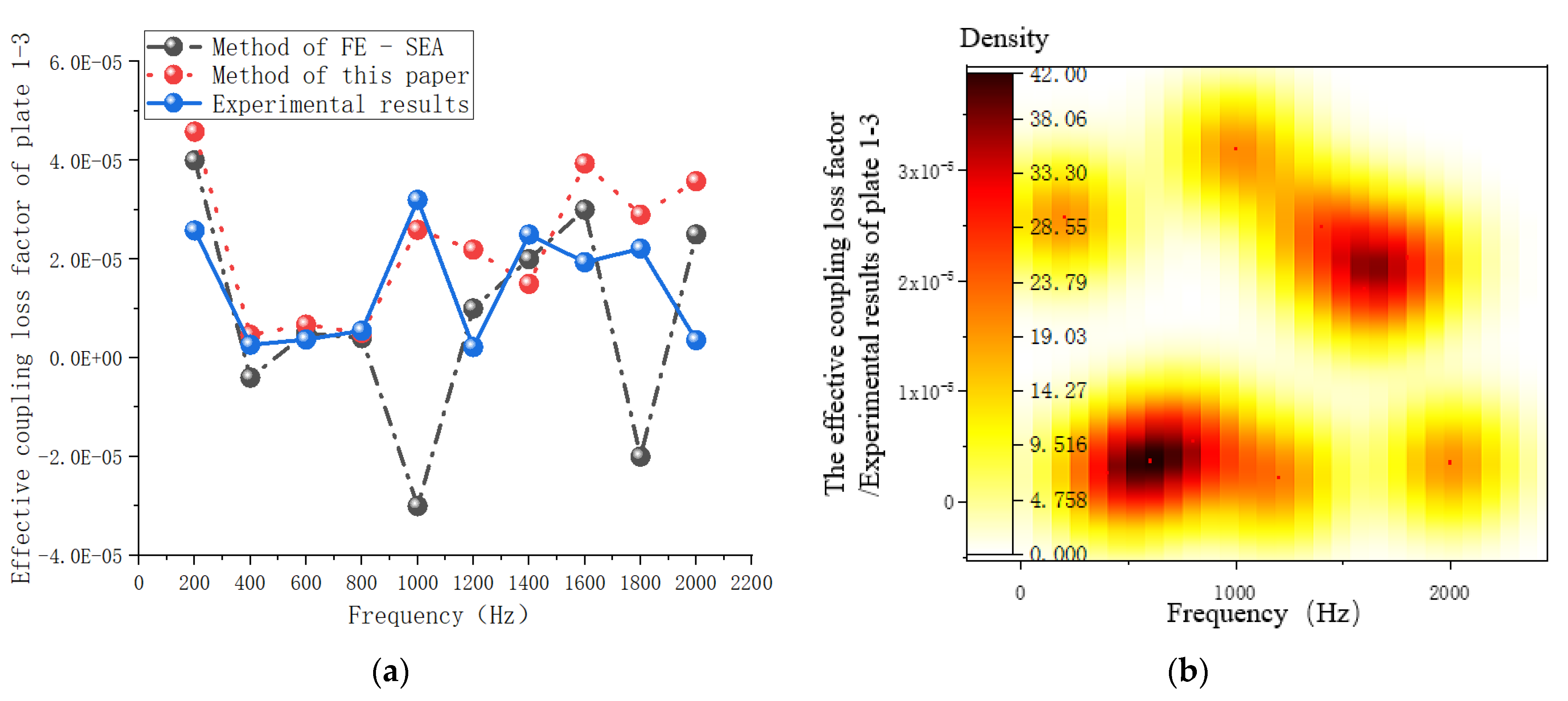
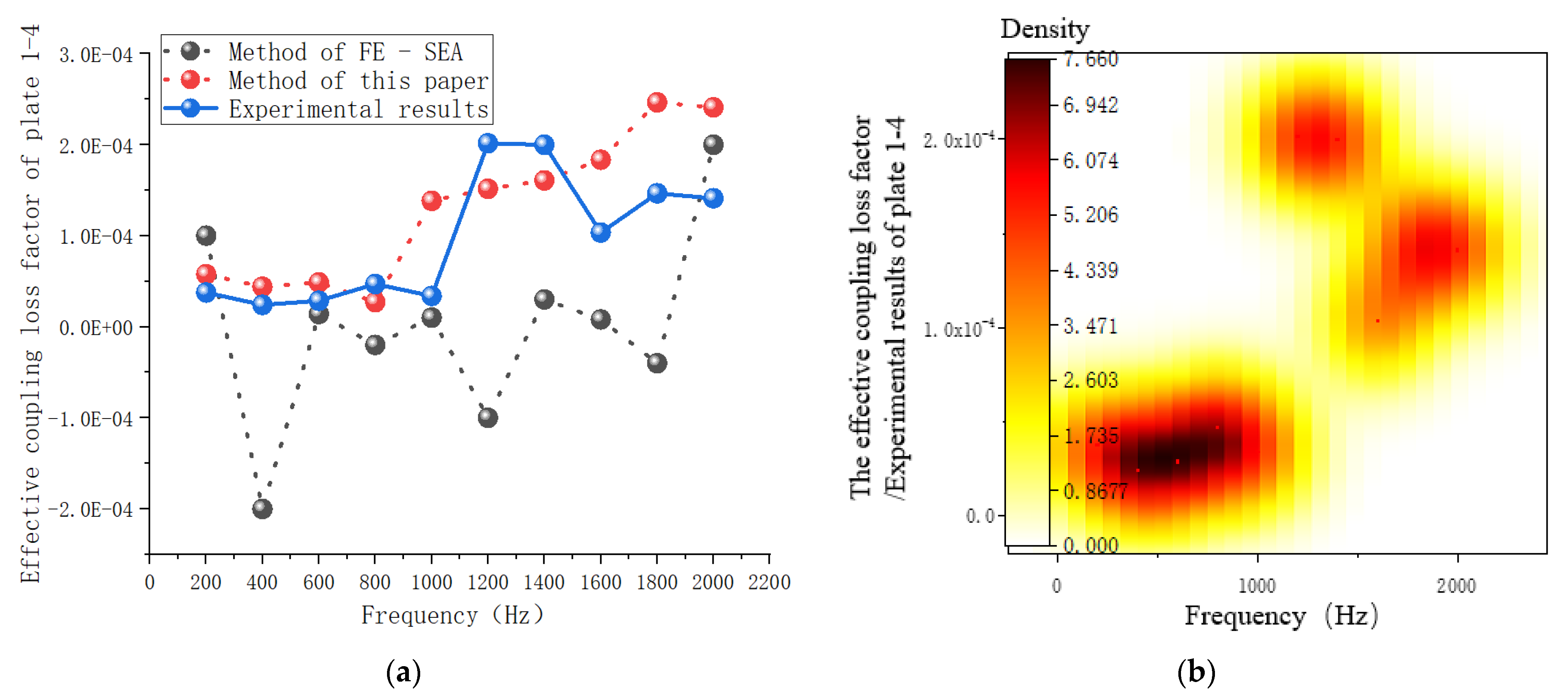
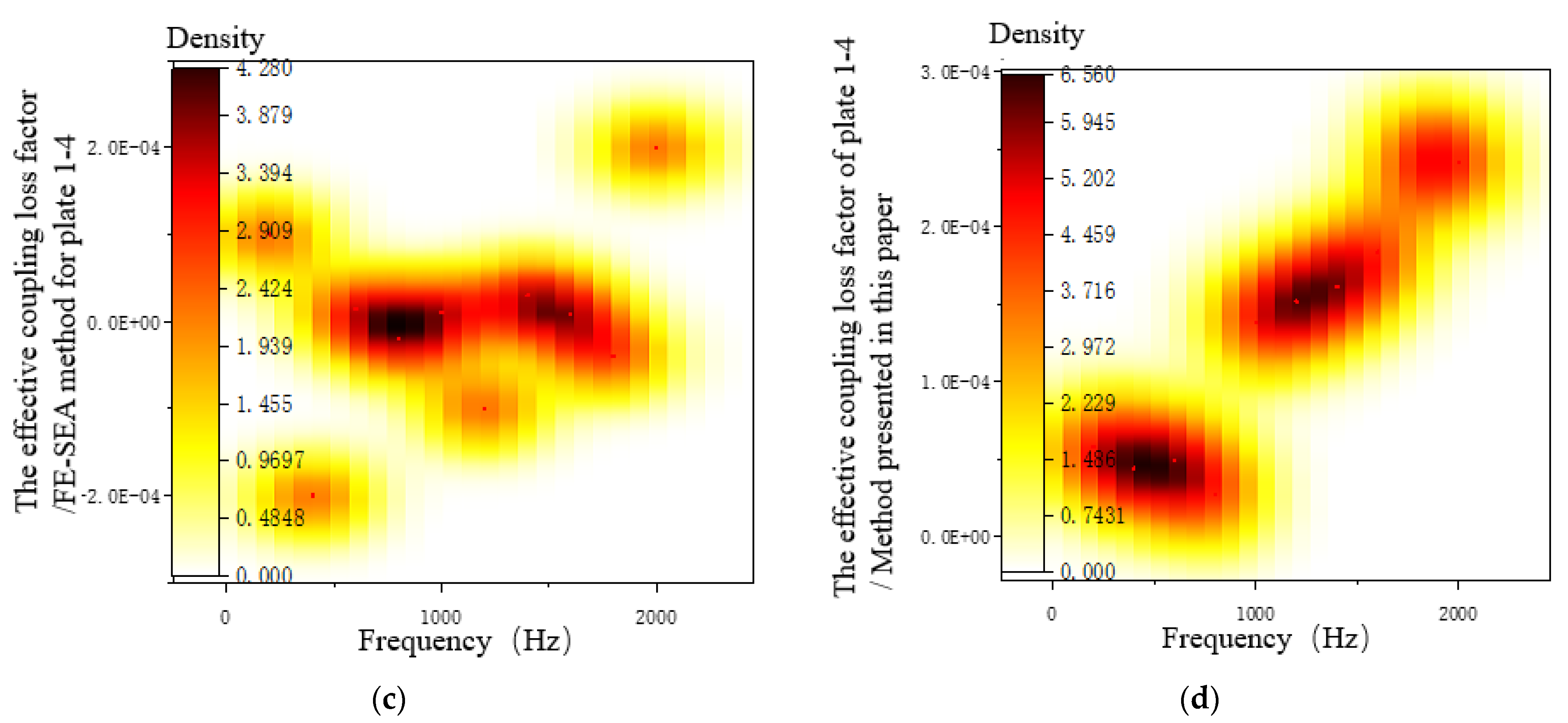
3.6.3. Coupling Loss-Factor Analysis of the System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Langley, R.S.; Bremner, P. A hybrid method for the vibration analysis of complex structural-acoustic systems. J. Acoust. Soc. Am. 1999, 105, 1657–1671. [Google Scholar] [CrossRef]
- Yan, H.H.; Parett, A.A. A FEA-Based Procedure to Perform Statistical Energy Analysis; SAE Technical Paper 2003-01-1553; SAE International: Warrendale, PA, USA, 2003. [Google Scholar]
- Cotoni, V.; Gardner, B.; Shorter, P.; Lane, S. Demonstration of Hybrid FE-SEA Analysis of Structure-Borne Noise in the Mid Frequency Range; SEA International Paper 2005-01-2331; SAE International: Warrendale, PA, USA, 2005. [Google Scholar]
- Chen, S.M.; Wang, D.F.; Zuo, A.K.; Chen, Z.; Zhao, X.M.; Zan, J.M. Calculation of coupling loss factors of several line junctions. J. Jilin Univ. 2010, 4, 920–924. [Google Scholar]
- Wu, J.L.; Zhang, Y.Q. The dynamic analysis of multibody systems with uncertain parameters using interval method. Appl. Mech. Mater. 2012, 152, 1555–1561. [Google Scholar] [CrossRef]
- Wu, J.; Luo, Z.; Zhang, Y.; Zhang, N.; Chen, L. Interval uncertain method for multibody mechanical systems using Chebyshev inclusion functions. Int. J. Numer. Methods Eng. 2013, 95, 608–630. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, Z. An interval perturbation method for exterior acoustic field prediction with uncertain-but-bounded parameters. J. Fluids Struct. 2014, 49, 441–449. [Google Scholar] [CrossRef]
- Zhang, J.G. A Method for static interval analysis of uncertain structures with interval parameters. In Advanced Materials Research; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2014; Volume 950. [Google Scholar]
- Su, J.B.; Liu, H.B.; De Zhao, H.; Zhang, D. Research on interval reversible inverse analysis method based on interval parameters. In Advanced Materials Research; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2013; pp. 556–559. [Google Scholar]
- Reynders, E.; Langley, R.S.; Dijckmans, A.; Vermeir, G. A hybrid finite element—Statistical energy analysis approach to robust sound transmission modeling. J. Sound Vib. 2014, 333, 4621–4636. [Google Scholar] [CrossRef]
- Moens, D.; Vandepitte, D. Recent advances in non-probabilistic approaches for non-deterministic dynamic finite element analysis. Arch. Comput. Methods Eng. 2006, 13, 389–464. [Google Scholar] [CrossRef]
- Moens, D.; Hanss, M. Non-probabilistic finite element analysis for parametric uncertainty treatment in applied mechanics: Recent advances. Finite Elem. Anal. Des. 2011, 47, 4–16. [Google Scholar] [CrossRef]
- Belyaev, A.K. Dynamic simulation of high-frequency vibration of extended complex structures. J. Struct. Mech. 2007, 20, 155–168. [Google Scholar] [CrossRef]
- Rao, S.S.; Berke, L. Analysis of uncertain structural systems using interval analysis. Aiaa J. 1997, 35, 727–735. [Google Scholar] [CrossRef]
- Qiu, Z.; Chen, S.; Elishakoff, I. Bounds of eigenvalues for structures with an interval description of uncertain-but-non-random parameters. Chaos Solitons Fractals 1996, 7, 425–434. [Google Scholar] [CrossRef]
- Xu, M.; Qiu, Z.; Wang, X. Uncertainty propagation in SEA for structural–acoustic coupled systems with non-deterministic parameters. J. Sound Vib. 2014, 333, 3949–3965. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Chen, L.; Luo, Z. A Chebyshev interval method for nonlinear dynamic systems under uncertainty. Appl. Math. Model. 2013, 37, 4578–4591. [Google Scholar] [CrossRef]
- He, Y.; Zhang, H.; Xia, X.; Xu, Z.; Zhang, Z. Analysis of Noise Reduction of Car Body Panel Based on FE-SEA Hybrid Method. J. Vib. Shock 2016, 35, 234–240. [Google Scholar]
- Ye, M.; Lang, Z.G.; Hao, Z.Y. Measurement of SEA Parameters in Vibration Energy Balance Equation of Complex System. Trans. CSICE 1998, 16, 469–474. [Google Scholar]
- Zhu, W.; Xing-Rui, M.A.; Han, Z.; Zou, Y. Research on Modeling Method of Hybrid FE-SEA Wire Connection. J. Vib. Eng. 2016, 5, 17–23. [Google Scholar]
- Wu, F.; Li, G.Y.; Cheng, A.G. Analysis of Acoustic-structure Coupling of Intermediate Frequency Based on Hybrid ES-FE-SEA Method. Chin. J. Mech. Eng. 2015, 2015, 73–80. [Google Scholar]
- Chen, S.M. Research on the Prediction and Control Method of High Frequency Noise in Car. Ph.D. Thesis, Jilin University, Changchun, China, 2011. [Google Scholar]


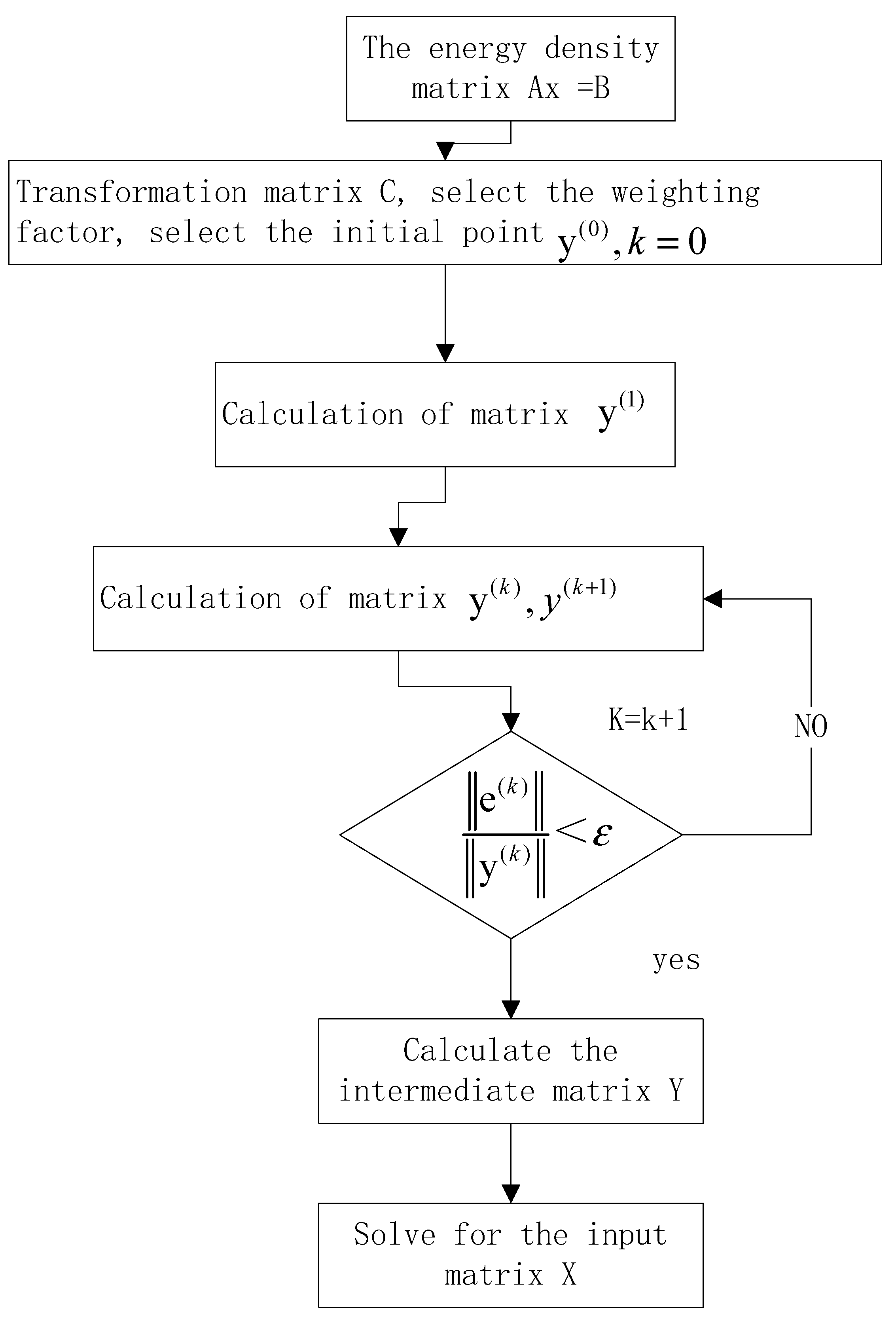


| Name | Density (kg/m3) | Poisson’s Ratio | Elasticity Modulus (GPa) | Damping Loss Factor | Steel Plate Size (mm) | Thickness of Steel Plate (mm) |
|---|---|---|---|---|---|---|
| steel plate | 7800 | 0.3 | 200 | 0.01 | 1000 × 1000 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.; Zheng, L. An Identification Method for the “Effective Coupling Loss Factor” Based on the Hybrid FE-SEA Model. Appl. Sci. 2023, 13, 3687. https://doi.org/10.3390/app13063687
Su J, Zheng L. An Identification Method for the “Effective Coupling Loss Factor” Based on the Hybrid FE-SEA Model. Applied Sciences. 2023; 13(6):3687. https://doi.org/10.3390/app13063687
Chicago/Turabian StyleSu, Jintao, and Ling Zheng. 2023. "An Identification Method for the “Effective Coupling Loss Factor” Based on the Hybrid FE-SEA Model" Applied Sciences 13, no. 6: 3687. https://doi.org/10.3390/app13063687





