Entangled Frequency-Tunable Microwave Photons in a Superconducting Circuit
Abstract
:1. Introduction
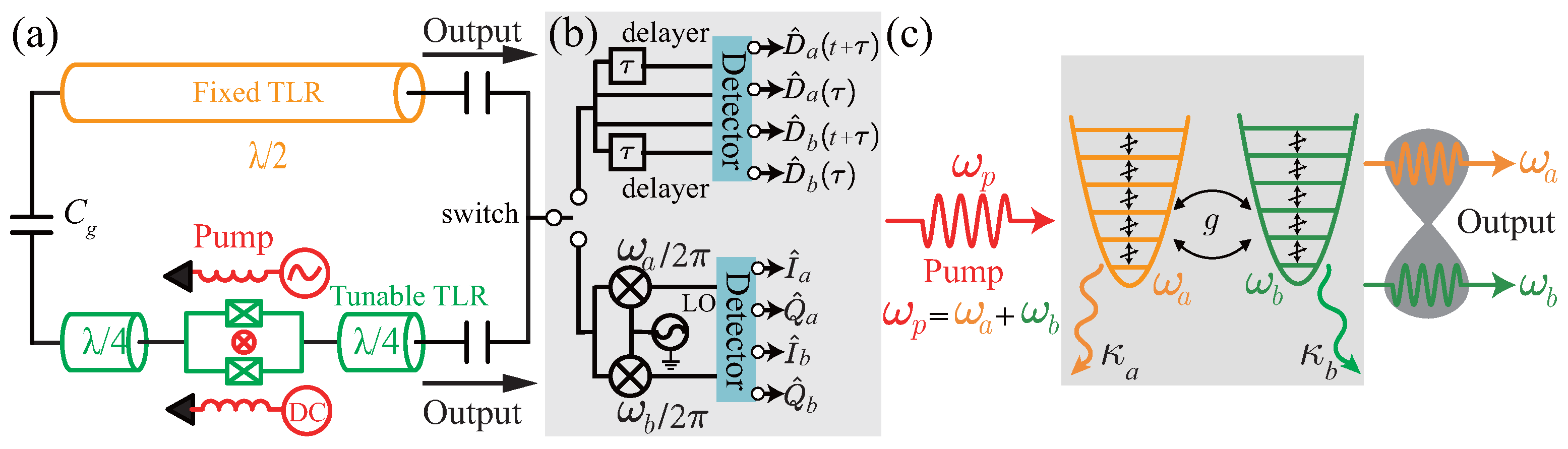
2. The Circuit Model
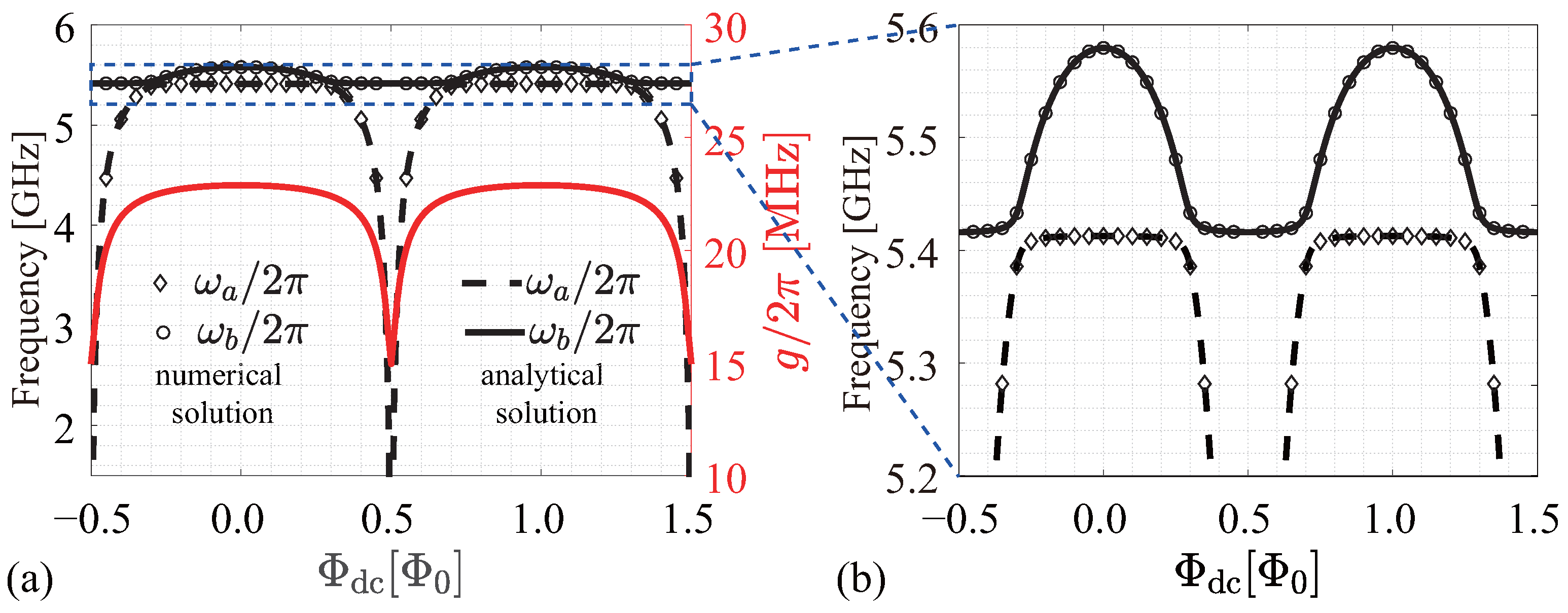
3. Parameters and Spectrum of the System
4. Numerical Results
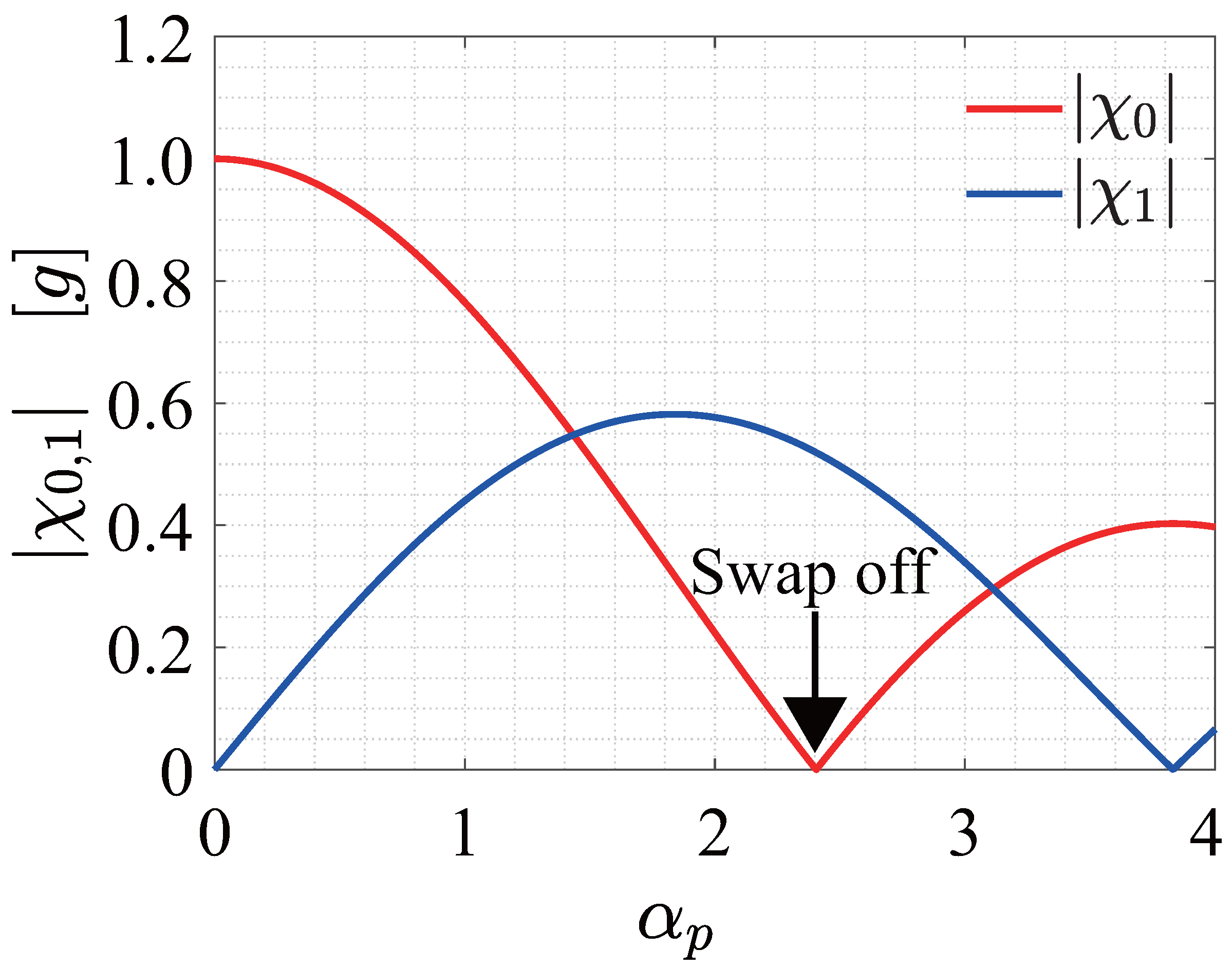
4.1. Creation of the Photon Pairs
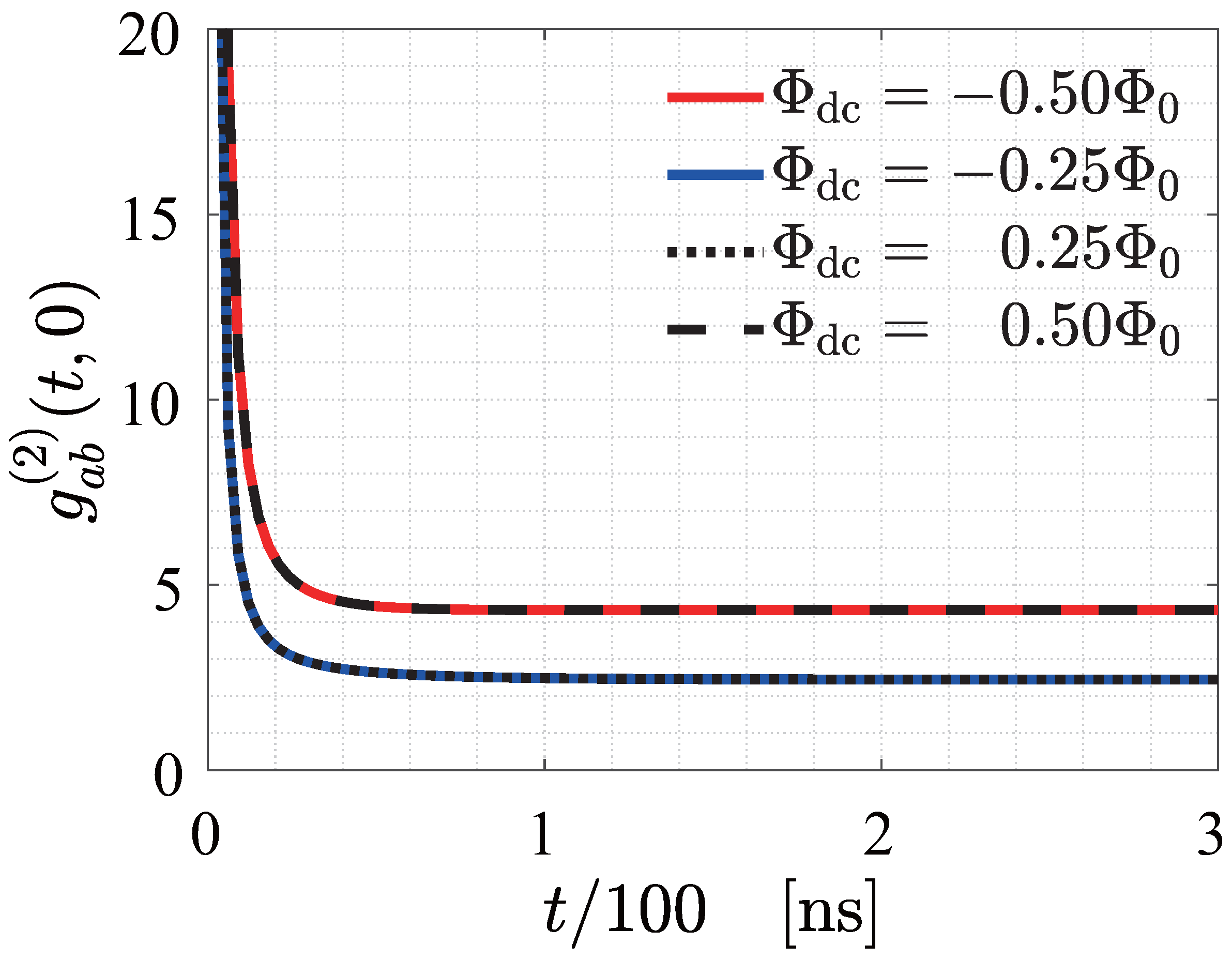
4.2. Two-Mode Entanglement
4.3. Frequency-Tunable Entangled Photon Pairs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wendin, G. Quantum information processing with superconducting circuits: A review. Rep. Prog. Phys. 2017, 80, 106001. [Google Scholar] [CrossRef] [Green Version]
- Peugeot, A.; Ménard, G.; Dambach, S.; Westig, M.; Kubala, B.; Mukharsky, Y.; Altimiras, C.; Joyez, P.; Vion, D.; Roche, P.; et al. Generating Two Continuous Entangled Microwave Beams Using a dc-Biased Josephson Junction. Phys. Rev. X 2021, 11, 031008. [Google Scholar] [CrossRef]
- Felicetti, S.; Sanz, M.; Lamata, L.; Romero, G.; Johansson, G.; Delsing, P.; Solano, E. Dynamical Casimir Effect Entangles Artificial Atoms. Phys. Rev. Lett. 2014, 113, 093602. [Google Scholar] [CrossRef] [Green Version]
- Agustí, A.; Solano, E.; Sabín, C. Entanglement through qubit motion and the dynamical Casimir effect. Phys. Rev. A 2019, 99, 052328. [Google Scholar] [CrossRef] [Green Version]
- Gómez, A.V.; Rodríguez, F.J.; Quiroga, L. Cross-entangling electronic and nuclear spins of distant nitrogen-vacancy centers in noisy environments by means of quantum microwave radiation. Phys. Rev. B 2018, 98, 075114. [Google Scholar] [CrossRef] [Green Version]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513–577. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.K.; Pan, J.W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Lin, D.K.; Wang, C.; Zeng, G.H. High-speed continuous-variable quantum key distribution without sending a local oscillator. Opt. Lett. 2015, 40, 3695–3698. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Sciarrino, F.; Laing, A.; Thompson, M.G. Integrated photonic quantum technologies. Nat. Photonics 2020, 14, 273–284. [Google Scholar] [CrossRef]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef] [Green Version]
- Reiserer, A.; Rempe, G. Cavity-based quantum networks with single atoms and optical photons. Rev. Mod. Phys. 2015, 87, 1379–1418. [Google Scholar] [CrossRef] [Green Version]
- Hillmann, T.; Quijandría, F.; Johansson, G.; Ferraro, A.; Gasparinetti, S.; Ferrini, G. Universal Gate Set for Continuous-Variable Quantum Computation with Microwave Circuits. Phys. Rev. Lett. 2020, 125, 160501. [Google Scholar] [CrossRef] [PubMed]
- Barzanjeh, S.; Pirandola, S.; Vitali, D.; Fink, J.M. Microwave quantum illumination using a digital receiver. Sci. Adv. 2020, 6. [Google Scholar] [CrossRef] [PubMed]
- Friberg, S.; Hong, C.K.; Mandel, L. Measurement of Time Delays in the Parametric Production of Photon Pairs. Phys. Rev. Lett. 1985, 54, 2011–2013. [Google Scholar] [CrossRef]
- Burnham, D.C.; Weinberg, D.L. Observation of Simultaneity in Parametric Production of Optical Photon Pairs. Phys. Rev. Lett. 1970, 25, 84–87. [Google Scholar] [CrossRef]
- Introini, V.; Steel, M.J.; Sipe, J.E.; Helt, L.G.; Liscidini, M. Spontaneous parametric down conversion in a doubly resonant one-dimensional photonic crystal. Opt. Lett. 2020, 45, 1244–1247. [Google Scholar] [CrossRef]
- Gosner, J.; Kubala, B.; Ankerhold, J. Relaxation dynamics and dissipative phase transition in quantum oscillators with period tripling. Phys. Rev. B 2020, 101, 054501. [Google Scholar] [CrossRef] [Green Version]
- Arndt, L.; Hassler, F. Period tripling due to Josephson parametric down-conversion beyond the rotating-wave approximation. Phys. Rev. B 2022, 106, 014513. [Google Scholar] [CrossRef]
- Arndt, L.; Hassler, F. Period Tripling due to Parametric Down-Conversion in Circuit QED. Phys. Rev. Lett. 2022, 128, 187701. [Google Scholar] [CrossRef]
- Denisenko, M.; Munyayev, V.; Satanin, A. Quantum fractional resonances in superconducting circuits with an embedded Josephson junction. J. Phys. Conf. Ser. 2016, 681, 012018. [Google Scholar] [CrossRef]
- Wilson, C.M.; Duty, T.; Sandberg, M.; Persson, F.; Shumeiko, V.; Delsing, P. Photon Generation in an Electromagnetic Cavity with a Time-Dependent Boundary. Phys. Rev. Lett. 2010, 105, 233907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sandbo Chang, C.W.; Simoen, M.; Aumentado, J.; Sabín, C.; Forn-Díaz, P.; Vadiraj, A.M.; Quijandría, F.; Johansson, G.; Fuentes, I.; Wilson, C.M. Generating Multimode Entangled Microwaves with a Superconducting Parametric Cavity. Phys. Rev. Appl. 2018, 10, 044019. [Google Scholar] [CrossRef]
- Agustí, A.; Chang, C.W.S.; Quijandría, F.; Johansson, G.; Wilson, C.M.; Sabín, C. Tripartite Genuine Non-Gaussian Entanglement in Three-Mode Spontaneous Parametric Down-Conversion. Phys. Rev. Lett. 2020, 125, 020502. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.W.S.; Sabín, C.; Forn-Díaz, P.; Quijandría, F.; Vadiraj, A.M.; Nsanzineza, I.; Johansson, G.; Wilson, C.M. Observation of Three-Photon Spontaneous Parametric Down-Conversion in a Superconducting Parametric Cavity. Phys. Rev. X 2020, 10, 011011. [Google Scholar] [CrossRef] [Green Version]
- Wustmann, W.; Shumeiko, V. Parametric effects in circuit quantum electrodynamics. Low Temp. Phys. 2019, 45, 848–869. [Google Scholar] [CrossRef] [Green Version]
- Wilson, C.M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J.R.; Duty, T.; Nori, F.; Delsing, P. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 2011, 479, 376–379. [Google Scholar] [CrossRef] [Green Version]
- Schneider, B.H.; Bengtsson, A.; Svensson, I.M.; Aref, T.; Johansson, G.; Bylander, J.; Delsing, P. Observation of Broadband Entanglement in Microwave Radiation from a Single Time-Varying Boundary Condition. Phys. Rev. Lett. 2020, 124, 140503. [Google Scholar] [CrossRef] [Green Version]
- Krantz, P.; Reshitnyk, Y.; Wustmann, W.; Bylander, J.; Gustavsson, S.; Oliver, W.D.; Duty, T.; Shumeiko, V.; Delsing, P. Investigation of nonlinear effects in Josephson parametric oscillators used in circuit quantum electrodynamics. New J. Phys. 2013, 15, 105002. [Google Scholar] [CrossRef] [Green Version]
- Bergeal, N.; Schackert, F.; Frunzio, L.; Devoret, M.H. Two-Mode Correlation of Microwave Quantum Noise Generated by Parametric Down-Conversion. Phys. Rev. Lett. 2012, 108, 123902. [Google Scholar] [CrossRef] [Green Version]
- Marković, D.; Jezouin, S.; Ficheux, Q.; Fedortchenko, S.; Felicetti, S.; Coudreau, T.; Milman, P.; Leghtas, Z.; Huard, B. Demonstration of an Effective Ultrastrong Coupling between Two Oscillators. Phys. Rev. Lett. 2018, 121, 040505. [Google Scholar] [CrossRef] [Green Version]
- Flurin, E.; Roch, N.; Mallet, F.; Devoret, M.H.; Huard, B. Generating Entangled Microwave Radiation Over Two Transmission Lines. Phys. Rev. Lett. 2012, 109, 183901. [Google Scholar] [CrossRef] [Green Version]
- Fedortchenko, S.; Felicetti, S.; Marković, D.; Jezouin, S.; Keller, A.; Coudreau, T.; Huard, B.; Milman, P. Quantum simulation of ultrastrongly coupled bosonic modes using superconducting circuits. Phys. Rev. A 2017, 95, 042313. [Google Scholar] [CrossRef] [Green Version]
- Flurin, E.; Roch, N.; Pillet, J.D.; Mallet, F.; Huard, B. Superconducting Quantum Node for Entanglement and Storage of Microwave Radiation. Phys. Rev. Lett. 2015, 114, 090503. [Google Scholar] [CrossRef] [Green Version]
- Johansson, J.R.; Johansson, G.; Wilson, C.M.; Delsing, P.; Nori, F. Nonclassical microwave radiation from the dynamical Casimir effect. Phys. Rev. A 2013, 87, 043804. [Google Scholar] [CrossRef] [Green Version]
- Pierre, M.; Sathyamoorthy, S.R.; Svensson, I.M.; Johansson, G.; Delsing, P. Resonant and off-resonant microwave signal manipulation in coupled superconducting resonators. Phys. Rev. B 2019, 99, 094518. [Google Scholar] [CrossRef] [Green Version]
- Pierre, M.; Svensson, I.M.; Raman Sathyamoorthy, S.; Johansson, G.; Delsing, P. Storage and on-demand release of microwaves using superconducting resonators with tunable coupling. Appl. Phys. Lett. 2014, 104, 232604. [Google Scholar] [CrossRef] [Green Version]
- Strand, J.D.; Ware, M.; Beaudoin, F.; Ohki, T.A.; Johnson, B.R.; Blais, A.; Plourde, B.L.T. First-order sideband transitions with flux-driven asymmetric transmon qubits. Phys. Rev. B 2013, 87, 220505. [Google Scholar] [CrossRef] [Green Version]
- Xue, Z.Y.; Zhou, J.; Wang, Z.D. Universal holonomic quantum gates in decoherence-free subspace on superconducting circuits. Phys. Rev. A 2015, 92, 022320. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Cai, W.; Ma, Y.; Mu, X.; Hu, L.; Chen, T.; Wang, H.; Song, Y.P.; Xue, Z.Y.; Yin, Z.Q.; et al. Single-Loop Realization of Arbitrary Nonadiabatic Holonomic Single-Qubit Quantum Gates in a Superconducting Circuit. Phys. Rev. Lett. 2018, 121, 110501. [Google Scholar] [CrossRef] [Green Version]
- DiCarlo, L.; Chow, J.M.; Gambetta, J.M.; Bishop, L.S.; Johnson, B.R.; Schuster, D.I.; Majer, J.; Blais, A.; Frunzio, L.; Girvin, S.M.; et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 2009, 460, 240–244. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [Green Version]
- Gong, M.; Wang, S.; Zha, C.; Chen, M.C.; Huang, H.L.; Wu, Y.; Zhu, Q.; Zhao, Y.; Li, S.; Guo, S.; et al. Quantum walks on a programmable two-dimensional 62-qubit superconducting processor. Science 2021, 372, 948–952. [Google Scholar] [CrossRef]
- Eichler, C.; Bozyigit, D.; Lang, C.; Baur, M.; Steffen, L.; Fink, J.M.; Filipp, S.; Wallraff, A. Observation of Two-Mode Squeezing in the Microwave Frequency Domain. Phys. Rev. Lett. 2011, 107, 113601. [Google Scholar] [CrossRef] [Green Version]
- Johansson, J.R.; Johansson, G.; Wilson, C.M.; Nori, F. Dynamical Casimir effect in superconducting microwave circuits. Phys. Rev. A 2010, 82, 052509. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Xiao, R.; Shen, H.Z.; Sun, C.; Xue, K. Simulating Anisotropic quantum Rabi model via frequency modulation. Sci. Rep. 2019, 9, 4569. [Google Scholar] [CrossRef] [Green Version]
- Rossatto, D.Z.; Felicetti, S.; Eneriz, H.; Rico, E.; Sanz, M.; Solano, E. Entangling polaritons via dynamical Casimir effect in circuit quantum electrodynamics. Phys. Rev. B 2016, 93, 094514. [Google Scholar] [CrossRef] [Green Version]
- Di Stefano, O.; Settineri, A.; Macrì, V.; Ridolfo, A.; Stassi, R.; Kockum, A.F.; Savasta, S.; Nori, F. Interaction of Mechanical Oscillators Mediated by the Exchange of Virtual Photon Pairs. Phys. Rev. Lett. 2019, 122, 030402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Macrì, V.; Ridolfo, A.; Di Stefano, O.; Kockum, A.F.; Nori, F.; Savasta, S. Nonperturbative Dynamical Casimir Effect in Optomechanical Systems: Vacuum Casimir-Rabi Splittings. Phys. Rev. X 2018, 8, 011031. [Google Scholar] [CrossRef] [Green Version]
- Minganti, F.; Garbe, L.; Le Boité, A.; Felicetti, S. Non-Gaussian superradiant transition via three-body ultrastrong coupling. Phys. Rev. A 2023, 107, 013715. [Google Scholar] [CrossRef]
- Seifoory, H.; Doutre, S.; Dignam, M.M.; Sipe, J.E. Squeezed thermal states: The result of parametric down conversion in lossy cavities. J. Opt. Soc. Am. B 2017, 34, 1587–1596. [Google Scholar] [CrossRef]
- Salmon, W.; Gustin, C.; Settineri, A.; Stefano, O.D.; Zueco, D.; Savasta, S.; Nori, F.; Hughes, S. Gauge-independent emission spectra and quantum correlations in the ultrastrong coupling regime of open system cavity-QED. Nanophotonics 2022, 11, 1573–1590. [Google Scholar] [CrossRef]
- Johansson, J.; Nation, P.; Nori, F. QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2012, 183, 1760–1772. [Google Scholar] [CrossRef] [Green Version]
- Johansson, J.; Nation, P.; Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2013, 184, 1234–1240. [Google Scholar] [CrossRef] [Green Version]
- Novikova, I.; Gorshkov, A.V.; Phillips, D.F.; Sørensen, A.S.; Lukin, M.D.; Walsworth, R.L. Optimal Control of Light Pulse Storage and Retrieval. Phys. Rev. Lett. 2007, 98, 243602. [Google Scholar] [CrossRef] [Green Version]
- Sete, E.A.; Mlinar, E.; Korotkov, A.N. Robust quantum state transfer using tunable couplers. Phys. Rev. B 2015, 91, 144509. [Google Scholar] [CrossRef] [Green Version]
- Caves, C.M.; Combes, J.; Jiang, Z.; Pandey, S. Quantum limits on phase-preserving linear amplifiers. Phys. Rev. A 2012, 86, 063802. [Google Scholar] [CrossRef] [Green Version]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Cao, C.; Chen, J.; Wang, H.; Sun, G.; Wu, P. Entangled Frequency-Tunable Microwave Photons in a Superconducting Circuit. Appl. Sci. 2023, 13, 3688. https://doi.org/10.3390/app13063688
Zhang K, Cao C, Chen J, Wang H, Sun G, Wu P. Entangled Frequency-Tunable Microwave Photons in a Superconducting Circuit. Applied Sciences. 2023; 13(6):3688. https://doi.org/10.3390/app13063688
Chicago/Turabian StyleZhang, Kaixuan, Chunhai Cao, Jian Chen, Huabing Wang, Guozhu Sun, and Peiheng Wu. 2023. "Entangled Frequency-Tunable Microwave Photons in a Superconducting Circuit" Applied Sciences 13, no. 6: 3688. https://doi.org/10.3390/app13063688
APA StyleZhang, K., Cao, C., Chen, J., Wang, H., Sun, G., & Wu, P. (2023). Entangled Frequency-Tunable Microwave Photons in a Superconducting Circuit. Applied Sciences, 13(6), 3688. https://doi.org/10.3390/app13063688







