1. Introduction
Because the wheels of a railway are guided by tracks, the condition of the tracks significantly affects the safety of the railway. Therefore, railway operators must manage tracks appropriately, safety should be ensured through inspections by track maintenance staff, and maintenance should be performed based on measurements using dedicated track geometry cars. However, conducting track maintenance for regional railways using conventional methods has become difficult because of their poor financial condition and lack of manpower.
Track condition monitoring using in-service vehicles has been the subject of worldwide research and development for the past quarter century [
1,
2,
3,
4,
5]. Determining the correlation between track irregularities and vehicle responses is crucial. The vehicle runs over the same track multiple times, allowing for efficient diagnosis of track condition deterioration. A number of methods have been proposed to monitor track conditions based on vehicle vibrations by installing sensors to detect vehicle vibrations on in-service vehicles. The use of vehicle responses in the track geometry assessment process allows for the identification of track defects that could not be identified from geometry parameters [
6].
There are three types of sensor configurations for track condition monitoring using in-service vehicles. The first is to mount the sensor on the axle-box. This method has the advantage of direct observation of the track condition, but it also creates new maintenance problems because the onboard sensors are exposed to severe vibration. Chen et al. analysed axle-box acceleration by using axle-box-mounted sensors to identify rail defects [
7]. The relation between axle-box accelerations and track irregularity was analysed by Karis et al. [
8]. Tsai et al. analysed the effect of track irregularities on axle-box acceleration and showed a method for monitoring the track defects [
9].
The second method is to mount the sensor on the bogie. This method is easier to maintain than mounting on the axle-box but requires careful consideration of the position of the sensor to be mounted on the bogie. A track irregularity monitoring method using bogie-mounted sensors was proposed by Weston et al. [
10,
11].
The method with the best maintainability and suitablity for unmanned measurement is to install sensors inside the car. In this method, vibrations generated by track geometry are transmitted to the car body via the primary and secondary suspensions. Therefore, it is necessary to examine the effect of track conditions on the acceleration of the car body. Bai et al. used low-cost accelerometers that were placed on or attached to the floors of in-service trains for analysing track quality [
12].
A track condition monitoring system has been developed to monitor track conditions by using accelerometers and microphones placed on the car body of in-service vehicles [
13,
14,
15,
16,
17,
18,
19]. A map-matching method that corrects the latitude and longitude information acquired by the global navigation satellite system (GNSS) on the track is used as the position identification method for this system. The system is currently installed in two regional railway lines in Japan and continuously monitors track conditions [
20,
21]. More recently, a track condition monitoring system using a smartphone has been proposed as an alternative to dedicated vehicle vibration measurement equipment [
22,
23,
24,
25].
If a mathematical model is available that can represent the vehicle’s motion, the model-based estimation method can be applied. In this case, it is necessary to solve the inverse problem of estimating the track geometry from the vibration of the vehicle. Kalman filter-based methods were proposed to estimate the track geometry from car-body motions [
26,
27,
28,
29,
30].
As large amounts of measurement data become available on a daily basis, it becomes necessary to process these data automatically to diagnose track conditions. The root mean square (RMS) of car-body acceleration is highly correlated to the general health of tracks [
31]. A machine learning technique for identifying track degradation based on the measured RMS values of a car-body acceleration has been developed [
20]. Tsunashima et al. proposed a new method for automatically classifying the type and degradation level of track faults using a convolutional neural network (CNN). In this study, the car-body acceleration was imaged using the continuous wavelet transform (CWT) [
32]. Dolezel et al. analysed possibilities for train-type identification in railway switches and crossings based on accelerometer data by using neural networks [
33].
Various methods of monitoring track conditions have been proposed. However, few papers refer to long-term changes in the condition of the track and future predictions. In this study, we conduct long-term measurements using the track condition monitoring system [
20,
21] and evaluate changes in the track conditions over time using car-body vibration data. The map-matching method causes an error of several tens of metres, depending on the GNSS reception conditions. Thus, to improve the position identification accuracy, we use the point at which changes are observed in the curvature estimated from the yaw angular velocity (yaw rate) of the vehicle to correct the position information obtained via the map-matching method; subsequently, we evaluate the effectiveness of the method and diagnose the track condition.
2. Track Condition Monitoring System
2.1. Overview of Track Condition Monitoring System
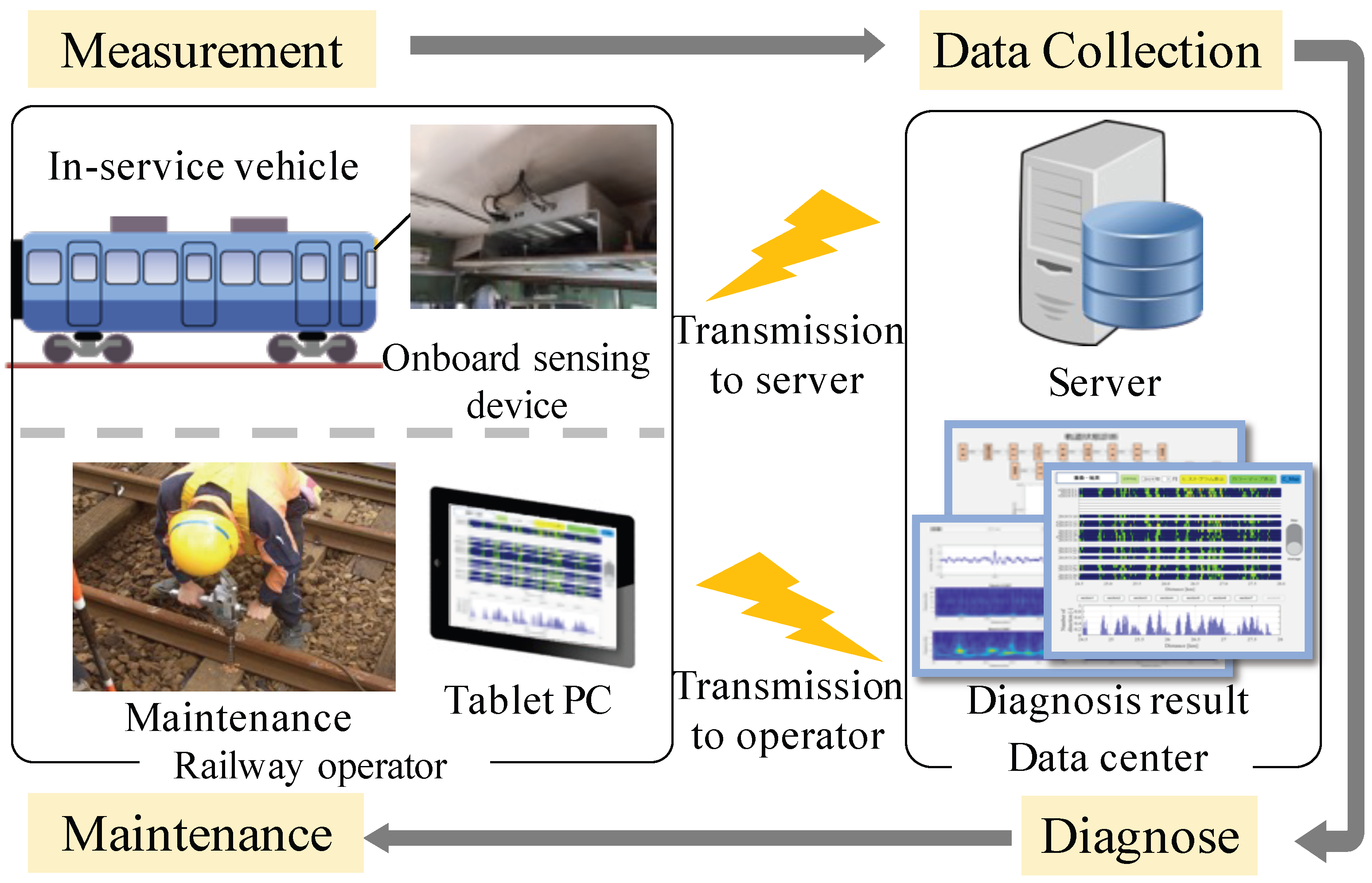
Figure 1 shows an overview of the proposed system. The system can be categorised into a measurement section for measuring the vibration acceleration of in-service vehicles and an analysis section for analysing the vibration acceleration data acquired. In the measurement section, an onboard sensing device comprising a three-axis sensor, rate gyroscope, and GNSS receiver was installed on the in-service vehicle.
The configuration enabled constant measurement of the car-body vibration acceleration by supplying power from the vehicle as it was operating. The vibration acceleration data acquired were transmitted to the server via a mobile phone network. A diagnosis based on the vibration acceleration data transmitted to the server is presented in the analysis section. Continuous monitoring of the track condition using this system enabled the detection of irregularities, such as track faults, and the provision of feedback to railway operators for maintenance planning.
2.2. Evaluation Value Used in the Track Condition Diagnostic System
The concept of a “track condition diagram”, which provides a visual representation of the results of a track irregularity analysis using measurement data obtained from an onboard sensing device, has been proposed. We used this concept in this study for track condition diagnosis.
Car-body vibrations are correlated significantly with track irregularity. Therefore, the single-sided maximum amplitude of vibration in a 10-m-long section was calculated based on the measured car-body vibration acceleration and then utilised in the evaluation. Here, the single-sided maximum amplitude used as a feature value was the absolute value of the half amplitude of the highest vibration acceleration in the section. The method used to calculate the single-sided maximum amplitude is illustrated in
Figure 2.
2.3. Car-Body Vibration Measurement in a Regional Railway
An actual vehicle test trial was conducted by installing an onboard sensing device in in-service vehicles on a regional railway for continuous measurements from October 2020 to August 2022. Owing to the general inspection of vehicles and software updates of the onboard sensing devices, almost no data were obtained between January 2022 and June 2022. In this study, we evaluated track conditions using the vertical and lateral acceleration data acquired during daily trials.
3. Track Condition Monitoring Results Using Vertical Vibration Acceleration
3.1. Locations at Which Extremely High Vertical Accelerations Were Measured
Figure 3 shows the locations at which extremely high vertical accelerations were measured. The blue line and light blue rectangles indicate the train tracks and stations, respectively; the accelerations measured at these locations are shown in orange and red, respectively.
As shown in
Figure 3, extremely high accelerations were measured in the CD, DE, and HI sections between the stations. Next, we focus our discussion on Section CD, where track maintenance was conducted partially in July 2022.
3.2. Track Condition Diagram
Figure 4 shows the track condition diagram for Section CD. The horizontal axis in
Figure 4 represents the distance, and the upper row shows the track condition diagram created based on the aforementioned single-sided maximum amplitude value. The vertical axis represents the measurement date; here, the date of the first measurement of each month is displayed as a reference value. At different times of day, the data with the highest one-sided maximum amplitude value are displayed as representative data.
The lower section of
Figure 4 is a histogram showing the frequency of threshold exceedance, where the number of times the one-sided maximum amplitude value of each datum exceeds the threshold of 1.0 [
] is normalised by the number of times the train operates. This enables the deterioration degree and track position to be estimated.
For cases in which multiple test trials were conducted in one day, the highest measured values of the one-sided maximum amplitude for the trials are shown herein as representative values. In the lower section of the diagram, the number of times the single-sided maximum amplitude of each test datum exceeded the threshold of 1.0 [] is normalised by the (total) number of test trials, and the histogram of the frequency of threshold exceedance is shown. The average velocity for all test data, as indicated by a red line, is used as a reference.
As shown in
Figure 4, high vibration accelerations occurred frequently in the sections from 1.1 to 1.2 km and from 1.4 to 1.5 km. Next, we investigated whether longitudinal-level irregularities occurred in these sections.
Table 1 and
Table 2 show the locations where the measurements exceeded the target value of track irregularity correction for riding comfort and the corresponding level of irregularity, as indicated by the track geometry measurement results for the sections from 1.1 to 1.2 km and from 1.4 to 1.5 km. The inspections were conducted in September 2020.
As shown in
Table 1 and
Table 2, track irregularity, which indicates track degradation, occurred continuously in both sections. Accordingly, sections with degraded tracks can be identified. In the next subsection, we discuss the changes in vibration acceleration over time in these sections.
The data presented in this paper include the effect of this train speed change. The authors also propose a more accurate evaluation method that does not depend on the effect of train speed [
21]. The sections evaluated in this paper have not been corrected for the effect of train speed, as the speed changes were small (AVE: 35.0 km/h, SD: 5.3 km/h at 1.15 km, AVE: 30.5 km/h, SD: 4.7 km/h at 1.45 km). Additionally, if the in-service train to be measured changes, the data to be measured will also change. For this reason, measurements are always taken on the same train.
3.3. Changes in Car-Body Vertical Acceleration over Time
To investigate the long-term changes in the track condition for each target section, the maximum car-body acceleration measured in one trial was regarded as one data point and plotted.
Figure 5 and
Figure 6 show the changes in vibration acceleration over time in the sections from 1.1 to 1.2 km and from 1.4 to 1.5 km.
The change from October 2020 to July 2022 shows that the maximum value of the maximum car-body vertical acceleration has been increasing steadily, indicating that the track condition has been deteriorating. There is a period between January 2021 and June 2022 when measurements are not available due to vehicle inspections.
The track beds were replenished and tamped down in July 2022, in the former section, primarily in the section from 1.110 to 1.145 km, where the measurements exceeded the target value of the track irregularity correction for riding comfort. However, for the section from 1.4 to 1.5 km, no track maintenance was performed, except in the section from 1.470 to 1.500 km.
As shown in
Figure 5, beginning from the time measurement commenced, the vibration acceleration gradually increased and then decreased after July 2022. Track maintenance was performed at this time, and its effects were confirmed.
Figure 6 shows changes in the maximum vertical acceleration in the section between 1.4 and 1.5 km. There is no significant change in the maximum values of the vertical acceleration of the car body between October 2020 and July 2021. However, it can be seen that significant vertical acceleration of the car body has been observed since July 2021. This indicates that the track condition degraded rapidly.
Track maintenance was performed in July 2022, but the vertical acceleration of the car body has not decreased since then.
Figure 5 and
Figure 6 show the maximum values for the 100 m section. Therefore, if the track irregularities generating large vertical accelerations are included in the maintenance section, the effect of maintenance should be confirmed. On the other hand, if the track irregularity was not included in the maintenance section, no decrease in the vibration acceleration can be observed. The details of the maintenance work shown in
Figure 5 and
Figure 6 were not provided by the railway operator. It is, therefore, necessary to re-examine why the maintenance effectiveness cannot be confirmed in the section shown in
Figure 6, based on future measurement data and detailed information about the new maintenance work.
Frequent track geometry measurements cannot be conducted on regional railways; therefore, such rapid track degradation cannot be detected through conventional track geometry measurements. Missing data for 6 months may have a significant impact on the accuracy of the diagnosis. Future re-validation should be carried out on the basis of data without the missing data period.
4. Track Condition Monitoring Results Using Lateral Vibration Acceleration
4.1. Effect of Centrifugal Acceleration
The lateral vibration acceleration of vehicles is correlated significantly with track alignment irregularity. However, lateral vibration acceleration includes a steady component owing to the centrifugal acceleration when the train operates on a curved track. This steady component must be eliminated to enable evaluation based on the vibration acceleration generated solely by the track irregularity. Therefore, the centrifugal acceleration was calculated based on the onboard sensing device measurements of travelling velocity and yaw angular velocity, which were then deducted from the lateral vibration acceleration measurements.
4.2. Diagnosis for Section CD
The diagnosis for Section CD was conducted in a manner similar to the vertical vibration acceleration-based diagnosis.
Figure 7 shows the track condition diagram for this section. The diagram can be described similarly as presented in
Section 3.2, except that the red line in the lower section shows the registered track curvature as a reference.
As shown in
Figure 7, significant vibrations occurred in the sections from 1.1 to 1.2 km and from 1.4 to 1.5 km. We investigated whether alignment irregularities occurred in these sections.
Table 3 and
Table 4 show the locations where the measurements exceeded the target value of track irregularity correction for riding comfort and the corresponding level of irregularity, as indicated by the track geometry measurement results for the sections from 1.05 to 1.15 km and from 1.4 to 1.5 km. As shown in
Table 3 and
Table 4, track irregularities occurred continuously in both sections, indicating track degradation. Hence, the sections with degraded tracks were identifiable. Next, we discuss the changes in the vibration acceleration over time in these sections.
4.3. Changes in Car-Body Lateral Acceleration over Time
Figure 8 and
Figure 9 show the changes in the vibration acceleration over time in the sections from 1.05 to 1.15 km and from 1.4 to 1.5 km.
No significant changes were indicated in the measurements from the time they commenced. Furthermore, the lateral accelerations decreased after June 2022. Between October 2020 and December 2021, the increase in car-body vibration acceleration is not significant but tends to increase gradually. Therefore, the deterioration of the track condition is considered to be progressing gradually.
Although the alignment correction for the track maintenance in June 2022 was not reported, the record of such work performed in November 2021 was confirmed. Thus, although detailed changes in the acceleration could not be confirmed because no measurements could be undertaken between January and June 2022, we believe that the effect of track maintenance in November 2021 was demonstrated. After track maintenance, the acceleration of car-body vibration decreased, confirming the effect of the track maintenance.
5. Improvement in Train Position Accuracy Based on Yaw Angular Velocity
5.1. Overview
A map-matching method that corrects the latitude and longitude information acquired by the GNSS on the track was used as the position identification method.
However, this method causes an error of several tens of metres, depending on the GNSS reception conditions. In this study, to improve the position identification accuracy, we used the point at which changes were observed in the curvature, estimated from the yaw angular velocity of the vehicle, to correct the position information obtained via the map-matching method; subsequently, we evaluated the effectiveness of the approach and diagnosed the track condition.
5.2. Map-Matching Based Train Position Identification
The map-matching technique used to estimate the train position is shown in
Figure 10. We created a database (DB) that associates the latitude and longitude measured in advance on the target route with the distance from the starting point, and each point in the DB was connected through a straight line.
We searched for the DB point that was the closest to the position measured by the onboard sensing device (DB_B) for the DB and determined the DB section with the shortest perpendicular length between the DB section before and after the point (DB_A and DB_C) as well as the measurement position (GNSS position). We calculated the distance from the aforementioned DB point to the intersection of the DB section and perpendicular line via linear interpolation. The distance obtained by adding the distance of the DB point to the distance above is defined as the distance converted from the GNSS position.
5.3. Track Condition Evaluation and Position Identification Issues
In the track condition diagrams shown in
Figure 4 and
Figure 7, the detection location differs depending on the day of measurement. The positions where the acceleration is from 1 to 1.5 [
], which varied depending on the day, are shown in green. Additionally, the histogram in the lower section of the figures confirms the variation in position.
5.4. Position Correction Method Using Yaw Rate
We applied the method proposed by Gion et al. to estimate the curve start/end points [
35]. Gion et al. calculated and corrected the train position using vehicle speed measured using a tachometer generator, which has high accuracy on vehicle speed. However, the proposed method has not been evaluated using vehicle speed measured by a GNSS. In this study, the correction target was the train position information obtained by map matching using a GNSS.
The curvature of the track can be estimated from the operating speed and yaw angular velocity measured using the onboard sensing device. The curve start/endpoints were estimated from the estimated curvatures and compared with the track information for track management to obtain and correct the error between the distance for track management and the distance obtained via map matching.
Figure 11 shows the position correction method.
The curvature
was calculated from the yaw angular velocity
[rad/s] obtained from the onboard sensing device and GNSS velocity
[m/s] using the following equation:
Subsequently, a linear approximation was performed using the value of the central section of the transition-curve region of the calculated curvature. We set the point at which the extension of the obtained approximated line intersected with the line where the curvature was 0 [1/m] as the curve start/endpoint. The track data used when the railway operator managed the track were used as the position data for the curve to be compared.
The magnification
A to be corrected is calculated as
where
[m] is the distance between the beginning and end of the curve obtained in the previous section, and
[m] is the position of the end of the curve in the track data.
The distance information was dilated and corrected by multiplying the calculated magnification A by the distance obtained via map matching.
5.5. Position Correction Results and Track Condition Monitoring Results
5.5.1. Measurement of Car-Body Vibration
We conducted an evaluation using the car-body vertical acceleration obtained from October 2020 to September 2021 at a regional railway, where onboard sensing devices were installed in in-service trains. The sampling frequency was 82 [Hz], and the operating data were used for 130 trials.
5.5.2. Overview of Field Test
In this study, we conducted a correction at two points in the section between stations at 1040 [m].
Figure 12 shows a satellite image of the section between the stations. We evaluated the car-body vertical acceleration of an inbound train operating from station B to station A. The yellow and red points in
Figure 12 indicate the positions of the end of the transition curve (ETC) and the beginning of the transition curve (BTC) used for correction, respectively; the curvature radii of the curves were
[m] and
[m], respectively, and the curve lengths were 245 and 432 [m], respectively, in the order of their proximities to station B. The statistical evaluation method for the position correction effect was implemented using the entire dataset for 130 trials.
5.5.3. Position Correction Result
Figure 13 and
Figure 14 show the curvatures of the data from all the trials without and with position correction, respectively. In addition, as a reference value, the curvature information of the midpoint of the curves is shown as a dotted red line, and the ETC and BTC positions used for position correction are indicated as a dotted blue line.
A comparison between
Figure 13 and
Figure 14 shows that the position correction method provided a slight variation in the estimated curvature at the midpoint of the curves. Subsequently, we calculated the variance and mean value of the position information (distance) at the midpoint of the transition-curve section (when measuring 50% of the maximum curvature value of the curve).
The results show that the standard deviations before correction were 12.5 and 8.6 [m], whereas, after correction, they was 7.6 and 3.9 [m], respectively, which indicates that the variation in the data owing to the GNSS error can be reduced. The mean values were 3942 and 4296 [m] before correction and 3948 and 4305 [m] after correction, respectively, whereas the actual values were 3946 and 4307 [m], respectively. This indicates that position correction using the yaw angular velocity is effective for the position information calculated via GNSS-based map matching.
5.5.4. Track Condition Monitoring Results after Position Correction
The track condition was monitored using the position-corrected data.
Figure 15 and
Figure 16 show the track condition diagrams before and after the position correction for the section between stations, respectively. The lower parts of
Figure 15 and
Figure 16 show histograms showing the threshold (1.0 [
]) exceedance frequency. Additionally, as a reference value, the track curvature is shown as a red line, and the BTC and ETC positions used for position correction are shown as red points.
The track conditions were monitored using position-corrected data.
Figure 15 and
Figure 16 show the track condition diagrams before and after position correction for the section between the stations, respectively. The lower sections of
Figure 15 and
Figure 16 present histograms that show the threshold (1.0 [
]) exceedance frequency. The reference value is indicated by a red line in the track curvature, whereas the BTC and ETC positions used for position correction are shown as red points.
First, we evaluated the acceleration occurring at approximately 4100 [m]. The variance and mean values were calculated before and after the correction. Before the correction, the variance was 104 [], and the mean value was 4105 [m]. After the correction, the variance was 75 [], the mean value was 4103 [m], and the data variation decreased owing to the position correction. Thus, the position where track irregularity occurs can be clarified via a position correction based on the curvature.
Additionally, we verified whether track irregularity occurred at this point by comparing it with the measurement results obtained using track inspection equipment. The results show significant longitudinal-level irregularities of 24.7 [mm] at 3985 [m], 22.4 [mm] at 4110 [m], and 21.6 [mm] at 4185 [m], all of which appeared within the range of ±10 [m] from the point indicated by the peak in the histogram of
Figure 16. Furthermore, on-site confirmation of the point shows the occurrence of mud pumping at the rail joint, which is believed to have caused significant longitudinal-level irregularities.
In the histograms shown in
Figure 15 and
Figure 16, the acceleration caused by multiple track irregularities is superimposed; hence, an evaluation is difficult to perform. To evaluate the effectiveness of the proposed method appropriately, we set the threshold to 1.5 [
] and extracted only relatively high accelerations caused by significant track irregularities (
Figure 17).
The results show that the position of the track irregularity can be identified more clearly via a position correction based on the curvature.
6. Detail Analysis of Track Condition Using Time-Frequency Analysis
6.1. Continuous Wavelet Transform (Cwt)
The wavelet transform is a tool that divides data or a function into its different frequency components and examines each component at a resolution appropriate to its scale. This method is used in various fields of engineering. The wavelet transform is well-known technique for analysing non-stationary signals [
36,
37].
A CWT gives simultaneous detection of the frequency and time characteristics for non-stationary signals,
, using a wavelet,
, which is a function of zero average. The CWT is calculated using the mother wavelet
as
where,
a and
b correspond to the dilatation and location parameters, respectively.
indicates the complex conjugate of
.
A CWT translates a source signal
using the mother wavelet transformed by a time shift
b in time and by
in frequency. In this study, we employed the
Morlet wavelet, which has a good performance between its localisation of time and frequency [
38].
The CWT is subject to the uncertainty principle in the time-frequency domain. In case of fault detection using the CWT, if we are focusing on the frequency related on the fault, the time when the fault occurred will be vague. If we are focusing on the time when the fault occurred, the frequency will spread widely on the time-frequency plane. The time and frequency variables cannot be treated independently. This fact is known as the uncertainty principle in the time-frequency plane.
6.2. Hilbert–Huang Transform (Hht)
A time-frequency analysis method called Hilbert–Huang transform (HHT) is not subject to the uncertainty principle on time-frequency domain mentioned above [
39,
40]. Thus, more localised fault detection is possible. The Hilbert–Huang transform (HHT) has been proposed for analysing nonlinear and non-stationary data by Hung et al. [
40].
The HHT consists of the empirical mode decomposition (EMD) and the Hilbert transform. The EMD breaks time domain data into intrinsic oscillatory modes called intrinsic mode functions (IMFs). An IMF satisfies that the number of local extrema and the number of zero crossings must either equal or differ by at most one and that the mean value of the envelopes of local maxima and local minima is zero at any point.
The iterative sifting process is applied for extracting IMFs from the original signal. Once the first IMF is calculated, it is subtracted from the original signal to obtain a residual. The EMD operation is applied again for the residual. This process repeats until the residual no longer contains any oscillation modes. The instantaneous amplitude and instantaneous phase of the IMFs are obtained by the Hilbert transform for each IMF component.
The original signal,
, can be expressed by an EMD operation as
where
is the
ith IMF and
is a residual.
It should be noted that the HHT is highly adaptive but IMFs are strongly depend on the data themselves. Thus, there is a possibility that similar source signals are decomposed in different IMFs.
6.3. Track Condition before and after Track Maintenance
It is known that when trains run on tracks with faults, characteristic vibrations corresponding to the types of track faults occur. It may be possible to identify the types and degradation levels of track faults and their locations by using the time-frequency plane. From the measured data, a time-frequency analysis was performed to identify and evaluate the detailed track conditions before and after track maintenance.
Figure 18 shows the time-frequency analysis of the car-body vertical acceleration before track maintenance. The top section of
Figure 18 shows the measured car-body acceleration (Measurement date: 16 December 2021, Train speed: V = 37 [km/h]). The middle section of
Figure 18 shows the time-frequency plane with the CWT. The bottom section of
Figure 18 shows the time-frequency plane with the HHT.
Figure 19 shows the time-frequency analysis of the car-body vertical acceleration after track maintenance. The top section of
Figure 19 shows the measured car-body acceleration (Measurement date: 28 June 2022, Train speed: V = 36 [km/h]). The middle section of
Figure 19 shows the time-frequency plane with the CWT. The bottom section of
Figure 19 shows the time-frequency plane with the HHT.
In December 2021, vibrations due to longitudinal track irregularities were detected at 1–2 Hz in the 3750–3800 m section but were no longer detected in July 2022, owing to the track maintenance carried out in May 2022. It should be noted that the time-frequency analysis with the CWT and the HHT gives detailed information about the track conditions, which is useful for evaluating the quality of track maintenance.
The vertical vibration acceleration of the car-body mainly consisted of vibration components between 1 and 2 Hz. In the CWT, the time resolution was widely spread due to uncertainty in lower frequency band. On the other hand, the HHT had a higher time resolution than the CWT. Thus, it is considered that more effective identification of track faults is possible using the HHT.
As indicated above, a time-frequency analysis of the vertical acceleration of the car-body can be used to evaluate longitudinal irregularities. It is also known that by focusing on higher frequency bands, joint depression can also be identified [
41].
7. Conclusions
We conducted long-term vibration measurements using in-service vehicles of regional railways, identified sections with degraded tracks using car-body vibration data, and presented figures that show changes in the track conditions over time. The track degradation trend can be constructed using the results obtained. Furthermore, this study demonstrated that the track maintenance effect could be confirmed.
Rapid track degradation and the effects of track maintenance in regional railways are difficult to understand owing to the difficulty in conducting frequent track geometry measurements because of their poor financial condition and lack of manpower. Therefore, the track condition must be monitored frequently based on the vibration acceleration data measured using in-service vehicles. Moreover, track geometry cars cannot operate on tracks in regional railways, and railway operators typically conduct only static track inspections without applying any load to the track. In a static inspection, the track condition differs from the state in which the vehicles operate on the track in actual scenarios. Therefore, car-body vibration accelerations measured using in-service trains must be utilised to maintain track conditions. This system can be used in conjunction with track recording car measurement data for efficient maintenance.
Position information calculated via map matching using a GNSS was corrected using the curvature obtained from the yaw angular velocity. Position correction using the curvature appeared to be effective for position information calculated via map matching using a GNSS. Additionally, the track irregularity position can be shown more clearly by monitoring the track condition using position-corrected data.
In future studies, we will add more correction points and verify other sections between the stations to confirm the effectiveness of the proposed method. In this study, we used the track data used by railway operators to manage the tracks as the reference positions for the curve start/end points (BTC, ETC); however, these data may not match the actual track geometry. Therefore, we will consider creating an accurate position information DB of the curve start/endpoints using high-precision positioning methods, such as the real-time kinematic method and quasi-zenith satellite system, and then use it for correction.
We also showed that a time-frequency analysis of the measured car-body vertical acceleration is effective for evaluating track conditions. We will evaluate the effect of track maintenance more comprehensively by comparing the vibration acceleration measurements with the track geometry measurement results after track maintenance. Furthermore, we plan to predict the progress of track condition degradation based on previous changes in the vibration acceleration.
Author Contributions
Conceptualization, H.T.; methodology, H.T.; software, H.O. and T.T.; validation, H.T., H.O. and T.T.; analysis, H.T., H.O. and T.T.; data curation, H.T., T.T., S.O. and H.O.; writing—original draft preparation, H.T.; writing—review and editing, H.O., T.T., S.O. and H.T.; visualization, H.T. and H.O.; supervision, H.T.; project administration, H.T.; funding acquisition, H.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Nihon University Research Grant for Social Implementation (19-006) (2019–2021) and JSPS KAKENHI Grant Number 20K04368.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AVE | average |
| BTC | beginning of transition curve |
| CNN | convolutional neural network |
| CWT | continuous wavelet transform |
| DB | database |
| ETC | end of transition curve |
| GNSS | global navigation satellite system |
| HHT | Hilbert–Huang transform |
| RMS | root mean square |
| SD | standard deviation |
References
- Weston, P.; Roberts, C.; Yeo, G.; Stewar, E. Perspectives on railway track geometry condition monitoring from in-service railway vehicles. Veh. Syst. Dyn. 2015, 53, 1063–1091. [Google Scholar] [CrossRef] [Green Version]
- Tsunashima, H. Railway Condition Monitoring, Present and Future. In 2016 1st International Workshop on Structural Health Monitoring for Railway Systems (IWSHM-RS 2016); DEStech Publications: Lancaster, PA, USA, 2016; ISBN 978-1-60595-371-7. [Google Scholar]
- Tsunashima, H. Railway Condition Monitoring, Present and Application for Regional Railways; Report of the Research Institute of Industrial Technology, Nihon University Number 102; Nihon University: Tokyo, Japan, 2018. [Google Scholar]
- Bernal, E.; Spiryagin, M.; Cole, C. Onboard Condition Monitoring Sensors, Systems and Techniques for Freight Railway Vehicles: A Review. IEEE Sens. J. 2019, 19, 4–24. [Google Scholar] [CrossRef]
- Kostrzewski, M.; Melnik, R. Condition Monitoring of the Rail Transport Systems: A Bibliometric Performance Analysis and Systematic Literature Review. Sensors 2021, 21, 4710. [Google Scholar] [CrossRef]
- Kraft, S.; Causse, J.; Coudert, F. Vehicle response based track geometry assessment using multi- body simulation. Veh. Syst. Dyn. 2018, 56, 190–220. [Google Scholar] [CrossRef]
- Chen, X.; Chai, X.; Cao, X. The time-frequency analysis of the train axle box acceleration signals using empirical mode decomposition. Comput. Model New Technol. 2014, 18, 356–360. [Google Scholar]
- Karis, T.; Berg, M.; Stichel, S. Correlation of track irregularities and vehicle responses based on measured data. Veh. Syst. Dyn. 2018, 56, 967–981. [Google Scholar] [CrossRef]
- Tsai, H.C.; Wang, C.Y.; Huang, N.E. Railway track inspection based on the vibration response to a scheduled train and the Hilbert–Huang transform. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2014, 229, 815–829. [Google Scholar] [CrossRef]
- Westeon, P.F.; Ling, C.S.; Roberts, C.; Goodman, C.J.; Li, P.; Goodall, R.M. Monitoring vertical track irregularity from in-service railway vehicles. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2007, 221, 75–88. [Google Scholar] [CrossRef]
- Weston, P.F.; Ling, C.S.; Goodman, C.J.; Roberts, C.; Li, P.; Goodall, R.M. Monitoring lateral track irregularity from in-service railway vehicles. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2007, 221, 89–100. [Google Scholar] [CrossRef]
- Bai, L.; Liu, R.; Li, Q. Data-driven bias correction and defect diagnosis model for in-service vehicle acceleration measurements. Sensors 2020, 20, 872. [Google Scholar] [CrossRef] [Green Version]
- Kojima, T.; Tsunashima, H.; Matsumoto, A. Fault detection of railway track by multi-resolution analysis. In Proceedings of the 4th International Conference on Wavelet Analysis and Its Applications, Macau, China, 21–28 November 2005. [Google Scholar]
- Kojima, T.; Tsunashima, H.; Matsumoto, A. Fault detection of railway track by multi-resolution analysis. In Computer in Railway X; WIT Press: Ashurst, UK, 2006; pp. 955–964. [Google Scholar]
- Hayashi, H.; Kojima, T.; Tsunashima, H.; Marumo, Y. Real Time Fault Detection of Railway Vehicles and Tracks. In Proceedings of the International Conference on Railway Condition Monitoring 2006, Birmingham, UK, 29–30 November 2006; pp. 20–25. [Google Scholar]
- Tsunashima, H.; Kojima, T.; Marumo, Y.; Matsumoto, A.; Mizuma, T. Condition Monitoring of Railway Track and Driver Using In-Service Vehicle. In Proceedings of the International Conference on Railway Condition Monitoring 2008, Derby, UK, 17–20 June 2008. [Google Scholar]
- Tsunashima, H.; Naganuma, Y.; Matsumoto, A. Japanese railway condition monitoring of tracks using in-service vehicle. In Proceedings of the 5th IET Conference on Railway Condition Monitoring (RCM 2011), Derby, UK, 29–30 November 2011. [Google Scholar]
- Tsunashima, H.; Naganuma, Y.; Matsumoto, A.; Mizuma, T.; Mori, H. Condition monitoring of railway track using in-service vehicle. In Reliability and Safety in Railway; Perpinya, X., Ed.; InTech: London, UK, 2012. [Google Scholar]
- Mori, H.; Ohno, H.; Tsunashima, H. Development of compact size onboard device for condition monitoring of railway tracks. J. Mech. Syst. Transp. Logistics 2013, 6, 142–149. [Google Scholar] [CrossRef] [Green Version]
- Tsunashima, H. Condition Monitoring of Railway Tracks from Car-Body Vibration Using a Machine Learning Technique. Appl. Sci. 2019, 9, 2734. [Google Scholar] [CrossRef] [Green Version]
- Ono, H.; Tsunashima, H.; Takata, T.; Ogata, S. Development and operation of a system for diagnosing the condition of regional railways tracks. Mech. Eng. J. 2023, in press. [Google Scholar] [CrossRef]
- Chellaswamy, C.; Geetha, T.S.; Vanathi, A.; Venkatachalam, K. An IoT based rail track condition monitoring and derailment prevention system. Int. J. Technol. 2020, 11, 81–107. [Google Scholar] [CrossRef]
- Rodríguez, A.; Sanudo, S.; Miranda, M.; Gomez, A.; Benavente, J. Smartphones and tablets applications in railways, ride comfort and track quality. Transition zones analysis. Measurement 2021, 182, 1–12. [Google Scholar] [CrossRef]
- Cong, J.; Gao, M.; Miranda, M.; Wang, Y.; Chen, R.; Wang, P. Subway rail transit monitoring by built-in sensor platform of smartphone. Front. Inf. Technol. Electron. Eng. 2020, 21, 1226–1238. [Google Scholar] [CrossRef]
- Paixão, A.; Fortunato, E.; Calçada, R. Smartphone’s Sensing Capabilities for On-Board Railway Track Monitoring: Structural Performance and Geometrical Degradation Assessment. Adv. Civ. Eng. 2019, 2019, 1729153. [Google Scholar] [CrossRef]
- Tsunashima, H.; Naganuma, Y.; Kobayashi, T. Track geometry estimation from car-body vibration. Veh. Syst. Dyn. 2014, 52, 207–219. [Google Scholar] [CrossRef]
- Naganuma, Y.; Azami, S.; Tsunashima, H. Track geometry estimation from car-body motions of Shinkansen vehicles. In Proceedings of the International Symposium on Speed-up and Sustainable Technology for Railway and Maglev Systems 2015 (STECH2015), Chiba, Japan, 10–12 November 2015. [Google Scholar]
- Odashima, M.; Azami, S.; Naganuma, Y.; Mori, H.; Tsunahsima, H. Trackg eometry estimation of a conventional railway from car-body acceleration measurement. Mech. Eng. J. 2017, 4, 16-00498. [Google Scholar] [CrossRef] [Green Version]
- Xiao, X.; Zhe Sun, Z.; Shen, W. A Kalman filter algorithm for identifying track irregularities of railway bridges using vehicle dynamic responses. Mech. Syst. Signal Process. 2020, 138, 106582. [Google Scholar] [CrossRef]
- Muñoz, S.; Ros, J.; Urda, P.; Escalona, J.L. Estimation of Lateral Track Irregularity Through Kalman Filtering Techniques. IEEE Access 2021, 9, 60010–60025. [Google Scholar] [CrossRef]
- Vinberg, E.; Martin, M.; Firdaus, A.; Tang, Y. Railway Applications of Condition Monitoring; KTH Royal Institute of Technology: Stockholm, Sweden, 2018. [Google Scholar] [CrossRef]
- Tsunashima, H.; Takikawa, M. Monitoring the Condition of Railway Tracks Using a Convolutional Neural Network. Recent Advances in Wavelet Transforms and Their Applications; IntechOpen: London, UK, 2022. [Google Scholar] [CrossRef]
- Dolezel, P.; Krc, R.; Podrouzek, J.; Kratochvilova, M.; Vukusic, I.; Plasek, O. Neural Network-Based Train Identification in Railway Switches and Crossings Using Accelerometer Data. J. Adv. Transp. 2020, 2020, 8841810. [Google Scholar] [CrossRef]
- Shinoda, N.; Tsunashima, H.; Matsumoto, A.; Sato, Y.; Ogata, S. Railway track management based on vibration data of in-service train measured by a mobile device. Jpn. Soc. Mech. Eng. (JSME) 2022, 88, 1–18. [Google Scholar] [CrossRef]
- Gion, A.; Kitano, Y.; Nakazawa, Y. A Study of Position Detection Method for Train Control Systems Using Inertial Sensors. Proceedings of TRANSLOG2021. Jpn. Soc. Mech. Eng. (JSME) 2021. (In Japanese) [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; CBMS-NSF Regional Conference Series in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1992; Volume 61. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Le, T. Use of the Morlet mother wavelet in the frequency-scale domain decomposition technique for the modal identification of ambient vibration responses. Mech. Syst. Signal Process. 2017, 95, 488–505. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Liu, H.H.; Yen, N.-C.; Tung, C.-C. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Attoh-Okine, N.O. Hilbert-Huang Transforms in Engineering; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Tsunashima, H.; Hirose, R. Condition monitoring of railway track from car-body vibration using time-frequency analysis. Veh. Syst. Dyn. 2020, 60, 1170–1187. [Google Scholar] [CrossRef]
Figure 1.
Track condition monitoring system.
Figure 1.
Track condition monitoring system.
Figure 2.
Maximum absolute values of the car-body vertical acceleration.
Figure 2.
Maximum absolute values of the car-body vertical acceleration.
Figure 3.
Locations where high accelerations were observed in a regional railway. It is pointed out that if the vertical acceleration exceeds 2.8 [
] in the driver’s cab, track maintenance should be carried out as soon as possible [
34]. For this reason, this figure defines an acceleration of 3 [
] or more as a significant car-body vertical acceleration.
Figure 3.
Locations where high accelerations were observed in a regional railway. It is pointed out that if the vertical acceleration exceeds 2.8 [
] in the driver’s cab, track maintenance should be carried out as soon as possible [
34]. For this reason, this figure defines an acceleration of 3 [
] or more as a significant car-body vertical acceleration.
Figure 4.
Track condition diagram of vertical acceleration for Section CD. Averaged speed profile for all runs is shown at the middle of the diagram. AVE: 35.0 km/h, SD: 5.3 km/h at 1.15 km, AVE: 30.5 km/h, SD: 4.7 km/h at 1.45 km. Speed profile for all runs is shown at the bottom of the diagram.
Figure 4.
Track condition diagram of vertical acceleration for Section CD. Averaged speed profile for all runs is shown at the middle of the diagram. AVE: 35.0 km/h, SD: 5.3 km/h at 1.15 km, AVE: 30.5 km/h, SD: 4.7 km/h at 1.45 km. Speed profile for all runs is shown at the bottom of the diagram.
Figure 5.
Changes in maximum vertical acceleration in a section between 1.1 and 1.2 km.
Figure 5.
Changes in maximum vertical acceleration in a section between 1.1 and 1.2 km.
Figure 6.
Changes in maximum vertical acceleration in a section between 1.4 and 1.5 km.
Figure 6.
Changes in maximum vertical acceleration in a section between 1.4 and 1.5 km.
Figure 7.
Track condition diagram of lateral acceleration for Section CD. Speed profile for all runs is shown at the bottom of the diagram.
Figure 7.
Track condition diagram of lateral acceleration for Section CD. Speed profile for all runs is shown at the bottom of the diagram.
Figure 8.
Changes in maximum lateral acceleration in a section between 1.05 and 1.15 km.
Figure 8.
Changes in maximum lateral acceleration in a section between 1.05 and 1.15 km.
Figure 9.
Changes in maximum lateral acceleration in a section between 1.4 and 1.5 km.
Figure 9.
Changes in maximum lateral acceleration in a section between 1.4 and 1.5 km.
Figure 10.
Map-matching-based train position identification.
Figure 10.
Map-matching-based train position identification.
Figure 11.
Position correction method.
Figure 11.
Position correction method.
Figure 12.
Satellite photo of the test section.
Figure 12.
Satellite photo of the test section.
Figure 13.
Estimated curvature without position correction. The color lines show the estimated curvatures for all runs without position correction.
Figure 13.
Estimated curvature without position correction. The color lines show the estimated curvatures for all runs without position correction.
Figure 14.
Estimated curvature with position correction. The color lines show the estimated curvatures for all runs with position correction.
Figure 14.
Estimated curvature with position correction. The color lines show the estimated curvatures for all runs with position correction.
Figure 15.
Track fault identification without position correction.
Figure 15.
Track fault identification without position correction.
Figure 16.
Track fault identification with position correction.
Figure 16.
Track fault identification with position correction.
Figure 17.
Comparison of track fault identification with and without position correction.
Figure 17.
Comparison of track fault identification with and without position correction.
Figure 18.
Time-frequency analysis of car-body vertical acceleration before track maintenance. The top section shows measured car-body acceleration (Measurement date: 16 December 2021, Train speed: V = 37 [km/h]). The middle section shows the time-frequency plane with CWT. The bottom section shows the time-frequency plane with HHT.
Figure 18.
Time-frequency analysis of car-body vertical acceleration before track maintenance. The top section shows measured car-body acceleration (Measurement date: 16 December 2021, Train speed: V = 37 [km/h]). The middle section shows the time-frequency plane with CWT. The bottom section shows the time-frequency plane with HHT.
Figure 19.
Time-frequency analysis of car-body vertical acceleration after track maintenance. The top section shows measured car-body acceleration (Measurement date: 28 June 2022, Train speed: V = 36 [km/h]). The middle section shows the time-frequency plane with CWT. The bottom section shows the time-frequency plane with HHT.
Figure 19.
Time-frequency analysis of car-body vertical acceleration after track maintenance. The top section shows measured car-body acceleration (Measurement date: 28 June 2022, Train speed: V = 36 [km/h]). The middle section shows the time-frequency plane with CWT. The bottom section shows the time-frequency plane with HHT.
Table 1.
Measured longitudinal level irregularity between 1.1 and 1.2 km.
Table 1.
Measured longitudinal level irregularity between 1.1 and 1.2 km.
| Distance [km] | 1.100 | 1.115 | 1.120 | 1.130 | 1.145 | 1.170 | 1.180 |
| Track irregularity [mm] | 9.7 | −7.5 | 7.5 | −7.3 | 16.3 | −7.6 | 9.3 |
Table 2.
Measured longitudinal level irregularity between 1.4 and 1.5 km.
Table 2.
Measured longitudinal level irregularity between 1.4 and 1.5 km.
| Distance [km] | 1.405 | 1.420 | 1.430 | 1.440 | 1.445 | 1.475 | 1.490 | 1.495 |
| Track irregularity [mm] | −10.9 | −9.6 | −10.9 | −18.6 | −19.4 | −9.5 | −10.9 | 23.5 |
Table 3.
Measured alignment irregularity between 1.05 and 1.15 km.
Table 3.
Measured alignment irregularity between 1.05 and 1.15 km.
| Distance [km] | 1.055 | 1.060 | 1.075 | 1.080 | 1.125 |
| Track irregularity [mm] | −8.3 | 7.6 | −8.1 | 9.8 | −8.0 |
Table 4.
Measured alignment irregularity between 1.4 and 1.5 km.
Table 4.
Measured alignment irregularity between 1.4 and 1.5 km.
| Distance [km] | 1.440 | 1.455 | 1.465 | 1.490 | 1.495 |
| Track irregularity [mm] | 11.3 | −13.2 | 11.0 | 15.1 | −9.2 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).