Performance of Pavement Temperature Prediction Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Literature Review
2.1.1. SHRP Superpave Model
2.1.2. Viljoen Model
2.1.3. Saudi Arabia Model
2.1.4. Diefenderfer Model
2.1.5. Oman Model
2.2. Selection of Models
2.3. Data Collection
2.3.1. Pretoria Data Collection
2.3.2. Ghana Data Collection
2.4. Analysis
2.4.1. Pavement Temperature Prediction
2.4.2. Data Randomization
2.4.3. Calibration
2.4.4. Statistical Analysis
- R2 measures goodness of fit, i.e., how well a linear regression model fits the measured data, where . R2 varies between 0 and 1; the closer it is to 1, the better the model, i.e., 100% of the variation in the model can be explained by the predictor variables;
- VAF measures the variance accounted for between measured values and predicted values, where . The closer the VAF is to 100, the better the model;
- MRE is defined as the ratio of the absolute error of the predicted value to the measured value, where . This provides a measure of how large the error is relative to measured values, so that the closer the value is to zero, the better the model;
- RMSE measures the extent to which predicted values deviate from measured/actual values, on average, where . RMSE decreases as the error in the predicted values decreases, so that the closer the value is to zero, the better the model.
3. Results
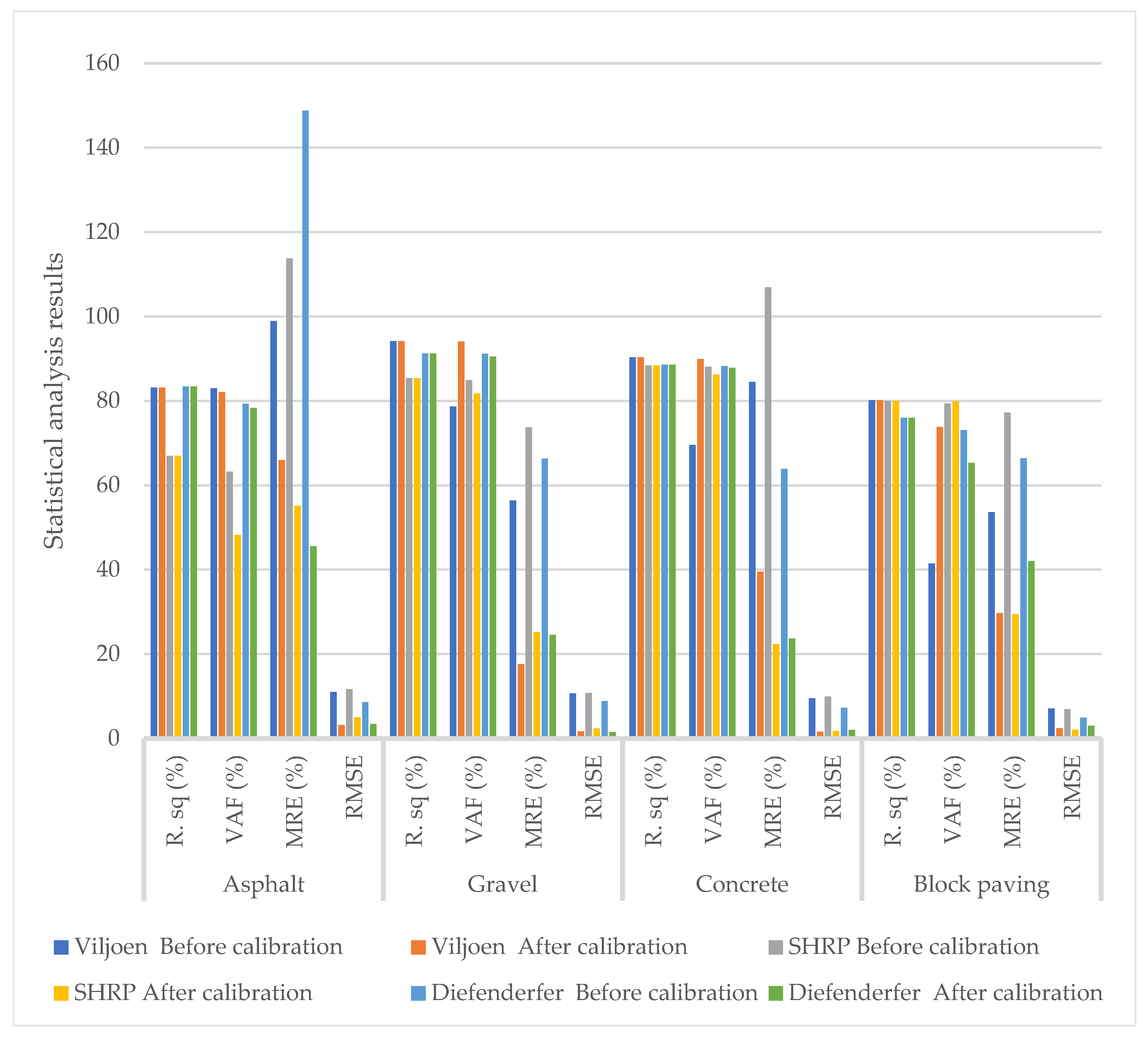
3.1. Performance of Pavement Temperature Prediction Models for Different Pavement Materials, before Calibration
3.1.1. Predicted Maximum Temperature
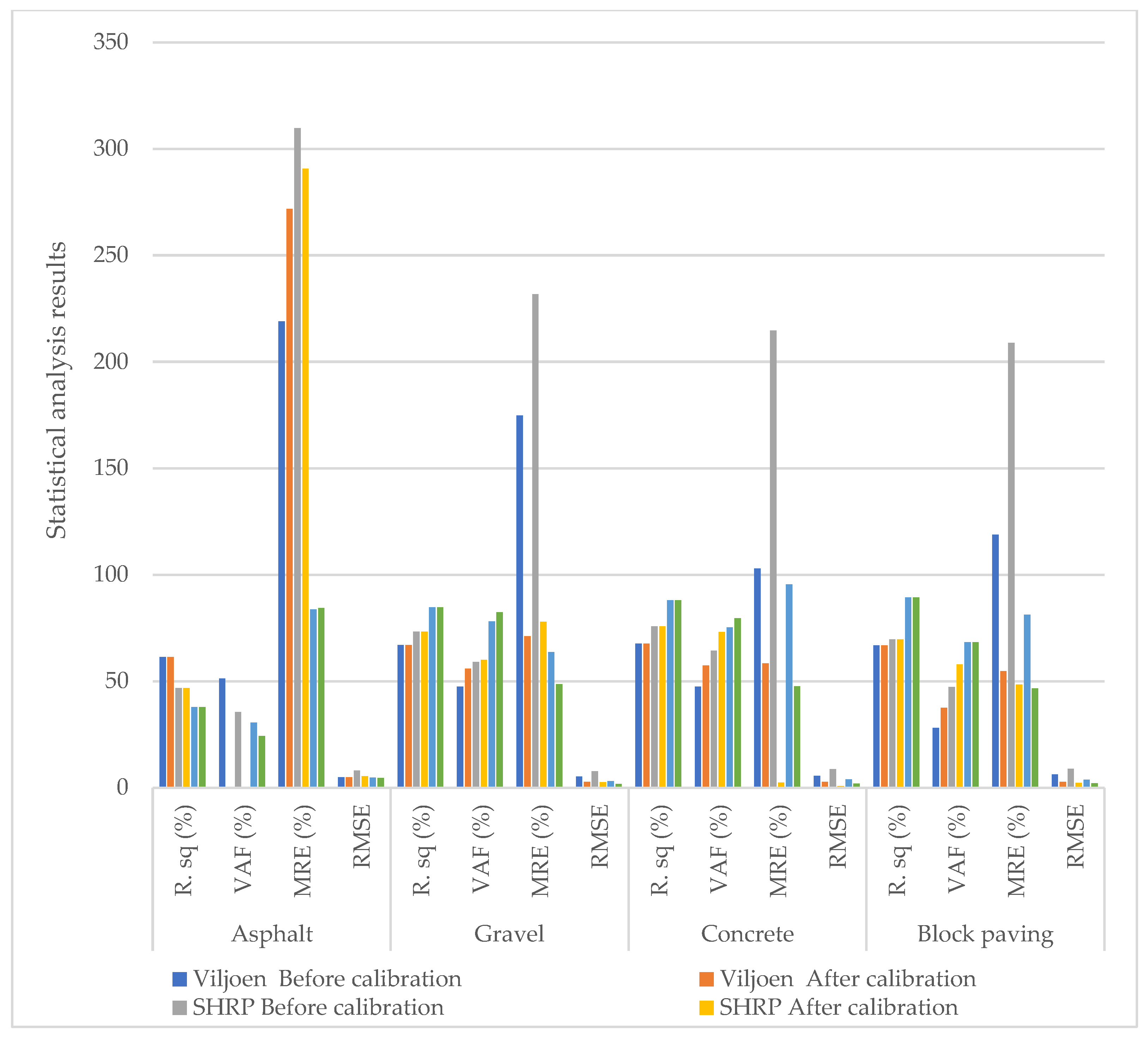
3.1.2. Predicted Minimum Temperature
3.2. Performance of Calibrated Models
3.2.1. Calibrated Maximum Temperature Models
3.2.2. Calibrated Minimum Temperature Models
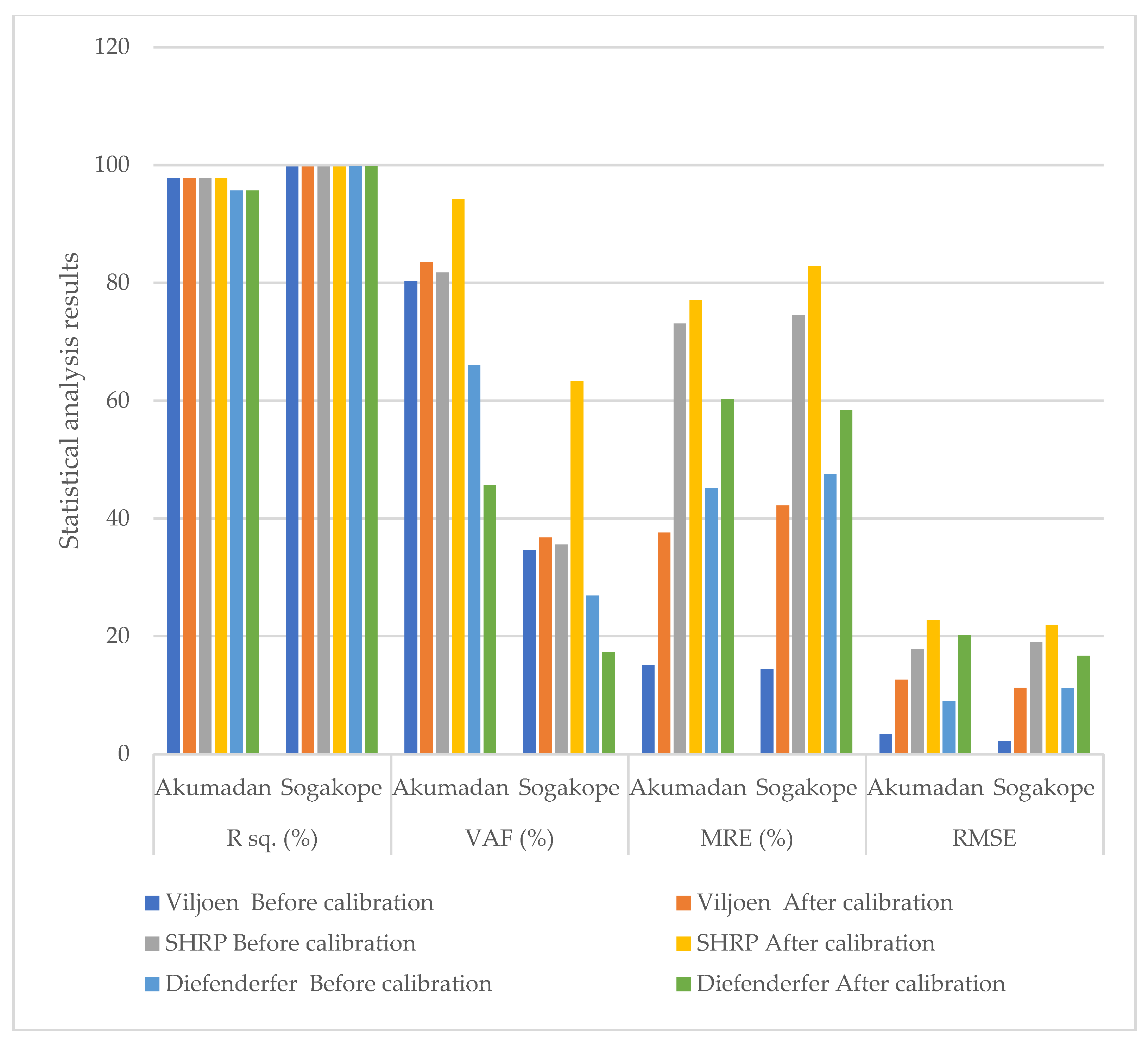
3.3. Performance of Models at Different Geographical Locations
4. Discussion
4.1. Materials Performance
4.2. Calibration
4.3. Effect of Geographical Location
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, L.; Qin, J. Prediction model on temperature field in asphalt pavement. J. Tongji Univ. (Nat. Sci.) 2006, 34, 480–483. [Google Scholar]
- Kennedy, T.; Huber, G.; Harringan, T.; Cominsky, R.; Hughes, C.; Von Quintis, H.; Moultrop, J. Superior Performing Asphalt Pavements (SUPERPAVE): The Product of the SHRP Asphalt Research Program; Report No: SHRP-A-410; Strategic Highway Research Program, National Research Council: Washington, DC, USA, 1994. [Google Scholar]
- Adwan, I.; Milad, A.; Memon, Z.A.; Widyatmoko, I.; Zanuri, N.A.; Memon, N.A.; Yusoff, N.I.M. Asphalt pavement tem-perature prediction models: A review. Appl. Sci. 2021, 11, 3794. [Google Scholar] [CrossRef]
- Mokoena, R.; Mturi, G.; Maritz, J.; Mateyisi, M.; Klein, P. African Case Studies: Developing Pavement Temperature Maps for Performance-Graded Asphalt Bitumen Selection. Sustainability 2022, 14, 1048. [Google Scholar] [CrossRef]
- Chao, J.; Jinxi, Z. Prediction Model for Asphalt Pavement Temperature in High-Temperature Season in Beijing. Adv. Civ. Eng. 2018, 2018, 1837952. [Google Scholar] [CrossRef] [Green Version]
- Kassem, E.; Bayomy, F.; Williams, C.; Saasita, E.; Lamichane, S.; Permadi, D.D. Development of Pavement Temperature Prediction Model (No. FHWA-ID-20-279); Idaho Transportation Department: Moscow, ID, USA, 2020.
- Chen, J.; Wang, H.; Xie, P. Pavement temperature prediction: Theoretical models and critical affecting factors. Appl. Therm. Eng. 2019, 158, 113755. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, X.; Tan, K.; Wang, J. A review on the influencing factors of pavement surface temperature. Environ. Sci. Pollut. Res. 2022, 29, 67659–67674. [Google Scholar] [CrossRef]
- Asefzadeh, A.; Hashemian, L.; Bayat, A. Development of statistical temperature prediction models for a test road in Edmonton, Alberta, Canada. Int. J. Pavement Res. Technol. 2017, 10, 369–382. [Google Scholar] [CrossRef]
- Dzotepe, G.A. The Effect of Environmental Factors on the Implementation of the Mechanistic-Empirical Pavement Design Guide (Mepdg); University of Wyoming: Laramie, WY, USA, 2011. [Google Scholar]
- Tutu, K.A.; Ntramah, S.; Tuffour, Y.A. Superpave performance graded asphalt binder selection for asphalt mixture design in Ghana. Sci. Afr. 2022, 17, e01348. [Google Scholar] [CrossRef]
- Abo-Hashema, M.A.; Mousa, R.M.; Al-Zedjali, S.A.; Abdullah, Q.; Al Balushi, M.M.; Al-Rashdi, M.H. Development of Oman performance grade paving map for superpave asphalt mix design. Int. J. Pavement Eng. Asph. Technol. 2016, 2016, 1–21. [Google Scholar] [CrossRef]
- Denneman, E.; Edmunds, A.; Alex, P.; Wilson, G. Application of pavement temperature prediction algorithms in per-formance grade (PG) binder selection for Australia. Aust. J. Civ. Eng. 2022, 2022, 2082632. [Google Scholar] [CrossRef]
- Viljoen, A. Estimating Asphalt Temperatures from Air Temperatures and Basic Sky Parameters; Internal Report; Transportek, CSIR: Pretoria, South Africa, 2001. [Google Scholar]
- Wahab, H.; Asia, I.; Ramadhan, R. Modelling resilient modulus and temperature correction for Saudi roads. J. Mater. Civ. Eng. 2001, 13, 298–305. [Google Scholar] [CrossRef]
- Diefenderfer, B.; Al-Qadi, I.; Diefenderfer, S. Model to predict pavement temperature profile: Development and validation. J. Transp. Eng. 2006, 132, 162–167. [Google Scholar] [CrossRef]
- Hassan, H.; Al-Nuaimi, A.; Taha, R.; Jafar, T. Development of Asphalt Pavement Temperature Models for Oman. J. Eng. Res. [TJER] 2005, 2, 32–42. [Google Scholar] [CrossRef] [Green Version]
- Huber, G. Weather Data Base for the Superpave Mix Design System; Report No. SHRP-A-648A; Strategic Highway Research Program, National Research Council: Washington, DC, USA, 1994. [Google Scholar]
- Denneman, E. The application of locally developed pavement temperature prediction algorithms in performance grade binder selection. In Proceedings of the 26th Southern African Transport Conference, CSIR International Convention Centre, Pretoria, South Africa, 9–12 July 2007. [Google Scholar]
- Diefenderfer, B.; Al-Qadi, I.; Reubush, S.; Freeman, E. Development and validation of a model to predict pavement temperature profile. In Proceedings of the TRB 2003 Annual Meeting, Transportation Research Board, Washington, DC, USA, 12–16 January 2003. [Google Scholar]
- Koranteng-Yorke, J.B. A Proposed Framework for Asphaltic Concrete Pavement Design for Tropical Soils—Case Study of Ghana. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2012. [Google Scholar]
- de Picado-Santos, L. Design Temperature on Flexible Pavements. Road Mater. Pavement Des. 2000, 1, 355–371. [Google Scholar] [CrossRef]
- Minhoto, M.J.; Pais, J.C.; Pereira, P.A.; Picado-Santos, L.G. Predicting asphalt pavement temperature with a three-dimensional finite element method. Transp. Res. Rec. 2005, 1919, 96–110. [Google Scholar] [CrossRef]
| Analysis | Material | Viljoen Model | SHRP Superpave Model | Diefenderfer Model | |||
|---|---|---|---|---|---|---|---|
| Before Calibration | After Calibration | Before Calibration | After Calibration | Before Calibration | After Calibration | ||
| R2 | Asphalt | 0.8313 | 0.8313 | 0.6694 | 0.6694 | 0.8338 | 0.8338 |
| Gravel | 0.9411 | 0.9411 | 0.8536 | 0.8536 | 0.9126 | 0.9126 | |
| Concrete | 0.9031 | 0.9031 | 0.8842 | 0.8842 | 0.8858 | 0.8858 | |
| Block paving | 0.8017 | 0.8017 | 0.7998 | 0.7998 | 0.7598 | 0.7598 | |
| RMSE | Asphalt | 11.0132 | 3.1463 | 11.6609 | 5.0166 | 8.5995 | 3.3905 |
| Gravel | 10.6601 | 1.7083 | 10.7882 | 2.3293 | 8.8178 | 1.5449 | |
| Concrete | 9.4748 | 1.5738 | 9.9504 | 1.7175 | 7.2553 | 1.9641 | |
| Block paving | 7.0864 | 2.4441 | 6.8919 | 2.1166 | 4.9582 | 3.0033 | |
| MRE (%) | Asphalt | 98.86 | 65.99 | 113.74 | 55.13 | 148.75 | 45.57 |
| Gravel | 56.34 | 17.62 | 73.71 | 25.20 | 66.27 | 24.54 | |
| Concrete | 84.51 | 39.55 | 106.91 | 22.34 | 63.91 | 23.65 | |
| Block paving | 53.62 | 29.65 | 77.22 | 29.42 | 66.42 | 41.99 | |
| VAF (%) | Asphalt | 83.01 | 82.06 | 63.23 | 48.17 | 79.30 | 78.34 |
| Gravel | 78.63 | 94.08 | 84.92 | 81.74 | 91.13 | 90.47 | |
| Concrete | 69.56 | 89.92 | 88.06 | 86.25 | 88.25 | 87.81 | |
| Block paving | 41.45 | 73.76 | 79.39 | 79.89 | 73.08 | 65.31 | |
| Analysis | Material | Viljoen Model | SHRP Superpave Model | Diefenderfer Model | |||
|---|---|---|---|---|---|---|---|
| Before Calibration | After Calibration | Before Calibration | After Calibration | Before Calibration | After Calibration | ||
| R2 | Asphalt | 0.6137 | 0.6137 | 0.4674 | 0.4674 | 0.3776 | 0.3776 |
| Gravel | 0.6702 | 0.6702 | 0.7321 | 0.7321 | 0.8471 | 0.8471 | |
| Concrete | 0.6766 | 0.6766 | 0.7572 | 0.7572 | 0.8794 | 0.8794 | |
| Block paving | 0.6678 | 0.6678 | 0.6962 | 0.6962 | 0.8939 | 0.8939 | |
| RMSE | Asphalt | 4.8524 | 4.8316 | 8.0644 | 5.3390 | 4.6242 | 4.5878 |
| Gravel | 5.1873 | 2.6673 | 7.6755 | 2.5906 | 2.9683 | 1.7031 | |
| Concrete | 5.5343 | 2.7527 | 8.6976 | 0.7572 | 3.8005 | 1.8192 | |
| Block paving | 6.1729 | 2.7966 | 8.7745 | 2.2907 | 3.7749 | 2.0786 | |
| MRE (%) | Asphalt | 219.06 | 271.73 | 309.69 | 290.59 | 83.69 | 84.40 |
| Gravel | 174.83 | 71.08 | 231.78 | 77.86 | 63.62 | 48.65 | |
| Concrete | 102.98 | 58.36 | 214.77 | 2.3315 | 95.46 | 47.58 | |
| Block paving | 118.74 | 54.72 | 208.96 | 48.36 | 81.19 | 46.59 | |
| VAF (%) | Asphalt | 51.30 | −3.30 | 35.43 | −13.29 | 30.48 | 24.20 |
| Gravel | 47.47 | 55.87 | 59.09 | 60.00 | 78.04 | 82.43 | |
| Concrete | 47.49 | 57.30 | 64.26 | 73.15 | 75.33 | 79.50 | |
| Block paving | 28.01 | 37.49 | 47.22 | 57.89 | 68.25 | 68.25 | |
| Analysis | Location | Viljoen Model | SHRP Superpave Model | Diefenderfer Model | |||
|---|---|---|---|---|---|---|---|
| Before Calibration | After Calibration | Before Calibration | After Calibration | Before Calibration | After Calibration | ||
| R2 | Akumadan | 0.9772 | 0.9772 | 0.9772 | 0.9772 | 0.9567 | 0.9567 |
| Sogakope | 0.9971 | 0.9971 | 0.9971 | 0.9971 | 0.9976 | 0.9976 | |
| RMSE | Akumadan | 3.38 | 12.60 | 17.76 | 22.76 | 8.95 | 20.22 |
| Sogakope | 2.18 | 11.26 | 18.96 | 21.91 | 11.20 | 16.69 | |
| MRE (%) | Akumadan | 15.14 | 37.59 | 73.09 | 77.03 | 45.12 | 60.27 |
| Sogakope | 14.38 | 42.21 | 74.56 | 82.87 | 47.60 | 58.39 | |
| VAF (%) | Akumadan | 80.30 | 83.47 | 81.71 | 94.17 | 66.04 | 45.68 |
| Sogakope | 34.63 | 36.78 | 35.57 | 63.33 | 26.91 | 17.32 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lekea, A.; Steyn, W.J.v. Performance of Pavement Temperature Prediction Models. Appl. Sci. 2023, 13, 4164. https://doi.org/10.3390/app13074164
Lekea A, Steyn WJv. Performance of Pavement Temperature Prediction Models. Applied Sciences. 2023; 13(7):4164. https://doi.org/10.3390/app13074164
Chicago/Turabian StyleLekea, Angella, and Wynand J. vdM. Steyn. 2023. "Performance of Pavement Temperature Prediction Models" Applied Sciences 13, no. 7: 4164. https://doi.org/10.3390/app13074164
APA StyleLekea, A., & Steyn, W. J. v. (2023). Performance of Pavement Temperature Prediction Models. Applied Sciences, 13(7), 4164. https://doi.org/10.3390/app13074164






