A Non-Destructive Method for Predicting Critical Load, Critical Thickness and Service Life for Corroded Spherical Shells under Uniform External Pressure Based on NDT Data
Abstract
:Featured Application
Abstract
1. Introduction
2. Problem Description
2.1. Before All, It Is Necessary to Solve the Estimation of the Critical Thickness, Critical Stress, and Service Life of the Shell Based on NDT Data in a Non-Corrosion and Temperature-Independent Environment
2.2. Then, on the Basis of the Previous Step 2.1, We Can Further Solve the Problem of Critical Load (Stress) and Service Life in an Environment Where Corrosion and Temperature Coexist
3. Problem Solving
3.1. First Step: Establish a Non-Destructive Method for Predicting Spherical Shell Life Regardless of Corrosion and Temperature
3.2. Second Step: Establish a Non-Destructive Method for Predicting Critical Load, Critical Thickness, and Service Life of Spherical Shells in the Presence of Corrosion and Temperature
4. Example Analysis
5. Practical Implementation of This Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation List
| S | slope of w vs. w/p line |
| u | displacement of the shell element in x direction |
| v | displacement of the shell element in y direction |
| w | displacement of the shell element in z direction |
| U0 | effect of initial imperfections |
| V | shearing force in straight members in y direction (buckling coefficient to be determined experimentally) |
| unit elongation or strain in x-direction | |
| unit elongation or strain in y-direction | |
| unit elongation of middle surface in x-direction | |
| unit elongation of middle surface in y-direction | |
| Poisson’s ratio | |
| change of curvature in x-direction | |
| change of curvature in y-direction | |
| t0 | thickness of the shell |
| pcr | buckling pressure |
| H( ) | mathematical operator |
| Nx, Ny | resultant forces |
| Qx, Qy | shear forces |
| Mx | My bending moments |
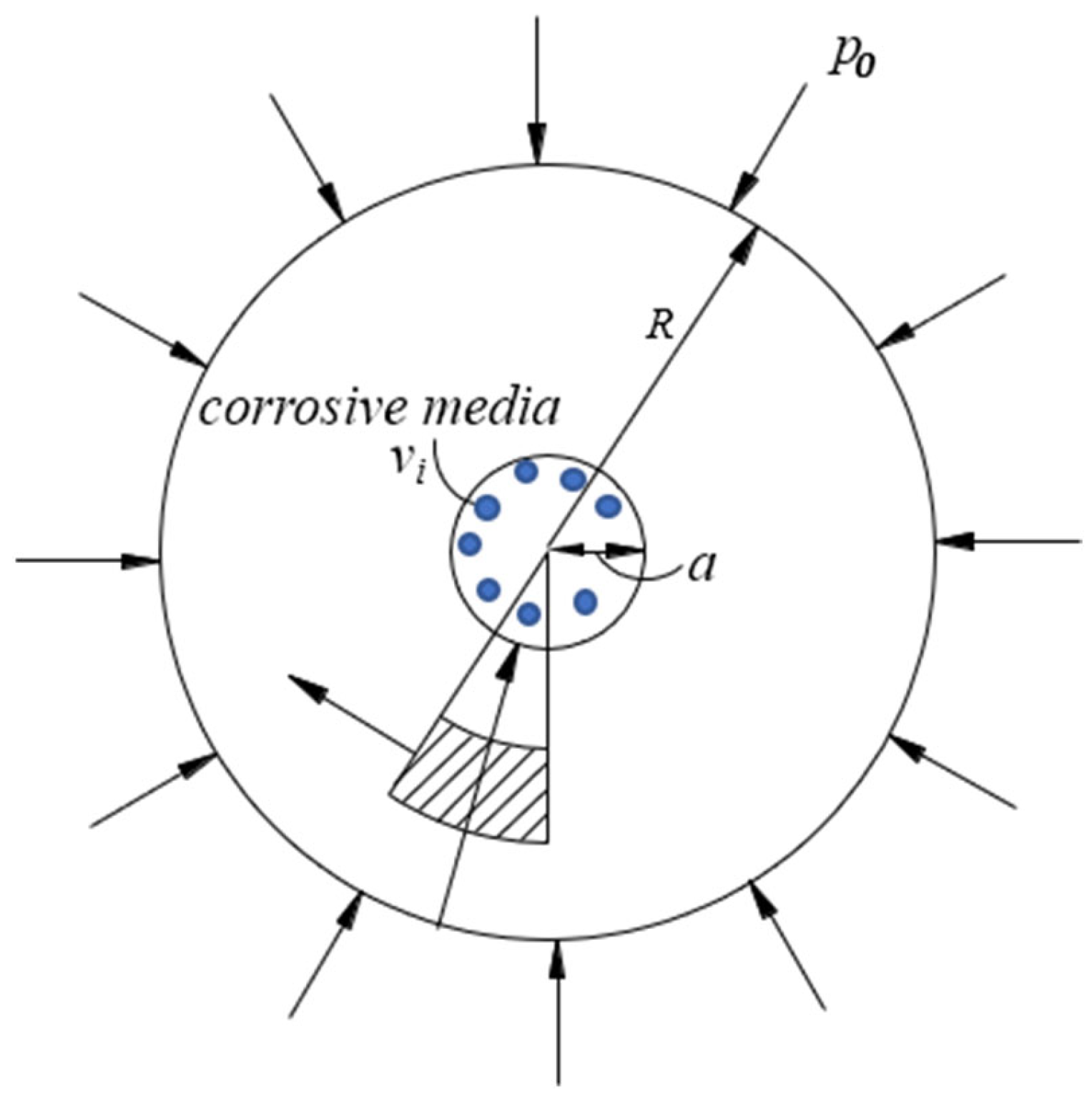
| po | outer pressure |
| vi | inner mechano-chemical corrosion rate |
| t | time |
| h | thickness |
| σ | principal stress |
| σe | effective stress |
| r | distance between a point in the shell material and the origin of the coordinate system/radius of two concentric spheres |
| ro | distance between the point in the outer shell surface and the origin of the coordinate system |
| b | corrosion inhibition effect |
| dr | radius of two concentric spheres |
| dθ, dφ | top angles of four wedge-shaped sections |
| rc | midsurface radius |
| x | thickness to midsurface radius ratio |
| t* | time required for a corroded pressure shell to fail for the first time due to buckling or yielding |
| h | corresponding thickness of the shell under the critical failure state |
Appendix A. Buckling Formulas for Spherical Shells in the Case of Section 2.1 (without Corrosion and Temperature)
Appendix A.1. Derivation of the Second-Order Critical Buckling Load (Stress)
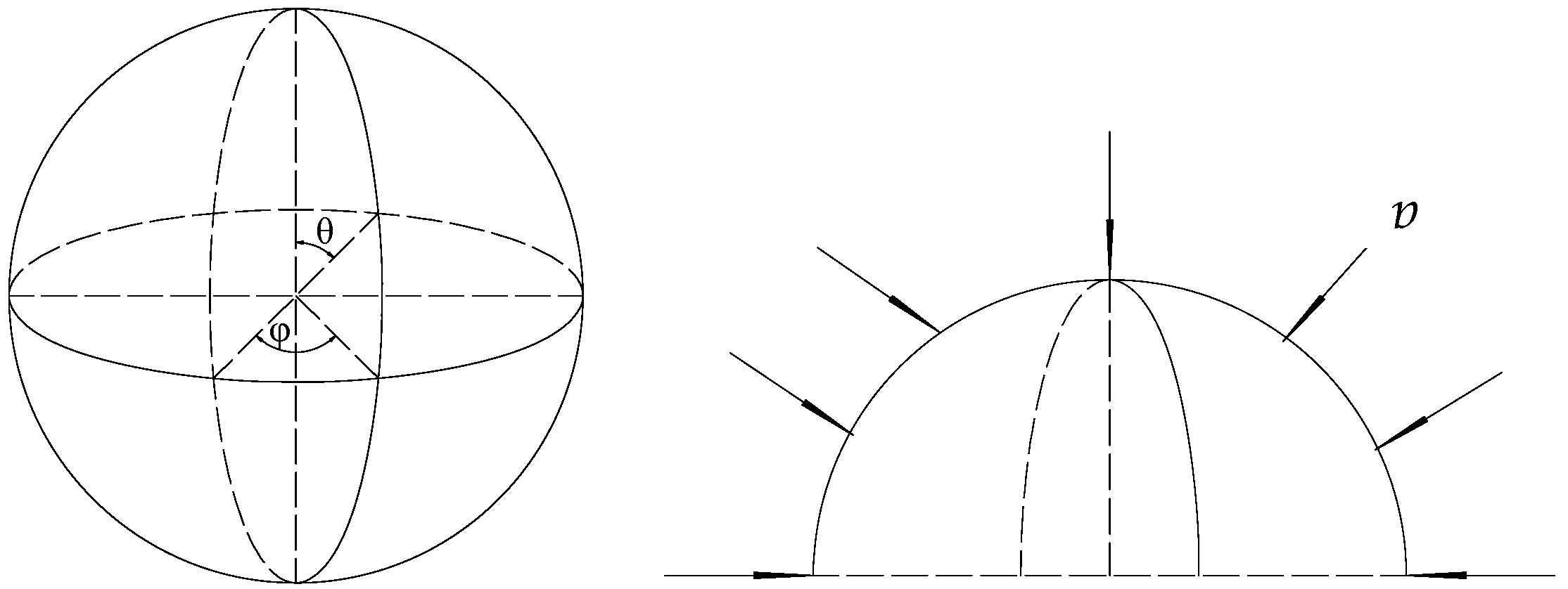
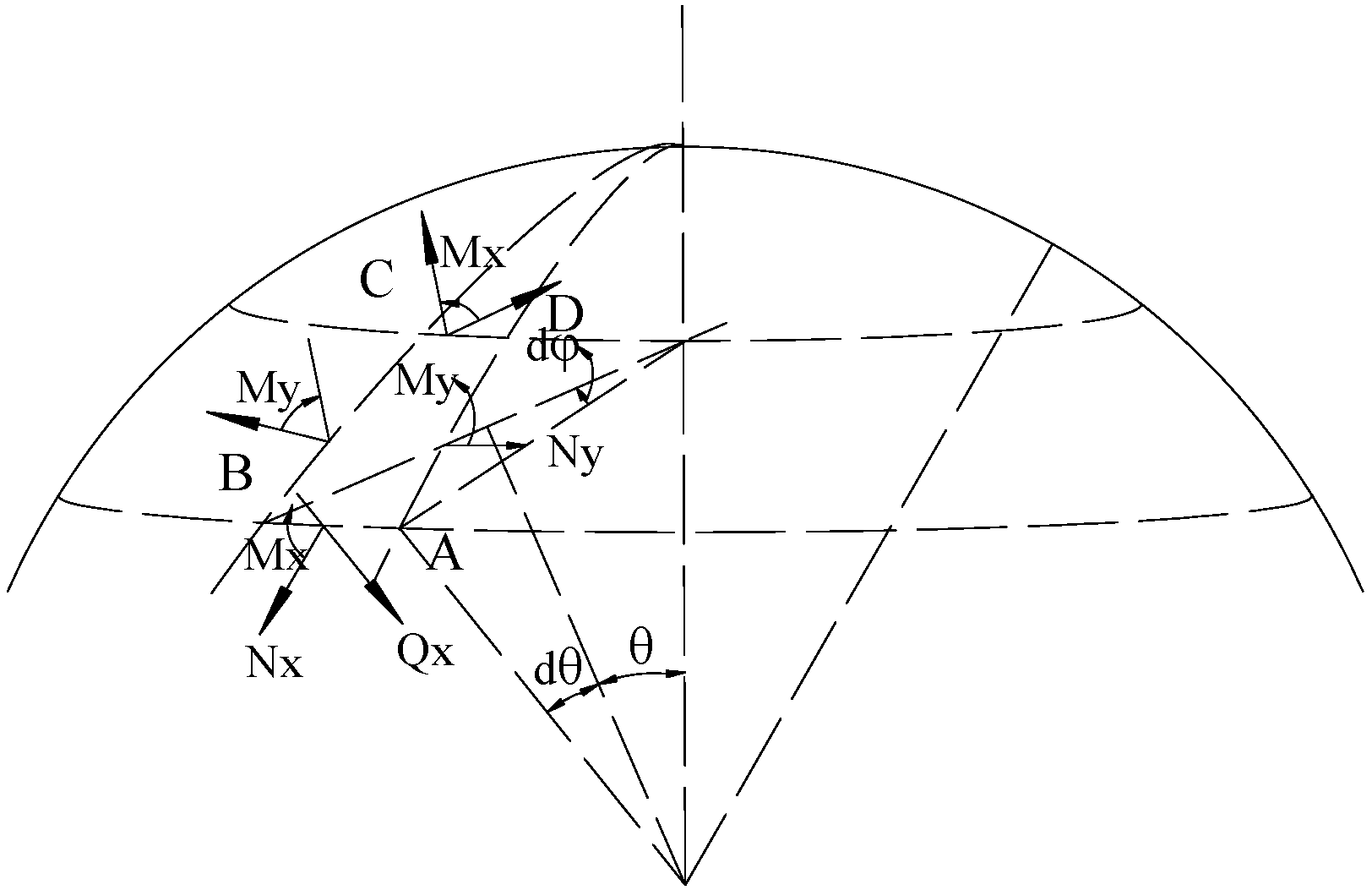
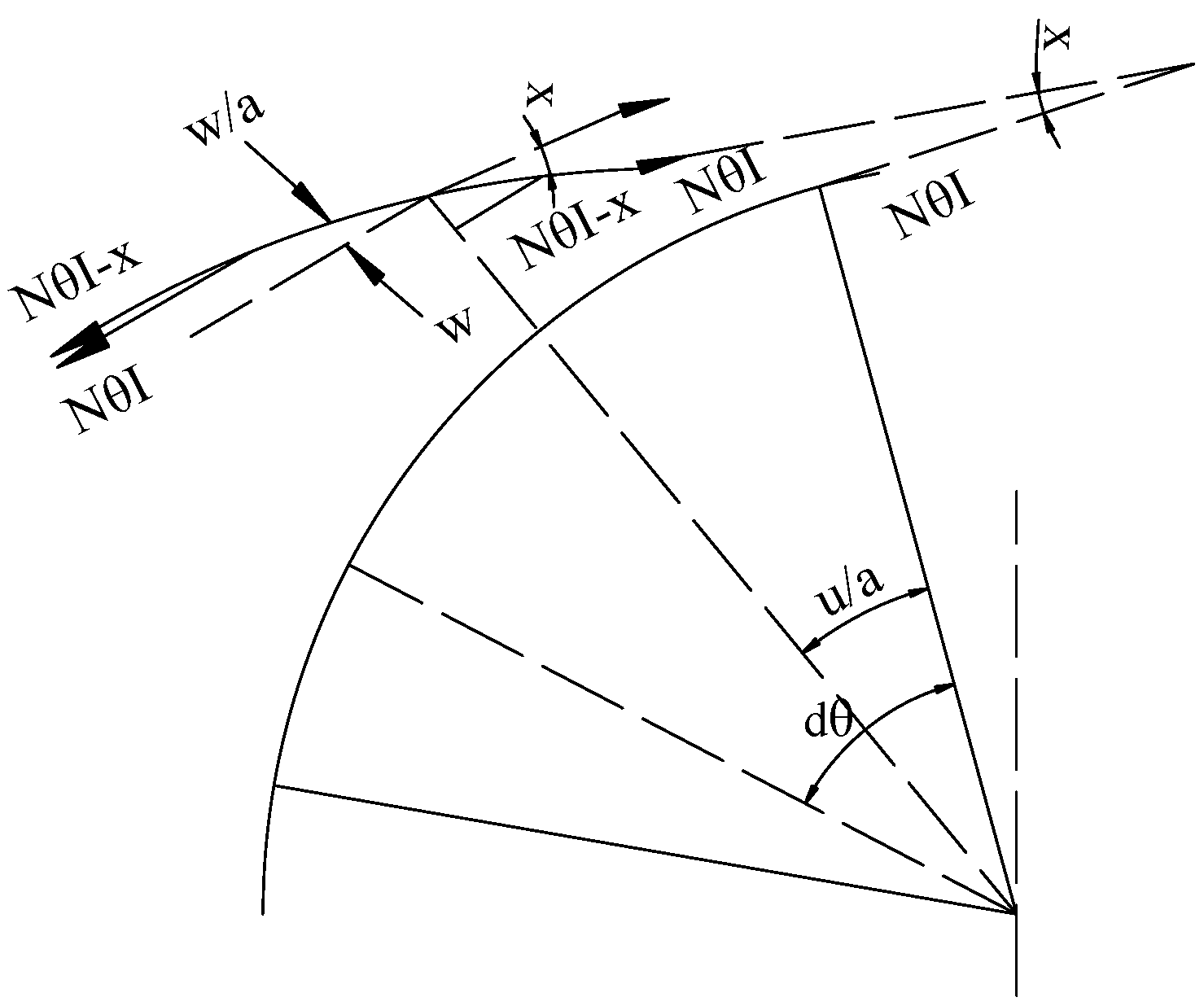
Appendix A.2. Derive the Relationship between w and φ of the Spherical Shell
Appendix B. Deriving the Corrosion Rate of the Spherical Shell as a Function of Temperature and Stress, Based on the Arrhenius Type
References
- Li, L.; Gao, J.; Wang, Y. Evaluation of cyto-toxicity and corrosion behavior of alkali-heat-treated magnesium in simulated body fluid. Surf. Coat. Technol. 2004, 185, 92–98. [Google Scholar] [CrossRef]
- Ben Seghier, M.E.A.; Höche, D.; Zheludkevich, M. Prediction of the internal corrosion rate for oil and gas pipeline: Implementation of ensemble learning techniques. J. Nat. Gas Sci. Eng. 2022, 99, 104425. [Google Scholar] [CrossRef]
- Islam, M.A. Corrosion behaviours of high strength TMT steel bars for reinforcing cement concrete structures. Procedia Eng. 2015, 125, 623–630. [Google Scholar] [CrossRef] [Green Version]
- Páczelt, I.; Kucharski, S.; Mróz, Z. The experimental and numerical analysis of quasi-steady wear processes for a sliding spherical indenter. Wear 2012, 274–275, 127–148. [Google Scholar] [CrossRef]
- Gutman, E.M. Mechanochemistry of Solid Surfaces; World Scientific Publishing Company: Singapore, 1994. [Google Scholar] [CrossRef]
- Kashani, M.M.; Crewe, A.J.; Alexander, N.A. Nonlinear stress-strain behaviour of corrosion-damaged reinforcing bars including inelastic buckling. Eng. Struct. 2013, 48, 417–429. [Google Scholar] [CrossRef]
- Möller, B.; Albrecht, S.; Wagener, R.; Melz, T. Fatigue strength of laser beam welded steel-aluminium joints considering variable amplitude loading and corrosive environment. Procedia Struct. Integr. 2019, 18, 556–559. [Google Scholar] [CrossRef]
- Popova, A.; Sokolova, E.; Raicheva, S.; Christov, M. AC and DC study of the temperature effect on mild steel corrosion in acid media in the presence of benzimidazole derivatives. Corros Sci. 2003, 45, 33–58. [Google Scholar] [CrossRef]
- Tanveer, N.; Mobin, M. Corrosion Protection of Carbon Steel by Poly (aniline-co-o-toluidine) and Poly (pyrrole-co-o-toluidine) Copolymer Coatings. J. Miner Mater. Charact. Eng. 2011, 10, 735–753. [Google Scholar] [CrossRef]
- Noor, E.A. Temperature effects on the corrosion inhibition of mild steel in acidic solutions by aqueous extract of fenugreek leaves. Int. J. Electrochem. Sci. 2007, 2, 996–1017. [Google Scholar]
- Al-Majedy, Y.K.; Ibraheem, H.H.; Falih, M.S.; Al-Amiery, A.A. New coumain derivatives as corrosion inhibitor. IOP Conf. Ser. Mater. Sci. Eng. 2019, 579, 012051. [Google Scholar] [CrossRef]
- Abdel-Azim, A.A.; Milad, R.; El-Ghazawy, R.; Kamal, R. Corrosion inhibition efficiency of water soluble ethoxylated trimethylol propane by gravimetric analysis. Egypt J. Pet. 2014, 23, 15–20. [Google Scholar] [CrossRef] [Green Version]
- AL-Saadie, K.; Abdul Karime, N.; Al-Mousawi, I.M. Corrosion Inhibition of Zinc in Hydrochloric Acid Medium Using Urea Inhibitor. J. Al-Nahrain Univ. Sci. 2007, 10, 31–38. [Google Scholar] [CrossRef]
- Patil, D.B.; Sharma, A.R. Study on the corrosion kinetics of iron in acid and base medium. E-J. Chem. 2011, 8 (Suppl. 1), 358–362. [Google Scholar] [CrossRef]
- Zhang, H.H.; Qin, C.K.; Chen, Y.; Zhang, Z. Inhibition behaviour of mild steel by three new benzaldehyde thiosemicarbazone derivatives in 0.5 M H2SO4: Experimental and computational study. R. Soc. Open Sci. 2019, 6, 190192. [Google Scholar] [CrossRef] [Green Version]
- Nicol, M.J. A comparative study of the kinetics of the oxidation of iron(II) by oxygen in acidic media - mechanistic and practical implications. Hydrometallurgy 2020, 192, 105246. [Google Scholar] [CrossRef]
- Hashim, N.Z.N.; Kassim, K. The effect of temperature on mild steel corrosion in 1 M HCL by Schiff bases. Malaysian J. Anal. Sci. 2014, 18, 28–36. [Google Scholar]
- Solutions, I.A. Electrodissolution Kinetics of Iron and Its Alloys Containing Titanium in Chloride Solutions. 1975. Available online: https://core.ac.uk/download/pdf/147423716.pdf (accessed on 31 October 2022).
- Gao, M.; Wang, H.; Song, Y.; Han, E.H. Corrosion behavior on carbon steel in a simulated soil solution under the interaction effect of chloride and bicarbonate ions. J. Mater. Res. Technol. 2022, 21, 3014–3024. [Google Scholar] [CrossRef]
- Piatti, R.C.V.; Arvía, A.J.; Podestá, J.J. The electrochemical kinetic behaviour of nickel in acid aqueous solutions containing chloride and perchlorate ions. Electrochim. Acta 1969, 14, 541–560. [Google Scholar] [CrossRef] [Green Version]
- Fassina, P.; Bolzoni, F.; Fumagalli, G.; Lazzari, L.; Vergani, L.; Sciuccati, A. Influence of hydrogen and low temperature on mechanical behaviour of two pipeline steels. Eng. Fract. Mech. 2012, 81, 43–55. [Google Scholar] [CrossRef]
- Garrigues, L.; Pebere, N.; Dabosi, F. An investigation of the corrosion inhibition of pure aluminum in neutral and acidic chloride solutions. Electrochim. Acta 1996, 41, 1209–1215. [Google Scholar] [CrossRef]
- Colacino, E.; Carta, M.; Pia, G.; Porcheddu, A.; Ricci, P.C.; Delogu, F. Processing and Investigation Methods in Mechanochemical Kinetics. ACS Omega 2018, 3, 9196–9209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bergman, R.M.; Levitsky, S.P.; Haddad, J.; Gutman, E.M. Stability loss of thin-walled cylindrical tubes, subjected to longitudinal compressive forces and external corrosion. Thin-Walled Struct. 2006, 44, 726–729. [Google Scholar] [CrossRef]
- Gutman, E.M.; Bergman, R.M.; Levitsky, S.P. Influence of internal uniform corrosion on stability loss of a thin-walled spherical shell subjected to external pressure. Corros. Sci. 2016, 111, 212–215. [Google Scholar] [CrossRef]
- Gutman, E.; Haddad, J.; Bergman, R. Stability of thin-walled high-pressure vessels subjected to uniform corrosion. Thin-Walled Struct. 2000, 38, 43–52. [Google Scholar] [CrossRef]
- Elso, M.I. Finite Element Method studies on the stability behavior of cylindrical shells under axial and radial uniform and non-uniform loads. Master’s Thesis, University of Applied Sciences, Krefeld, Germany, May 2012. [Google Scholar]
- Wang, H.; Zhu, Y.; He, X.; Guan, W.; Zhan, M.; Zhang, J. Strength Prediction of Spherical Electronic Cabins with Pitting Corrosion. Metals 2022, 12, 1120. [Google Scholar] [CrossRef]
- Naseri Ghalghachi, R.; Showkati, H.; Eyvazinejad Firouzsalari, S. Buckling behaviour of GFRP cylindrical shells subjected to axial compression load. Compos. Struct. 2021, 260, 113269. [Google Scholar] [CrossRef]
- Amaya-Gómez, R.; Sánchez-Silva, M.; Bastidas-Arteaga, E.; Schoefs, F.; Muñoz, F. Reliability assessments of corroded pipelines based on internal pressure—A review. Eng. Fail. Anal. 2019, 98, 190–214. [Google Scholar] [CrossRef]
- De Meo, D.; Oterkus, E. Finite element implementation of a peridynamic pitting corrosion damage model. Ocean Eng. 2017, 135, 76–83. [Google Scholar] [CrossRef] [Green Version]
- Do, V.D.; Le Grognec, P.; Rohart, P. Closed-form solutions for the elastic—Plastic buckling design of shell structures under external pressure. Eur. J. Mech. A Solids 2023, 98, 104861. [Google Scholar] [CrossRef]
- Nayyeri Amiri, S.; Rasheed, H.A. Nondestructive method to predict the buckling load in elastic spherical shells. Eng. Struct. 2017, 150, 300–317. [Google Scholar] [CrossRef]

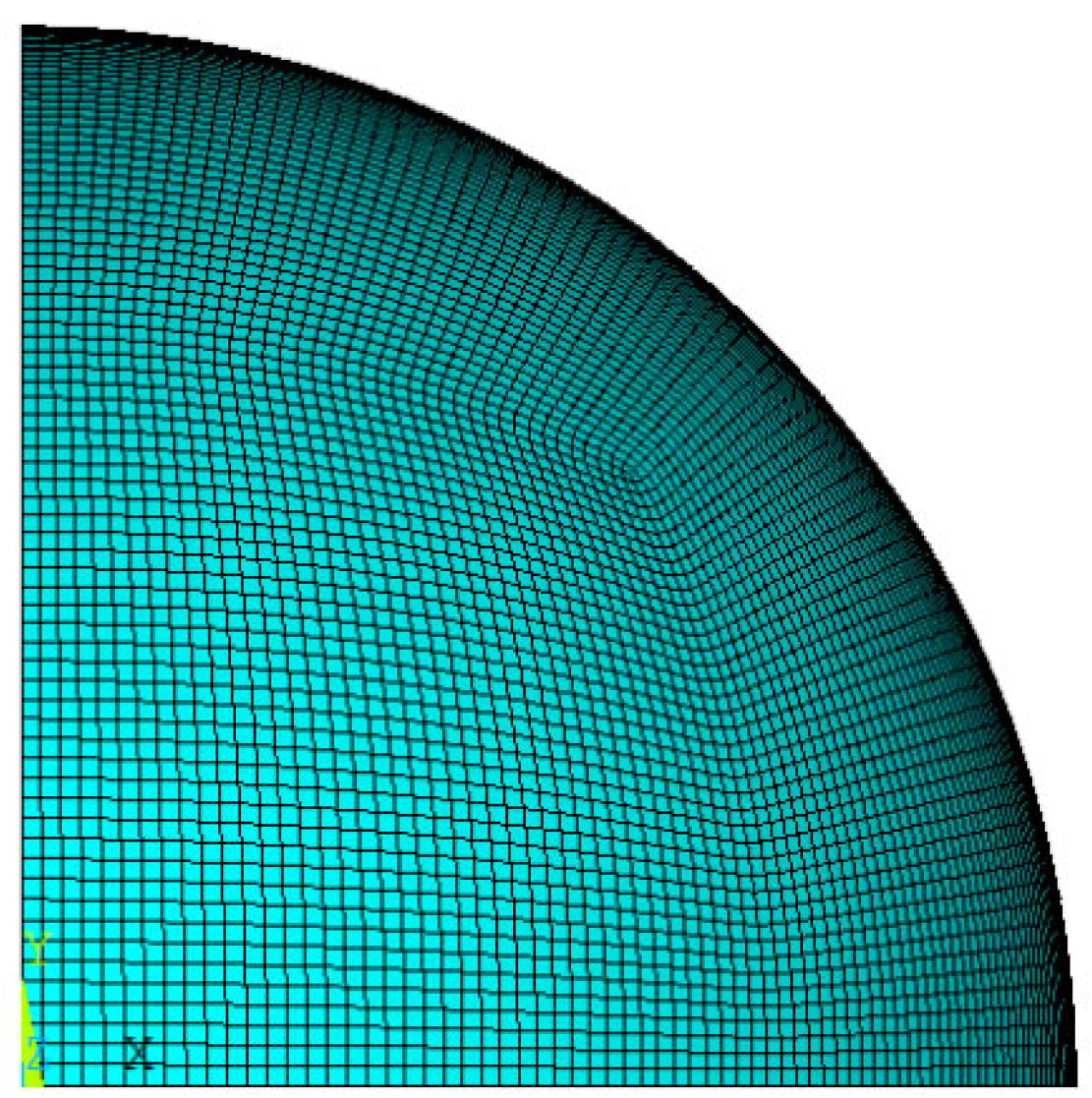
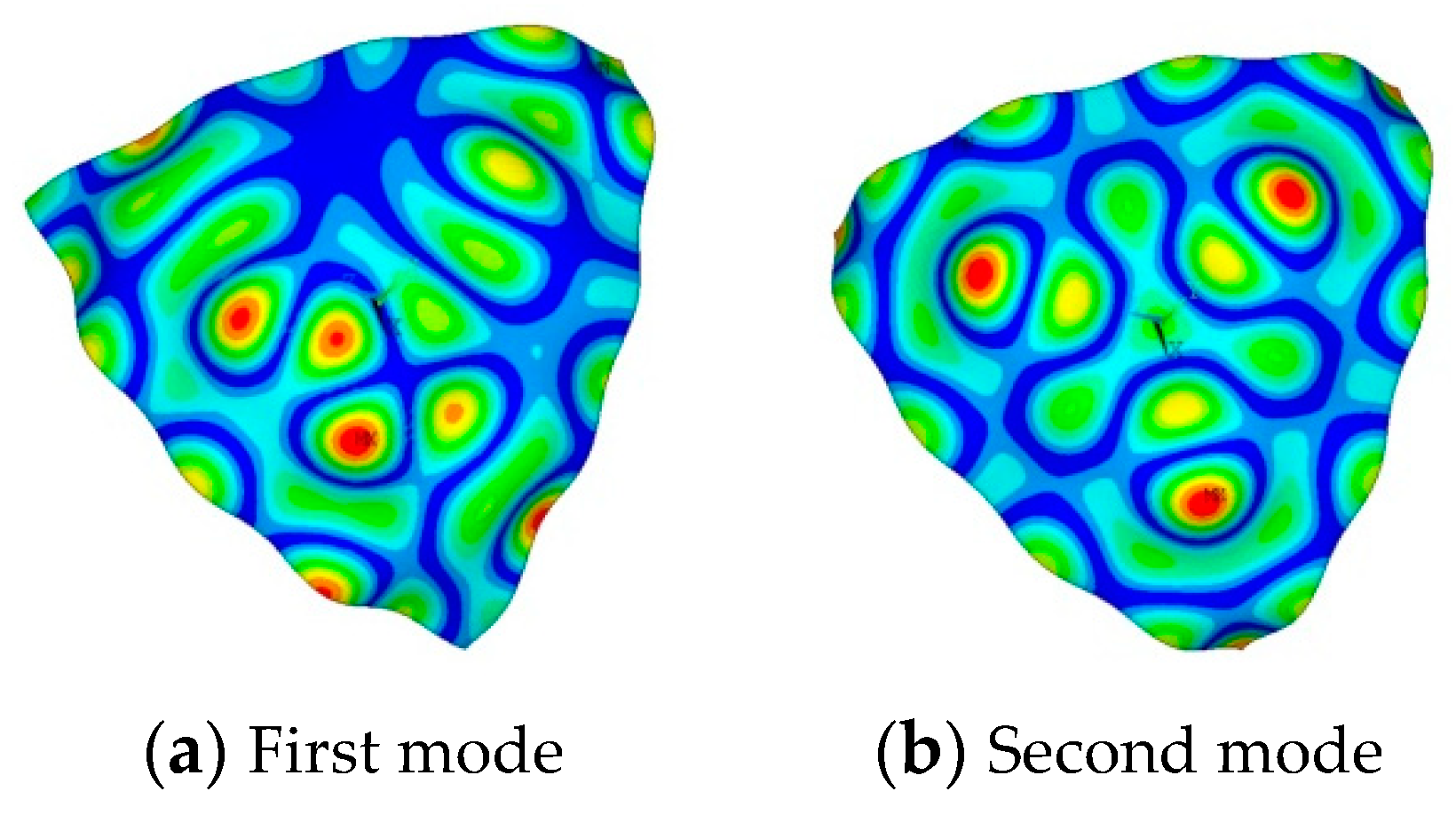

| Method No. | 1st | 2nd | 3rd | 4th | 5th | 6th |
|---|---|---|---|---|---|---|
| Method name | The lowest Eigenvalue method | Traditional one-order analytical method | Non-destruction | Analytical two-order method [33] | Numerical method [33] | Experimental method [33] |
| Our method | ||||||
| Critical load value | 0.081574 | 0.08127 | 0.08593 | 0.08189 | 0.08790 | 0.07800 |
| Formulas | Here [K],[S] are the constants, is the buckling load multiplier, is the buckling mode. | Ansys FEM software. | Non-destructive Testing | |||
| Relative Error | 0.03718 | 0.04193 | 0.10167 | 0.04988 | 0.12692 | Reference |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.H.; Lacidogna, G. A Non-Destructive Method for Predicting Critical Load, Critical Thickness and Service Life for Corroded Spherical Shells under Uniform External Pressure Based on NDT Data. Appl. Sci. 2023, 13, 4172. https://doi.org/10.3390/app13074172
Liu CH, Lacidogna G. A Non-Destructive Method for Predicting Critical Load, Critical Thickness and Service Life for Corroded Spherical Shells under Uniform External Pressure Based on NDT Data. Applied Sciences. 2023; 13(7):4172. https://doi.org/10.3390/app13074172
Chicago/Turabian StyleLiu, Cheng Huijuan, and Giuseppe Lacidogna. 2023. "A Non-Destructive Method for Predicting Critical Load, Critical Thickness and Service Life for Corroded Spherical Shells under Uniform External Pressure Based on NDT Data" Applied Sciences 13, no. 7: 4172. https://doi.org/10.3390/app13074172
APA StyleLiu, C. H., & Lacidogna, G. (2023). A Non-Destructive Method for Predicting Critical Load, Critical Thickness and Service Life for Corroded Spherical Shells under Uniform External Pressure Based on NDT Data. Applied Sciences, 13(7), 4172. https://doi.org/10.3390/app13074172







