Author Contributions
Conceptualization, P.W. and S.W.; methodology, P.W. and S.W.; software, P.W.; validation, P.W. and S.W.; formal analysis, P.W.; investigation, P.W.; resources, P.W.; data curation, P.W.; writing—original draft preparation, P.W.and S.W.; writing—review and editing, P.W. and S.W.; visualization, P.W.; supervision, S.W.; project administration, P.W.; funding acquisition, P.W. All authors have read and agreed to the published version of the manuscript.
Figure 1.
CAC rule ordering.
Figure 1.
CAC rule ordering.
Figure 2.
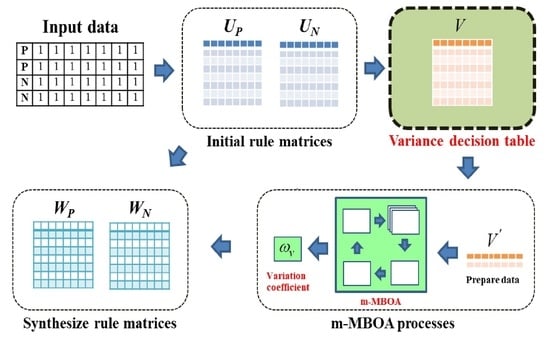
An overview of the proposed CAV methods.
Figure 2.
An overview of the proposed CAV methods.
Figure 3.
The initial rule matrices process consists of three steps: (a) converting the input data into binary data using a gray code encoder; (b) creating initial rule matrices with periodic boundary conditions; and (c) generating initial rule matrices for both positive and negative data.
Figure 3.
The initial rule matrices process consists of three steps: (a) converting the input data into binary data using a gray code encoder; (b) creating initial rule matrices with periodic boundary conditions; and (c) generating initial rule matrices for both positive and negative data.
Figure 4.
The Create Variance Decision Table process. (a) Initial rule matrix of positive data; (b) initial rule matrix of negative data; and (c) generating variance decision table.
Figure 4.
The Create Variance Decision Table process. (a) Initial rule matrix of positive data; (b) initial rule matrix of negative data; and (c) generating variance decision table.
Figure 5.
The m-MBOA process. (a) Variance decision table; (b) Create vector V′ by de-duplicate and sort data; (c) process m-MBOA algorithm to create the variation coefficient; and (d) variation coefficient.
Figure 5.
The m-MBOA process. (a) Variance decision table; (b) Create vector V′ by de-duplicate and sort data; (c) process m-MBOA algorithm to create the variation coefficient; and (d) variation coefficient.
Figure 6.
Synthesis rule matrices.
Figure 6.
Synthesis rule matrices.
Figure 7.
Illustration of dataset distribution using the PCA technique.
Figure 7.
Illustration of dataset distribution using the PCA technique.
Figure 8.
CAV with other classifiers; accuracy comparison for the test datasets.
Figure 8.
CAV with other classifiers; accuracy comparison for the test datasets.
Figure 9.
CAV with other classifiers; precision comparison for the test datasets.
Figure 9.
CAV with other classifiers; precision comparison for the test datasets.
Figure 10.
CAV with other classifiers; recall comparison for the test datasets.
Figure 10.
CAV with other classifiers; recall comparison for the test datasets.
Figure 11.
CAV with other classifiers; F1 comparison for the test datasets.
Figure 11.
CAV with other classifiers; F1 comparison for the test datasets.
Figure 12.
CAV with other classifiers; specificity comparison for the test datasets.
Figure 12.
CAV with other classifiers; specificity comparison for the test datasets.
Figure 13.
CAV with other classifiers; G-mean comparison for the test datasets.
Figure 13.
CAV with other classifiers; G-mean comparison for the test datasets.
Figure 14.
Illustration of the average Friedman rank for CAV, CAC, SVM, kNN, DNN-1, DNN-2, and Naïve Bayes. The green bar graph represents the value of the average Friedman rank in the proposed model, while the blue bar graph represents the corresponding value of the classifier used for comparison with the proposed model.
Figure 14.
Illustration of the average Friedman rank for CAV, CAC, SVM, kNN, DNN-1, DNN-2, and Naïve Bayes. The green bar graph represents the value of the average Friedman rank in the proposed model, while the blue bar graph represents the corresponding value of the classifier used for comparison with the proposed model.
Table 1.
Notation.
| Notation | Description |
|---|
|
| Number of datasets (binary data) features, number of possible ECA configuration |
| k | Number of samples from and = 2 |
|
| Initial rule matrix of the data in positive class |
|
| Initial rule matrix of the data in negative class |
|
| Variance Decision Table matrix |
|
| Variance Decision Table vector |
|
| Rule matrix of the positive class |
|
| Rule matrix of the negative class |
|
| Mean of each and |
| S | Standard deviation of each and |
|
| Percentage coefficient of variance |
|
| Training data |
|
| The variation coefficient |
Table 2.
Classification method parameters.
Table 2.
Classification method parameters.
| Classifier | Parameters | Value |
|---|
| CAV | Population | 100 |
| | Probability switch (p) | 0.5 |
| | Power exponent | 0.4 |
| | Sensory modality | 0.03 |
| | Max iteration | 20 |
| CAC | Sample | 100 |
| | Crossover probability | 48 |
| | Mutation probability | 40 |
| | Max iteration | 20 |
| SVM | SVM type | C-SVM |
| | Kernel type | Rbf |
| | Class weight | 1.0 |
| kNN | K (neighbor) | 5 |
| | Weighted vote | Yes |
| DNN-1 | Activation | Rectifier |
| | Hidden layer number | 2 |
| | Hidden layer size | 50 |
| DNN-2 | Activation | Maxout |
| | Hidden layer number | 3 |
| | Hidden layer size | 100 |
| Naïve Bayes | Laplace correction | Yes |
Table 3.
Datasets.
| Dataset | Class | Instances | Features |
|---|
| Soybean (small) | 4 | 47 | 35 |
| SPECT heart | 2 | 80 | 23 |
| Analcatdata boxing2 | 2 | 132 | 10 |
| Tae | 3 | 151 | 6 |
| Hayes-Roth | 3 | 160 | 5 |
| Wisconsin | 2 | 194 | 33 |
| Sonar | 2 | 208 | 61 |
| Prnn synth | 2 | 256 | 3 |
| Thyroid Disease | 2 | 306 | 3 |
| Ecoli | 8 | 336 | 8 |
| Congressional Voting | 2 | 435 | 16 |
| Monk Problem 2 | 2 | 601 | 7 |
| Breast w | 2 | 699 | 10 |
| Pima Indians Diabetes | 2 | 768 | 8 |
| Mammographic Mass | 2 | 961 | 6 |
Table 4.
The accuracy of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2, and naïve Bayes (the bold number indicates the maximum value).
Table 4.
The accuracy of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2, and naïve Bayes (the bold number indicates the maximum value).
| Dataset | Classification Accuracy (K = 10) | Average Improvement |
|---|
| CAV | CAC | SVM | kNN | DNN-1 | DNN-2 | Naïve Bayes |
|---|
| Analcatdata boxing2 | 72.360 | 69.200 | 71.970 | 64.390 | 56.820 | 63.640 | 67.420 | |
| Breast w | 97.420 | 96.850 | 96.850 | 97.000 | 96.570 | 96.570 | 95.990 | |
| Congressional voting | 96.980 | 95.270 | 92.240 | 93.970 | 95.260 | 95.260 | 94.830 | |
| Ecoli | 88.240 | 67.510 | 43.740 | 85.120 | 81.850 | 79.510 | 79.170 | |
| Hayes-Roth | 78.950 | 77.250 | 43.750 | 66.250 | 58.750 | 66.870 | 70.000 | |
| Mammographic mass | 82.640 | 82.430 | 80.480 | 79.520 | 82.170 | 81.330 | 80.600 | |
| Monk’s problems 2 | 67.500 | 63.400 | 82.530 | 66.560 | 63.890 | 74.210 | 64.390 | |
| Pima indian diabetes | 72.700 | 69.263 | 72.010 | 71.740 | 74.220 | 74.350 | 75.520 | |
| Prnn synth | 83.279 | 78.704 | 84.400 | 81.600 | 83.200 | 82.800 | 84.400 | |
| Sonar | 74.550 | 74.143 | 87.020 | 80.290 | 80.290 | 81.250 | 67.790 | |
| Soybean small | 100.000 | 100.000 | 100.000 | 97.870 | 100.000 | 100.000 | 100.000 | |
| SPECTheart | 75.000 | 62.500 | 68.750 | 63.750 | 71.250 | 71.250 | 68.750 | |
| Tae | 59.040 | 57.536 | 47.020 | 47.680 | 46.360 | 41.720 | 51.660 | |
| Thyroid disease | 93.960 | 94.892 | 80.930 | 95.350 | 93.490 | 93.490 | 96.740 | |
| Wisconsin | 97.510 | 97.217 | 97.070 | 97.360 | 96.930 | 96.930 | 96.190 | |
| Average | 82.675 | 79.078 | 76.584 | 79.230 | 78.737 | 79.945 | 79.563 | |
| Improvement | | 3.60 | 6.09 | 3.45 | 3.94 | 2.73 | 3.11 | 4.58 |
Table 5.
The precision of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2 and naïve Bayes (the bold number indicates the maximum value).
Table 5.
The precision of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2 and naïve Bayes (the bold number indicates the maximum value).
| Dataset | Classification Accuracy (K = 10) | Average Improvement |
|---|
| CAV | CAC | SVM | kNN | DNN-1 | DNN-2 | Naïve Bayes |
|---|
| Analcatdata boxing2 | 0.720 | 0.750 | 0.873 | 0.747 | 0.521 | 0.648 | 0.761 | |
| Breast w | 0.993 | 0.994 | 0.972 | 0.974 | 0.965 | 0.965 | 0.952 | |
| Congressional voting | 0.983 | 0.977 | 0.887 | 0.927 | 0.944 | 0.960 | 0.960 | |
| Ecoli | 0.880 | 0.723 | 0.088 | 0.558 | 0.595 | 0.739 | 0.547 | |
| Hayes-Roth | 0.835 | 0.830 | 0.366 | 0.637 | 0.631 | 0.693 | 0.751 | |
| Mammographic mass | 0.815 | 0.803 | 0.873 | 0.814 | 0.772 | 0.757 | 0.811 | |
| Monk’s problems 2 | 0.889 | 0.727 | 0.779 | 1.000 | 0.527 | 0.676 | 0.980 | |
| Pima indian diabetes | 0.809 | 0.846 | 0.466 | 0.519 | 0.474 | 0.489 | 0.605 | |
| Prnn synth | 0.854 | 0.789 | 0.832 | 0.920 | 0.776 | 0.760 | 0.848 | |
| Sonar | 0.744 | 0.786 | 0.814 | 0.722 | 0.773 | 0.835 | 0.804 | |
| Soybean small | 1.000 | 1.000 | 1.000 | 0.975 | 1.000 | 1.000 | 1.000 | |
| SPECTheart | 0.815 | 0.583 | 0.450 | 0.450 | 0.700 | 0.700 | 0.450 | |
| Tae | 0.629 | 0.622 | 0.468 | 0.475 | 0.461 | 0.410 | 0.518 | |
| Thyroid disease | 0.927 | 0.940 | 0.580 | 0.910 | 0.863 | 0.911 | 0.965 | |
| Wisconsin | 0.991 | 0.991 | 0.973 | 0.978 | 0.964 | 0.964 | 0.955 | |
| Average | 0.859 | 0.824 | 0.695 | 0.774 | 0.731 | 0.767 | 0.794 | |
| Improvement | | 0.035 | 0.164 | 0.085 | 0.128 | 0.092 | 0.065 | 0.114 |
Table 6.
The recall of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2 and naïve Bayes (the bold number indicates the maximum value).
Table 6.
The recall of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2 and naïve Bayes (the bold number indicates the maximum value).
| Dataset | Classification Accuracy (K = 10) | Average Improvement |
|---|
| CAV | CAC | SVM | kNN | DNN-1 | DNN-2 | Naïve Bayes |
|---|
| Analcatdata boxing2 | 0.631 | 0.500 | 0.689 | 0.646 | 0.617 | 0.667 | 0.675 | |
| Breast w | 0.967 | 0.958 | 0.980 | 0.980 | 0.982 | 0.982 | 0.986 | |
| Congressional voting | 0.960 | 0.935 | 0.965 | 0.958 | 0.967 | 0.952 | 0.944 | |
| Ecoli | 0.835 | 0.700 | 0.200 | 0.551 | 0.571 | 0.755 | 0.563 | |
| Hayes-Roth | 0.798 | 0.783 | 0.601 | 0.735 | 0.615 | 0.679 | 0.742 | |
| Mammographic mass | 0.834 | 0.851 | 0.760 | 0.775 | 0.847 | 0.843 | 0.794 | |
| Monk’s problems 2 | 0.400 | 0.400 | 0.849 | 0.663 | 0.874 | 0.908 | 0.653 | |
| Pima indian diabetes | 0.760 | 0.646 | 0.635 | 0.612 | 0.690 | 0.686 | 0.664 | |
| Prnn synth | 0.791 | 0.808 | 0.853 | 0.762 | 0.874 | 0.880 | 0.841 | |
| Sonar | 0.819 | 0.728 | 0.898 | 0.833 | 0.798 | 0.779 | 0.619 | |
| Soybean small | 1.000 | 1.000 | 1.000 | 0.986 | 1.000 | 1.000 | 1.000 | |
| SPECTheart | 0.700 | 0.500 | 0.857 | 0.628 | 0.718 | 0.718 | 0.857 | |
| Tae | 0.589 | 0.576 | 0.469 | 0.479 | 0.511 | 0.282 | 0.513 | |
| Thyroid disease | 0.927 | 0.925 | 0.806 | 0.960 | 0.962 | 0.911 | 0.942 | |
| Wisconsin | 0.971 | 0.966 | 0.982 | 0.982 | 0.989 | 0.989 | 0.986 | |
| Average | 0.799 | 0.752 | 0.769 | 0.770 | 0.801 | 0.802 | 0.785 | |
| Improvement | | 0.047 | 0.029 | 0.029 | −0.002 | −0.003 | 0.014 | 0.023 |
Table 7.
The F1 of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2 and naïve Bayes (the bold number indicates the maximum value).
Table 7.
The F1 of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2 and naïve Bayes (the bold number indicates the maximum value).
| Dataset | Classification Accuracy (K = 10) | Average Improvement |
|---|
| CAV | CAC | SVM | kNN | DNN-1 | DNN-2 | Naïve Bayes |
|---|
| Analcatdata boxing2 | 0.662 | 0.600 | 0.770 | 0.693 | 0.565 | 0.657 | 0.715 | |
| Breast w | 0.980 | 0.975 | 0.976 | 0.977 | 0.974 | 0.974 | 0.969 | |
| Congressional voting | 0.971 | 0.971 | 0.924 | 0.943 | 0.955 | 0.956 | 0.953 | |
| Ecoli | 0.850 | 0.921 | 0.122 | 0.553 | 0.574 | 0.738 | 0.544 | |
| Hayes-Roth | 0.786 | 0.788 | 0.310 | 0.663 | 0.622 | 0.685 | 0.742 | |
| Mammographic mass | 0.823 | 0.825 | 0.813 | 0.794 | 0.808 | 0.797 | 0.803 | |
| Monk’s problems 2 | 0.552 | 0.516 | 0.812 | 0.797 | 0.657 | 0.775 | 0.783 | |
| Pima indian diabetes | 0.784 | 0.732 | 0.538 | 0.562 | 0.562 | 0.571 | 0.633 | |
| Prnn synth | 0.817 | 0.789 | 0.842 | 0.833 | 0.822 | 0.816 | 0.845 | |
| Sonar | 0.773 | 0.748 | 0.854 | 0.774 | 0.785 | 0.806 | 0.700 | |
| Soybean small | 1.000 | 1.000 | 1.000 | 0.980 | 1.000 | 1.000 | 1.000 | |
| SPECTheart | 0.730 | 0.529 | 0.590 | 0.651 | 0.709 | 0.709 | 0.590 | |
| Tae | 0.569 | 0.551 | 0.464 | 0.474 | 0.445 | 0.327 | 0.501 | |
| Thyroid disease | 0.914 | 0.927 | 0.600 | 0.932 | 0.971 | 0.911 | 0.953 | |
| Wisconsin | 0.980 | 0.978 | 0.977 | 0.980 | 0.976 | 0.976 | 0.970 | |
| Average | 0.813 | 0.790 | 0.706 | 0.774 | 0.762 | 0.780 | 0.780 | |
| Improvement | | 0.023 | 0.107 | 0.039 | 0.051 | 0.033 | 0.033 | 0.057 |
Table 8.
The specificity of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2 and naïve Bayes (the bold number indicates the maximum value).
Table 8.
The specificity of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2 and naïve Bayes (the bold number indicates the maximum value).
| Dataset | Classification Accuracy (K = 10) | Average Improvement |
|---|
| CAV | CAC | SVM | kNN | DNN-1 | DNN-2 | Naïve Bayes |
|---|
| Analcatdata boxing2 | 0.804 | 0.857 | 0.786 | 0.640 | 0.528 | 0.603 | 0.673 | |
| Breast w | 0.988 | 0.988 | 0.947 | 0.951 | 0.936 | 0.936 | 0.914 | |
| Congressional voting | 0.981 | 0.973 | 0.881 | 0.920 | 0.937 | 0.953 | 0.953 | |
| Ecoli | 0.850 | 0.921 | 0.000 | 0.978 | 0.973 | 0.948 | 0.969 | |
| Hayes-Roth | 0.887 | 0.873 | 0.718 | 0.819 | 0.777 | 0.823 | 0.837 | |
| Mammographic mass | 0.820 | 0.799 | 0.861 | 0.816 | 0.801 | 0.791 | 0.818 | |
| Monk’s problems 2 | 0.675 | 0.857 | 0.807 | 1.000 | 0.485 | 0.583 | 0.000 | |
| Pima indian diabetes | 0.727 | 0.780 | 0.750 | 0.762 | 0.759 | 0.763 | 0.798 | |
| Prnn synth | 0.872 | 0.767 | 0.836 | 0.899 | 0.799 | 0.789 | 0.847 | |
| Sonar | 0.663 | 0.753 | 0.850 | 0.782 | 0.807 | 0.846 | 0.768 | |
| Soybean small | 1.000 | 1.000 | 1.000 | 0.993 | 1.000 | 1.000 | 1.000 | |
| SPECTheart | 0.800 | 0.750 | 0.627 | 0.649 | 0.707 | 0.707 | 0.627 | |
| Tae | 0.795 | 0.789 | 0.737 | 0.739 | 0.735 | 0.724 | 0.768 | |
| Thyroid disease | 0.960 | 0.960 | 0.809 | 0.975 | 0.935 | 0.951 | 0.971 | |
| Wisconsin | 0.983 | 0.983 | 0.951 | 0.959 | 0.936 | 0.936 | 0.921 | |
| Average | 0.854 | 0.870 | 0.771 | 0.859 | 0.808 | 0.824 | 0.791 | |
| Improvement | | −0.016 | 0.083 | −0.005 | 0.046 | 0.030 | 0.063 | 0.040 |
Table 9.
The G-mean of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2, and naïve Bayes (the bold number indicates the maximum value).
Table 9.
The G-mean of the proposed CAV compared with CAC, SVM, k-NN, DNN-1, DNN-2, and naïve Bayes (the bold number indicates the maximum value).
| Dataset | Classification Accuracy (K = 10) | Average Improvement |
|---|
| CAV | CAC | SVM | kNN | DNN-1 | DNN-2 | Naïve Bayes |
|---|
| Analcatdata boxing2 | 0.712 | 0.655 | 0.736 | 0.643 | 0.571 | 0.634 | 0.674 | |
| Breast w | 0.977 | 0.973 | 0.963 | 0.965 | 0.959 | 0.959 | 0.950 | |
| Congressional voting | 0.970 | 0.954 | 0.922 | 0.939 | 0.952 | 0.953 | 0.949 | |
| Ecoli | 0.843 | 0.803 | 0.000 | 0.734 | 0.745 | 0.846 | 0.738 | |
| Hayes-Roth | 0.841 | 0.827 | 0.657 | 0.776 | 0.691 | 0.748 | 0.788 | |
| Mammographic mass | 0.827 | 0.825 | 0.809 | 0.795 | 0.824 | 0.816 | 0.806 | |
| Monk’s problems 2 | 0.520 | 0.585 | 0.827 | 0.814 | 0.651 | 0.728 | 0.000 | |
| Pima indian diabetes | 0.743 | 0.710 | 0.690 | 0.683 | 0.724 | 0.723 | 0.728 | |
| Prnn synth | 0.831 | 0.787 | 0.844 | 0.827 | 0.835 | 0.833 | 0.844 | |
| Sonar | 0.737 | 0.740 | 0.874 | 0.807 | 0.802 | 0.812 | 0.690 | |
| Soybean small | 1.000 | 1.000 | 1.000 | 0.990 | 1.000 | 1.000 | 1.000 | |
| SPECTheart | 0.748 | 0.612 | 0.733 | 0.638 | 0.713 | 0.713 | 0.733 | |
| Tae | 0.684 | 0.674 | 0.587 | 0.595 | 0.612 | 0.452 | 0.628 | |
| Thyroid disease | 0.943 | 0.942 | 0.808 | 0.967 | 0.948 | 0.931 | 0.956 | |
| Wisconsin | 0.977 | 0.974 | 0.966 | 0.970 | 0.962 | 0.962 | 0.953 | |
| Average | 0.824 | 0.804 | 0.761 | 0.810 | 0.799 | 0.807 | 0.762 | |
| Improvement | | 0.020 | 0.063 | 0.014 | 0.024 | 0.016 | 0.061 | 0.040 |