Robustness of Deep Learning Models for Vision Tasks
Abstract
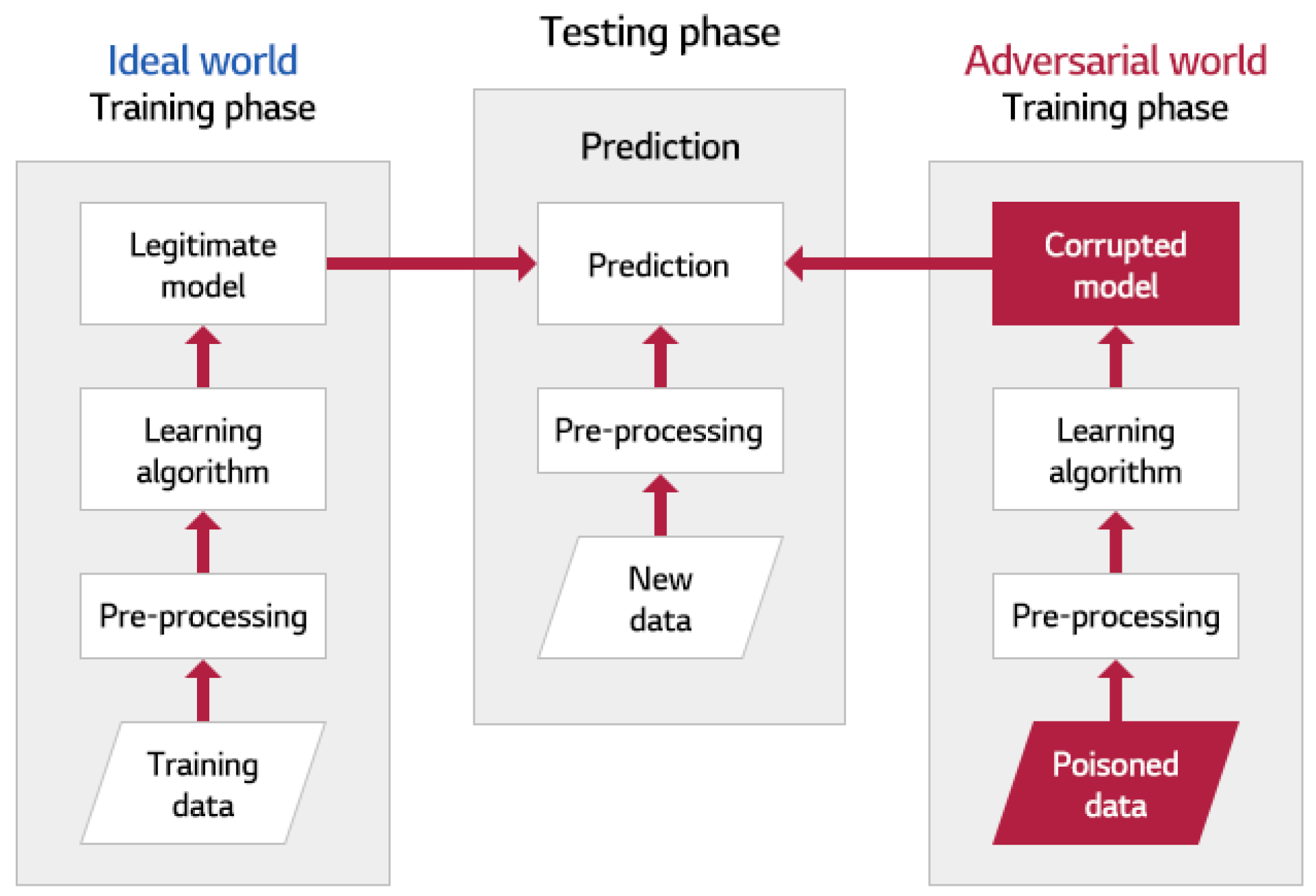
1. Introduction
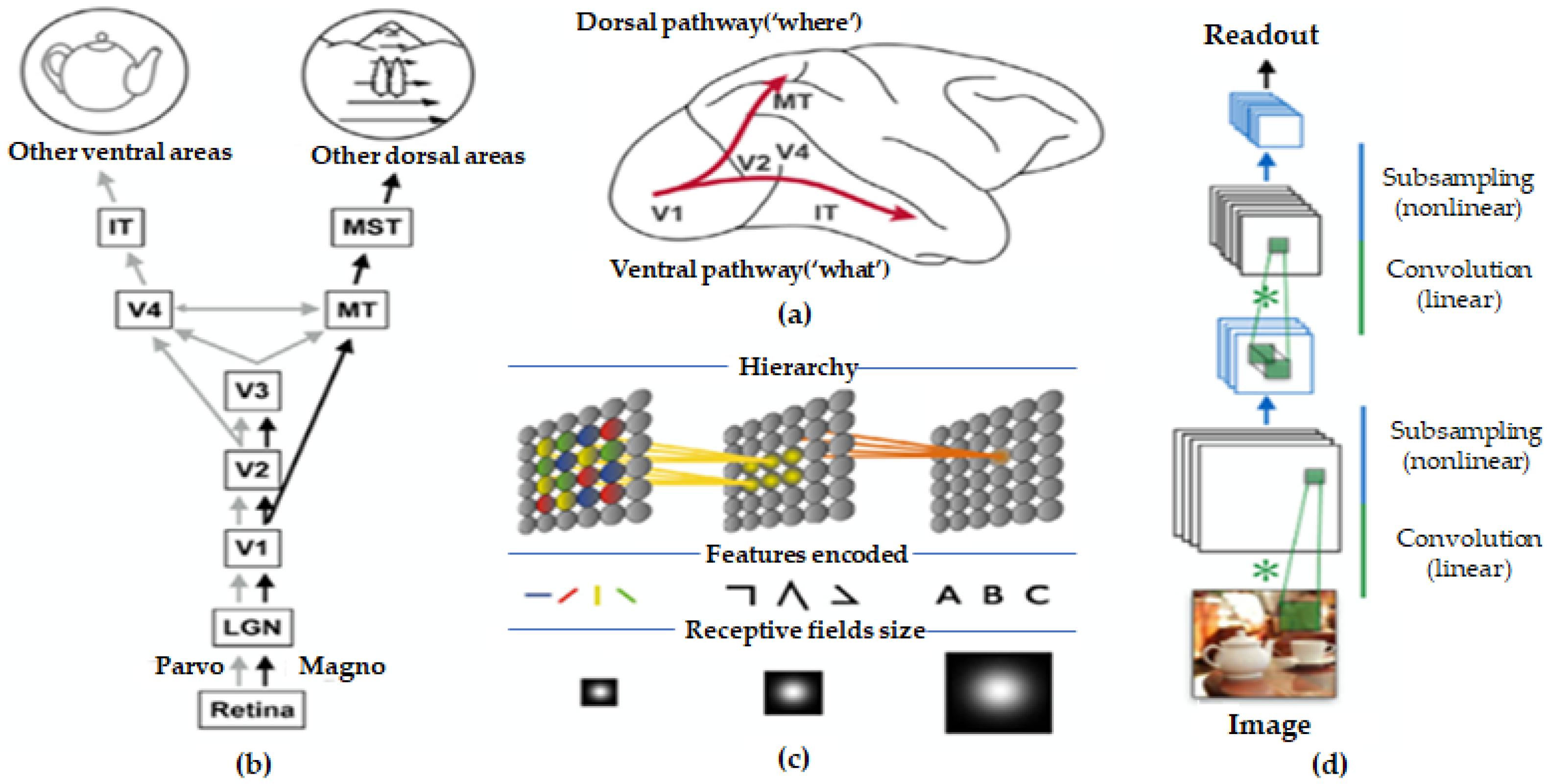
2. Biological Hierarchical Vision Processing
2.1. Biological Vision in Brain
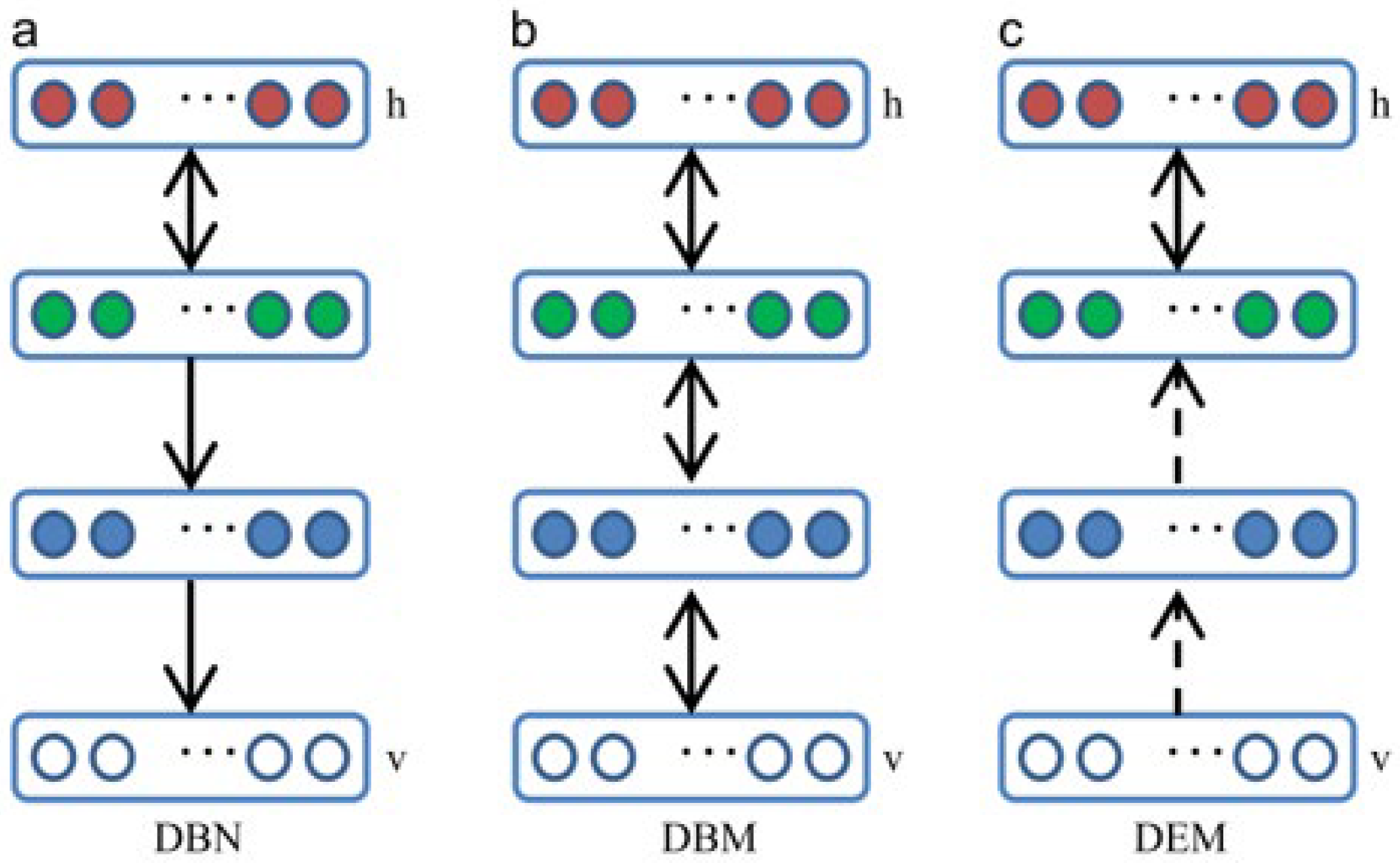
2.2. Categorization of Deep Learning in Vision Tasks
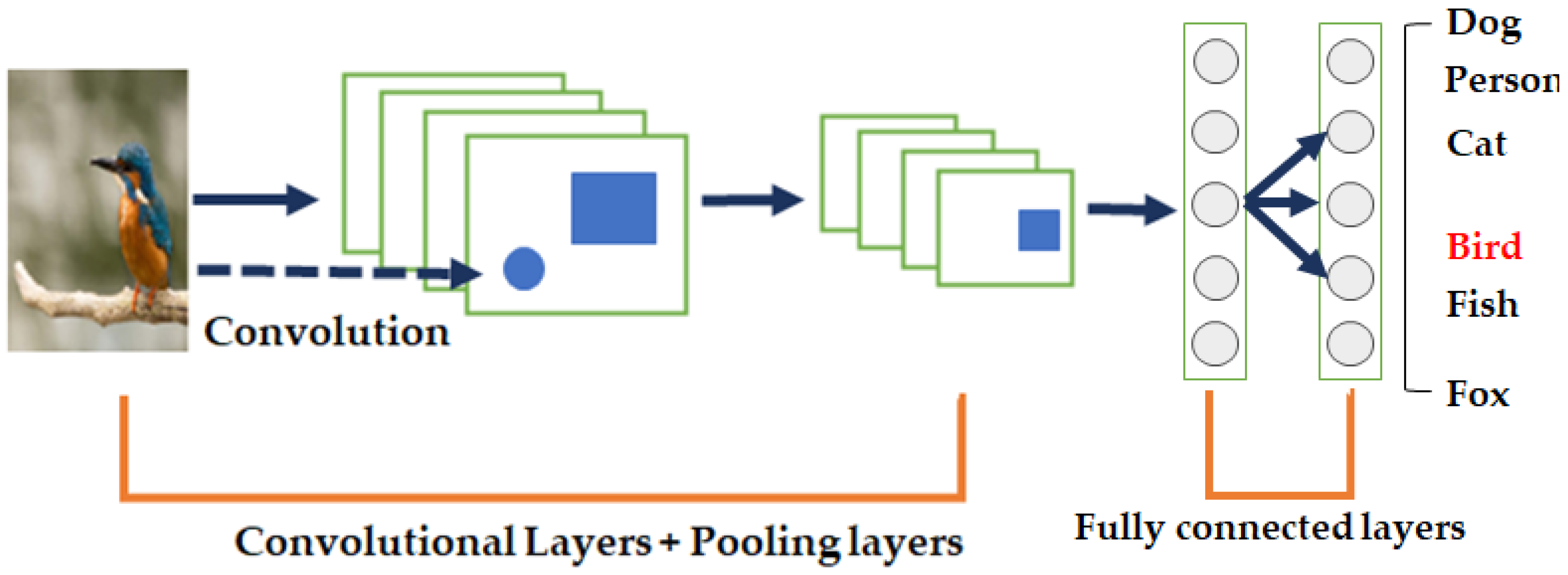
2.3. CNN: Basis of Deep Neural Networks for Vision Tasks
- Convolutional layer: The input format of the CNN is a multichannel image, whereas the inputs of the conventional neural network architectures are in vector format. During the operation of the convolutional layer, the process involves sliding the kernel over all the pixels in the image both horizontally and vertically. The feature map of the output is created by performing a dot product between the values of the kernel and the pixel values within the region covered by the kernel, resulting in a single value, where the calculated dot product represents the feature map of the output. Figure 6 shows the primary calculation of the convolution operation in each step. Here, the blue color represents the 2 2 kernels, and the green color represents the input region for taking the dot product in the input image. After the dot product operation, the resulting value (brown) is used for constructing the output feature map. The size of the output feature map depends on the stride value, the step size of the kernel in the horizontal and vertical directions, and the padding number to represent the border-side information of the image. Consequently, the size of the feature map increases with the input image size.
- Pooling layer: The purpose of the pooling layer is to perform subsampling on the feature maps. A pooling operation transforms a large feature map into a smaller one, and the input to the pooling layer retains most of the information from the feature map. After the initial stride value and padding number are assigned, the pooling operation is initiated. Generally, three types of pooling algorithms, max pooling, average pooling, and global average pooling, are executed in the pooling layer. The max pooling algorithm selects the maximum value as the output feature map from the dot products of the kernel and local region of the image. The average pooling algorithm calculates the average value through the pooling operation, and the average value is representative the local region of the image. Finally, global average pooling is used to significantly reduce the number of CNN parameters to fully overcome the connection in the layer. Figure 7 shows a conceptual illustration of the three pooling methods. The pooling layer cannot avoid information loss owing to its operational characteristics, and it allows the CNN to determine whether features are available in the input image. Therefore, it affects the performance of the CNN.
- Fully connected layer: At the end of the CNN architecture, each neuron of the fully connected layer is connected to all the neurons of the previous layer. Similar to a conventional multilayer perceptron neural network, the fully connected layer is used as a classifier. The inputs of the fully connected layer are derived from the last pooling or convolutional layer as vectors. After flattening, the output of the fully connected layer is the output of the CNN. Figure 8 shows a schematic of the fully connected layer.
- Activation functions, cost functions, and optimizers: The activation function leads to a nonlinear output of the layer for the linear summation of neurons as the input at the end of all the layers in the CNN architecture. Along with nonlinearity, the condition of differentiability must be satisfied. The differentiability condition is crucial for error backpropagation for updating the weight values of neurons in the training process. In most cases, the ReLU function or its variations are used as the activation functions, which convert all the input values the into nonnegative numbers. To solve the dying ReLU problem, the leaky ReLU, a variation of the ReLU that operates as the ReLU for positive inputs and assigns a precise small negative value for negative inputs, is used. Occasionally, the noisy ReLU is employed by adding Gaussian distribution noise to the ReLU.
- During the training process, the last layer of the CNN outputs the estimated result for the underlying input and compares it with the label as an answer. The difference between the predicted value and the answer is the predicted error, which must be corrected close to the answer. A cost function is applied as the criterion to minimize the prediction error. Several types of cost functions have been employed in different cases. A commonly employed cost function is the cross-entropy criterion, which expresses outputs as a probability distribution in the range by applying the softmax function. The network parameters should be updated according to the cost function to minimize the prediction error. This requires repetitive calculations using the optimizer during every training epoch. The optimizer operates the gradient of the cost function by taking the first-order derivative with respect to the network parameters, and the updating process is performed through network backpropagation in which the gradient of all neurons is backpropagated to all neurons in the preceding layer.
2.4. CNN Variations
- 6.
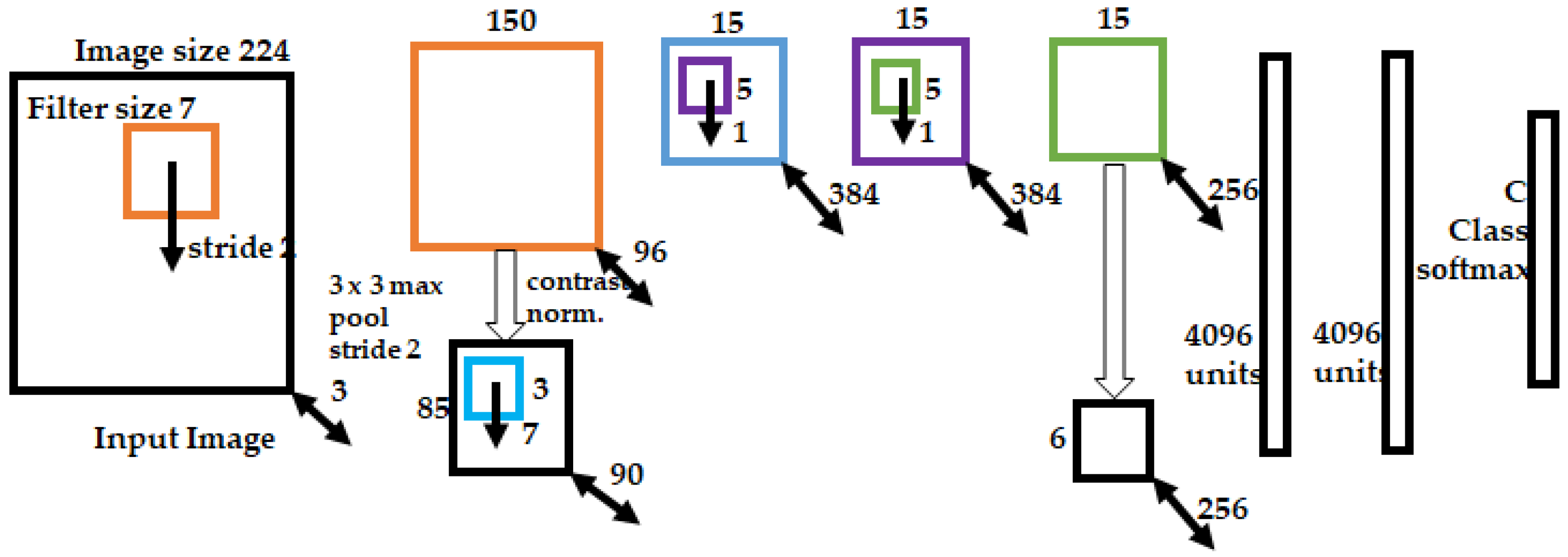
- AlexNet achieved remarkable improvements in performance and applicability compared with the previously developed LeNet. Although the applicable areas of vision tasks in the early days of deep neural networks (DNNs) were limited to handwritten digit recognition, remarkable performance was achieved considering the hardware of the time. Compared with LeNet, AlexNet significantly improves the performance by innovating the structure of the CNN and the implemented hardware.
- 7.
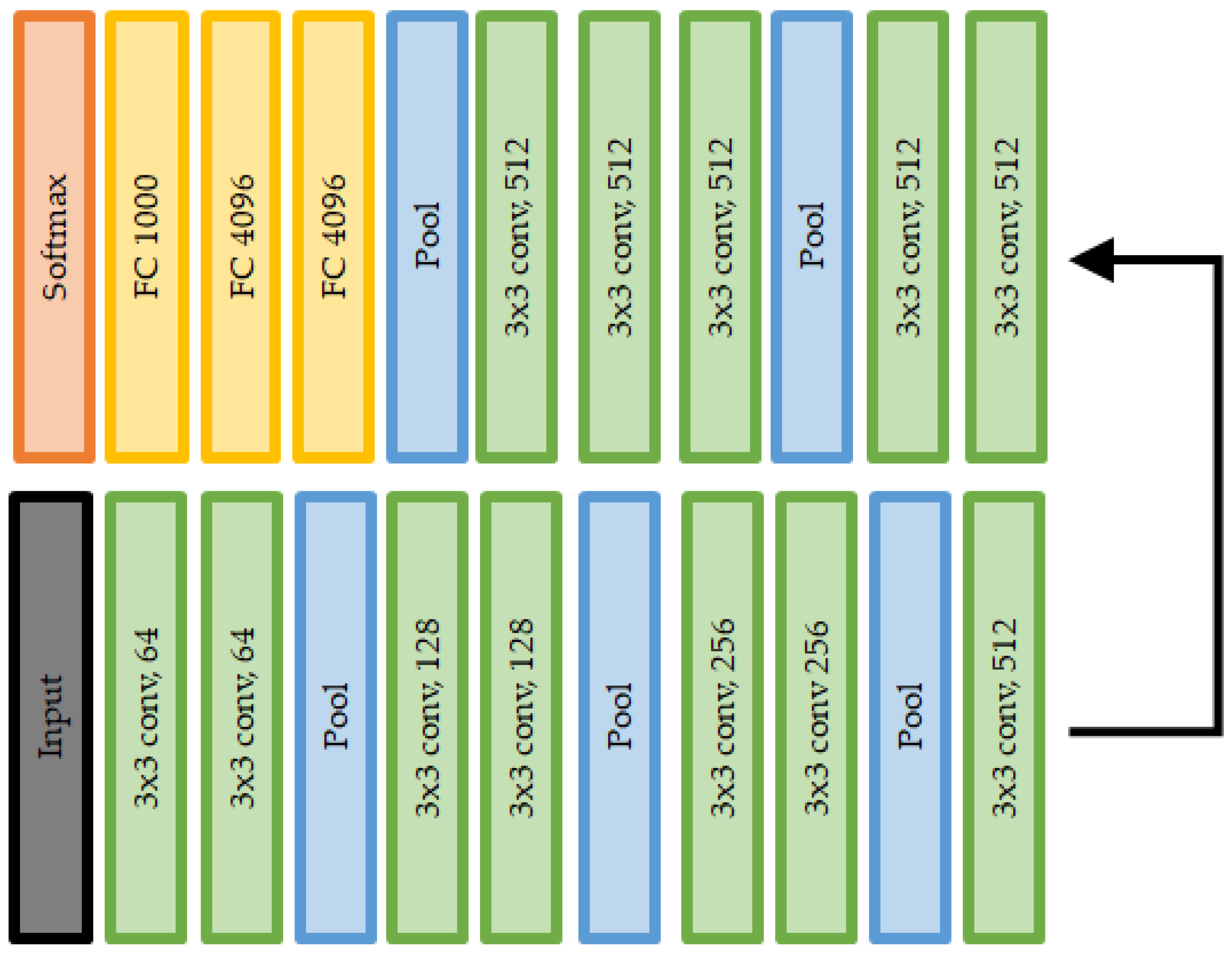
- Visual geometry group network (VGGNet): As indicated by the first paper [92] related to VGGNet, the relationship between the depth of the network and performance has been an important issue in vision tasks using CNN structures. Before the advent of VGGNet, ZefNet and AlexNet were the winners of the ILSVRC (ImageNet large-scale visual recognition challenge) competition [93] in 2012 and 2013, respectively. The depth of the CNN structure is only eight layers, with 5 and 11 filters. VGGNet is a CNN structure with a depth of 19 layers, wherein the existing CNN structure is significantly changed to improve the performance. Even if the filter size is reduced to 3 , an efficiency similar to that for the larger filters 5 and 11 can be achieved.
- 8.
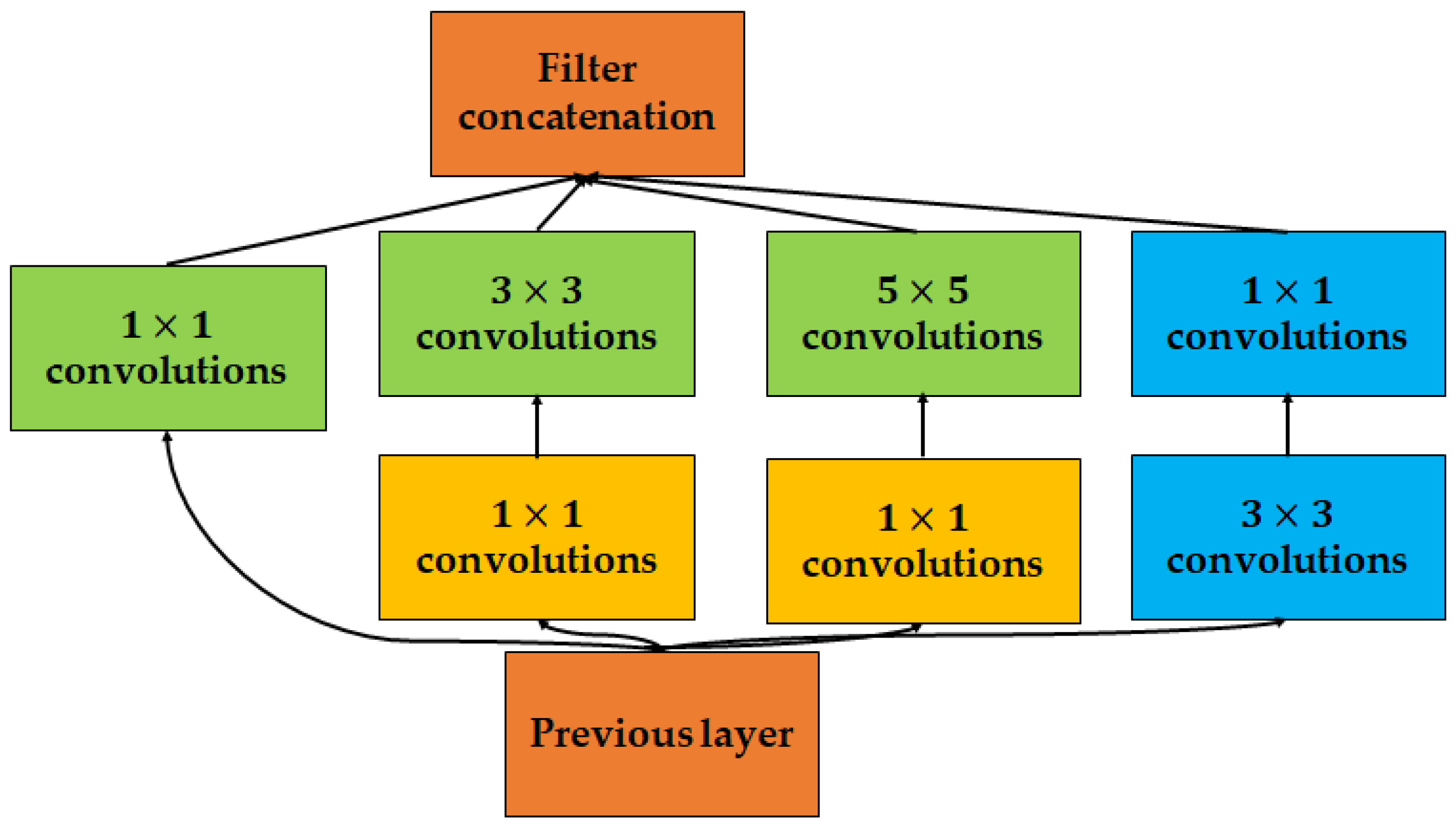
- GoogLeNet, the winner of the ILSVRC 2014 competition (also called Inception V1) [94] achieved a 6.67% error rate, which was the best at the time and a reduction in computational cost, which was the purpose of its implementation. The core of GoogLeNet is an inception block that employs multiscale convolutional transformation based on merging, transforming, and split functions for feature extraction. The inception block architecture integrates filters of varying sizes to gather channel information across a broad range of spatial resolutions. Figure 13 shows the basic structure of the inception block in GoogLeNet. GoogLeNet aims to increase the efficiency of the CNN parameters and enhance learning. The sparse connection applied to GoogLeNet removes redundant information that increases the computation cost owing to the operations of an irrelevant channel. Additionally, the GAP layer is applied as an end layer instead of a fully connected layer to reduce the density of the connection. Consequently, the number of parameters is significantly reduced from 40 million to 5 million. To increase the learning capacity, GoogLeNet employs auxiliary learners that accelerate the rate of convergence and solve the gradient vanishing problem. The main weakness of this method is the heterogeneous topology of the structure, which implies that information flow from one block to another requires an adaptation block.
- 9.
- ResNet: As the performance of the model improves, the depth of the network tends to increase. The most significant difference of ResNet from the existing model is that the network is deeper [95]. The depth initially applied to ResNet was 34 layers, which is more than four times that of AlexNet. Later, the depth of ResNet was increased to 1202 layers, and ResNet50, the most widely used variation of ResNet, consisted of 49 convolutional layers and one fully connected layer. The objectives of ResNet are to solve the gradient vanishing problem and to increase the network depth. Gradient vanishing that is a fatal weakness of the extreme deep model was resolved using the bypass concept in ResNet. The bypass concept was proposed for Highway networks [96]. Though there are differences between the two concepts, their basic meanings are the same. Figure 14 shows the basic structure of the ResNet. ResNet is composed of the conventional feedforward of the CNN structure and residual connection. The output of the residual layer is delivered from the preceding layer. Using residual layers, ResNet can reduce the gradient vanishing according to the deep network and accelerate the deep network convergence. ResNet was the winner of the ILSVCR 2015 competition. It had 152 layers, exceeding the depth of the previous year’s winner, i.e., GoogLeNet.
- 10.
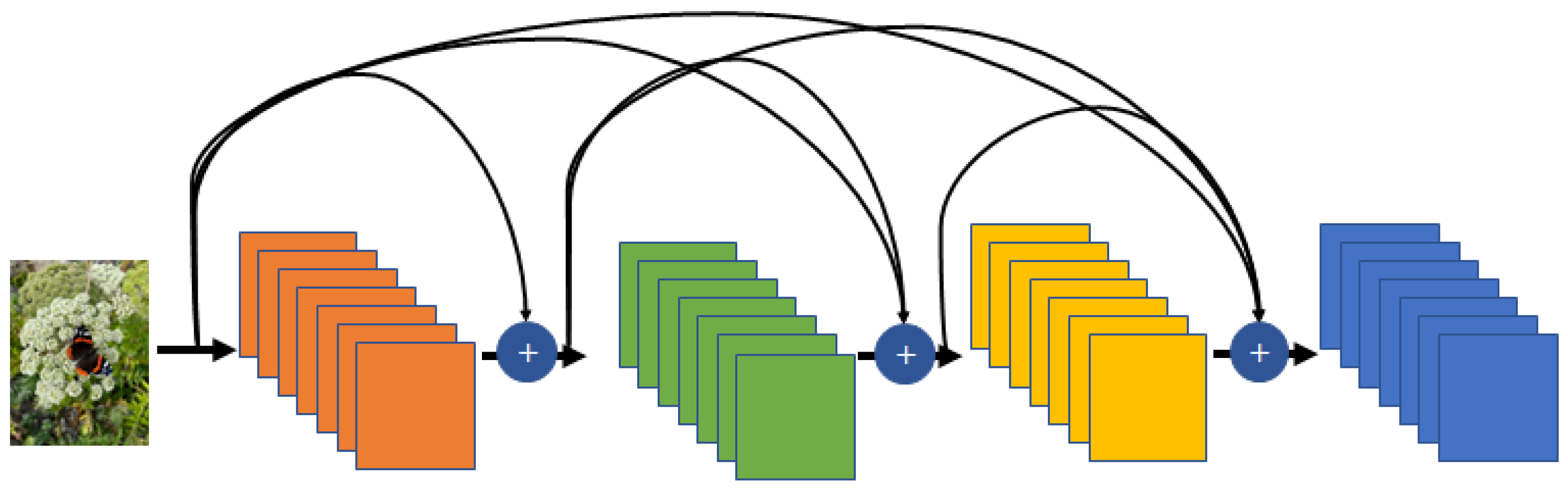
- DenseNet: The strategy of DenseNet [97] for solving the gradient vanishing problem is identical to that of ResNet. The causal difference between DenseNet and ResNet is that DenseNet involves channel-wise concatenation that connects to neurons not only on the next layer but also subsequent layers, whereas ResNet employs element-wise addition, which results in an addition path with a skip connection. As a unique parameter in DenseNet, the growth rate is defined to control the number of features that increase the number of channels. As shown in Figure 15, DenseNet is also helpful in learning because it can receive gradients through various paths, such as ResNet.

3. Adversarial Attacks and Defenses
3.1. Adversarial Attacks
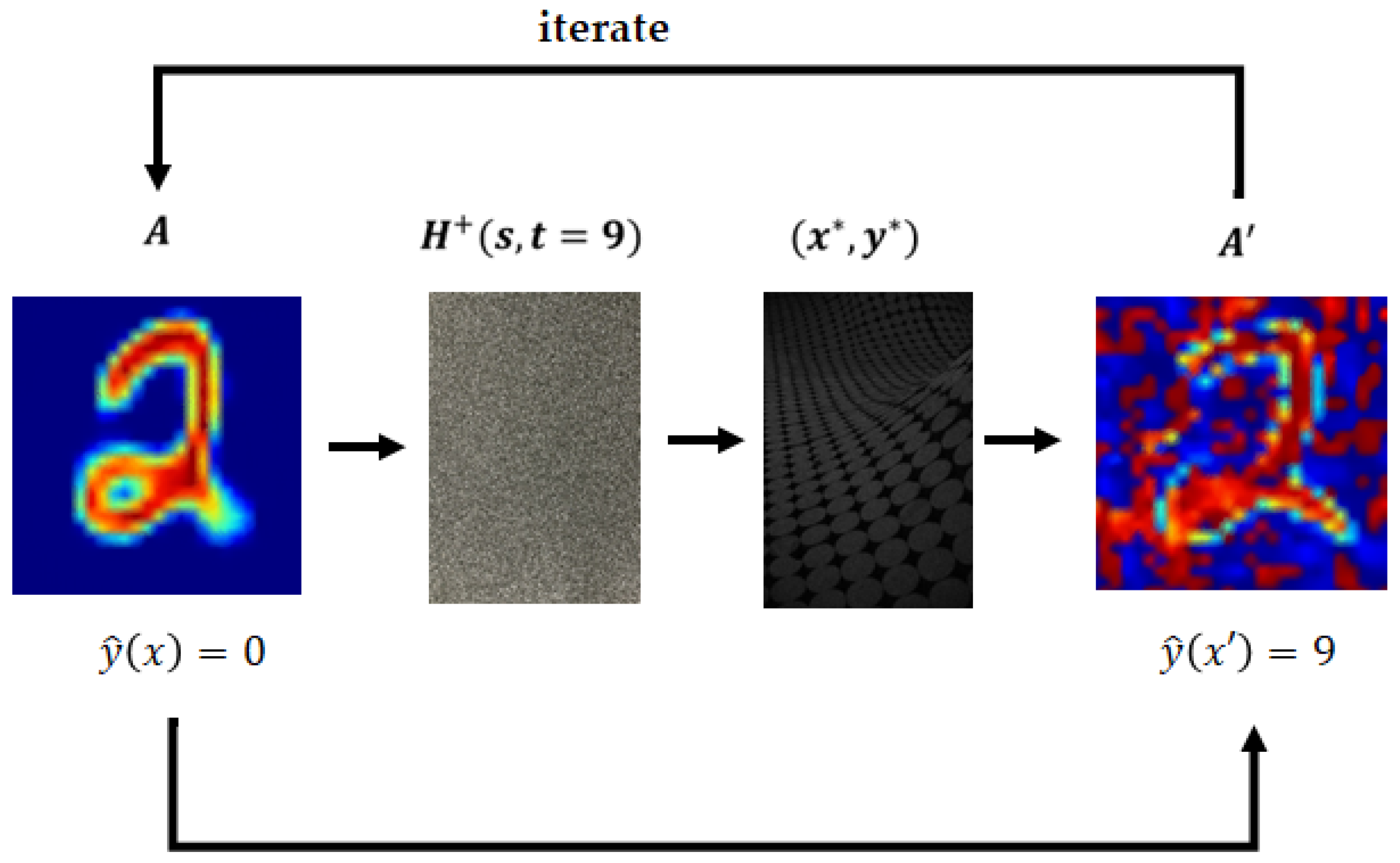
3.1.1. L-BFGS Attack
3.1.2. FGSM Attack
3.1.3. DeepFool Attack
3.1.4. JSMA
3.1.5. CW Attacks
3.2. Adversarial Defenses
3.2.1. Adversarial Training
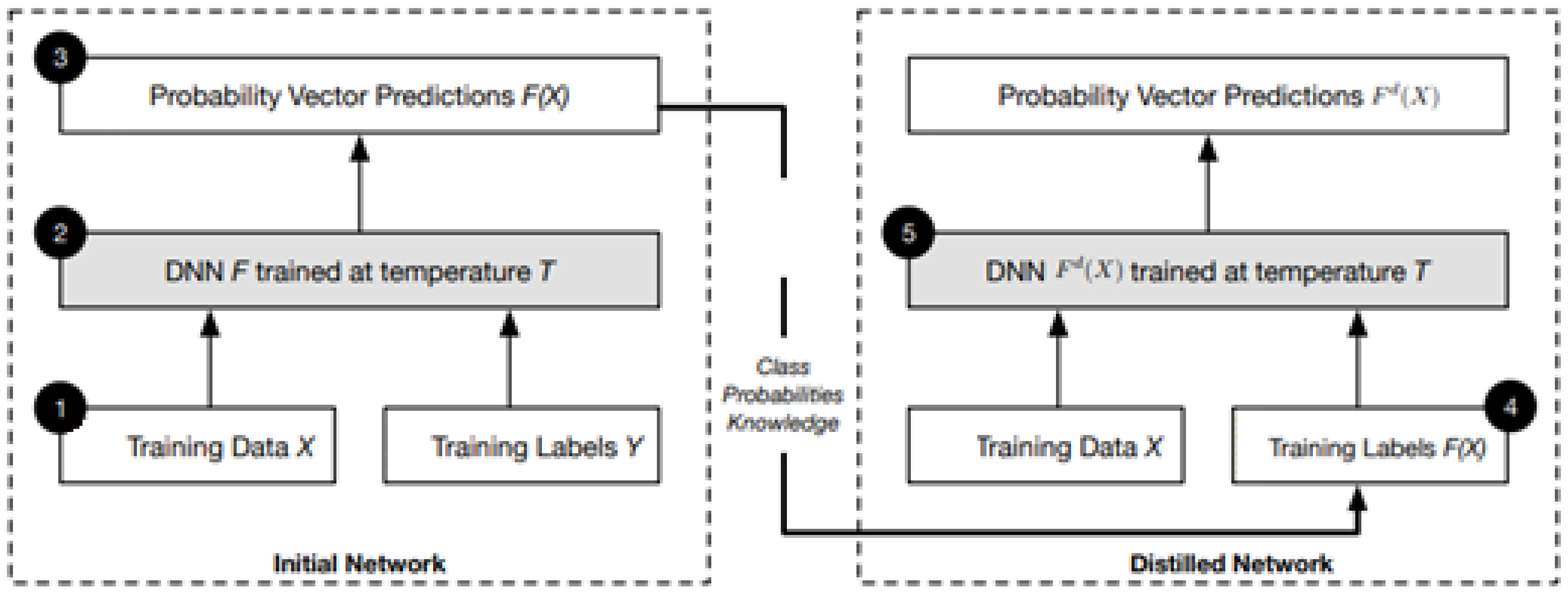
3.2.2. Defensive Distillation
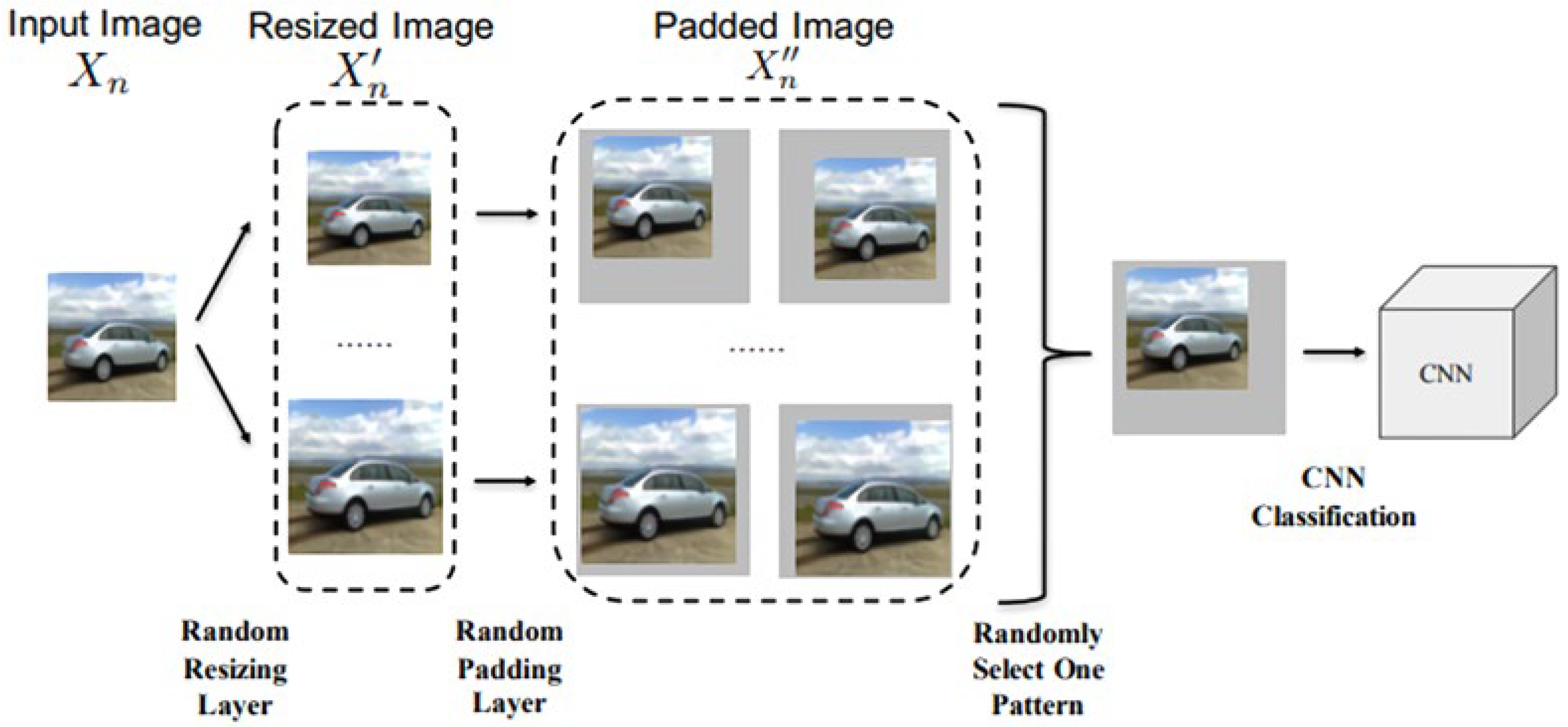
3.2.3. Randomization
3.2.4. Defense-GAN
- Defense-GAN can be utilized with any classifier and does not alter the classifier’s design. It functions as an auxiliary step or a preprocessing step before the classification process.
- If the GAN has a strong representation, there is no need to retrain the classifier and the integration of Defense-GAN should not cause a significant drop in performance.
- Defense-GAN can be applied as a defense against any type of attack as it does not rely on a specific attack model. It simply takes advantage of the generative capabilities of GANs to reconstruct adversarial examples.
- Defense-GAN is highly nonlinear, making it challenging for white-box gradient-based attacks due to the gradient descent loop.

3.2.5. Adversary Detector Networks
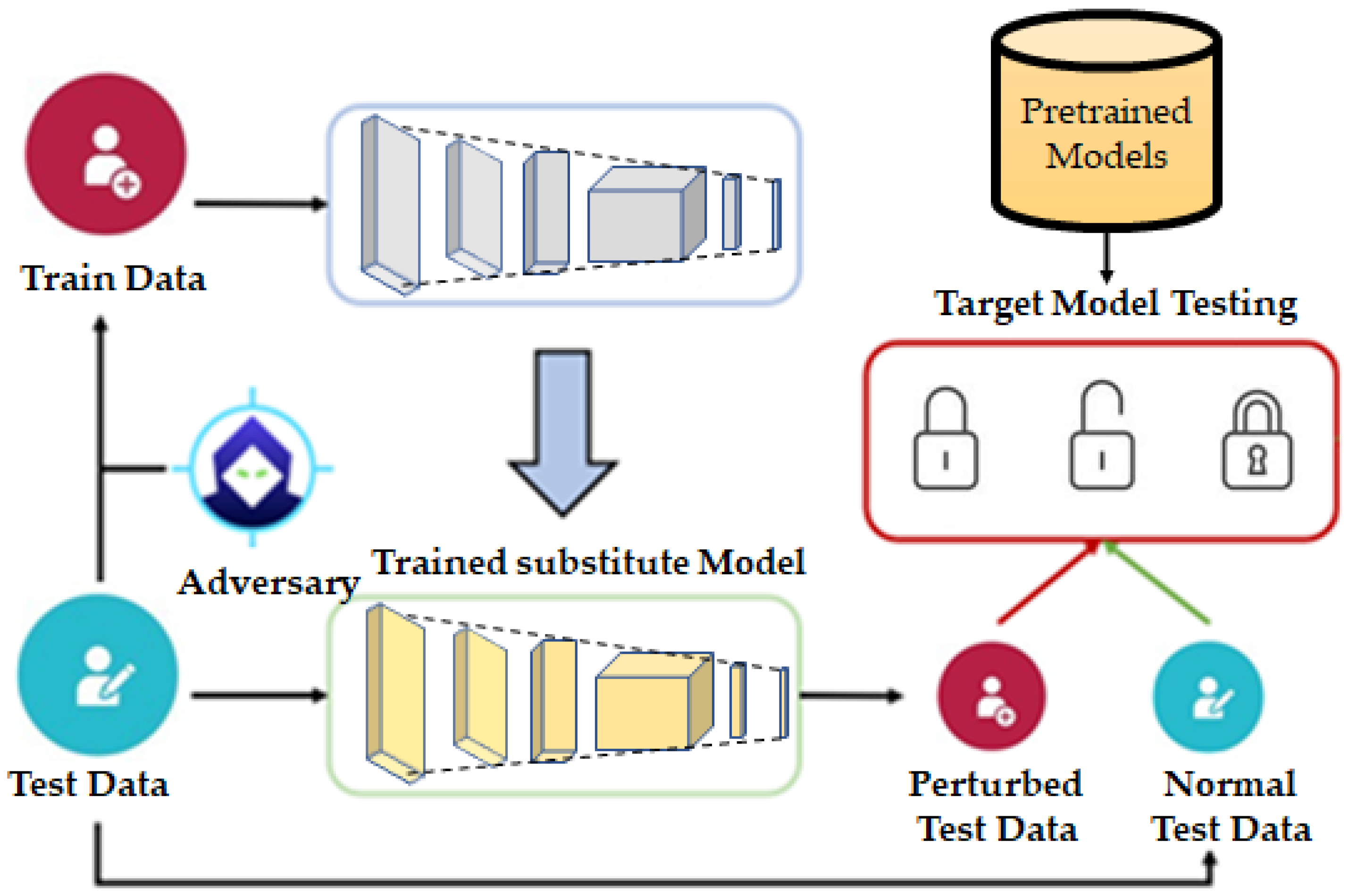
4. Brain-Inspired Neural Architectures against Adversarial Attacks
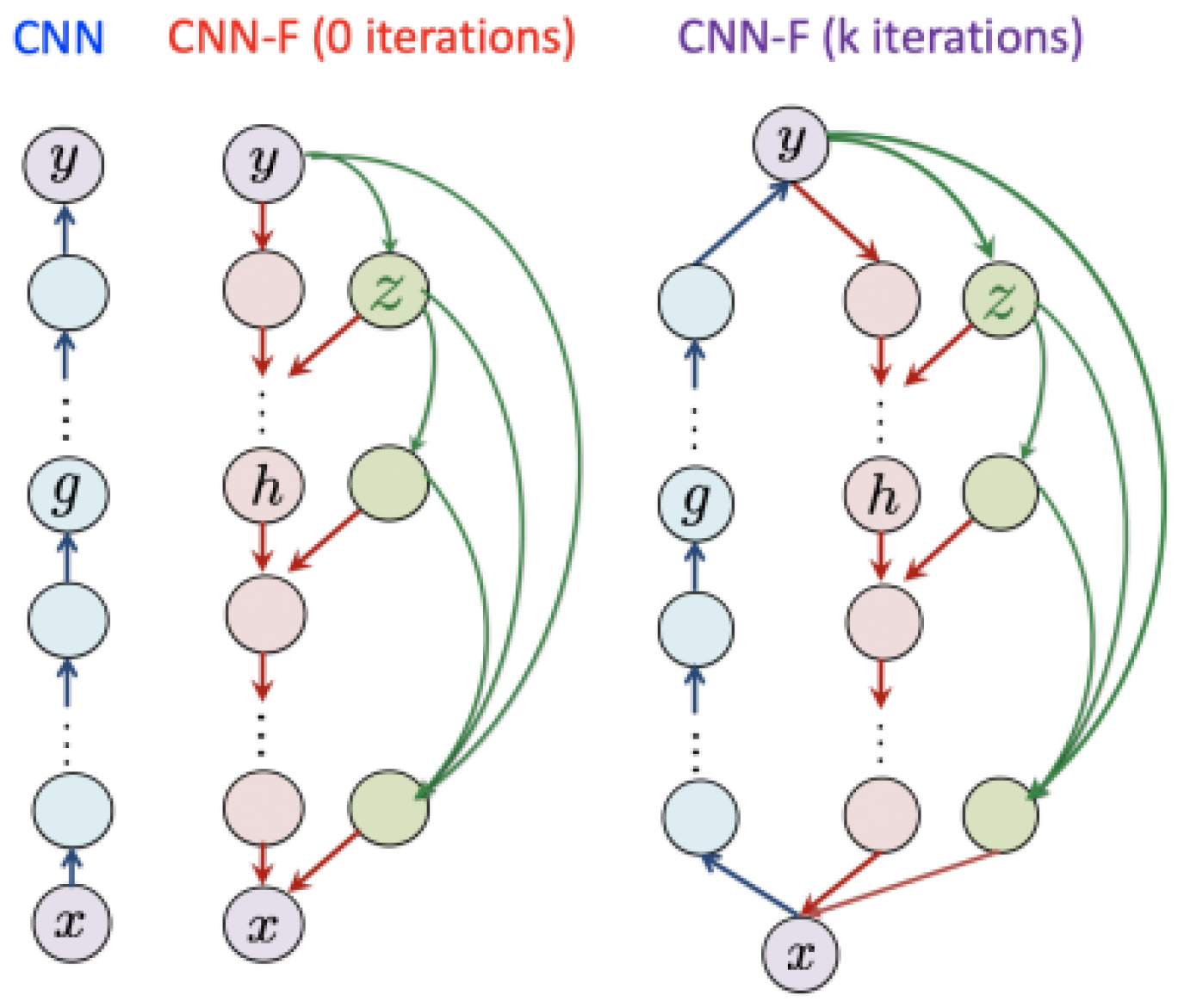
4.1. CNN with Feedback Model
4.2. Hyperdimensional Computing Model
4.3. Integrated Contour Model
4.4. Generalized Likelihood Ratio Model
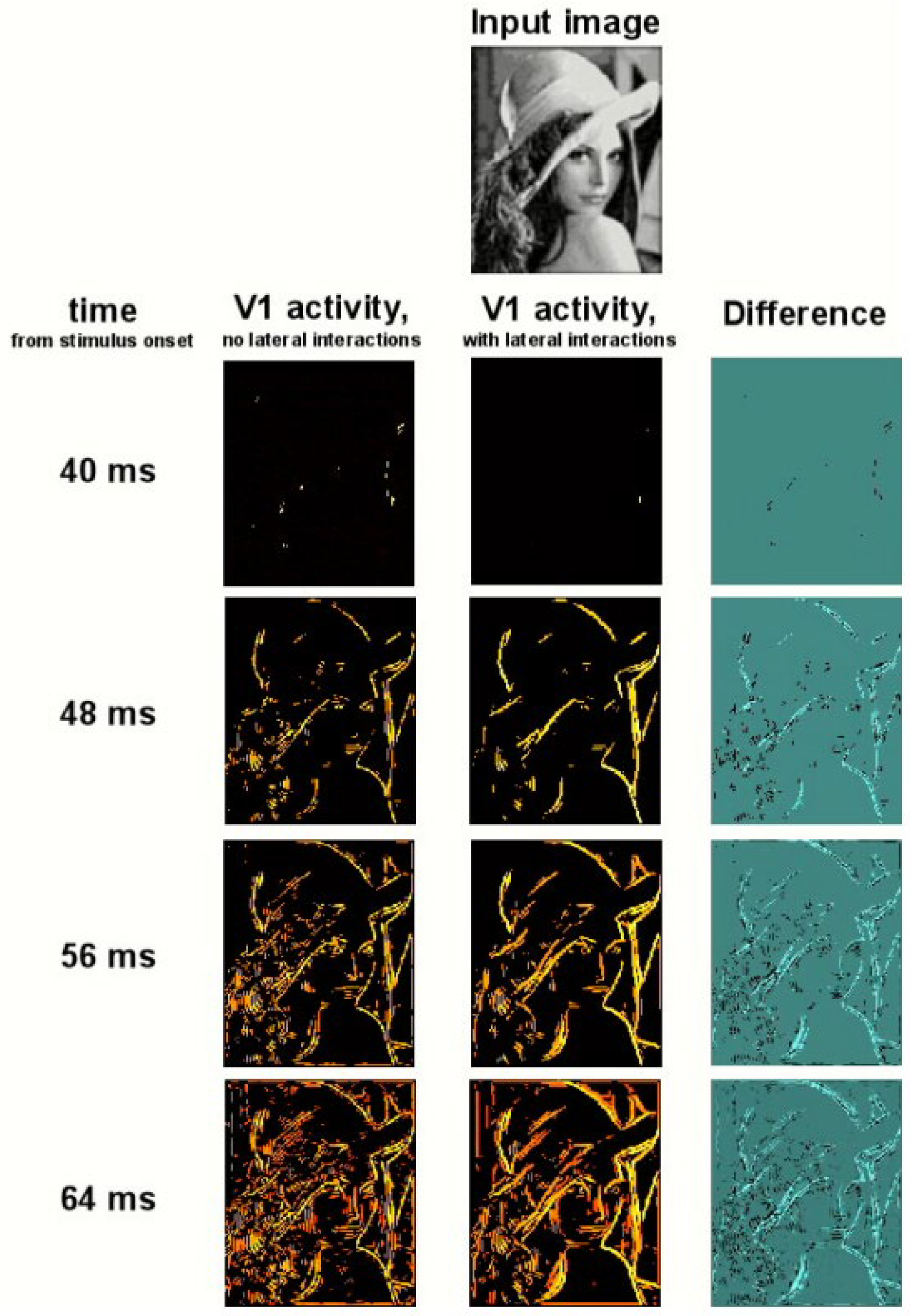
4.5. Biological Mechanism Model
4.6. CNN-Based Visual Cortex Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hinton, G.; Neural, R.S.-A. Using Deep Belief Nets to Learn Covariance Kernels for Gaussian Processes. In Proceedings of the 20th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 7 December 2007. [Google Scholar]
- Ahmed, A.; Yu, K.; Xu, W.; Gong, Y.; Xing, E. Training Hierarchical Feed-Forward Visual Recognition Models Using Transfer Learning from Pseudo-Tasks; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy Layer-Wise Training of Deep Networks. In Proceedings of the 19th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2006. [Google Scholar]
- Larochelle, H.; Erhan, D.; Courville, A.; Bergstra, J.; Bengio, Y. An Empirical Evaluation of Deep Architectures on Problems with Many Factors of Variation. ACM Int. Conf. Proc. Ser. 2007, 227, 473–480. [Google Scholar] [CrossRef]
- Lee, H.; Grosse, R.; Ranganath, R.; Ng, A.Y. Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 609–616. [Google Scholar] [CrossRef]
- Ranzato, M.; Boureau, Y.L.; Cun, Y. Sparse Feature Learning for Deep Belief Networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2007; Volume 20. [Google Scholar]
- Aurelio, M.; Poultney, R.C.; Chopra, S.; Lecun, Y. Efficient Learning of Sparse Representations with an Energy-Based Model. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2006; Volume 19. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and Composing Robust Features with Denoising Autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Montreal, QC, Canada, 11–15 April 2008; pp. 1096–1103. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Salakhutdinov, R.; Hinton, G. Learning a Nonlinear Embedding by Preserving Class Neighbourhood Structure. In Proceedings of the Eleventh International Conference on Artificial Intelligence and Statistics, San Juan, Puerto Rico, 21–24 March 2007. [Google Scholar]
- Taylor, G.W.; Hinton, G.E. Factored Conditional Restricted Boltzmann Machines for Modeling Motion Style. ACM Int. Conf. Proc. Ser. 2009, 382, 1025–1032. [Google Scholar] [CrossRef]
- Taylor, G.; Hinton, G.E.; Roweis, S. Modeling Human Motion Using Binary Latent Variables. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2006; Volume 19. [Google Scholar]
- Osindero, S.; Hinton, G.E. Modeling Image Patches with a Directed Hierarchy of Markov Random Fields. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2007; Volume 20. [Google Scholar]
- Ranzato, M.; Szummer, M. Semi-Supervised Learning of Compact Document Representations with Deep Networks. In Proceedings of the Twenty-Fifth International Conference (ICML 2008), Helsinki, Finland, 5–9 June 2008. [Google Scholar]
- Salakhutdinov, R.; Approximate, G.H.-I.J. Semantic Hashing; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Utgoff, P.; Stracuzzi, D.J. Many-Layered Learning. Neural Comput. 2002, 14, 2497–2529. [Google Scholar] [CrossRef] [PubMed]
- Hadsell, R.; Erkan, A.; Sermanet, P.; Scoffier, M.; Muller, U.; LeCun, Y. Deep Belief Net Learning in a Long-Range Vision System for Autonomous off-Road Driving. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008. [Google Scholar]
- Xie, D.; Bai, L. A Hierarchical Deep Neural Network for Fault Diagnosis on Tennessee-Eastman Process. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015. [Google Scholar]
- Zhang, L.; Yang, F.; Zhang, Y.D.; Zhu, Y.J.I. Road Crack Detection Using Deep Convolutional Neural Network. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016. [Google Scholar]
- Lee, J.; Jun, S.; Cho, Y.; Lee, H.; Kim, G.B.; Seo, J.B.; Kim, N. Deep Learning in Medical Imaging: General Overview. Korean J. Radiol. 2017, 18, 570–584. [Google Scholar] [CrossRef] [PubMed]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing Properties of Neural Networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Drenkow, N.; Sani, N.; Shpitser, I.; Unberath, M. A Systematic Review of Robustness in Deep Learning for Computer Vision: Mind the Gap? arXiv 2021, arXiv:2112.00639. [Google Scholar] [CrossRef]
- Yan, H.; Tan, V.Y.F. Towards Adversarial Robustness of Deep Vision Algorithms. arXiv 2020, arXiv:2211.10670. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, Y.; Li, Y.; Wu, S.; Yu, X. Towards Evaluating the Robustness of Adversarial Attacks Against Image Scaling Transformation. Chin. J. Electron. 2023, 32, 151–158. [Google Scholar]
- Ren, C.; Xu, Y. Robustness Verification for Machine-Learning-Based Power System Dynamic Security Assessment Models Under Adversarial Examples. IEEE Trans. Control. Netw. Syst. 2022, 9, 1645–1654. [Google Scholar] [CrossRef]
- Ibrahim, M.S.; Dong, W.; Yang, Q. Machine learning driven smart elctric power systems: Current trens and new perspectives. Appl. Energy 2020, 272, 115237. [Google Scholar] [CrossRef]
- Chattopadhyay, N.; Chatterjee, S.; Chattopadhyay, A. Robustness Against Adversarial Attacks Using Dimensionality. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2022; pp. 226–241. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, K.; Xu, Z. Re-Thinking Model Robustness from Stability: A New Insight to Defend Adversarial Examples. Mach. Learn. 2022, 111, 2489–2513. [Google Scholar] [CrossRef]
- Borji, A.; Ai, Q.; Francisco, S. Overparametrization Improves Robustness against Adversarial Attacks: A Replication Study. arXiv 2002, arXiv:2202.09735. [Google Scholar]
- Borji, A.; Ai, Q.; Francisco, S. Is Current Research on Adversarial Robustness Addressing the Right Problem? arXiv 2022, arXiv:2208.00539. [Google Scholar]
- Wang, Y.; Tan, Y.A.; Baker, T.; Kumar, N.; Zhang, Q. Deep Fusion: Crafting Transferable Adversarial Examples and Improving Robustness of Industrial Artificial Intelligence of Things. In IEEE Transactions on Industrial Informatics; IEEE: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Jankovic, A.; Mayer, R. An Empirical Evaluation of Adversarial Examples Defences, Combinations and Robustness Scores. In Proceedings of the IWSPA ’22: Proceedings of the 2022 ACM on International Workshop on Security and Privacy Analytics, Baltimore, MD, USA, 27 April 2022. [Google Scholar]
- Poggio, T. Marr’s Computational Approach to Vision; Elsevier: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Ungerleider, L.; Haxby, J.V. ’What’ and ’Where’ in the Human Brain; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Markov, N.T.; Ercsey-Ravasz, M.; van Essen, D.C.; Knoblauch, K.; Toroczkai, Z.; Kennedy, H. Cortical High-Density Counterstream Architectures. Science 2013, 342, 1238406. [Google Scholar] [CrossRef] [PubMed]
- Fattori, P.; Pitzalis, S.; Galletti, C. The Cortical Visual Area V6 in Macaque and Human Brains; Elsevier: Amsterdam, The Netherlands, 2009; Volume 103, pp. 88–97. [Google Scholar] [CrossRef]
- DeYoe, E.A.; van Essen, D.C. Concurrent Processing Streams in Monkey Visual Cortex. Trends. Neurosci. 1988, 11, 219–226. [Google Scholar] [CrossRef]
- Bassett, D.S.; Cullen, K.E.; Eickhoff, S.B.; Farah, M.J.; Goda, Y.; Haggard, P.; Hu, H.; Hurd, Y.L.; Josselyn, S.A.; Khakh, B.S.; et al. Reflections on the Past Two Decades of Neuroscience. Nat. Rev. Neurosci. 2020, 21, 524–534. [Google Scholar] [CrossRef]
- Cadieu, C.; Kouh, M.; Pasupathy, A.; Connor, C.E.; Riesenhuber, M.; Poggio, T. A Model of V4 Shape Selectivity and Invariance. J. Neurophysiol. 2007, 98, 1733–1750. [Google Scholar] [CrossRef]
- Serre, T.; Wolf, L.; Bileschi, S.; Riesenhuber, M.; Poggio, T. Robust Object Recognition with Cortex-like Mechanisms. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 411–426. [Google Scholar] [CrossRef]
- Hinton, G.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Cox, D.D.; Dean, T. Neural Networks and Neuroscience-Inspired Computer Vision. Curr. Biol. 2014, 24, R921–R929. [Google Scholar] [CrossRef] [PubMed]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Cai, Z.; Vasconcelos, N. Cascade R-Cnn: Delving into High Quality Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6154–6162. [Google Scholar]
- Shreyas, E.; Sheth, M.H. 3D Object Detection and Tracking Methods Using Deep Learning for Computer Vision Applications. In Proceedings of the 2021 International Conference on Recent Trends on Electronics, Information, Communication & Technology (RTEICT), Bangalore, India, 27–28 August 2021. [Google Scholar] [CrossRef]
- Dai, X.; Lei, Y.; Roper, J.; Chen, Y.; Bradley, J.D.; Curran, W.J.; Liu, T.; Yang, X.; Xiaofeng Yang, C. Deep Learning—Based Motion Tracking Using Ultrasound Images. Wiley Online Libr. 2021, 48, 7747–7756. [Google Scholar] [CrossRef] [PubMed]
- Kiran, S.; Khan, M.; Javed, M.; Alhaisoni, M.; Tariq, U. Multi-Layered Deep Learning Features Fusion for Human Action Recognition. CMC Comput. Mater. Contin. 2021, 69, 3. [Google Scholar] [CrossRef]
- Ronald, M.; Poulose, A.; Han, D.S. ISPLInception: An Inception-ResNet Deep Learning Architecture for Human Activity Recognition. IEEE Access 2021, 9, 68985–69001. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, H.; Feng, R.; Wu, S.; Ji, S.; Yang, B.; Wang, X. Deep Dual Consecutive Network for Human Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 525–534. [Google Scholar]
- Wang, J.; Jin, S.; Liu, W.; Liu, W.; Qian, C.; Luo, P. When Human Pose Estimation Meets Robustness: Adversarial Algorithms and Benchmarks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 11855–11864. [Google Scholar]
- Lecun, Y.; Haffner, P.; Eon Bottou, L.; Bengio, Y.; Abstract|, P.H. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Carreira-Perpinan, M.; Hinton, G. On Contrastive Divergence Learning. In Proceedings of the Machine Learning Research, New York, NY, USA, 24 June 2016. [Google Scholar]
- Hinton, G.E. A Practical Guide to Training Restricted Boltzmann Machines. In Lecture Notes in Computer Science (Including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2012; pp. 599–619. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines; Department of Computer Science, University of Toronto: Toronto, ON, Canada, 2010. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Stochastic Pooling for Regularization of Deep Convolutional Neural Networks. arXiv 2013, arXiv:1301.355. [Google Scholar]
- Liou, C.; Cheng, W.; Liou, J.; Liou, D.R. Autoencoder for Words; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Hyvärinen, A.; Hoyer, P. Emergence of Phase-and Shift-Invariant Features by Decomposition of Natural Images into Independent Feature Subspaces. Neural Comput. 2000, 12, 1705–1720. [Google Scholar] [CrossRef]
- Olshausen, B.; Field, D.J. Sparse Coding with an Overcomplete Basis Set: A Strategy Employed by V1? Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Yu, K.; Zhang, T.; Gong, Y. Nonlinear Learning Using Local Coordinate Coding. In Proceedings of the 23rd Annual Conference on Neural Information Processing Systems 2009, Vancouver, BC, Canada, 7–10 December 2009. [Google Scholar]
- Raina, R.; Battle, A.; Lee, H.; Packer, B.; Ng, A.Y. Self-Taught Learning: Transfer Learning from Unlabeled Data. ACM Int. Conf. Proceeding Ser. 2007, 227, 759–766. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Yu, K.; Huang, T.; Gong, Y. Locality-Constrained Linear Coding for Image Classification. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Ouyang, W.; Zeng, X.; Wang, X.; Luo, P.; Tian, Y.; Li, H.; Yang, S.; Wang, Z.; Li, H.; Wang, K.; et al. DeepID-Net: Object Detection with Deformable Part Based Convolutional Neural Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1320–1334. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Lay, N.; Wei, Z.; Lu, L.; Kim, L.; Turkbey, E.; Summers, R.M. Colitis Detection on Abdominal CT Scans by Rich Feature Hierarchies. Proc. SPIE 2016, 9785, 423–429. [Google Scholar]
- Luo, G.; An, R.; Wang, K.; Zhang, H. A Deep Learning Network for Right Ventricle Segmentation in Short-Axis MRI. In Proceedings of the 2016 Computing in Cardiology Conference (CinC), Vancouver, BC, Canada, 11–14 September 2016. [Google Scholar] [CrossRef]
- Diao, W.; Sun, X.; Zheng, X.; Dou, F.; Wang, H.; Fu, K. Efficient Saliency-Based Object Detection in Remote Sensing Images Using Deep Belief Networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 137–141. [Google Scholar] [CrossRef]
- Shin, H.-C.; Orton, M.R.; Collins, D.J.; Doran, S.J.; Leach, M.O. Stacked Autoencoders for Unsupervised Feature Learning and Multiple Organ Detection in a Pilot Study Using 4D Patient Data. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 1930–1943. [Google Scholar] [CrossRef] [PubMed]
- Doulamis, N.; Doulamis, A. Fast and Adaptive Deep Fusion Learning for Detecting Visual Objects. In Lecture Notes in Computer Science (Including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2012; pp. 345–354. [Google Scholar] [CrossRef]
- Lawrence, S.; Lee Giles, C.; Member, S.; Chung Tsoi, A.; Back, A.D. Face Recognition: A Convolutional Neural-Network Approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef] [PubMed]
- Amos, B.; Ludwiczuk, B.; Satyanarayanan, M. Openface: A General-Purpose Face Recognition Library with Mobile Applications. CMU Sch. Comput. Sci. 2016, 6, 20. [Google Scholar]
- Voulodimos, A.; Kosmopoulos, D.; Doulamis, N.; Varvarigou, T.; Voulodimos, A.S.; Kosmopoulos, D.I.; Doulamis, N.D.; Varvarigou, T.A.; Voulodimos, A.S.; Doulamis, N.D.; et al. A Top-down Event-Driven Approach for Concurrent Activity Recognition. Multimed. Tools Appl. 2014, 69, 293–311. [Google Scholar] [CrossRef]
- Voulodimos, A.S.; Doulamis, N.D.; Kosmopoulos, D.I.; Varvarigou, T.A. Improving Multi-Camera Activity Recognition by Employing Neural Network Based Readjustment. Appl. Artif. Intell. 2012, 26, 97–118. [Google Scholar] [CrossRef]
- Makantasis, K.; Doulamis, A.; Doulamis, N.; Psychas, K. Deep Learning Based Human Behavior Recognition in Industrial Workflows. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016. [Google Scholar] [CrossRef]
- Gan, C.; Wang, N.; Yang, Y.; Yeung, D.-Y.; Hauptmann, A.G. Devnet: A Deep Event Network for Multimedia Event Detection and Evidence Recounting. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Kautz, T.; Groh, B.H.; Hannink, J.; Jensen, U.; Strubberg, H.; Eskofier, B.M. Activity Recognition in Beach Volleyball Using a Deep Convolutional Neural Network: Leveraging the Potential of Deep Learning in Sports. Data Min. Knowl. Discov. 2017, 31, 1678–1705. [Google Scholar] [CrossRef]
- Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei-Fei, L. Large-Scale Video Classification with Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 1725–1732. [Google Scholar]
- Ronao, C.; Cho, S.-B. Human Activity Recognition with Smartphone Sensors Using Deep Learning Neural Networks. Expert Syst. Appl. 2016, 59, 235–244. [Google Scholar] [CrossRef]
- Shao, J.; Loy, C.; Kang, K.; Wang, X. Crowded Scene Understanding by Deeply Learned Volumetric Slices. IEEE Trans. Circuits Syst. Video Technol. 2016, 27, 613–623. [Google Scholar] [CrossRef]
- Tang, K.; Yao, B.; Fei-Fei, L.; Koller, D. Combining the Right Features for Complex Event Recognition. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013. [Google Scholar] [CrossRef]
- Song, S.; Chandrasekhar, V.; Mandal, B.; Li, L.; Lim, J.-H.; Sateesh Babu, G.; Phyo San, P.; Cheung, N.-M. Multimodal Multi-Stream Deep Learning for Egocentric Activity Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Kavi, R.; Kulathumani, V.; Kecojevic, V. Multiview Fusion for Activity Recognition Using Deep Neural Networks. J. Electron. Imaging 2016, 25, 043010. [Google Scholar] [CrossRef]
- Kitsikidis, A.; Dimitropoulos, K.; Douka, S.; Grammalidis, N. Dance Analysis Using Multiple Kinect Sensors; SciTePress: Odense, Denmark, 2014. [Google Scholar]
- Felzenszwalb, P.F.; Huttenlocher, D.P. Pictorial Structures for Object Recognition. Int. J. Comput. Vis. 2005, 61, 55–79. [Google Scholar] [CrossRef]
- Jain, A.; Tompson, J.; Andriluka, M.; Taylor, G.W.; Bregler, C. Learning Human Pose Estimation Features with Convolutional Networks. arXiv 2013, arXiv:1312.7302. [Google Scholar]
- Hubel, D.H.; Wiesel, T.N. Receptive Fields of Single Neurones in the Cat’s Striate Cortex. J. Physiol. 1959, 148, 574. [Google Scholar] [CrossRef]
- Fukushima, K. Neocognitron: A Hierarchical Neural Network Capable of Visual Pattern Recognition; Elsevier: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Yan, L.; Yoshua, B.; Hinton, G. Deep Learning. Nature 2016, 521, 436–444. [Google Scholar]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A Survey of the Recent Architectures of Deep Convolutional Neural Networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef]
- Bhatt, D.; Patel, C.; Talsania, H.; Patel, J.; Vaghela, R.; Pandya, S.; Modi, K.; Ghayvat, H. CNN Variants for Computer Vision: History, Architecture, Application, Challenges and Future Scope. Electronics 2021, 10, 2470. [Google Scholar] [CrossRef]
- Zeiler, M.; Vision, R.F.-E. Visualizing and Understanding Convolutional Networks; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Zeiler, M.; Taylor, G.; Fergus, R. Adaptive Deconvolutional Networks for Mid and High Level Feature Learning. In Proceedings of the 2011 IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Lee, S.; Sung, Y.; Kim, Y.; Cha, E.-Y. Variations of AlexNet and GoogLeNet to Improve Korean Character Recognition Performance. J. Inf. Process. Syst. 2018, 14, 205–217. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Highway Networks. arXiv 2015, arXiv:1505.00387. [Google Scholar]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 261–2269. [Google Scholar] [CrossRef]
- Zagoruyko, S.; Komodakis, N. Wide Residual Networks. In Proceedings of the British Machine Vision Conference (BMVC), York, UK, 19–22 September 2016; pp. 1–12. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic Routing between Capsules. arXiv 2017, arXiv:1710.09829. [Google Scholar]
- Quang, N.V.; Chun, J.; Tokuyama, T. CapsuleNet for Micro-Expression Recognition. In Proceedings of the 2019 14th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2019), Lille, France, 14–18 May 2019. [Google Scholar]
- Arun, P.; Buddhiraju, K.M.; Porwal, A. Capsulenet-Based Spatial–Spectral Classifier for Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1849–1865. [Google Scholar] [CrossRef]
- Stoica, A.; Kadar, T.; Lemnaru, C.; Potolea, R.; Dîns, M. Intent Detection and Slot Filling with Capsule Net Architectures for a Romanian Home Assistant. Sensors 2021, 21, 1230. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Lin, Y.; Lin, H.I. ATMPA: Attacking Machine Learning-Based Malware Visualization Detection Methods via Adversarial Examples. In Proceedings of the International Symposium on Quality of Service, IWQoS 2019, Phoenix, AZ, USA, 24–25 June 2019. [Google Scholar]
- Biggio, B.; Roli, F. Wild Patterns: Ten Years after the Rise of Adversarial Machine Learning Half-Day Tutorial. Proc. ACM Conf. Comput. Commun. Secur. 2018, 2154–2156. [Google Scholar] [CrossRef]
- Bhatnagar, S.; Cotton, T.; Brundage, M.; Avin, S.; Clark, J.; Toner, H.; Eckersley, P.; Garfinkel, B.; Dafoe, A.; Scharre, P.; et al. The Malicious Use of Artificial Intelligence: Forecasting, Prevention, and Mitigation. arXiv 2018, arXiv:1802.07228. [Google Scholar]
- Wittel, G. On Attacking Statistical Spam Filters. In Proceedings of the CEAS 2004—First Conference on Email and Anti-Spam, Mountain View, CA, USA, 30–31 July 2004. [Google Scholar]
- Zhang, J.; Li, C. Adversarial Examples: Opportunities and Challenges. IEEE Trans. Neural Netw. Learn. Syst. 2019, 1–16. [Google Scholar] [CrossRef]
- Biggio, B.; Didaci, L.; Fumera, G.; Roli, F. Poisoning Attacks to Compromise Face Templates. In Proceedings of the 2013 International Conference on Biometrics (ICB), Madrid, Spain, 4–7 June 2013. [Google Scholar]
- Biggio, B.; Corona, I.; Maiorca, D.; Nelson, B.; Šrndić, N.; Laskov, P.; Giacinto, G.; Roli, F. Evasion Attacks against Machine Learning at Test Time. Lect. Notes Comput. Sci. 2013, 8190, 387–402. [Google Scholar] [CrossRef]
- Grosse, K.; Papernot, N.; Manoharan, P.; Backes, M.; Mcdaniel, P. Adversarial Examples for Malware Detection; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Abaid, Z.; Kaafar, M.; Jha, S. Quantifying the Impact of Adversarial Evasion Attacks on Machine Learning Based Android Malware Classifiers. In Proceedings of the 2017 IEEE 16th International Symposium on Network Computing and Applications (NCA), Cambridge, MA, USA, 30 October–1 November 2017. [Google Scholar]
- Jagielski, M.; Oprea, A.; Biggio, B.; Liu, C.; Nita-Rotaru, C.; Li, B. Manipulating Machine Learning: Poisoning Attacks and Countermeasures for Regression Learning. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 21–23 May 2018. [Google Scholar]
- Bulò, S.; Biggio, B.; Pillai, I.; Pelillo, M.; Roli, F. Randomized Prediction Games for Adversarial Machine Learning. IEEE Trans. Neural Networks Learn. Syst. 2016, 28, 2466–2478. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceeding, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Papernot, N.; McDaniel, P.; Ian, G. Transferability in Machine Learning: From Phenomena to Black-Box Attacks Using Adversarial Samples. arXiv 2016, arXiv:1605.07277. [Google Scholar]
- Liu, Y.; Chen, X.; Liu, C.; Song, D. Delving into Transferable Adversarial Examples and Black-Box Attacks. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017—Conference Track Proceedings, Toulon, France, 24–26 April 2017. [Google Scholar]
- Arpit, D.; Jastrz, S.; Ballas, N.; Krueger, D.; Bengio, E.; Kanwal, M.S.; Maharaj, T.; Fischer, A.; Courville, A.; Bengio, Y.; et al. A Closer Look at Memorization in Deep Networks. arXiv 2017, arXiv:1706.05394. [Google Scholar]
- Jo, J.; Bengio, Y. Measuring the Tendency of CNNs to Learn Surface Statistical Regularities. arXiv 2017, arXiv:1711.11561. [Google Scholar]
- Liu, D.; Nocedal, J. On the Limited Memory BFGS Method for Large Scale Optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Kurakin, A.; Goodfellow, I.; Samy, B. Adversarial Examples in the Physical World. arXiv 2017, arXiv:1607.02533. [Google Scholar]
- Moosavi-Dezfooli, S.-M.; Fawzi, A.; Frossard’, P.F.; Polytechnique, F.; de Lausanne, F. Deepfool: A Simple and Accurate Method to Fool Deep Neural Networks. arXiv 2015, arXiv:1511.04599. [Google Scholar]
- Xu, H.; Ma, Y.; Liu, H.C.; Deb, D.; Liu, H.; Tang, J.L.; Jain, A.K. Adversarial Attacks and Defenses in Images, Graphs and Text: A Review. Int. J. Autom. Comput. 2020, 17, 151–178. [Google Scholar] [CrossRef]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Papernot, N.; Mcdaniel, P.; Jha, S.; Fredrikson, M.; Berkay Celik, Z.; Swami, A. The Limitations of Deep Learning in Adversarial Settings. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbruecken, Germany, 21–24 March 2016. [Google Scholar]
- Carlini, N.; Wagner, D. Towards Evaluating the Robustness of Neural Networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017. [Google Scholar]
- Moosavi-Dezfooli, S.-M.; Fawzi, A.; Fawzi, O.; Frossard, P. Universal Adversarial Perturbations. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Kingma, D.; Welling, M. An Introduction to Variational Autoencoders. Found. Trends® Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, H.; Sharma, Y.; Yi, J.; Hsieh, C.-J. Zoo: Zeroth Order Optimization Based Black-Box Attacks to Deep Neural Networks without Training Substitute Models. In Proceedings of the AISec ’17, the 10th ACM Workshop on Artificial Intelligence and Security, Dallas, TX, USA, 3 November 2017. [Google Scholar]
- Tramèr, F.; Kurakin, A.; Brain, G.; Papernot, N.; Goodfellow, I.; Boneh, D.; Mcdaniel, P. Ensemble Adversarial Training: Attacks and Defenses. arXiv 2020, arXiv:1705.07204. [Google Scholar]
- Papernot, N.; McDaniel, P.; Wu, X.; Jha, S.; Swami, A. Distillation as a Defense to Adversarial Perturbations against Deep Neural Networks. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2016. [Google Scholar]
- Adry, A.M.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar]
- Fischer, V.; Kumar, M.C.; Metzen, J.H.; Brox, T. Adversarial Examples for Semantic Image Segmentation. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017—Workshop Track Proceedings, Toulon, France, 24–26 April 2017. [Google Scholar]
- Gong, Z.; Wang, W.; Ku, W.-S. Adversarial and Clean Data Are Not Twins. arXiv 2017, arXiv:1704.04960. [Google Scholar]
- Grosse, K.; Manoharan, P.; Papernot, N.; Backes, M.; Mcdaniel, P. On the (Statistical) Detection of Adversarial Examples. arXiv 2017, arXiv:1702.06280. [Google Scholar]
- Feinman, R.; Curtin, R.; Shintre, S.; Gardner, A.B. Detecting Adversarial Samples from Artifacts. arXiv 2017, arXiv:1703.00410. [Google Scholar]
- Chen, P.; Sharma, Y.; Zhang, H.; Yi, J.; Hsieh, C.-J. Ead: Elastic-Net Attacks to Deep Neural Networks via Adversarial Examples. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 3–7 February 2018; Volume 32. [Google Scholar] [CrossRef]
- Sharma, Y.; Chen, P.Y. Attacking the Madry Defense Model with L1-Based Adversarial Examples. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018—Workshop Track Proceedings, Vancouver, BC, Canada, 3 May 2018. [Google Scholar]
- Lee, H.; Han, S.; Lee, J. Generative Adversarial Trainer: Defense to Adversarial Perturbations with GAN. arXiv 2017, arXiv:1705.03387. [Google Scholar]
- Odena, A.; Olah, C.; Shlens, J. Conditional Image Synthesis with Auxiliary Classifier Gans. arXiv 2017, arXiv:1610.09585. [Google Scholar]
- Liu, X.; Hsieh, C.J. Rob-Gan: Generator, Discriminator, and Adversarial Attacker. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Carlini, N.; Wagner, D.A. Defensive Distillation Is Not Robust to Adversarial Examples. arXiv 2016, arXiv:1607.04311. [Google Scholar]
- Xie, C.; Zhang, Z.; Yuille, A.L.; Wang, J.; Ren, Z. Mitigating Adversarial Effects through Randomization. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018—Conference Track Proceedings, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Uesato, J.; O’donoghue, B.; van den Oord, A.; Kohli, P. Adversarial Risk and the Dangers of Evaluating against Weak Attacks. arXiv 2018, arXiv:1802.05666. [Google Scholar]
- Athalye, A.; Engstrom, L.; Ilyas, A.; Kwok, K. Synthesizing Robust Adversarial Examples. arXiv 2018, arXiv:1707.07397. [Google Scholar]
- Samangouei, P.; Kabkab, M.; Chellappa, R. Defense-Gan: Protecting Classifiers against Adversarial Attacks Using Generative Models. arXiv 2018, arXiv:1805.06605. [Google Scholar]
- Athalye, A.; Carlini, N.; David, N.W. Obfuscated Gradients Give a False Sense of Security: Circumventing Defenses to Adversarial Examples. arXiv 2018, arXiv:1802.00420. [Google Scholar]
- Metzen, J.; Genewein, T.; Fischer, V.; Bischoff, B. On Detecting Adversarial Perturbations. arXiv 2017, arXiv:1702.04267. [Google Scholar]
- Rao, R.; Ballard, D.H. Predictive Coding in the Visual Cortex: A Functional Interpretation of Some Extra-Classical Receptive-Field Effects. Nat. Neurosci. 1999, 2, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Gornet, J.; Dai, S.; Yu, Z.; Nguyen, T.; Tsao, D.; Anandkumar, A. Neural Networks with Recurrent Generative Feedback. Adv. Neural Inf. Process. Syst. 2020, 33, 535–545. [Google Scholar]
- Gungor, O.; Rosing, T.; Aksanli, B. RES-HD: Resilient Intelligent Fault Diagnosis Against Adversarial Attacks Using Hyper-Dimensional Computing. arXiv 2022, arXiv:2203.08148. [Google Scholar]
- Bhambri, S.; Muku, S.; Tulasi, A.; Buduru, A.B. A Survey of Black-Box Adversarial Attacks on Computer Vision Models. arXiv 2019, arXiv:1912.01667. [Google Scholar]
- Lei, J.; Liu, C.; Jiang, D. Fault Diagnosis of Wind Turbine Based on Long Short-Term Memory Networks. Renew. Energy 2019, 133, 422–432. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, X.; Sánchez, R.; Yang, S.; Bai, Y. Spur Gear Fault Diagnosis Using a Multilayer Gated Recurrent Unit Approach with Vibration Signal. IEEE Access 2019, 7, 56880–56889. [Google Scholar] [CrossRef]
- Shenfield, A.; Howarth, M. A Novel Deep Learning Model for the Detection and Identification of Rolling Element-Bearing Faults. Sensors 2020, 20, 5112. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Piëch, V.; Gilbert, C.D. Contour Saliency in Primary Visual Cortex. Neuron 2006, 50, 951–962. [Google Scholar] [CrossRef]
- VanRullen, R.; Delorme, A.; Thorpe, S. Feed-Forward Contour Integration in Primary Visual Cortex Based on Asynchronous Spike Propagation. Neurocomputing 2001, 38–40, 1003–1009. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M. Mobilenets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Khan, S.; Wong, A.; Tripp, B. Guarding against Adversarial Attacks Using Biologically Inspired Contour Integration. J. Comput. Vis. Imaging Syst. 2018, 4, 3. [Google Scholar] [CrossRef]
- Li, Z. A Neural Model of Contour Integration in the Primary Visual Cortex. Neural. Comput. 1998, 10, 903–940. [Google Scholar] [CrossRef]
- Xiao, L.; Peng, Y.; Hong, J.; Ke, Z.; Yang, S. Training Artificial Neural Networks by Generalized Likelihood Ratio Method: Exploring Brain-like Learning to Improve Robustness. arXiv 2019, arXiv:1902.00358. [Google Scholar]
- Ursino, M.; La Cara, G.E. A Model of Contextual Interactions and Contour Detection in Primary Visual Cortex. Neural Netw. 2004, 17, 719–735. [Google Scholar] [CrossRef] [PubMed]
- Stettler, D.; Das, A.; Bennett, J.; Gilbert, C.D. Lateral Connectivity and Contextual Interactions in Macaque Primary Visual Cortex. Neuron 2002, 36, 739–750. [Google Scholar] [CrossRef] [PubMed]
- Dapello, J.; Marques, T.; Schrimpf, M.; Geiger, F.; Cox, D.D.; Dicarlo, J.J. Simulating a Primary Visual Cortex at the Front of CNNs Improves Robustness to Image Perturbations. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar] [CrossRef]













| Model | Top-1 Accuracy | Pixels | Attack Success |
|---|---|---|---|
| AlexNet | 36.1 ± 0.4 | 1 | 8.5 ± 0.4% |
| 3 | 10.6 ± 2.2% | ||
| 5 | 10.4 ± 2.1% | ||
| AlexNet + Contour | 38.0 ± 1.1 | 1 | 8.22 ± 1.8% |
| 3 | 9.76 ± 20% | ||
| 5 | 9.55 ± 1.75% |
| Activations + Entropy | Orig. | Adv_L_BFGS | Adv_FGSM |
|---|---|---|---|
| Sigmoid (trained by BP) | 0.96 | 0.57 | 0.28 |
| Sigmoid | 0.94 | 0.77 | 0.45 |
| Threshold | 0.93 | 0.73 | 0.52 |
| 0.94 | 0.78 | 0.53 | |
| Activations + 0–1 loss | Orig. | Adv_L_BFGS | Adv_FGSM |
| Sigmoid | 0.84 | 0.76 | 0.58 |
| Threshold | 0.83 | 0.72 | 0.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.; Kim, J. Robustness of Deep Learning Models for Vision Tasks. Appl. Sci. 2023, 13, 4422. https://doi.org/10.3390/app13074422
Lee Y, Kim J. Robustness of Deep Learning Models for Vision Tasks. Applied Sciences. 2023; 13(7):4422. https://doi.org/10.3390/app13074422
Chicago/Turabian StyleLee, Youngseok, and Jongweon Kim. 2023. "Robustness of Deep Learning Models for Vision Tasks" Applied Sciences 13, no. 7: 4422. https://doi.org/10.3390/app13074422
APA StyleLee, Y., & Kim, J. (2023). Robustness of Deep Learning Models for Vision Tasks. Applied Sciences, 13(7), 4422. https://doi.org/10.3390/app13074422






