Optimization of Pile Driver Frame Based on Sensitivity Analysis
Abstract
:1. Introduction
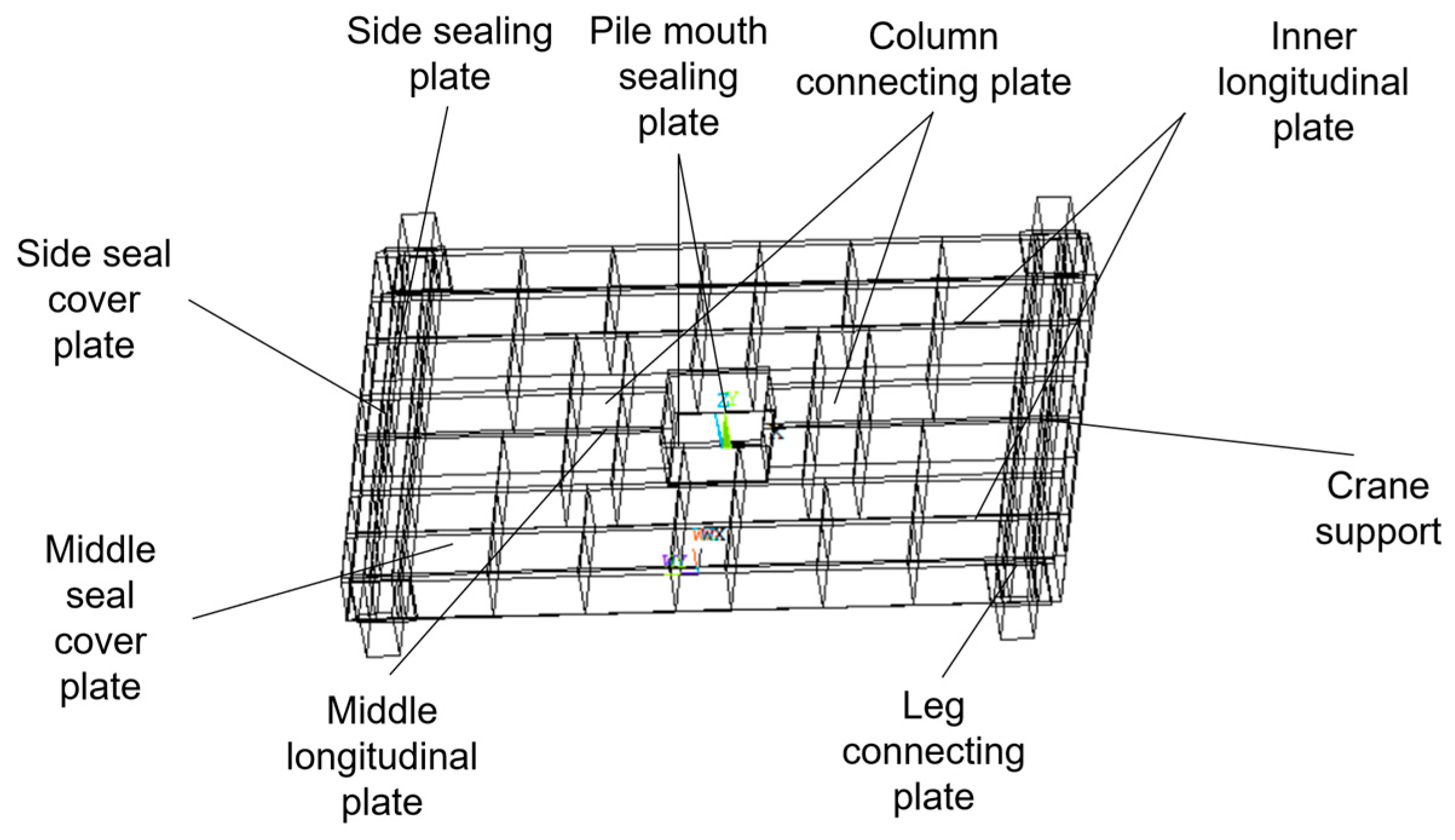
2. Body Model Structure and Analysis
2.1. Finite Element Model (FEM)
2.2. Static Analysis
2.2.1. Typical Working Condition Selection
2.2.2. Analysis of Stress Results in Typical Working Conditions
3. Theoretical Foundations of Sensitivity Analysis
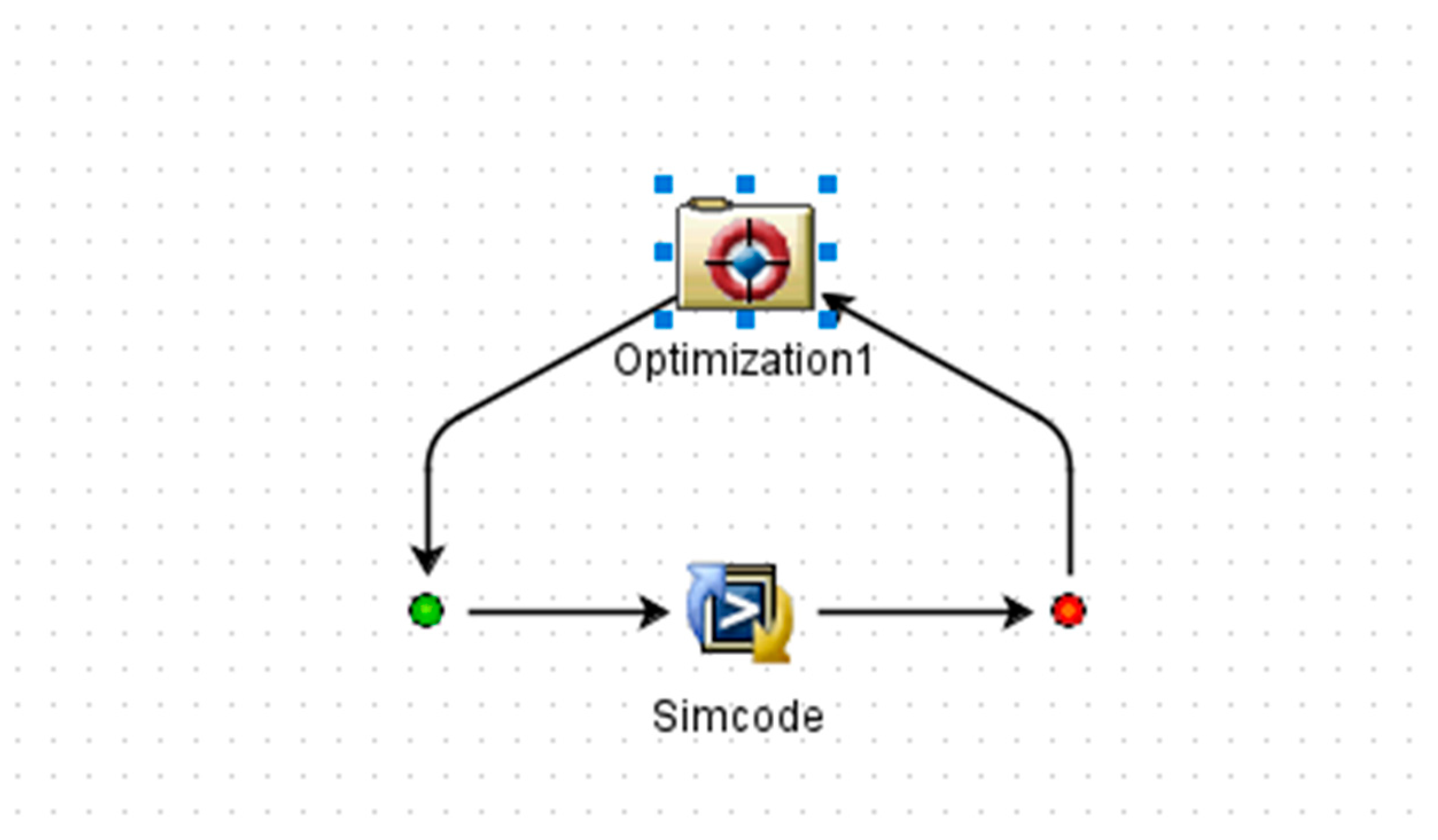
4. Optimized Design of Structures
4.1. Sensitivity Analysis
4.2. Constructing Optimal Design Model
- (1)
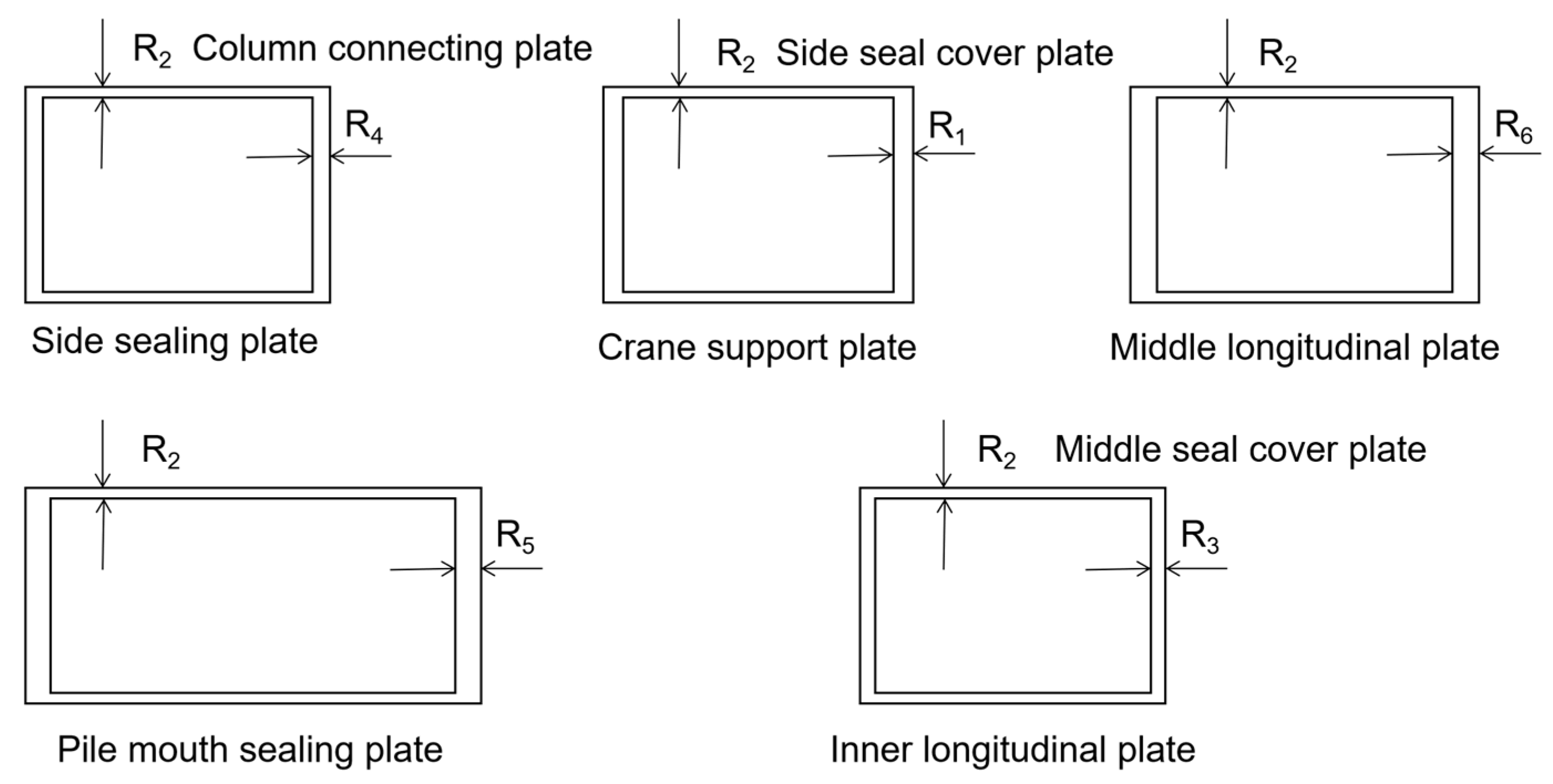
- Design variables: The large body skeleton of the pile driver is mainly made of thin steel plates welded together, and the steel plate thickness R is chosen as the design variable.
- (2)
- Constraints: The strength and stiffness of the large body skeleton are the constraints.
- (3)
- Objective function: The large body skeleton mass M is minimized as the objective.
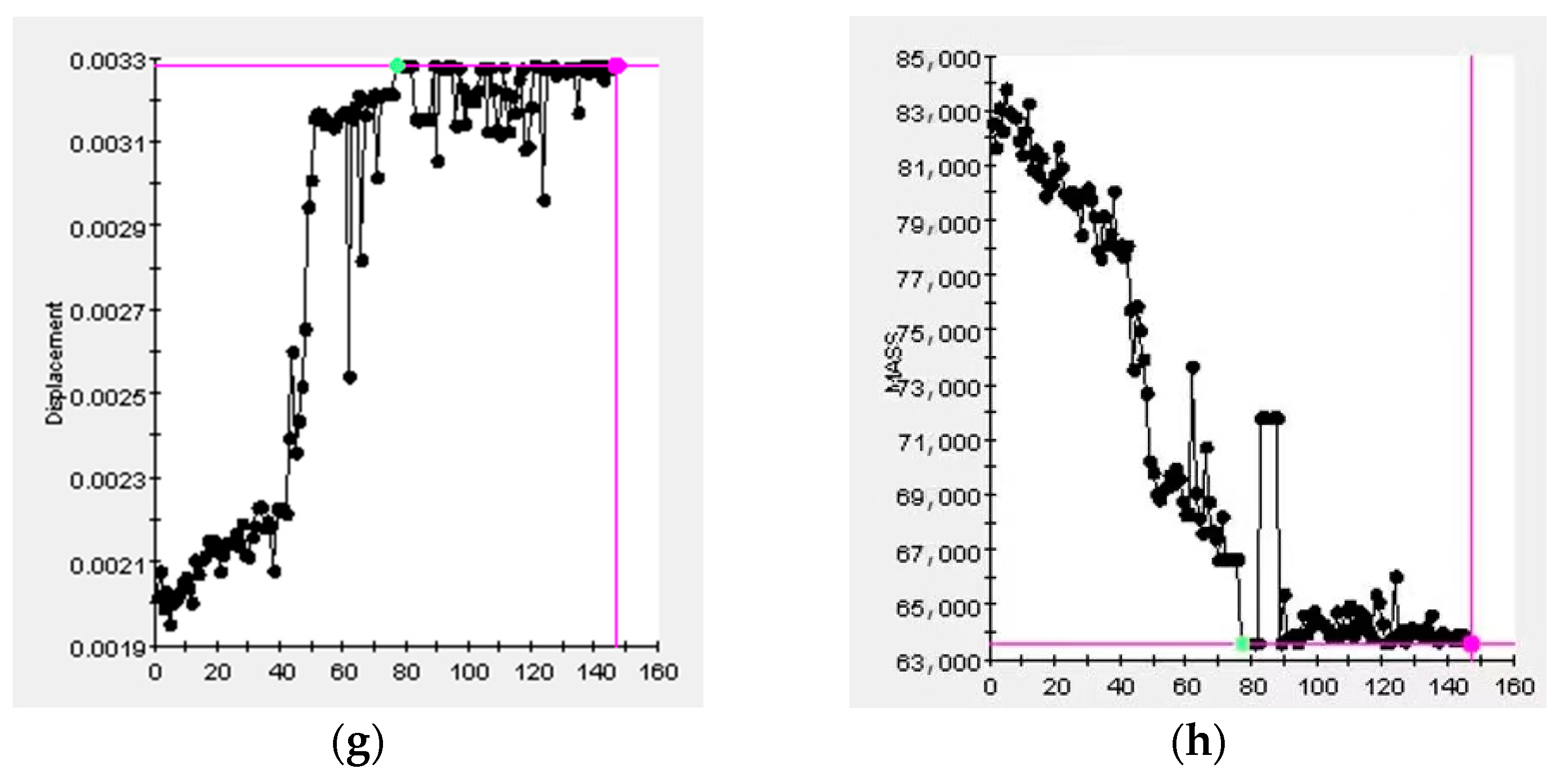
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sfiligoj, E. Pile drivers. Croplife 2010, 1736, 86–89. [Google Scholar]
- Liew, S.S.; Ho, S.F. Fallacy of capacity performance & innovation improvement of jack-in piling in Malaysia. Geotech. Eng. 2016, 47, 134–143. [Google Scholar]
- Noor, S.T.; Islam, M.S.; Mumtarin, M.; Chakraborty, N. Dynamic load test of full-scale pile for the construction and rehabilitation of bridges. IOP Conf. Ser. Mater. Sci. Eng. 2019, 513, 12017. [Google Scholar] [CrossRef]
- Ai, Z.; Gu, G.; Li, P. Analysis of interaction between fractional viscoelastic saturated soils and laterally loaded pile groups. Yantu Lixue/Rock Soil Mech. 2022, 43, 2933–2940. [Google Scholar]
- Worku, A.; Lulseged, A. Kinematic pile-soil interaction using a rigorous two-parameter foundation model. Soil Dyn. Earthq. Eng. 2023, 165, 107701. [Google Scholar] [CrossRef]
- Hama, K.; Horii, Y.; Nakanishi, Y.; Watanabe, T. Field trials of large-diameter multi-belled piling method. In Geotechnics for Sustainable Infrastructure Development; Springer: Singapore, 2020; pp. 161–168. [Google Scholar]
- Jiang, Y.; Xu, C.; Shao, S. Analysis on the piling mechanism of the jacked pile in layered soil. Arab. J. Geosci. 2022, 15, 1399. [Google Scholar] [CrossRef]
- Hisao, Y.; Hisashi, H.; Masanori, K. Challenges in the past and for the future of design and installation technologies on steel pipe piles in Japan. Doboku Gakkai Ronbunshuu F 2010, 663, 34–36. [Google Scholar]
- ZuoJian, D. Research on Lightweight Technology of YZY800D Pile Driver Frame Structure; Southwest Jiaotong University: Chengdu, China, 2015; Available online: https://kns.cnki.net/ (accessed on 30 August 2022).
- Lim, G.T. Applications of press-in piling in south-east asia countries. Spec. Present. 4th IPA Int. Workshop 2012, 12, 6–7. [Google Scholar]
- Tang, J.; Song, C.; Liu, F.Y.; Xu, Y.E. Research on lightweight method of commercial vehicle cab based on structural parameter sensitivity analysis. Mech. Des. 2021, 38, 97–101. [Google Scholar]
- Wang, L.; Diskin, B.; Biedron, R.T.; Nielsen, E.J.; Bauchau, O.A. High-Fidelity Multidisciplinary Sensitivity Analysis and Design Optimization for Rotorcraft Applications. AIAA J. 2019, 57, 3117–3131. [Google Scholar] [CrossRef]
- Yu, T.; Shi, Y.; He, X.; Kang, C.; Deng, B.; Song, S. Optimization of Parameter Ranges for Composite Tape Winding Process Based on Sensitivity Analysis. Appl. Compos. Mater. 2017, 24, 821–836. [Google Scholar] [CrossRef]
- Liu, Q.M. Exact sensitivity analysis of stresses and lightweight design of Timoshenko composite beams. Compos. Struct. 2016, 143, 272–286. [Google Scholar] [CrossRef]
- Kiendl, J.; Schmidt, R.; Wüchner, R.; Bletzinger, K.U. Isogeometric shape optimization of shells using semi-analytical sensitivity analysis and sensitivity weighting. Comput. Methods Appl. Mech. Eng. 2014, 274, 148–167. [Google Scholar] [CrossRef]
- Liu, S.H.; Du, Y.B.; Lin, M. Study on lightweight structural optimization design system for gantry machine tool. Concurr. Eng. Res. Appl. 2019, 27, 170–185. [Google Scholar] [CrossRef]
- Jun, P.; Hu, H.; Dong, Z.; Li, K.J. Stress Research and Finite Element Analysis of Pile Clamping Mechanism of Hydraulic Static Pile Driver. Adv. Mater. Res. 2014, 3103, 908. [Google Scholar]
- Xiong, F.; Wang, D.; Ma, Z.; Chen, S.; Lv, T.; Lu, F. Structure-material integrated multi-objective lightweight design of the front end structure of automobile body. Struct. Multidiscip. Optim. 2018, 57, 829–847. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Q.; Zhang, X.; Wang, X.; Chen, J.; Shen, X. Lightweight Design of Special Axle Hub Based on ANSYS Consider Different Working Conditions for Low Carbon. Math. Probl. Eng. 2022, 2022, 3738996. [Google Scholar] [CrossRef]
- Wu, M. Design Research of Crawler Type Multifunctional Static Pile Driver; Northeast Petroleum University: Daqing, China, 2017; Available online: https://kns.cnki.net/ (accessed on 30 August 2022).
- Ning, H.E.; Delong, Z.; Qinghua, Z. Reliability Sensitivity Analysis for Drum Brake on Modal Stress. Int. J. Plant Eng. Manag. 2021, 26, 193–214. [Google Scholar]
- Zuo, W.; Yu, J.; Saitou, K. Stress sensitivity analysis and optimization of automobile body frame consisting of rectangular tubes. Int. J. Automot. Technol. 2016, 17, 843–851. [Google Scholar] [CrossRef]
- Jin, W.; Mao, Z.; Zhou, S.; Zhang, T.; Hu, Y.; Wu, Z. Research on Multi-Optimal Project of Outlet Guide Vanes of Nuclear Grade Axial Flow Fan Based on Sensitivity Analysis. Appl. Sci. 2022, 12, 3029. [Google Scholar] [CrossRef]
- Sha, L.; Lin, A.; Zhao, X.; Kuang, S. A topology optimization method of robot lightweight design based on the finite element model of assembly and its applications. Sci. Prog. 2020, 103, 36850420936482. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H. Study on the Strength and Fatigue Life of ZYB800M Pile Press Clamp Pile Box; Central South University: Changsha, China, 2014; Available online: https://kns.cnki.net/ (accessed on 30 August 2022).

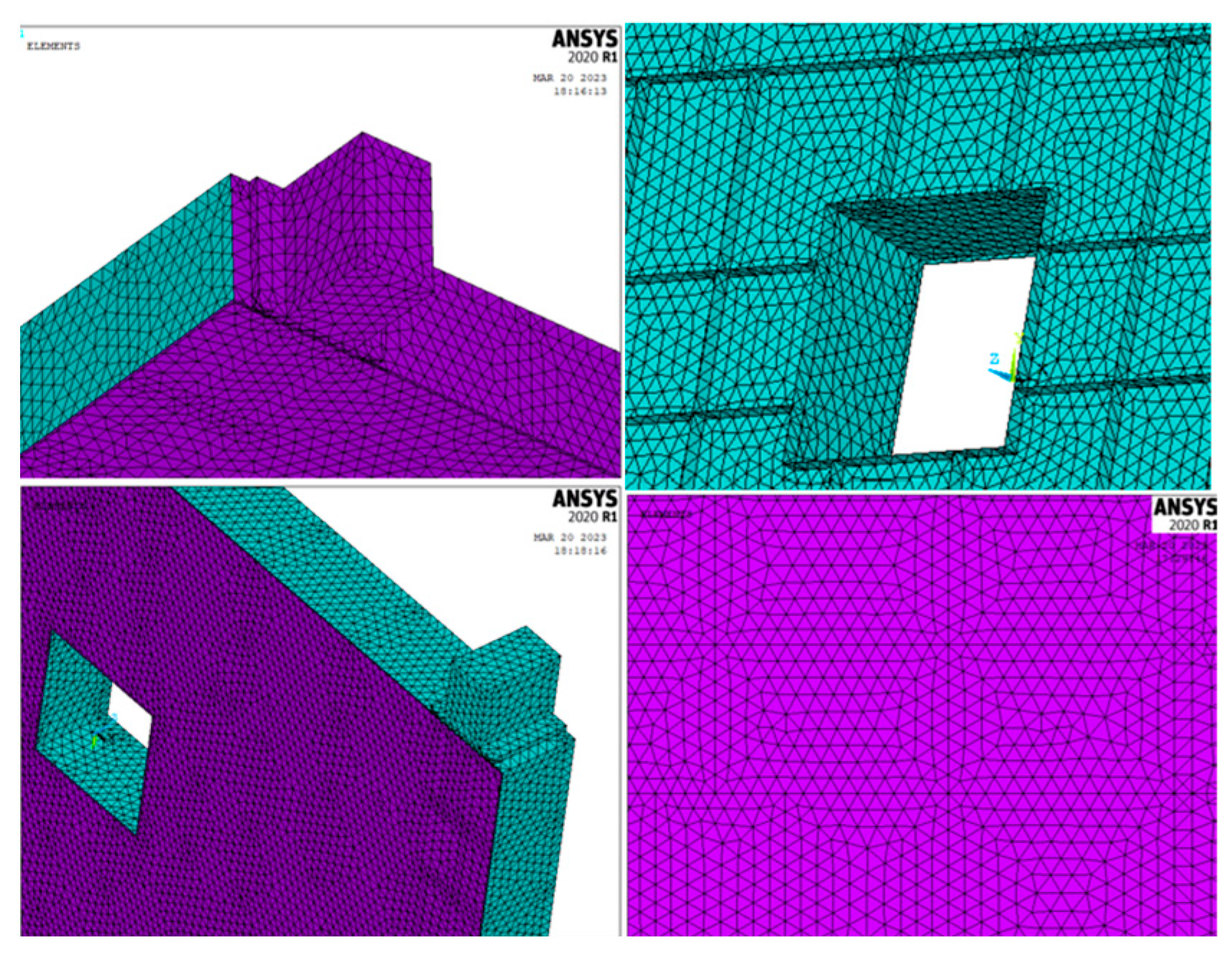

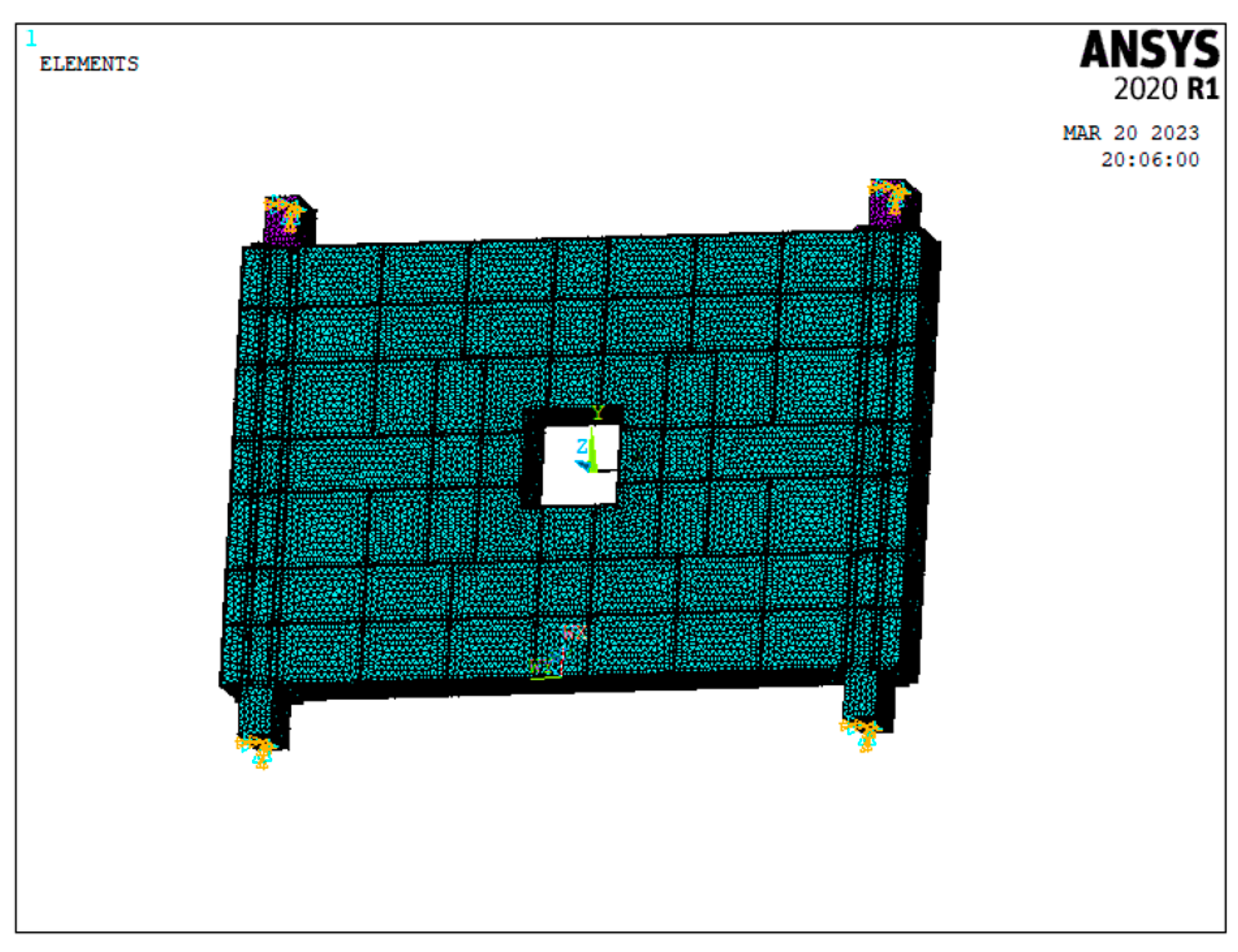


| Parameter | Numerical Value | Parameter | Numerical Value | ||
|---|---|---|---|---|---|
| Total mass | 140 t | Crane rated lifting | 16 t | ||
| Piling capacity | 400 t | Whole machine size | 12.9 10.0 7.38 m3 | ||
| Grounding specific voltage | Longship | 0.119 MPa | Line Size | Longship | 3.3 m |
| Shortship | 0.127 MPa | Shortship | 0.8 m | ||
| Pressing piles Speed | Maximum speed | 4.7 m/min | Stake size | Square pile | 250, 300, 400 mm |
| Minimum speed | 1.3 m/min | Round pile | 300, 400, 500 mm | ||
| Parameter Name | Quality Sensitivity | Parameter Name | Quality Sensitivity |
|---|---|---|---|
| R1 | 0.94 | R4 | 0.21 |
| R2 | 0.16 | R5 | 0.23 |
| R3 | 0.12 | R6 | 0.12 |
| Parameter Name | Displacement Sensitivity | Parameter Name | Displacement Sensitivity |
|---|---|---|---|
| R1 | −0.95 | R4 | 0.04 |
| R2 | 0.21 | R5 | −0.21 |
| R3 | −0.02 | R6 | 0.05 |
| Parameter Name | Stress Sensitivity | Parameter Name | Stress Sensitivity |
|---|---|---|---|
| R1 | −0.95 | R4 | −0.08 |
| R2 | 0.21 | R5 | −0.22 |
| R3 | −0.04 | R6 | 0.03 |
| Variable Name | Thickness before Optimization /m | Optimized Thickness /m | Thickness after Rounding /m |
|---|---|---|---|
| R1 | 0.04 | 0.03 | 0.03 |
| R3 | 0.03 | 0.02 | 0.02 |
| R4 | 0.035 | 0.025 | 0.025 |
| R5 | 0.05 | 0.0599979 | 0.06 |
| R6 | 0.06 | 0.0500 | 0.05 |
| Maximum Stress /Mpa | Mass /kg | Maximum Displacement /m | |||
|---|---|---|---|---|---|
| Before optimization | After optimization | Before optimization | After optimization | Before optimization | After optimization |
| 110 | 162 | 82,556.1 | 64,282.6 | 0.00201 | 0.00326 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Yang, Y.; Hu, J. Optimization of Pile Driver Frame Based on Sensitivity Analysis. Appl. Sci. 2023, 13, 4774. https://doi.org/10.3390/app13084774
Wu J, Yang Y, Hu J. Optimization of Pile Driver Frame Based on Sensitivity Analysis. Applied Sciences. 2023; 13(8):4774. https://doi.org/10.3390/app13084774
Chicago/Turabian StyleWu, Jinmei, Yanqing Yang, and Jiameng Hu. 2023. "Optimization of Pile Driver Frame Based on Sensitivity Analysis" Applied Sciences 13, no. 8: 4774. https://doi.org/10.3390/app13084774
APA StyleWu, J., Yang, Y., & Hu, J. (2023). Optimization of Pile Driver Frame Based on Sensitivity Analysis. Applied Sciences, 13(8), 4774. https://doi.org/10.3390/app13084774





