Experimental Investigation and Theoretical Prediction Model of Flexural Bearing Capacity of Pre-Cracked RC Beams
Abstract
:1. Introduction
2. Experimental Programs
2.1. Specimen Design
2.2. Loading and Measuring-Point Arrangement
3. Experimental Results and Discussion
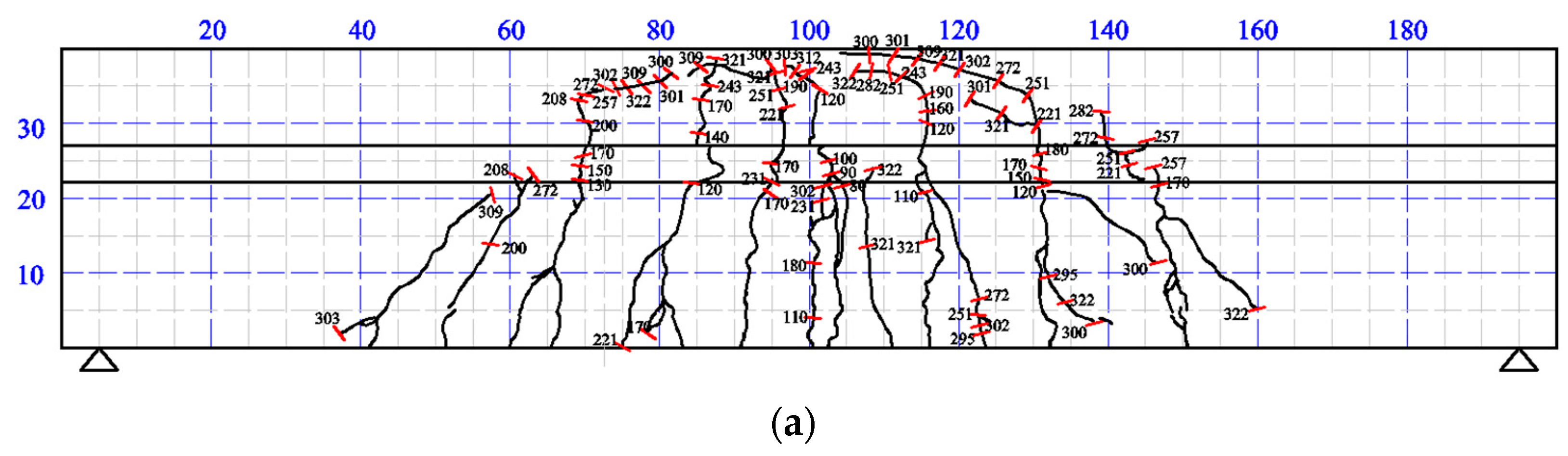
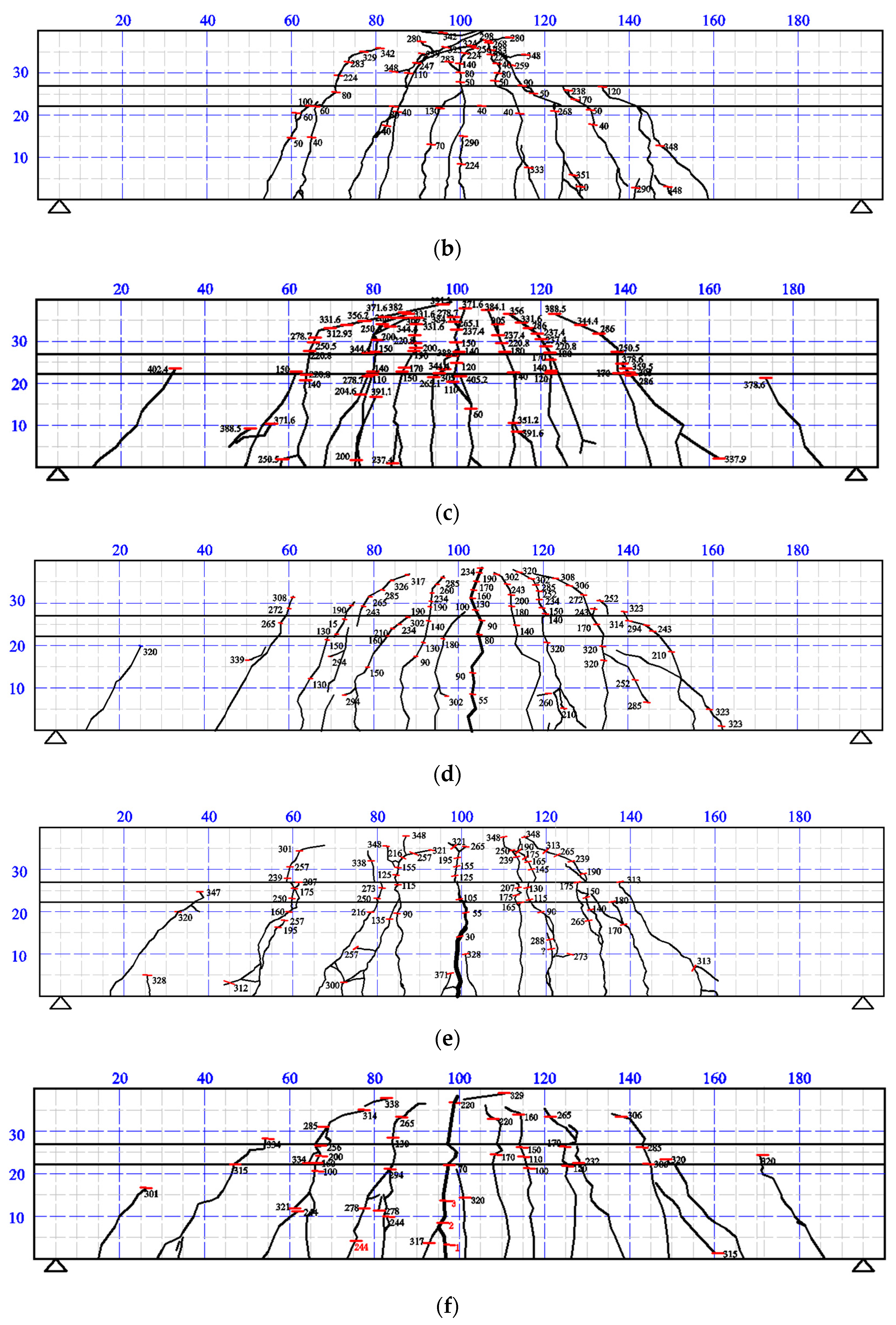
3.1. Crack Distribution and Failure Mode
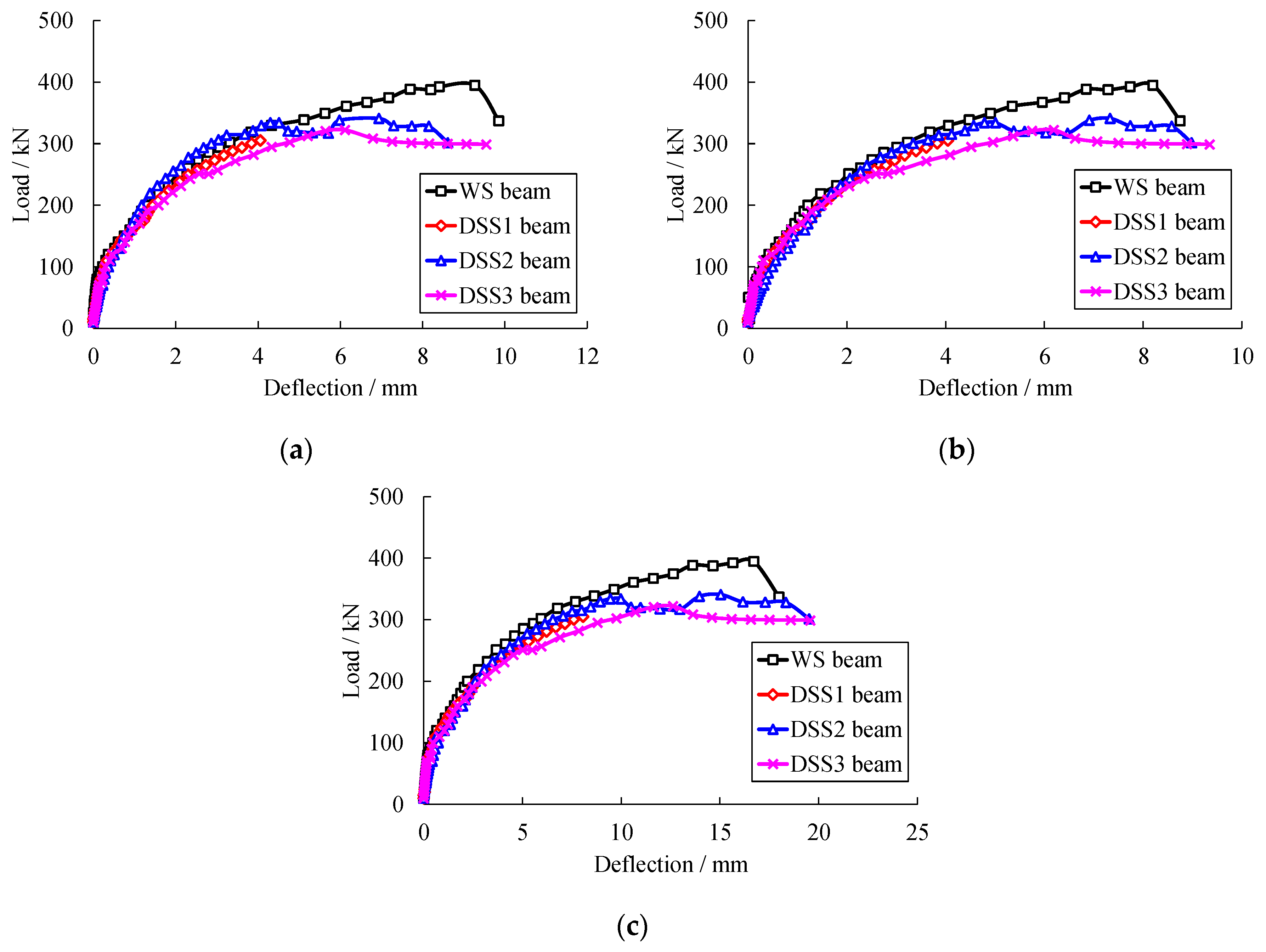
3.2. Load-Deflection Curves
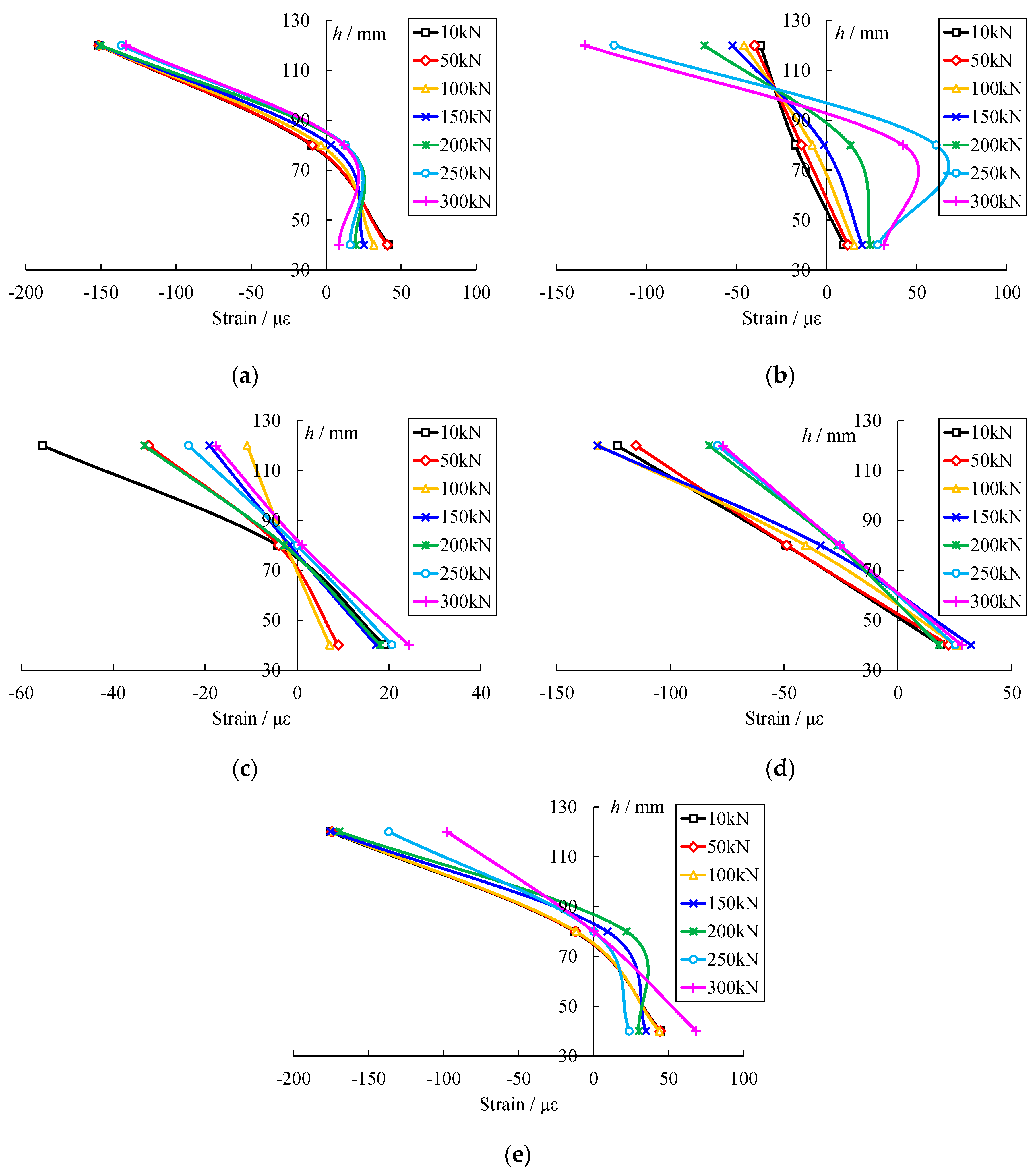
3.3. Strain Distribution of Concrete and Reinforcing Steel
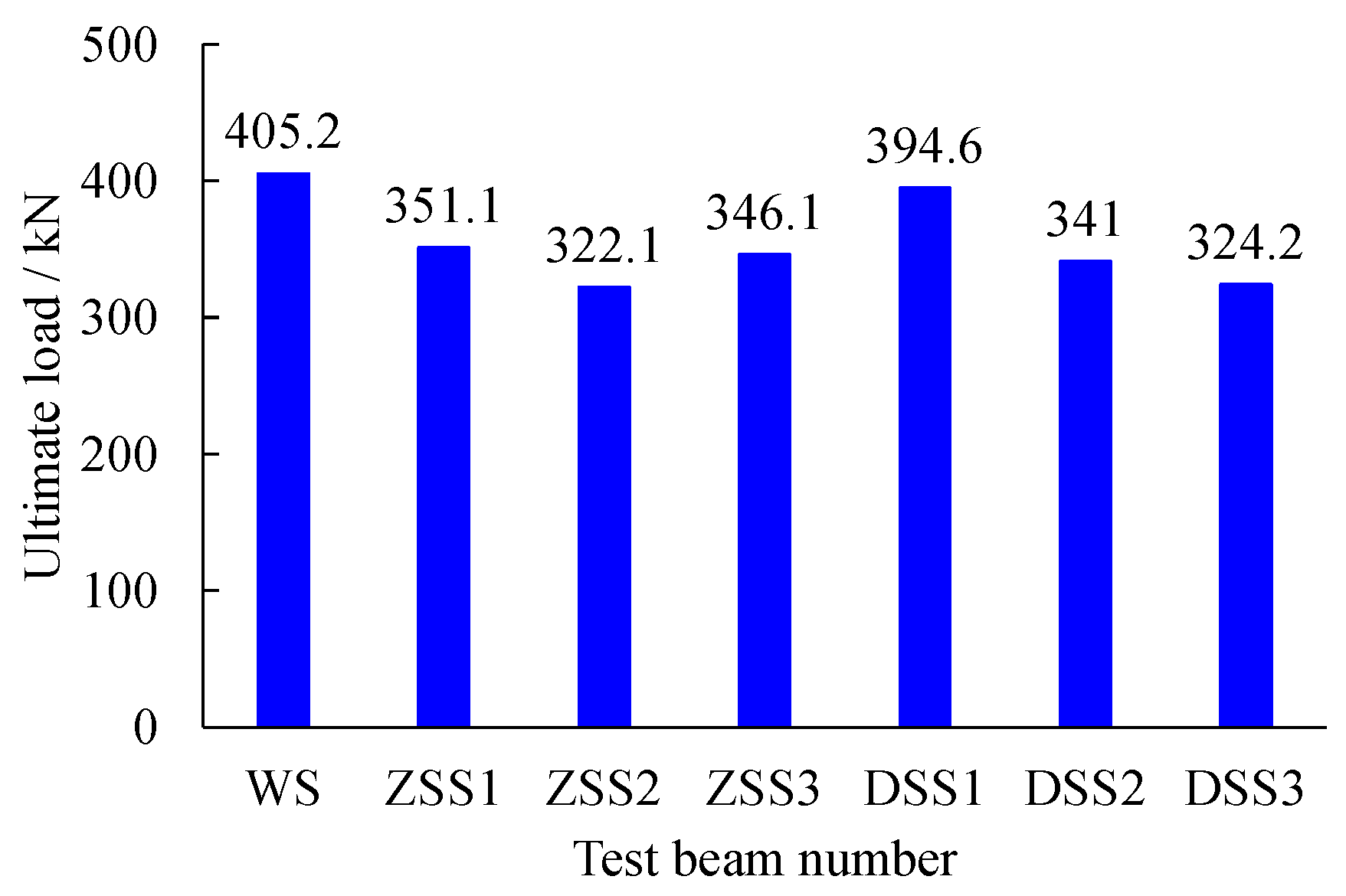
3.4. The Cracking Load and Ultimate Load
4. FE Numerical Model of Pre-Cracked Beam
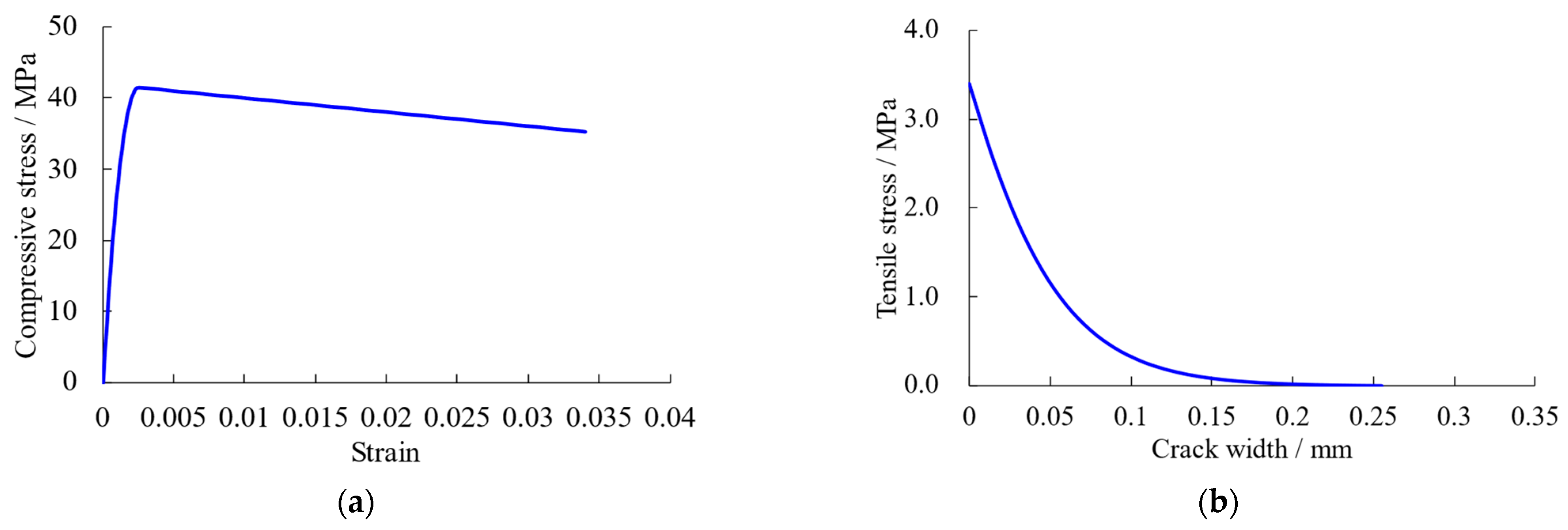
4.1. Overview of FE Numerical Models
4.2. Numerical Simulation Results
5. Theoretical Model of Flexural Bearing Capacity of Pre-Cracked Beam
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| σc | the compressive stress of concrete |
| Ec | the elastic modulus of concrete |
| εc | the compressive strain of concrete |
| fc | the compressive strength of the concrete cylinder |
| k | the plasticity value |
| η | the ratio of strain to peak strain |
| σt | the tensile stress of concrete |
| ft | the tensile strength of concrete |
| w | the crack width |
| wc | the crack width when the stress is completely released |
| c1, c2 | the constant items |
| dc | the compression damage factor |
| dt | the tension damage factor |
| εcpl | the plastic strain |
| wpl | the plastic crack width |
| bc, bt | the constant items |
| ξn | the height of the relative boundary compression zone |
| h0 | the height of the current section from the neutral axis |
| εs | the rebar strain |
| εtu | the section strain in the tension zone |
| htu | the height of the current section from the neutral axis |
| σ0 | the peak stress in the elastic stage of concrete |
| φ | the geometric parameters |
| b | the width of the cross section |
| fy | the tensile design strength of reinforcement |
| ρ | the reinforcement ratio |
| h | the height of the beam |
| Mu | the ultimate bending moment |
| α | the influence coefficient which relates to support conditions and load forms |
| l | the calculated span |
| f | the mid-span deflection |
| M | the mid-span bending moment |
| B | the bending stiffness |
| Pu | the vertical concentrated load |
| l | the calculation span of the simply supported beam |
| h | the height of the cross section |
| c | the thickness of the concrete protection layer |
| hc | the height of the prefabricated crack |
| η | the impact factor of the prefabricated crack |
References
- Giuriani, E.; Plizzari, G.A. Interrelation of splitting and flexural cracks in RC beams. J. Struct. Eng. 1998, 124, 1032–1049. [Google Scholar] [CrossRef]
- Ma, Y.; Peng, A.; Su, X.; Wang, L.; Zhang, J. Modeling constitutive relationship of steel bar removed from corroded PC beams after fatigue considering spatial location effect. J. Mater. Civ. Eng. 2021, 33, 04021019. [Google Scholar] [CrossRef]
- Ma, Y.; Guo, Z.; Wang, L.; Zhang, J. Experimental investigation of corrosion effect on bond behavior between reinforcing bar and concrete. Constr. Build. Mater. 2017, 152, 240–249. [Google Scholar] [CrossRef]
- Aasim, B.A.; Karimi, A.K.; Tomiyama, J.; Suda, Y. Horizontal end crack control and load-bearing capacity performance of hollow-type pretensioned girders through experimentally calibrated finite element models. Eng. Sci. Technol. Int. J. 2021, 24, 1262–1271. [Google Scholar] [CrossRef]
- Nasser, H.; Vandewalle, L.; Verstrynge, E. Effect of pre-existing longitudinal and transverse corrosion cracks on the flexural behaviour of corroded RC beams. Constr. Build. Mater. 2022, 319, 126141. [Google Scholar] [CrossRef]
- Triantafyllou, G.G.; Rousakis, T.C.; Karabinis, A.I. Analytical assessment of the bearing capacity of RC beams with corroded steel bars beyond concrete cover cracking. Compos. Part B Eng. 2017, 119, 132–140. [Google Scholar] [CrossRef]
- Hoseinzade, M.; Esfahani, M.; Arbab, F.; Shakiba, M.; Yekrangnia, M. Residual flexural capacity of pre-cracked RC beams exposed to chloride penetration at the sea surface temperature. Constr. Build. Mater. 2022, 343, 128126. [Google Scholar] [CrossRef]
- Zhang, M.; Akiyama, M.; Shintani, M.; Xin, J.; Frangopol, D.M. Probabilistic estimation of flexural loading capacity of existing RC structures based on observational corrosion-induced crack width distribution using machine learning. Struct. Saf. 2021, 91, 102098. [Google Scholar] [CrossRef]
- Ma, Y.; Guo, Z.; Wang, L.; Zhang, J. Probabilistic life prediction for reinforced concrete structures subjected to seasonal corrosion-fatigue damage. J. Struct. Eng. 2020, 146, 04020117. [Google Scholar] [CrossRef]
- Thoma, K. Finite element analysis of experimentally tested RC and PC beams using the cracked membrane model. Eng. Struct. 2018, 167, 592–607. [Google Scholar] [CrossRef]
- Minh, H.; Mutsuyoshi, H.; Niitani, K. Influence of grouting condition on crack and load-carrying capacity of post-tensioned concrete beam due to chloride-induced corrosion. Constr. Build. Mater. 2007, 21, 1568–1575. [Google Scholar] [CrossRef]
- Kumar, P.; Kodur, V. Response of prestressed concrete beams under combined effects of fire and structural loading. Eng. Struct. 2021, 246, 113025. [Google Scholar] [CrossRef]
- Gencturk, B.; Hossain, K.; Kapadia, A.; Labib, E.; Mo, Y. Use of digital image correlation technique in full-scale testing of prestressed concrete structures. Measurement 2014, 47, 505–515. [Google Scholar] [CrossRef]
- Wang, C.; Shen, Y.; Zou, Y.; Li, T.; Feng, X. Stiffness degradation characteristics destructive testing and finite-element analysis of prestressed concrete T-beam. Comput. Model. Eng. Sci. 2018, 114, 75–93. [Google Scholar] [CrossRef]
- Jeng, C.; Chao, M.; Chuang, H. Torsion experiment and cracking-torque formulae of hollow prestressed concrete beams. Eng. Struct. 2019, 196, 109325. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, P.; Guo, W.; Gong, X.; Wang, C.; Chen, Y. Controlling roof with potential rock burst risk through different pre-crack length: Mechanism and effect research. J. Cent. South Univ. 2022, 29, 3706–3719. [Google Scholar] [CrossRef]
- Visintin, P.; Oehlers, D.; Wu, C.; Haskett, M. A mechanics solution for hinges in RC beams with multiple cracks. Eng. Struct. 2012, 36, 61–69. [Google Scholar] [CrossRef]
- Lucas, W.; Oehlers, D.; Ali, M. Formulation of a shear resistance mechanism for inclined cracks in RC beams. J. Struct. Eng. 2011, 137, 1480–1488. [Google Scholar] [CrossRef]
- Xie, J.; Li, J.; Lu, Z.; Liu, D.; Huang, P. Effects of pre-existing damage and cyclic overloading on the flexural behaviour of RC beams strengthened with prestressed CFRP plates. Eng. Struct. 2021, 247, 113078. [Google Scholar] [CrossRef]
- Blomfors, M.; Berrocal, C.G.; Lundgren, K.; Zandi, K. Incorporation of pre-existing cracks in finite element analyses of reinforced concrete beams without transverse reinforcement. Eng. Struct. 2021, 229, 116101. [Google Scholar] [CrossRef]
- Hamrat, M.; Bouziadi, F.; Boulekbache, B.; Daouadji, T.; Chergui, S.; Labed, A.; Amziane, S. Experimental and numerical investigation on the deflection behavior of pre-cracked and repaired reinforced concrete beams with fiber-reinforced polymer. Constr. Build. Mater. 2020, 249, 118745. [Google Scholar] [CrossRef]
- Pimanmas, A.; Maekawa, K. Finite element analysis and behaviour of pre-cracked reinforced concrete members in shear. Mag. Concr. Res. 2001, 53, 263–282. [Google Scholar] [CrossRef]
- Ngidi, S.D.; Dundu, M. Composite action of pre-cracked reinforced concrete beams repaired with adhesive bonded steel plates. Structures 2018, 14, 400–408. [Google Scholar] [CrossRef]
- Nie, J.; Cai, C. Deflection of cracked RC beams under sustained loading. J. Struct. Eng. 2000, 126, 708–716. [Google Scholar] [CrossRef]
- Capozucca, R. A reflection on the application of vibration tests for the assessment of cracking in PRC/RC beams. Eng. Struct. 2013, 48, 508–518. [Google Scholar] [CrossRef]
- Kaklauskas, G.; Ghaboussi, J. Stress-strain relations for cracked tensile concrete from RC beam tests. J. Struct. Eng. 2001, 127, 64–73. [Google Scholar] [CrossRef]
- Fayyad, T.; Lees, J. Integrated fracture-based model formulation for RC crack analysis. J. Struct. Eng. 2018, 144, 04018083. [Google Scholar] [CrossRef] [Green Version]
- Davoudi, R.; Miller Gregory, R.; Kutz, J. Structural load estimation using machine vision and surface crack patterns for shear-critical RC beams and slabs. J. Comput. Civ. Eng. 2018, 32, 04018024. [Google Scholar] [CrossRef]
- Pimanmas, A.; Tisavipat, J. Effect of existing cracks on shear failure behaviour of reinforced concrete members. Mag. Concr. Res. 2005, 57, 485–495. [Google Scholar] [CrossRef]
- Faron, A.; Rombach, G. Simulation of crack growth in reinforced concrete beams using extended finite element method. Eng. Fail. Anal. 2020, 116, 104698. [Google Scholar] [CrossRef]
- Cervenka, V.; Rimkus, A.; Gribniak, V.; Cervenka, J. Simulation of the crack width in reinforced concrete beams based on concrete fracture. Theor. Appl. Fract. Mech. 2022, 121, 103428. [Google Scholar] [CrossRef]
- Jiki, P. Buckling analysis of pre-cracked beam-columns by Liapunov’s second method. Eur. J. Mech. A/Solids 2007, 26, 503–518. [Google Scholar] [CrossRef]
- Ma, Y.; He, Y.; Wang, G.; Wang, L.; Zhang, J.; Lee, D. Corrosion fatigue crack growth prediction of bridge suspender wires using Bayesian gaussian process. Int. J. Fatigue 2023, 168, 107377. [Google Scholar] [CrossRef]
- Ismail, Z.; Kuan, K.; Yee, K.; Chao, O. Examining the trend in loss of flexural stiffness of simply supported RC beams with various crack severity using model updating. Measurement 2014, 50, 43–49. [Google Scholar] [CrossRef]
- Castel, A.; Gilbert, R.; Ranzi, G. Instantaneous stiffness of cracked reinforced concrete including steel-concrete interface damage and long-term effects. J. Struct. Eng. 2014, 140, 04014021. [Google Scholar] [CrossRef]
- Yu, K.; Zhang, C.; Shooshtarian, M.; Zhao, W.; Shu, J. Automated finite element modeling and analysis of cracked reinforced concrete beams from three dimensional point cloud. Structural concrete. J. FIB 2021, 22, 3213–3227. [Google Scholar] [CrossRef]
- Qu, Y.; Li, X.; Kong, X.; Zhang, W.; Wang, X. Numerical simulation on dynamic behavior of reinforced concrete beam with initial cracks subjected to air blast loading. Eng. Struct. 2016, 128, 96–110. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Peng, A.; Wang, L.; Dai, L.; Zhang, J. Structural performance degradation of cable-stayed bridges subjected to cable damage: Model test and theoretical prediction. Struct. Infrastruct. Eng. 2021, in press. [Google Scholar] [CrossRef]
- Zheng, S.; Liu, Y.; Yoda, T.; Lin, W. Parametric study on shear capacity of circular-hole and long-hole perfobond shear connector. J. Constr. Steel Res. 2016, 117, 64–80. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture and Building Press: Beijing, China, 2015. (In Chinese)
- JTG 3362-2018; Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridge and Culverts. China Communications Press: Beijing, China, 2018. (In Chinese)
- Ma, Y.; Wang, G.; Su, X.; Wang, L.; Zhang, J. Experimental and modelling of the flexural performance degradation of corroded RC beams under fatigue load. Constr. Build. Mater. 2018, 191, 994–1003. [Google Scholar] [CrossRef]
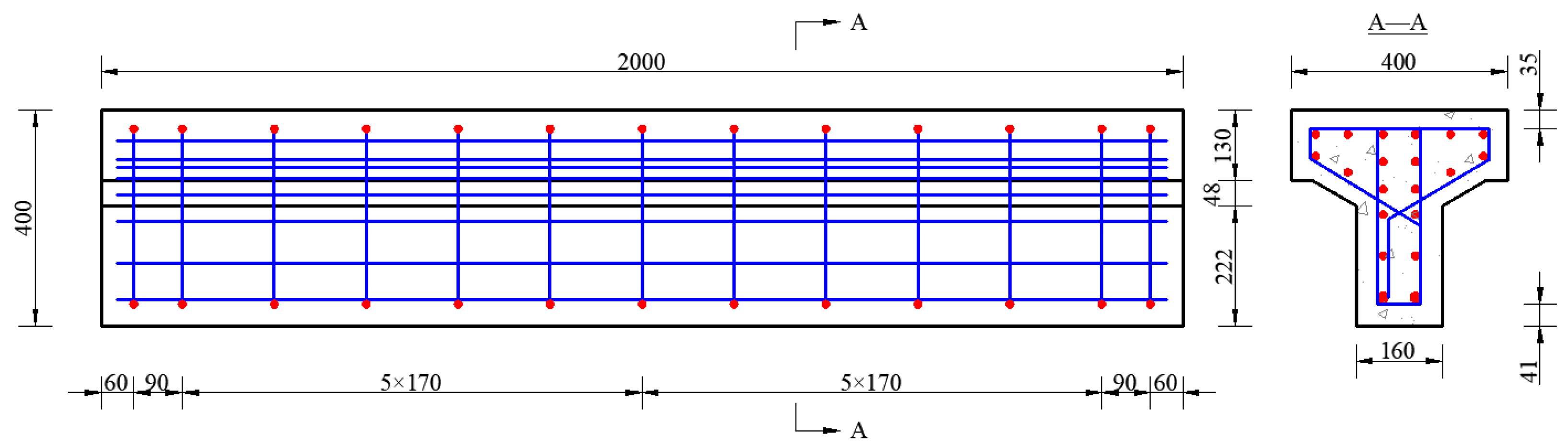
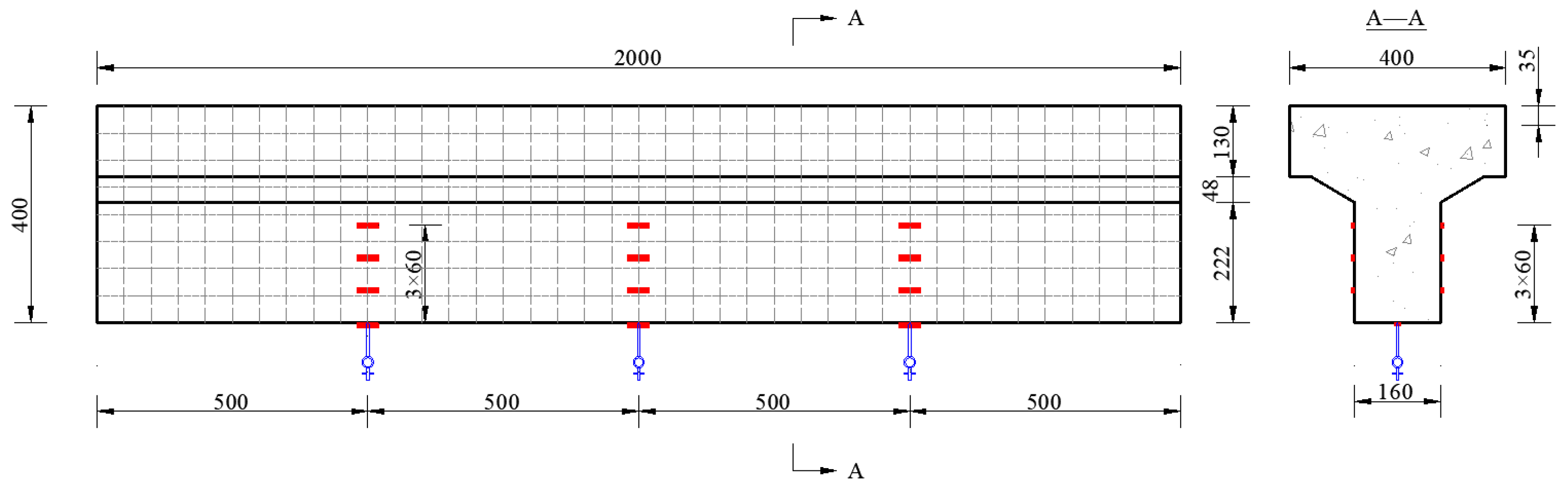









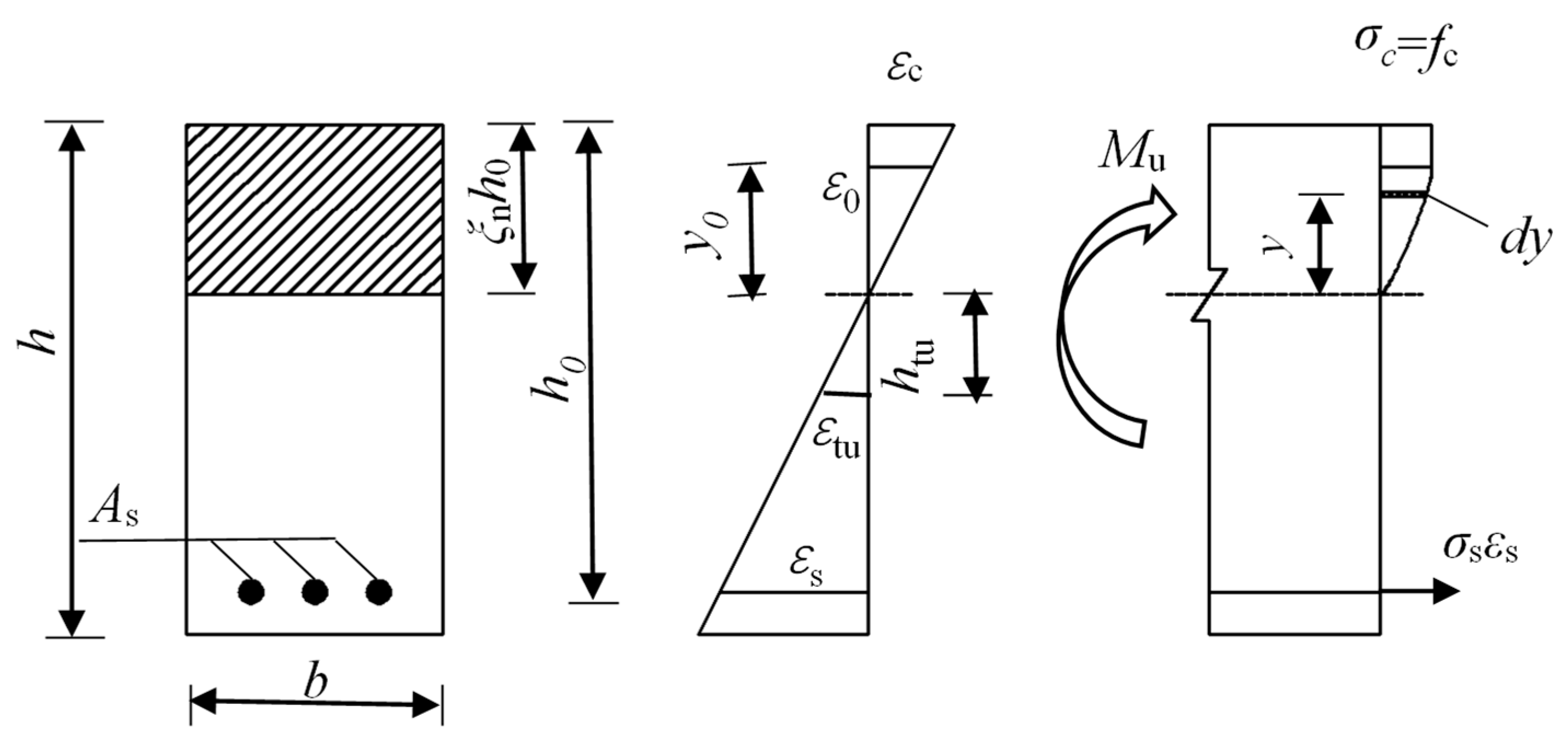
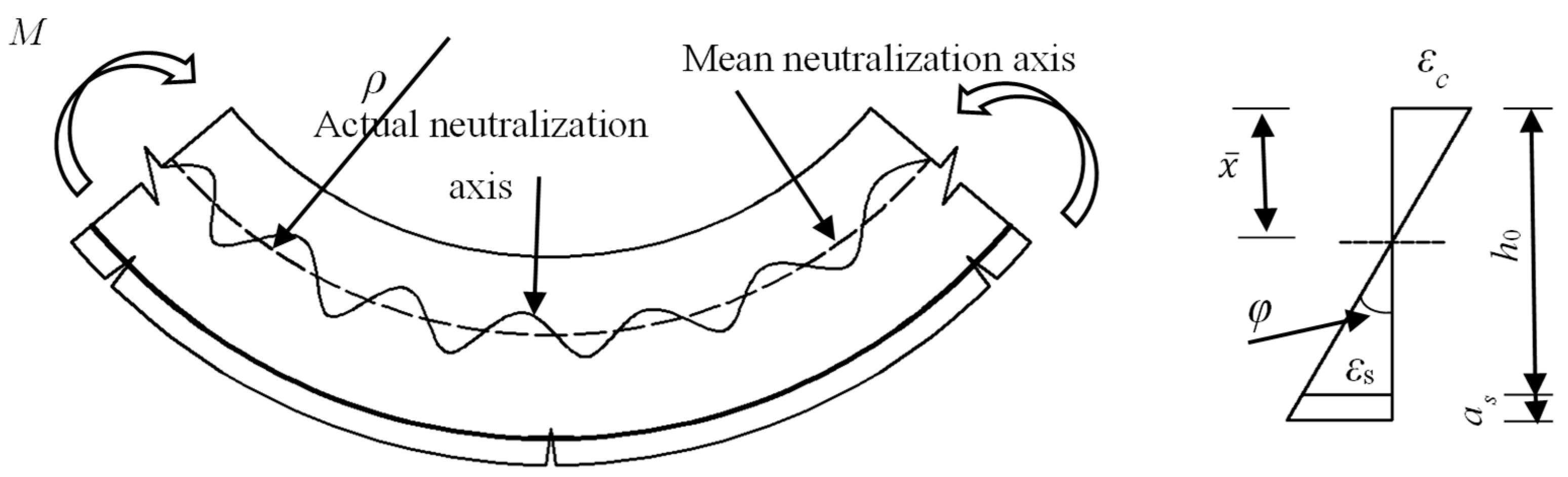


| Number of Test Beam | Location of Crack | Depth of Crack/mm | Diameter of Steel Bar at Crack/mm |
|---|---|---|---|
| WS | - | - | - |
| ZSS1 | mid-span | 20 | 12 |
| ZSS2 | mid-span | 60 | 12 |
| ZSS3 | mid-span | 60 | 10 |
| DSS1 | l/4 position | 20 | 12 |
| DSS2 | l/4 position | 60 | 12 |
| DSS3 | l/4 position | 60 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Yan, D. Experimental Investigation and Theoretical Prediction Model of Flexural Bearing Capacity of Pre-Cracked RC Beams. Appl. Sci. 2023, 13, 4775. https://doi.org/10.3390/app13084775
Zhou S, Yan D. Experimental Investigation and Theoretical Prediction Model of Flexural Bearing Capacity of Pre-Cracked RC Beams. Applied Sciences. 2023; 13(8):4775. https://doi.org/10.3390/app13084775
Chicago/Turabian StyleZhou, Shuming, and Donghuang Yan. 2023. "Experimental Investigation and Theoretical Prediction Model of Flexural Bearing Capacity of Pre-Cracked RC Beams" Applied Sciences 13, no. 8: 4775. https://doi.org/10.3390/app13084775
APA StyleZhou, S., & Yan, D. (2023). Experimental Investigation and Theoretical Prediction Model of Flexural Bearing Capacity of Pre-Cracked RC Beams. Applied Sciences, 13(8), 4775. https://doi.org/10.3390/app13084775





