Thermo-Mechanical Buckling and Non-Linear Free Oscillation of Functionally Graded Fiber-Reinforced Composite Laminated (FG-FRCL) Beams
Abstract
1. Introduction
2. Theoretical Problem
3. Solution of the Nonlinear Problem
3.1. The Galerkin Method
3.2. Approximate Analytical Solution for Nonlinear Oscillation
3.3. Thermal Buckling Temperature
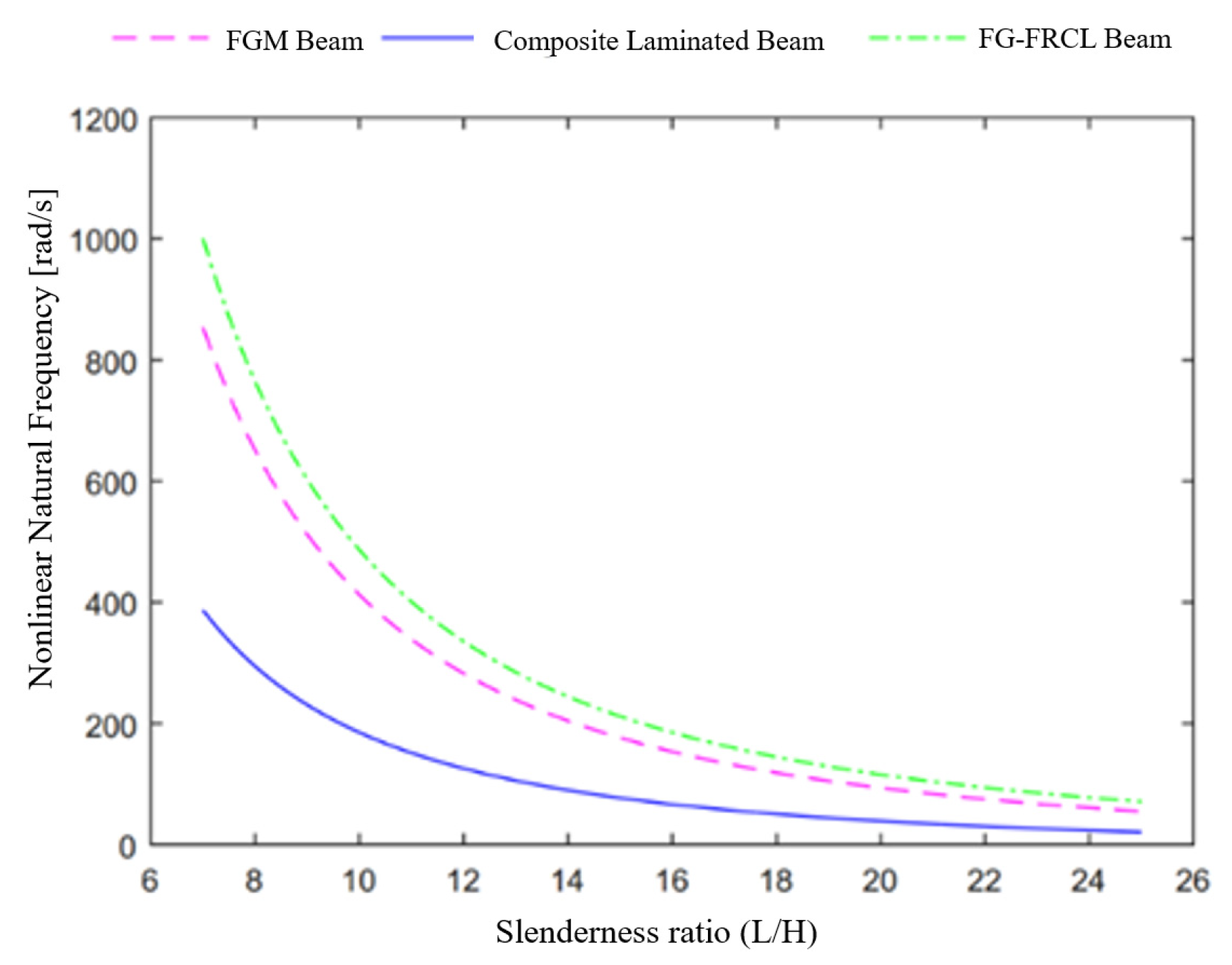
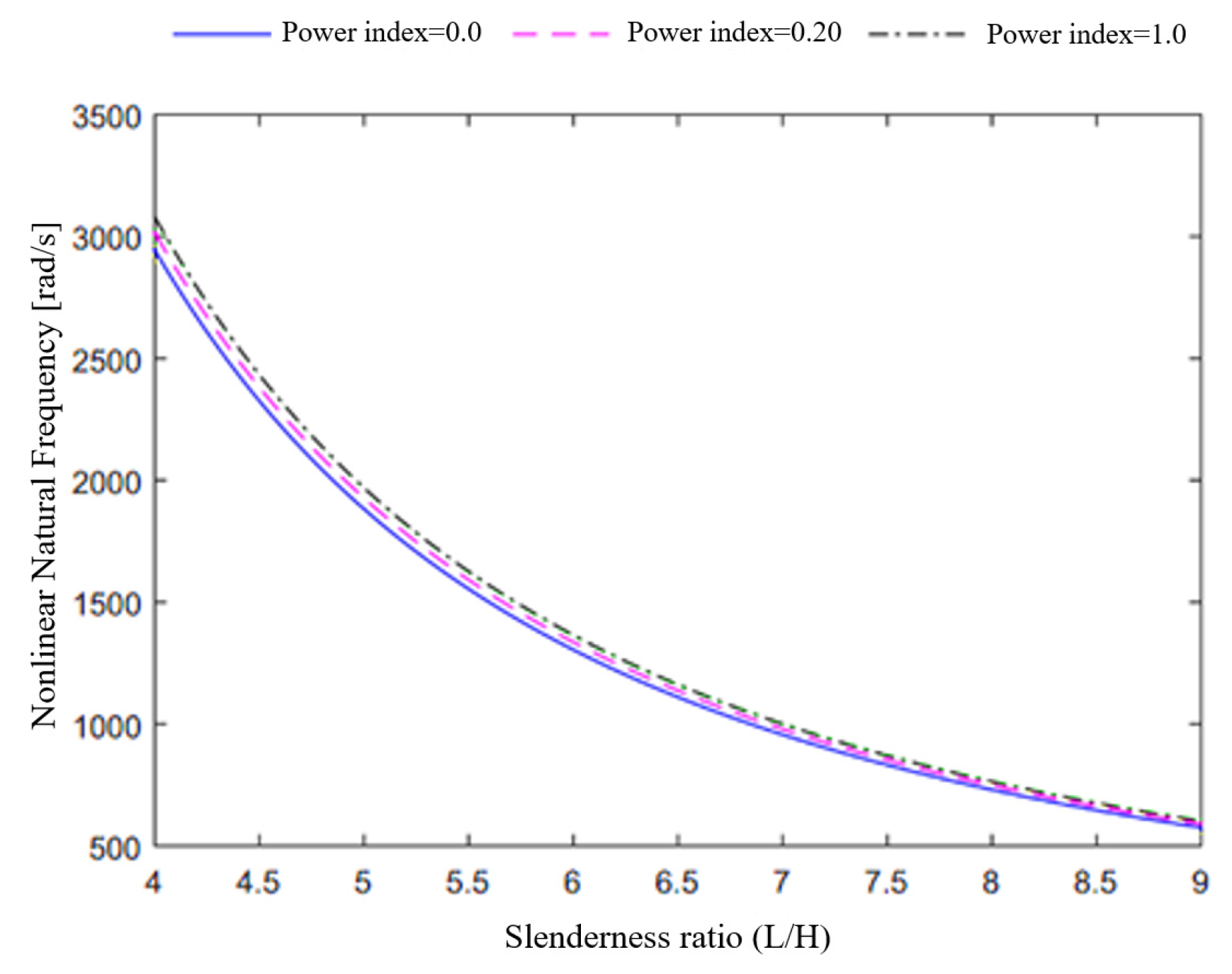
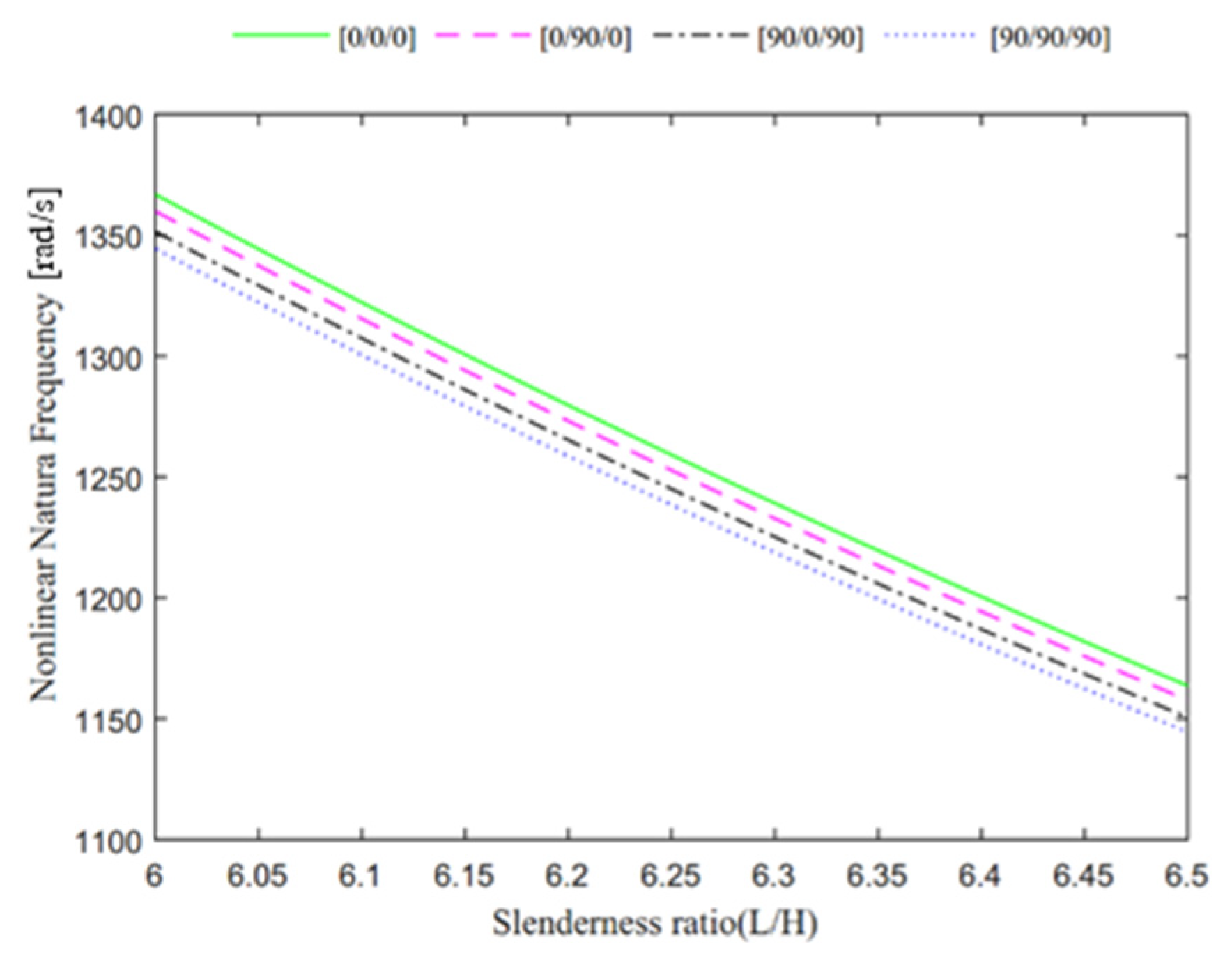
4. Numerical Results
5. Conclusions
- (1)
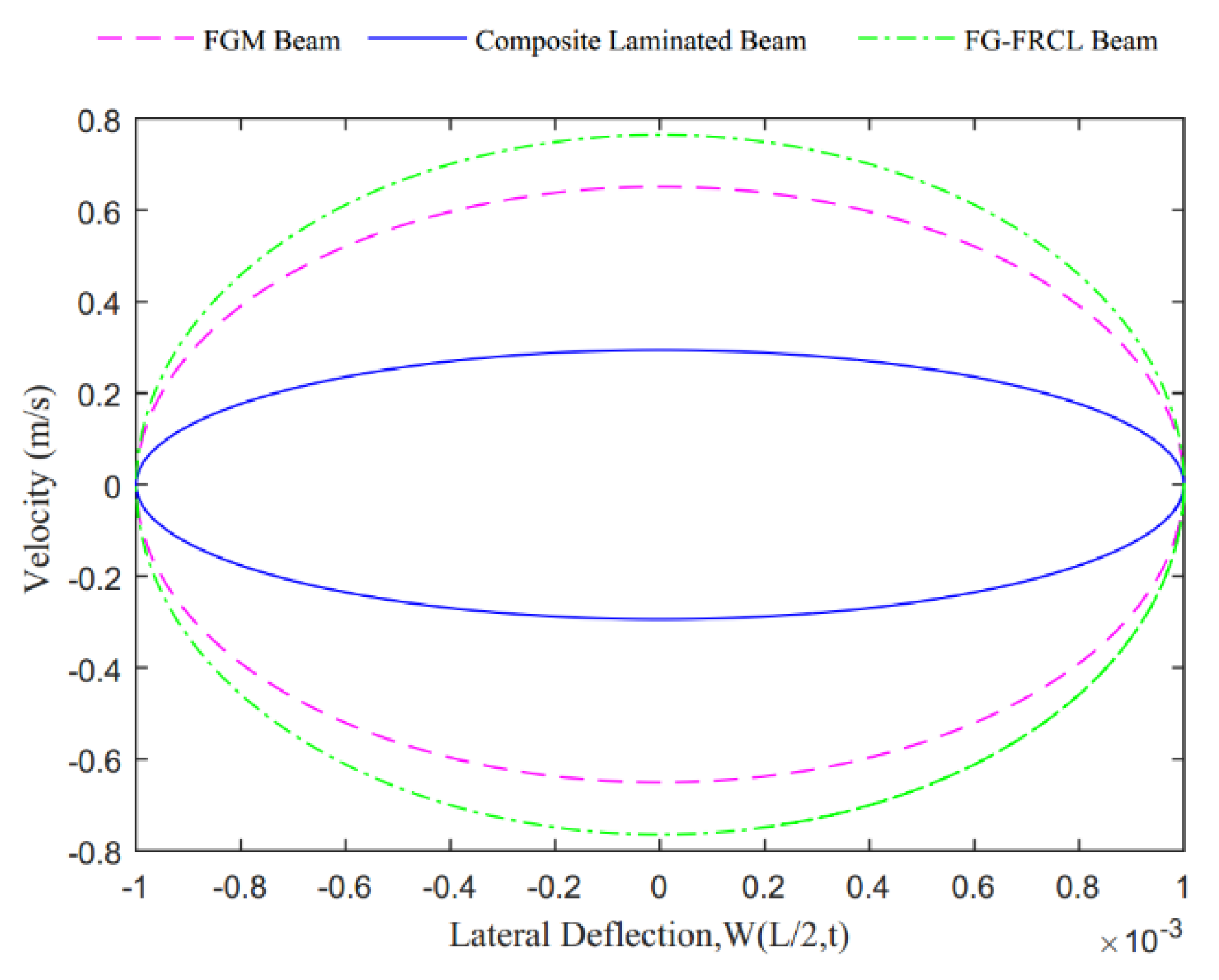
- FG-FRCL beams showed the highest nonlinear natural frequency response, followed by FGM beams and composite laminated beams;
- (2)
- The nonlinear fundamental frequency increased for an increased power index, whose effect became more pronounced for lower slenderness ratios;
- (3)
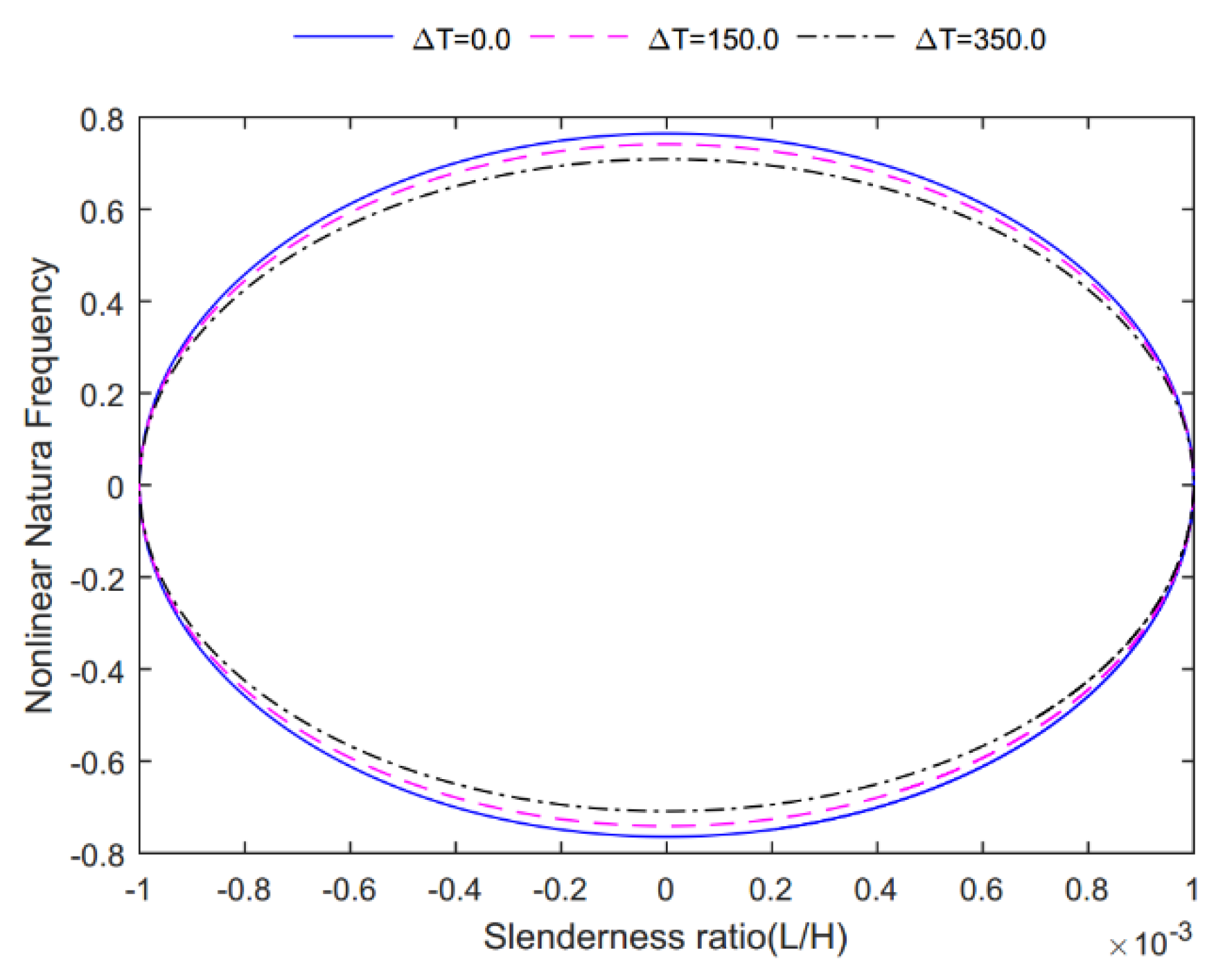
- The fundamental frequency decreased for an increased temperature, especially for higher slenderness ratios;
- (4)
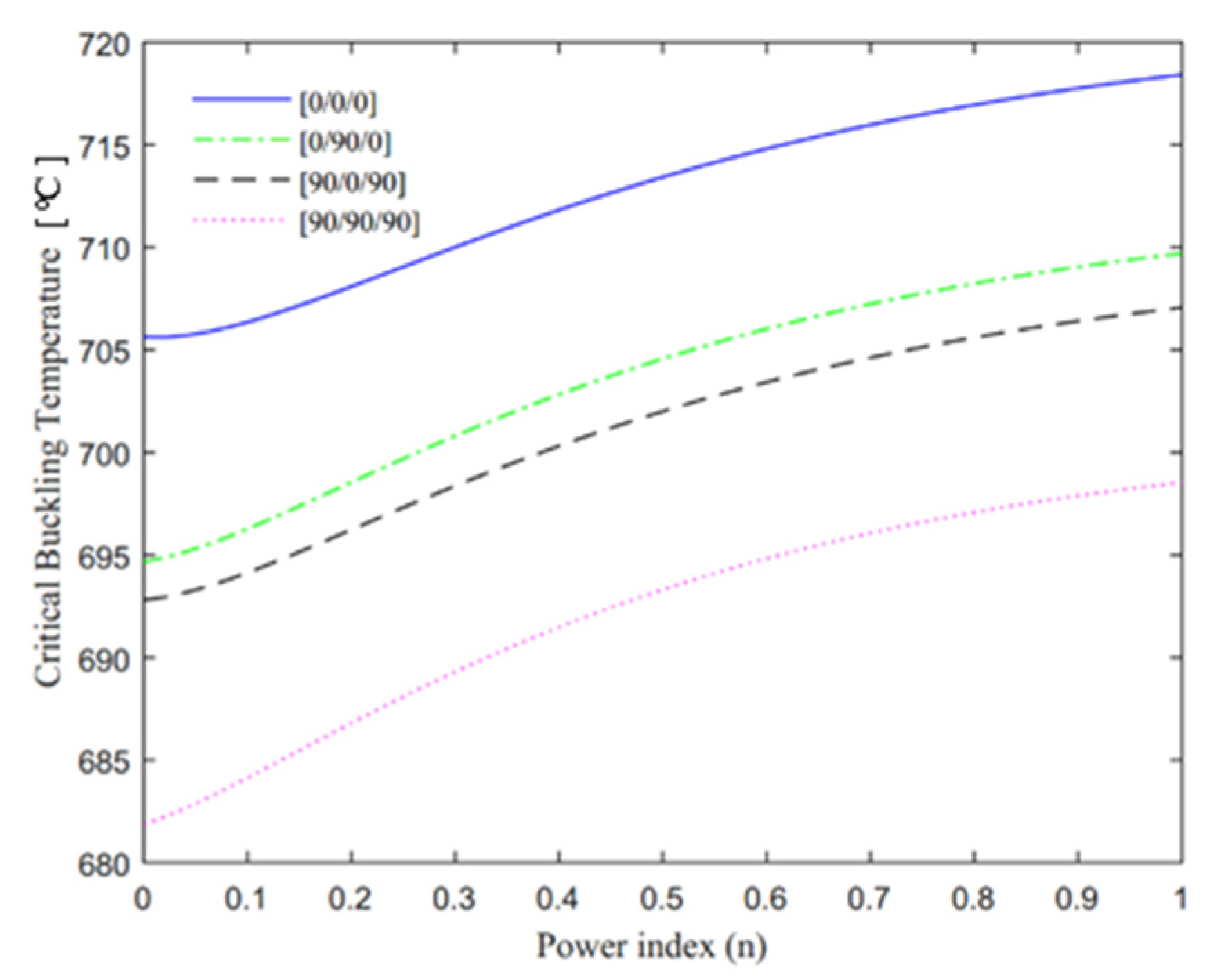
- Based on a parametric evaluation of the response for different reinforcement lay-ups, FG-FRCL beams with [0/0/0] lay-ups showed the highest nonlinear natural frequency and thermal buckling temperature, followed by [0/90/0], [90/0/90] and [90/90/90] lay-ups, in sequence;
- (5)
- An increased power index provided an increased critical buckling temperature of the system, whereas the nonlinear oscillation velocity of FG-FRCL beams assumed the highest value followed by FGM beams and composite laminated beams, which, in turn, featured the lowest oscillation velocity;
- (6)
- An increased power index expanded outward the phase trajectory and yielded an increased oscillation velocity. At the same time, for an increased temperature, the phase trajectory shrank inward and the oscillation velocity decreased, while the system maintained its own stability.
Author Contributions
Funding
Conflicts of Interest
References
- Mohamed, M.; Hussein, R.; Abutunis, A.; Huo, Z.; Chandrashekhara, K.; Sneed, L.H. Manufacturing and evaluation of polyurethane composite structural insulated panels. J. Sandw. Struct. Mat. 2016, 18, 769–789. [Google Scholar] [CrossRef]
- Sobhani Aragh, B.; Yas, M.H. Effect of continuously grading fiber orientation face sheets on vibration of sandwich panels with FGM core. Int. J. Mech. Sci. 2011, 53, 628–638. [Google Scholar] [CrossRef]
- Feli, S.; Jafari, S. Analytical investigation of perforation of aluminum—Foam sandwich panels under ballistic impact. J. Modares Mech. Eng. 2013, 13, 52–59. [Google Scholar]
- Duc, N.D.; Seung-Eock, K.; DucTuan, N.; Tran, P.; DinhKhoa, N. New approach to study nonlinear dynamic response and vibration of sandwich composite cylindrical panels with auxetic honeycomb core layer. Aerosp. Sci. Technol. 2017, 70, 396–404. [Google Scholar] [CrossRef]
- Ameri, B.; Moradi, M.; Talebitooti, R. Effect of Honeycomb Core on Free Vibration Analysis of Fiber Metal Laminate (FML) Beams Compared to Conventional Composites. Compos. Struct. 2021, 261, 113281. [Google Scholar] [CrossRef]
- Arleo, L.; Bondì, G.; Albini, A.; Maselli, M.; Cianchetti, M. Design methodology for the development of variable stiffness devices based on layer jamming transition. Eng. Res. Express 2020, 2, 035033. [Google Scholar] [CrossRef]
- Tornabene, F.; Viscoti, M.; Dimitri, R.; Aiello, M.A. Higher order formulations for doubly-curved shell structures with a honeycomb core. Thin-Wall. Struct. 2021, 164, 107789. [Google Scholar] [CrossRef]
- Duc, N.D.; Cong, P.H. Nonlinear vibration of thick FGM plates on elastic foundation subjected to thermal and mechanical loads using the first-order shear deformation plate theory. Cogent Eng. 2015, 2, 1045222. [Google Scholar]
- Shen, H.-S. A comparison of buckling and postbuckling behavior of FGM plates with piezoelectric fiber reinforced composite actuators. Compos. Struct. 2009, 91, 375–384. [Google Scholar] [CrossRef]
- Kiani, Y.; Eslami, M.R. Thermal buckling and post-buckling response of imperfect temperature-dependent sandwich FGM plates resting on elastic foundation. Arch. Appl. Mech. 2012, 82, 891–905. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.H. Thermomechanical vibration and stability of effectively homogenized FGM beam with temperature-dependent shear correction factors. J. Compos. Mat. 2023, 57, 253–264. [Google Scholar] [CrossRef]
- Arioui, O.; Belakhdar, K.; Kaci, A.; Tounsi, A. Thermal buckling of FGM beams having parabolic thickness variation and temperature dependent materials. Steel Compos. Struct. 2018, 27, 777–788. [Google Scholar]
- Iurlaro, L.; Gherlone, M.; Di Sciuva, M. Bending and free vibration analysis of functionally graded sandwich plates using the Refined Zigzag Theory. J. Sandw. Struct. Mater. 2014, 16, 669–699. [Google Scholar] [CrossRef]
- Li, Q.; Iu, V.P.; Kou, K.P. Three-dimensional vibration analysis of functionally graded material sandwich plates. J. Sound Vibr. 2008, 311, 498–515. [Google Scholar] [CrossRef]
- Kong, S.; Zhou, S.; Nie, Z.; Wang, K. The size-dependent natural frequency of Bernoulli–Euler micro-beams. Int. J. Eng. Sci. 2008, 46, 427–437. [Google Scholar] [CrossRef]
- Shojaa, R. A micro scale geometrically non-linear Timoshenko beam model based on strain gradient elasticity theory. Int. J. Nonlinear Mech. 2012, 47, 863–873. [Google Scholar]
- Fernandes, R.; Mousavi, S.M.; El-Borgi, S. Free and forced vibration nonlinear analysis of a microbeam using finite strain and velocity gradients theory. Acta Mech. 2016, 227, 2657–2670. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Jafari, A. A higher-order thermomechanical vibration analysis of temperature-dependent FGM beams with porosities. J. Eng. 2016, 2016, 9561504. [Google Scholar] [CrossRef]
- Dabbagh, A.; Rastgoo, A.; Ebrahimi, F. Thermal buckling analysis of agglomerated multiscale hybrid nanocomposites via a refined beam theory. Mech. Based Des. Struct. Mach. 2021, 49, 403–429. [Google Scholar] [CrossRef]
- Khorasani, M.; Lampani, L.; Dimitri, R.; Tornabene, F. Thermomechanical Buckling Analysis of the E&P-FGM Beams Integrated by Nanocomposite Supports Immersed in a Hygrothermal Environment. Molecules 2021, 26, 6594. [Google Scholar]
- Founda, N.; El-midany, T.; Sadoun, A.M. Bending, Buckling and Vibration of a Functionally Graded Porous Beam Using Finite Elements. J. Appl. Comput. Mech. 2017, 3, 274–282. [Google Scholar]
- Kamarian, S.; Salim, M.; Dimitri, R.; Tornabene, F. Free vibration analysis of conical shells reinforced with agglomerated Carbon Nanotubes. Int. J. Mech. Sci. 2016, 108–109, 157–165. [Google Scholar] [CrossRef]
- Zhang, L.; Lai, S.; Wang, C.; Yang, J. DSC regularized Dirac-delta method for dynamic analysis of FG graphene platelet-reinforced porous beams on elastic foundation under a moving load. Compos. Struct. 2021, 255, 112865. [Google Scholar] [CrossRef]
- Chen, Y.; Fu, Y.; Zhong, J.; Tao, C. Nonlinear dynamic responses of fiber-metal laminated beam subjected to moving harmonic loads resting on tensionless elastic foundation. Comp. Part B Eng. 2017, 15, 131, 253–259. [Google Scholar] [CrossRef]
- Xiao, B.J.; Li, X.F. Exact solution of buckling load of axially exponentially graded columns and its approximation. Mech. Res. Commun. 2019, 101, 103414. [Google Scholar] [CrossRef]
- Li, S.-R.; Batra, R.C. Relations between buckling loads of functionally graded Timoshenko and homogeneous Euler–Bernoulli beams. Compos. Struct. 2013, 95, 5–9. [Google Scholar] [CrossRef]
- Huang, Y.; Li, X.-F. Buckling Analysis of Nonuniform and Axially Graded Columns with Varying Flexural Rigidity. J. Eng. Mech. 2011, 137, 73–81. [Google Scholar] [CrossRef]
- von Kármán, T.; Dunn, L.G.; Tsien, H. The influence of curvature on the buckling characteristics of structures. J. Aeron. Sci. 1940, 7, 276–289. [Google Scholar] [CrossRef]
- von Kármán, T.; Tsien, H. The buckling of thin cylindrical shells under axial compression. J. Aeron. Sci. 1941, 8, 303–312. [Google Scholar] [CrossRef]
- Mandal, P.; Calladine, C.R. Buckling of thin cylindrical shells under axial compression. Int. J. Solids Struct. 2000, 37, 4509–4525. [Google Scholar] [CrossRef]
- Mahaffey, P.B. Bending, Vibration and Buckling Response of Conventional and Modified Euler-Bernoulli and Timoshenko Beam Theories Accounting for the von Karman Geometric Nonlinearity. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2013. [Google Scholar]
- Daniel, I.M.; Ishai, O.; Daniel, I.M.; Daniel, I. Engineering Mechanics of Composite Materials; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Xiang, H.J.; Yang, J. Free and forced vibration of a laminated FGM Timoshenko beam of variable thickness under heat conduction. Comp. Part B Eng. 2008, 39, 292–303. [Google Scholar] [CrossRef]
- Chen, W.J.; Li, X.P. Size-dependent free vibration analysis of composite laminated Timoshenko beam based on new modified couple stress theory. Arch. Appl. Mech. 2013, 83, 431–444. [Google Scholar] [CrossRef]
- Mohammad-Abadi, M.; Daneshmehr, A.R. Modified couple stress theory applied to dynamic analysis of composite laminated beams by considering different beam theories. Int. J. Eng. Sci. 2015, 87, 83–102. [Google Scholar] [CrossRef]
- Samadpour, M.; Asadi, H.; Wang, Q. Nonlinear aero-thermal flutter postponement of supersonic laminated composite beams with shape memory alloys. Eur. J. Mech. A Solids. 2016, 57, 18–28. [Google Scholar] [CrossRef]
- Inman, D.J. Vibration with control. In Computational and Systems Oncology; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Norouzi, H.; Younesian, D. Chaotic vibrations of beams on nonlinear elastic foundations subjected to reciprocating loads. Mech. Res. Commun. 2015, 69, 121–128. [Google Scholar] [CrossRef]
- Şimşek, M. Nonlinear static and free vibration analysis of microbeams based on the nonlinear elastic foundation using modified couple stress theory and He’s variational method. Compos. Struct. 2014, 112, 264–272. [Google Scholar] [CrossRef]
- Laura, P.A.; Pombo, J.L.; Susemihl, E.A. A note on the vibrations of a clamped-free beam with a mass at the free end. J. Sound Vib. 1974, 37, 161–168. [Google Scholar] [CrossRef]
- He, J.-H. Variational approach for nonlinear oscillators. Chaos Solitons Fractals 2007, 34, 1430–1439. [Google Scholar] [CrossRef]
- Ventsel, E.; Krauthammer, T.; Carrera, E.J. Thin plates and shells: Theory, analysis, and applications. Appl. Mech. Rev. 2002, 55, B72–B73. [Google Scholar] [CrossRef]
- Tao, C.; Fu, Y.M.; Dai, H.L. Nonlinear dynamic analysis of fiber metal laminated beams subjected to moving loads in thermal environment. Compos. Struct. 2016, 140, 410–416. [Google Scholar] [CrossRef]
- Wang, C.M.; Ke, L.; Chowdhury, A.R.; Yang, J.; Kitipornchai, S.; Fernando, D. Critical examination of midplane and neutral plane formulations for vibration analysis of FGM beams. Eng. Struct. 2017, 130, 275–281. [Google Scholar] [CrossRef]
- Alimoradzadeh, M.; Akbas, S.D.; Esfrajani, S.M. Nonlinear dynamic and stability of a beam resting on the nonlinear elastic foundation under thermal effect based on the finite strain theory. Struct. Eng. Mech. 2021, 80, 275–284. [Google Scholar]
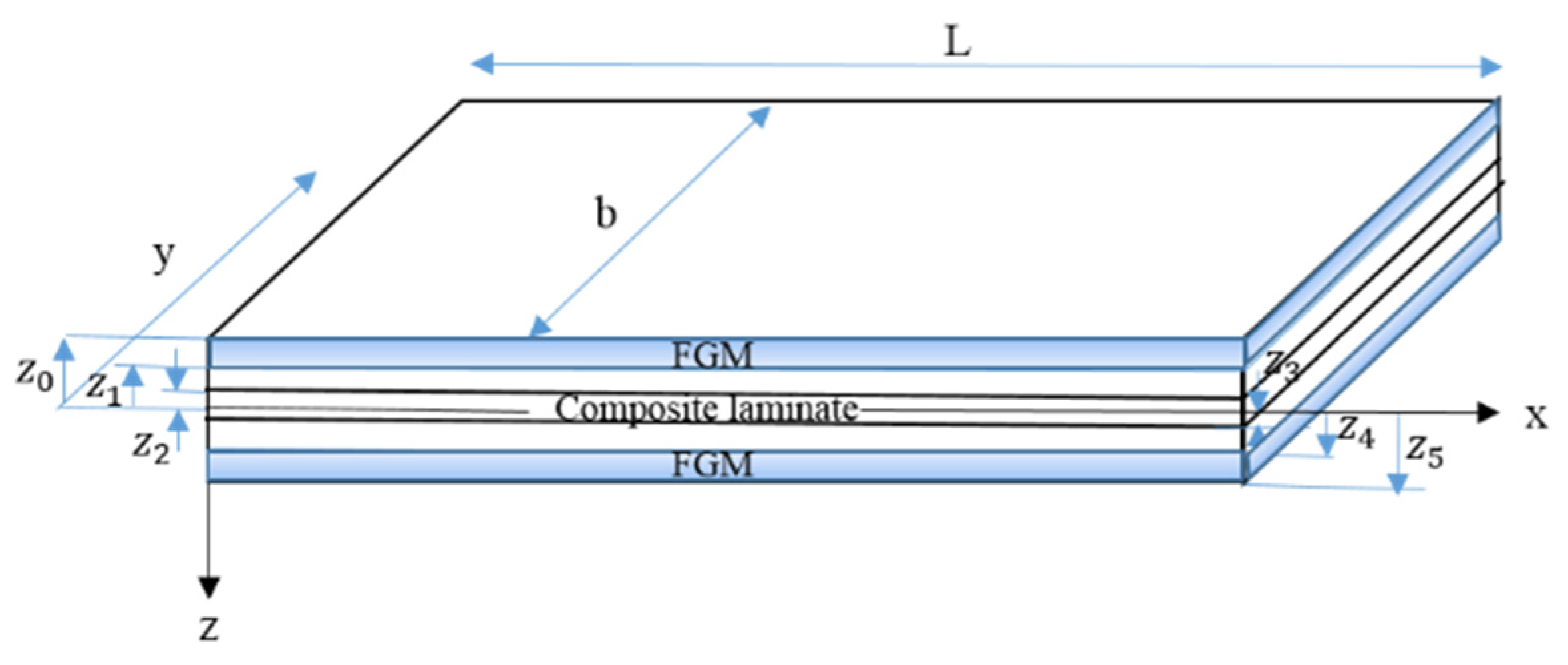


| Material | Properties | |||
|---|---|---|---|---|
| E(GPa) | ||||
| 348.43 | 2370 | 0.24 | 5.8723 × 10−6 | |
| SUS304 | 201.04 | 8166 | 0.3262 | 12.330 × 10−6 |
| Material Properties (Glass-Polymer Composite) | |||||
|---|---|---|---|---|---|
| (GPa) | () | ||||
| 50, 15.2 | 4.7 | 2000.0 | 0.254 | 6.34 × 10−6 | 23.3 × 10−6 |
| Slenderness Ratio | Linear Fundamental Frequency (rad/s) | |
|---|---|---|
| Present Study | Reference [34] | |
| 5.0 | 1370.2 | 1370.2 |
| 10.0 | 342.6 | 342.6 |
| 20.0 | 85.6 | 85.6 |
| 30.0 | 38.1 | 38.1 |
| 40.0 | 21.4 | 21.4 |
| 50.0 | 13.7 | 13.7 |
| Slenderness Ratio | Linear Fundamental Frequency (rad/s) | Nonlinear Fundamental Frequency (rad/s) | ||
|---|---|---|---|---|
| FGM Beam (n = 1) | FGM Beam (n = 0) | |||
| Present Study | Ref. [44] | Present Study | Ref. [45] | |
| 5.0 | 8485.27 | 8485.3 | 5655.3 | 5655.6 |
| 10.0 | 2121.3 | 2121.3 | 1413.8 | 1413.9 |
| 20.0 | 530.3 | 530.3 | 353.5 | 353.5 |
| 30.0 | 235.7 | 235.7 | 157.1 | 157.1 |
| 40.0 | 132.6 | 132.6 | 88.4 | 88.4 |
| 50.0 | 84.9 | 84.9 | 56.6 | 56.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alimoradzadeh, M.; Heidari, H.; Tornabene, F.; Dimitri, R. Thermo-Mechanical Buckling and Non-Linear Free Oscillation of Functionally Graded Fiber-Reinforced Composite Laminated (FG-FRCL) Beams. Appl. Sci. 2023, 13, 4904. https://doi.org/10.3390/app13084904
Alimoradzadeh M, Heidari H, Tornabene F, Dimitri R. Thermo-Mechanical Buckling and Non-Linear Free Oscillation of Functionally Graded Fiber-Reinforced Composite Laminated (FG-FRCL) Beams. Applied Sciences. 2023; 13(8):4904. https://doi.org/10.3390/app13084904
Chicago/Turabian StyleAlimoradzadeh, Mehdi, Habib Heidari, Francesco Tornabene, and Rossana Dimitri. 2023. "Thermo-Mechanical Buckling and Non-Linear Free Oscillation of Functionally Graded Fiber-Reinforced Composite Laminated (FG-FRCL) Beams" Applied Sciences 13, no. 8: 4904. https://doi.org/10.3390/app13084904
APA StyleAlimoradzadeh, M., Heidari, H., Tornabene, F., & Dimitri, R. (2023). Thermo-Mechanical Buckling and Non-Linear Free Oscillation of Functionally Graded Fiber-Reinforced Composite Laminated (FG-FRCL) Beams. Applied Sciences, 13(8), 4904. https://doi.org/10.3390/app13084904








