The Time Variation Law of Concrete Compressive Strength: A Review

Abstract

Concrete is a building material that is most widely used because of its excellent mechanical performance and durability. Compressive strength is an essential property of concrete, which changes with time under various factors. In this paper, the time variation law of the compressive strength of concrete was reviewed from three aspects: single, multiple and material internal factors. The mathematical models of compressive strength relative to time under single factors such as carbonization, freeze–thaw cycle, temperature effect and sulfate attack were summarized. Based on the statistical analysis of laboratory experimental data and field test data, the time variation laws of concrete under the coupling action of two or more factors were analyzed. The results show that the strength loss of concrete under the coupling effect of multiple factors is more serious than under the effect of a single factor. In addition, the time variation models of compressive strength in existing buildings were discussed, and it was observed that there are obvious differences between these models. After analysis, it is known that the different data sources and normalization methods are the primary causes of differences. Finally, the influences of concrete internal factors on compressive strength were outlined. The main conclusions of the time variation law of compressive strength were summarized, and further research directions were also proposed.

1. Introduction

Concrete is one of the most widely used construction materials because of its good strength and durability relative to its cost [1,2,3,4,5,6,7,8,9,10,11,12]. However, it is not an everlasting construction material. Due to the interaction of various factors in the surrounding environment, concrete materials will gradually deteriorate over time, thus reducing their mechanical properties [13,14,15]. Among them, compressive strength is an essential mechanical index of concrete [16,17,18,19,20,21].

Many factors cause variations in the compressive strength of concrete, such as carbonation, temperature effect, chloride ion erosion, freeze–thaw cycle, sulfate attack, etc. [17,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Currently, the research methods for studying the time variation law of compressive strength generally include taking statistical analyses on laboratory experimental data or field test data. The statistical analysis of laboratory experimental data is the main method for studying single factors affecting concrete, such as carbonation, freeze–thaw cycle, temperature effect, etc. [37,38,39,40,41,42,43]. In many cases, however, the variation in concrete strength is the result of the comprehensive effects of various factors. The superposition of carbonation and freeze–thaw cycles, dry and wet cycles and sulfate attack, loading and freeze–thaw cycles, carbonation and chloride ion attack and other influencing factors on the compressive strength of concrete were studied based on laboratory experimental data [30,44,45,46,47,48,49]. In addition, the long-term time variation law of concrete specimens under the coupling effect of multiple factors was studied [50,51,52,53]. However, concrete compressive strength is influenced by a number of factors, and concrete structures mostly experience long-term loads in practical engineering. This phenomenon is generally difficult to emulate in a laboratory environment. Therefore, the statistical analysis of field test data is becoming the main method for studying the time variation law of compressive strength. Many researchers analyzed the field test data of existing concrete buildings and obtained a long-term time variation law [54,55,56]. In addition, the compressive strength of concrete is also influenced by internal factors such as cement type, curing conditions, and water–cement ratio [37,57,58,59,60,61,62,63].

The study of the time variation law of concrete compressive strength, which is the basis of structural resistance calculations, is very necessary for assessing time-dependent reliability and predicting the subsequent service life of structures or components. There are many studies on the time variation law of the compressive strength of concrete. However, there is a lack of summary and comparison of its variation laws. In this paper, the time variation law of compressive strength was reviewed from both external and internal factors. External factors include carbonization, freeze–thaw cycle, temperature effect, sulfate attacks, etc. The internal factors include cement type, curing conditions, and water–cement ratio, etc. Firstly, the mathematical models of single external factors on concrete compressive strength with time were summarized. Secondly, the time variation laws of concrete under the coupling action of two or more factors were analyzed, and the time variation models of compressive strength in existing buildings were compared. Finally, the influences of internal factors on the strength of concrete were briefly outlined.

2. Study on Single Factors

Physical and chemical attacks such as carbon dioxide, temperature effect, sulfate attack and freeze–thaw cycle can lead to the degradation of the mechanical properties of concrete [55,64,65,66,67]. The various factors affecting the changes in concrete strength can be studied by controlling each certain variable. Currently, conducting accelerated tests in the laboratory is the main method for studying the effect of a single factor on the strength of concrete.

2.1. Carbonization

Carbonation is an essential factor affecting the strength of concrete exposed to the atmosphere [25,68,69,70]. Consideration needs to be given to the effect of carbonation on the strength of concrete in different time periods. Early carbonation improves the concrete compactness, which leads to an increase in its surface strength [71,72,73,74]. However, over time, carbonation will cause the PH of cement-based materials in concrete to decrease, which will cause the corrosion of steel, and eventually lead to a decrease in the durability of the concrete’s structure [25,75,76,77]. Due to the relatively low concentration of CO₂ in the atmosphere, the carbonation rate of concrete in the natural environment is quite slow. Thus, the accelerated carbonation test is usually adopted to study the effect of concrete carbonation [78,79,80,81,82]. Loo et al. [38] established a carbonation prediction model considering CO₂ concentration, temperature, etc., by conducting accelerated carbonation tests on concrete cylindrical specimens, as shown in Equation (1):

$$K=\alpha f_{28}^{-1.08}{C}_0^{0.158}{e}^{0.012T}{t}_{\mathrm{wc}}^{-0.126}+\beta$$

(1)

where $K$ is the carbonation coefficient; $\alpha$ and $\beta$ are constants for a specific exposure condition; $f_{28}$ is the standard 28 d strength, MPa; $C_0$ is the CO₂ concentration, %; $e$ is the exponential constant; $T$ is the temperature, °C; $t_{\mathrm{wc}}$ is the curing period, in days.

From Equation (1), it can be seen that the carbonation coefficient is mostly dependent on the CO₂ concentration under accelerated conditions. In addition, the carbonation of concrete exposed to the natural environment was also monitored and the results showed that the carbonation rates of the accelerated carbonation test were considerably higher than that of the natural carbonation [83,84,85]. The relationship between natural and accelerated carbonation is dependent on concrete quality, as well as the type of admixture [83].

2.2. Freeze–Thaw Cycles

The freeze–thaw cycle is one of the factors that cause the deterioration of the mechanical properties of concrete structures, especially in cold environments [26,49,86,87,88,89,90]. The volume expansion and internal pressure of the concrete will be induced due to the freezing [91,92,93,94]. The continuous cycles will eventually lead to concrete fatigue damage. An accelerated laboratory test is the most commonly used method for studying the relationship between the number of freeze–thaw cycles and compressive strength [91,95].

It was found that the concrete compressive strength decreased with the increasing number of freeze–thaw cycles in the freeze–thaw cycle tests on polypropylene fiber concrete specimens [26,49,93,96]. Further, 70% of the compressive strength remained after 350 freeze–thaw cycles [26]. The normalized compressive strength formula was obtained by 0, 25, 50, 75, 100 and 125 freeze–thaw cycles data [97], as shown in Equation (2):

$$\begin{array}{l}\overline{f}=-12\times {10}^{-4}{N}^2-aN+99.8\\ a=5\times {10}^{-5}{f}_{\mathrm{cu},\mathrm{k}}^3-6\times {10}^{-3}{f}_{\mathrm{cu},\mathrm{k}}^2+0.24f_{\mathrm{cu},\mathrm{k}}-2.57\end{array}$$

(2)

where $\overline{f}$ is the normalized compressive strength after freeze–thaw cycles to the standard value of cube compressive strength; $f_{\mathrm{cu},\mathrm{k}}$ is the standard value of cube compressive strength; $N$ is the number of freeze–thaw cycles.

Shang et al. [98] obtained the relationship between the number of freeze–thaw cycles and the normalized compressive strength of plain concrete under biaxial compressive stress (${\sigma }_2$, ${\sigma }_3$), as shown in Equation (3):

$${\overline{f}}_3=\frac{A+B\times \alpha }{{\left(1+\alpha \right)}^2}\begin{array}{cc}& 0\le N\le \end{array}75$$

(3)

where ${\overline{f}}_3$ is the ratio of principal stress ${\sigma }_3$ to uniaxial compressive strength before freeze–thaw cycles; $\alpha$ is the ratio of ${\sigma }_2$ to ${\sigma }_3$, $0<\alpha <1$; $A$ and $B$ are functions of $N$, $A=-0.0050544\times N+1.02214$, $B=-0.0087264\times N+3.75944$.

2.3. High and Low Temperature Effect

The effect of high temperature on the concrete compressive strength cannot be ignored, especially under the fire or after fire with cooling system [99,100,101]. The several important models of the compressive strength of concrete at high temperatures are summarized in

Table 1. Compressive strength models of concrete at high temperature.

Literature	Models at Elevated Temperature
ASCE Manuals (1992) [102]	$\begin{array}{l}{f}_{\mathrm{cT}}=f_{\mathrm{c}}^{\prime }\begin{array}{cc}& 20\le T<450 °\mathrm{C}\end{array}\\ f_{\mathrm{cT}}=f_{\mathrm{c}}^{\prime }\left(2.011-2.353\times \frac{T-20}{1000}\right)\begin{array}{cc}& T\ge 450 °\mathrm{C}\end{array}\end{array}$
Chang et al. (2006) [103]	$\begin{array}{l}{f}_{\mathrm{cT}}=f_{\mathrm{c}}^{\prime }\left(1.01-0.00055T\right)\begin{array}{cc}& 20 °\mathrm{C}<T\le 200 °\mathrm{C}\end{array}\\ f_{\mathrm{cT}}=f_{\mathrm{c}}^{\prime }\left(1.15-0.00125T\right)\begin{array}{cc}& 200 °\mathrm{C}\le T<800 °\mathrm{C}\end{array}\end{array}$
Krishna et al. (2019) [39]	$\begin{array}{l}{f}_{\mathrm{cT}}=f_{\mathrm{c}}^{\prime }\left(1.0032-0.00044T\right)\begin{array}{cc}& 20 °\mathrm{C}\le T\le 400 °\mathrm{C}\end{array}\\ f_{\mathrm{cT}}=f_{\mathrm{c}}^{\prime }\left(1.4163-0.0016T\right)\begin{array}{cc}& 400 °\mathrm{C}\le T<800 °\mathrm{C}\end{array}\\ f_{\mathrm{cT}}=0\begin{array}{cc}& T\ge 800 °\mathrm{C}\end{array}\end{array}$

$f_{\mathrm{cT}}$ is the compressive strength of concrete at a temperature of $T °\mathrm{C}$; $f_{\mathrm{c}}^{\prime }$ is the compressive strength of concrete at ambient temperature.

.

Krishna et al. [39] showed that the compressive strength decreased obviously but quite steadily with temperatures ranging from 20 °C to 500 °C, while the decline was more obvious above 500 °C. Husem [32] compared the compressive strength of normal and high-performance concrete at high temperatures (200, 400, 600, 800 and 1000 °C) with also different cooling conditions (air and water). The results showed that the strength of concrete decreased with increasing temperature, and the strength of normal concrete has a higher decrease than that of high-performance concrete [32,104]. In addition, the strength of concrete cooled in water decreased more than in air.

Based on the compressive strength versus porosity equation proposed by Ryshkewitch [105] and Griffith’s fracture theory [106], Shen et al. [40] developed a compressive strength model related to temperature, as shown in Equation (4):

$$\sigma =\sqrt{\frac{2E_0\exp \left(-t\mathrm{P}+m\mathrm{P}{S}_{\mathrm{r}}+n{P}_{\mathrm{c}}\right){\gamma }_0\exp \left(-q\mathrm{P}{S}_{\mathrm{r}}\right)}{\pi l}}$$

(4)

where $\sigma$ denotes the concrete compressive strength after various drying processes; $E_0$ is the modulus of elasticity at zero porosity; $t$, $m$, $n$, and $q$ are constants, which are obtained by experience; $\mathrm{P}$ is the porosity of the concrete; $S_{\mathrm{r}}$ is the concrete specimen’s saturation degree; $P_{\mathrm{c}}$ is the capillary pressure; ${\gamma }_0$ is the fracture energy corresponding to zero porosity. The results showed that a decrease in compressive strength in the early stage and an increase in the later stage, due to the simultaneous factors of capillary pressure and the micro-cracks on concrete during the heating.

Jessie et al. [42] tested the steel fiber-reinforced concrete at high temperatures (28 °C to 750 °C) and established a compressive strength model related to steel fiber content and temperature, as shown in Equation (5). The results indicated that quite an increase in strength was exhibited due to the steel fibers. Meanwhile, Zaki et al. [35] studied steel fiber concrete at low temperatures (0 °C to −20 °C) and found that the compressive strength of concrete increased when the temperature was lower than room temperature.

$$f_{\mathrm{c}}=42.58+1.13A-5.7\times {10}^{-3}T+4\times {10}^{-3}AT+1.96A^2-1.57\times {10}^{-5}{T}^2$$

(5)

where $A$ is the steel fiber content.

In addition, Jian et al. [41] studied the axial compressive properties of concrete at low temperatures and established a normalized compressive strength model considering temperature, as shown in Equation (6). The results show that the strength of concrete increased linearly from 20 °C to −120 °C and decreased slightly from −120 °C to 160 °C:

$${\overline{f}}_{\mathrm{T}}=\left\{\begin{array}{ll}-0.004T+1.08,& -120 °\mathrm{C}\le T\le 20°\mathrm{C}\\ 1.56,& -160 °\mathrm{C}\le T\le -120 °\mathrm{C}\end{array}\right.$$

(6)

where ${\overline{f}}_{\mathrm{T}}$ is the ratio of the compressive strength of concrete at $T$ °C to the compressive strength of concrete at 20 °C.

2.4. Sulfate Attacks

Concrete in saline soils, underground water, seawater and other environments is liable to severe sulfate attacks [29,107,108,109]. A sulfate attack is one of the most harmful chemical attacks on concrete [2,110]. The change in the compressive strength of concrete under sulfate attacks can be divided into two stages, where compressive strength increased with time in the early stage and gradually decreased in the later stage [29]. Sulfate attacks on concrete involved sulfate concentrations and the concrete’s strength grade [28]. The concrete strength decreased with an increase in sulfate concentrations with the same concrete strength grade, and the higher the concrete strength grade, the less loss of compressive strength with the same sulfate concentration [28].

Zhang et al. [43] established a sulfate attack model for mixed fiber fly ash concrete based on the fractal dimension and fly ash content, as shown in Equation (7):

$$\begin{array}{l}{D}_{\mathrm{v}}=a+b{e}^{c{D}_{\mathrm{c}}}\\ D_{\mathrm{v}}=1-\frac{V_{\mathrm{n}}^2}{V_0^2}\\ D_{\mathrm{c}}=1-\frac{f_{\mathrm{cn}}}{f_{\mathrm{c}0}}\end{array}$$

(7)

where $D_{\mathrm{v}}$ and $D_{\mathrm{c}}$ are the relative dynamic modulus of elasticity and the relative damage variable, respectively; $a$, $b$ and $c$ are the coefficients; $V_{\mathrm{n}}$ and $V_0$ are, respectively, a value after $n$ days of sulfate attacks and the initial ultrasonic velocity ($\mathrm{m}/\mathrm{s}$); $f_{\mathrm{cn}}$ and $f_{\mathrm{c}0}$ are the relative compressive strength after $n$ days and initial, respectively. It was shown that the concrete with 10% fly ash has a significantly higher compressive strength than that without fly ash under the same sulfate attack.

3. Comprehensive Study on Multiple Factors

The interaction of two or more factors can usually deteriorate concrete performance in practical engineering [26]. At the same time, the deterioration of the concrete will be more severe under the action of multiple damages [26,30,49,111,112,113,114,115,116,117,118]. At present, the studies of concrete compressive strength under the influence of various factors were mainly by statistical analysis of laboratory experimental data or field test data.

3.1. Statistical Analysis of Laboratory Experimental Data

The time variation law study of concrete compressive strength mainly used the multi-factor coupling method in the laboratory.

The variation laws of concrete strength under the combined conditions of freeze–thaw cycles and sulfate attacks were studied [47,48,49]. The results showed that the lower temperature during the freeze–thaw cycle slowed down the diffusion of sulfate ions in concrete. At the same time, the sulfate attack accelerated the formation of concrete cracks, which resulted in more severely damage during the freeze–thaw cycle. In addition, the dry–wet cycles also accelerated the sulfate attacks [30,45]. The concrete compressive strength increased first and then decreased rapidly when the dry–wet cycle and sulfate attack acted simultaneously, and the compressive strength was much lower than that only with sulfate attacks.

Based on the test data, Chen et al. [46] established a degradation model of concrete compressive strength under the combined actions of freeze–thaw cycles and external loads, as shown in Equation (8). It can be observed that the external load will reduce the frost resistance of concrete and accelerate the damage rate of concrete.

$$\left\{\begin{array}{l}\frac{1.671}{f_{\left(N\right)}{}^{3/2}}{\rho }^{3/2}+\frac{7.656}{f_{\left(N\right)}}\rho \cos \theta +\frac{5.817}{f_{\left(N\right)}}\xi =1\begin{array}{cc}& 0°\le \theta \le 60°\end{array}\\ f_{\left(N\right)}=f_{\left(0\right)}\left(1+K_{\mathrm{ass}}\times N\right)\end{array}\right.$$

(8)

where $\rho$, $\theta$ and $\xi$ are functions of the invariants ($I_1$, $J_2$ and $J_3$) of the principal stress tensor components [119]; $f_{\left(N\right)}$ is residual compressive strength; $f_{\left(0\right)}$ is initial compressive strength; $K_{\mathrm{ass}}$ is damage velocity, $K_{\mathrm{ass}}=\left(f_{\left(N+1\right)}-f_{\left(N\right)}\right)/f_{\left(0\right)}$.

Actually, the main way to study the long-term time variation law of concrete strength was to expose concrete specimens both indoors and outdoors considering the interaction of various factors. The University of Wisconsin–Madison carried out a long-term concrete testing program of over 2500 standard cylindrical specimens in 1910, 1923 and 1937 [52]. The research object was to study the concrete strength variations from 50 to 100 years under the combined actions of various factors and to establish long-term models.

According to the data in the literature [51], the time variation law of the compressive strength of concrete (1910 series) was obtained, as shown in Figure 1a. The fitting function in Figure 1a can be expressed as follows:

$$\begin{array}{l}{f}_1=24.133+8.240\lg t\\ f_2=15.169+4.585\lg t\end{array}$$

(9)

where $f$ is the compressive strength of concrete specimens; $t$ is the service age, in years.

It can be seen from Figure 1a, there are two different increase segments of concrete strength: one is within 1 year, and the other is within a period ranging from 10 to 30 years. The average compressive strength, on the whole, increased with time. The literature [50] summarized the compressive strength of concrete specimens (1923 series) over a period of 50 years. Accordingly, the time variation of the mean value of the concrete compressive strength was obtained, as shown in Figure 1b. From Figure 1b, it can be observed that the compressive strength of concrete reached its peak value at around 25 years. Washa et al. [52] studied the variation in the performance of concrete specimens (1937 series) under the influence of different cement types, mix proportions and other factors. It was observed that the average compressive strength increased by 65% from 28 days to 10 years, and it decreased by 5% from 10 years to 25 years and increased again by 3% from 25 years to 50 years [52]. Based on the data in the literature [52], the time average compressive strength curve can be obtained, as shown in Figure 1c.

It can be seen from Figure 1 that the time variation laws of compressive strength for different series of concrete specimens were quite different. It was explained that aggregate coarseness and C₂S content were the influence factors [50].

3.2. Statistical Analysis of Field Test Data

In reality, the environment of concrete is very complex and not a simple superposition of influencing factors. Moreover, in addition to the service environment, the variation in loading conditions will also influence the strength. The concrete structures are basically under long-term load. Thus, the field test data of existing buildings provide more advantages for studying the time variation law of concrete compressive strength in practical engineering.

The probability distribution of concrete strength was analyzed according to the field test data, and the normal distribution was verified [54,55,56,120]. In contrast, Wang et al. [120] pointed out that the gamma distribution was more suitable compared to the normal distribution. In addition to the distribution analysis, many researchers studied the time variation model of concrete compressive strength [54,55,56]. There were mainly three models, described as follows.

• Niu’s model

Niu et al. [54] established a time variation model of the mean and standard deviation of the normalized compressive strength based on a large number of long-term exposure tests, and field test data of existing buildings. The compressive strength data of Niu’s model was normalized by dividing the mean value of the 28-day strength, to eliminate the influences of construction processes, curing conditions, mix proportions and other factors. Niu’s model was expressed as follows:

$$\begin{array}{l}{\mu }_1\left(t\right)=1.4529\exp \left[-0.0246{\left(\ln t-1.7154\right)}^2\right]\\ {\sigma }_1\left(t\right)=0.0305t+1.2368\end{array}$$

(10)

where $\mu$ and $\sigma$ are the mean and standard deviation of normalized compressive strength, respectively.

2.

Gao’s model

Gao et al. [55] established the time variation models of normalized compressive strength based on the data obtained by the rebound hammer method, and core test method from existing buildings in Shanghai, China. The compressive strength of Gao’s model was normalized by dividing the mean value of the cube compressive strength. Gao’s model can be formulated as follows:

$$\begin{array}{l}{\mu }_{\mathrm{R}-1}=-2.0\times {10}^{-4}{t}^2+8.6\times {10}^{-3}t+0.84\\ {\mu }_{\mathrm{C}-1}=-3.0\times {10}^{-4}{t}^2+1.3\times {10}^{-2}t+0.8819\end{array}$$

(11)

where ${\mu }_{\mathrm{R}}$ and ${\mu }_{\mathrm{C}}$ are the dimensionless mean values of the strengths measured by the rebound and core drilling methods, respectively.

3.

Wang’s model

Wang [56] established a time variation model of normalized compressive strength based on the data obtained by the rebound hammer method and core test method from existing buildings in Shandong, China. The normalized compressive strength of Wang’s model is the ratio of the field test data to the mean value of axial compressive strength. Wang’s model can be presented as follows:

$$\begin{array}{l}{\mu }_{\mathrm{R}-2}=-1.8\times {10}^{-4}{t}^2+0.01t+1.06\\ {\mu }_{\mathrm{C}-2}=-2.4\times {10}^{-4}{t}^2+0.01t+1.30\end{array}$$

(12)

4.

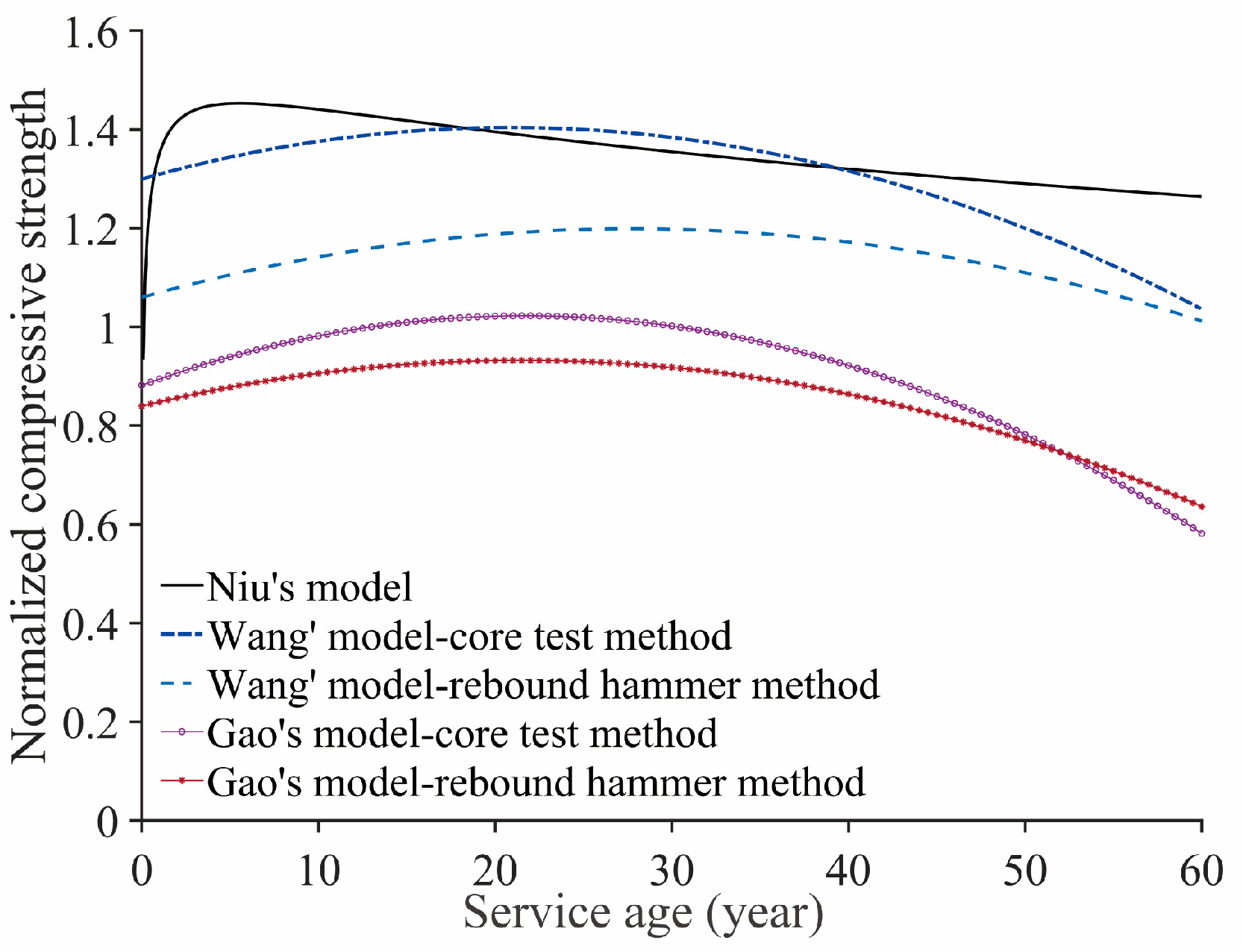
Comparative analysis of time variation models

From the above model, it is observed that data normalization is usually processed via division by the mean value of the 28 d strength, or of the cubic compressive strength, or of the axial compressive strength. In order to study the similarities and differences, the above models are drawn under the same coordinate system, as shown in Figure 2.

It can be seen in Figure 2 that the three models all show a trend of increases first, and then decreases with time. In addition, obvious differences between the models are observed due to the differences in data sources and normalization methods. First of all, with the exception of Niu’s model, which is an exponential function, all other models are quadratic functions. The maximum value of normalized compressive strength in the models occurs at different service ages, which is about 5 years in Niu’s model, about 30 years in Wang’s model and about 25 years in Gao’s model. It can be observed that Niu’s model is very different from Wang’s model and Gao’s model. The main reason for this difference is that the data sources of the model are different. On the one hand, this difference is caused by regional differences. The data for Niu’s model were mainly taken from abroad, while those for Wang’s model and Gao’s model were taken from Shandong and Shanghai, China, respectively. On the other hand, there is a certain deviation in Niu’s exponential model, which cannot accurately reflect the change in the compressive strength of existing buildings in 60 years. It can be observed in

Table 2. Normalized compressive strengths collected by Niu.

Service Age (Year)	Normalized Compressive Strength
0	1.0
1	1.38
2	1.411
2.5	1.347
3	1.41
5	1.5
7	1.336
10	1.53
12	1.344
17	1.351
20	1.58
24	1.40
25	1.56
30	1.35
45	1.21
60	1.16

that 82% of the data for Niu were obtained within 25 years, and the normalized compressive strength corresponding to 20 and 25 years was much greater than those for 5 years.

It can also be seen from Figure 2 that the normalized intensity in Wang’s model is always greater than that in Gao’s model. This is mainly due to the different normalization methods. Wang’s normalized strength was obtained by taking the field test data and dividing the data by the mean value of axial compressive strength, while Gao’s model was divided by the mean value of cubic compressive strength. The mean value of the axial compressive strength $f_{\mathrm{cm}}$ and the mean value of the cubic compressive strength $f_{\mathrm{cu},\mathrm{m}}$ can be expressed as follows:

$$f_{\mathrm{cm}}=f_{\mathrm{ck}}/\left(1-1.645{\delta }_{\mathrm{c}}\right)$$

(13)

$$f_{\mathrm{cu},\mathrm{m}}=f_{\mathrm{cu},\mathrm{k}}/\left(1-1.645{\delta }_{\mathrm{c}}\right)$$

(14)

where $f_{\mathrm{ck}}$ and $f_{\mathrm{cu},\mathrm{k}}$ is the standard value of the compressive strength of a cube and cuboid, respectively. The relationship between $f_{\mathrm{ck}}$ and $f_{\mathrm{cu},\mathrm{k}}$ is expressed as follows [121]:

$$f_{\mathrm{ck}}=0.88\times {\alpha }_1{\alpha }_2{f}_{\mathrm{cu},\mathrm{k}}$$

(15)

where 0.88 is the correction coefficient considering the difference between the structure and the specimen of concrete; ${\alpha }_1$ is the ratio of the prism’s strength to the cube’s strength, ${\alpha }_1<1$; ${\alpha }_2$ is the reduced coefficient of concrete considering brittleness, ${\alpha }_2\le 1$.

From the above analysis, it is clear that the average value of axial compressive strength was less than 0.88 times the average value of cubic compressive strength, i.e., $f_{\mathrm{cm}}<0.88f_{\mathrm{cu},\mathrm{m}}$. Hence, the normalized strength in Wang’s model was always greater than that of Gao’s model.

In addition, Wang’s model and Ga’s model have a consistency, i.e., the normalized compressive strength of the core test was higher than that of the rebound hammer test. The difference between the rebound hammer test and the core test becomes smaller with an increase in service age, which is related to the measuring mechanism of the rebound hammer test and the core test. The rebound hammer test measures the concrete surface hardness and then transformed it into the strength data. Additionally, the core test measures the inner strength of the concrete. The concrete surface hardness can be affected by many factors and decreased with time. Although certain modification is also considered, the strength obtained by the rebound hammer test is generally lower than the core test data. However, in the long term, the normalized compressive strength of the rebound hammer test and core test will gradually converge.

4. Study on Internal Factors of Concrete

The type of cement, water–cement ratio, curing conditions and other internal factors have a certain influence on the time variation of concrete strength, and their effects cannot be ignored. The model established by Chidiac et al. [62] and Moutassem et al. [63] shows that the compressive strength of concrete was related to the type of cement, the cement’s degree of hydration, aggregate types, gradation, etc. David et al. [122] studied the strength of concrete specimens with or without fly ash and of concrete specimens under moist-cured versus air-cured conditions. The results showed that the compressive strength of concrete with fly ash was higher than that without fly ash within 100 days, and then the opposite phenomenon occurred. In addition, the compressive strength of concrete under moist-cured conditions was higher than concrete under air-cured conditions. In addition, the compressive strength of concrete was mainly affected by the water–cement ratio, and strength increased with a decrease in the water–cement ratio [51,59,63].

The CEB-FIP Model Code [123] uses the following equation for the development of concrete compressive strength with time:

$$f_{\mathrm{c}}\left(t\right)=f_{\mathrm{c}}^{\prime }\left(28\right)\cdot \exp \left[s\cdot {\left(1-\frac{28}{t/t_1}\right)}^{1/2}\right]$$

(16)

where $f_{\mathrm{c}}\left(t\right)$ is the compressive strength of concrete at time $t$; $f_{\mathrm{c}}^{\prime }\left(28\right)$ is the 28 d compressive strength of concrete; $s$ is a coefficient which depends on the type of cement; $t_1$ is the time of 1 day.

Mckinnie et al. [59] summarized the existing theoretical models for the variation in compressive strength with time, which involved factors such as cement type, conditioning conditions, mineral admixtures, etc. In addition, Mckinnie et al. [59] performed regression analysis by Freiesleben model, CEB-FIP model, Hyperbolic model and Nykanen model based on the strength data of fly ash concrete, and the results showed that the Freiesleben model exhibited the lowest average error for cement types I, II and III. The Freiesleben model is shown in Equation (17):

$$f_{\mathrm{c}}\left(t\right)=f_{ult}\exp \left[-{\left(\frac{\tau }{t}\right)}^a\right]\cdot f_{\mathrm{c}}^{\prime }\left(28\right)$$

(17)

where $f_{\mathrm{c}}\left(t\right)$ and $f_{\mathrm{c}}^{\prime }\left(28\right)$ have the same meaning as above; $f_{ult}$ is the ultimate compressive strength of concrete; $\tau$ and $a$ are the variables related to cement type.

5. Conclusions and Discussions

Based on the review above, the time variation law of compressive strength can be summarized as follows:

• The strength loss of concrete under the coupling effect of multiple factors has been found to be more serious than the single factor. On the whole, the compressive strength of concrete decreased under the action of various factors in the long term. However, the effect of carbonation and sulfate attacks on concrete needs to be divided into two stages, where the compressive strength increases with time in the early stage and gradually decreases in a later stage.
• The compressive strength of concrete first increased and then decreased under long-term variations in existing concrete buildings. Due to different data sources and normalization methods, there are obvious differences in time variation models.
• The compressive strength of concrete is not only influenced by external factors but also internal factors such as cement type and water–cement ratio, and curing conditions also exhibit remarkable influences.

It can be observed from the above review that there were more studies on the time variation models of concrete compressive strength based on laboratory experimental data than on-site data from existing buildings. Therefore, more site data were needed for the statistical analysis of the concrete compressive strength, including different regions, different temperatures, humidity, salt ion content, etc. A well-established time variation model can be used to assess the reliability and predict the subsequent service life of existing buildings in different regions.