Investigating the Fracture Process and Tensile Mechanical Behaviours of Brittle Materials under Concentrated and Distributed Boundary Conditions
Abstract
1. Introduction
2. Methodology
2.1. Basic Theories
2.2. Experimental Program
2.2.1. Material and Specimen
2.2.2. Setups and Data Acquisition
3. Application and Results
3.1. Loads and Loading-Rate
3.2. Crack-Pattern Profiles
4. Discussion
4.1. Evolution of Failure
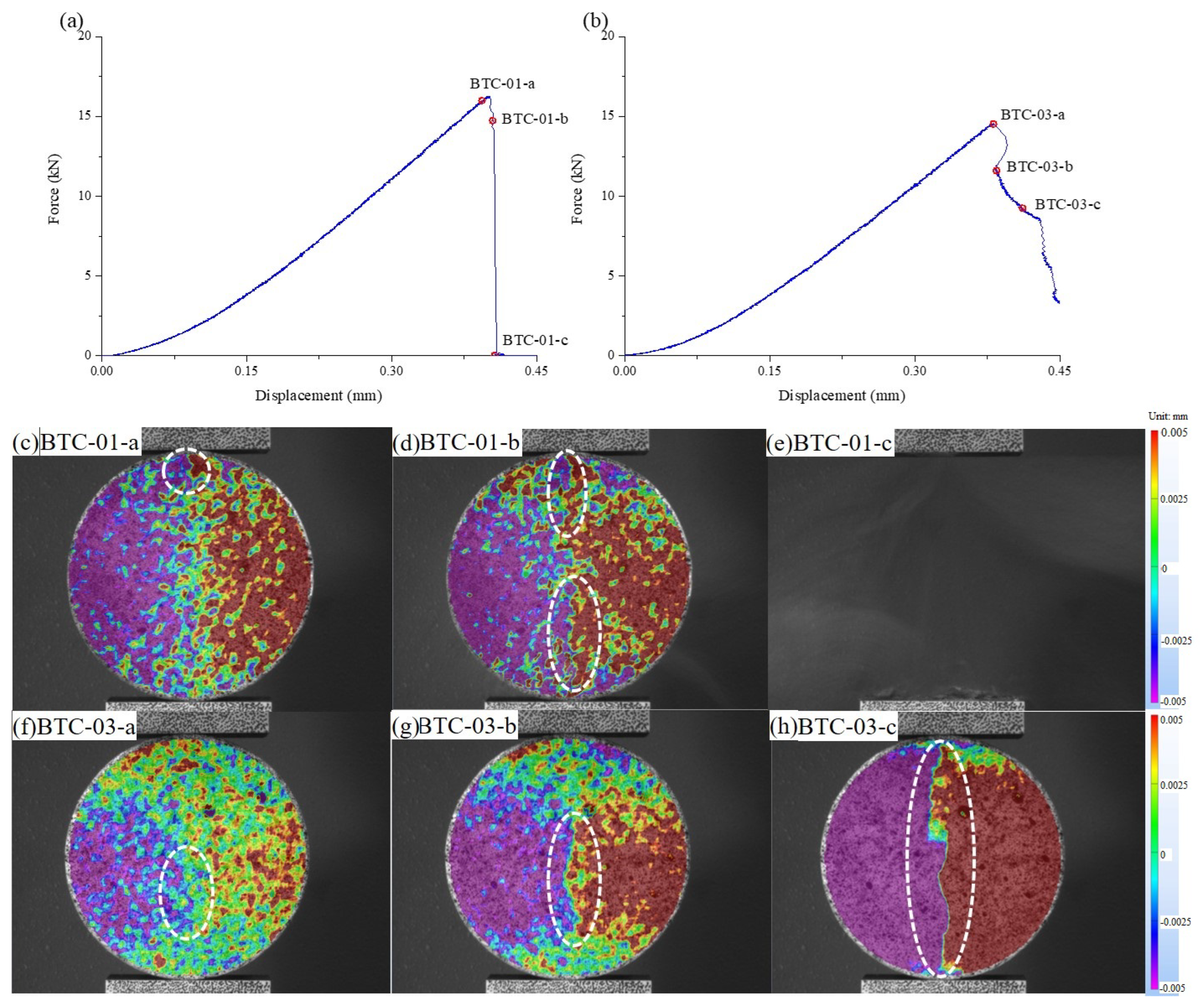
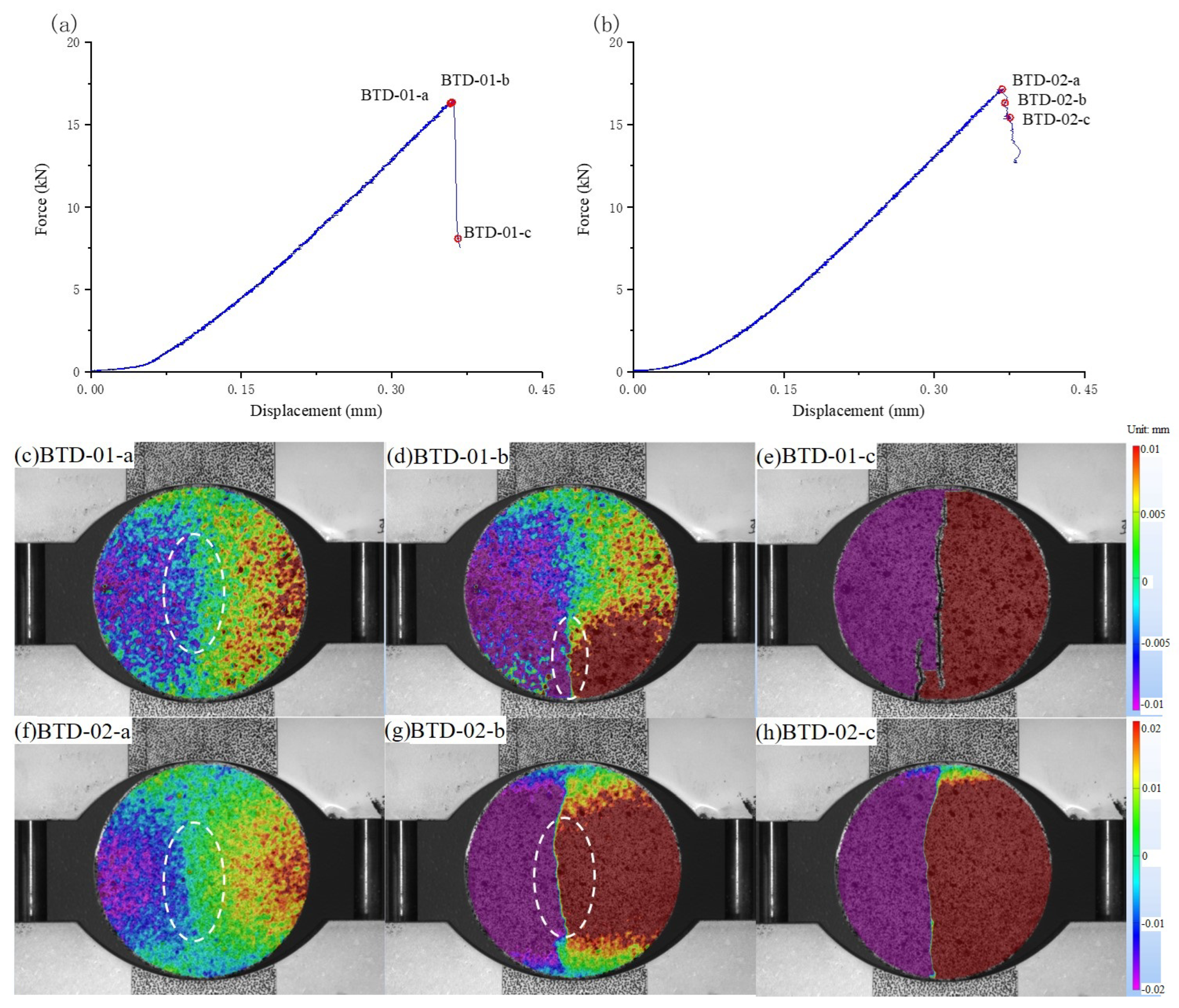
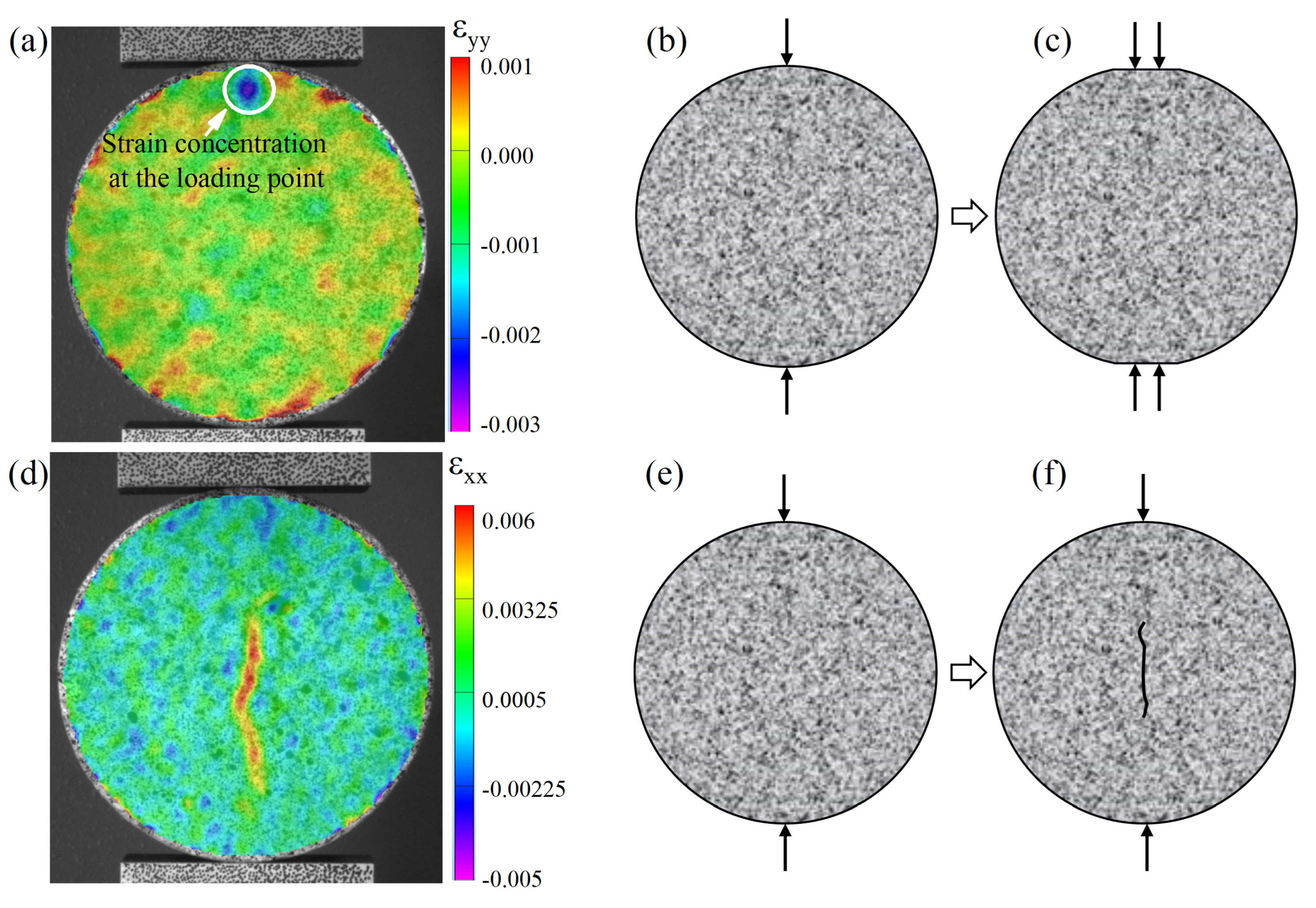
4.1.1. Characteristics of Fracture Profiles
4.1.2. Fractures of BTC
4.1.3. Fractures of BTD
4.2. Tensile Strength
4.2.1. Tensile Strength of BTC Tests
4.2.2. Tensile Strength of BTD Tests
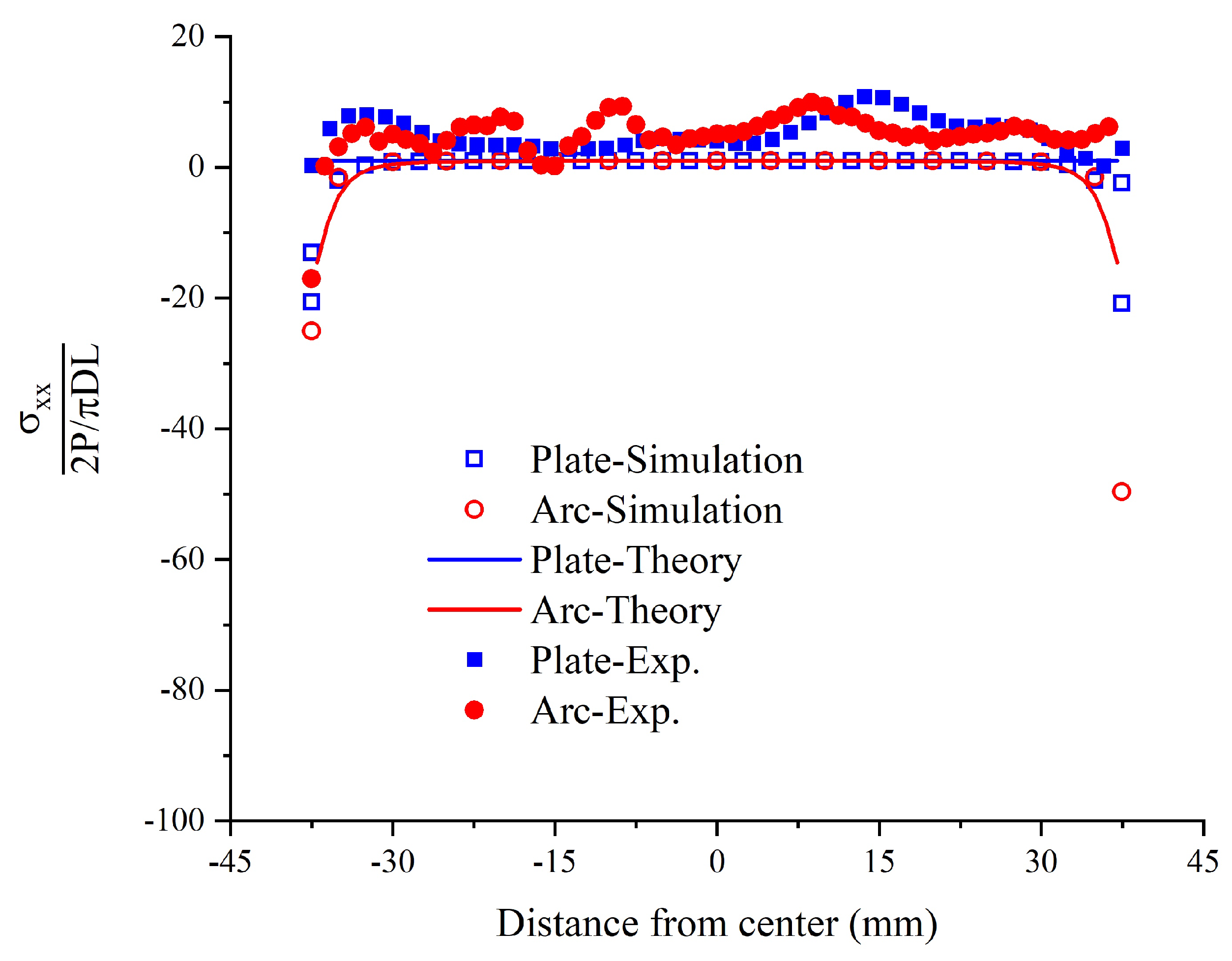
4.3. Numerical Analysis
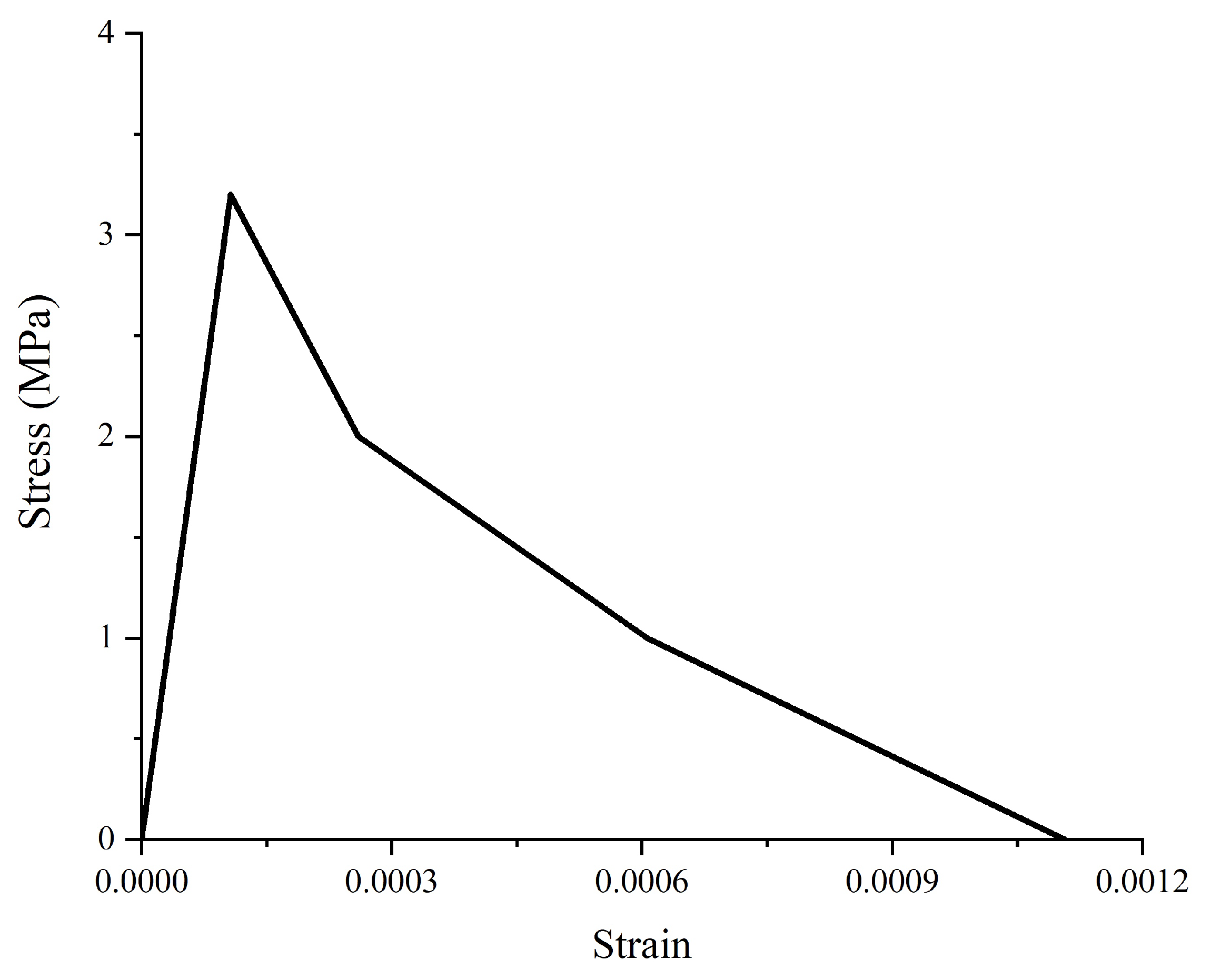
4.3.1. Material Model
4.3.2. Geometry and Elements
4.3.3. Numerical Results and Analysis
5. Conclusions
- (1)
- The tensile strength and failure process was evaluated in Brazilian tests using a high-resolution camera and the DIC method.
- (2)
- In the BTC, cracks were confirmed to randomly initiate at the centre and boundary of the discs in most BTD with the validation of the DIC method.
- (3)
- The nominal tensile strength measured by the Brazilian test was related to the failure process of discs. The average nominal tensile strength of specimens cracking at the boundary was larger than that of specimens cracking at the centre in the BTC.
- (4)
- The tensile strength measured by the Brazilian test was associated with the boundary conditions. The average tensile strength of the BTD was close to that of the BTC. In addition, the equation recommended by the ISRM may slightly overestimate the tensile strength of brittle materials based on the pure elastic theory and hyperbolic-distributed loading conditions at the boundaries.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Abbreviations
| 2-D | Two-dimension |
| ASME | American Society of Mechanical Engineers |
| BTC | Brazilian test with concentrated loading boundary |
| BTD | Brazilian test with distributed loading boundary |
| DIC | Digital image correlation |
| ISRM | International Society for Rock Mechanics |
| RILEM | International Union of Laboratories and Experts in Construction Materials, Systems and Structures |
| D | Diameter of disc |
| L | Thickness of disc |
| P | Loading force |
| t | Time |
| U | Horizontal displacement |
| V | Vertical displacement |
| Loading rate | |
| Average loading rate | |
| Horizontal strain | |
| Vertical strain | |
| Horizontal stress | |
| Vertical stress | |
| Shear stress | |
| Tensile strength | |
| Contact angle |
References
- Berenbaum, R.; Brodie, I. Measurement of the tensile strength of brittle materials. Br. J. Appl. Phys. 1959, 10, 281. [Google Scholar] [CrossRef]
- Sedlacek, R.; Halden, F.A. Method for tensile testing of brittle materials. Rev. Sci. Instrum. 1962, 33, 298–300. [Google Scholar] [CrossRef]
- Labuz, J.; Biolzi, L. Characteristic strength of quasi-brittle materials. Int. J. Solids Struct. 1998, 35, 4191–4203. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Cornetti, P. On the mechanics of quasi-brittle materials with a fractal microstructure. Eng. Fract. Mech. 2003, 70, 2321–2349. [Google Scholar] [CrossRef]
- Efimov, V. The rock strength in different tension conditions. J. Min. Sci. 2009, 45, 569–575. [Google Scholar] [CrossRef]
- You, T.; Zhu, Q.Z.; Li, P.F.; Shao, J.F. Incorporation of tension-compression asymmetry into plastic damage phase-field modeling of quasi brittle geomaterials. Int. J. Plast. 2020, 124, 71–95. [Google Scholar] [CrossRef]
- Fu, Y.; Yu, X.; Dong, X.; Zhou, F.; Ning, J.; Li, P.; Zheng, Y. Investigating the failure behaviors of RC beams without stirrups under impact loading. Int. J. Impact Eng. 2020, 137, 103432. [Google Scholar] [CrossRef]
- Yu, X.; Fu, Y.; Dong, X.; Zhou, F.; Ning, J. An Improved Lagrangian-Inverse Method for Evaluating the Dynamic Constitutive Parameters of Concrete. Materials 2020, 13, 1871. [Google Scholar] [CrossRef]
- Hudson, W.R.; Kennedy, T.W. An Indirect Tensile Test for Stabilized Materials; Center for Highway Research, University of Texas at Austin: Austin, TX, USA, 1968. [Google Scholar]
- Fakhimi, A.; Labuz, J. A simple apparatus for tensile testing of rock. Int. J. Rock Mech. Min. Sci. 2022, 158, 105208. [Google Scholar] [CrossRef]
- Liu, J.; Lyu, C.; Lu, G.; Shi, X.; Li, H.; Liang, C.; Deng, C. Evaluating a new method for direct testing of rock tensile strength. Int. J. Rock Mech. Min. Sci. 2022, 160, 105258. [Google Scholar] [CrossRef]
- Elvery, R.H.; Haroun, W. A direct tensile test for concrete under long- or short-term loading. Mag. Concr. Res. 1968, 20, 111–116. [Google Scholar] [CrossRef]
- Zhang, Q.; Duan, K.; Xiang, W.; Yuan, S.; Jiao, Y.Y. Direct tensile test on brittle rocks with the newly developed centering apparatus. Geotech. Test. J. 2017, 41, 92–102. [Google Scholar] [CrossRef]
- Mesbah, A.; Morel, J.; Walker, P.; Ghavami, K. Development of a direct tensile test for compacted earth blocks reinforced with natural fibers. J. Mater. Civ. Eng. 2004, 16, 95–98. [Google Scholar] [CrossRef]
- Lu, Y.; Li, Q. About the dynamic uniaxial tensile strength of concrete-like materials. Int. J. Impact Eng. 2011, 38, 171–180. [Google Scholar] [CrossRef]
- Guo, H.; Aziz, N.; Schmidt, L. Rock fracture-toughness determination by the Brazilian test. Eng. Geol. 1993, 33, 177–188. [Google Scholar] [CrossRef]
- Newman, D.; Bennett, D. The effect of specimen size and stress rate for the Brazilian test—A statistical analysis. Rock Mech. Rock Eng. 1990, 23, 123–134. [Google Scholar] [CrossRef]
- Li, D.; Wong, L.N.Y. The Brazilian disc test for rock mechanics applications: Review and new insights. Rock Mech. Rock Eng. 2013, 46, 269–287. [Google Scholar] [CrossRef]
- Andreev, G. A review of the Brazilian test for rock tensile strength determination. Part I: Calculation formula. Min. Sci. Technol. 1991, 13, 445–456. [Google Scholar] [CrossRef]
- Andreev, G. A review of the Brazilian test for rock tensile strength determination. Part II: Contact conditions. Min. Sci. Technol. 1991, 13, 457–465. [Google Scholar] [CrossRef]
- Fairhurst, C. On the validity of the ‘Brazilian’ test for brittle materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1964, 1, 535–546. [Google Scholar] [CrossRef]
- Claesson, J.; Bohloli, B. Brazilian test: Stress field and tensile strength of anisotropic rocks using an analytical solution. Int. J. Rock Mech. Min. Sci. 2002, 39, 991–1004. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Serati, M.; Masoumi, H.; Rahimi, E. Numerical assessment of rupture mechanisms in Brazilian test of brittle materials. Int. J. Solids Struct. 2019, 180, 1–12. [Google Scholar] [CrossRef]
- Kovári, K.; Tisa, A.; Einstein, H.H.; Franklin, J.A. Suggestion methods for determining the strength of rock materials in triaxial compression: Revised version. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 283–290. [Google Scholar]
- ASTM International Committee. Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens1; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- RILEM. RILEM Recommendations for the Testing and Use of Constructions Materials: CPC 6 Tension by Splitting of Concrete Specimens; Springer: London, UK, 1975. [Google Scholar]
- Ministry of Hosing and Urban-Rural Development of People’s Republic of China. Standard for Tests Method of Engineering Rock Masses (English Version); China Plan Press: Beijing, China, 1999. [Google Scholar]
- Timoshenko, S. Theory of Elasticity; Engineering Societies Monographs; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Mazel, V.; Guerard, S.; Croquelois, B.; Kopp, J.; Girardot, J.; Diarra, H.; Busignies, V.; Tchoreloff, P. Reevaluation of the diametral compression test for tablets using the flattened disc geometry. Int. J. Pharm. 2016, 513, 669–677. [Google Scholar] [CrossRef]
- Hondros, G. The evaluation of Poisson’s ratio and the modulus of materials of low tensile resistance by the Brazilian (indirect tensile) test with particular reference to concrete. Aust. J. Appl. Sci. 1959, 10, 243–268. [Google Scholar]
- Ma, C.C.; Hung, K.M. Exact full-field analysis of strain and displacement for circular disks subjected to partially distributed compressions. Int. J. Mech. Sci. 2008, 50, 275–292. [Google Scholar] [CrossRef]
- Wei, X.; Chau, K.T. Three dimensional analytical solution for finite circular cylinders subjected to indirect tensile test. Int. J. Solids Struct. 2013, 50, 2395–2406. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, J.; Zhang, J. A modified Brazilian disk tension test. Int. J. Rock Mech. Min. Sci. 2009, 46, 421–425. [Google Scholar] [CrossRef]
- Kourkoulis, S.; Markides, C.F.; Chatzistergos, P. The standardized Brazilian disc test as a contact problem. Int. J. Rock Mech. Min. Sci. 2013, 57, 132–141. [Google Scholar] [CrossRef]
- Xu, J.; Dong, X.; Fu, Y.; Yu, X.; Zhou, F. Experimental analysis of process and tensile strength for concrete Brazilian splitting test with different loading boundaries by DIC method. Chin. J. Theor. Appl. Mech. 2020, 52, 864–876. [Google Scholar]
- Wang, Q.; Li, L.; Wu, L.; Huan, R. Improvement of Brazilian test: From flattened Brazilian disc to grooved Brazilian disc. Chin. J. Theor. Appl. Mech. 2017, 49, 793–801. [Google Scholar]
- Liu, Y.; Dai, F.; Xu, N.; Zhao, T.; Feng, P. Experimental and numerical investigation on the tensile fatigue properties of rocks using the cyclic flattened Brazilian disc method. Soil Dyn. Earthq. Eng. 2018, 105, 68–82. [Google Scholar] [CrossRef]
- Wang, Q.; Jia, X.; Kou, S.; Zhang, Z.; Lindqvist, P.A. The flattened Brazilian disc specimen used for testing elastic modulus, tensile strength and fracture toughness of brittle rocks: Analytical and numerical results. Int. J. Rock Mech. Min. Sci. 2004, 41, 245–253. [Google Scholar] [CrossRef]
- Markides, C.F.; Pasiou, E.D.; Stavropoulou, M.; Papagiannopoulos, A.; Sakaropoulos, F.; Kourkoulis, S.K. Revisiting the flattened Brazilian disc configuration-Part I: The actual boundary conditions. Procedia Struct. Integr. 2022, 41, 351–360. [Google Scholar] [CrossRef]
- Blikharskyy, Y.; Kopiika, N.; Khmil, R.; Selejdak, J.; Blikharskyy, Z. Review of Development and Application of Digital Image Correlation Method for Study of Stress–Strain State of RC Structures. Appl. Sci. 2022, 12, 10157. [Google Scholar] [CrossRef]
- Chu, T.; Ranson, W.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Stirling, R.A.; Simpson, D.J.; Davie, C.T. The application of digital image correlation to Brazilian testing of sandstone. Int. J. Rock Mech. Min. Sci. 2013, 60, 1–11. [Google Scholar] [CrossRef]
- Li, D.; Li, B.; Han, Z.; Zhu, Q. Evaluation on Rock Tensile Failure of the Brazilian Discs under Different Loading Configurations by Digital Image Correlation. Appl. Sci. 2020, 10, 5513. [Google Scholar] [CrossRef]
- Abaqus. ABAQUS Analysis User’s Manual; Dassault Systemes: Vélizy-Villacoublay, France, 2009. [Google Scholar]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Forquin, P.; Lukić, B.; Saletti, D.; Sallier, L.; Pierron, F. A benchmark testing technique to characterize the stress–strain relationship in materials based on the spalling test and a photomechanical method. Meas. Sci. Technol. 2019, 30, 125006. [Google Scholar] [CrossRef]









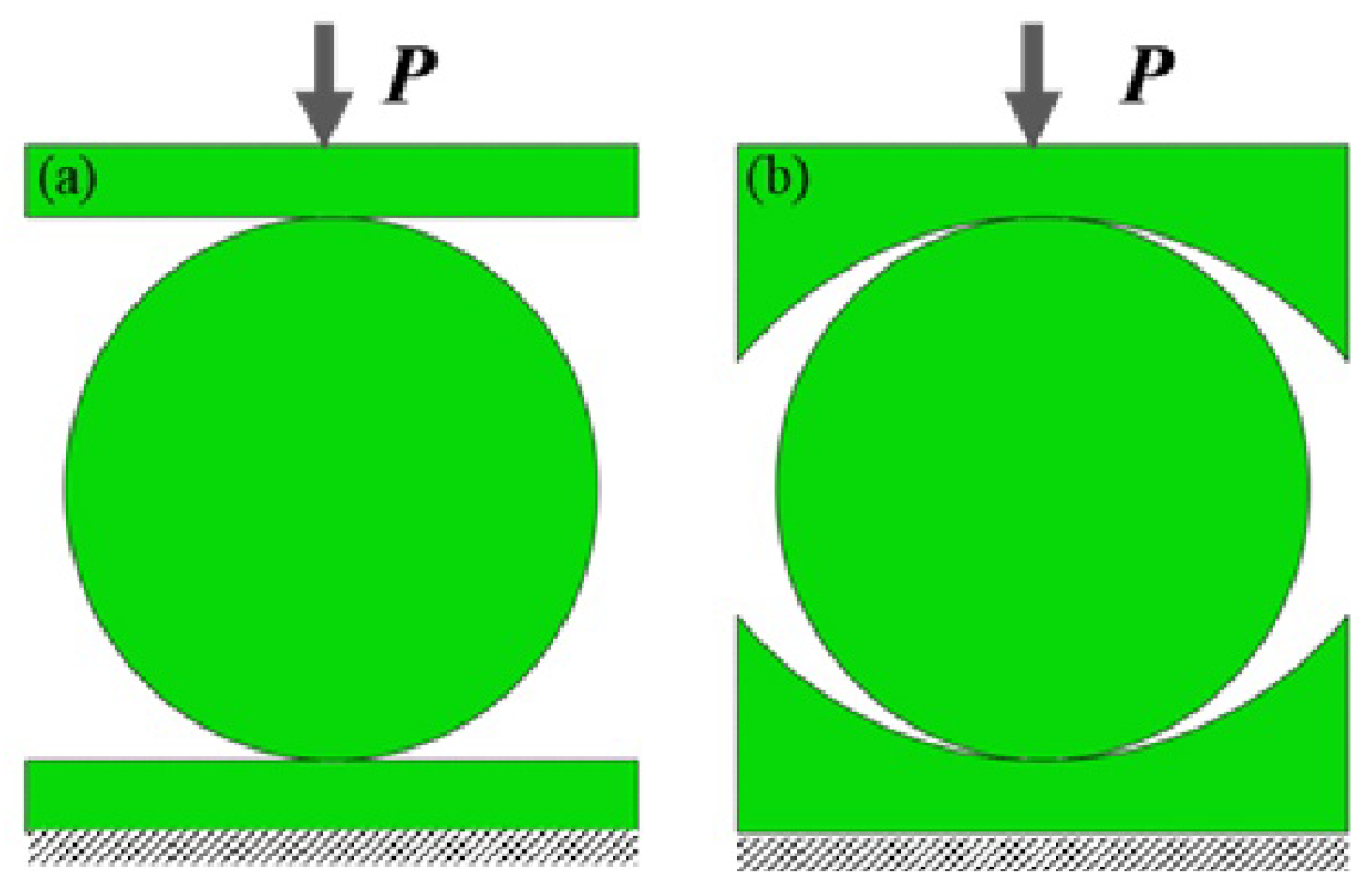


| Boundary Conditions | Loading Types | Stress field in Central Line | Tensile Strength at the Center of the Disc | Source |
|---|---|---|---|---|
 | 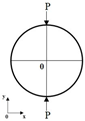 | [25,28] | ||
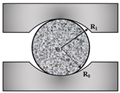 | 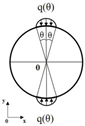 | [26,30,31,38] |
| Density | Compressive Strength | Passion’s Ratio | Compressive Young’s Modulus |
|---|---|---|---|
| GPa | kg/m3 | MPa | |
| 32 | 2430 | 60 | 0.21 |
| Parameters | Setting |
|---|---|
| Subset | 15 × 15 pixel2 |
| Step | 10 pixel |
| Magnification factor | 55 mm/pixel |
| Strain filter size | Gaussian (5) |
| Matching criterion | Normalized squared differences |
| Interpolation | Optimized 8-tap interpolation |
| Shape function | Affine |
| Number | Loading Rate/kN/s | Maximum Load/kN | Crack Initiation | Tensile Strength/MPa |
|---|---|---|---|---|
| 03 | 0.478 | 14.53 | Center | 3.291 |
| 04 | 0.513 | 15.12 | 3.424 | |
| 07 | 0.509 | 15.45 | 3.499 | |
| Average | 0.500 | 15.03 | 3.405 | |
| 01 | 0.515 | 16.25 | Boundary | 3.680 |
| 02 | 0.544 | 16.90 | 3.490 | |
| 05 | 0.480 | 15.41 | 3.691 | |
| 06 | 0.476 | 16.30 | 3.506 | |
| 08 | 0.514 | 15.48 | 3.827 | |
| Average | 0.506 | 16.07 | 3.639 |
| Number | Loading Rate/kN/s | Maximum Load/kN | Contact Angle 2/ | Tensile Strength/MPa |
|---|---|---|---|---|
| 01 | 0.593 | 16.44 | 15.9 | 3.641 |
| 02 | 0.605 | 17.15 | 17.8 | 3.777 |
| 03 | 0.596 | 16.13 | 18.9 | 3.539 |
| 04 | 0.459 | 16.79 | 16.7 | 3.709 |
| Average | 0.563 | 16.63 | 17.3 | 3.667 |
| Materials | Density kg/m3 | Elastic Modulus GPa | Poisson Ratio | Tensile Strength MPa | Fracture Energy N/m |
|---|---|---|---|---|---|
| Concrete | 2400 | 30 | 0.2 | 3.2 | 120 |
| Steel | 7800 | 210 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, H.; Fang, X.; Yu, X.; Fu, Y.; Zhou, G. Investigating the Fracture Process and Tensile Mechanical Behaviours of Brittle Materials under Concentrated and Distributed Boundary Conditions. Appl. Sci. 2023, 13, 5273. https://doi.org/10.3390/app13095273
Liang H, Fang X, Yu X, Fu Y, Zhou G. Investigating the Fracture Process and Tensile Mechanical Behaviours of Brittle Materials under Concentrated and Distributed Boundary Conditions. Applied Sciences. 2023; 13(9):5273. https://doi.org/10.3390/app13095273
Chicago/Turabian StyleLiang, Haozhe, Xiaozu Fang, Xinlu Yu, Yingqian Fu, and Gangyi Zhou. 2023. "Investigating the Fracture Process and Tensile Mechanical Behaviours of Brittle Materials under Concentrated and Distributed Boundary Conditions" Applied Sciences 13, no. 9: 5273. https://doi.org/10.3390/app13095273
APA StyleLiang, H., Fang, X., Yu, X., Fu, Y., & Zhou, G. (2023). Investigating the Fracture Process and Tensile Mechanical Behaviours of Brittle Materials under Concentrated and Distributed Boundary Conditions. Applied Sciences, 13(9), 5273. https://doi.org/10.3390/app13095273







