Dynamical Neural Network Based Dynamic Inverse Control Method for a Flexible Air-Breathing Hypersonic Vehicle

Featured Application

The method proposed can be used for the identification and control of multivariable nonlinear systems.

Abstract

A novel dynamic inverse control method based on a dynamical neural network (DNN) is proposed for the trajectory tracking control of a flexible air-breathing hypersonic vehicle (FAHV). Firstly, considering that the accurate model of FAHV is difficult to obtain, the FAHV is regarded as a completely unknown system, and a DNN is designed to identify its nonlinear model. On the basis of Lyapunov’s second law, the weight vectors of the DNN are adaptively updated. Then, a dynamic inverse controller is designed based on the identification model, which avoids the transformation of the nonlinear model of FAHV, thereby simplifying the controller design process. The simulation results verify that the DNN can identify FAHV accurately, and velocity and altitude can track the given reference signal accurately with the proposed dynamic inverse control method. Compared with the back-stepping control method, the proposed method has better tracking accuracy, and the amplitude of the initial control law is smaller.

1. Introduction

Hypersonic Vehicles (HVs) refer to a new type of aircraft flying at a speed of more than Mach 5, which has received widespread attention in the civilian and military fields because of its advantages of global fast arrival and efficient cost [1,2]. The unknown aerodynamic parameters, actuator saturation limitations, and integrated airframe/engine design make the dynamics of the HV uncertain, nonlinear, and strongly coupled, which brings great difficulties to the controller design [3,4,5]. In addition, these unfavourable factors seriously affect the flight performance of HVs and even can lead to system instability.

With the above-mentioned challenges, the design of the guidance and control system for HV has attracted a great deal of attention in the past few years. In terms of trajectory planning, researchers have conducted extensive research on guidance laws under special constraints and made important achievements. In the design of guidance law, the most wide studies are the optimal guidance method. The idea is to transform the design of the guidance law into an optimal control problem and obtain an explicit guidance equation by reasonable assumption and simplification [6,7]. The optimal guidance law method can establish the mathematical model according to different constraint conditions. However, due to the influence of external disturbance, measurement error, and high manoeuvrability of the target in the flight process of HV, there will be a large error in the mathematical model, which can greatly reduce the guidance accuracy [8]. To deal with the disadvantages of optimal guidance, Ref. [9] proposed a search-resampling-optimization (SRO) framework. Numerical simulations demonstrate that the SRO framework is efficient and robust even with narrow accessible tunnels for autonomous dispatch trajectory planning on the flight deck. The SRO is inherently flexible and can be easily extended to the trajectory planning problem for HVs. In addition, Wang et al. [10] proposed a comprehensive investigation of techniques and research progress for the carrier aircraft’s dispatch path planning on the deck, and they provided an exploratory prospect of the knowledge or method learned from other fields. These solutions also can provide some reference for the trajectory planning of HVs.

In terms of trajectory tracking and attitude control, scholars have proposed many control methods for the characteristics of HVs. Considering the constraints of HVs and their complex external disturbances, a predictive control method based on various types of disturbance observers was proposed [11,12,13]. Additionally, considering that sliding mode control is insensitive to parameter variations and external disturbance, sliding mode control for HVs has been extensively studied [14,15,16]. In addition, to improve the anti-interference performance of HVs, reinforcement learning methods [17,18,19] are proposed to estimate various uncertain disturbances of HVs. These methods are conceptually intuitive and improve the robust tracking performance from different aspects, but they are based on the approximate linearization around specified trim conditions or input–output linearization techniques.

However, due to the complex flight environment and unique dynamic characteristics of HVs, accurate models of HVs are difficult or even impossible to obtain. Therefore, in order to expand the practicality of the control methods, the fuzzy logic system [20] and neural network [21,22,23,24,25,26] are proposed to approximate unknown dynamics of HVs. By taking the nonlinear model and external disturbance as an unknown system, a radial basis function neural network (RBFNN) is employed to approximate them [21,22,23]. Moreover, based on RBFNN, Ref [24] takes the FAHV model as an unknown nonaffine system and designs an adaptive neural controller. Additionally, fuzzy wavelet neural network (FWNN) is proposed to estimate the unknown model of HVs to improve the transient performance [25,26]. These methods have been proven to have good control performance, but the adaptive law is related to the control law needed to be designed together with the control law, which will lead to inconvenience in some cases.

The dynamical neural network identifier, proposed by George A. Rovithakis, can not only approximate unknown nonlinear dynamic systems well, but also dynamically adjust weighted parameters independent of control law [27,28]. And it has been applied in DC motors [27,28], unmanned quadrotor formation flight [29], wastewater treatment bioprocess [30], etc. Inspired by this, a dynamic inverse tracking control design method for a FAHV based on DDN is proposed. The main contributions of this paper include the following:

(1)

A DNN is used to identify the FAHV model. The weighted parameters of the neural network are updated by the adaptive law and compared with conventional system identification techniques, such as maximum likelihood estimation method [31,32] and Kalman filtering method [33], this approach does not require the exact mathematical model of the object.

(2)

Compared with the widely used adaptive neural network control [21,22,23,24], the DNN system identification method adopted in this paper is independent of the control law design, which is convenient for system identification and control law design.

(3)

A dynamic inverse controller is designed based on the identification model, which avoids complex model transformations; thus, the controller design process is simplified.

The remainder of this paper is organized as follows. Section 2 presents the FAHV model and preliminaries. The neural network identification model and the dynamic inverse controller are developed in Section 3 and Section 4, respectively. Simulation studies are made in Section 5 and the conclusions are presented in Section 6.

2. Problem Description

2.1. FAHV Model Description

The model adopted in this study is developed by Bolender and Doman for the longitudinal dynamics of a FAHV [34]. The nonlinear equations of the longitudinal motion, derived from Lagrange’s equations, including flexible effects by modeling the fuselage as a free beam and the vehicle as a single flexible structure with mass-normalized mode shapes [35], are formulated as

$$\begin{array}{l}\dot{V}=\frac{T\cos \alpha -D}{m}-g\sin \gamma \\ \dot{\gamma }=\frac{L+T\sin \alpha }{mV}-g\cos \gamma \\ \dot{h}=V\sin \gamma \\ \dot{\alpha }=Q-\dot{\gamma }\\ \dot{Q}=\frac{M}{I_{yy}}\\ {\ddot{\eta }}_i=-2{\zeta }_i{\omega }_i{\dot{\eta }}_i-{\omega }_i^2{\eta }_i+N_i,i=1,2,3\end{array}.$$

(1)

This FAHV model is composed of eleven flight states, i.e., $x={[V,\gamma ,h,\alpha ,Q,{\eta }_1,{\dot{\eta }}_1,{\eta }_2,{\dot{\eta }}_2,{\eta }_3,{\dot{\eta }}_3]}^T$ for the five rigid-body states with velocity $V$, flight-path angle (FPA) $\gamma$, altitude $h$, the angle of attack (AOA) $\alpha$, pitch rate $Q$, and the flexible modes $\mathit{\eta }={[{\eta }_1,{\dot{\eta }}_1,{\eta }_2,{\dot{\eta }}_2,{\eta }_3,{\dot{\eta }}_3]}^T$. Here, $g$ and $I_{yy}$ denote the gravitational acceleration and the moment of inertia, respectively. As shown in Table 1, the vehicle mass $m$ and the modal frequencies $({\omega }_i,i=1,2,3)$ of the flexible structure are different at different fuel levels. It is also seen from Table 1 that the modal frequencies increase as the vehicle mass decreases with the fuel consumption, but, in fact, the vehicle mass decreases on a slower timescale than the velocity $V$ and altitude $h$ during hypersonic cruise flight [36]. Therefore, nominal values of mass and modal frequencies at the 50% fuel level are considered. While for all flexible modes, the damping ratio is constant, and that is ${\zeta }_i=0.02$.

Table 1. Vehicle mass and modal frequencies at different fuel levels.

Fuel Level	0%	30%	50%	70%	100%
$m$ (slug/ft)	93.57	126.1	147.9	169.6	202.2
${\omega }_1$ (rad/s)	22.78	21.71	21.17	20.73	20.17
${\omega }_2$ (rad/s)	68.94	57.77	53.92	51.24	48.4
${\omega }_3$ (rad/s)	140	117.8	109.1	102.7	95.6

Besides, the definitions of $T,D,L,M$ and $N_i(i=1,2,3)$ that are given by [36,37]:

$$\begin{array}{l}T\approx \overline{q}S\left[C_{T,\varphi }(\alpha )\varphi +C_T(\alpha )+C_T^{\eta }\mathit{\eta }\right]\\ D\approx \overline{q}S{C}_D(\alpha ,\delta ,\mathit{\eta })\\ L\approx \overline{q}S{C}_L(\alpha ,\delta ,\mathit{\eta })\\ M\approx z_{T}T+\overline{q}S\overline{c}{C}_M(\alpha ,\delta ,\mathit{\eta })\\ N_i\approx \left[N_i^{{\alpha }^2}{\alpha }^2+N_i^{\alpha }\alpha +N_i^0+N_i^{\eta }\mathit{\eta }+N_i^{{\delta }_e}{\delta }_e+N_i^{{\delta }_c}{\delta }_c\right]=N_i(\alpha ,\mathit{\eta })+N_i(\delta )\delta ,i=1,2,3\end{array},$$

(2)

where $\delta ={\left[{\delta }_c,{\delta }_e\right]}^T$.

The correlation coefficients under nominal operating conditions in Equation (2) are

$$\begin{array}{l}{C}_{T,\varphi }(\alpha )=C_T^{\varphi {\alpha }^3}{\alpha }^3+C_T^{\varphi {\alpha }^2}{\alpha }^2+C_T^{\varphi \alpha }\alpha +C_T^{\varphi }\\ C_T(\alpha )=C_T^3{\alpha }^3+C_T^2{\alpha }^2+C_T^1\alpha +C_T^0\\ C_L(\alpha ,\delta ,\mathit{\eta })=C_L^{\alpha }\alpha +C_L^0+C_L^{\eta }\mathit{\eta }+C_L^{{\delta }_e}{\delta }_e+C_L^{{\delta }_c}{\delta }_c\\ \hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=C_{L,\alpha ,\mathit{\eta }}(\alpha ,\mathit{\eta })+C_{L,\delta }(\delta )\delta \\ C_D(\alpha ,\delta ,\mathit{\eta })=C_D^{{\alpha }^2}{\alpha }^2+C_D^{\alpha }\alpha +C_D^0+C_D^{\eta }\mathit{\eta }+C_D^{{\delta }_e^2}{\delta }_e^2+C_D^{{\delta }_e}{\delta }_e+C_D^{{\delta }_c^2}{\delta }_c^2+C_D^{{\delta }_c}{\delta }_c\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}=C_{D,\alpha ,\mathit{\eta }}(\alpha ,\mathit{\eta })+C_{D,\delta }(\delta )\delta \\ C_M(\alpha ,\delta ,\mathit{\eta })=C_M^{{\alpha }^2}{\alpha }^2+C_M^{\alpha }\alpha +C_M^0+C_M^{\eta }\mathit{\eta }+C_M^{{\delta }_e}{\delta }_e+C_M^{{\delta }_c}{\delta }_c\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}=C_{M,\alpha ,\mathit{\eta }}(\alpha ,\mathit{\eta })+C_{M,\delta }(\delta )\delta \end{array}.$$

(3)

There are three control inputs $\varphi$, ${\delta }_c$, and ${\delta }_e$ which are defined as the fuel equivalence ratio, the canard deflection, and the elevator deflection. The canard deflection ${\delta }_c$ is ganged with the elevator deflection ${\delta }_e$ with a negative gain $k_{ec}$, i.e., ${\delta }_c=k_{ec}{\delta }_e$. Therefore, the actual control input that needs to be designed is $u={\left[\varphi ,{\delta }_e\right]}^T$. Here, $S$, $z_T$, and $\overline{c}$ denote the reference area, thrust moment arm, and mean aerodynamic chord, respectively. The dynamic pressure is calculated as $\overline{q}=0.5\rho V^2$, where the air density $\rho$ is modeled as $\rho ={\rho }_0\exp (-h/h_0)$ with ${\rho }_0=1.2266$ kg/m³ and $h_0$ = 7315.2 m. The meaning of the coefficients and the specific values are referred to [35]. Additionally, from the aerodynamic parameter Formulas (2) and (3) of FAHVs, it can be seen that the various states of FAHVs are highly coupled, and the elastic modes have great influences on its thrust, lift, drag, and pitch moment.

2.2. Model Conversion and Control Objective

The nonlinear dynamic model of FAHV (1) can be written as the following matrix form:

$$\begin{array}{l}\dot{x}\approx f(x)+g(x)u\\ y=x\\ z=Cx\end{array}.$$

(4)

where $y$ is the measurable output and z is the controlled output.

$$f(x)=\left[\begin{array}{c}\frac{\overline{q}S\left(C_T(\alpha )+C_T^{\eta }(\mathit{\eta })\right)\cos \alpha -\overline{q}S{C}_{D,\alpha ,\eta }(\alpha ,\mathit{\eta })}{m}-g\sin \gamma \\ \frac{\overline{q}S{C}_{L,\alpha ,\eta }(\alpha ,\mathit{\eta })+\overline{q}S\left(C_T(\alpha )+C_T^{\eta }(\mathit{\eta })\right)\sin \alpha }{mV}-g\cos \gamma \\ V\sin \gamma \\ Q-\frac{\overline{q}S{C}_{L,\alpha ,\eta }(\alpha ,\mathit{\eta })+\overline{q}S\left(C_T(\alpha )+C_T^{\eta }(\mathit{\eta })\right)\sin \alpha }{mV}+g\cos \gamma \\ \frac{z_T\overline{q}S\left(C_T(\alpha )+C_T^{\eta }(\mathit{\eta })\right)+\overline{q}S\overline{c}{C}_{M,\alpha ,\eta }(\alpha ,\mathit{\eta })}{I_{yy}}\\ {\dot{\eta }}_1\\ -2{\zeta }_1{\omega }_1{\dot{\eta }}_1-{\omega }_1^2{\eta }_1+N_1(\alpha ,\mathit{\eta })\\ {\dot{\eta }}_2\\ -2{\zeta }_2{\omega }_2{\dot{\eta }}_2-{\omega }_2^2{\eta }_2+N_2(\alpha ,\mathit{\eta })\\ {\dot{\eta }}_3\\ -2{\zeta }_3{\omega }_3{\dot{\eta }}_3-{\omega }_3^2{\eta }_3+N_3(\alpha ,\mathit{\eta })\end{array}\right]$$

$$g(x)=\left[\begin{array}{cc}\frac{\overline{q}S{C}_{T,\varphi }(\alpha )\cos \alpha }{m}& -\frac{\overline{q}S{C}_{D,\delta }(\delta )}{m}\\ \frac{\overline{q}S{C}_{T,\varphi }(\alpha )\sin \alpha }{mV}& \frac{\overline{q}S{C}_{L,\delta }(\delta )}{mV}\\ 0& 0\\ -\frac{\overline{q}S{C}_{T,\varphi }(\alpha )\sin \alpha }{mV}& -\frac{\overline{q}S{C}_{L,\delta }(\delta )}{mV}\\ \frac{z_T\overline{q}S{C}_{T,\varphi }(\alpha )}{I_{yy}}& \frac{\overline{q}S\overline{c}{C}_{M,\delta }(\delta )}{I_{yy}}\\ 0& 0\\ 0& N_1(\delta )\\ 0& 0\\ 0& N_2(\delta )\\ 0& 0\\ 0& N_3(\delta )\end{array}\right],\mathrm{and}C=\left[\begin{array}{ccccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right].$$

Remark 1. 

In order to accurately identify all states of the nonlinear system (4), it is assumed that all states of the FAHV system are measurable.

The control objective is to design a control law so that the velocity $V$ and the altitude $h$ of the FAHV track given reference signals when the motion model of the FAHV is completely unknown.

3. Establishment of Adaptive Identification Model for Flexible Air-Breathing Hypersonic Vehicle

3.1. Dynamical Neural Network

Dynamical neural networks are recurrent, fully interconnected nets containing dynamical elements in their neurons [27,28]. By dynamically adjusting the weighting coefficients of the neural network, it has been proven that the approximation of a nonlinear function can be achieved with high precision [27,28].

The nonlinear dynamic system of the form (4) can be described by the following system of coupled the first-order differential equation [27,28]

$$\begin{array}{l}\dot{\widehat{x}}=A\widehat{x}+B\widehat{W}\Phi (\widehat{x})+B\widehat{\beta }\Psi (\widehat{x})u\\ \widehat{y}=\widehat{x}\\ z=C\widehat{x}\end{array},$$

(5)

where $\widehat{x}\in R^{11}$ is an estimation of the state $x$ of the FAHV, the input $u\in R^2$, the output $\widehat{y}\in R^{11}$, $W$ is a $11\times 11$ matrix of adjustable synaptic weights, $\beta$ is a $11\times 11$ diagonal matrix of adjustable synaptic weights, $A$ is a $11\times 11$ diagonal matrix with negative eigenvalues $a_i$, and $B$ is a $11\times 11$ diagonal matrix with scalar elements $b_i$, i.e.,

$$\begin{array}{l}A={\left[\begin{array}{cccc}{a}_1& 0& \cdots & 0\\ 0& a_2& & ⋮\\ ⋮& & \ddots & 0\\ 0& \cdots & 0& a_{11}\end{array}\right]}_{11\times 11},a_i<0,i=1,2,\dots ,11\\ B={\left[\begin{array}{cccc}{b}_1& 0& \cdots & 0\\ 0& b_2& & ⋮\\ ⋮& & \ddots & 0\\ 0& \cdots & 0& b_{11}\end{array}\right]}_{11\times 11}\end{array}.$$

(6)

$\Phi (\widehat{x})$ is a 11-dimensional vector with elements of $\varphi ({\widehat{x}}_i)$, and $\Psi (\widehat{x})$ is a $11\times 2$ matrix with elements of $\psi ({\widehat{x}}_i)$. $\varphi ({\widehat{x}}_i)$ and $\psi ({\widehat{x}}_i)$ are represented by sigmoids of the form

$$\begin{array}{l}\varphi ({\widehat{x}}_i)=\frac{m_1}{1+e^{-{\delta }_1{\widehat{x}}_i}}\\ \psi ({\widehat{x}}_i)=\frac{m_2}{1+e^{-{\delta }_2{\widehat{x}}_i}}+k\hspace{1em}i=1,2,\cdots ,11\end{array},$$

(7)

where $m_1,m_2,{\delta }_1$ and ${\delta }_2$ are constants representing the bound and slope of the sigmoid’s curvature and $k>0$ is a constant that shifts the sigmoid, such that $\psi ({\widehat{x}}_i)>0,i=1,2,\cdots ,11$.

3.2. Online Updating for DNN

Assume there exists weight values $W^{\ast }$ and ${\beta }^{\ast }$ such that the system (4) can be approximated by the model

$$\begin{array}{l}\dot{x}=Ax+B{W}^{\ast }\Phi (x)+B{\beta }^{\ast }\Psi (x)u+\omega (x,u)\\ y=x\end{array}.$$

(8)

Define the error between (5) and (8) as $e=y-\widehat{y}=x-\widehat{x}$. Assuming $\omega (x,u)$ is zero, we obtain

$$\dot{e}=Ae+B\tilde{W}\Phi (\widehat{x})+B\tilde{\beta }\Psi (\widehat{x})u,$$

(9)

where $\tilde{W}=W^{\ast }-\widehat{W}$ and $\tilde{\beta }={\beta }^{\ast }-\widehat{\beta }$ which are undated by the adaptive law (15) and (16) derived later.

To obtain the stable updating laws, the Lyapunov second law is used. Considering the following Lyapunov function

$$V=\frac{1}{2}{e}^{T}Pe+{\displaystyle \sum _{i=1}^{11}\frac{1}{2{\eta }_i}{\tilde{W}}_i}{\tilde{W}}_i^T+{\displaystyle \sum _{i=1}^{11}\frac{1}{2{\lambda }_i}{\tilde{\beta }}_i{\tilde{\beta }}_i^T},$$

(10)

where ${\eta }_i$ and ${\lambda }_i$ are positive constant which is referred to as the learning rate of the DNN, ${\tilde{W}}_i$ and ${\tilde{\beta }}_i$ is the ith row vector of matrix $\tilde{W}$ and $\tilde{\beta }$, respectively, i.e. $\tilde{W}={\left[\begin{array}{cccc}{\tilde{W}}_1& {\tilde{W}}_2& \cdots & {\tilde{W}}_{11}\end{array}\right]}^T,\tilde{\beta }={\left[\begin{array}{cccc}{\tilde{\beta }}_1& {\tilde{\beta }}_2& \cdots & {\tilde{\beta }}_{11}\end{array}\right]}^T$. And because $\beta$ is a $11\times 11$ diagonal matrix, then ${\tilde{\beta }}_i=\left[\begin{array}{ccccccc}0& \cdots & 0& {\tilde{\beta }}_{ii}& 0& \cdots & 0\end{array}\right],i=1,2,\dots ,11$.

The derivative of the Lyapunov function is

$$\dot{V}=\frac{1}{2}{\dot{e}}^{T}Pe+\frac{1}{2}{e}^{T}P\dot{e}+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\eta }_i}}{\tilde{W}}_i{\dot{\tilde{W}}}_i^T+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\lambda }_i}}{\tilde{\beta }}_i{\dot{\tilde{\beta }}}_i^T.$$

(11)

When Substituted (9) into (11), we obtain

$$\begin{array}{l}\dot{V}=\frac{1}{2}{e}^T{A}^{T}Pe+\frac{1}{2}{e}^{T}PAe+\frac{1}{2}{\left(B\tilde{W}\Phi (\widehat{x})+B\tilde{\beta }\Psi (\widehat{x})u\right)}^{T}Pe\\ \hspace{1em}\hspace{0.17em}+\frac{1}{2}{e}^{T}P\left(B\tilde{W}\Phi (\widehat{x})+B\tilde{\beta }\Psi (\widehat{x})u\right)+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\eta }_i}}{\tilde{W}}_i{\dot{\tilde{W}}}_i^T+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\lambda }_i}}{\tilde{\beta }}_i{\dot{\tilde{\beta }}}_i^T\end{array},$$

(12)

where $P>0$ satisfies the Lyapunov equation $PA+A^{T}P=-Q$.

Since ${\Phi }^T(\widehat{x}){\tilde{W}}^T{B}^{T}Pe$ and $u^T{\Psi }^T(\widehat{x}){\tilde{\beta }}^T{B}^{T}Pe$ are scalars, that is

$$\begin{array}{l}{\Phi }^T(\widehat{x}){\tilde{W}}^T{B}^{T}Pe=e^{T}PB\tilde{W}\Phi (\widehat{x})\\ u^T{\Psi }^T(\widehat{x}){\tilde{\beta }}^T{B}^{T}Pe=e^{T}PB\tilde{\beta }\Psi (\widehat{x})u\end{array}.$$

(13)

Hence, Equation (12) will be

$$\begin{array}{l}\dot{V}=-\frac{1}{2}{e}^{T}Qe+e^{T}P\left(B\tilde{W}\Phi (\widehat{x})+B\tilde{\beta }\Psi (\widehat{x})u\right)+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\eta }_i}}{\tilde{W}}_i{\dot{\tilde{W}}}_i^T+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\lambda }_i}}{\tilde{\beta }}_i{\dot{\tilde{\beta }}}_i^T\\ \hspace{1em}=-\frac{1}{2}{e}^{T}Qe+e^{T}PB\tilde{W}\Phi (\widehat{x})+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\eta }_i}}{\tilde{W}}_i{\dot{\tilde{W}}}^T+e^{T}PB\tilde{\beta }\Psi (\widehat{x})u+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\lambda }_i}}{\tilde{\beta }}_i{\dot{\tilde{\beta }}}_i^T\\ \hspace{1em}=-\frac{1}{2}{e}^{T}Qe+e^{T}PB\left[\begin{array}{c}{\tilde{W}}_1\\ {\tilde{W}}_2\\ ⋮\\ {\tilde{W}}_{11}\end{array}\right]\Phi (\widehat{x})+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\eta }_i}}{\tilde{W}}_i{\dot{\tilde{W}}}^T+e^{T}PB\left[\begin{array}{c}{\tilde{\beta }}_1\\ {\tilde{\beta }}_2\\ ⋮\\ {\tilde{\beta }}_{11}\end{array}\right]\Psi (\widehat{x})u+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\lambda }_i}}{\tilde{\beta }}_i{\dot{\tilde{\beta }}}_i^T\\ \hspace{1em}=-\frac{1}{2}{e}^{T}Qe+{\displaystyle \sum _{i=1}^{11}{e}_i{p}_i{b}_i{\tilde{W}}_i}\Phi (\widehat{x})+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\eta }_i}}{\tilde{W}}_i{\dot{\tilde{W}}}_i{}^T+{\displaystyle \sum _{i=1}^{11}{e}_i{p}_i{b}_i{\tilde{\beta }}_i}\Psi (\widehat{x})u+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\lambda }_i}}{\tilde{\beta }}_i{\dot{\tilde{\beta }}}_i^T\end{array},$$

(14)

where $e=\left[\begin{array}{c}{e}_1\\ e_2\\ ⋮\\ e_{11}\end{array}\right],P=\left[\begin{array}{cccc}{p}_1& 0& \cdots & 0\\ 0& p_2& & ⋮\\ ⋮& & \ddots & 0\\ 0& \cdots & 0& p_{11}\end{array}\right]$.

If ${\displaystyle \sum _{i=1}^{11}{e}_i{p}_i{b}_i{\tilde{W}}_i}\Phi (\widehat{x})+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\eta }_i}}{\tilde{W}}_i{\dot{\tilde{W}}}^T=0$, i.e.,

$${\dot{\tilde{W}}}_i{}^T=-{\eta }_i{e}_i{p}_i{b}_i\Phi (\widehat{x}),i=1,2,\cdots ,11$$

(15)

and ${\displaystyle \sum _{i=1}^{11}{e}_i{p}_i{b}_i{\tilde{\beta }}_i}\Psi (\widehat{x})u+{\displaystyle \sum _{i=1}^{11}\frac{1}{{\lambda }_i}}{\tilde{\beta }}_i{\dot{\tilde{\beta }}}_i^T=0$, i.e.,

$${\dot{\tilde{\beta }}}_i^T=-{\lambda }_i{e}_i{p}_i{b}_i\Psi (\widehat{x})u,i=1,2,\cdots ,11.$$

(16)

$\beta$ is a $11\times 11$ diagonal matrix,

$${\dot{\tilde{\beta }}}_{ii}=-{\lambda }_i{e}_i{p}_i{b}_i{\Psi }_i(\widehat{x})u,i=1,2,\cdots ,11,$$

(17)

where ${\Psi }_i(\widehat{x})$ is the ith row vector of matrix $\Psi (\widehat{x})$.

Then,

$$\dot{V}=-\frac{1}{2}{e}^{T}Qe\le 0.$$

(18)

The above equation illustrates that $\dot{V}$ is negative semidefinite and the identification error is convergent. Using Barbalat’s lemma [38,39], it can be seen that as $t\to \infty$ and $e\to 0$.

4. Dynamic Inverse Controller Design Based on the DNN Model

In order to realize the tracking control of FAHV velocity and altitude, a controller is designed based on the DNN model (5).

Assume that the reference signal is $z_r$, the output tracking error is

$$e_m=z_r-z.$$

(19)

Taking time derivative of $e_m$ and using (5), we have

$$\begin{array}{l}{\dot{e}}_m={\dot{z}}_r-C\dot{\widehat{x}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\dot{z}}_r-CA\widehat{x}-CB\widehat{W}\Phi (\widehat{x})-CB\widehat{\beta }\Psi (\widehat{x})u\end{array}.$$

(20)

Design the linearizing feedback control law as

$$u={\left(CB\widehat{\beta }\Psi (\widehat{x})\right)}^{-1}\left({\dot{z}}_r-CA\widehat{x}-CB\widehat{W}\Phi (\widehat{x})+K{e}_m\right),$$

(21)

where $K=diag\left\{k_i\right\},k_i>0,i=1,2$.

Then, substituting (21) into (20), we obtain

$${\dot{e}}_m=-K{e}_m.$$

(22)

Therefore, the error $e_m$ will converge to the origin exponentially.

Remark 2. 

To apply the control law (21), we have to assure the existence of ${\left(CB\widehat{\beta }\Psi (\widehat{x})\right)}^{-1}$.

To analyze the existence of ${\left(CB\widehat{\beta }\Psi (\widehat{x})\right)}^{-1}$, the learning laws (15) and (17) can be written in matrix form as

$$\begin{array}{l}\dot{\widehat{W}}=-\dot{\tilde{W}}=\eta EPBS\\ \dot{\widehat{\beta }}=-\dot{\tilde{\beta }}=\lambda EPB{S}_{1}U\end{array},$$

(23)

where $\eta =\left[\begin{array}{cccc}{\eta }_1& & & \\ & {\eta }_2& & \\ & & \ddots & \\ & & & {\eta }_{11}\end{array}\right],$ $E=\left[\begin{array}{cccc}{e}_1& & & \\ & e_2& & \\ & & \ddots & \\ & & & e_{11}\end{array}\right],$ $S=\left[\begin{array}{c}{\Phi }^T(\widehat{x})\\ {\Phi }^T(\widehat{x})\\ ⋮\\ {\Phi }^T(\widehat{x})\end{array}\right],$$\lambda =\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_{11}\end{array}\right],$$S_1=\left[\begin{array}{cccc}{\Psi }_1(\widehat{x})& & & \\ & {\Psi }_2(\widehat{x})& & \\ & & \ddots & \\ & & & {\Psi }_3(\widehat{x})\end{array}\right],$ $U=\left[\begin{array}{cccc}u& & & \\ & u& & \\ & & \ddots & \\ & & & u\end{array}\right]$, B, and P are as listed in Equations (6) and (14), respectively.

For our problem, expand matrix $CB\widehat{\beta }\Psi (\widehat{x})$, and we have

$$\begin{array}{l}CB\widehat{\beta }\Psi (\widehat{x})=\left[\begin{array}{cccccc}1& 0& 0& 0& \cdots & 0\\ 0& 0& 1& 0& \cdots & 0\end{array}\right]\left[\begin{array}{cccc}{b}_1& & & \\ & b_2& & \\ & & \ddots & \\ & & & b_{11}\end{array}\right]\left[\begin{array}{cccc}{\widehat{\beta }}_{11}& 0& \cdots & 0\\ 0& {\widehat{\beta }}_{22}& & ⋮\\ ⋮& & \ddots & 0\\ 0& \cdots & 0& {\widehat{\beta }}_{11,11}\end{array}\right]\left[\begin{array}{cc}{\psi }_{11}& {\psi }_{12}\\ {\psi }_{21}& {\psi }_{22}\\ ⋮& ⋮\\ {\psi }_{11,1}& {\psi }_{11,2}\end{array}\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left[\begin{array}{cc}{b}_1{\widehat{\beta }}_{11}{\psi }_{11}& b_1{\widehat{\beta }}_{11}{\psi }_{12}\\ b_3{\widehat{\beta }}_{33}{\psi }_{31}& b_3{\widehat{\beta }}_{33}{\psi }_{32}\end{array}\right]\end{array}.$$

(24)

Since B and $\widehat{\beta }$ are diagonal matrices and $b_i\ne 0,\forall i=1,2,\cdots ,n$, and because the outputs of the FAHV are the velocity and the altitude, we only need to meet the condition ${\widehat{\beta }}_{11}\ne 0$ and ${\widehat{\beta }}_{33}\ne 0$. A projection algorithm was proposed to assure the condition [27,28,40], but it needs to know the optimal value of ${\beta }^{\ast }$, and this is difficult to obtain.

As can be seen from (24), to guarantee that $CB\widehat{\beta }\Psi (\widehat{x})$ is reversible, one can make the elements ${\psi }_{12}$ and ${\psi }_{31}$ equal to zero when generating matrix $\Psi (\widehat{x})$. Additionally, it is seen from (23) that the condition ${\widehat{\beta }}_{11}\ne 0$ and ${\widehat{\beta }}_{33}\ne 0$ can be satisfied by adjusting the parameters $\lambda$ and $B$.

5. Simulation Results and Analysis

To illustrate the effectiveness of the proposed adaptive identification model and dynamic inverse control, simulation studies were carried out under stochastic constant control and dynamic inverse control. The parameters of the identification model are selected as $A=-0.001I$,$B=0.1I$, $m_1=0.5$, $m_2=1.3$, ${\delta }_1={\delta }_2=0.0001$, $k=0.4$, ${\eta }_i=1,i=1,2,\cdots ,11$, and ${\lambda }_i=1,i=1,2,\cdots ,11$. The initial velocity and altitude errors of the real system and identification system are taken as 10 and 30, respectively.

5.1. System Identification under Stochastic Constant Control

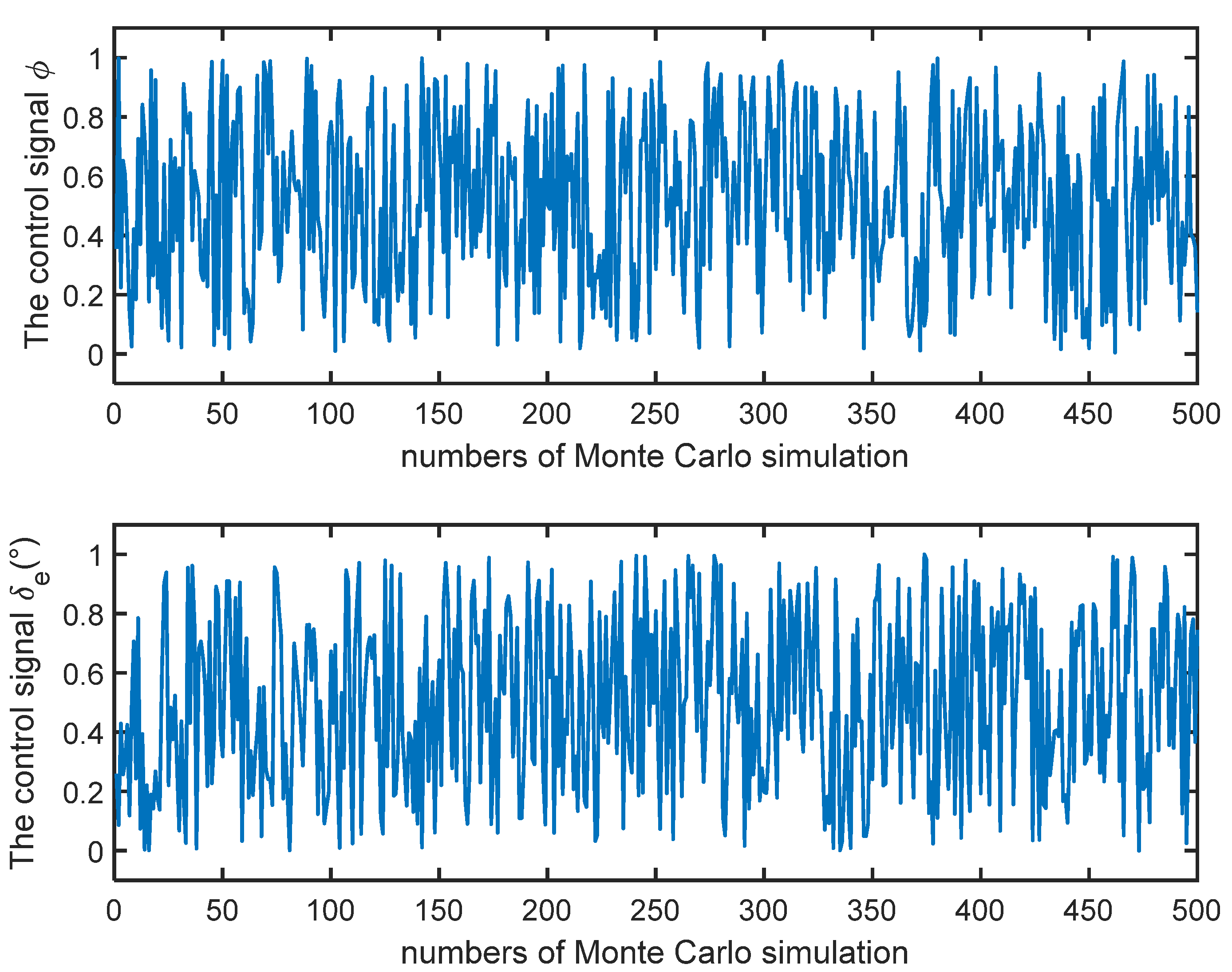
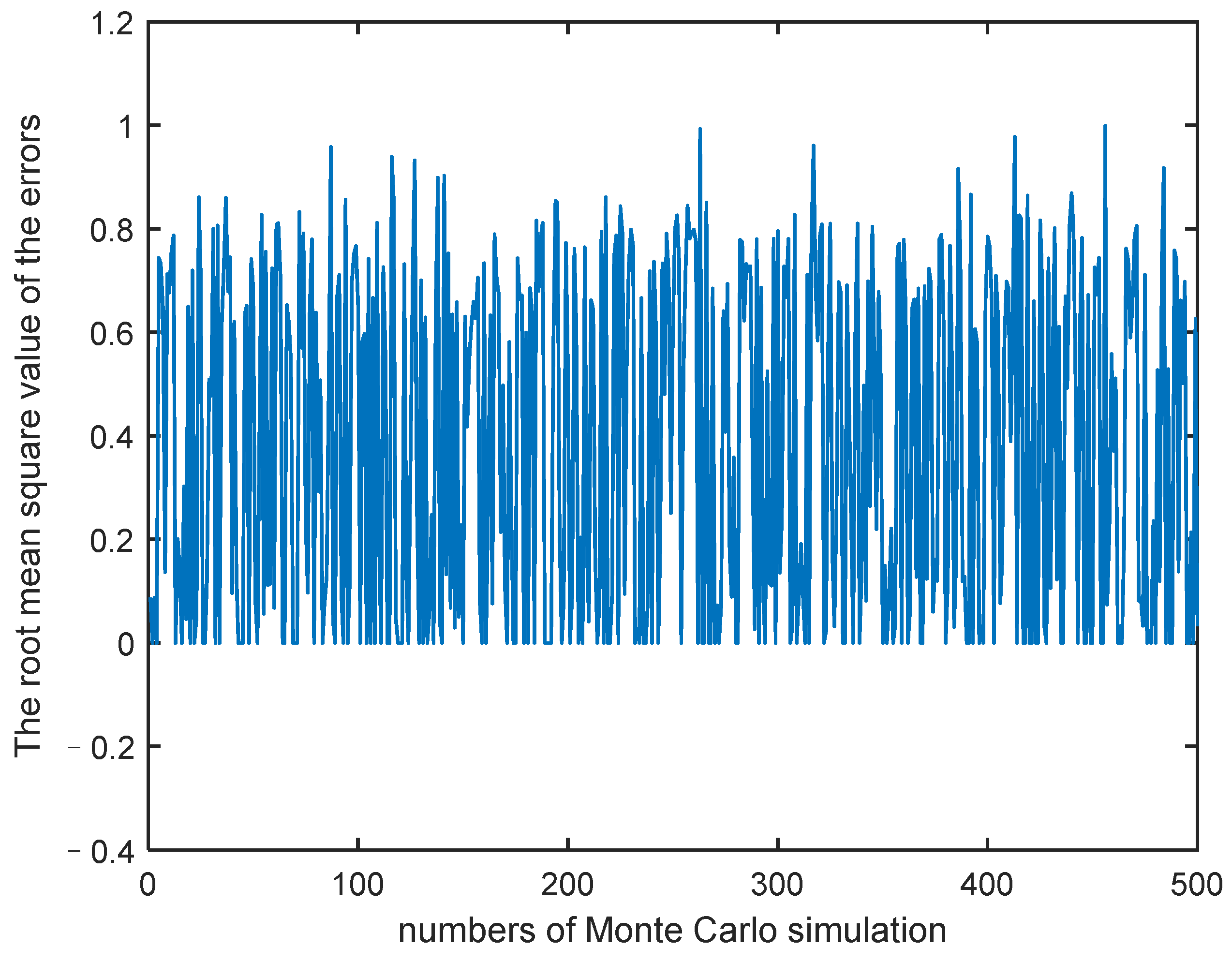
Firstly, in order to verify the effectiveness of the identification method, simulation analysis is carried out under the randomly generated constant control signals. A total of 500 times Monte Carlo simulations is performed. The constant control quantity of 500 times is shown in Figure 1, and the root mean square (RMS) values of the errors of the true system and identification system are shown in Figure 2. It is seen from Figure 2 that the RMS value of the final error is less than one, indicating that the identification model has high precision.

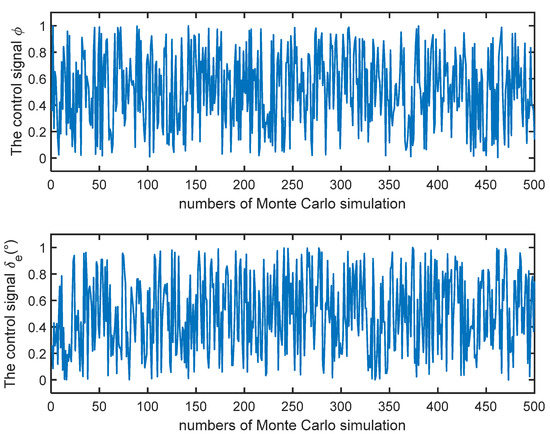
Figure 1. 500 times random control signals.

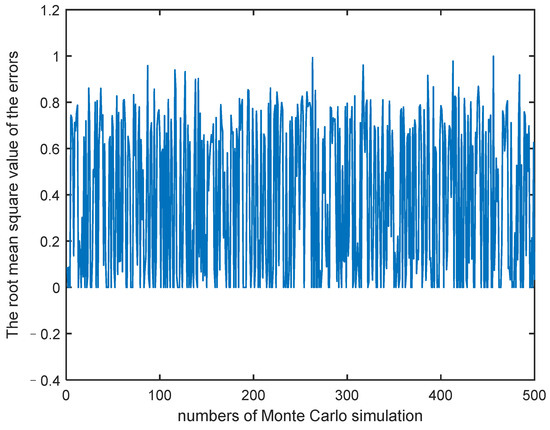
Figure 2. The root mean square values of the errors of true system (TS) and identification system (IS).

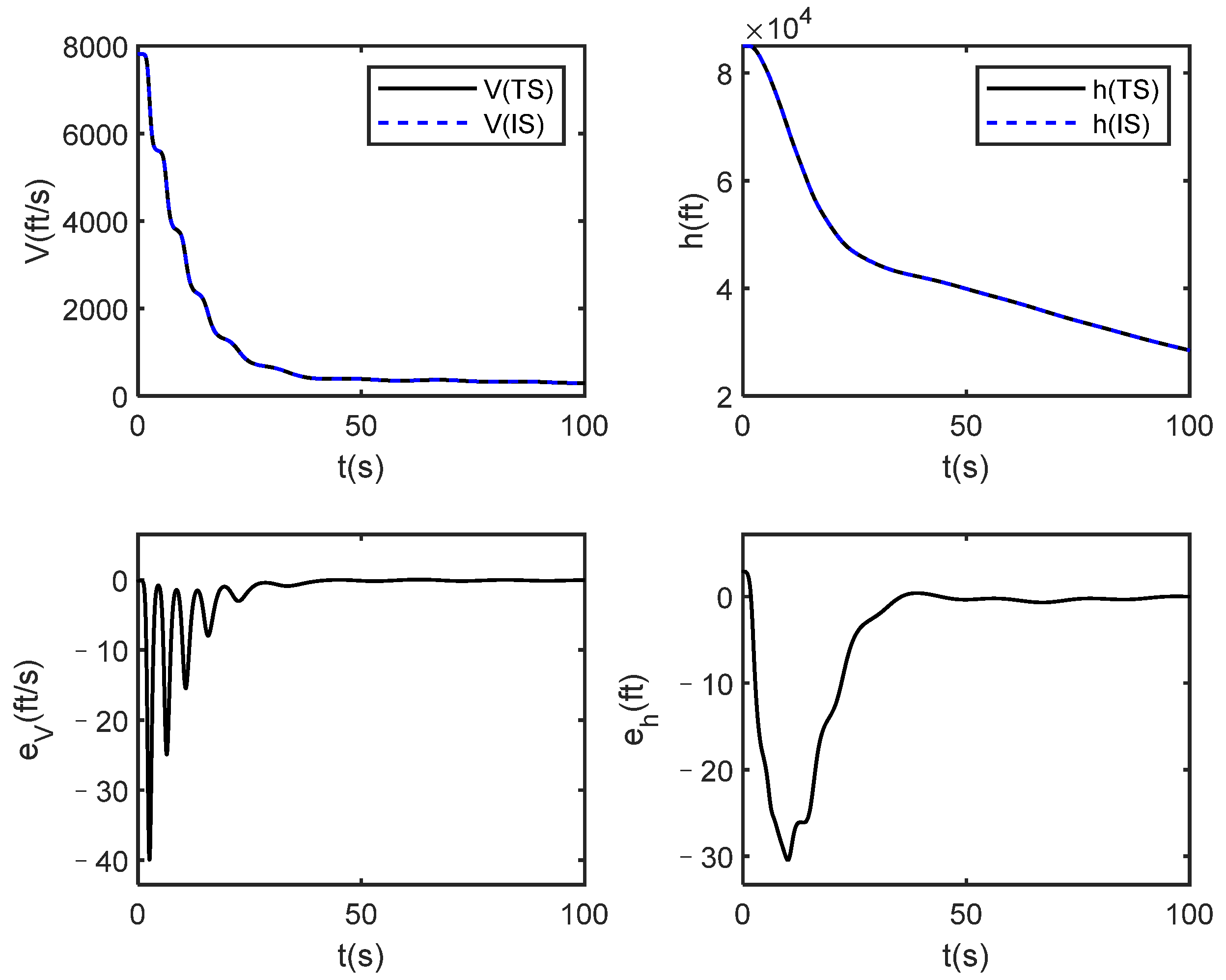
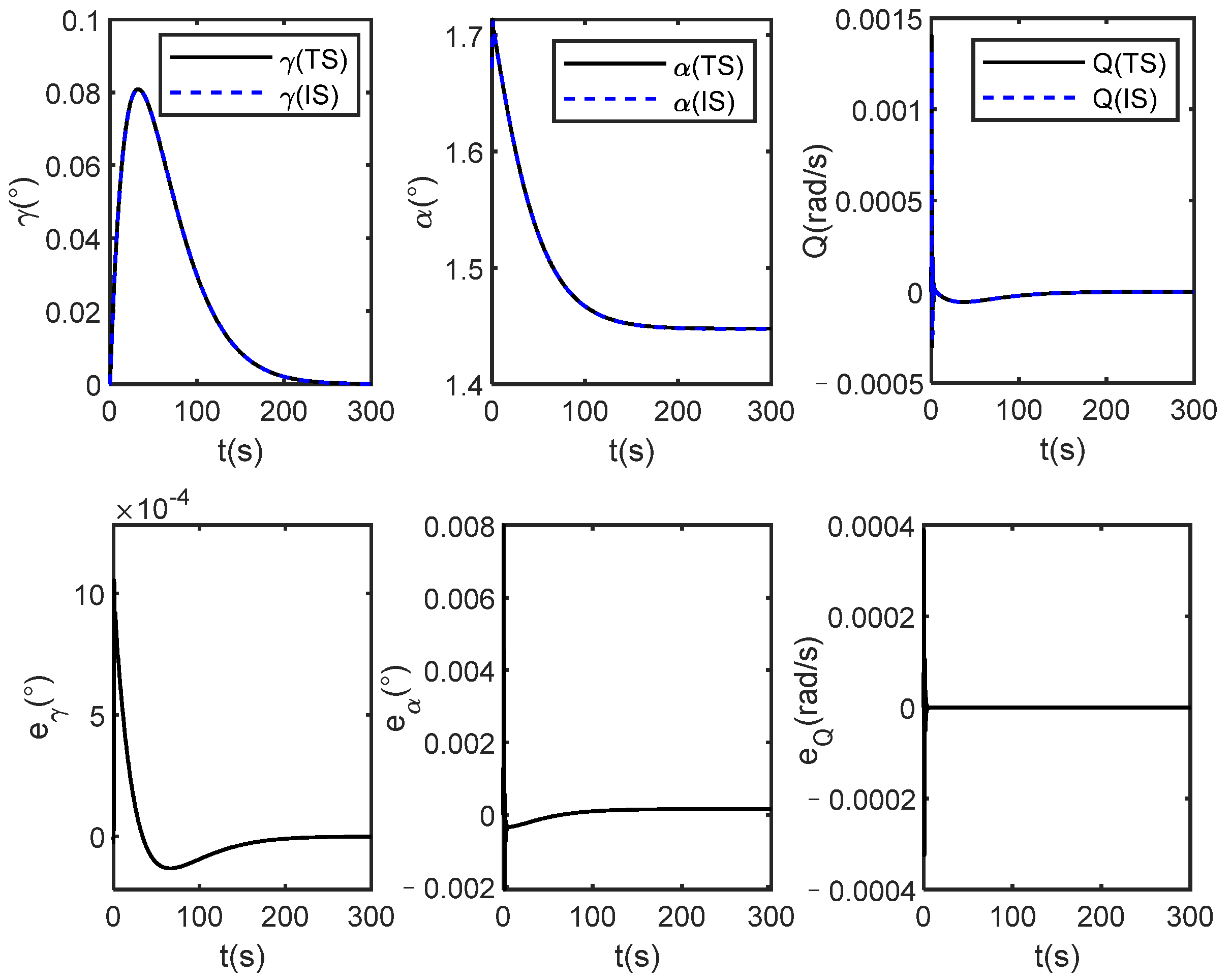
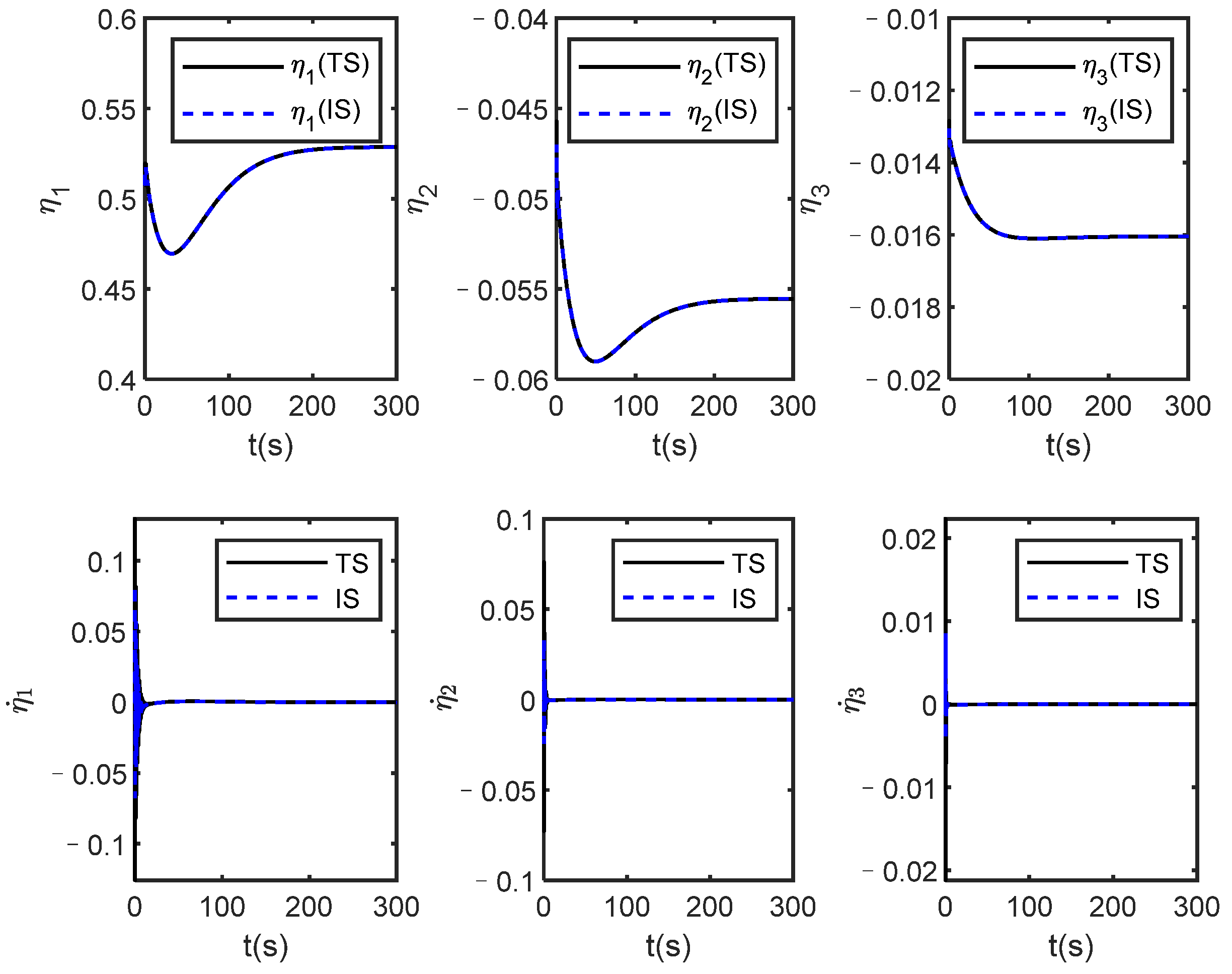
Figure 3, Figure 4, Figure 5 and Figure 6 show the simulation results under one of the constant control signals, and the control law is $u={\left[\begin{array}{cc}0.013& {6.303}^{\circ }\end{array}\right]}^T$. In this case, since the control law is arbitrarily given, the rigid body states are divergent, but the states of the identification system are infinitely close to the actual system from the upper part of Figure 2 and Figure 3. In addition, it can be seen from the bottom half of Figure 2, Figure 3 and Figure 4 that all state errors finally converge to 0, which verifies that the proposed identification method is effective, and it is independent of the controller design.

Figure 3. Control signals—stochastic constant control law u.

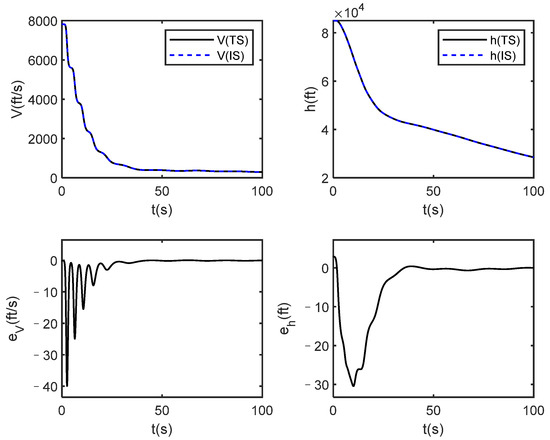
Figure 4. Outputs and errors of true system (TS) and identification system (IS) under stochastic constant control law u.

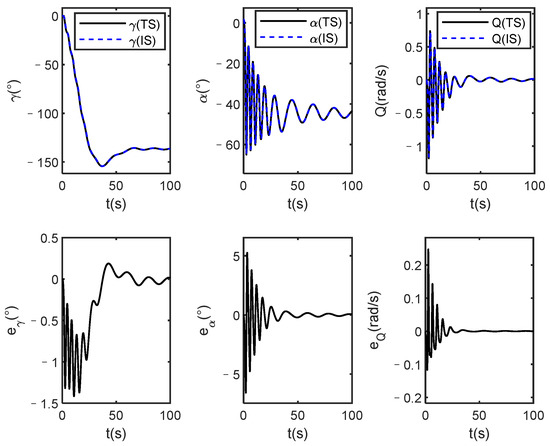
Figure 5. Altitude angles and errors of true system (TS) and identification system (IS) under stochastic constant control law u.

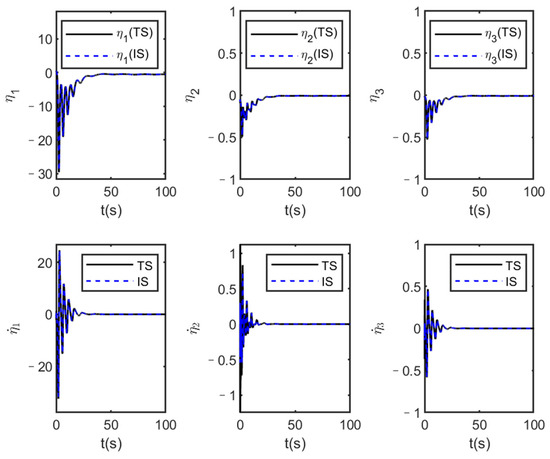
Figure 6. The flexible states of true system (TS) and identification system (IS) under stochastic constant control law u.

5.2. System Identification and Tracking under Dynamic Inverse Control

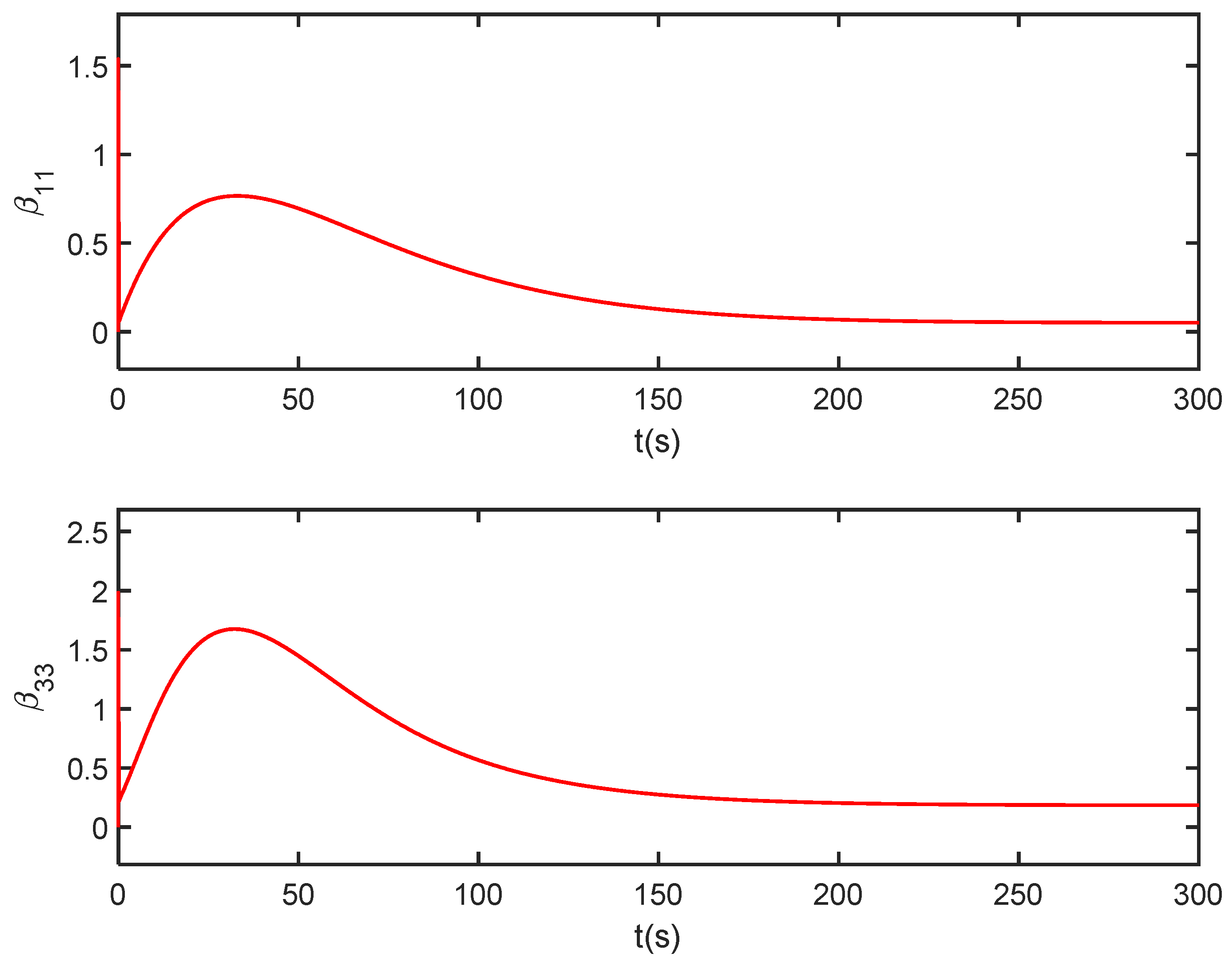
Secondly, in order to verify the effectiveness of the dynamic inverse control based on the identification model. The simulation results under dynamic inverse control law are given, as shown in Figure 7, Figure 8, Figure 9 and Figure 10, and the curves of the estimated parameter ${\beta }_{11}$ and ${\beta }_{33}$ are shown in Figure 11.

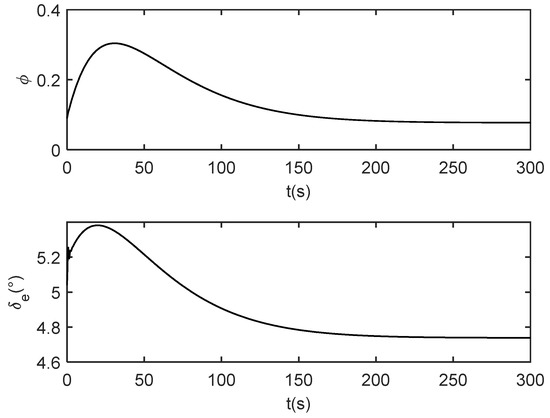
Figure 7. Dynamic inverse control law.

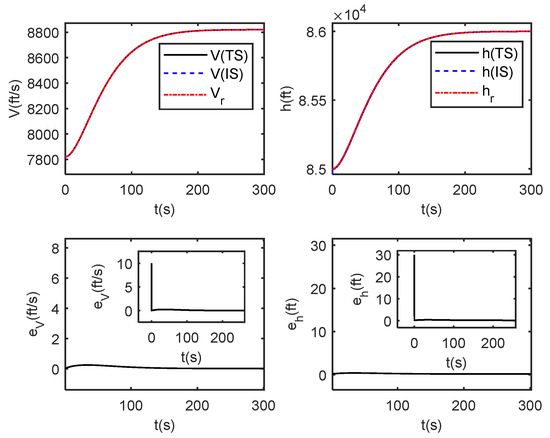
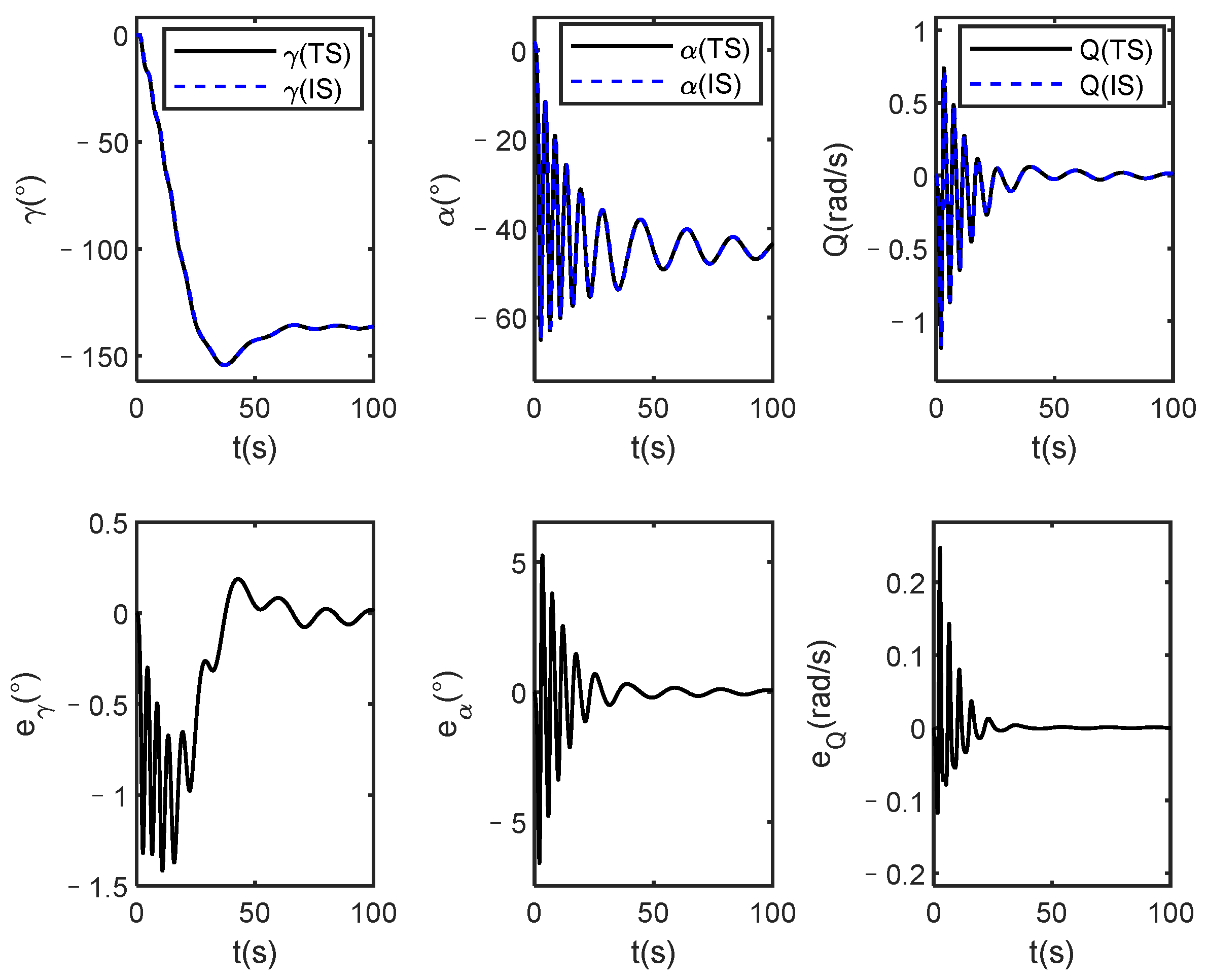
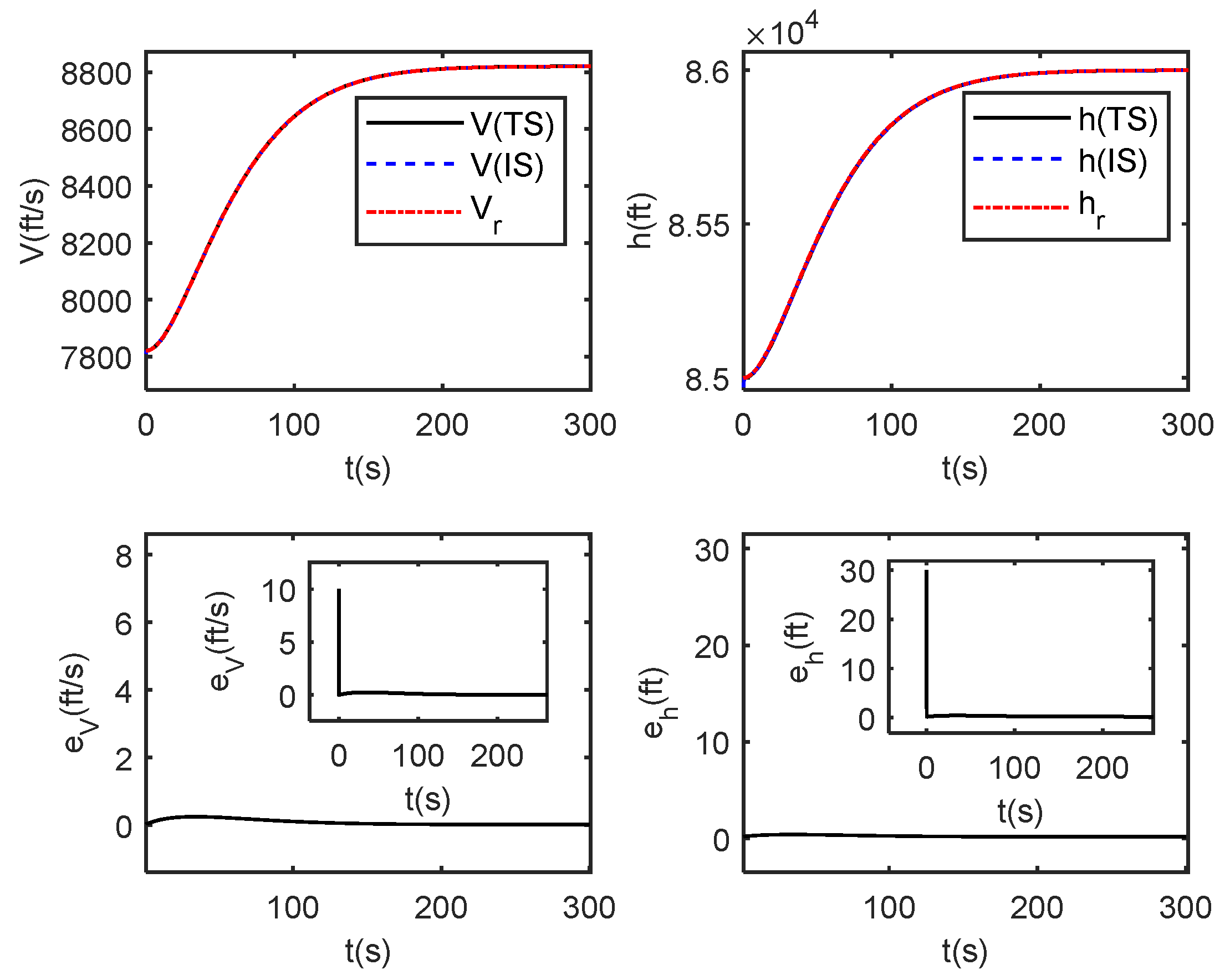
Figure 8. Output tracking curves and errors between true system (TS) and identification system (IS) under dynamic inverse control.

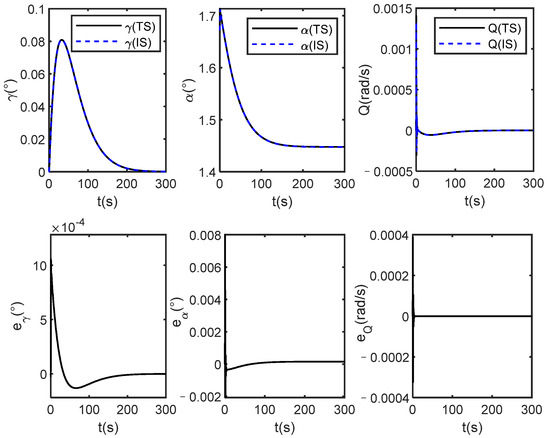
Figure 9. Altitude angles and errors of true system (TS) and identification system (IS) under dynamic inverse control.

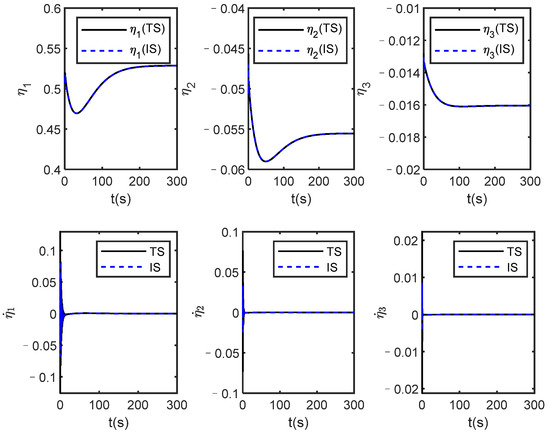
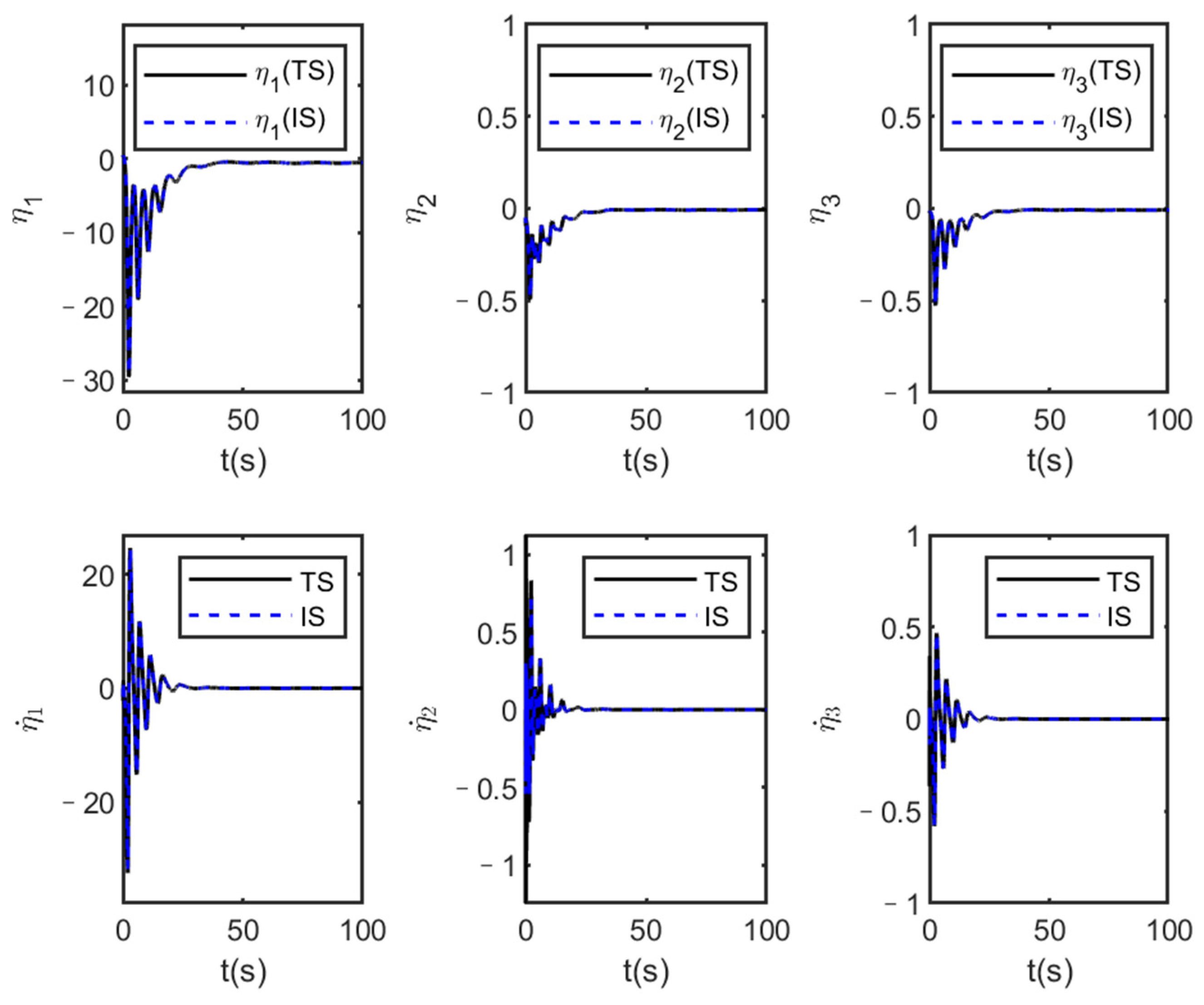
Figure 10. The flexible states of true system (TS) and identification system (IS) under dynamic inverse control.

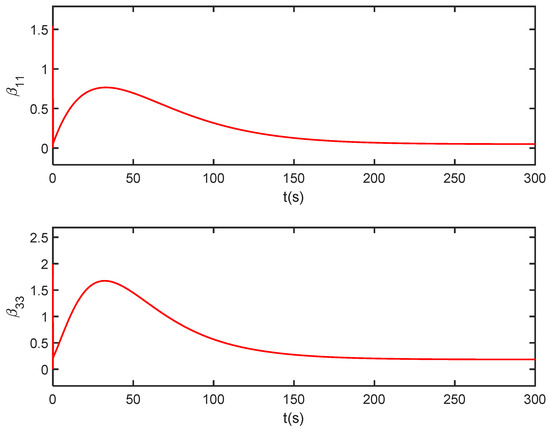
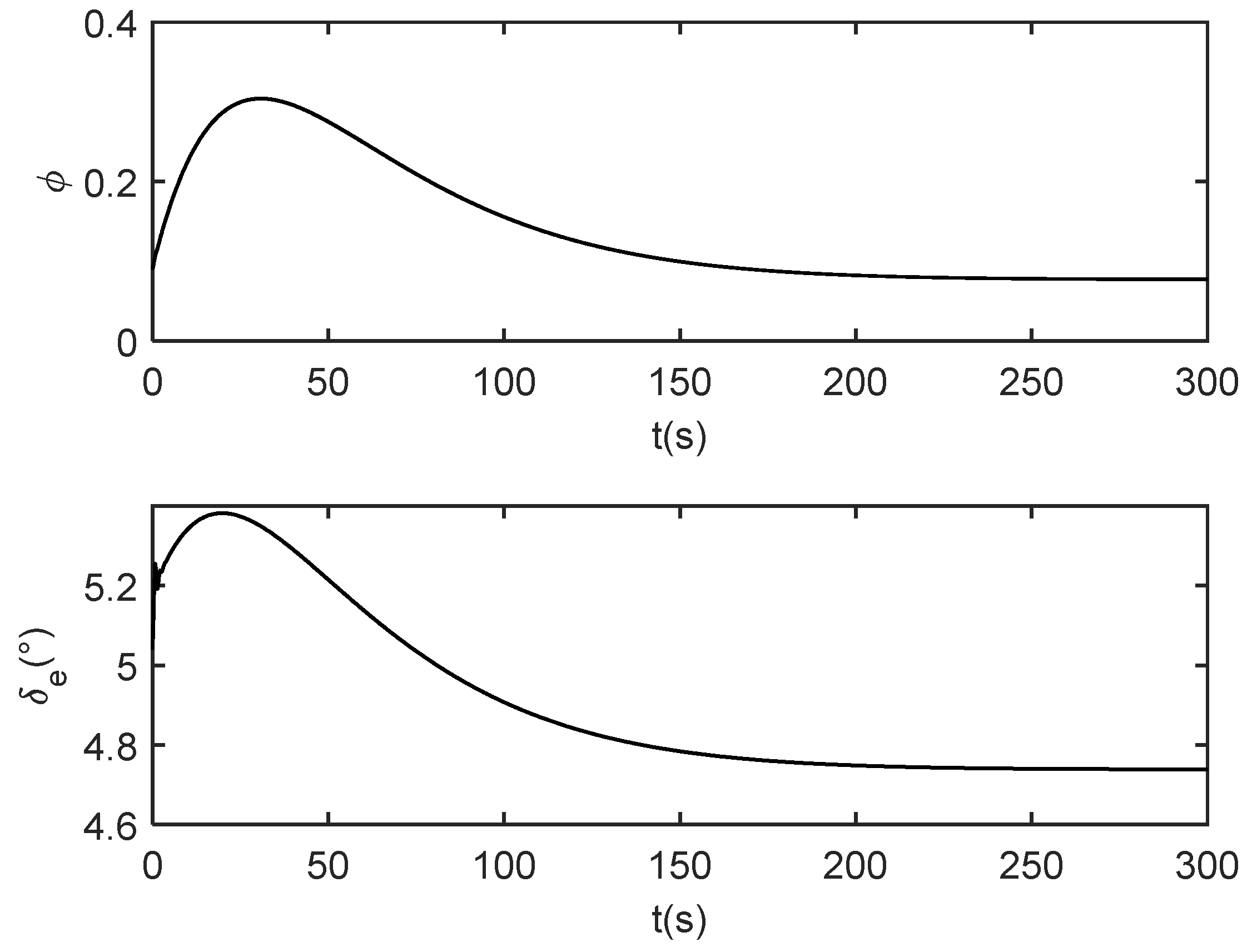
Figure 11. Curves of the estimated parameter ${\beta }_{11}$ and ${\beta }_{33}$ under dynamic inverse control.

In this case, the vehicle starts at initial trim conditions as listed in Table 2. and tracks the reference trajectories of velocity and altitude generated by the second-order filters with natural frequency $\omega =0.03 \mathrm{rad}/\mathrm{s}$ and the damping ratio $\varsigma =0.95$.

$$\begin{array}{l}{V}_{ref}(s)={\omega }^2{V}_c(s)/\left(s^2+2\varsigma \omega s+{\omega }^2\right)\\ h_{ref}(s)={\omega }^2{h}_c(s)/\left(s^2+2\varsigma \omega s+{\omega }^2\right)\end{array},$$

(25)

where the final reference commands are $V_c=8820 \mathrm{ft}/\mathrm{s}$ and $h_c=\mathrm{86,000} \mathrm{ft}$.

Table 2. States at initial trim conditions.

State	Value	State	Value
V (ft/s)	7820	${\eta }_1$	0.5099
$\gamma$ (deg)	0	${\dot{\eta }}_1$	0
h (ft)	85,000	${\eta }_2$	−0.0493
$\alpha$ (deg)	1.6444	${\dot{\eta }}_2$	0
Q (rad/s)	0	${\eta }_3$	−0.0136
		${\dot{\eta }}_3$	0

It is seen from Figure 8 that both the output of the actual system and the identification system track the given reference signal, and it is also seen that the identification system state quickly follows the actual system state. In addition, the attitude angle and elastic state of the identification system can also quickly converge to the state of the actual system as shown in Figure 9 and Figure 10. These show that the designed adaptive DNN identification method and dynamic inverse controller are effective. Additionally, from Figure 11, it is seen that the estimated values of the parameter ${\beta }_{11}$ and ${\beta }_{33}$ are not equal to 0 throughout the flight process which indicates that the selected parameters are valid.

Further observation of the simulation results under constant control law and dynamic inverse control, and it can be seen that under dynamic inverse control, the states of the identification system approach the states of the real system faster, because the weighting coefficient of the DNN is affected by the control law as shown in Equation (16).

In summary, although the DNN identification method is independent of the control law design, its performance will be affected by the control law.

5.3. Comparison with Back-Stepping Control Method

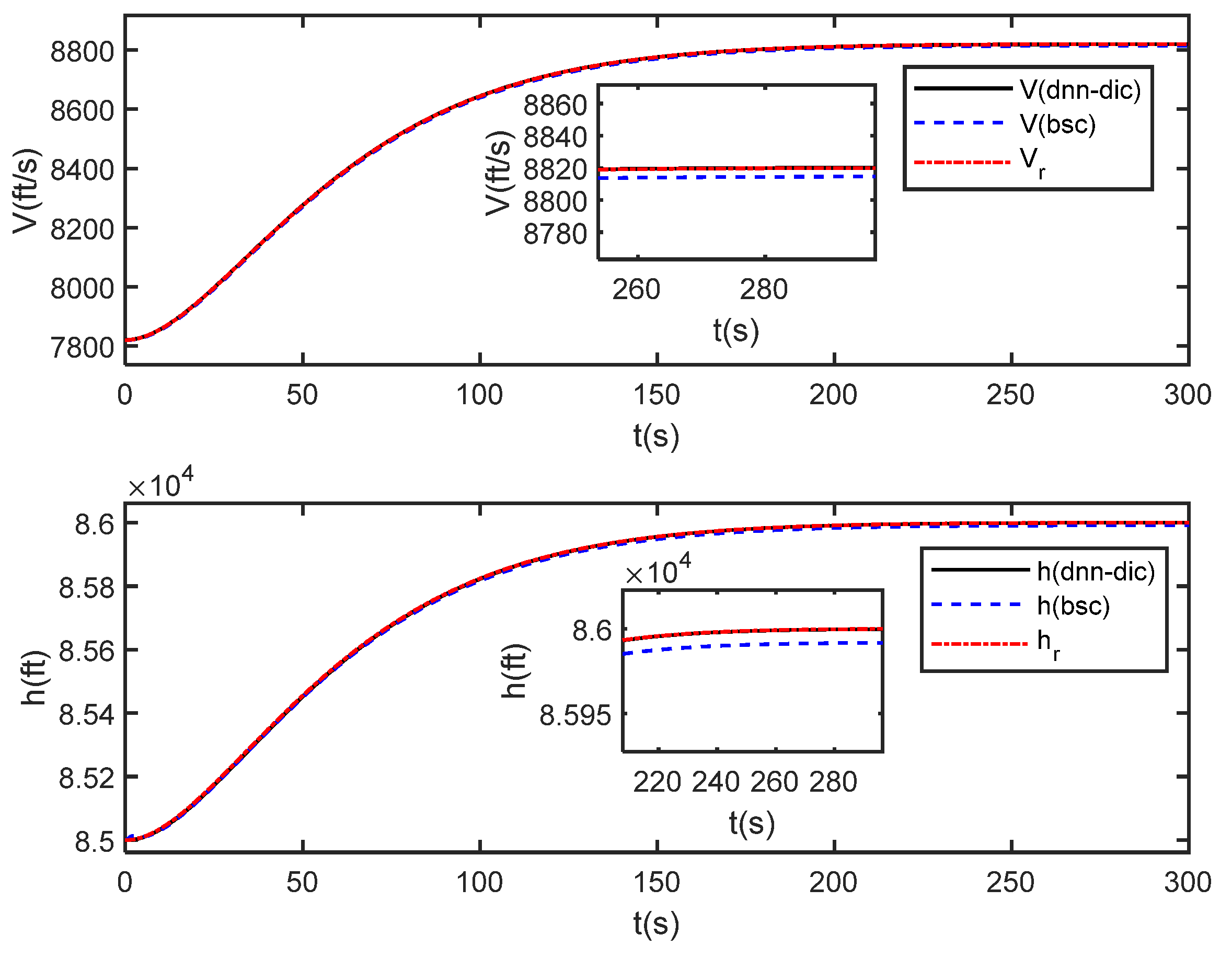
In order to illustrate the advantages of the proposed method, the proposed method is compared with the back-stepping control method [41]. The simulation conditions are set the same as Section 5.2, and the comparison curves of simulation results are shown in Figure 12, Figure 13 and Figure 14.

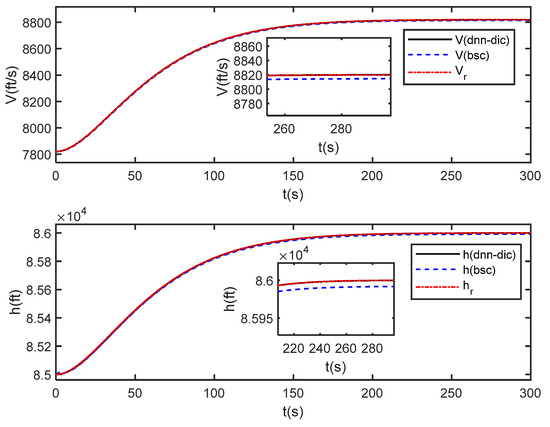
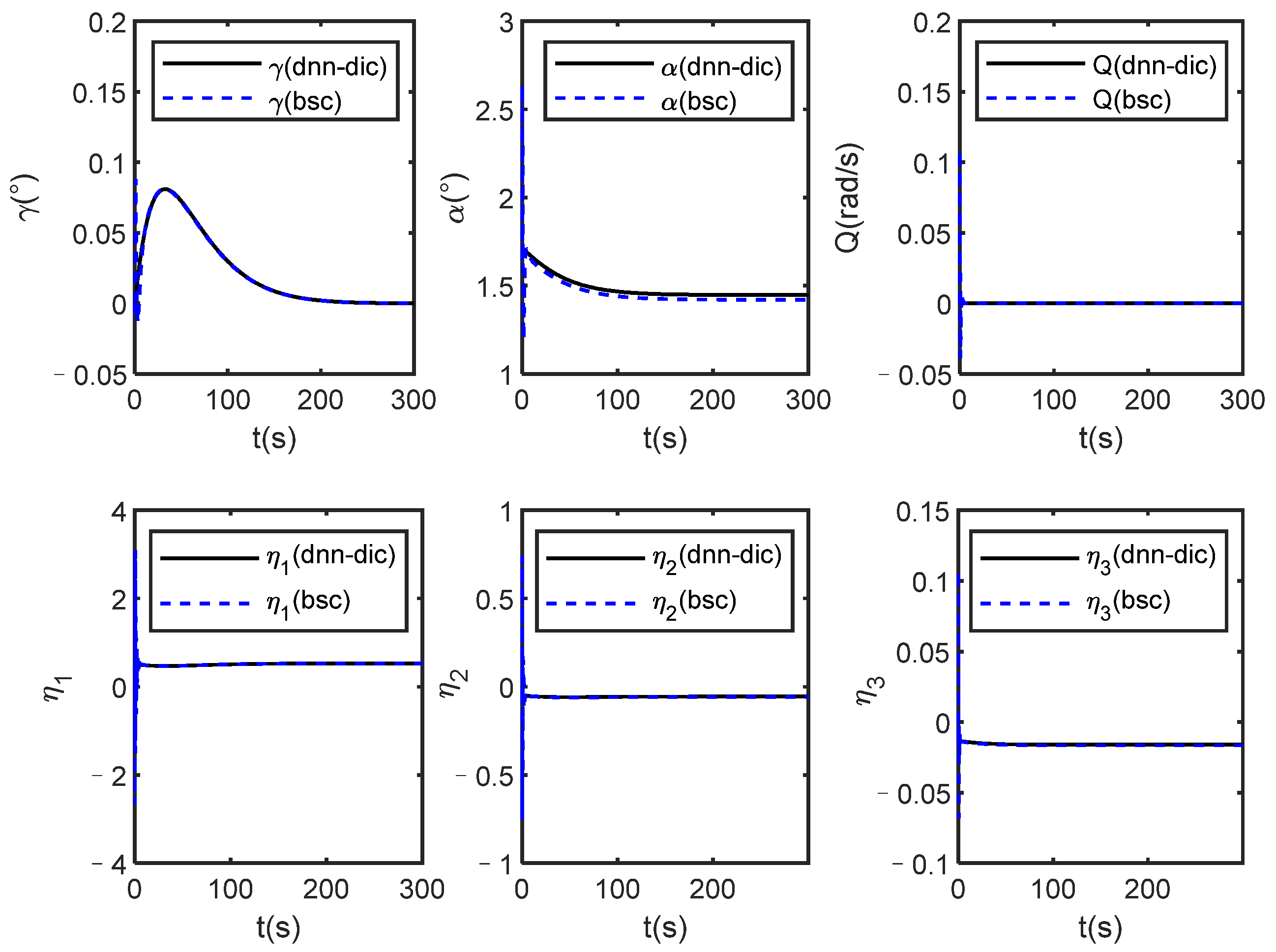
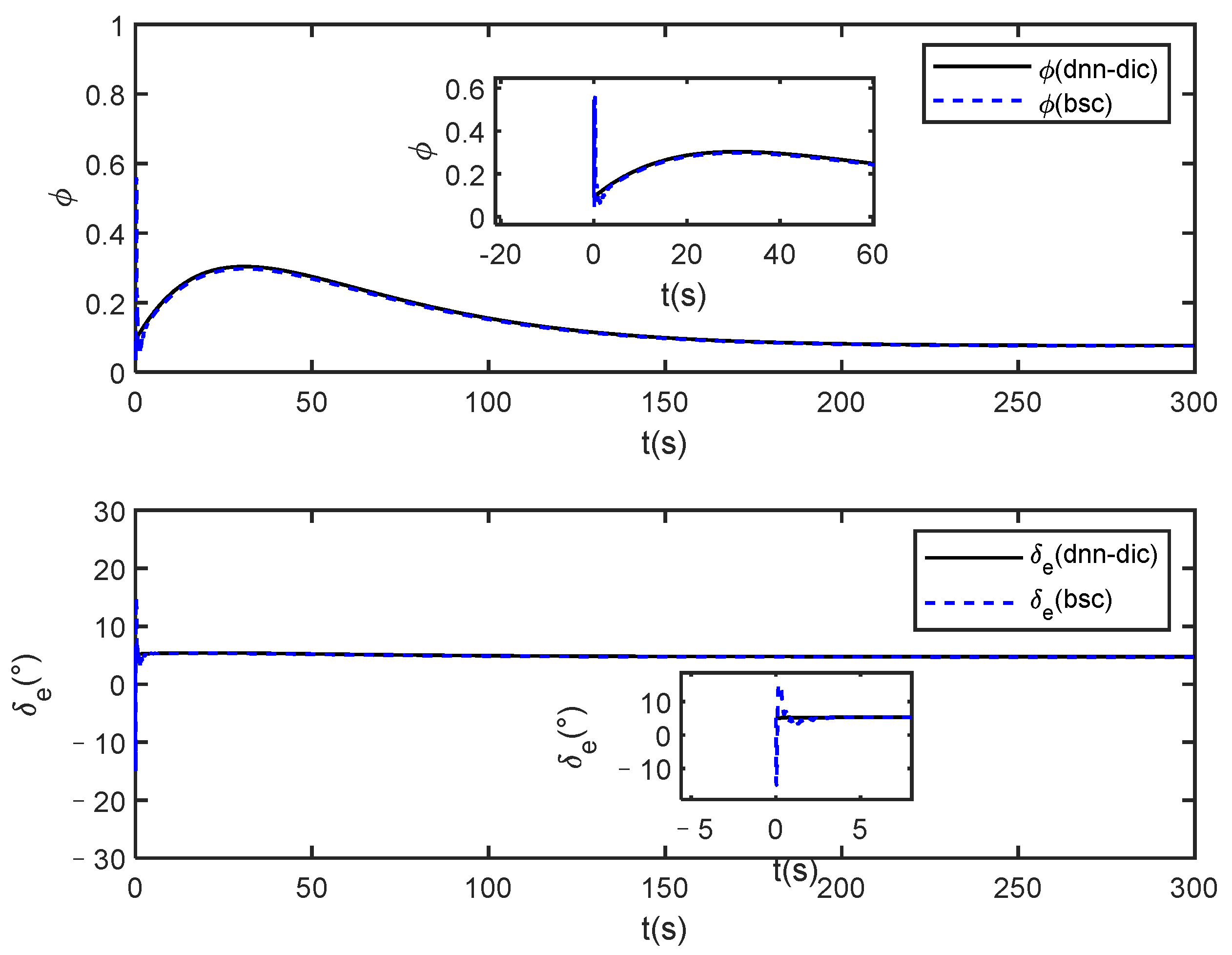
Figure 12. Comparison of trajectory tracking curves under dynamic neural network based dynamic inverse control (dnn-dic) and back-stepping control (bsc).

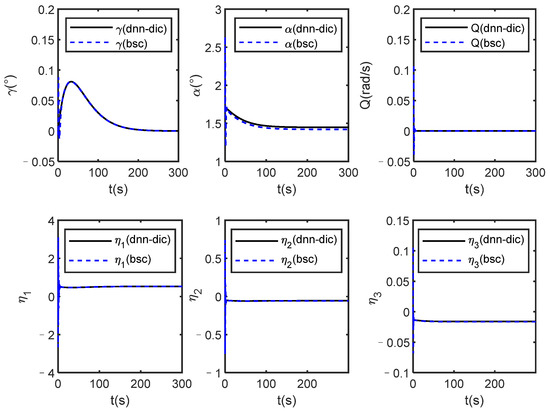
Figure 13. Comparison curves of other states under dnn-dic and bsc.

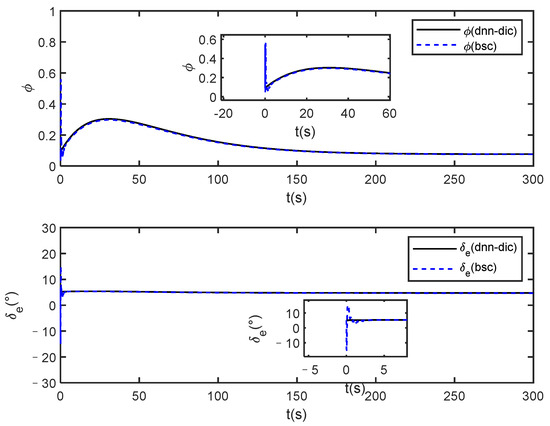
Figure 14. Control law comparison curve.

It can be seen from Figure 12 that both methods can track the given reference signals, and the local magnifications show that the proposed method has smaller steady-state tracking errors. The states of the HVs all converge under the two methods from Figure 13, and the back-stepping control method requires greater control initially from the local magnification of Figure 14.

6. Conclusions

In this article, a dynamic inverse control method based on DNN is proposed to achieve the trajectory tracking control for a FAHV. The designed DNN identification model does not need to know the motion equation of FAHV, and the parameters can be designed independently of the control law which is beneficial to engineering applications. The dynamic inverse control law is designed based on the identification model, the complex model transformations are avoided, and the controller design process is simplified which can be verified by the simulation. In future research, more practical problems faced by FAHV, such as constraints, external interference, and unpredictable elastic modes, will be considered.