Rapid Parametric Modeling and Robust Analysis for the Hypersonic Ascent Based on Gap Metrics
Abstract
:1. Introduction
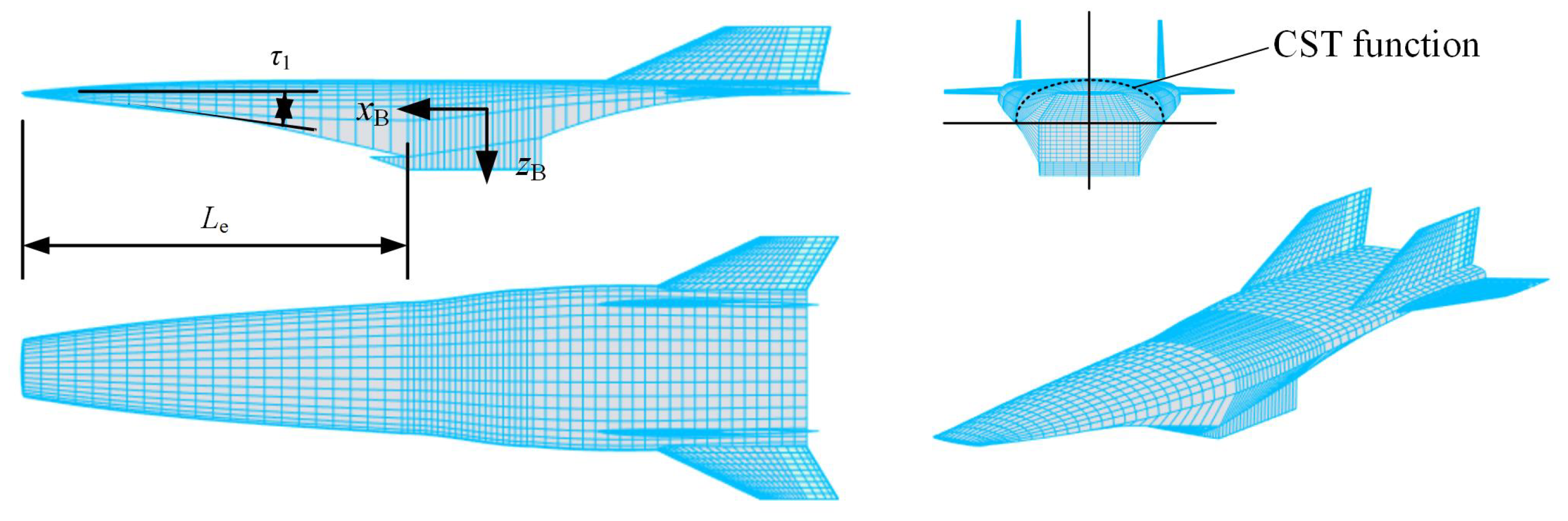
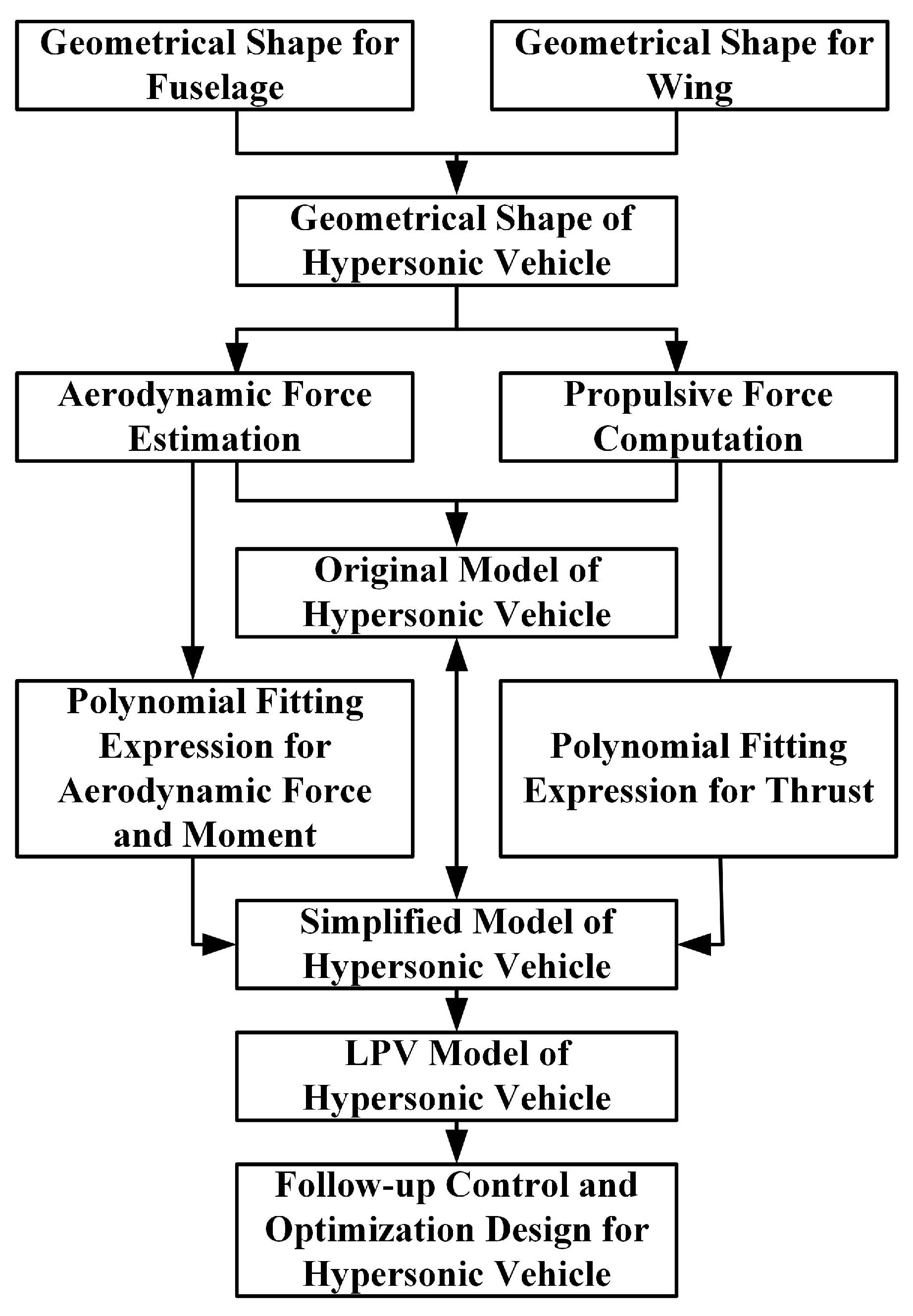
2. Model Description
2.1. Force Estimation
2.2. Longitudinal Dynamics
2.3. Polynomial Fitting Modeling
3. LPV Modeling Based on Gap Metric
4. Climbing Command and Track Controller Design
4.1. Velocity-Driven Climbing Command
4.2. Track Controller Design
5. Simulation Analysis
5.1. Static and Dynamic Analysis
5.2. Tracking Control
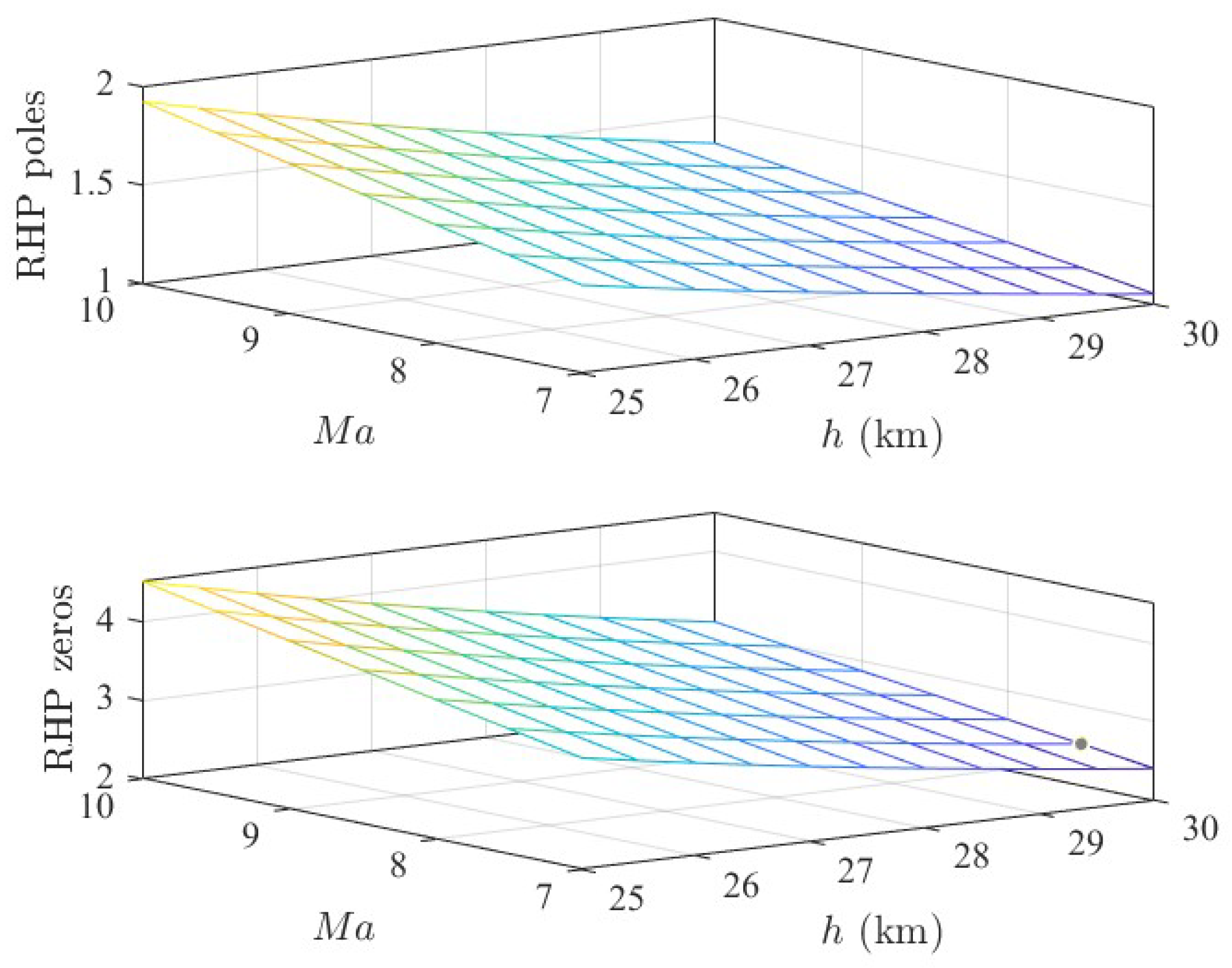
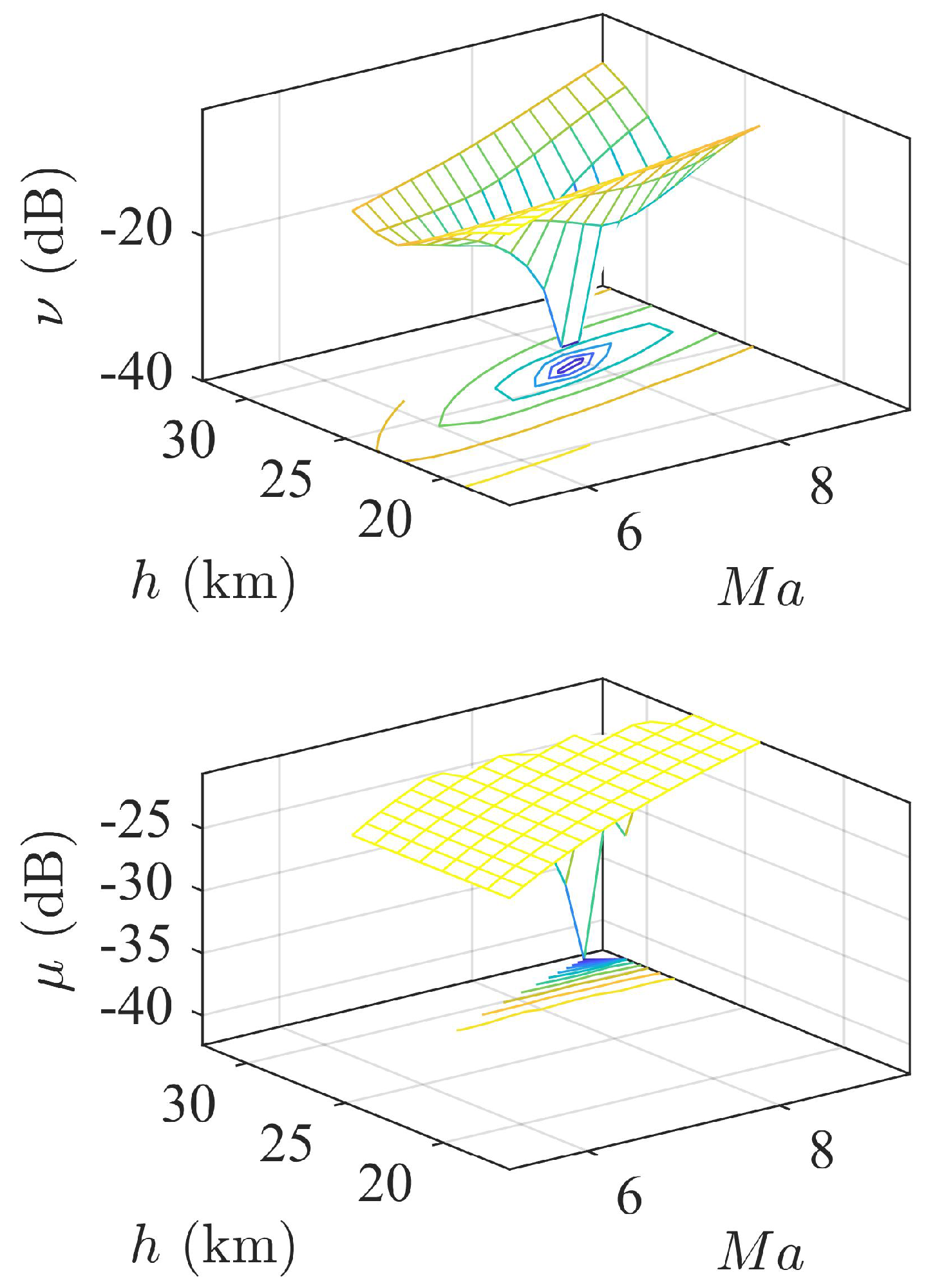
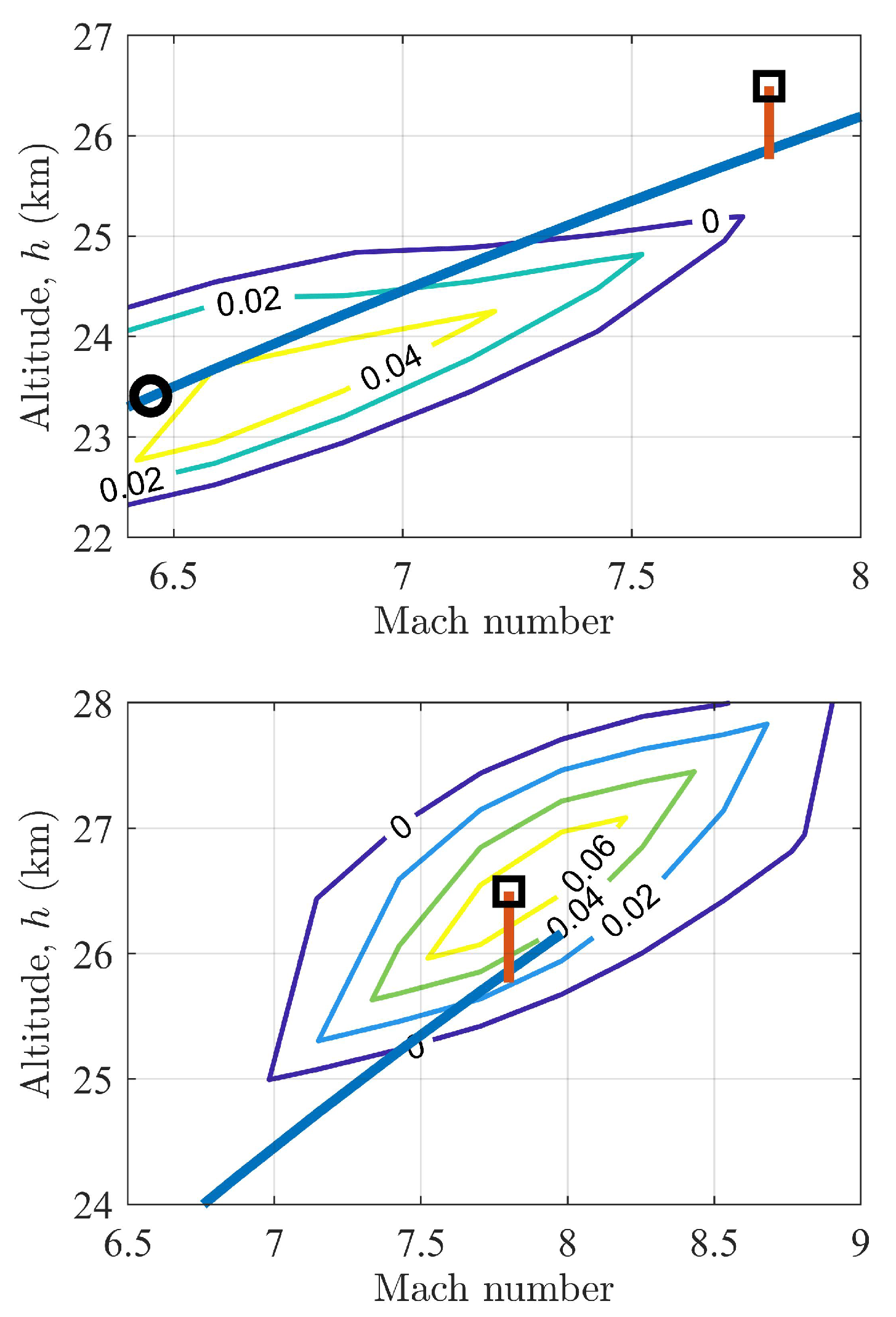
5.3. Robust Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, K.; Pei, S.; Shen, F.; Liu, S. Tightly Coupled Integrated Navigation Algorithm for Hypersonic Boost-Glide Vehicles in the LCEF Frame. Aerospace 2021, 8, 124. [Google Scholar] [CrossRef]
- Wang, G.Z.; Huang, W.; Yan, L. Multidisciplinary design optimization approach and its application to aerospace engineering. Chin. Sci. Bull. 2014, 59, 5338–5353. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, B.; Li, Y.; Shen, H. Overview of control-centric integrated design for hypersonic vehicles. Astrodynamics 2018, 2, 307–324. [Google Scholar] [CrossRef]
- Chavez, F.R.; Schmidt, D.K. Analytical Aeropropulsive/Aeroelastic Hypersonic-Vehicle Model with Dynamic Analysis. J. Guid. Control Dyn. 1994, 17, 1308–1319. [Google Scholar] [CrossRef]
- Clark, A.; Mirmirani, M.; Choi, S.; Wu, C.; Mathew, K. An Aero-Propulsion Integrated Elastic Model of a Generic Airbreathing Hypersonic Vehicle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Bolender, M.A.; Doma, D.B. Nonlinear Longitudinal Dynamical Model of an Air-Breathing Hypersonic Vehicle. J. Spacecr. Rocket. 2007, 44, 374–387. [Google Scholar] [CrossRef]
- Oppenheimer, M.W.; Doman, D.B. A Hypersonic Vehicle Model Developed With Piston Theory. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Parker, J.T.; Serrani, A.; Yurkovich, S.; Bolender, M.A.; Doman, D.B. Control-Oriented Modeling of an Air-Breathing Hypersonic Vehicle. J. Guid. Control. Dyn. 2007, 30, 856–869. [Google Scholar] [CrossRef]
- Frendreis, S.G.; Cesniky, C.E. 3D Simulation of Flexible Hypersonic Vehicles. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Whitmer, C.; Kelkar, A.; Vogel, J.; Chaussee, D.; Ford, C. Control Centric Parametric Trade Studies for Scramjet-Powered Hypersonic Vehicles. In Proceedings of the 2010 AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Tsuchiya, T.; Takenaka, Y.; Taguchi, H. Multidisciplinary Design Optimization for Hypersonic Experimental Vehicle. AIAA J. 2007, 45, 1655–1662. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Y.; Lei, H.; Shen, H.; Lu, Y. Ascent trajectory tracking for an air-breathing hypersonic vehicle with guardian maps. Int. J. Adv. Robot. Syst. 2017, 14, 1–11. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Y.; Shen, H.; Lu, Y. Surrogate modeling of a 3D scramjet-powered hypersonic vehicle based on screening method IFFD. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2017, 231, 265–278. [Google Scholar]
- Starkey, R.P.; Rankins, F.; Pines, D. Coupled Waverider/Trajectory Optimization for Hypersonic Cruise. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Chen, B.; Liu, Y.; Shen, H.; Lei, H.; Lu, Y. Performance limitations in trajectory tracking control for air-breathing hypersonic vehicles. Chin. J. Aeronaut. 2019, 32, 167–175. [Google Scholar] [CrossRef]
- Xu, B. Robust adaptive neural control of flexible hypersonic flight vehicle with dead-zone input nonlinearity. Nonlinear Dyn. 2015, 80, 1509–1520. [Google Scholar] [CrossRef]
- Qin, W.; He, B.; Liu, G.; Zhao, P. Robust model predictive tracking control of hypersonic vehicles in the presence of actuator constraints and input delays. J. Frankl. Inst. 2016, 353, 4351–4367. [Google Scholar]
- Xiao, D.; Liu, M.; Liu, Y.; Lu, Y. Switching control of a hypersonic vehicle based on guardian maps. Acta Astronaut. 2016, 202, 294–306. [Google Scholar] [CrossRef]
- Kulfan, B.M. Universal Parametric Geometry Representation Method. J. Aircr. 2007, 45, 142–158. [Google Scholar] [CrossRef]
- Skujins, T.; Cesnik, C.E.; Oppenheimer, M.W.; Doman, D.B. Canard-Elevon Interactions on a Hypersonic Vehicle. J. Spacecr. Rocket. 2010, 47, 90–100. [Google Scholar] [CrossRef]
- Torrez, S.M.; Driscoll, J.F.; Dalle, D.J. Hypersonic Vehicle Thrust Sensitivity to Angle of Attack and Mach Number. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Chicago, IL, USA, 10–13 August 2009. [Google Scholar]
- Dalle, D.J.; Torrez, S.M.; Driscoll, J.F.; Bolender, M.A.; Bowcutt, K.G. Minimum-Fuel Ascent of a Hypersonic Vehicle Using Surrogate Optimization. J. Aircr. 2014, 51, 1973–1986. [Google Scholar] [CrossRef]
- Dickeson, J.; Rodriguez, A.; Sridharan, S.; Korad, A. Elevator Sizing, Placement, and Control-Relevant Tradeoffs for Hypersonic Vehicles. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Kelkar, A.G.; Vogel, J.M.; Inger, G.; Whitmer, C.; Sidlinger, A.; Ford, C. Modeling and Analysis Framework for Early Stage Trade-off Studies for Scramjet-Powered Hypersonic Vehicles. In Proceedings of the 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, Norfolk, VA, USA, 19–22 October 2009. [Google Scholar]
- Morelli, E.A. Flight-Test Experiment Design for Characterizing Stability and Control of Hypersonic Vehicles. J. Guid. Control. Dyn. 2009, 32, 949–959. [Google Scholar] [CrossRef]
- Frendreis, S.G.; Skujins, T.; Cesnik, C.E. Six-Degree-of-Freedom Simulation of Hypersonic Vehicles. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Chicago, IL, USA, 10–13 August 2009. [Google Scholar]
- Wang, S.X.; Zhang, Y.; Jin, Y.Q.; Zhang, Y.Q. Neural control of hypersonic flight dynamics with actuator fault and constraint. Sci. China Inf. Sci. 2015, 58, 1–10. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Li, Z.Y. L1 Adaptive Loss Fault Tolerance Control of Unmanned Hypersonic Aircraft with Elasticity. Aerospace 2021, 8, 176. [Google Scholar] [CrossRef]
- Marcos, A.; Balas, G.J. Development of Linear-Parameter-Varying Models for Aircraft. J. Guid. Control Dyn. 2004, 27, 218–228. [Google Scholar] [CrossRef]
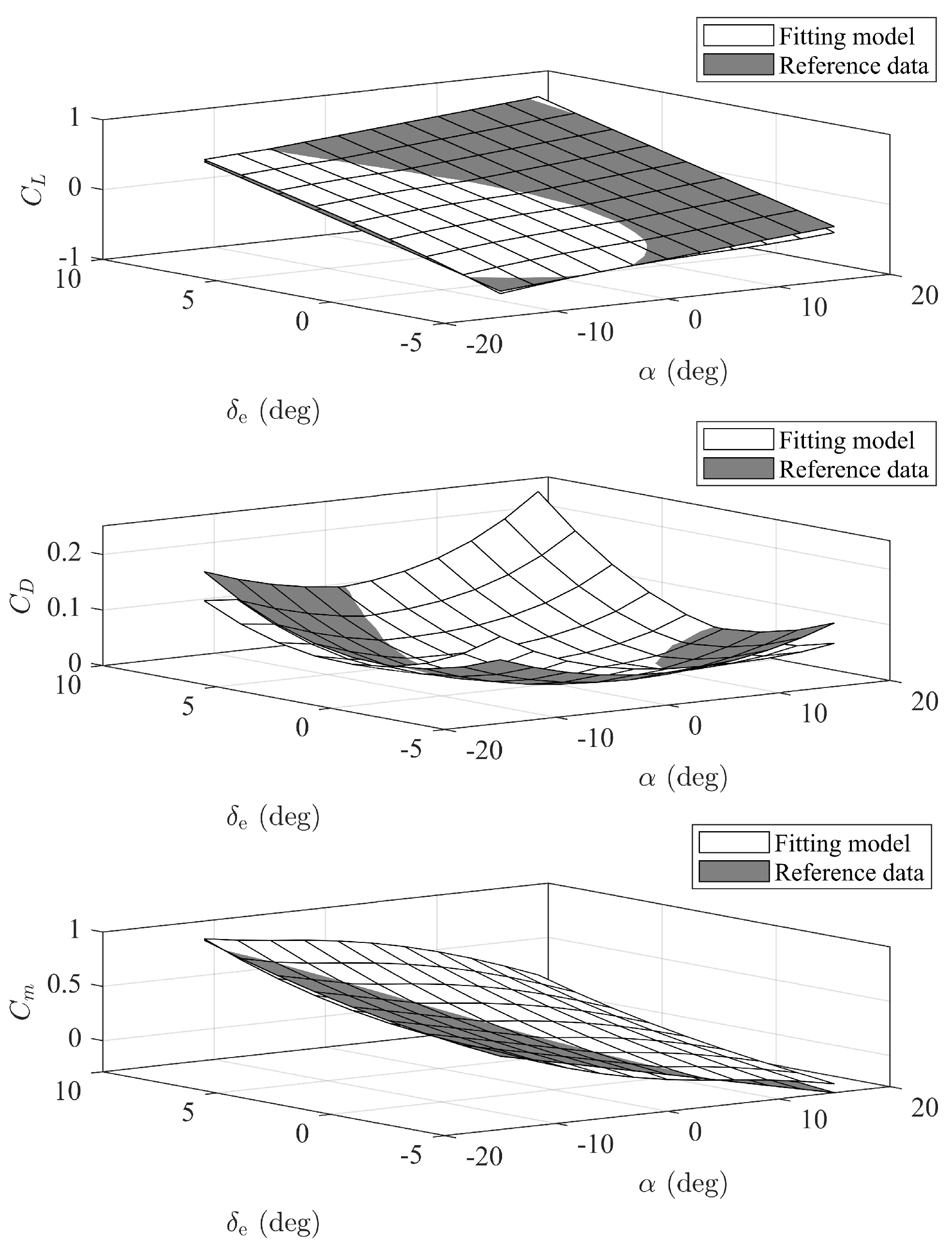



| Coefficients | VAF | RMSE |
|---|---|---|
| 99.08% | 0.0007 | |
| 98.04% | 0.00008 | |
| 98.36% | 0.0022 | |
| 90.82% | 0.0094 |
| Mach | Altitude (km) | AOA (deg) | Elevon Deflection Angle (deg) | FER |
|---|---|---|---|---|
| 6 | 25 | 2.1645 | 14.4488 | 0.391 |
| 7 | 26 | 1.9073 | 13.6513 | 0.4044 |
| 8 | 27 | 1.7253 | 13.1218 | 0.4393 |
| 9 | 28 | 1.6016 | 12.7670 | 0.4811 |
| 10 | 29 | 1.5224 | 12.5351 | 0.5309 |
| Phases | ||||
|---|---|---|---|---|
| Constant dynamic pressure | 23,408 | 25,769 | 6.5 | 7.8 |
| Constant Mach number | 25,769 | 26,495 | 7.8 | 7.8 |
| Cruise flight | 26,495 | 26,495 | 7.8 | 7.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, B.; Chen, J.; Liu, Y. Rapid Parametric Modeling and Robust Analysis for the Hypersonic Ascent Based on Gap Metrics. Appl. Sci. 2023, 13, 5189. https://doi.org/10.3390/app13085189
Liu Y, Chen B, Chen J, Liu Y. Rapid Parametric Modeling and Robust Analysis for the Hypersonic Ascent Based on Gap Metrics. Applied Sciences. 2023; 13(8):5189. https://doi.org/10.3390/app13085189
Chicago/Turabian StyleLiu, Yiran, Boyi Chen, Jinbao Chen, and Yanbin Liu. 2023. "Rapid Parametric Modeling and Robust Analysis for the Hypersonic Ascent Based on Gap Metrics" Applied Sciences 13, no. 8: 5189. https://doi.org/10.3390/app13085189
APA StyleLiu, Y., Chen, B., Chen, J., & Liu, Y. (2023). Rapid Parametric Modeling and Robust Analysis for the Hypersonic Ascent Based on Gap Metrics. Applied Sciences, 13(8), 5189. https://doi.org/10.3390/app13085189







