Light-to-Plasma Momentum Transfer

Abstract

The momentum of light in a plasma and the momentum transfer from light to plasma is calculated for a uniform plane of light incident into a uniform plasma. At low irradiance, the Minkowski and Abraham expressions for photon momentum are shown to be equivalent. We evaluate relativistic electron motion at a high irradiance for a plasma and show that most light momentum is transferred to the electrons associated with motion parallel to the light propagation at an irradiance corresponding to the reduced vector potential $a_o\approx 3.7$ (reduced irradiance $I{\lambda }^2\approx 2\times {10}^{19}$ W cm${}^{-2}$ μm${}^2$). Our results show that to ensure the maximum momentum transfer from photons to electrons in motion parallel to the $\mathbf{k}$-direction for fixed laser pulse energy, the laser focusing should be adjusted to achieve $a_o\approx 3.7$, even if tighter focusing, and thus higher $a_o$ values, are possible.

1. Introduction

We consider the momentum transfer from light to plasma when light propagates through plasma. Many experiments involving high-power lasers depend directly or indirectly on the momentum transfer from light to plasma. For example, the electron density profile of plasma material expanding from laser-irradiated solid targets has been modified due to light pressure [1,2,3], and there have been proposals to use direct light momentum to compress plasma material for inertial fusion studies [4,5,6]. Light pressure can accelerate electrons in laser-plasmas to high energies that are useful for many applications [7,8,9,10,11]. Electrons accelerated by light pressure may be used as a heating source for fusion ignition when the electrons or co-moving ions are injected into laser-compressed deuterium/tritium [12,13,14]. The interaction of light with electrons in the conduction band of solids can be modeled as light–plasma interactions. For a first approximation, the refractive indices of a conductor or semiconductor can exhibit similar dependencies to plasmas with “free” electrons. Quantum plasmonics involves the study of the quantum properties of light and its interaction with such electrons, usually when there are solid nanoscale interfaces, and often involving applications where the light is confined to below-diffraction distances [15]. The momentum of light and light-momentum transfer to electrons in solids is important in solid-state plasmonics.

Special relativity predicts the vacuum momentum of a photon of light to be $\hslash \omega /c=|\hslash {\mathbf{k}}_{\mathbf{0}}|$, where ${\mathbf{k}}_{\mathbf{0}}$ is the vacuum wave-vector of the photon, $\omega$ is the photon angular frequency, and c is the vacuum speed of light. To many commentators, the appropriate value of the momentum of a photon in a dielectric medium has been less clear-cut. Over 100 years ago, Minkowski [16] proposed a photon momentum of $\eta \hslash {\mathbf{k}}_{\mathbf{0}}$ and Abraham [17], a photon momentum of $(1/\eta )\hslash {\mathbf{k}}_{\mathbf{0}}$, where $\eta$ is the refractive index of the medium of propagation. The different and seemingly incompatible proposals for photon momentum have become known as the Abraham–Minkowski controversy with many experiments, “thought experiments”, and much theoretical work undertaken in an effort to resolve the controversy (for reviews, see [18,19,20,21,22]).

Quantum theories of light propagation have determined a momentum operator for a radiation field in order to evaluate the progression of electromagnetic waves [23,24]. Quantum optics then associated the Minkowski photon momentum with the momentum of the field, plus the momentum associated with the medium polarization, while the Abraham photon momentum considered the momentum of the electromagnetic field alone [25]. The momentum of light has become an increasingly important parameter in structured light studies where, for example, orbital angular momentum due to the field spatial distribution is produced [26]. In plasmas, an electromagnetic wave interacts with free electrons. Considering the classical (non-quantum) electron motion in an electromagnetic wave, we show in this paper that for a plasma, the Minkowski and Abraham expressions for photon momentum are equivalent.

With focused laser light, the number of photons in a laser pulse can be large. For example, for a peak irradiance of ${10}^{16}$ W cm${}^{-2}$ and 1 micron wavelength, there are typically ≈${10}^{16}$ photons per picosecond per micron focused radius in a laser pulse. Nevertheless, the energy or momentum transferred from light to plasma can be usefully evaluated per unit of photon energy $\hslash \omega$ or photon momentum $\hslash \mathbf{k}$. We follow this “per photon” approach in our treatment in this paper, as it aids comment on the Abraham–Minkowski controversy. We evaluate the energy and momentum per photon transferred from light to plasma over a range of irradiances, including the extremely high irradiances now possible with focused high-power, short-duration laser pulses.

2. Photon Momentum at Low Irradiance

When an electromagnetic wave of low irradiance is incident into a plasma, the motion of the free electrons in the plasma are, to a good approximation, parallel to the electric field of the wave in a direction transverse to the wave-vector $\mathbf{k}$. We consider a plasma with an electron number density $n_e$ much less than the critical electron density, so that wave reflection, light scattering, and electron-collision processes are negligible. A plasma profile could reflect light (and to a lesser extent, scatter light), but in a “gedanken” experiment, we can assume sufficiently small refractive index deviations from unity that these processes are negligible or, alternatively, only consider the light impinging on a uniform plasma that had not been reflected or scattered. For most laser-plasma experiments, ignoring collisions in the light–plasma interaction has resulted in very accurate approximations. Even at electron densities approaching critical density, the mean free path for collisions is much greater than the electron oscillation range in an electromagnetic wave. For example, the electron–electron mean free path is ≈2 $\mathsf{\mu }$m at a temperature of 30 eV and an electron density of ${10}^{20}$ cm${}^{-3}$ (see Section 5.3 [27]), while the electromagnetic oscillation distance is ≈0.02 $\mathsf{\mu }$m for a wavelength of 1 micron and an irradiance of ${10}^{16}$ W cm${}^{-2}$ (see Section 4.1 [28]). Due to the mass difference between electrons and ions, the electron–ion interaction difference is much greater than the electron–electron mean free path. The assumption that electron oscillation in an electromagnetic field is collision-less and local over distances much smaller than typical focal point sizes has been an excellent approximation used widely to evaluate local refractive indices and other parameters in laser-produced plasmas.

A linearly polarized electromagnetic wave varying in time as $E=E_{0}cos\left(\omega t\right)$ with a frequency of $\omega$ accelerates an initially stationary free electron at a rate of $-Ee/m_0$, where e is the charge on the electron and $m_0$ is the rest mass of the electron. Integrating the electron acceleration with respect to time gives the electron velocity as $v=-e{E}_0/\left(m_0\omega \right)sin\left(\omega t\right)$ with an electron energy U, given by:

$$U=(1/2)m_0{v}^2=\frac{e^2{E}_0^2}{2m_0{\omega }^2}{sin}^2\left(\omega t\right).$$

(1)

The average of a period of oscillation yields the time-averaged ponderomotive, or quiver energy, $<U>$ of an electron in a propagating electromagnetic wave with an electric-field amplitude of $E_0$:

$$<U>=\frac{e^2{E}_0^2}{4m_0{\omega }^2}.$$

(2)

The ponderomotive energy of a single electron in an electromagnetic wave has been discussed in many texts (see, for example, Section 2.4.1 of Tallents [29]). The ponderomotive energy per unit volume in a plasma of electron number density $n_e$ is given by $n_e<U>$.

The energy density $U_L$ of an electromagnetic wave in a vacuum is related to the electric-field amplitude $E_0$ by the following:

$$U_L=(1/2){ϵ}_0{E}_0^2$$

(3)

where ${ϵ}_0$ is the vacuum dielectric constant. The vacuum density of photons per unit of volume is then simply $U_L/(\hslash \omega )$. The ponderomotive energy per incident photon $W_P$ in a plasma is given by the ponderomotive energy per unit of volume $n_e<U>$ divided by the vacuum density of photons per unit of volume $U_L/(\hslash \omega )$. We find the following:

$$W_P=\frac{n_e<U>}{U_L/(\hslash \omega )}=\frac{n_e{e}^2}{2m_0{ϵ}_0{\omega }^2}\hslash \omega =(1/2)\frac{{\omega }_p^2}{{\omega }^2}\hslash \omega$$

(4)

where the natural oscillation frequency ${\omega }_p$ of the electrons in a plasma (known as the plasma frequency, see, e.g., Section 8.1 of Rybicki and Lightman [30]) is given in SI units by the following:

$${\omega }_p^2=\frac{n_e{e}^2}{m_0{ϵ}_0}.$$

(5)

The relationship between the wave-vector $\mathbf{k}$ in plasma and the wave-vector ${\mathbf{k}}_0$ in a vacuum is readily obtained by the dispersion relationship of light in a plasma (see, e.g., Section 4.4 of Tallents [28]). A plasma medium has a dispersion relationship according to the following:

$$k^2=\frac{{\omega }^2-{\omega }_p^2}{c^2}.$$

(6)

Re-arranging Equation (6), we find the following:

$$k={\left(1-\frac{{\omega }_p^2}{{\omega }^2}\right)}^{1/2}\frac{\omega }{c}={\left(1-\frac{{\omega }_p^2}{{\omega }^2}\right)}^{1/2}{k}_0$$

(7)

Refractive indices vary depending on whether the index is related to the phase or the group velocity of a propagating electromagnetic wave. The phase velocity $v_p$ is defined by $\omega /k$, where k is the amplitude of the wave-vector of the wave, while the group velocity $v_g=d\omega /dk$. In a vacuum, both the phase and group velocities are at the same speed-of-light c, but in a dielectric medium, $v_p=c/{\eta }_p$, and $v_g=c/{\eta }_g$, where ${\eta }_p$ is the phase refractive index and ${\eta }_g$ is the group refractive index. For a plasma, the phase refractive index is given by the following:

$${\eta }_p={\left(1-\frac{{\omega }_p^2}{{\omega }^2}\right)}^{1/2}.$$

(8)

Similarly, the group refractive index is given by the following:

$${\eta }_g={\left(1-\frac{{\omega }_p^2}{{\omega }^2}\right)}^{-1/2}.$$

(9)

The standard derivation of the phase and group refractive index expressions has been given, for example, in Section 8.1 of Rybicki and Lightman [30] and in Section 2.1.2 of Tallents [29]. Using Equations (7)–(9), we have two expressions for the photon momentum:

$$p_{phot}=\hslash k={\eta }_p\hslash k_0,$$

(10)

and

$$p_{phot}=\hslash k=\frac{1}{{\eta }_g}\hslash k_0.$$

(11)

Equation (10) corresponds to the Minkowski description of the photon momentum [16], while Equation (11) corresponds to the Abraham description of the photon momentum [17].

The Abraham–Minkowski controversy has been generally resolved if an appropriate phase or group refractive index is employed, respectively, in the Minkowski and Abraham expressions [31,32], though this conclusion has been obscured by associating Minkowski’s interpretation with the words “canonical or wave momentum” and Abraham’s interpretation with the “kinetic momentum”, rather than referring directly to the phase (Minkowski) or group (Abraham) velocities of light (see [19,20,33,34]). For example, the diffraction of light was determined by the phase of the light, so in diffraction calculations, the Minkowski photon momentum should be used (see, for example, the diffraction “thought experiment” discussed by Padgett [35]). The propagation of information and the energy of light in a medium depends on the group velocity and, thus, requires the Abraham photon momentum.Our short discussion here has demonstrated that the distinction between the Minkowski and the Abraham evaluations of photon momentum vanishes for a plasma medium.

3. Light Momentum Transfer to Plasma at High Irradiance

At higher electromagnetic wave irradiances, the motion of the accelerated electrons parallel to the direction of the wave propagation becomes important. At the highest irradiances, we also need to use an appropriate relativistic expression for the electron kinetic energies, and during the electron-acceleration calculations, we need to make an allowance for a relativistic “mass increase” from the electron rest mass of $m_0$ to $\gamma m_0$, where $\gamma$ is the Lorentz parameter. We also need to consider the dielectric plasma effect on the electric and magnetic fields of the electromagnetic wave. When the electron density is below the critical electron density, the plasma refractive index ${\eta }_P$ modifies the vacuum electric field E to $E/\sqrt{{\eta }_p}$ and the vacuum magnetic field B to $\sqrt{{\eta }_P}B$.

Electrons accelerated by an electromagnetic wave in the direction of the electric field are accelerated by the magnetic field $\mathbf{B}$ of the wave due to the Lorentz $-e\mathbf{v}\times \mathbf{B}$ force. The magnetic field of a linearly polarized electromagnetic wave produces acceleration in the direction of the beam propagation (the wave-vector $\mathbf{k}$-direction) with an acceleration magnitude of $(-e/\gamma m_0)vB\sqrt{{\eta }_P}$, where B is the vacuum magnetic field. Given a velocity oscillation in the form of $v=-e{E}_0/\left(\sqrt{{\eta }_P}\gamma m_0\omega \right)sin\left(\omega t\right)$, where $E_0$ is the vacuum electric field and the magnetic field oscillation in the form of $B=B_{0}cos\left(\omega t\right)$, the acceleration in the $\mathbf{k}$ direction has a magnitude $e^2{E}_0^2/\left({\gamma }^2{m}_0^2\omega c\right)sin\left(\omega t\right)cos\left(\omega t\right)$, provided that the electron motion in the $\mathbf{k}$-direction is small. Integrating in time, we obtain the velocity $v_k$ of an electron in the direction of the $\mathbf{k}$-vector when irradiated by an electromagnetic wave:

$$v_k=\frac{e^2{E}_0^2}{2{\gamma }^2{m}_0^2{\omega }^{2}c}{sin}^2\left(\omega t\right).$$

(12)

Integrating again, we can obtain the electron position $z_k$ parallel to the $\mathbf{k}$-vector:

$$z_k=\frac{e^2{E}_0^2}{4{\gamma }^2{m}_0^2{\omega }^{3}c}\left(\omega t-(1/2)sin\left(2\omega t\right)\right)$$

(13)

For a small relativistic mass increase (i.e., $\gamma$ approaching unity) and linearly polarized light, an electron oscillates in the $\mathbf{k}$-direction at a frequency of $2\omega$ with a time-averaged drift velocity in the $\mathbf{k}$-direction. 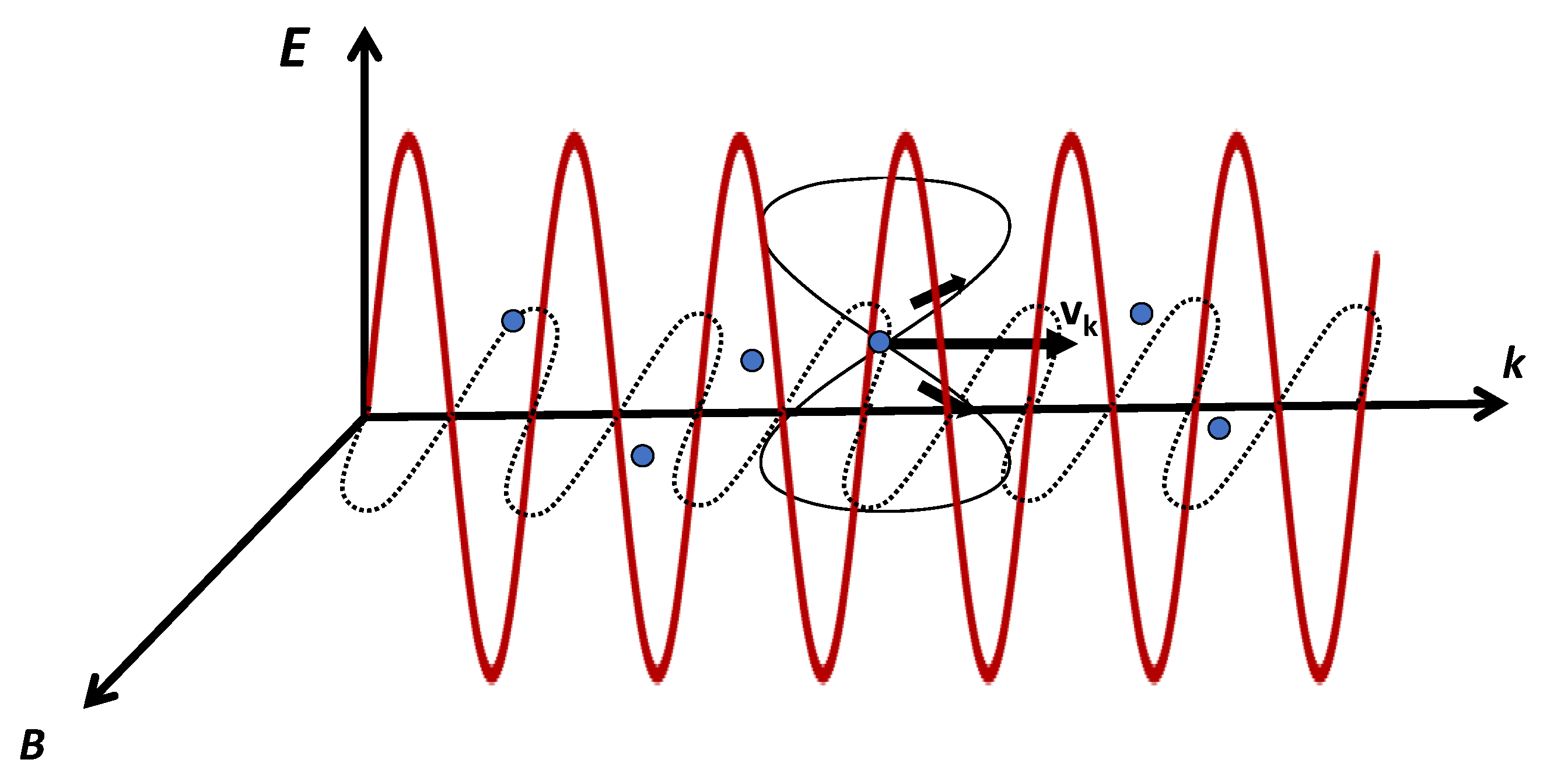The electron oscillates at a frequency of $\omega$ perpendicular to $\mathbf{k}$ and $2\omega$ parallel to $\mathbf{k}$, so the electron trajectory follows a figure-eight motion with a superimposed time-averaged drift velocity in the direction of the $\mathbf{k}$-vector (see Figure 1). After averaging a period of oscillation of the electromagnetic wave, the time-averaged drift velocity in the $\mathbf{k}$-direction becomes the following:

$$<v_k>=\frac{e^2{E}_0^2}{4<\gamma {>}^2{m}_0^2{\omega }^{2}c}$$

(14)

where $<\gamma >$ is the cycle-averaged Lorentz factor for the oscillating electron. After averaging over the time of a cycle of electromagnetic oscillation, the net velocity of an electron in an electromagnetic field is given by Equation (14).

The quantities in Equation (14) can be conveniently grouped into a single parameter, known as the reduced vector potential $a_o$, and defined by the following:

$$a_o^2=\frac{e^2{E}_0^2}{m_0^2{\omega }^2{c}^2}.$$

(15)

For small values of $a_o$, the drift velocity of an electron in an electromagnetic field is $<v_k>=a_o^2/4$. A useful quantitative indication of the value of $a_o$ in laser-plasma experiments has been found by relating the electric-field amplitude $E_0$ to the irradiance I of an electromagnetic wave measured in units of W cm${}^{-2}$. Converting the angular frequency $\omega$ to wavelength ${\lambda }_{\mu m}$ in microns, we can write the dimensionless reduced vector potential as the following:

$$a_o^2=\frac{I{\lambda }_{\mu m}^2}{1.37\times {10}^{18}}.$$

(16)

Inertial fusion experiments have typically utilized laser pulses with $a_o<<1$, but some short-pulse (<100 fs) laser-plasma experiments have achieved $a_o>100$. It has been shown (see, for example, Landau and Lifshitz [36], Umstadter [37] and Section 4.3 Tallents [28]) that the cycle-averaged relativistic Lorentz factor for the electrons accelerated in an electromagnetic field can be found by the following:

$$<\gamma >={\left(1+\frac{a_o^2}{2}\right)}^{1/2}.$$

(17)

Allowing for the “de-phasing” of the electron in the electromagnetic wave oscillation due to the $\mathbf{k}$-directed motion, it was also readily shown (see Section 4.1 Tallents [28]) that, when motion in the $\mathbf{k}$-direction was large, the time-averaged velocity in the $\mathbf{k}$-direction at large values of $a_o$ can be expressed as the following:

$$\frac{<v_k>}{c}=\frac{a_o^2}{4+a_o^2}.$$

(18)

In the laboratory frame, the kinetic energy of an electron in a frame of velocity v with Lorentz factor $\gamma$ can be written as $({\gamma }^2/(1+\gamma ))m_0{v}^2$. The energy of electrons moving parallel to $\mathbf{k}$ with a drift velocity $<v_k>$ in a plasma of electron density $n_e$ is expressed by the following: $<\gamma {>}^2$/$(1+<\gamma >)n_e{m}_0<v_k{>}^2$. Using Equations (3) and (18), the energy per incident photon is given by the following:

$$n_e<U_k>=n_e\left(\frac{<\gamma {>}^2}{1+<\gamma >}\right)\frac{m_0<v_k{>}^2}{U_L/(\hslash \omega )}=\left(\frac{<\gamma {>}^2}{1+<\gamma >}\right)\frac{n_e{m}_0{c}^2}{(1/2){ϵ}_0{E}_0^2/(\hslash \omega )}{\left(\frac{a_o^2}{4+a_o^2}\right)}^2.$$

Using Equation (17) for the Lorentz parameter $<\gamma >$, Equation (15) to convert the maximum electric field $E_0$ to the reduced vector potential $a_o$, and Equation (5) for the plasma frequency ${\omega }_p$, we can write the following for the directed electron energy per incident photon:

$$n_e<U_k>=\frac{{\omega }_p^2}{{\omega }^2}\left(\frac{1+a_o^2/2}{1+{(1+a_o^2/2)}^{1/2}}\right)\frac{2a_o^2}{{(4+a_o^2)}^2}\hslash \omega$$

(19)

At low irradiances (small $a_o$), $n_e<U_k>$ varies as $(1/16)({\omega }_p^2/{\omega }^2)a_o^2\hslash \omega$. At high irradiances (large $a_o$), the directed electron energy per photon $n_e<U_k>$ varies as $(1/\left(9\sqrt{2}\right))({\omega }_p^2/{\omega }^2){\left(a_o\right)}^{-1}\hslash \omega$, suggesting a drop in the “efficiency” of the energy transfer from the photons to the $\mathbf{k}$-directed electrons. The $\mathbf{k}$-directed electron energy $n_e<U_k>$ decreases as the irradiance of the beam increases to extreme values (high $a_o$). The “optimum” irradiance for the maximum transfer of kinetic energy in the direction of the light propagation per photon is the reduced vector potential $a_o\approx 3.7$ (see Figure 2).

4. Discussion

The acceleration of the electrons parallel to $\mathbf{k}$ in a plasma has often been referred to as $\mathbf{J}\times \mathbf{B}$ acceleration in the laser-plasma literature, as it is caused by the electron current flow $\mathbf{J}$, parallel to the electric field producing a force due to the magnetic field $\mathbf{B}$ of the electromagnetic wave. For a pulse of light incident into a plasma, $\mathbf{J}\times \mathbf{B}$ acceleration can be equivalently expressed as being caused by the ponderomotive force on each electron, which is represented by the gradients $-\nabla <U>$ in the $\mathbf{k}$-direction of the time-averaged ponderomotive energy $<U>$ (see Section 4.1 Tallents [28]). The leading edge of a light pulse incident into a plasma with increasing ponderomotive energy accelerates electrons in the direction of the light propagation, while the trailing edge with decreasing ponderomotive energy de-accelerates the electrons back to a zero velocity. When a light pulse interacts with a low-density plasma in front of a solid target, the electrons can be accelerated to collide with the high-density plasma before being de-accelerated (resulting in the term $\mathbf{J}\times \mathbf{B}$ “heating” of the target used in the laser-plasma literature; for example, in [2,38]).

Recently measured and simulated electron temperatures at laser irradiances from $I{\lambda }^2={10}^{19}$ to ${10}^{22}$ W cm${}^{-2}\mathsf{\mu }$m${}^2$ have shown evidence that the focal spot size can affect the temperatures in laser-plasmas produced at high, constant irradiances [39]. We showed that the electron kinetic energy per photon for the electron motion in the direction of a beam, as shown in Figure 2, exhibites a maximum at a laser irradiance corresponding to the reduced vector potential $a_o\approx 3.7$. For fixed laser pulse energy (and, hence, a fixed photon number), this result suggests that to ensure the maximum energy transfer from photons to electron motion, parallel to the $\mathbf{k}$-direction, the laser focus should be adjusted to achieve $a_o\approx 3.7$ (reduced irradiance $I{\lambda }^2\approx 2\times {10}^{19}$ W cm${}^{-2}\mathsf{\mu }$m${}^2$), even if a tighter focus, with consequent higher $a_o$ values, is possible.

5. Conclusions

The momentum of light in a plasma was evaluated from low to extreme irradiances. Expressing the energy and momentum of light propagating in a plasma in terms of the average incident photon energy and the photon momentum enabled a direct comment on the 100-years-old Abraham–Minkowski controversy regarding light in a plasma dielectric: The photon momentum is ${\eta }_p\hslash {\mathbf{k}}_{\mathbf{0}}$ (the Minkowski determination) and equivalently $1/{\eta }_g\hslash {\mathbf{k}}_{\mathbf{0}}$ (the Abraham determination), where ${\eta }_p$ is the phase velocity refractive index and ${\eta }_g$ is the group velocity refractive index. We evaluated the relativistic electron motion at high-to-extreme irradiances and showed that most of the energy per photon is transferred to the electron energy associated with the motion parallel to the light propagation, at an irradiance corresponding to the reduced vector potential $a_o\approx 3.7$.