Topology and Polarization of Optical Vortex Fields from Atomic Phased Arrays

Abstract

We developed a theoretical formalism for the generation of optical vortices by phased arrays of atoms. Using the Jacobi–Anger expansion, we demonstrated the resulting field topology and determined the least number of individual atoms necessary for the generation of vortices with a given topological charge. Vector vortices were considered, taking into account both the spin and orbital angular momenta of electromagnetic fields. It was found for the vortex field that, in the far field limit, the spatial variation in spin-density matrix parameters—orientation and alignment—is independent of the distance to the radiation source.

1. Introduction

Studies and applications of optical angular momentum (OAM) beams attract a lot of interest from the photonics research community, and the methods for the generation of optical vortices are rapidly progressing [1]. Most recently, new results were obtained on the use of metasurfaces for the synthesis and multiplexing of terahertz vortices [2] and optical vortices [3], the generation of supercontinuum vortices with femtosecond pulses [4], the breakup of vortices with high topological charges [5], and stability studies of vortex solitons in matter [6]. Of particular interest are the enhanced capabilities of OAM beams to transmit information encoded in orthogonal angular-momentum eigenstates [7,8]. OAM radio has the potential to improve the bandwidth of radio communications [9].

In view of the robustness of information transfer by OAM light, here we address the problem of its coupling to artificial arrays of atoms prepared with optical traps. Our work is motivated in particular by studies of two-dimensional arrays for quantum memory [10], topological states of optical excitations in two-dimensional atomic arrays [11], free-space radiation entanglement by atomic arrays (Ref. [12]), and the possible application of phased atomic arrays as antennas in chiral photonic quantum links for quantum networks [13].

Given the limited number of atoms in an array, the question arises of what number of atoms is required to generate OAM light radiation—or an optical vortex—with a certain topological charge. In fact, the formation of OAM modes of light from discrete radiation sources was demonstrated experimentally using coherent laser beam arrays [14] or an array of small apertures (Ref. [15]). In the previous theoretical study [16], we considered scalar fields from 2D arrays of point-like emitters. In the present paper, we extend our formalism to 3D vector fields of a phased atomic antenna array and analyze the topological and polarization properties of the emitted radiation.

The paper is organized as follows. In Section 2, we analyze radiation from a circular array of polarized atoms and obtain an analytic formula for the case of a large number of atoms. In Section 3, the case of a finite number of atoms is treated via the Jacobi–Anger expansion, which enables us to perform an analytic summation for all individual emitters. Section 4 provides a review of the formalism of the 3D polarization of optical fields and gives analytic results of polarization parameters in limiting cases. Section 5 gives a detailed numerical analysis of atomic-array radiation intensity and polarization as a function of the propagation distance and number of radiating atoms. The results are summarized in Section 6.

2. Radiation of an Atomic Phased Array with Many Elements

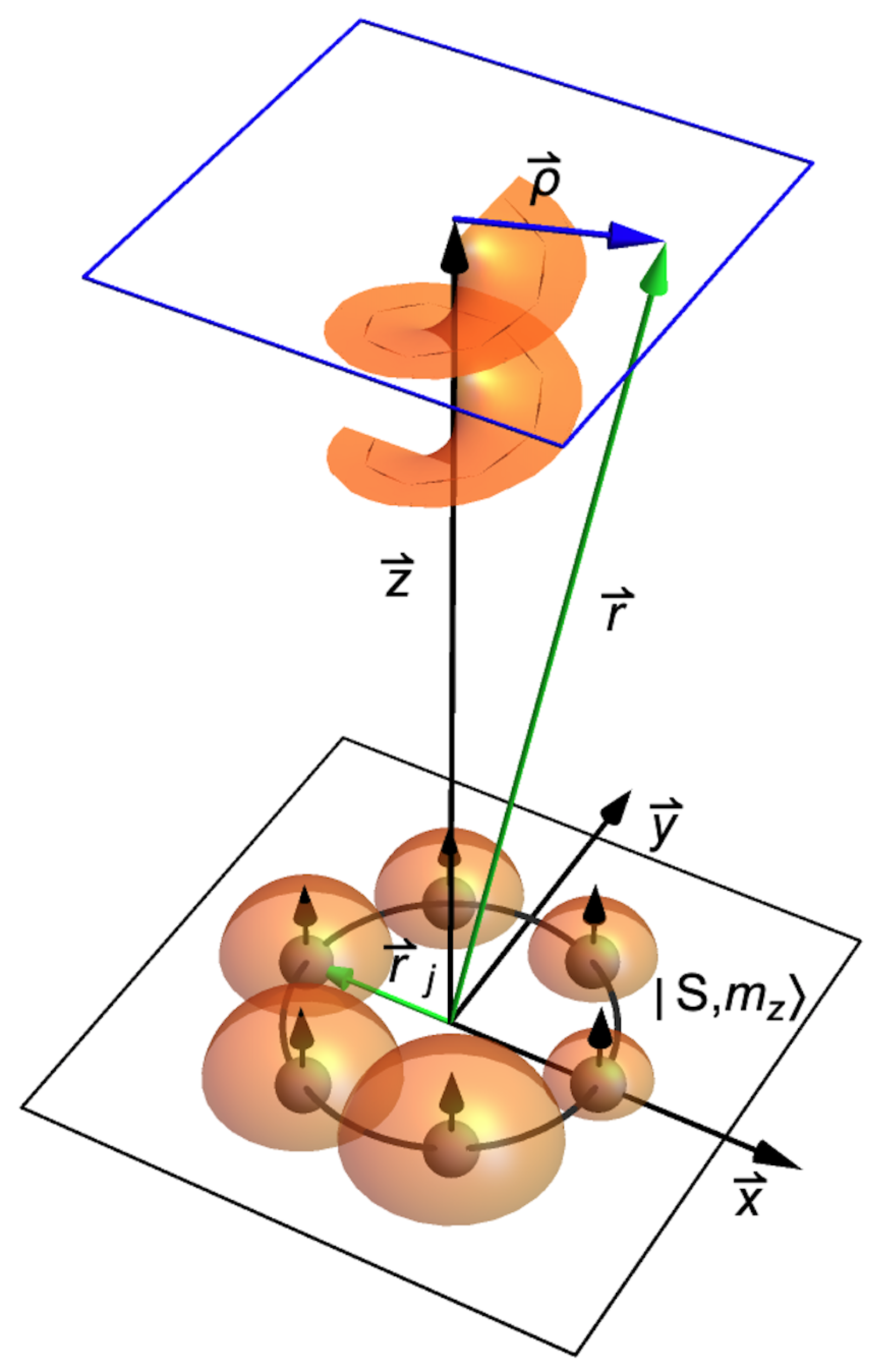
Consider a circular array of N excited atoms, each carrying an angular momentum S and its projection $m_z$. The array geometry is shown in Figure 1, along with the observation plane located at a distance z parallel to the atomic array. Let us denote a state vector of light emitted by the individual j-th atom located at a polar angle ${\varphi }_j$ on the ring as $\left|{\varphi }_j,S,m_z\right.〉$. Each adjacent atom radiates with a phase difference $\Delta \varphi =\frac{2\pi l}{N}$, where l is an externally controlled phase parameter. The phase difference could be achieved, depending on the specific application, through laser assistance [13] or through incoming OAM light modes. The state vector of a photon emitted by the j-th atom is

$$\begin{array}{c}\hfill \left|{\varphi }_j,S,m_z\right.〉\to e^{il{\varphi }_j}{\left|m_z\right.〉}_j,\end{array}$$

(1)

where the position dependence for the individual source is indicated by the source number j.

Using the photon field operator ${\widehat{A}}^{\mu }$, the total field of the emitted light of an atomic phased ring array is

$$\begin{array}{c}\hfill A_{m_z}^{\mu }(\overrightarrow{r})=\sum _j{e}^{il{\varphi }_j}\left.〈0\right|{\widehat{A}}^{\mu }{\left|m_z\right.〉}_j.\end{array}$$

(2)

For each atom, the polarization state of the emitted light can be expanded in the basis formed by left- and right-circularly polarized light in its propagation direction along $\overrightarrow{r}-{\overrightarrow{r}}_j$,

$$\begin{array}{c}\hfill {\left|m_z\right.〉}_j={\alpha }_{+}^{(j)}\left|\Lambda =+1\right.〉+{\alpha }_{-}^{(j)}\left|\Lambda =-1\right.〉,\end{array}$$

(3)

where $\Lambda =\pm 1$ defines the photon’s helicity and the expansion coefficients are

$${\alpha }_{\pm }^{(j)}=\left.〈m_z^{(j)}\phantom{\Lambda =\pm 1}\right|\Lambda =\pm 1\phantom{m_z^{(j)}}〉.$$

(4)

It should be noted that the observation of the light emitted by the atom is near a point on the z-axis aligned with the center of the ring array. The light propagating in the $\left|\Lambda =\pm 1\right.〉$ state in the above expansion has an angle ${\theta }_j$ with respect to the z-axis. The angle is the same for all the atoms ${\theta }_j\equiv {\theta }_k$. In order to choose the quantization along the z-axis, we have to rotate the coordinate system attached to the atom by a rotation operator $R(-{\varphi }_j,{\theta }_k,{\varphi }_j)$. Therefore, the coefficients become

$$\begin{array}{c}\hfill {\alpha }_{+}^{(j)}=\left.〈m_z\right|R(-{\varphi }_j,{\theta }_k,{\varphi }_j)\left|\Lambda =+1\right.〉\\ \hfill {\alpha }_{-}^{(j)}=\left.〈m_z\right|R(-{\varphi }_j,{\theta }_k,{\varphi }_j)\left|\Lambda =-1\right.〉.\end{array}$$

(5)

The above expressions give Wigner d-matrices for the considered case of electric dipole emission (while generalization to higher multipoles is straightforward):

$$\begin{array}{c}\hfill {\alpha }_{+}^{(j)}=d_{1m_z}^1({\theta }_k)e^{i(m_z-1){\varphi }_j}\\ \hfill {\alpha }_{-}^{(j)}=d_{-1m_z}^1({\theta }_k)e^{i(m_z+1){\varphi }_j},\end{array}$$

(6)

where $d_{\pm 1m_z}^1({\theta }_k)=(1\pm m_{z}cos{\theta }_k)/2$.

The total field of the emitted light of an atomic phased ring array can then be expressed in the basis formed by left- and right-circularly polarized light by the above coefficients. The angles ${\varphi }_j$ and ${\theta }_k$ define the orientation of the wave vector ${\overrightarrow{k}}_j$ of light emitted by the j-th atom in the spherical coordinate system.

$$\begin{array}{cc}\hfill & A_{m_z}^{\mu }=\sum _j{e}^{il{\varphi }_j}\hfill \\ \hfill & ({\alpha }_{+}^{(j)}\left.〈0\right|{\widehat{A}}^{\mu }\left|{\overrightarrow{k}}_j,\Lambda =+1\right.〉+{\alpha }_{-}^{(j)}\left.〈0\right|{\widehat{A}}^{\mu }\left|{\overrightarrow{k}}_j,\Lambda =-1\right.〉).\hfill \end{array}$$

(7)

If the number of atoms in the ring goes to infinity, it gives us the continuous case. We notice that in the momentum space, an infinite number of states of light ${\left|\Lambda \right.〉}_j$ lying on a cone with an opening angle $2{\theta }_k$ form a vortex state of light. Hence, with infinitely many atoms,

$$\sum _j\to \int \frac{d{\varphi }_j}{2\pi },$$

the total field generated by the atomic phased ring array can be expressed by two vector vortices with a potential $A_{\Lambda =\pm 1}^{\mu }$ with opposite helicities,

$$\begin{array}{c}\hfill A_{m_z}^{\mu }={\alpha }_{+}{A}_{\Lambda =+1}^{\mu }+{\alpha }_{-}{A}_{\Lambda =-1}^{\mu },\end{array}$$

(8)

where ${\alpha }_{\pm }=\frac{1}{2}(1\pm m_{z}cos{\theta }_k)$. Note that ${({\alpha }_{-}^2+{\alpha }_{+}^2)}^{-1/2}={[(1+cos{({\theta }_k)}^2)/2]}^{-1/2}$ has to be factored in for proper normalization of the field amplitude.

A vector vortex field formed by a cone of light rays with helicity $\Lambda$ can be expressed as [17,18]

$$\begin{array}{cc}\hfill A_{\Lambda }^{\mu }=e^{-i(\omega t-k_{z}z)}& \sqrt{\frac{\kappa }{2\pi }}A\hfill \\ \hfill & \int \frac{d{\varphi }_j}{2\pi }{(-i)}^{m_{\gamma }}{e}^{i{m}_{\gamma }{\varphi }_j}{e}^{i\overrightarrow{{\kappa }_j}·\overrightarrow{\rho }}{\overrightarrow{ϵ}}_{\Lambda },\hfill \end{array}$$

(9)

$m_{\gamma }=l+\Lambda$, where $m_{\gamma }$ is the total angular momentum projection of the vortex photon, while l can be interpreted as the orbital angular momentum projection of the photon in a paraxial limit ${\theta }_k\to 0$. The quantities $\kappa$ and $\rho$ are the transverse components of the wave vector and position vector in an observation plane, respectively; ${\overrightarrow{\kappa }}_j·\overrightarrow{\rho }={\overrightarrow{k}}_j·\overrightarrow{\rho }=\kappa \rho cos({\varphi }_j)$ and A is an overall normalization factor. Consider the term with $\Lambda =+1$. The unit vectors are

$$\begin{array}{c}\hfill {ϵ}_{\Lambda =+1}^{\mu }=e^{-i{\varphi }_j}{cos}^2\frac{{\theta }_k}{2}{\eta }_{+1}^{\mu }+e^{i{\varphi }_j}{sin}^2\frac{{\theta }_k}{2}{\eta }_{-1}^{\mu }+\frac{1}{\sqrt{2}}sin{\theta }_k{\eta }_0^{\mu },\end{array}$$

(10)

where

$$\begin{array}{c}\hfill {\eta }_{\pm 1}^{\mu }=\frac{1}{\sqrt{2}}\left(\begin{array}{cccc}0;& \mp 1,& -i,& 0\end{array}\right)\\ \hfill {\eta }_0^{\mu }=\frac{1}{\sqrt{2}}\left(\begin{array}{cccc}0;& 0,& 0,& 1\end{array}\right)\end{array}$$

(11)

are the spherical-basis vectors with a z-axis orthogonal to the array, as shown in Figure 1, and $\mu$ denotes the four-dimensional Lorentz space–time indices, where $+1,-1$, and 0 stand for left-circular, right-circular, and z unit vectors, respectively. Hence, we have

$$\begin{array}{c}\hfill A_{m_z}^{\mu }=e^{-i(\omega t-k_{z}z)}\sqrt{\frac{\kappa }{2\pi }}A\int \frac{d{\varphi }_j}{2\pi }{e}^{i\overrightarrow{{\kappa }_j}·\overrightarrow{\rho }}\\ \hfill [\frac{1}{2}(1+m_{z}cos{\theta }_k)e^{i(m_z-1){\varphi }_j}{(-i)}^{l+1}{e}^{i(l+1){\varphi }_j}{ϵ}_{+1}^{\mu }\\ \hfill +\frac{1}{2}(1-m_{z}cos{\theta }_k)e^{i(m_z+1){\varphi }_j}{(-i)}^{l-1}{e}^{i(l-1){\varphi }_j}{ϵ}_{-1}^{\mu }].\end{array}$$

(12)

Substituting expression (11) for basis vectors, we obtain

$$\begin{array}{c}\hfill A_{m_z}^{\mu }=e^{-i(\omega t-k_{z}z)}\sqrt{\frac{\kappa }{2\pi }}A\int \frac{d{\varphi }_j}{2\pi }{e}^{i\overrightarrow{{\kappa }_j}·\overrightarrow{\rho }}{e}^{i(l+m_z){\varphi }_j}\\ \hfill [\frac{1}{2}(1+m_{z}cos{\theta }_k){(-i)}^{l+1}\\ \hfill (e^{-i{\varphi }_j}{cos}^2\frac{{\theta }_k}{2}{\eta }_1^{\mu }+e^{i{\varphi }_j}{sin}^2\frac{{\theta }_k}{2}{\eta }_{-1}^{\mu }+\frac{1}{\sqrt{2}}sin{\theta }_k{\eta }_0^{\mu })\\ \hfill +\frac{1}{2}(1-m_{z}cos{\theta }_k){(-i)}^{l-1}\\ \hfill (e^{i{\varphi }_j}{cos}^2\frac{{\theta }_k}{2}{\eta }_{-1}^{\mu }+e^{-i{\varphi }_j}{sin}^2\frac{{\theta }_k}{2}{\eta }_1^{\mu }-\frac{1}{\sqrt{2}}sin{\theta }_k{\eta }_0^{\mu })].\end{array}$$

(13)

The integral over ${\varphi }_j$ can be expressed in terms of Bessel functions,

$$\begin{array}{c}\hfill \int \frac{d{\varphi }_j}{2\pi }{e}^{i\overrightarrow{{\kappa }_j}·\overrightarrow{\rho }}{e}^{i(l+m_z-1){\varphi }_j}=-i{J}_{l+m_z-1}(\kappa \rho )e^{i(l+m_z-1){\varphi }_{\rho }}.\end{array}$$

(14)

As a result, a vector potential for radiation from continuously distributed atoms ($N\to \infty$) around the ring array is

$$\begin{array}{ccc}\hfill & & A_{m_z}^{\mu }=e^{-i(\omega t-k_{z}z)}\sqrt{\frac{\kappa }{2\pi }}A\hfill \\ & & (-\frac{i}{2}{e}^{i(l+m_z-1){\varphi }_{\rho }}{J}_{l+m_z-1}(\kappa \rho )(1+m_z{cos}^2{\theta }_k){\eta }_1^{\mu }\hfill \\ & & +\frac{i}{2}{e}^{i(l+m_z+1){\varphi }_{\rho }}{J}_{l+m_z+1}(\kappa \rho )(1-m_z{cos}^2{\theta }_k){\eta }_{-1}^{\mu }\hfill \\ & & +\frac{m_z}{2\sqrt{2}}{e}^{i(l+m_z){\varphi }_{\rho }}{J}_{l+m_z}(\kappa \rho )sin2{\theta }_k{\eta }_0^{\mu }).\hfill \end{array}$$

(15)

3. Radiation Field from a Finite Number of Atomic Sources

In the discrete case, recall the expression Equation (2). The light emitted by the j-th atom has the same angular distribution as the light emitted by an oscillating dipole [19].

$$\begin{array}{c}\hfill \left.〈0\right|{\widehat{A}}^{\mu }{\left|m_z\right.〉}_j=\frac{A_N}{16\pi }\frac{{\omega }_0^2{e}^2}{{ϵ}_0{c}^2}\frac{1}{|\overrightarrow{r}-{\overrightarrow{r}}_j|}{e}^{ik|\overrightarrow{r}-{\overrightarrow{r}}_j|}{e}^{-i\omega t}\\ \hfill [(1+m_z{cos}^2{\theta }_j)e^{i(m_z-1){\varphi }_j}{\eta }_{+1}^{\mu }\\ \hfill +(1-m_z{cos}^2{\theta }_j)e^{i(m_z+1){\varphi }_j}{\eta }_{-1}^{\mu }\\ \hfill +\frac{1}{\sqrt{2}}sin2{\theta }_j{e}^{i{m}_z{\varphi }_j}{\eta }_0^{\mu }],\end{array}$$

(16)

where the normalization constant is $A_N=A/N$. The angles are

$$\begin{array}{cc}\hfill & cos{\varphi }_j^{\prime }=\frac{\rho cos{\varphi }_{\rho }-Rcos{\varphi }_j}{|\overrightarrow{\rho }-{\overrightarrow{r}}_j|}\hfill \\ \hfill & sin{\varphi }_j^{\prime }=\frac{\rho sin{\varphi }_{\rho }-Rsin{\varphi }_j}{|\overrightarrow{\rho }-{\overrightarrow{r}}_j|}\hfill \\ \hfill & cos{\theta }_j^{\prime }=\frac{z}{|\overrightarrow{r}-{\overrightarrow{r}}_j|}\hfill \\ \hfill & sin{\theta }_j^{\prime }=\frac{|\overrightarrow{\rho }-{\overrightarrow{r}}_j|}{|\overrightarrow{r}-{\overrightarrow{r}}_j|}.\hfill \end{array}$$

(17)

We are interested in large distances z; therefore, we assume that $\frac{1}{|\overrightarrow{r}-{\overrightarrow{r}}_j|}\approx \frac{1}{z}$. The field is

$$\begin{array}{c}\hfill \left.〈0\right|{\widehat{A}}^{\mu }{\left|m_z\right.〉}_j=A\frac{{\omega }_0^2{e}^2}{3{ϵ}_0{c}^2}\frac{1}{z}{e}^{ik|\overrightarrow{r}-\overrightarrow{r}|}{e}^{-i\omega t}\\ \hfill [\frac{3}{16\pi }(1+m_z{cos}^2{\theta }_j^{\prime })e^{i(m_z-1){\varphi }_j^{\prime }}{\eta }_{+1}^{\mu }\\ \hfill +\frac{3}{16\pi }(1-m_z{cos}^2{\theta }_j^{\prime })e^{i(m_z+1){\varphi }_j^{\prime }}{\eta }_{-1}^{\mu }\\ \hfill +\frac{3}{16\sqrt{2}\pi }sin2{\theta }_j^{\prime }{e}^{i{m}_z{\varphi }_j^{\prime }}{\eta }_0^{\mu }].\end{array}$$

(18)

We also assume that $z\gg R\gg \rho$, $\frac{1}{|\overrightarrow{\rho }-{\overrightarrow{r}}_j|}\to \frac{1}{R}$. Then,

$$\begin{array}{c}\hfill cos{\varphi }_j^{\prime }=\frac{1}{R}(\rho cos{\varphi }_{\rho }-Rcos{\varphi }_j)\\ \hfill sin{\varphi }_j^{\prime }=\frac{1}{R}(\rho sin{\varphi }_{\rho }-Rsin{\varphi }_j)\end{array}$$

(19)

and

$$\begin{array}{c}\hfill e^{i2{\varphi }_j^{\prime }}=\frac{1}{R^{2}2}{(\rho e^{i{\varphi }_{\rho }}-R{e}^{i{\varphi }_j})}^2\approx e^{i2{\varphi }_j};\end{array}$$

(20)

therefore, ${\varphi }_j^{\prime }\approx {\varphi }_j$.

Note that ${\theta }_k$ is defined as ${\theta }_k=arctan(\frac{R}{z})\approx \frac{R}{z}$. Further expanding

$$\begin{array}{cc}\hfill {cos}^2{\theta }_j^{\prime }=\frac{z^2}{z^2+{\rho }^2+R^2-2R\rho cos({\varphi }_{\rho }-{\varphi }_j)}& \approx 1-{\theta }_k^2\hfill \\ \hfill {sin}^2{\theta }_j^{\prime }=\frac{{\rho }^2+R^2-2R\rho cos({\varphi }_{\rho }-{\varphi }_j)}{z^2+{\rho }^2+R^2-2R\rho cos({\varphi }_{\rho }-{\varphi }_j)}& \approx {\theta }_k^2\hfill \end{array}$$

(21)

leads to approximately equal ${\theta }_j^{\prime }\approx {\theta }_k$.

The total vector field of the atomic ring array with a finite number of sources is

$$\begin{array}{cc}\hfill & A_{m_z}^{\mu }(\overrightarrow{r},t)=\frac{A_N}{16\pi }\frac{{\omega }_0^2{e}^2}{{ϵ}_0{c}^2}\frac{1}{z}{e}^{-i\omega t}\hfill \\ \hfill \sum _{j=0}^{N-1}[& (1+m_z{cos}^2{\theta }_k)e^{i(m_z-1){\varphi }_j}{\eta }_{+1}^{\mu }\hfill \\ \hfill & +(1-m_z{cos}^2{\theta }_k)e^{i(m_z+1){\varphi }_j}{\eta }_{-1}^{\mu }\hfill \\ \hfill & +\frac{1}{\sqrt{2}}sin2{\theta }_k{e}^{i{m}_z{\varphi }_j}{\eta }_0^{\mu }]e^{il{\varphi }_j}{e}^{ik|\overrightarrow{r}-{\overrightarrow{r}}_j|}.\hfill \end{array}$$

(22)

The sum over sources j can be evaluated using the Jacobi–Anger expansion:

$$\begin{array}{cc}\hfill & \sum _{j=0}^{N-1}{e}^{i(l+m_z){\varphi }_j}{e}^{ik|\overrightarrow{r}-{\overrightarrow{r}}_j|}\hfill \\ \hfill & =e^{ik(z+\frac{R^2}{z})}\sum _{j=0}^{N-1}{e}^{i(l+m_z){\varphi }_j}{e}^{-i\kappa \rho cos({\varphi }_{\rho }-{\varphi }_j)}\hfill \\ \hfill & =N{e}^{ik(z+\frac{R^2}{z})}\sum _{j=0}^{N-1}\sum _{n=-\infty }^{n=\infty }{(-i)}^n{J}_n(\kappa \rho )e^{in({\varphi }_{\rho }-{\varphi }_j)}{e}^{i(l+m_z){\varphi }_j}.\hfill \end{array}$$

(23)

The above result corresponds to the ${\eta }_0^{\mu }$ component of the vector field in Equation (22). For $+1$ and $-1$ spherical-vector components (i.e., the factors in front of ${\eta }_{+1}^{\mu }$ and ${\eta }_{-1}^{\mu }$ in Equation (22)), we have

$$\begin{array}{c}\hfill N{e}^{ik(z+\frac{R^2}{z})}\sum _{j=0}^{N-1}\sum _{n=-\infty }^{n=\infty }{(-i)}^n{J}_n(\kappa \rho )e^{in({\varphi }_{\rho }-{\varphi }_j)}{e}^{i(l+m_z-1){\varphi }_j}\end{array}$$

(24)

and

$$\begin{array}{c}\hfill N{e}^{ik(z+\frac{R^2}{z})}\sum _{j=0}^{N-1}\sum _{n=-\infty }^{n=\infty }{(-i)}^n{J}_n(\kappa \rho )e^{in({\varphi }_{\rho }-{\varphi }_j)}{e}^{i(l+m_z+1){\varphi }_j}.\end{array}$$

(25)

Summation over j selects certain orders of Bessel vortices n, while other order terms are canceled, as was demonstrated for scalar fields in [16]. After the summation of radiation from individual atoms, the final result for the field is:

$$\begin{array}{cc}\hfill & A_{m_z}^{\mu }(\overrightarrow{r},t)=\frac{A}{16\pi }\frac{{\omega }_0^2{e}^2}{{ϵ}_0{c}^2}\frac{1}{z}{e}^{-i\omega t}{e}^{ik(z+\frac{R^2}{z})}\hfill \\ \hfill & [(1+m_z{cos}^2{\theta }_k)C_{+1}{\eta }_{+1}^{\mu }+(1-m_z{cos}^2{\theta }_k)C_{-1}{\eta }_{-1}^{\mu }\hfill \\ \hfill & +\frac{1}{\sqrt{2}}sin2{\theta }_k{C}_0{\eta }_0^{\mu }],\hfill \end{array}$$

(26)

where the coefficient for the ${\eta }_0^{\mu }$ field component is

$$\begin{array}{c}\hfill C_0=\sum _{m=-\infty }^{m=\infty }{[{(-i)}^n{J}_n(\kappa \rho )e^{in{\varphi }_{\rho }}]}_{n=l+m_z+mN},\end{array}$$

(27)

and for the $+1$ and $-1$ field components, we obtain

$$\begin{array}{c}\hfill C_{\pm 1}=\sum _{m=-\infty }^{m=\infty }{\left[{(-i)}^n{J}_n(\kappa \rho )e^{in{\varphi }_{\rho }}\right]}_{n=l+m_z\mp 1+mN},\end{array}$$

(28)

where m is an integer that also serves as a summation index: $m=0,\pm 1,\pm 2,\dots$.

The above Equations (26)–(28) represent a result for the total vector potential of a phased atomic array with N atoms and a phase parameter l expressed in terms of an infinite series of Bessel vortices. The quantity $m=0$ corresponds to the leading order terms $n=l+m_z\pm 1$ and $n=l+m_z$ of each of the three spherical components of the vector vortex field. In general, we have an infinite series of Bessel vortices contributing. However, a closer look reveals a crucial role of the number of emitters N: the next non-vanishing order corresponds to the addition/subtraction of an integer number of N, so the larger N is, the wider the “gap” is between the orders of contributing Bessel vortices.

The result also sets a requirement for the minimal number of atoms necessary to form a vortex. To generate a vortex of order l for each field component, we find that the necessary conditions $N\ge 2(l+m_z)-1$ for the positive-helicity component, $N\ge 2(l+m_z)+3$ for the negative-helicity component, and $N\ge 2(l+m_z)+1$ for the zeroth (or longitudinal) component are satisfied. The strongest of the above conditions is $N\ge 2(l+m_z)+3$. If it is satisfied, then all three components of the field have vortex structures (i.e., show a phase singularity). When $m_z=-1$, the condition becomes $N\ge 2l+1$, which is the condition for a scalar vortex field [16]. However, for $m_z=+1$, the conditions are different. The difference is due to the different azimuthal variations in the phase $e^{i(l+m_z-1){\varphi }_{\rho }}$, $e^{i(l+m_z+1){\varphi }_{\rho }}$ and $e^{i(l+m_z){\varphi }_{\rho }}$ in the three spherical components of the vector vortex field.

If we only keep the leading-order terms in Equations (27) and (28), the vortex field exactly matches the continuous ($N\to \infty$) limit given by Equation (15).

Let us discuss the role of spin in our approach. For a ray of twisted light, the helicity $\Lambda =\pm 1$ plays the role of spin angular momentum projection. In our case, each individual ray of light is generated by an atom from an array. As required by the conservation of angular momentum, the corresponding atomic states $m_z=\pm 1$ emit right- or left-circularly polarized light, if the quantization axis is along the ray’s direction. The atom’s magnetic quantum number $m_z$, in our theory, plays the role of the spin angular momentum projection of the generated vortex field, if taken in a paraxial approximation ${\theta }_k\ll 1$. The quantity $l+m_z$ is therefore similar to the total angular momentum projection of the vortex field, the same as $m_{\gamma }=l+\Lambda$ for the Bessel beam with a circular polarization [18].

4. Polarization Parameters of Atomic-Array Radiation

The presence of a longitudinal electric field component in the vector vortices requires the definition of a 3 × 3 spin density matrix described by nine independent parameters (including the field’s intensity). One possibility is to use expansion coefficients of nine Gell-Mann matrices [20,21]. It is also possible to describe the electromagnetic field in terms of state multipoles. Using this approach, it was shown in Ref. [22] that the polarization parameters of twisted photons are in one-to-one correspondence with the related parameters of the spin-density matrix of optically polarized atoms excited through a dominant electric dipole mechanism.

We will briefly describe the polarization formalism here. An arbitrary (pure) state of a spin 1 particle $|{\chi }_1\rangle$, or a three-dimensional vector field, can be expanded in terms of basis kets $|{\chi }_{1i}\rangle$$(i=x,y,z)$ in a Cartesian basis

$$|{\chi }_1\rangle =\sum _i{a}_i|{\chi }_{1i}\rangle ,$$

or, equivalently, in a spherical basis

$$|{\chi }_1\rangle =a^{+}|{\chi }_{1+}\rangle +a^0|{\chi }_{10}\rangle +a^{-}|{\chi }_{1-}\rangle ,$$

where $a_i$ and $a^{\pm }$ are complex amplitudes related by

$$a^{\pm }=\frac{(\mp a_x+i{a}_y)}{\sqrt{2}},a_0=a_z,\sum _i{\left|a_i\right|}^2=1.$$

The spin density matrix is ${\rho }_{ij}=a_i{a}_j^{\ast }$, and we will use the parameterization and normalization conventions from Refs. [22,23]:

$$\begin{array}{ccc}\hfill {\rho }_{ij}=& & \frac{1}{3}\{I+\frac{3}{2}(p_x{\mathcal{P}}_x+p_y{\mathcal{P}}_y+p_z{\mathcal{P}}_z)+\hfill \\ & & \frac{2}{3}(p_{xy}{\mathcal{P}}_{xy}+p_{yz}{\mathcal{P}}_{yz}+p_{xz}{\mathcal{P}}_{xz})+\hfill \\ & & \frac{1}{6}(p_{xx}-p_{yy})({\mathcal{P}}_{xx}-{\mathcal{P}}_{yy})+\frac{1}{2}{p}_{zz}{\mathcal{P}}_{zz}{\}}_{ij},\hfill \end{array}$$

(29)

where ${\mathcal{P}}_i,{\mathcal{P}}_{ij}$ are the operators of the spin and quadrupole moments, and $p_i,p_{ij}$ are the corresponding vector and quadrupole polarizations, which can be expressed in terms of the above amplitudes $a_i$ and $a^{\pm ,0}$,

$$p_i=i\sum _{jk}{ϵ}_{ijk}{a}_j{a}_k^{\ast };p_{ik}=-\frac{3}{2}(a_i{a}_k^{\ast }+a_k{a}_i^{\ast }-\frac{2}{3}{\delta }_{ik}).$$

(30)

In particular,

$$\begin{array}{cc}\hfill & p_{xx}-p_{yy}=3(a^{+}{a}^{-\ast }+a^{-}{a}^{+\ast });\hfill \\ & p_{zz}=|a^{+}{|}^2+|a^{-}{|}^2-2{\left|a^0\right|}^2;\hfill \\ \hfill & p_{xy}=i\frac{3}{2}(a^{+}{a}^{-\ast }-a^{-}{a}^{+\ast })\hfill \\ \hfill & p_{xz}=\frac{3}{2\sqrt{2}}(a^{+}{a}^{0\ast }+a^0{a}^{+\ast }-a^{-}{a}^{0\ast }-a^0{a}^{-\ast })\hfill \\ \hfill & p_{yz}=i\frac{3}{2\sqrt{2}}(a^{+}{a}^{0\ast }-a^0{a}^{+\ast }+a^{-}{a}^{0\ast }-a^0{a}^{-\ast }).\hfill \end{array}$$

(31)

The components of polarization have the following bounds: $-3\le p_{xx}-p_{yy}\le 3$, $-2\le p_{ii}\le 1$, $-\frac{3}{2}\le p_{ij}\le \frac{3}{2}$ ($i\ne j$), and $-1\le p_i\le 1$. These quantities are commonly referred to in atomic and nuclear physics as orientation $p_i$ and alignment $p_{ik}$. For a comprehensive formalism of spin 1 particle polarization, see also Ref. [24], noting that the definition of $p_{nm}$ used here has an extra factor of 3. Another convention for the description of optical polarization in 3D fields uses an expansion in terms of Gell-Mann matrices [25] and is equivalent to the approach presented here.

Let us derive expressions for the vector polarization $p_z$ (or orientation) and quadrupole polarization $p_{zz}$ (or alignment) of the vector vortex field generated by the phased ring array of atoms. The simplest expressions are obtained for $N\to \infty$ with the electric field from the vector potential Equation (15):

$$\begin{array}{c}\hfill E_{m_z}^{\mu }=\frac{\partial }{\partial t}{A}_{m_z}^{\mu }=-i\omega A_{m_z}^{\mu }=-i\omega A{e}^{-i(\omega t-k_{z}z)}\sqrt{\frac{\kappa }{2\pi }}\\ \hfill (-\frac{i}{2}{e}^{i(l+m_z-1){\varphi }_{\rho }}{J}_{l+m_z-1}(\kappa \rho )(1+m_z{cos}^2{\theta }_k){\eta }_1^{\mu }\\ \hfill +\frac{i}{2}{e}^{i(l+m_z+1){\varphi }_{\rho }}{J}_{l+m_z+1}(\kappa \rho )(1-m_z{cos}^2{\theta }_k){\eta }_{-1}^{\mu }\\ \hfill +\frac{m_z}{2\sqrt{2}}{e}^{i(l+m_z){\varphi }_{\rho }}{J}_{l+m_z}(\kappa \rho )sin2{\theta }_k{\eta }_0^{\mu }).\end{array}$$

(32)

To evaluate the orientation and alignment parameters, $p_z$ and $p_{zz}$, we use the definitions from Equations (30) and (31) and the electric field components from the above equation,

$$\begin{array}{c}\hfill p_z=\frac{|E_{+1}^{\mu }{|}^2-{\left|E_{-1}^{\mu }\right|}^2}{|E_{+1}^{\mu }{|}^2+|E_{-1}^{\mu }{|}^2+{\left|E_0^{\mu }\right|}^2}\end{array}$$

(33)

$$\begin{array}{c}\hfill p_{zz}=\frac{|E_{+1}^{\mu }{|}^2+|E_{-1}^{\mu }{|}^2-2{\left|E_0^{\mu }\right|}^2}{|E_{+1}^{\mu }{|}^2+|E_{-1}^{\mu }{|}^2+{\left|E_0^{\mu }\right|}^2}.\end{array}$$

(34)

We are interested in particular in the far-field polarization properties of the array’s radiation in the vicinity of phase singularity, where ${\theta }_k\approx \frac{R}{z}\ll 1$; therefore, Taylor expansion in ${\theta }_k$ is justified. Keeping only the leading terms in ${\theta }_k$, we obtain for the positive-helicity component (${\eta }_1$),

$$\begin{array}{cc}\hfill & (1+m_z{cos}^2{\theta }_k){(-i)}^{-1}{J}_{l+m_z-1}(\kappa \rho )\approx \hfill \\ \hfill & (1+m_z-m_z{\theta }_k^2){(-i)}^{-1}\frac{1}{(l+m_z-1)!}{(\frac{x{\theta }_k}{2})}^{|l+m_z-1|},\hfill \end{array}$$

(35)

where $x=k\rho =\frac{2\pi }{\lambda }\rho$. For the negative-helicity component (${\eta }_{-1}$), we have

$$\begin{array}{cc}\hfill & (1-m_z{cos}^2{\theta }_k)(-i)J_{l+m_z+1}(\kappa \rho )\approx \hfill \\ \hfill & (1-m_z+m_z{\theta }_k^2)(-i)\frac{1}{(l+m_z+1)!}{(\frac{x{\theta }_k}{2})}^{|l+m_z+1|},\hfill \end{array}$$

(36)

and for the longitudinal field component (${\eta }_0$),

$$\begin{array}{cc}\hfill & \frac{1}{\sqrt{2}}sin2{\theta }_k{J}_{l+m_z}(\kappa \rho )\approx \hfill \\ \hfill & \sqrt{2}{\theta }_k\frac{1}{(l+m_z)!}{(\frac{x{\theta }_k}{2})}^{|l+m_z|},\hfill \end{array}$$

(37)

where we left out a common factor that can be restored from Equation (32).

Substituting $m_z=+1$ in the above expressions, we obtain

$$\begin{array}{cc}\hfill |E_{-1}^{\mu }{|}^2& \sim {\theta }_k^{2(l+4)}\frac{1}{(l+2){!}^2}{(\frac{x}{2})}^{2|l+2|}\hfill \\ \hfill |E_{+1}^{\mu }{|}^2& \sim \frac{4}{l{!}^2}{(\frac{x}{2})}^{2l}{\theta }_k^{2\left|l\right|}\hfill \\ \hfill |E_0^{\mu }{|}^2& \sim \frac{2{\theta }_k^{2(l+2)}}{(l+1){!}^2}{(\frac{x}{2})}^{2|l+1|},\hfill \end{array}$$

(38)

where a common factor is omitted since it does not affect polarization parameters. The term $|E_{+1}^{\mu }{|}^2$ contains the lowest order of ${\theta }_k^{2l}$. Therefore, in the leading order of ${\theta }_k$ expansion

$$\begin{array}{c}\hfill p_z\approx \frac{|E_{+1}^{\mu }{|}^2}{|E_{+1}^{\mu }{|}^2}=1\\ \hfill p_{zz}\approx \frac{|E_{+1}^{\mu }{|}^2}{|E_{+1}^{\mu }{|}^2}=1.\end{array}$$

(39)

Therefore, both $p_z$ (orientation) and $p_{zz}$ (alignment) are equal to unity in the leading order of ${\theta }_k$, i.e., in the far field case, provided that the l and $m_z$ parameters have the same sign. The same result, $p_z=p_{zz}=1$, is obtained for l=0.

When $m_z=-1$, we have for the field components

$$\begin{array}{cc}\hfill |E_{-1}^{\mu }{|}^2& \sim \frac{4{\theta }_k^{2l}}{l{!}^2}{(\frac{x}{2})}^{2\left|l\right|}\hfill \\ \hfill |E_{+1}^{\mu }{|}^2& \sim \frac{{\theta }_k^{2l}}{(l-2){!}^2}{(\frac{x}{2})}^{2|l-2|}\hfill \\ \hfill |E_0^{\mu }{|}^2& \sim \frac{2{\theta }_k^{2l}}{(l-1){!}^2}{(\frac{x}{2})}^{2|l-1|},\hfill \end{array}$$

(40)

where $|E_{-1}^{\mu }{|}^2$ and $|E_0^{\mu }{|}^2$ have the same orders ${\theta }_k^{2(l+m_z)+2}$ and $|E_{+1}^{\mu }{|}^2$ remains the order ${\theta }_k^{2(l+m_z)+2}$.

$$\begin{array}{c}\hfill p_z=\frac{\frac{1}{(l-2){!}^2}{(\frac{x}{2})}^{2|l-2|}-\frac{4}{l{!}^2}{(\frac{x}{2})}^{2\left|l\right|}}{\frac{1}{(l-2){!}^2}{(\frac{x}{2})}^{2|l-2|}+\frac{4}{l{!}^2}{(\frac{x}{2})}^{2\left|l\right|}+\frac{2}{(l-1){!}^2}{(\frac{x}{2})}^{2|l-1|}}.\end{array}$$

(41)

$$\begin{array}{c}\hfill p_{zz}=\frac{\frac{1}{(l-2){!}^2}{(\frac{x}{2})}^{2|l-2|}+\frac{4}{l{!}^2}{(\frac{x}{2})}^{2\left|l\right|}-\frac{4}{(l-1){!}^2}{(\frac{x}{2})}^{2|l-1|}}{\frac{1}{(l-2){!}^2}{(\frac{x}{2})}^{2|l-2|}+\frac{4}{l{!}^2}{(\frac{x}{2})}^{2\left|l\right|}+\frac{2}{(l-1){!}^2}{(\frac{x}{2})}^{2|l-1|}}.\end{array}$$

(42)

Specifically for $l=0$, $m_z=-1$,

$$\begin{array}{cc}\hfill p_z& =-1,\hfill \\ \hfill p_{zz}& =1.\hfill \end{array}$$

(43)

For $l=1$, $m_z=-1$,

$$\begin{array}{cc}\hfill p_z& =\frac{-{(\frac{x}{2})}^2}{{(\frac{x}{2})}^2+0.5},\hfill \\ \hfill p_{zz}& =\frac{{(\frac{x}{2})}^2-1}{{(\frac{x}{2})}^2+0.5}.\hfill \end{array}$$

(44)

For $l=2$, $m_z=-1$,

$$\begin{array}{cc}\hfill p_z& =\frac{1-{(\frac{x}{2})}^2}{1+{(\frac{x}{2})}^2},\hfill \\ \hfill p_{zz}& =\frac{1+{(\frac{x}{2})}^4-4{(\frac{x}{2})}^2}{1+{(\frac{x}{2})}^4+2{(\frac{x}{2})}^2}.\hfill \end{array}$$

(45)

The derived expressions demonstrate that for opposite sign values of l and $m_z$, in the vicinity of phase singularity, the polarization parameters depend only on l and the transverse position with respect to the z-axis, but are independent on z, i.e., on a longitudinal distance to the source array. If we evaluate the polarization parameters in the vortex center ($x=0$), Equation (40) shows that when $l=1$, left- and right-circular components are both one order of $x=kb$ smaller than the z component. In this case, $p_z=0$, which is a measure of the difference between the left and right components. At the same time, $p_{zz}=-2$, which is a measure of the difference between the transverse and longitudinal components of the field. If $l>1$, the field components dominate in the following sequence when approaching the vortex center: right-circular, longitudinal, and left-circular components. Hence, $p_z=1$ is dominated by right-circular components, while $p_{zz}=1$ is dominated by transverse components. For the optical vortex beams, a similar effect was demonstrated to follow from Maxwell’s equations [26].

5. Numerical Results and Discussion

Let us supplement the above results with numerical examples. Assume that the wavelength is the unit of length and the atoms are prepared in $m_z=-1$ states. The atomic ring array has a radius of $R=1000\lambda$. We evaluate the energy flux density,

$$f(\overrightarrow{\rho },z)=cos({\theta }_k){(|E|}^2+{\left|B\right|}^2)/4,$$

and polarization parameters $p_z$ and $p_{zz}$ for several distances $z=z_R,1.5z_R,2z_R$ from the array, where $z_R=\frac{\pi w_0^2}{\lambda }=3.14$ is the Rayleigh range and $w_0=R=1000\lambda$ is the beam’s waist equal to the array radius. For each value of phase parameter $l=1,2,3$, the results are analyzed for different numbers of radiating atoms, $N=3,6,12$.

As shown in Figure 2 and Figure 3, the peaks of light energy flux are located in a transverse plane in the range of a few waist radii for $z<2z_R$, that is in 1000 s of wavelengths. We can also see in Figure 3 that increasing the number of emitters N results in a transition from a lattice of peaks to a ring-like structure (described by three Bessel functions of different orders in the limit $N\to \infty$). For the scalar fields, this transition was previously demonstrated in Ref. [16]. The present paper fully considers a vector nature of the electromagnetic fields. In contrast to the spatial inhomogeneity of the flux, the spatial scales for the change in polarizations $p_z$ and $p_{zz}$ are about one wavelength around the phase singularity (Figure 4), and, quite remarkably, are independent of the propagation distance z.

As shown in Figure 5, the position dependence of the polarization parameters near the vortex center is affected by the phase parameter l, which, for large N, may be associated with a topological charge of the electromagnetic vortex. Note from the same figure that the vector polarization $p_z$ turns to zero in the vortex center if l and $m_z$ are equal in magnitude but opposite in sign.

The effect on polarization of varying the number of emitters N can be seen in Figure 6. It should be noted that for $l=2$ and $N=3$, the leading-order vortex contribution has a topological charge $n=-1$ (equal in sign to $m_z$), according to Equations (27) and (28), which results in a different behavior of polarizations (shown in Figure 6) as opposed to large values of $N=6,12$. In other words, if the condition for the number of sources needed to generate a vortex vector field is not met, the topological charge changes its sign with respect to the applied phase parameter l, the spin and OAM become aligned, and the longitudinal component of the field is suppressed. As evidence, $p_{zz}=1$, which is dominated by the transverse field. At the same time, $p_z$ is fully determined throughout the entire wave front by the sign of $m_z$, which shows left- and right-circularly polarized light.

For sparse arrays, $N=3,6$, polarization singularities form a lattice, as shown in Figure 7 for $p_z$. The condition for generating a vortex field is met. The peaks shown in (c) and (d) are exactly the sign of vortex fields generated. Since they are all vortex fields, the properties of the polarizations near the vortex center are the same no matter how many sources we use. Therefore, (c) and (d) in Figure 7 are similar. The distributions of the peaks of $p_z$ and $p_{zz}$ are closely related to the lattice-like distribution of the intensities, while the spatial separation between the singularities increases with the propagation distance z. However, the spatial extent of an individual singularity in the vortex center remains propagation-independent and N-independent (once the requirement for the least number N is met), as seen in the bottom plots in Figure 7. The polarization $p_{zz}$ shows similar behavior.

6. Summary

Let us summarize the obtained results. We considered a circular array of N atoms excited into a P-state with a definite magnetic quantum number $m_z$ and analyzed the topological properties of their coherent radiation, provided that it is controlled with a phase parameter l. We found that for $N\to \infty$, the resulting radiation near the array axis is described by a superposition of circularly polarized Bessel beams with different topological charges. Next, we derived a result for the total vector potential of a phased atomic array with N atoms and a phase parameter l expressed in terms of an infinite series of Bessel vortices. We obtained the necessary conditions for the least number N required to generate vortex states with a given topological charge l for all components of the vector field: $N\ge 2(l+m_z)+3$.

In analyzing the resulting vortex field properties, we applied a formalism of 3D-polarization [22] with a spin-density matrix of the twisted photons defined in terms of eight polarization parameters. We demonstrated that if the spin and orbital angular momentum of the radiation are anti-aligned, then the spatial variation in the radiation’s polarization in the plane parallel to the atomic array near the vortex axis is independent of the distance to the source. The presence of a longitudinal component in the field plays a significant role in this behavior. In order to fulfill Maxwell’s equations, optical vortex beams have to include non-zero longitudinal components [26], with the field ratios showing propagation-independent spatial features. Here, we found similar propagation-invariant polarization features in radiation from atomic arrays.

The developed formalism can be extended and applied in several areas, from conventional polarized phased antenna arrays to complex geometries of multi-atom Dicke states to the transfer of quantum information between atomic ensembles.