Analysis of the Bearing Capacity of Reinforced Concrete Dapped-End Beams
Abstract
:1. Introduction
2. Analytical Methods for Calculating the Failure Load
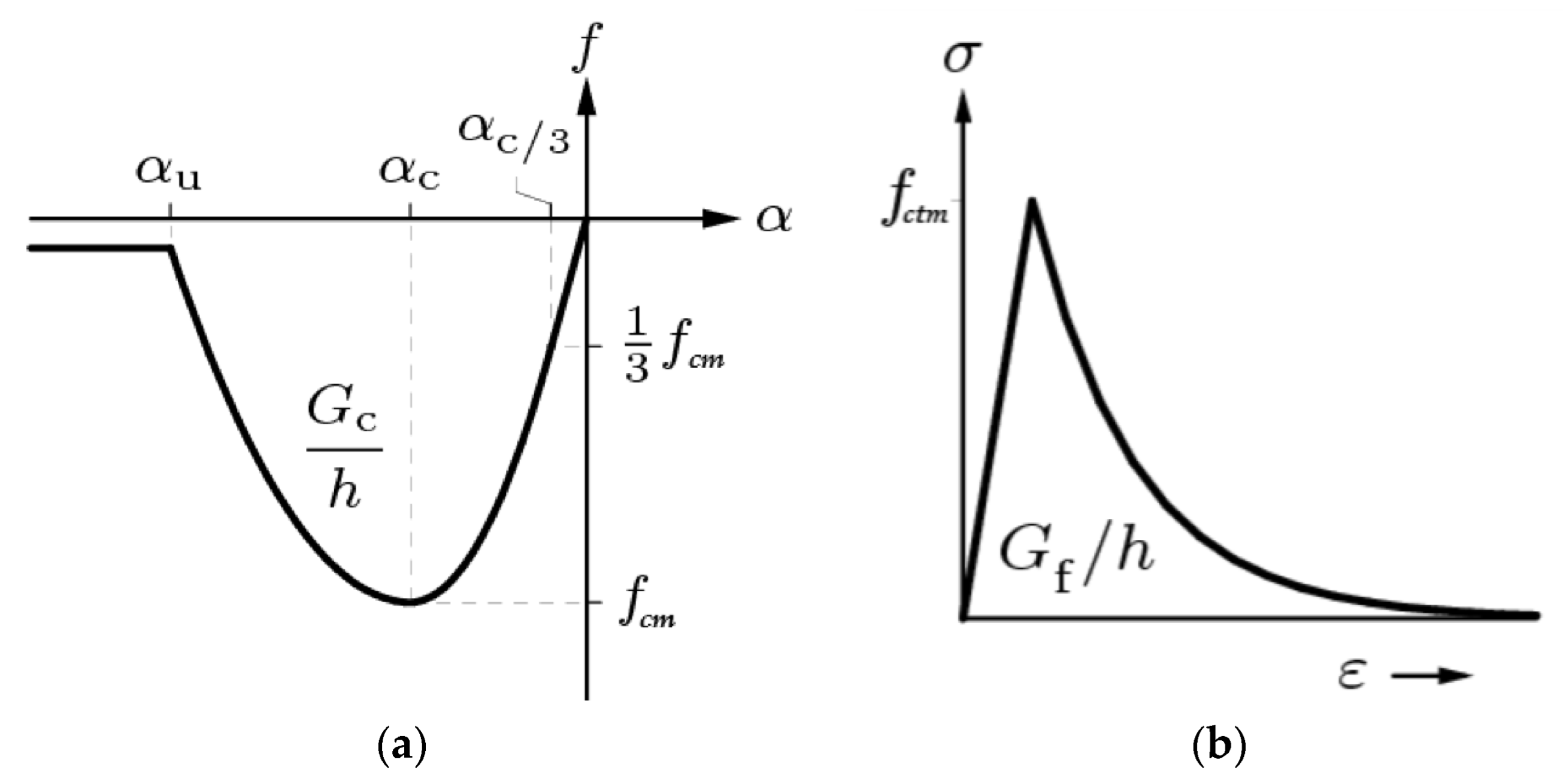
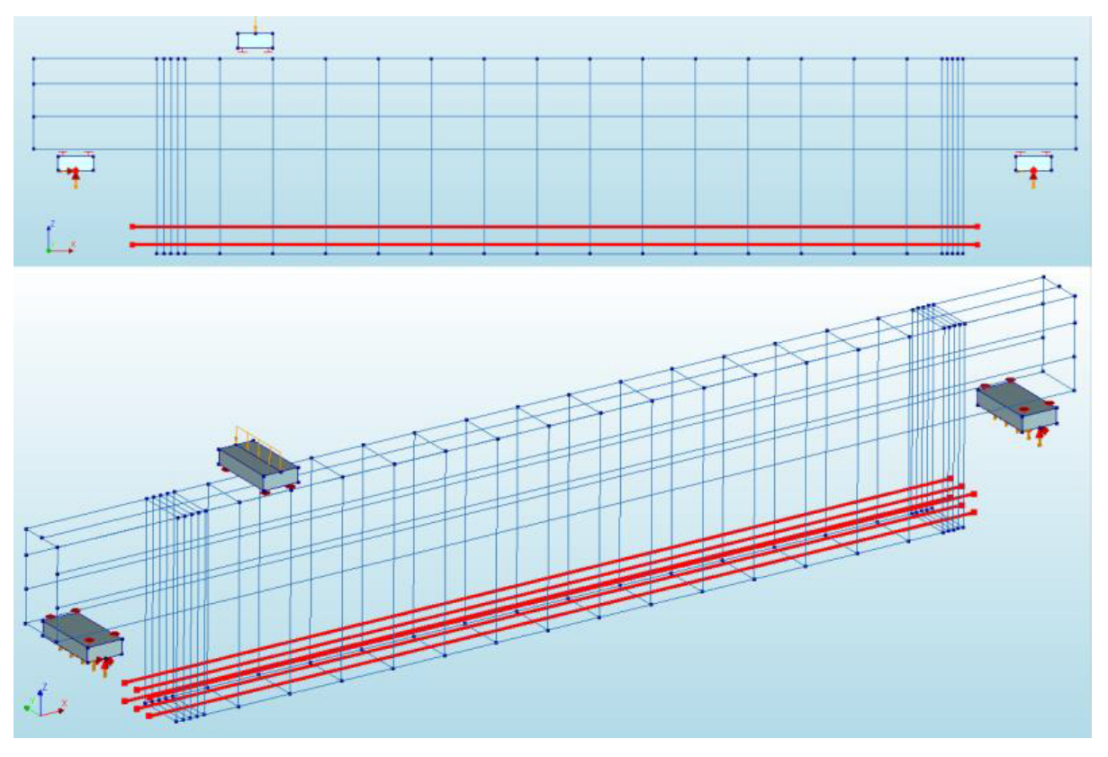
3. Numerical Modelling of the Dapped-End Beam
4. Results
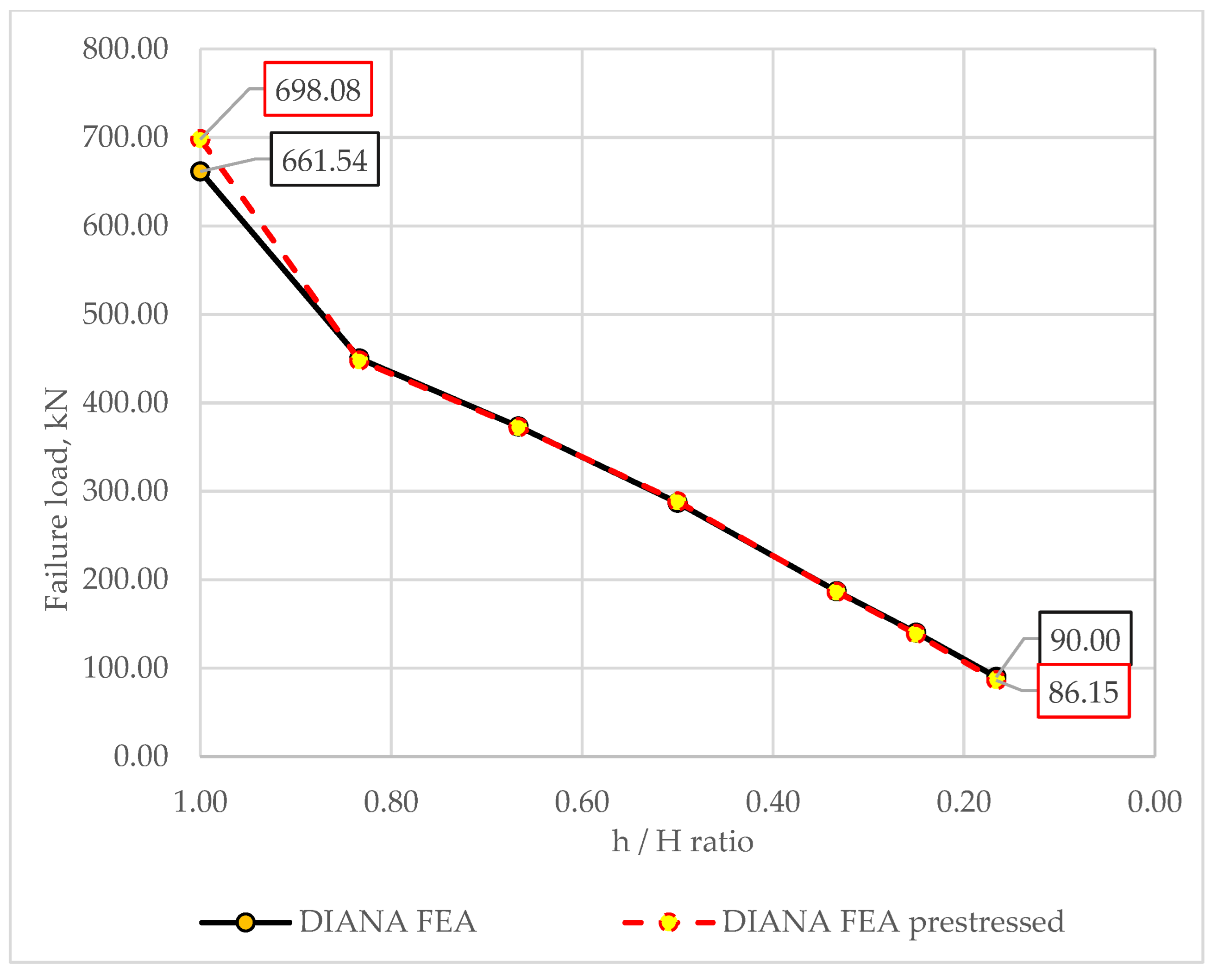
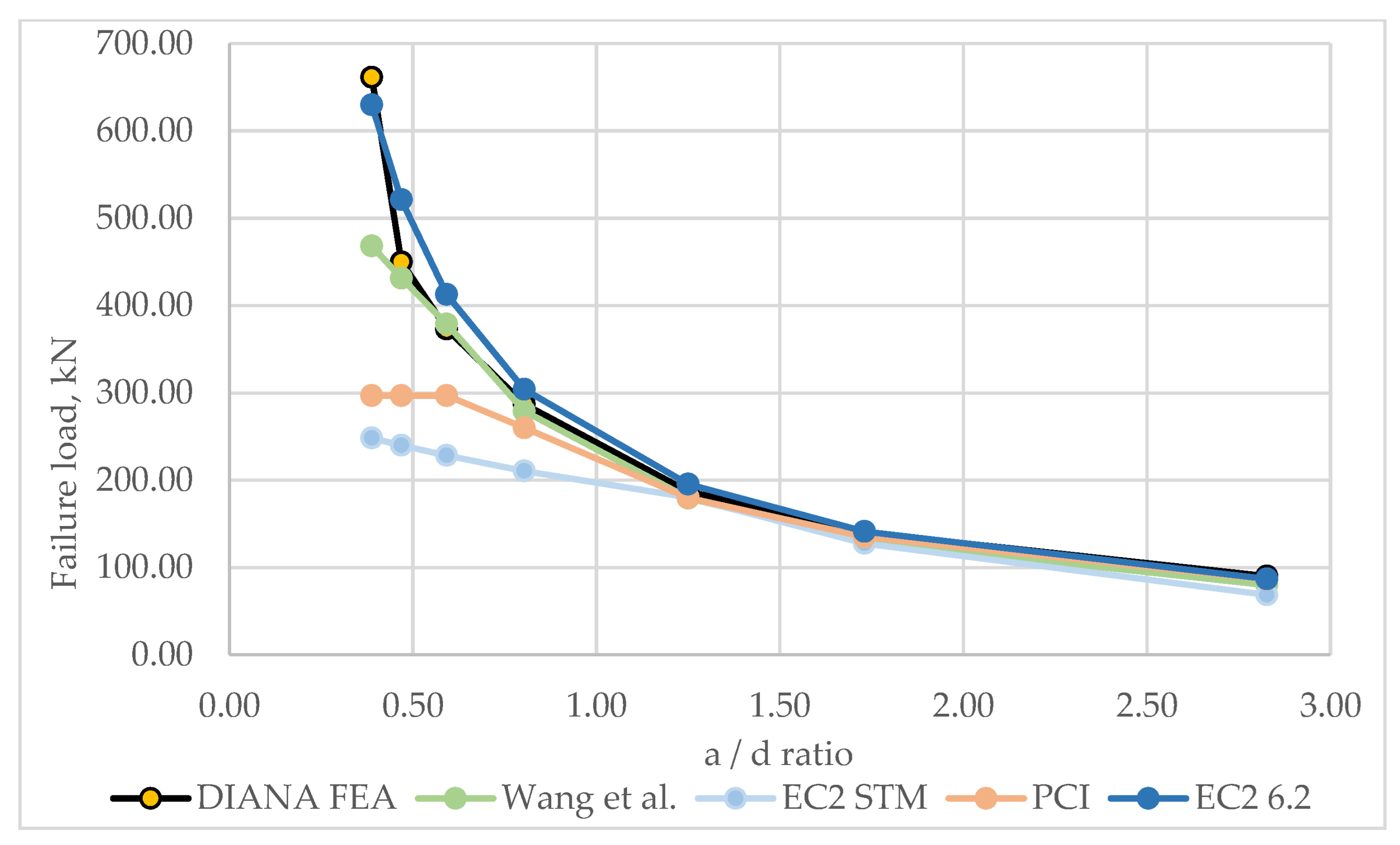
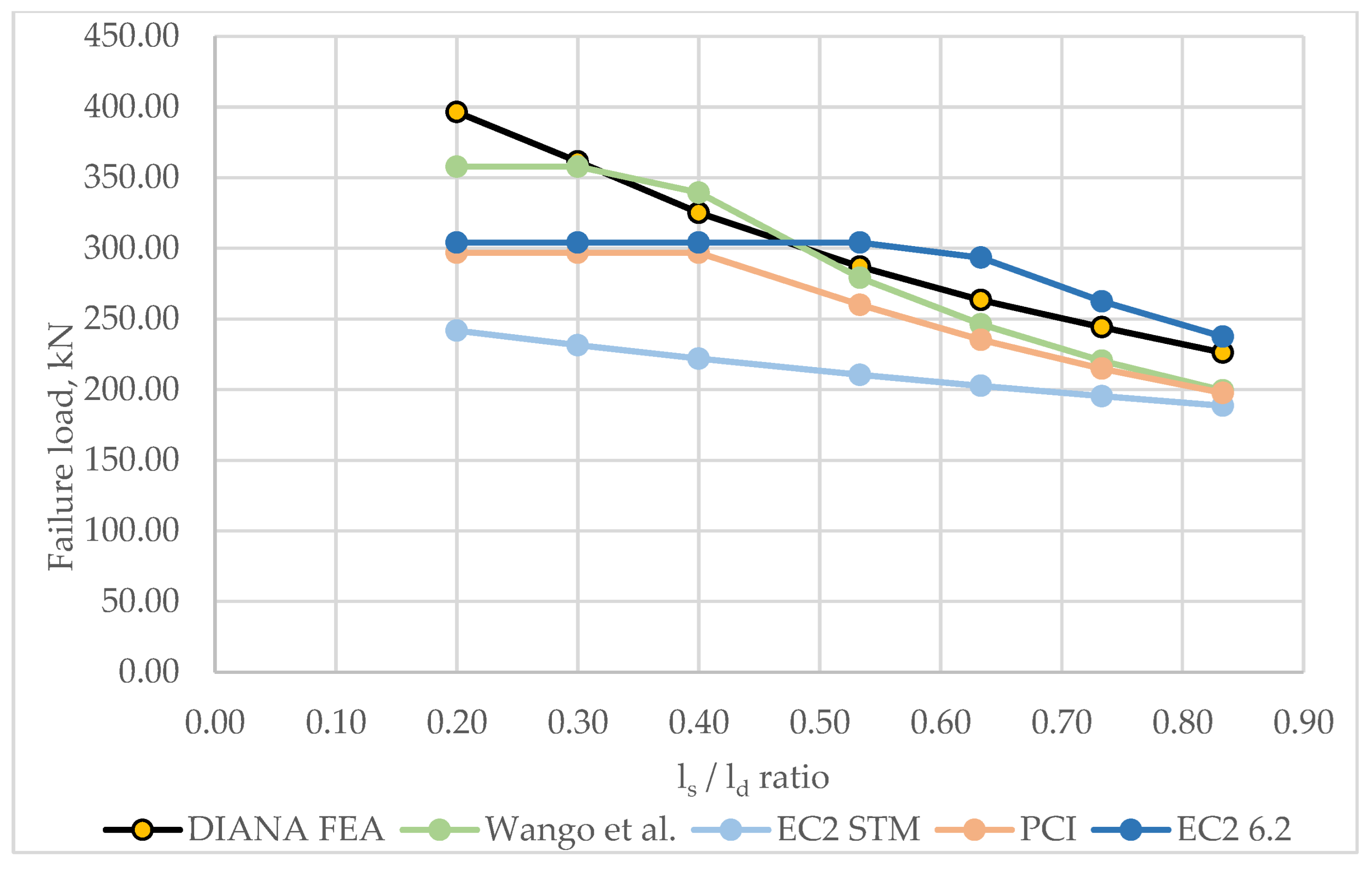
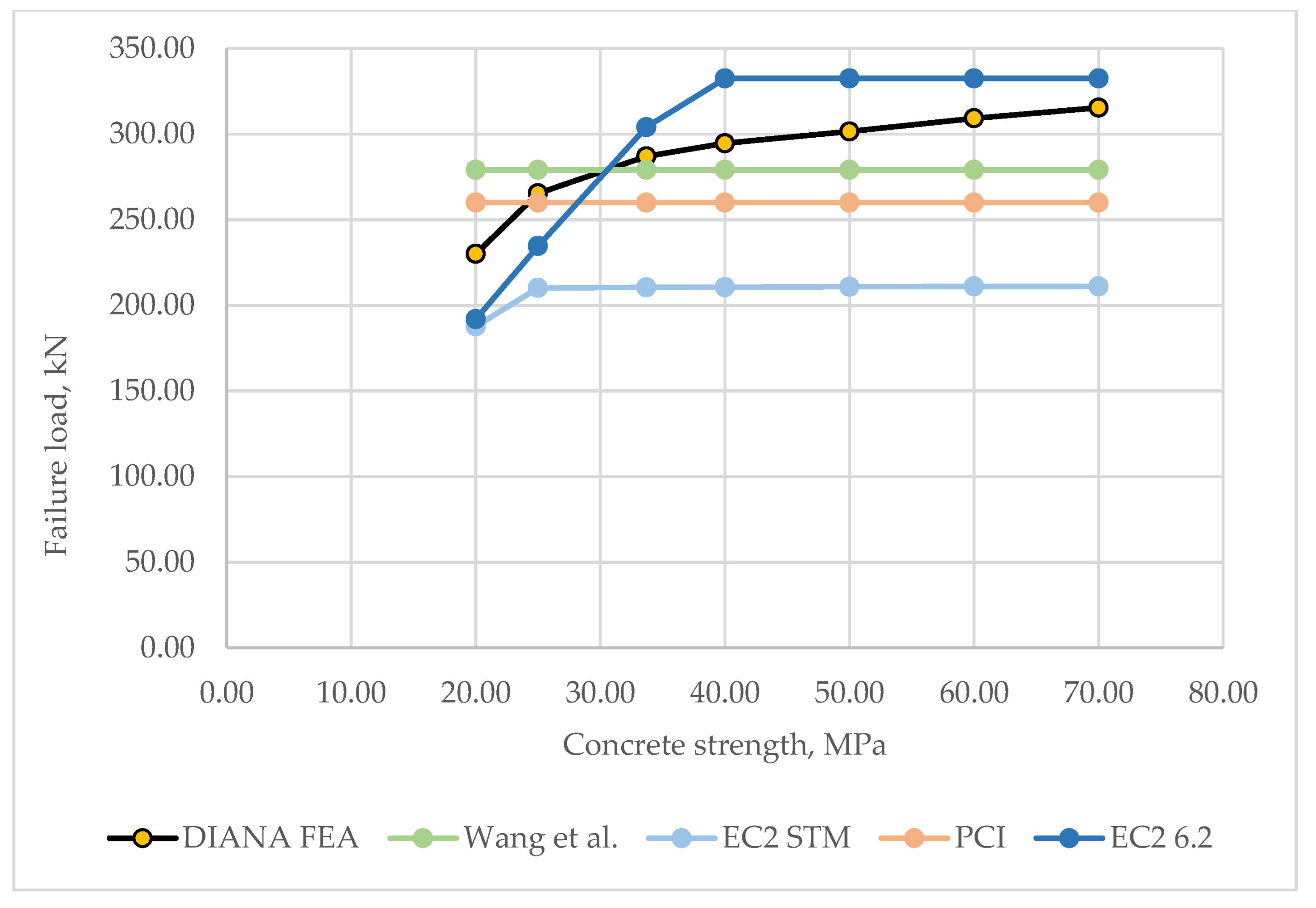
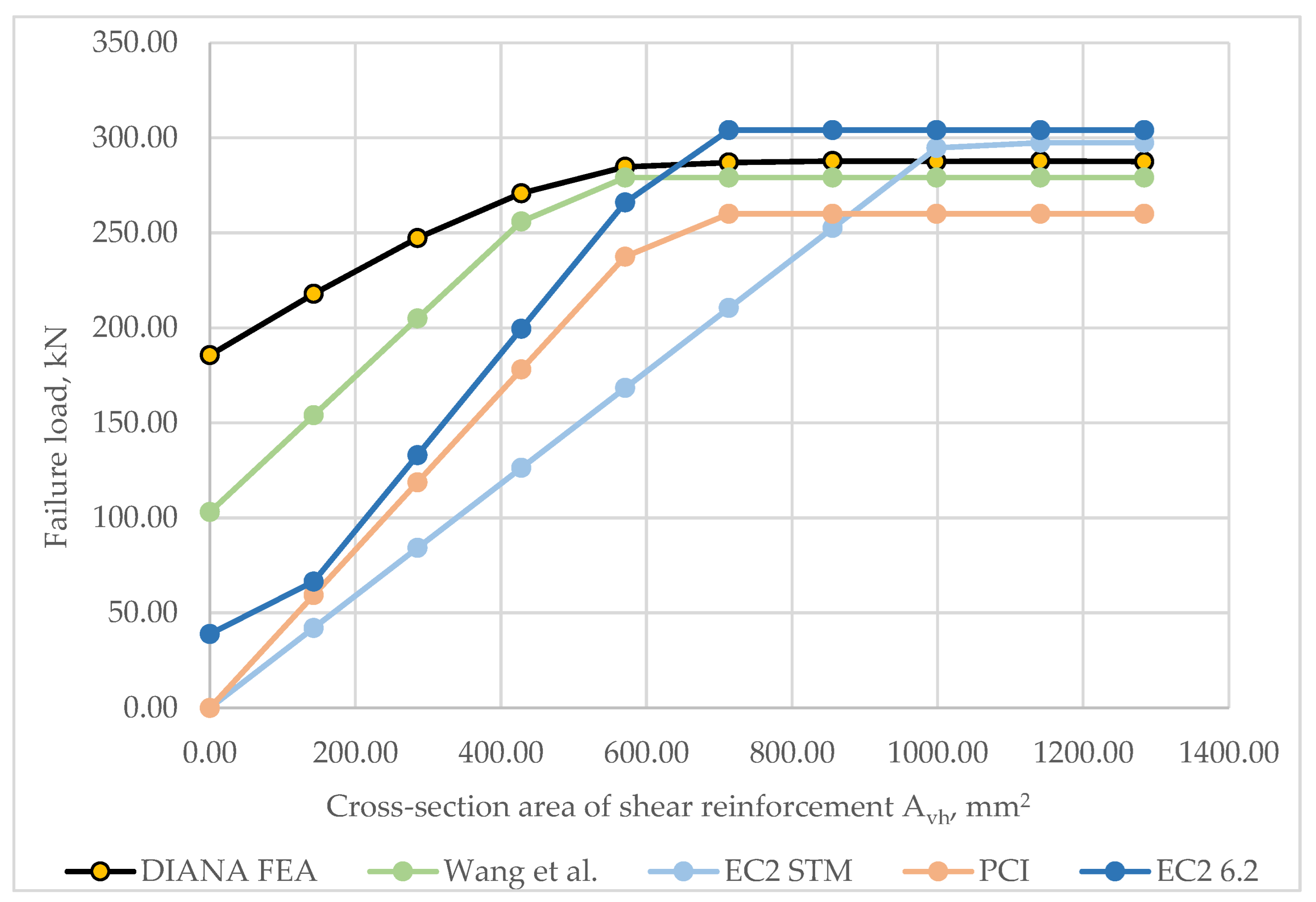
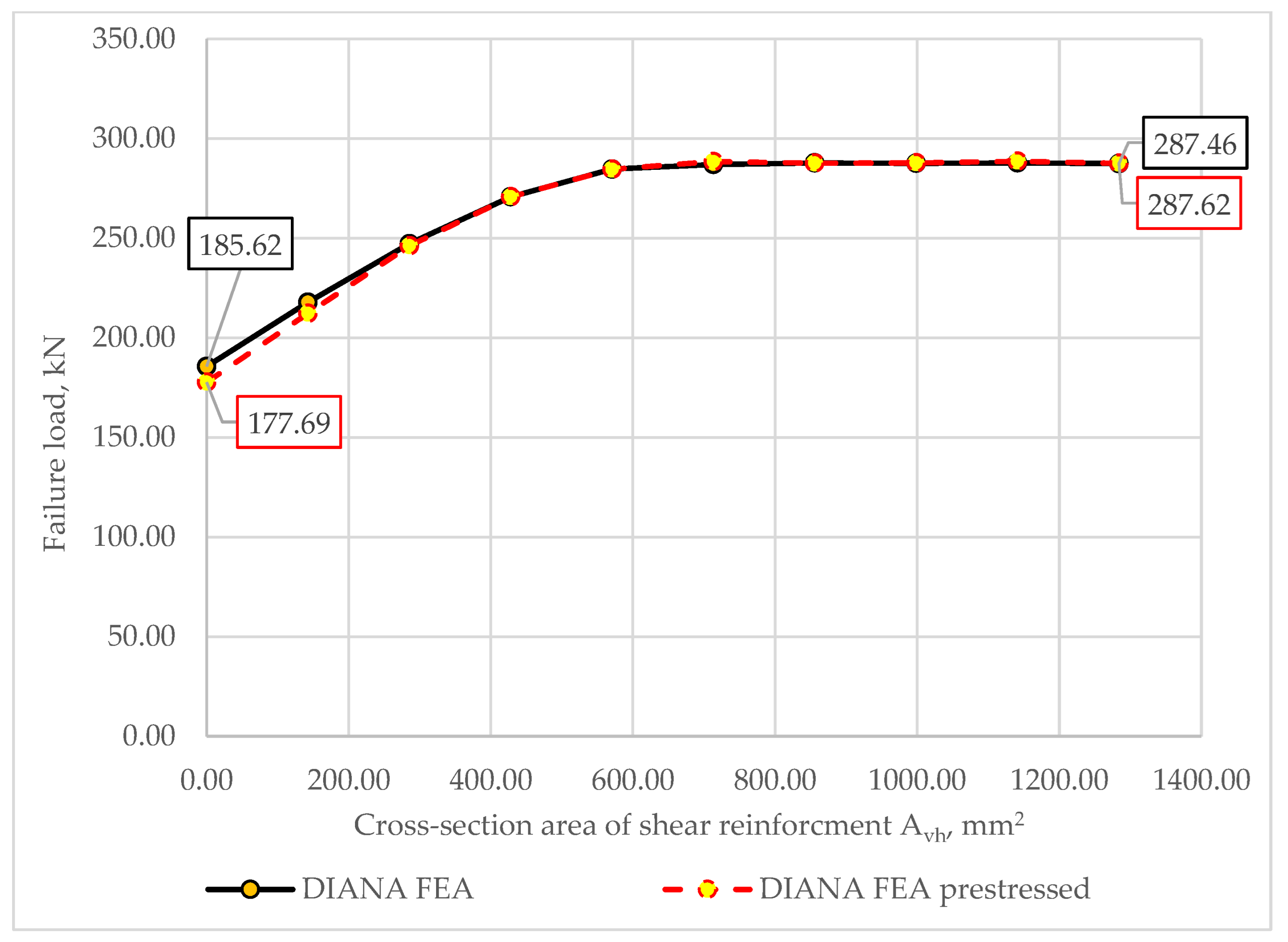
4.1. Parametric Analysis of the Failure Load
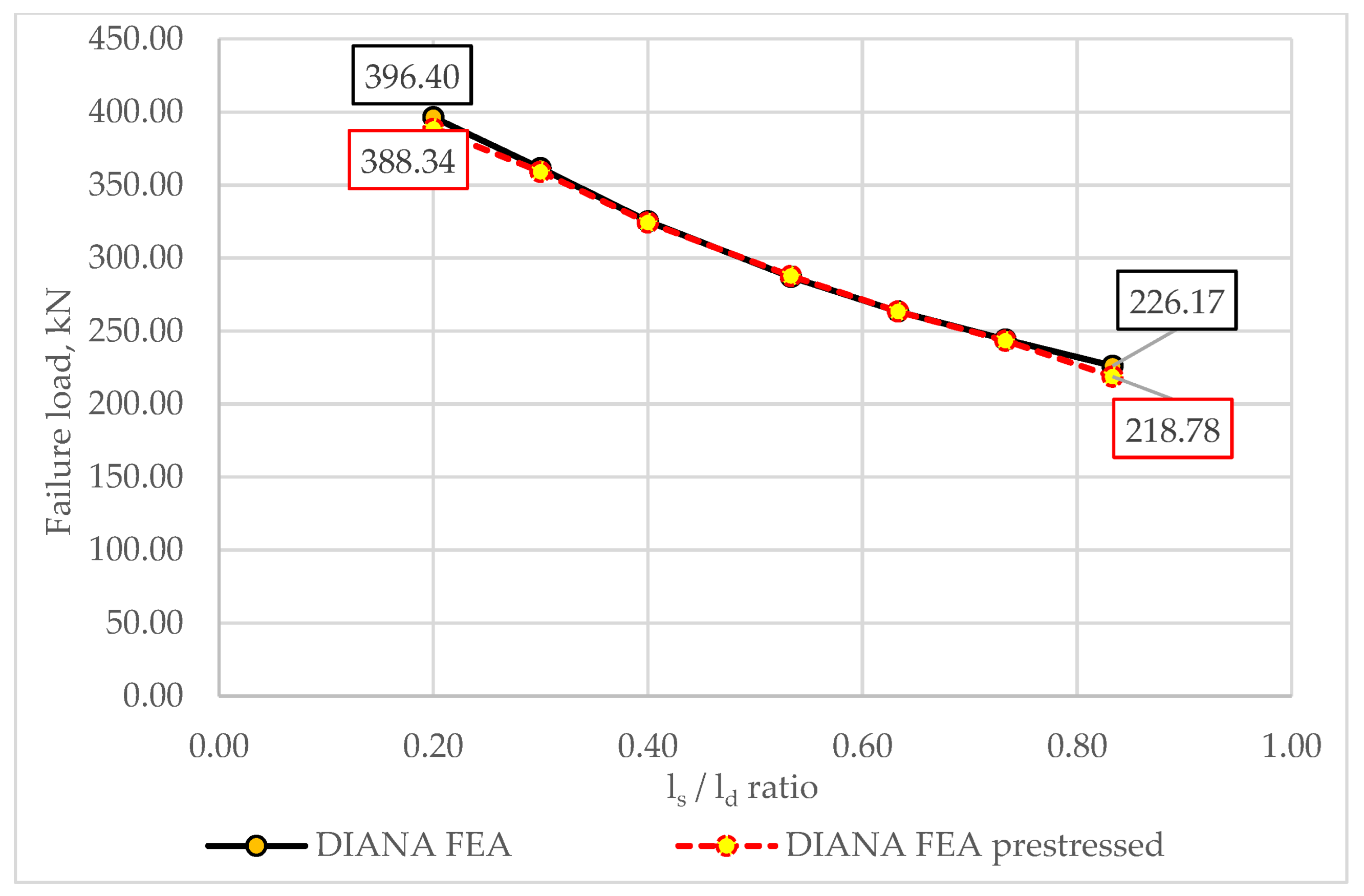
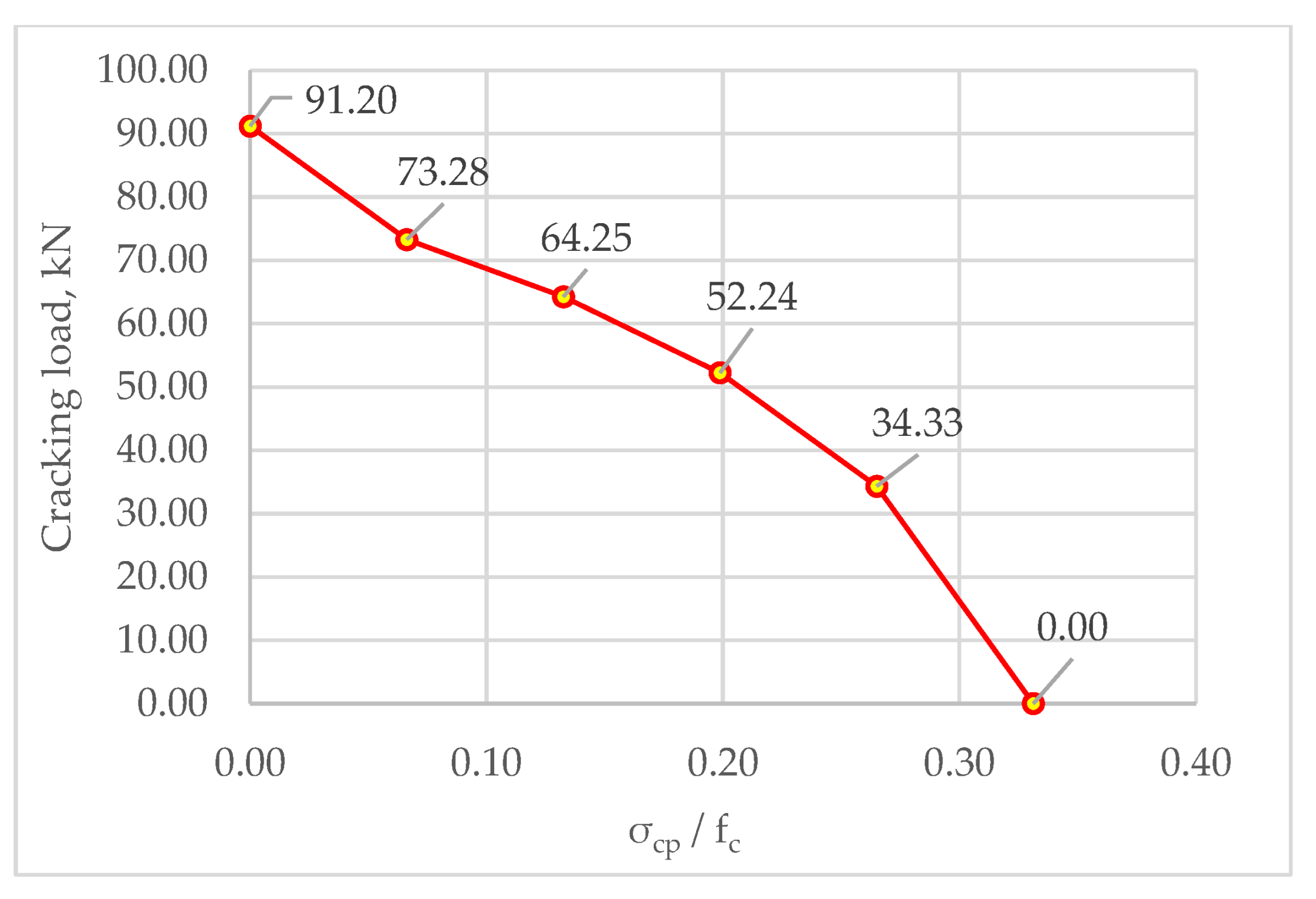
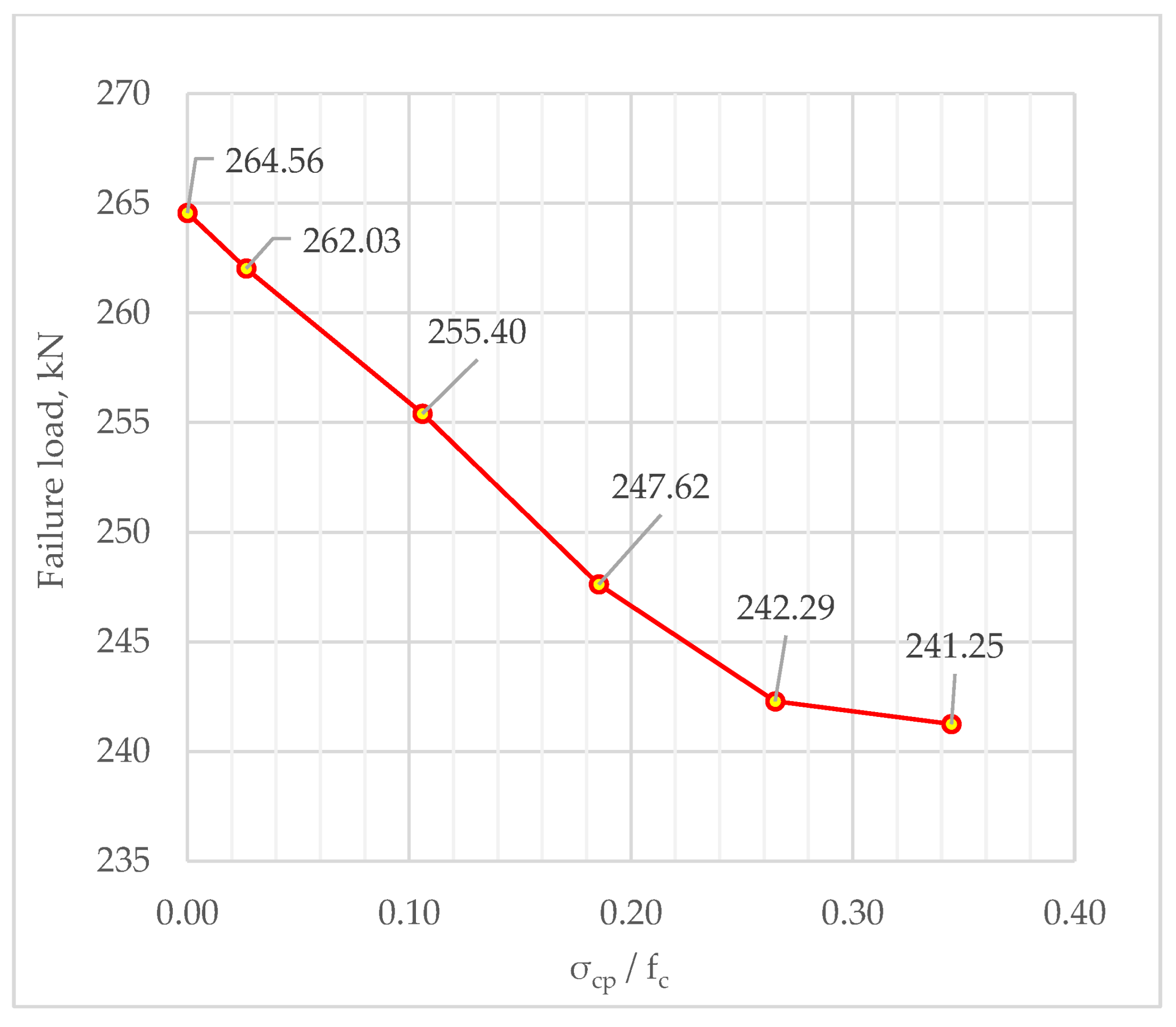
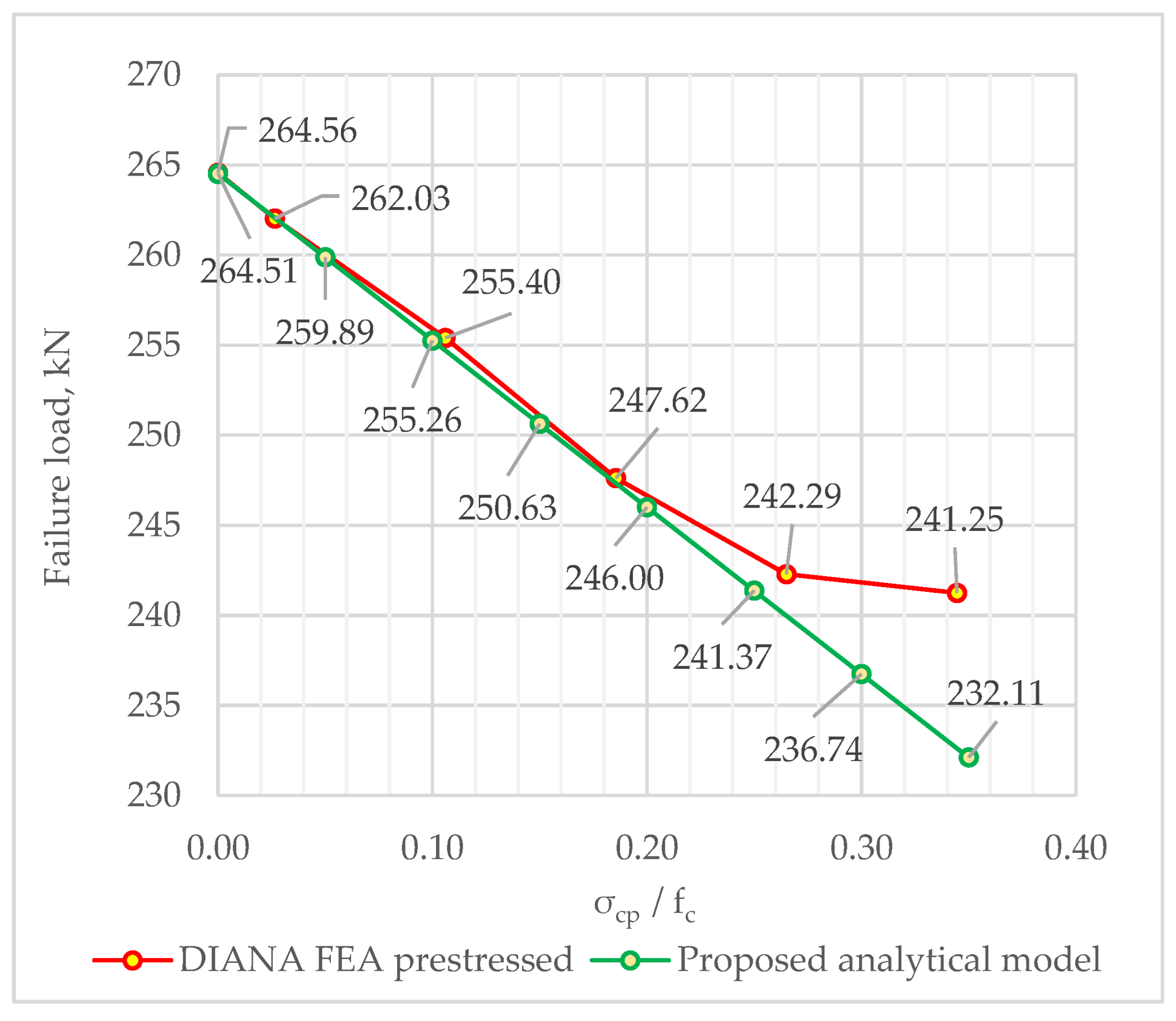
4.2. Impact of Prestressing Intensity
5. Conclusions
- The most significant factors affecting the bearing capacity of a dapped-end beam were found to be the amount of shear reinforcement and the height of the dap, whereas the concrete strength had the least impact.
- The parametric analysis comparing analytical and numerical methods showed that the EC2 STM method yields the highest bearing capacity estimates. However, ST models require proper adjustments to accurately capture acting forces in analyzed zones, and they should primarily be used for designing or as a baseline to be modified for configuration-specific analyses. The PCI method is less conservative, and the Wang et al. method demonstrates the best correlation with the numerical model. The EC2 6.2 section often overestimates shear strength, making it less suitable for dapped-end beam design.
- The results of the numerical parametric analysis revealed the significant effects of prestressing in certain dapped-end configurations. Prestressed reinforcement compressing the dap wall reduced resistance to cracking at the re-entrant corner, with severity depending on the prestressing intensity. A 50% reduction in cracking load was observed at a compressive stress ratio of 0.20–0.25. With higher prestressing, cracks appeared in the re-entrant corner before the external load exposure.
- When the prestressed reinforcement compressed the wall of the dap, the induced tensile stresses reduced the bearing capacity of the dapped-end beam. The significance of this effect was dependent on the intensity of the prestressing. A decrease of up to 8.81% in the bearing capacity was observed in the conducted analysis.
- The proposed analytical model for the assessment of the bearing capacity reduction caused by prestressing in dapped-end beams proved to be in good correlation with the results of the numerical model.
- The results of this study indicate that if prestressed reinforcement is used in the design of dapped-end beams and it is not possible to extend the tendons to the end of the nib above the dap, then it is essential to assess the reduction of the bearing capacity and implement strategies to mitigate cracking in the re-entrant corner.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shakir, Q.M. Reinforced Concrete Dapped End Beams—State of the Art. Int. J. Appl. Sci. 2018, 1, 44. [Google Scholar] [CrossRef]
- Aswin, M.; Mohammed, B.; Liew, M.S.; Syed, Z. Root Cause of Reinforced Concrete Dapped-End Beams Failure. Adv. Mater. Sci. Eng. 2015, 10, 42927–42933. [Google Scholar]
- Aswin, M.; Mohammed, B.S.; Liew, M.S.; Syed, Z.I. Shear Failure of RC Dapped-End Beams. Adv. Mater. Sci. Eng. 2015, 2015, 309135. [Google Scholar] [CrossRef]
- Mattock, A.H.; Chan, T.C. Design and Behavior of Dapped-End Beams. PCI J. 1979, 24, 28–45. [Google Scholar] [CrossRef]
- Shah, A.; Haq, E.; Khan, S. Analysis and Design of Disturbed Regions in Concrete Structures. Procedia Eng. 2011, 14, 3317–3324. [Google Scholar] [CrossRef]
- Precast/Prestressed Concrete Institute. PCI Design Handbook: Precast and Prestressed Concrete, 7th ed.; Precast/Prestressed Concrete Institute: Chicago, IL, USA, 2010. [Google Scholar]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- Fib International Federation for Structural Concrete. Fib Model Code for Concrete Structures 2010; Fib—Federation Internationale du Beton: Lausanne, Switzerland, 2013. [Google Scholar] [CrossRef]
- Mattock, A.H. Strut-and-Tie Models for Dapped-End Beams. Concr. Int. 2012, 34, 35–40. [Google Scholar]
- Mitchell, D.; Cook, W.D.; Peng, T. Example 14: Importance of Reinforcement Detailing. SP-273 Furth. Ex. Des. Struct. Concr. Strut-Tie Model. 2010, 273, 237–252. [Google Scholar]
- Sanders, D.H. Example 2: Dapped-End T-Beam Supported by an Inverted T-Beam. SP-208 Ex. Des. Struct. Concr. Strut-Tie Model. 2002, 208, 91–103. [Google Scholar] [CrossRef]
- ACI Committee 318. Building Code Requirements for Structural Concrete: (ACI 318-19) and Commentary (ACI 318R-19); American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Al-Khazraji, S.D.M. Response of Dapped-End Prestressed Concrete Girders to Static and Impact Loads. Ph.D. Thesis, University of Baghdad, Baghdad, Iraq, 2014. [Google Scholar]
- Werner, M.P.; Dilger, W.H. Shear Design of Prestressed Concrete Stepped Beams. PCI J. 1973, 18, 37–49. [Google Scholar] [CrossRef]
- Hamoudi, A.A.; Phang, M.K.S. Shear Strength of Post-Tensioned Daps in Prestressed Concrete Beams. J. Struct. Div. 1974, 100, 2403–2418. [Google Scholar] [CrossRef]
- Mattock, A.H.; Theryo, T.S. Strength of Precast Prestressed Concrete Members with Dapped Ends. PCI J. 1986, 31, 58–75. [Google Scholar] [CrossRef]
- Brinkley, M.C. Behavior of Prestressed, Precast Concrete Thin-Stemmed Members with Dapped Ends. Master’s Thesis, North Carolina State University, Raleigh, NC, USA, 2013; 224p. [Google Scholar]
- Botros, A.W.; Klein, G.J.; Lucier, G.W.; Rizkalla, S.H.; Zia, P. Dapped Ends of Prestressed Concrete Thin-Stemmed Members: Part 1, Experimental Testing and Behavior. PCI J. 2017, 62, 61–82. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, Z.; Hoogenboom, P.C.J. Experimental Investigation on the Shear Capacity of RC Dapped End Beams and Design Recommendations. Struct. Eng. Mech. 2005, 21, 221–235. [Google Scholar] [CrossRef]
- DIANA FEA BV. Compressive Behavior. 2015. Available online: https://manuals.dianafea.com/d100/MatLib/node328.html (accessed on 27 February 2022).
- DIANA FEA BV. Tensile Behavior. 2015. Available online: https://manuals.dianafea.com/d96/MatLib/node84.html (accessed on 21 March 2022).
- Lu, W.Y.; Lin, I.J.; Hwang, S.J.; Lin, Y.H. Shear Strength of High-Strength Concrete Dapped-End Beams. J. Chin. Inst. Eng. 2003, 26, 671–680. [Google Scholar] [CrossRef]
- Valivonis, J.; Jonaitis, B.; Zavalis, R.; Skuturna, T.; Šneideris, A. Flexural capacity and stiffness of monolithic biaxial hollow slabs. J. Civil Eng. Manag. 2014, 20, 693–701. [Google Scholar] [CrossRef]
- MC90. CEB-FIB Model Code 1990 for Concrete Structures; CEB Bull. d’Information 1993, No. 213/214; Comité Euro-International du Béton: Lausanne, Switzerland, 1993. [Google Scholar]
- Desnerck, P.; Lees, J.M.; Morley, C.T. Impact of the Reinforcement Layout on the Load Capacity of Reinforced Concrete Half-Joints. Eng. Struct. 2016, 127, 227–239. [Google Scholar] [CrossRef]
- Shakir, Q.M.; Abd, B.B.; Jasim, A.T. Experimental and Numerical Investigation of Self Compacting Reinforced Concrete Dapped End Beams Strengthened with CFRP Sheets. J. Univ. Babylon Eng. Sci. 2018, 26, 16–35. [Google Scholar] [CrossRef]
- Ahmad, S.; Elahi, A.; Hafeez, J.; Fawad, M.; Ahsan, Z. Evaluation of the Shear Strength of Dapped Ended Beam. Life Sci. J. 2013, 10, 1038–1044. Available online: https://www.researchgate.net/publication/289708665_Evaluation_of_the_shear_strength_of_dapped_ended_beam (accessed on 10 February 2022).
- Shakir, Q.M. A Review on Structural Behavior, Analysis, and Design of RC Dapped End Beams. IOP Conf. Ser. Mater. Sci. Eng. 2020, 978, 012003. [Google Scholar] [CrossRef]
- Barton, D. Design of Dapped Beams Using the Strut-and-Tie-Model; University of Texas: Austin, TX, USA, 1988. [Google Scholar]

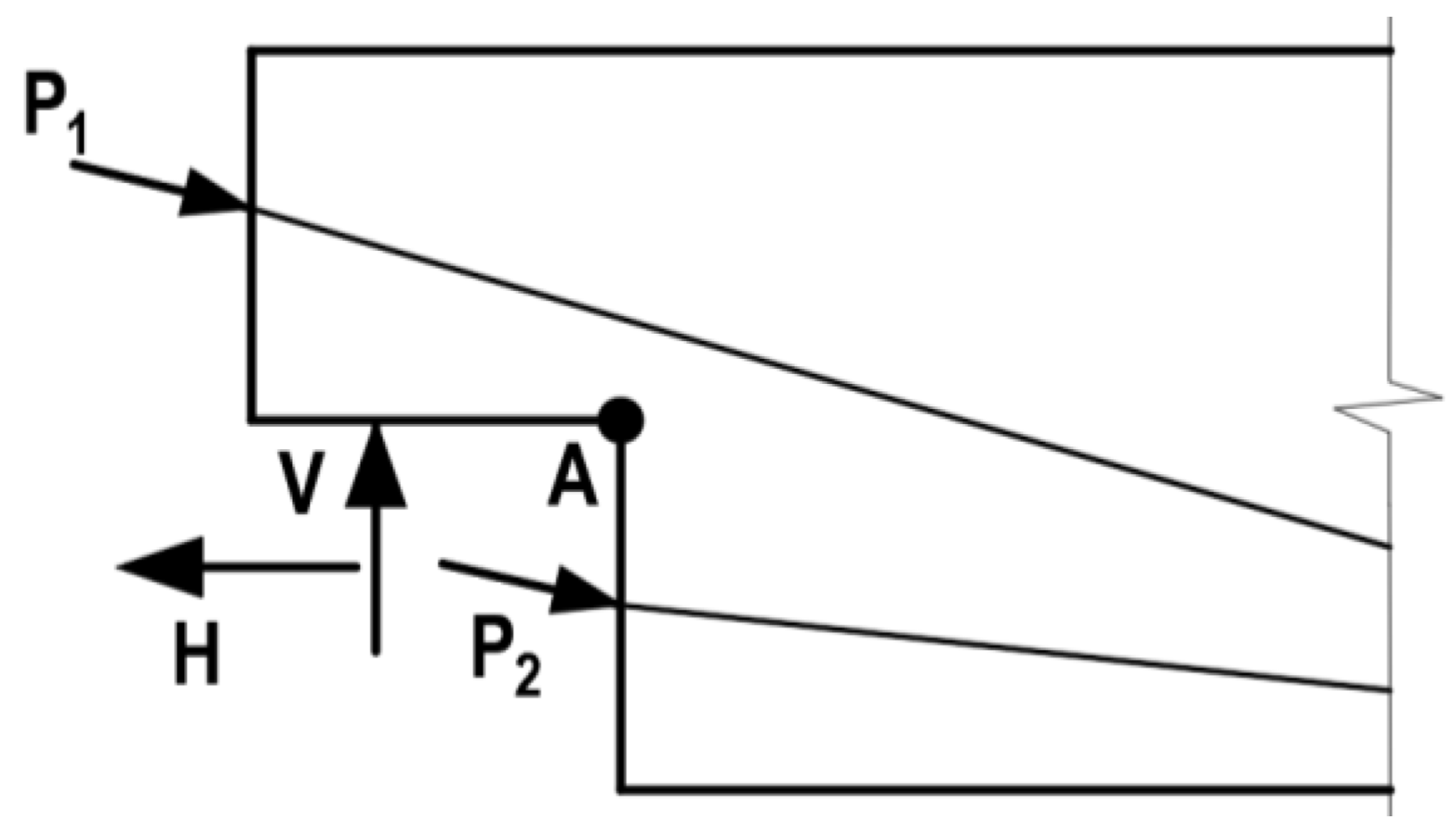
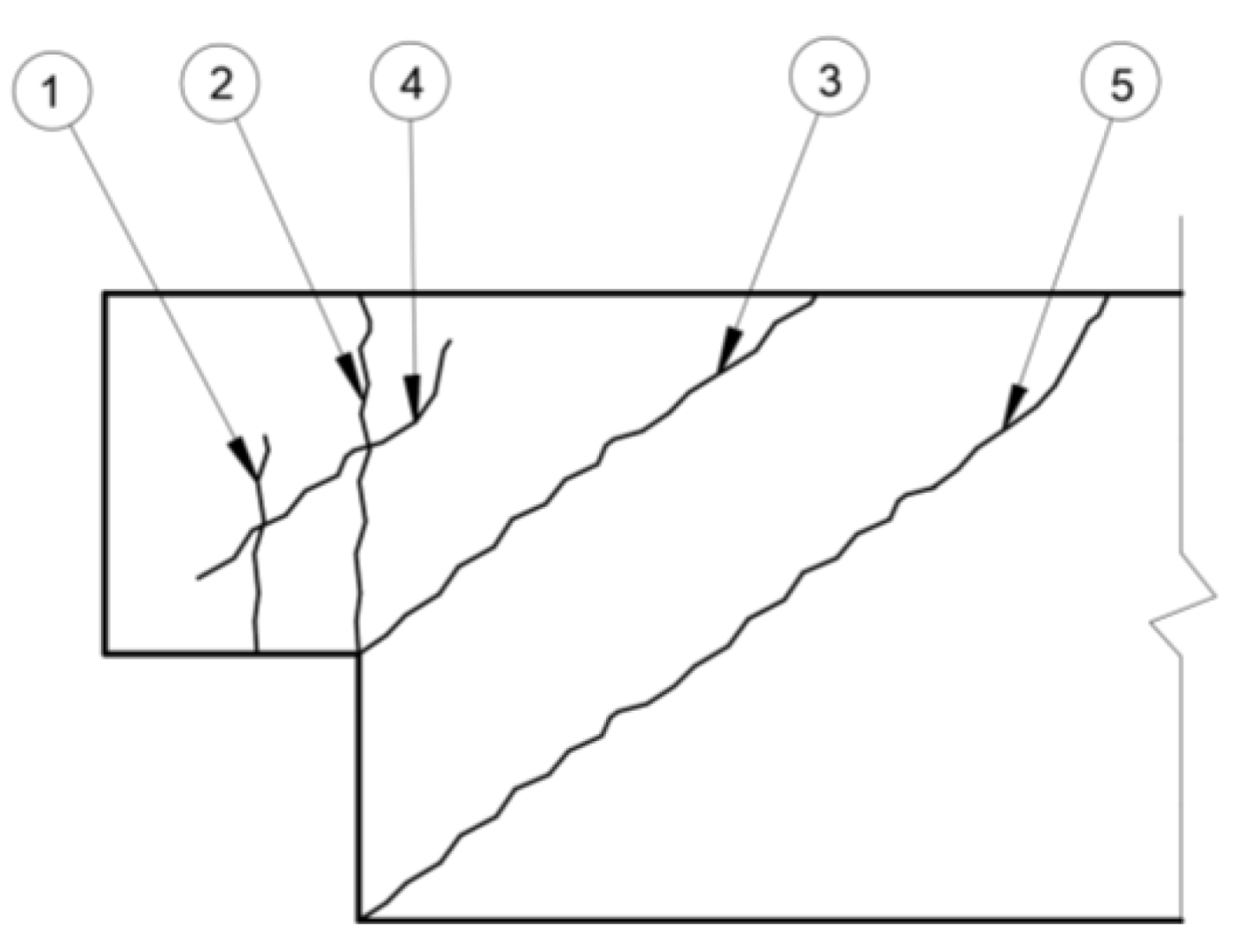

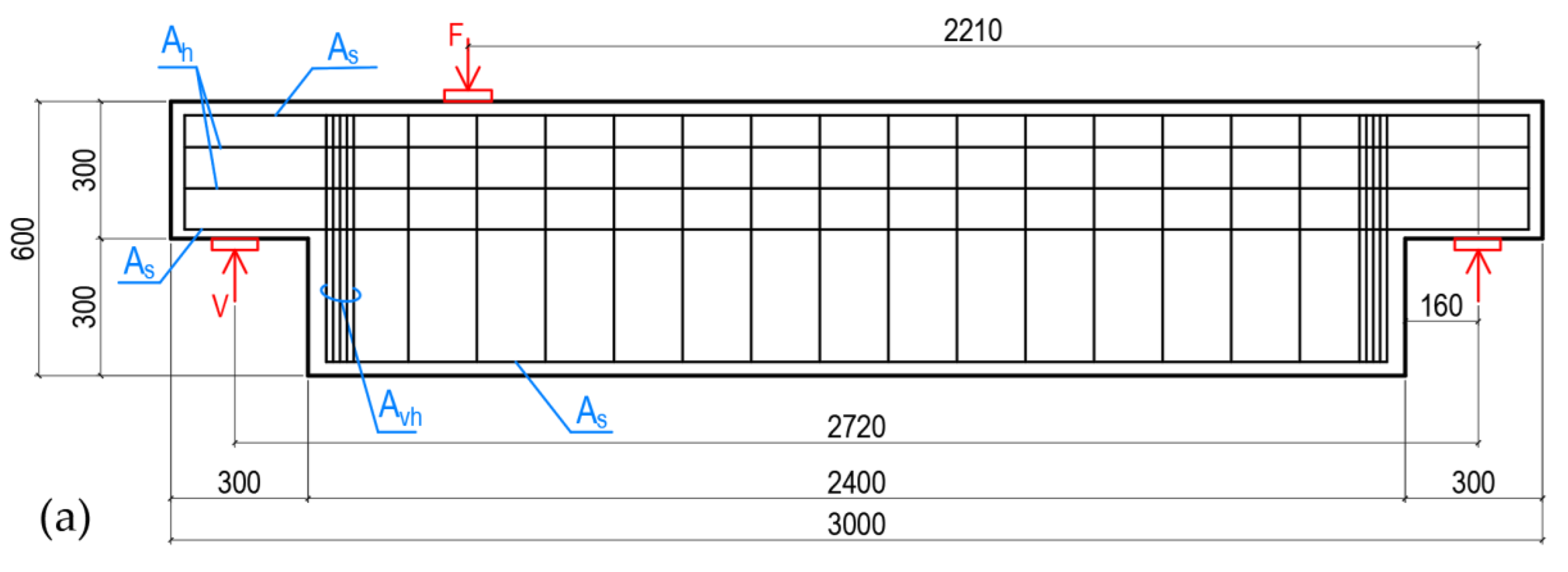


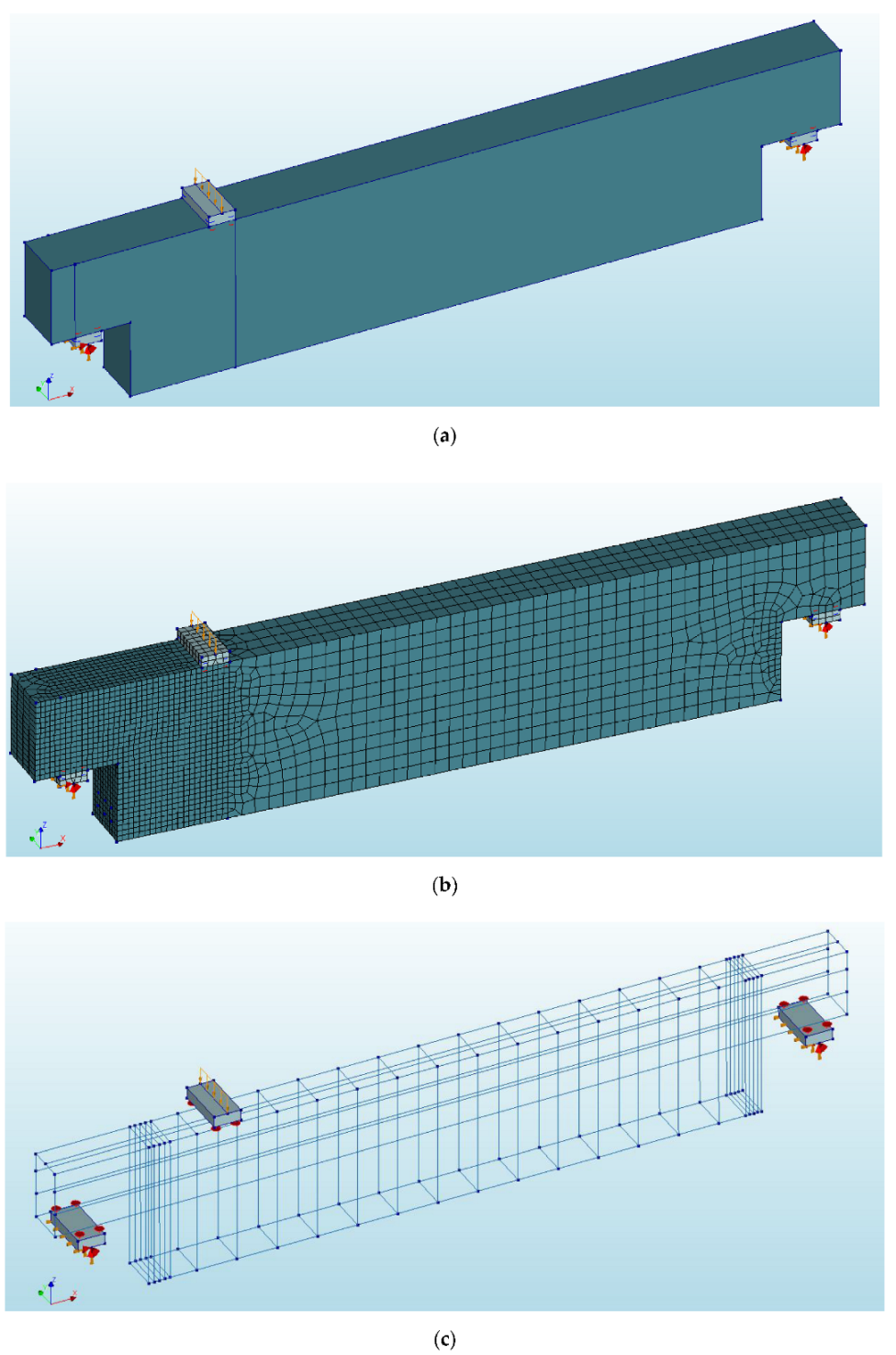





| Reinforcement Group | Material Model | Modulus of Elasticity, GPa | Yield Stress, MPa |
|---|---|---|---|
| Von Mises plasticity | 200 | 461.82 | |
| Von Mises plasticity | 200 | 368.00 | |
| Von Mises plasticity | 200 | 416.14 | |
| Von Mises plasticity | 195 | 1600.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masėnas, V.; Meškėnas, A.; Valivonis, J. Analysis of the Bearing Capacity of Reinforced Concrete Dapped-End Beams. Appl. Sci. 2023, 13, 5228. https://doi.org/10.3390/app13095228
Masėnas V, Meškėnas A, Valivonis J. Analysis of the Bearing Capacity of Reinforced Concrete Dapped-End Beams. Applied Sciences. 2023; 13(9):5228. https://doi.org/10.3390/app13095228
Chicago/Turabian StyleMasėnas, Vilius, Adas Meškėnas, and Juozas Valivonis. 2023. "Analysis of the Bearing Capacity of Reinforced Concrete Dapped-End Beams" Applied Sciences 13, no. 9: 5228. https://doi.org/10.3390/app13095228
APA StyleMasėnas, V., Meškėnas, A., & Valivonis, J. (2023). Analysis of the Bearing Capacity of Reinforced Concrete Dapped-End Beams. Applied Sciences, 13(9), 5228. https://doi.org/10.3390/app13095228







